Finanse przedsiębiorstw
Wykład 5
Finanse przedsiębiorstw
Wykład 5
2
Zapasy: korzyści
Zapasy materiałów umożliwiają:
◦
zabezpieczenie przed zmianami cen
materiałów
◦
ochronę przed zmianami / brakiem podaży
materiałów
◦
ułatwiają planowanie produkcji
◦
zdolność do magazynowania zapasów daje
możliwość korzystania z dyskonta
ilościowego
3
Zapasy: jeszcze korzyści
zapasy produkcji w toku
◦
zapewnienie płynności produkcji
(buforowanie)
zapasy wyrobów gotowych
◦
stabilizacja produkcji
◦
możliwość natychmiastowej realizacji
zamówień
4
Zapasy: koszty
Koszty trzymania zapasów
◦
koszt zaangażowanego kapitału (albo KUM)
◦
koszty magazynowania
◦
koszty ubezpieczenia
◦
straty spowodowane
psuciem się zapasów
starzeniem się zapasów
5
Zapasy: więcej kosztów
Koszty zamawiania / wyprodukowania:
◦
koszty transportu
◦
rozładunku
◦
opłaty telefoniczne, pocztowe etc.
◦
koszty produkcji
6
Zapasy: jeszcze więcej kosztów
Koszt braku zapasów
◦
strata sprzedaży
◦
strata klientów
◦
koszty przerwania produkcji (przestoje)
◦
koszty wymuszone potrzebą
natychmiastowego zakupu towaru (wyższa
cena, droższa przesyłka etc.)
7
Modele zapasów: mają dać
odpowiedź na pytania
Jaki powinien być optymalny rozmiar
zamówienia?
Kiedy składać zamówienia?
◦
Jaki powinien być poziom zapasów przy
którym należy złożyć nowe zamówienie?
◦
Jak często składać zamówienia?
Czy warto kupić więcej i skorzystać z
dyskonta?
8
Model EOQ: założenia
(Economic order quantity model)
W modelu uwzględnia się
◦
koszty trzymania zapasów - zakłada się, że
są wprost proporcjonalne do wielkości
zapasów
◦
koszty zamawiania - zakłada się, że są
wprost proporcjonalne do liczby zamówień
(!)
◦
czas od złożenia zamówienia do jego
realizacji (okres dostawy), z tym, że
niekoniecznie
9
Model EOQ: więcej założeń
Zakłada się, że
◦
zamówiony towar po dostarczeniu trafia
natychmiast w całości do magazynu
(zerowy czas rozładowania towaru !)
◦
zapasy są zużywane w stałym tempie i
odnawiane w stałych okresach
w modelu nie uwzględnia się
◦
kosztów braku zapasów
◦
dyskonta ilościowego
10
Model EOQ: oznaczenia
F
- koszt złożenia jednego zamówienia
T
- roczne zużycie zapasów
K
- koszt utraconych możliwości czyli
stopa procentowa kapitału
finansującego zapasy
G
- wielkość pojedynczego zamówienia
P
- cena jednostkowa zapasów
Konsekwencje:
◦
G/2 = średni zapas
◦
T/G = liczba zamówień w ciągu roku
11
Model EOQ: wersja podstawowa
Nie uwzględnia się okresu dostawy
(zamówienie jest natychmiast
realizowane)
Zatem:
Nowe zamówienie jest składane gdy
zapas spada do zera
12
EOQ: przykład
Firma sprzedaje rocznie ok. T = 250
ton. Koszt jednej tony wynosi P = 1000
zł.
Koszt zamówienia wynosi F = 295 zł;
sklep ma linię kredytową o
oprocentowaniu K = 20%. Oblicz:
◦
optymalny poziom zamówienia
◦
jak często trzeba będzie składać
zamówienia
13
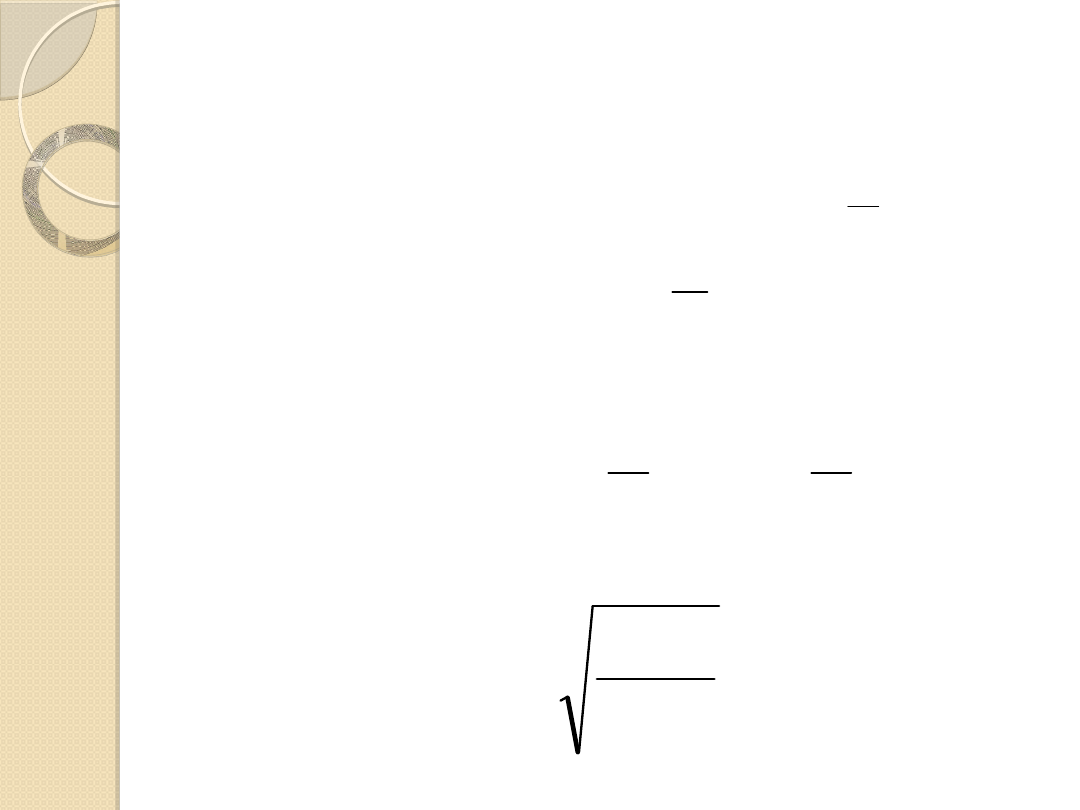
Model EOQ: wersja podstawowa
Koszt Trzymania Zapasów
Koszt Zamówień
Ogólny koszt:
Optymalna wielkość zamówienia:
G
T F
K P
2
P
K
G
KTZ
2
F
G
T
KZ
F
G
T
P
K
G
KZ
KTZ
OK
2
14
Model EOQ: punkt zamówienia
(order point)
Zmiany:
◦
uwzględniamy okres dostawy
◦
Nowe zamówienie jest składane gdy zapas
spada do określonego poziomu (zwanego
punktem zamówienia)
punkt zamówienia
= okres dostawy x dzienne
zużycie zapasów
15
EOQ: przykład - ciąg
dalszy
Zakładając, że okres dostawy wynosi 2
tygodnie,
◦
oblicz punkt zamówienia,
◦
odpowiedz ile dni upływa pomiędzy
kolejnymi zamówieniami
16
EOQ: przykład - ciąg
dalszy
Zakładamy, że zużycie może
wzrosnąć: nie możemy dopuścić by
zapasy spadły poniżej poziomu 5 ton
◦
jaki jest teraz punkt zamówienia,
◦
jaki jest minimalny poziom zapasów
◦
jaki jest teraz ogólny koszt?
17
EOQ: przykład – wariacje na
temat
Producent zaoferował następujące
upusty:
◦
2% zniżki za każdą partię 35 ton
◦
50% zniżki na koszty zamówień za każdą
partię 30 ton, lub
Jaka jest optymalna wielkość
zamówienia?