Stabilność liniowych układów automatyki
Liniowy układ automatyki będziemy uważać za stabilny, jeśli przy
dowolnych warunkach początkowych zerowych wymuszeniach (zerowych
sygnałach sterujących i zakłócających) sygnał błędu e dąży do wartości
zero, gdy t . Dla zamkniętego układu automatyki mamy:
E(p)(1+K(p)) = (p)Z
k
(p).
n
k
zk
K
0
Podstawiając w równaniu Z
k
(p) = 0, możemy przedstawić lewą stronę
równania jako E(p) pomnożone przez pewien wielomian. Uwzględniając to,
że iloczynowi p
(i)
E(p) odpowiada w dziedzinie funkcji czasu
e
(i)
=
otrzymujemy dla rozpatrywanego przypadku następujące równanie
różniczkowe:
a
0
e
(n)
+ a
1
e
(n-1)
+ … + a
n
e = 0,
rozwiązania tego równania przy dowolnych warunkach początkowych mają
postać:
i
i
dt
e
d
e(t) =
n
k
k
C
1
t
k
p
e
gdzie C
k
– stałe zależne od warunków początkowych, p
k
– są pierwiastkami
równania charakterystycznego, które w rozważanym przypadku ma postać:
1 + K(p) = 0
jeżeli wszystkie pierwiastki równania mają części rzeczywiste ujemne
R
e
[p
k
] < 0,
e(t) = 0
wtedy układ jest stabilny.
Jeżeli natomiast dowolny z pierwiastków p ma część rzeczywistą
dodatnią
R
e
[p
k
] > 0,
e(t) ≠ 0
i wtedy układ jest niestabilny
lim
t
lim
t
Jeżeli równanie ma pierwiastki wielokrotne to pojawiają się wyrazy
typu :
t
l
t
k
p
e
l – liczba całkowita.
Funkcja t
l
rośnie wolniej niż funkcja wykładnicza. Jeżeli więc spełniony jest
warunek
R
e
[p
k
] < 0,
lim
t
t
k
p
e
t
l
= 0
= 0.
Warunek ten jest koniecznym i wystarczającym
warunkiem stabilności.
Stabilność układu automatycznej regulacji – niezbędny warunek pracy
układu automatycznej regulacji
mówiący o tym, że układ po wyprowadzeniu go
ze stanu równowagi sam powraca do tego stanu.
Ponieważ stan równowagi może być różnie interpretowany stosuje się także
definicję stabilności wg Laplace'a która mówi, że układ liniowy jest stabilny,
jeżeli jego odpowiedź na wymuszenie (
zakłócenie
) o ograniczonej wartości jest
ograniczona.
Klasyczne kryteria stabilności układów
ciągłych
•
Kryterium biegunów
Wszystkie pierwiastki
równania charakterystycznego
(Równanie
charakterystyczne — równanie, powstające w wyniku przyrównania
mianownika
transmitancji operatorowej
do zera)
a
0
e
(n)
+ a
1
e
(n-1)
+ … + a
n
e = 0,
układu zamkniętego powinny być ujemne, czyli znajdować się w lewej
półpłaszczyźnie
płaszczyzny zmiennej zespolonej s
.
•Kryterium odpowiedzi skokowej
Układ zamknięty
w odpowiedzi na
skok jednostkowy
(
funkcją
nieciągłą
która
przyjmuje wartość 0 dla ujemnych argumentów i wartość 1 w pozostałych
przypadkach) powinien osiągać
stan ustalony
(w którym opis tego układu jest
niezależny od zmiennej
czasu
. Należy zwrócić uwagę, iż nie oznacza to braku
ruchu
, przepływu
ciepła
itp., a jedynie niezmienność tych wielkości w czasie.) w
czasie dążącym do nieskończoności.
•Kryterium Hurwitza – podaje warunki, jakie powinny spełniać
współczynniki równania algebraicznego, aby pierwiastki tego
równania miały części rzeczywiste ujemne.
Według kryterium Hurwitza zachodzi to wówczas:
•wszystkie współczynniki równania istnieją i są większe od zera
a
0
> 0, a
1
> 0, …, a
n
> 0,
•wszystkie podwyznaczniki (aż do rzędu n-1) wyznacznika
utworzonego ze współczynników równania w sposób podany
poniżej są większe od zera
Δ
n
=
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
...
...
...
...
...
0
...
0
...
...
4
2
0
5
3
1
6
4
2
0
7
5
3
1
czyli
Δ
1
= a
1
> 0,
Δ
2
=
2
0
3
1
a
a
a
a
>0,
Δ
3
= >0
...
...
...
0
3
1
4
2
0
5
3
1
a
a
a
a
a
a
a
a
aż do rzędu
n-1
Dodatnia wartość współczynników jest koniecznym warunkiem stabilności
(dla wielomianów 1 i 2 stopnia jest również warunkiem dostatecznym).
Jeżeli któryś z podwyznaczników jest równy zeru to równanie może mieć
między innymi pierwiastki czysto urojone i wtedy mówimy, że układ znajduje
się na granicy stabilności (w przebiegu e(t) występują drgania o stałej
amplitudzie). Jeżeli któryś z współczynników jest ujemny albo któryś z
podwyznaczników jest mniejszy od zera, to układ jest nie stabilny.
•Kryterium Michajłowa
Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki
w lewej półpłaszczyźnie
płaszczyzny
zmiennej zespolonej s, jeśli przyrost
argumentu równania charakterystycznego w postaci widmowej M(jω) przy
zmianie pulsacji ω od 0 do wynosi nπ / 2, gdzie n jest stopniem równania.
Płaszczyzna zmiennej zespolonej s - geometryczna reprezentacja
współrzędnych
zespolonych
, tworzona przez oś rzeczywistą i oś urojoną.
Można ją określić jako zmodyfikowany
kartezjański układ współrzędnych
, z
częścią rzeczywistą reprezentowaną przez oś "x" i częścią urojoną
reprezentowaną przez oś "y".
W
teorii sterowania
, płaszczyznę zespoloną określa się mianem płaszczyzny "s".
Używana jest do graficznego przedstawienia pierwiastków
równania charakterystycznego
, występującego w postaci wielomianu o
niewiadomej w postaci zmiennej zespolonej "s" (stąd nazwa), symbolizującej
tranformatę Laplace'a
.
Dodatkowo, płaszczyznę tę używa się do badania
stabilności układu
metodą
Nyquista, która polega na analizie
charakterystyki amplitudowo-fazowej
układu
opisanego
transmitancją operatorową
.
Odpowiednikiem płaszczyzny "s" w czasie ciągłym jest płaszczyzna "z" w czasie
dyskretnym, gdzie użyta jest
transformata Z
zamiast transmormaty Laplace'a.
•Kryterium Nyquista
Układ zamknięty jest stabilny, jeżeli
charakterystyka amplitudowo-fazowa
układu otwartego
nie obejmuje punktu (-1, j0).
Charakterystyka amplitudowo-fazowa
- układu to, w
automatyce
, wykres
transmitancji widmowej
tego układu na płaszczyźnie zmiennej zespolonej. Można
ją wyznaczyć doświadczalnie, dokonując
pomiarów
(w
stanie ustalonym
)
amplitudy
oraz
przesunięcia fazowego
sygnału
wyjściowego układu, gdy
sygnałem
wejściowym jest
sygnał
sinusoidalny o stałej amplitudzie i częstotliwości.
Jeśli układ otwarty jest stabilny, to zamknięty układ
jest
stabilny wówczas, gdy charakterystyka
amplitudowo-fazowa układu otwartego nie obejmuje
punktu (-1,j0), przy czym termin „obejmuje”
oznacza, że rozpatrujemy wektor, którego początek
znajduje się w punkcie (-1,j0), koniec zaś na
charakterystyce amplitudo-fazowej w punkcie
odpowiadającym wybranej wartości pulsacji ω.
Na wykresie umieszcza się punkty odpowiadające wartościom transmitancji
widmowej dla kolejnych wartości pulsacji ω є (0 ; ∞) . Kierunek strzałki
oznacza kierunek wzrostu ω.
Na osi rzędnych odłożona zostaje wartość części urojonej, a na osi odciętych
wartość części rzeczywistej transmitancji widmowej. Charakterystyki
amplitudowo-fazowe układów realizowalnych fizycznie, dążą do początku
układu współrzędnych.
Analiza
Każdemu pierwiastkowi p
k
równania
1+ K(p) = 0,
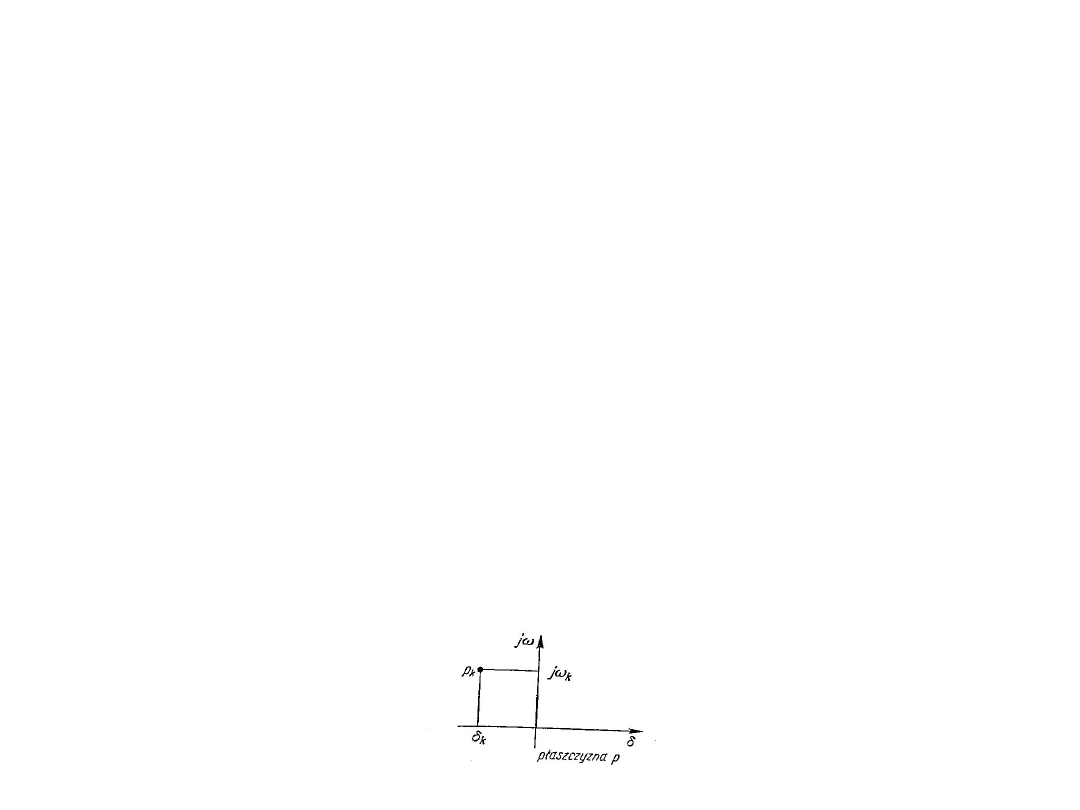
można podporządkować jeden punkt na płaszczyźnie zmiennej zespolonej p.
Jeżeli oznaczymy
p
k
= δ
k
+ jω
k
,
to współrzędne punktu odpowiadającego pierwiastkowi p
k
są (δ
k
, ω
k
).
Operując pojęciem płaszczyzny p, można warunek stabilności
Re[p
k
] > 0
lim e(t) = 0,
określić jako warunek znajdowania się wszystkich pierwiastków równania
1+ K(p) = 0,
na lewej płaszczyźnie zmiennej p.
Istota kryterium Nyquista polega na kontroli położenia pierwiastków p
k
,
poprzez odwzorowanie płaszczyzny p na płaszczyznę K.
Funkcję transformującą jest funkcja przejścia badanego układu w stanie
otwartym, to znaczy, że funkcja K(p).
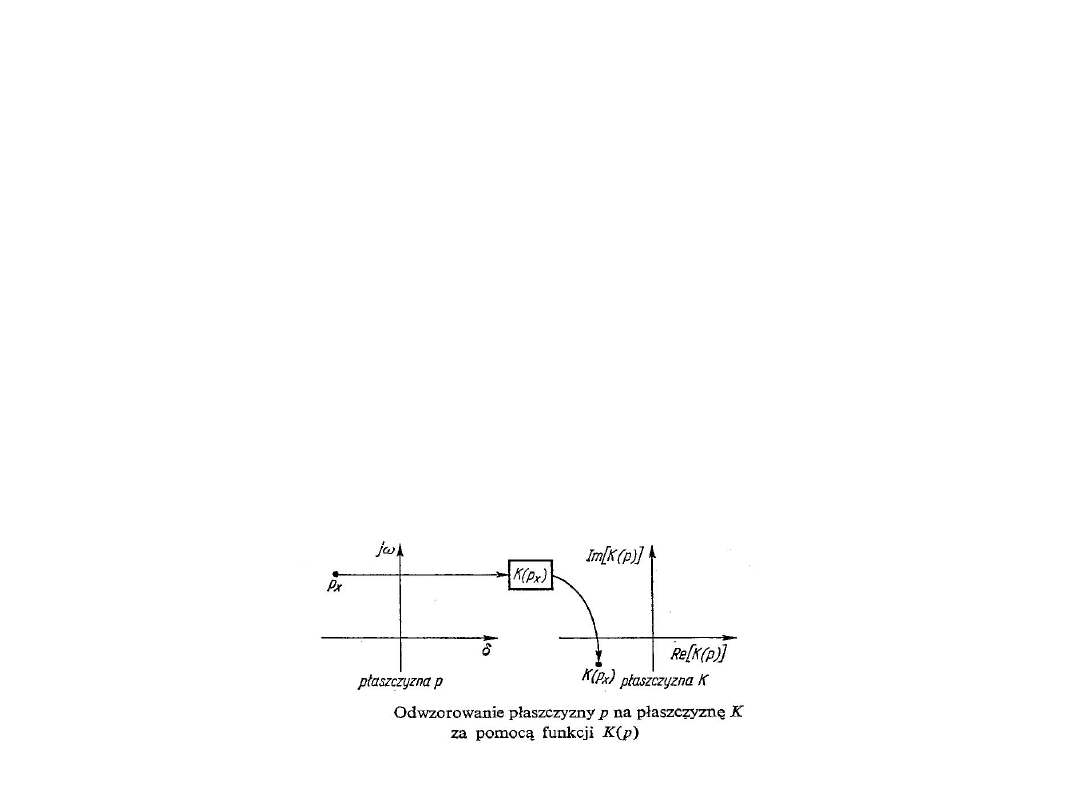
Aby znaleźć na płaszczyźnie punkt K punkt odpowiadający punktowi p
x
płaszczyzny p, należy wstawić wartość p
x
do funkcji K(p), a z otrzymanego
wyodrębnić część rzeczywistą i urojoną według relacji
K(p) = Re [K(p
x
)] + j Im [K(p
x
)].
Wartości Re [K(p
x
)] i Im [K(p
x
)] są współrzędnymi punktu odpowiadającego
na płaszczyźnie K punktowi p
x
płaszczyzny p.
Jeżeli p
x
jest jednym z pierwiastków równania K(p) + 1 = 0, czyli jeżeli K(p
k
)
= -1, to takiemu punktowi p
k
płaszczyzny p odpowiada na płaszczyźnie K
punkt o współrzędnych (-1,j0).
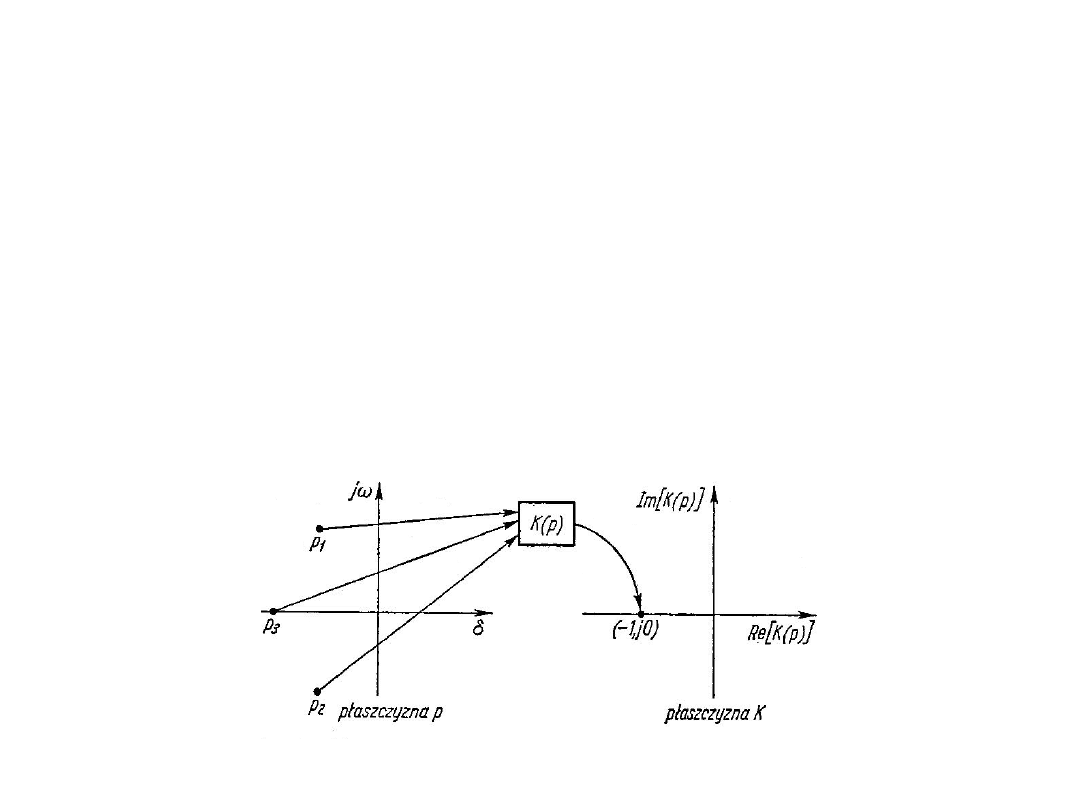
Po dokonaniu omawianej transformacji wszystkie punkty p
k
płaszczyzny p
przejdą zatem w jeden punkt o współrzędnych (-1,j0) na płaszczyźnie K.
Dla sprawdzenia stabilności wystarczy zatem skontrolować czy na
płaszczyźnie K punkt
(-1,j0) znajduje się w obszarze odpowiadającym lewej półpłaszczyźnie
zmiennej p lub
– jest równoważne – czy znajduje się poza obszarem odpowiadającym
prawej półpłaszczyźnie zmiennej p.
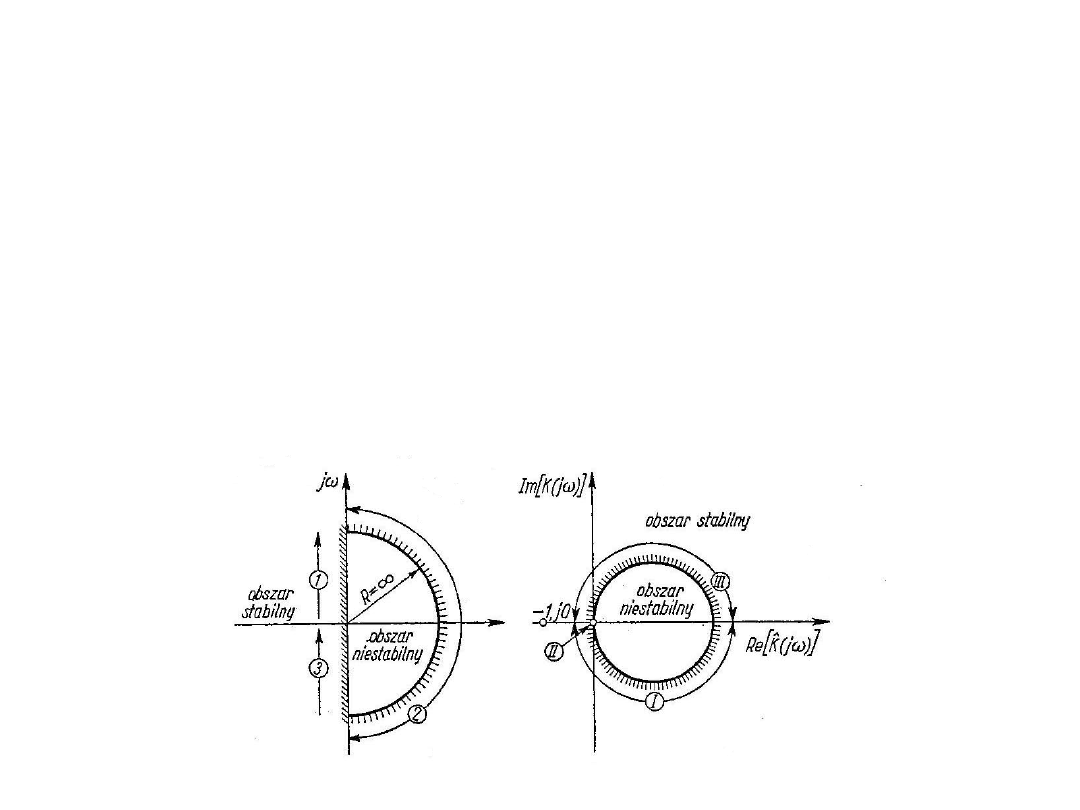
Dokonujemy w tym celu odwzorowania brzegów prawej półpłaszczyzny
zmiennej p, dzieląc je na trzy części tak jak to przedstawiono dla
przypadku funkcji transformującej
K(p) = k/(1 + pT).
Półprosta 1 (ω = 0 ω = - ∞) przechodzi po transformacji w krzywą I, wykres K(jω)
dla ω zmieniającego się od 0 do ∞.
Półprosta 3 (ω = - ∞ ω = 0) przechodzi po transformacji w krzywą III, wykres
K(jω) dla ω zmieniającego się od - ∞ do 0.
Półprosta 2 (ω = 0) przechodzi po transformacji w punkt II o współrzędnych (0,0)
czyli początek układu. Jest tak dlatego, że K(jω) = 0.
Wykres K(jω) nazywany charakterystyką częstotliwościową otwartego układu
regulacji. Jest to krzywa symetryczna względem osi Re[K(p)]. Funkcje K(jω) i K(-
jω) są bowiem funkcjami sprzężonymi i zachodzą związki:
Re [K(jω)] = Re [K(-jω)],
Im[K(jω)] = - Im [K(-jω)],
Jeżeli zatem znamy przebieg funkcji K(jω) dla ω = 0 aż do ω = ∞ , czyli jeżeli
znamy odcinek I charakterystyki częstotliwościowej, to odcinek III możemy
narysować bez obliczeń jako lustrzane odbicie krzywej względem osi Re [K(p)].
Na podstawie przeprowadzonej analizy można powiedzieć, że układ automatyki
będzie po zamknięciu stabilny, jeżeli punkt (-1, j0) leży na płaszczyźnie K „na
zewnątrz” charakterystyki częstotliwościowej układu otwartego. Przez wyrażenie
„na zewnątrz” rozumie się „w obszarze odpowiadającym lewej półpłaszczyźnie
zmiennej p”.
Document Outline