„Jak ty rodzicom, tak dzieci
tobie.”
Tales z Miletu
„Jak ty rodzicom, tak dzieci
tobie.”
Tales z Miletu
TWIERDZENIE TALESA.
Tales z Miletu to jeden z najwybitniejszych
mędrców starożytności. Zasłynął nie tylko
jako filozof ale także jako matematyk i
astronom. Potrafił przewidywać zaćmienia
słońca, czym prawdopodobnie przyczynił się
do wyniku bitwy nad rzeką Halys.
Twierdzenie Talesa przedstawione w tej
prezentacji to potężne narzędzie w geometrii.
Tales dzięki swojej wiedzy już w VI w p. n. e.
potrafił obliczać wysokość m. in. piramid tylko
w oparciu o pomiar długości ich cienia…
TALES Z MILETU
ODCINKI
PROPORCJONALNE.
Co to oznacza, że dane odcinki są
proporcjonalne?
Oznacza
to,
że
jeśli
podzielimy przez siebie ich długości, to
otrzymamy tę samą liczbę.
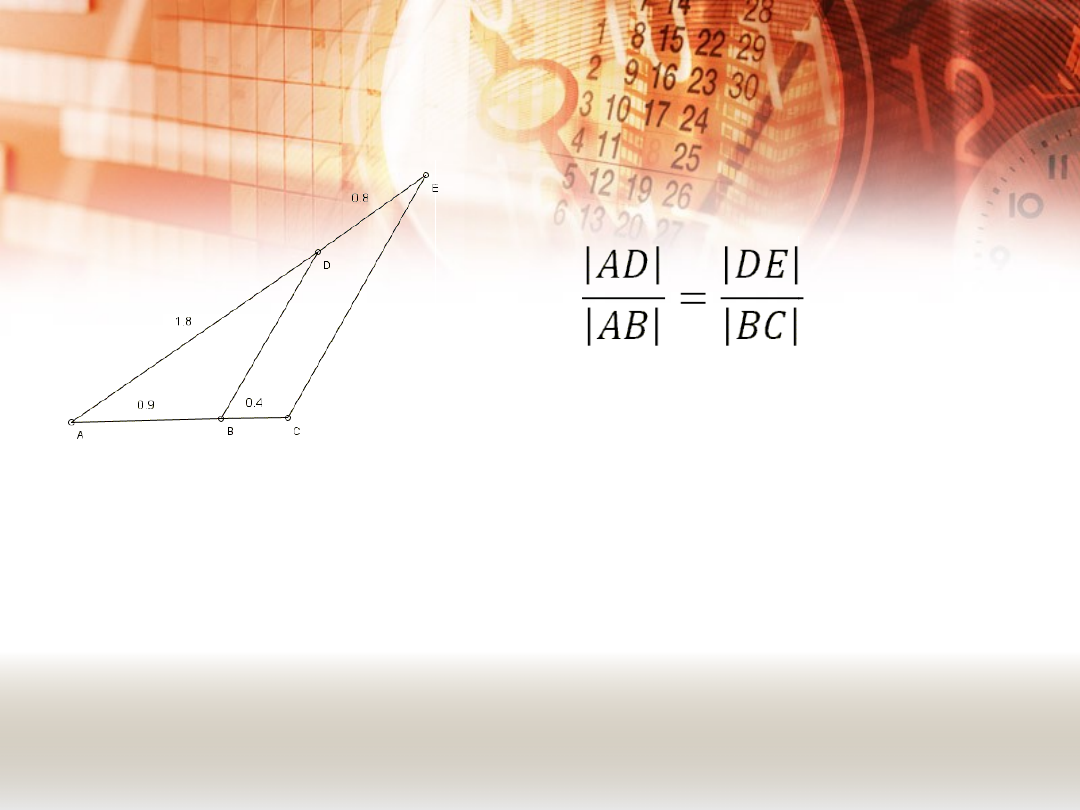
PRZYKŁAD:
|AB|= 0,9
|BC| = 0,4
|AD| = 1,8
|DE| = 0,8
ODCINKI
PROPORCJONALNE.
Jeżeli zachodzi powyższa proporcja, to o
odcinkach AD I DE mówimy, że są
proporcjonalne do odcinków AB i BC.
TWIERDZENIE TALESA.
Jeżeli ramiona kąta przetniemy prostymi
równoległymi, to odcinki wyznaczone przez
te proste na jednym ramieniu kąta są
proporcjonalne do odpowiednich odcinków
na drugim ramieniu kąta.
m ||
n
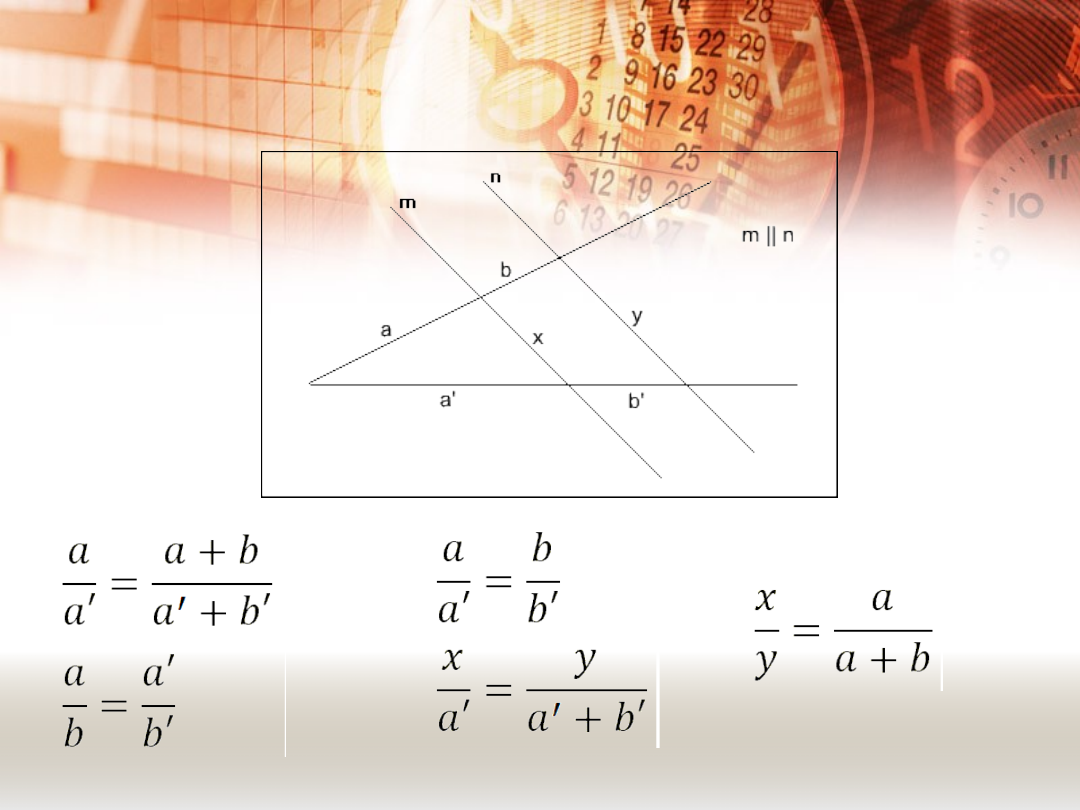
PROPORCJE WYNIKAJĄCE Z
TWIERDZENIA TALESA.
PRZYKŁADY.
PRZYKŁAD 1.
Oblicz długość odcinka oznaczonego literą x.
Rozwiązujemy
proporcję
wynikającą
z
twierdzenia Talesa:
2,4 ∙ 3,5 = 1 ∙ x
x = 8,4
PRZYKŁADY.
PRZYKŁAD 2.
Oblicz długość odcinka oznaczonego literą a.
Rozwiązujemy
proporcję
wynikającą
z
twierdzenia Talesa:
2 ∙ (2 + 6) = 2a
16 = 2a
a = 8
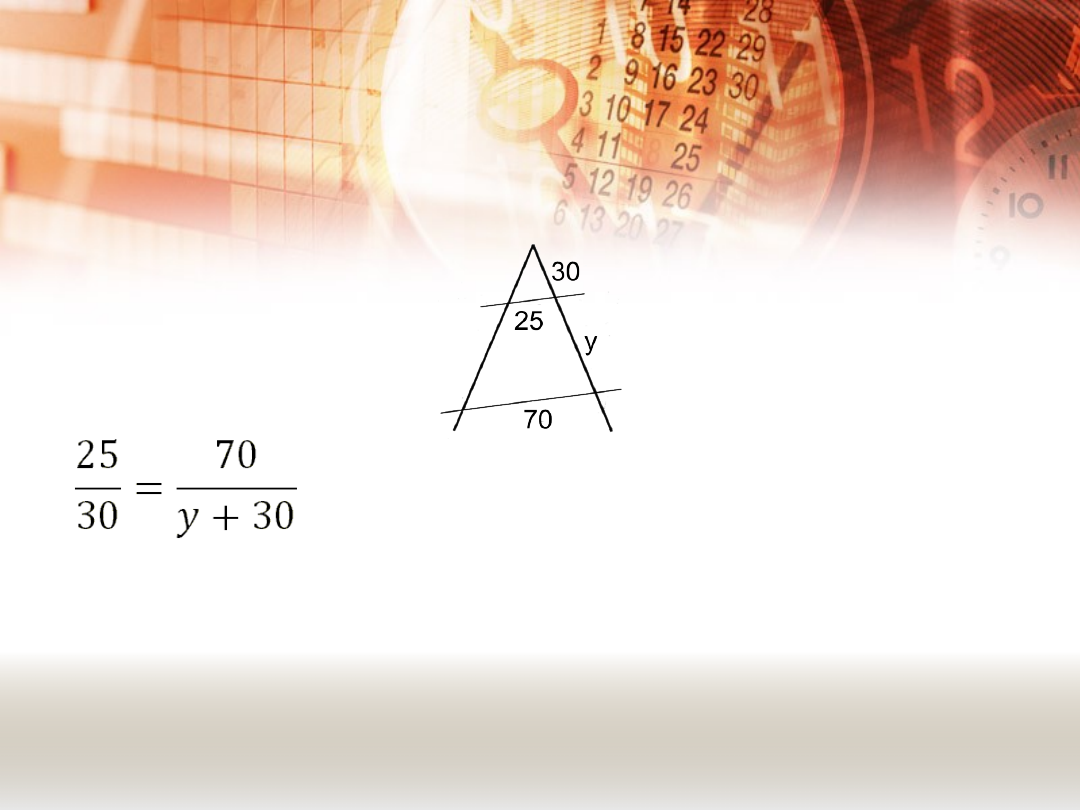
PRZYKŁADY.
PRZYKŁAD 3.
Oblicz długość odcinka oznaczonego literą y.
25 ∙ (y + 30) = 30 ∙ 70
25y + 750 = 2100
25y = 1350 | : 25
y = 54
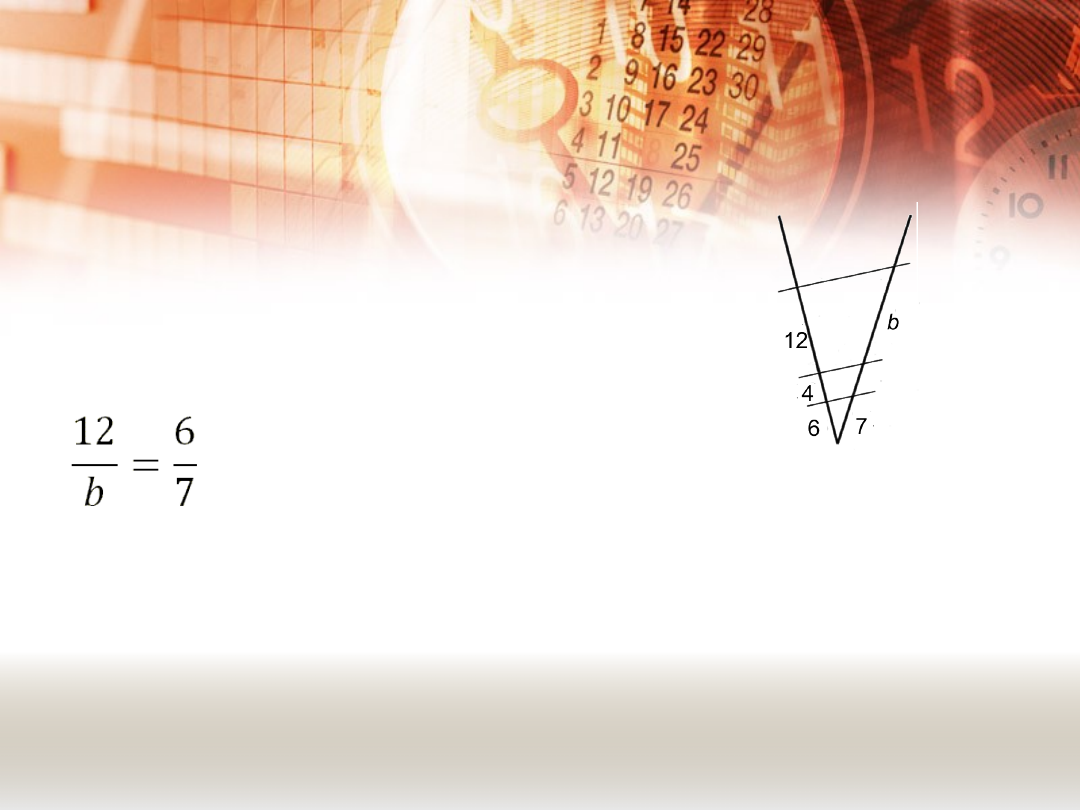
PRZYKŁADY.
PRZYKŁAD 4.
Oblicz długość odcinka oznaczonego literą b.
W tym przypadku także „działa”
twierdzenie Talesa.
Układamy proporcję dla odpowiednich
odcinków.
12 ∙ 7 = b ∙ 6
6b = 84 | : 6
b = 14
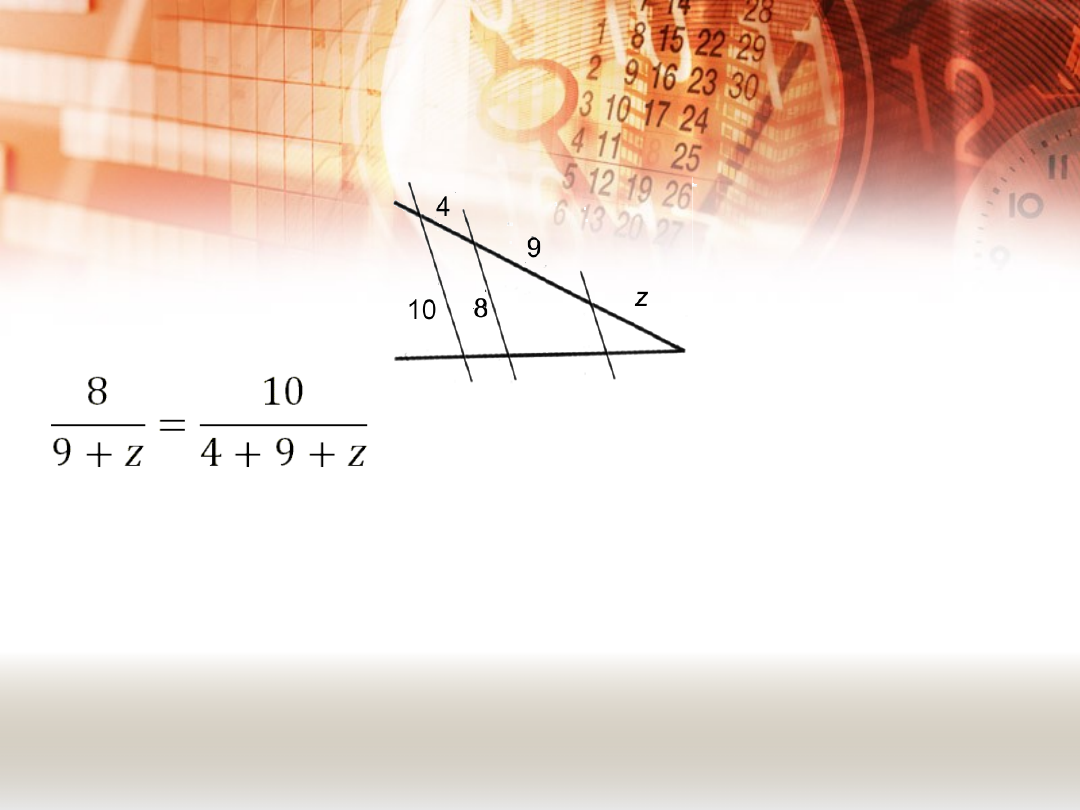
PRZYKŁADY.
PRZYKŁAD 5.
Oblicz długość odcinka oznaczonego literą z.
8 ∙ (13 + z) = (9 + z) ∙ 10
104 + 8z = 90 + 10z
8z – 10z = 90 – 104
-2z = -14 | : (-2)
z = 7
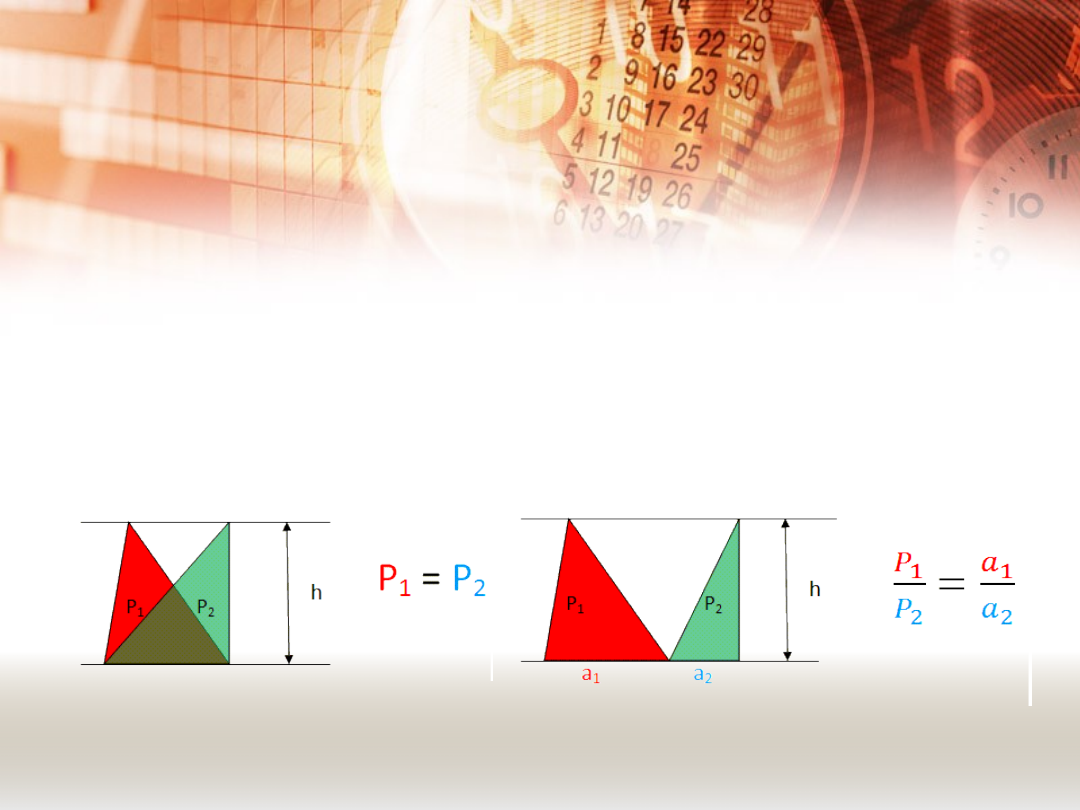
DOWÓD TWIERDZENIA
TALESA.
Dowód tego twierdzenia jest dość prosty.
Opiera się na dwóch faktach:
1.Pola trójkątów, które mają wspólną
podstawę i równe wysokości, są takie same.
2. Stosunek pól trójkątów, które mają taką
samą wysokość, jest równy stosunkowi ich
podstaw.
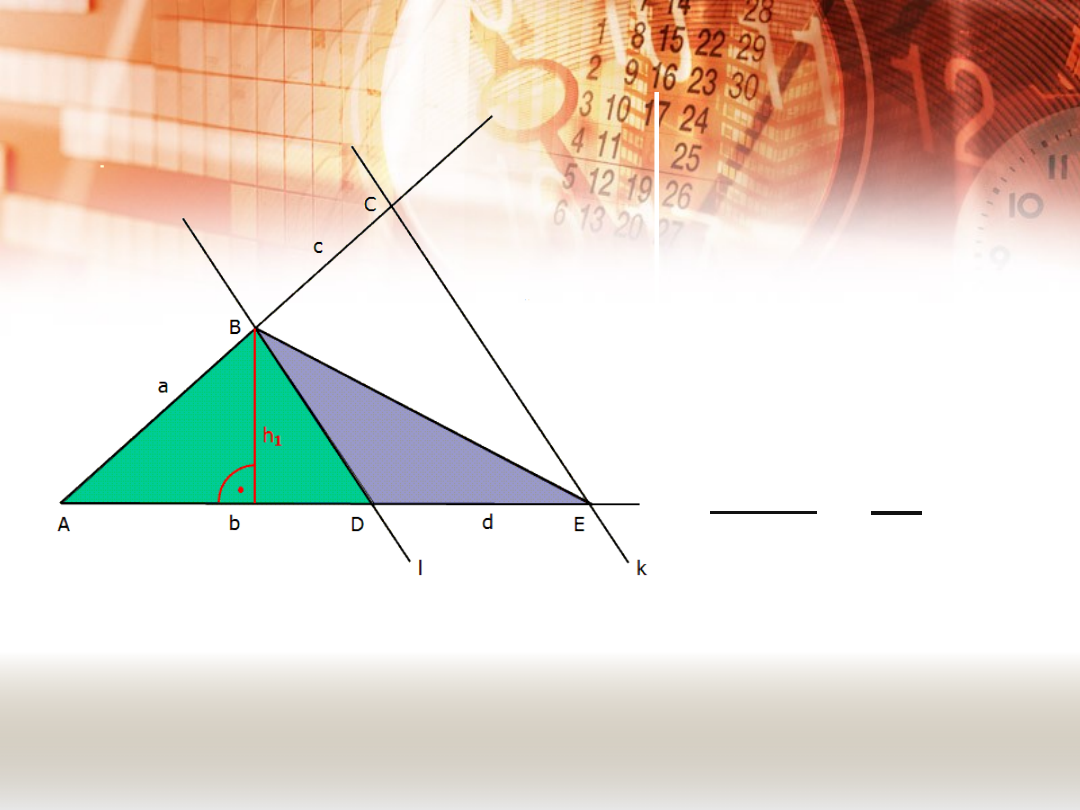
DOWÓD TWIERDZENIA
TALESA.
Trójkąty ADB i
DEB mają
wspólną
wysokość h
1
.
Zgodnie z
podanymi
powyżej
faktami
zachodzi:
P
ΔADB
P
ΔDEB
=
b
d
k || l
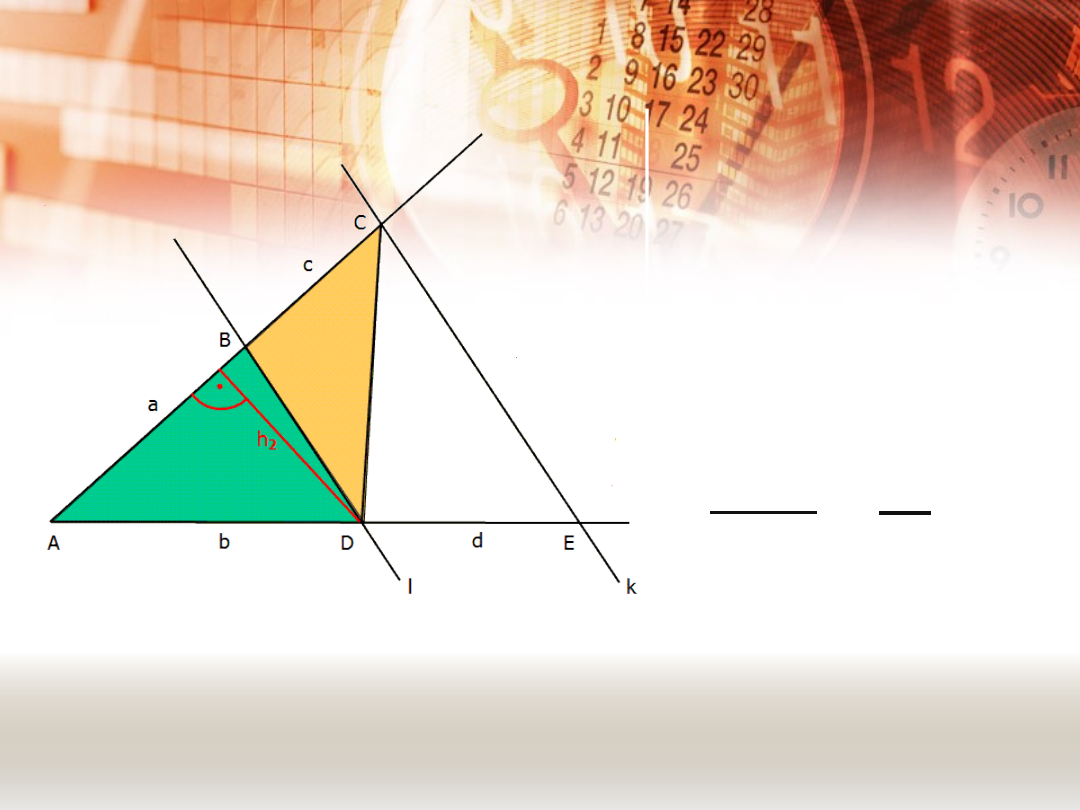
DOWÓD TWIERDZENIA
TALESA.
Trójkąty ADB i
DCB mają
wspólną
wysokość h
2
.
Analogicznie:
=
k || l
P
ΔADB
P
ΔDCB
a
c
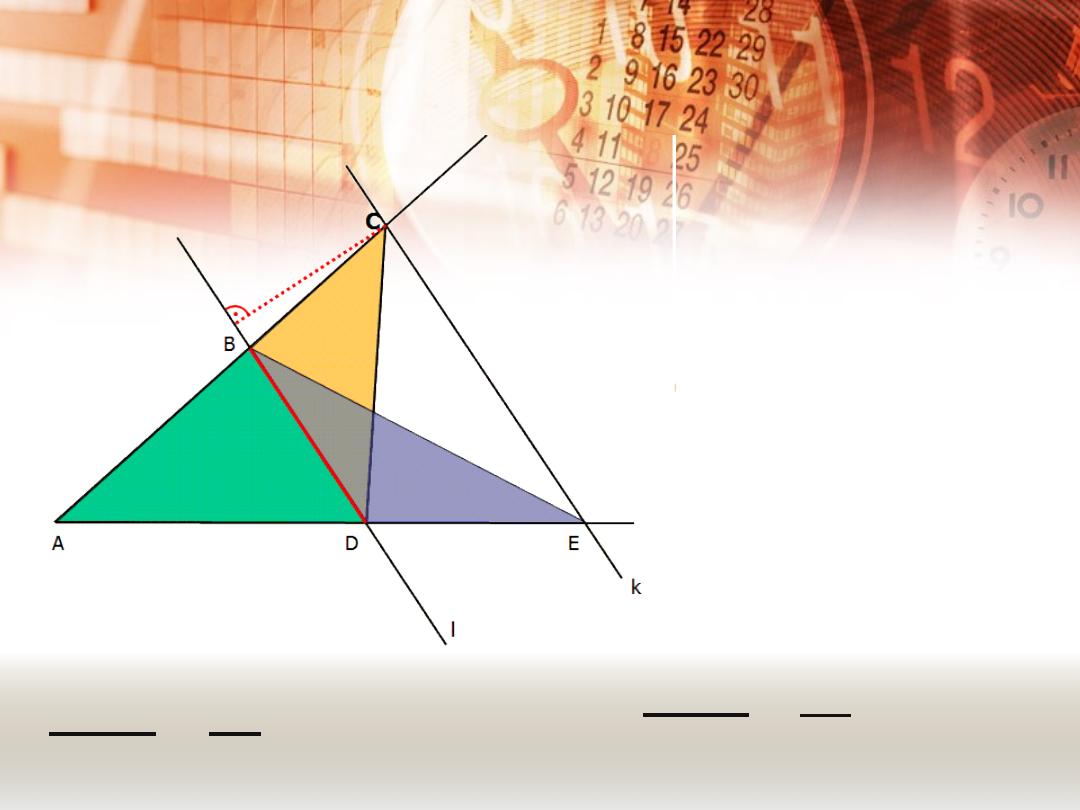
DOWÓD TWIERDZENIA
TALESA.
Godnie z
pierwszym
faktem
zachodzi:
k || l
P
ΔDEB
=
P
ΔDCB
Mamy zatem:
P
ΔAD
B
P
ΔDC
B
=
a
c
P
ΔDEB
=
P
ΔDCB
P
ΔAD
B
P
ΔDE
B
=
b
d
DOWÓD TWIERDZENIA
TALESA.
Po uporządkowaniu dostajemy:
,
zachodzi więc równość:
co kończy dowód.
P
ΔAD
B
P
ΔDC
B
=
a
c
P
ΔAD
B
P
ΔDE
B
=
b
d
=
a
c
=
b
d
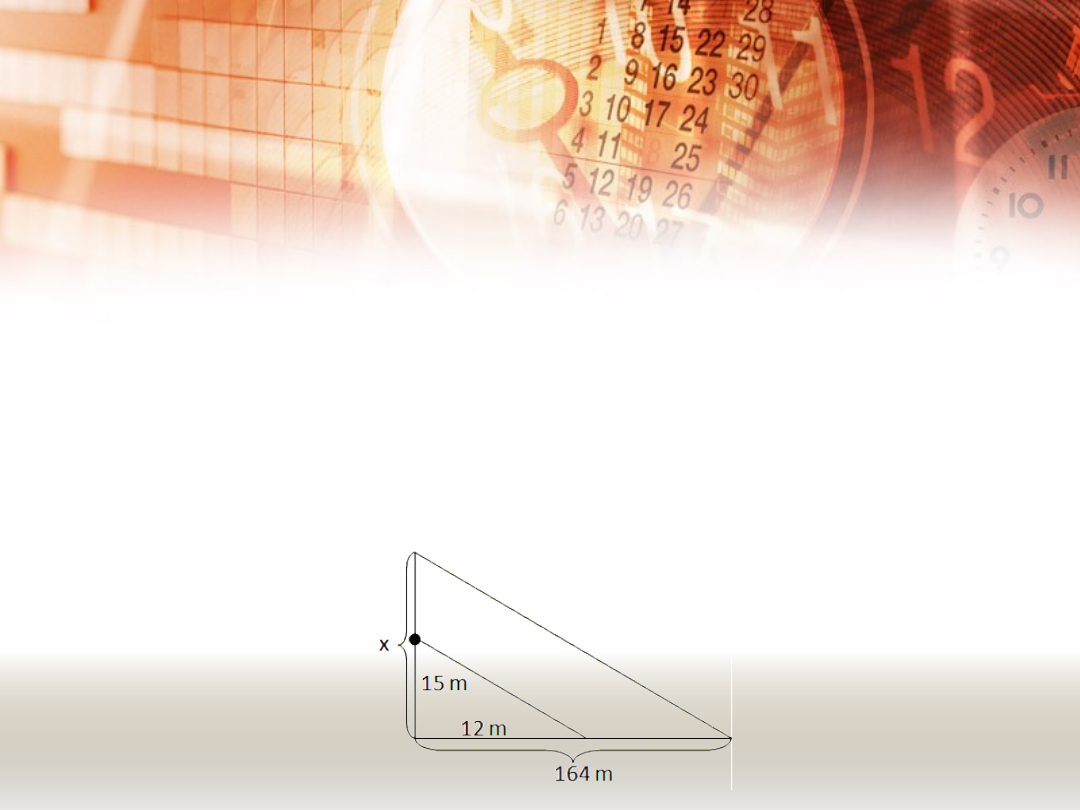
PRZYKŁADOWE ZADANIA.
ZADANIE 1.
Maszt rzuca cień długości 164 m. Na maszcie
umieszczono anteny stacji nadawczych
telefonii komórkowej. Najniżej umieszczona
antena jest na wysokości 15m nad ziemią.
Cień anteny zaczyna się w odległości 12m od
masztu. Jak wysoki jest maszt?
Rozwiązanie najlepiej zacząć od wykonania
rysunku pomocniczego
PRZYKŁADOWE ZADANIA.
ZADANIE 1 – ciąg dalszy.
Zgodnie z twierdzeniem
Talesa zachodzi równość:
Rozwiązujemy proporcje:
15 ∙ 164 = x ∙ 12
12x = 2460 |: 12
x = 205 (m)
Odpowiedź: Maszt ma 205 m wysokości.
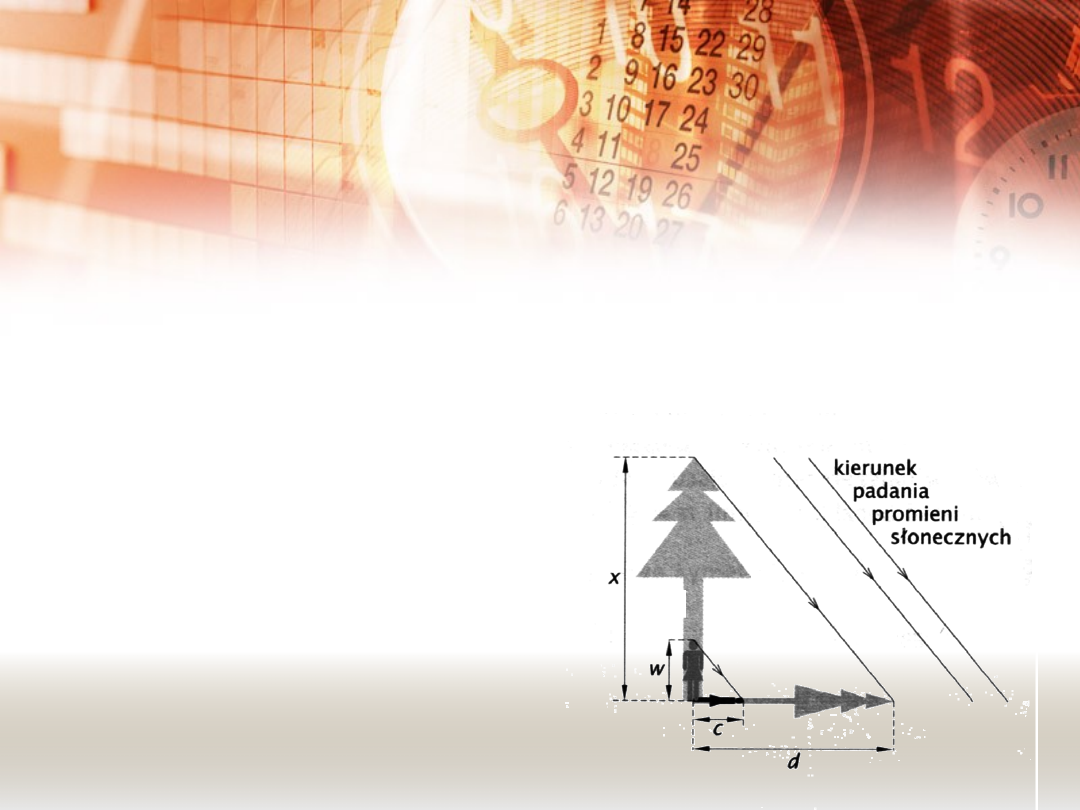
PRZYKŁADOWE ZADANIA.
ZADANIE 2.
Przy drodze rosło samotne drzewo. Aby
poznać jego wysokość, uczniowie dokonali
odpowiednich
pomiarów.
Następnie,
korzystając ze schematu, obliczyli jego
wysokość. Przedstaw ich obliczenia.
Uzyskane przez gimnazjalistów pomiary:
długość cienia drzewa – 5,6 m
długość cienia Basi – 1,4 m
wzrost Basi – 1,7 m
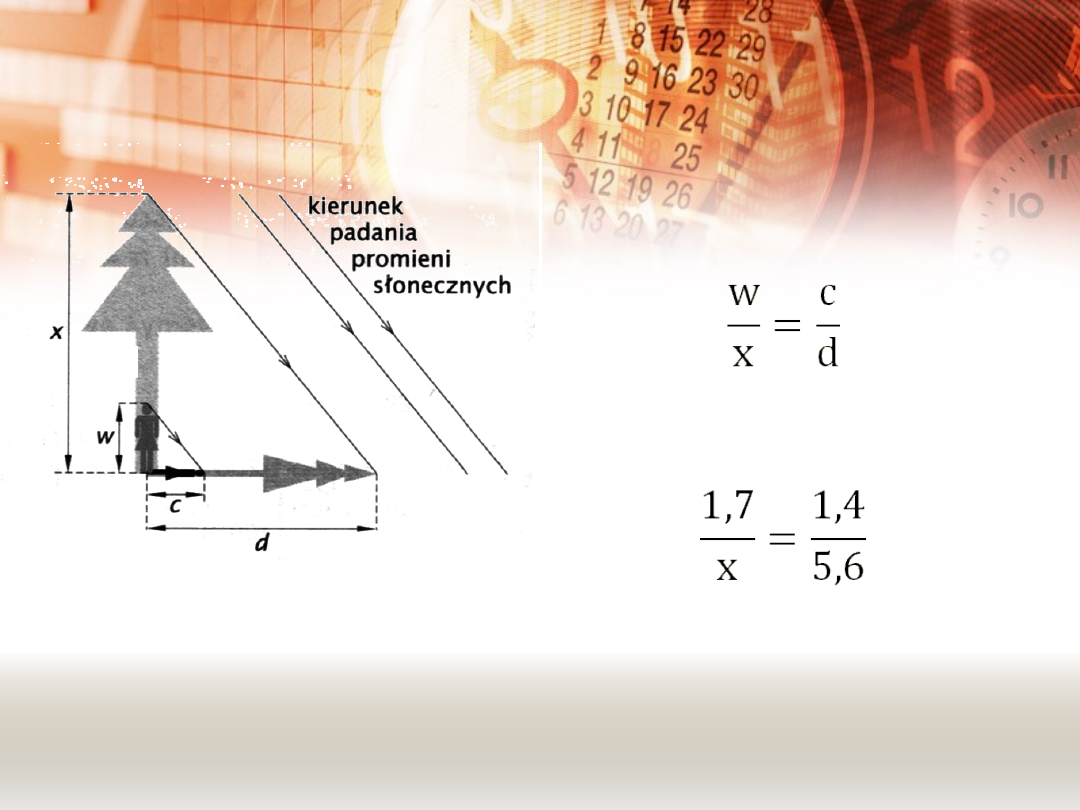
PRZYKŁADOWE ZADANIA.
ZADANIE 2 – ciąg dalszy.
Zgodnie
z
twierdzeniem Talesa
zachodzi proporcja:
Po
podstawieniu
danych otrzymujemy:
1,7 ∙ 5,6 = x ∙ 1,4
1,4x = 9,52 |: 1,4
x = 6,8
Odpowiedź: Drzewo ma wysokość 6,8 m.