Piotr Łukowski, Wykład dla studentów prawa

1

Logiczne podstawy prawoznawstwa

Piotr Łukowski

Piotr Łukowski, Wykład dla studentów prawa

2

WYKŁAD 9

klasyczny rachunek nazw

relacje

Piotr Łukowski, Wykład dla studentów prawa

3

Ludwik Borkowski, Elementy logiki formalnej, PWN, Warszawa 1977, s.154

(cienka książka)

(nie korzystamy z Ziębińskiego)

Piotr Łukowski, Wykład dla studentów prawa

4

Rachunek nazw (Arystoteles)

Zdanie kategoryczne, to zdanie o budowie podmiotowo-orzecznikowej, w którym występują
dwie nazwy (w roli podmiotu i w roli orzecznika) połączone funktorem zdaniotwórczym „jest”.

Wyróżniamy cztery typy zdań kategorycznych:

1. zdanie ogólno-twierdzące „Każde S jest P” (SaP)
2. zdanie ogólno-przeczące „śadne S nie jest P” (SeP)
3. zdanie szczegółowo-twierdzące „Niektóre S są P” (SiP)
4. zdanie szczegółowo-przeczące „Niektóre S nie są P” (SoP)

S -

s

ubiectum (podmiot)

SaP, SiP -

a

ff

i

rmo (twierdzę)

P -

p

raedicatum (orzecznik)

SeP, SoP - n

e

g

o

(przeczę)

Przykład
Każdy adwokat jest prawnikiem.

(SaP)

ś

aden sędzia nie jest prokuratorem.

(SeP)

Niektórzy prawnicy są prokuratorami.

(SiP)

Niektórzy prawnicy nie są prokuratorami.

(SoP)

Ex(S)

↔

SiS

(zdanie Ex(S) stwierdza istnienie obiektu będącego S, czyli stwierdza niepustość S)

Piotr Łukowski, Wykład dla studentów prawa

5

Zdania SaP i SiP mają tę samą JAKOŚĆ (w tym przypadku twierdzącą), zaś
zdania SaP i SeP mają tę samą ILOŚĆ (w tym przypadku ogólną).
Podobnie,
zdania SeP i SoP mają te samą JAKOŚĆ (w tym przypadku przeczącą), zaś
zdania SiP i SoP mają tę samą ILOŚĆ (w tym przypadku szczegółową).


Zmiana jakości zdania bez zmiany jego ilości oznacza zamianę,

albo SaP na SeP, albo SeP na SaP, albo SiP na SoP, albo zamianę SoP na SiP.

Zmiana ilości zdania bez zmiany jego jakości oznacza zamianę,

albo SaP na SiP, albo SiP na SaP, albo SeP na SoP, albo zamianę SoP na SeP.

Jednoczesna zmiana ilości i jakości zdania oznacza zamianę,

albo SaP na SoP, albo SoP na SaP, albo SeP na SiP, albo zamianę SiP na SeP.

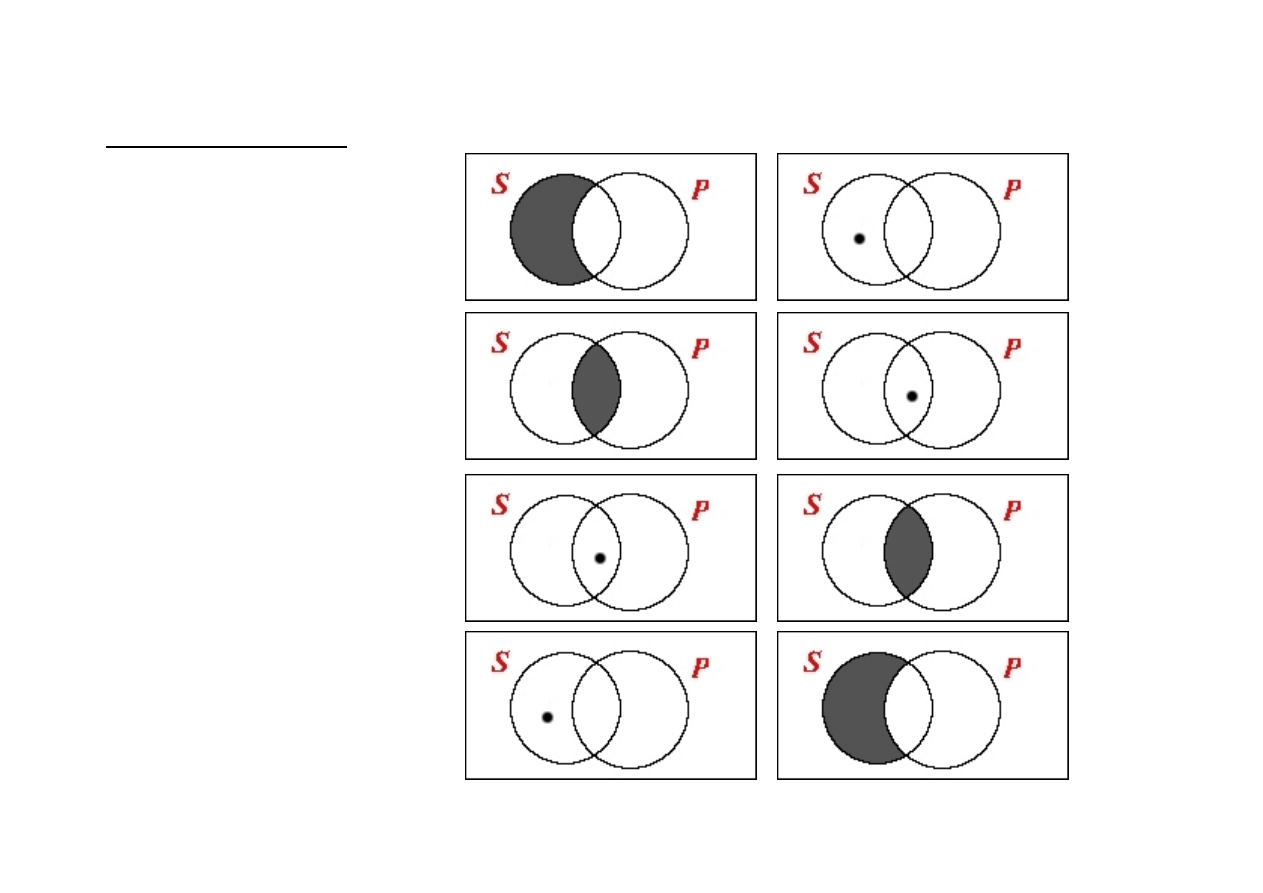
Piotr Łukowski, Wykład dla studentów prawa

6

diagramy Venna

zdanie prawdziwe

zdanie fałszywe

SaP

SeP

SiP

SoP

Piotr Łukowski, Wykład dla studentów prawa

7

Prawa z kwadratu logicznego

SaP

↔

∀

x (x

∈

S

→

x

∈

P)

↔

¬∃

x (x

∈

S

∧

x

∉

P)

↔

¬

SoP

SeP

↔

∀

x (x

∈

S

→

x

∉

P)

↔

¬∃

x (x

∈

S

∧

x

∈

P)

↔

¬

SiP

SiP

↔

∃

x (x

∈

S

∧

x

∈

P)

↔

¬∀

x (x

∈

S

→

x

∉

P)

↔

¬

SeP

SoP

↔

∃

x (x

∈

S

∧

x

∉

P)

↔

¬∀

x (x

∈

S

→

x

∈

P)

↔

¬

SaP

(SaP

∧

Ex(S))

→

¬

SeP

(

¬

SiP

∧

Ex(S))

→

SoP

(SaP

∧

Ex(S))

→

SiP

(SeP

∧

Ex(S))

→

¬

SaP

(

¬

SoP

∧

Ex(S))

→

SiP

(SeP

∧

Ex(S))

→

SoP

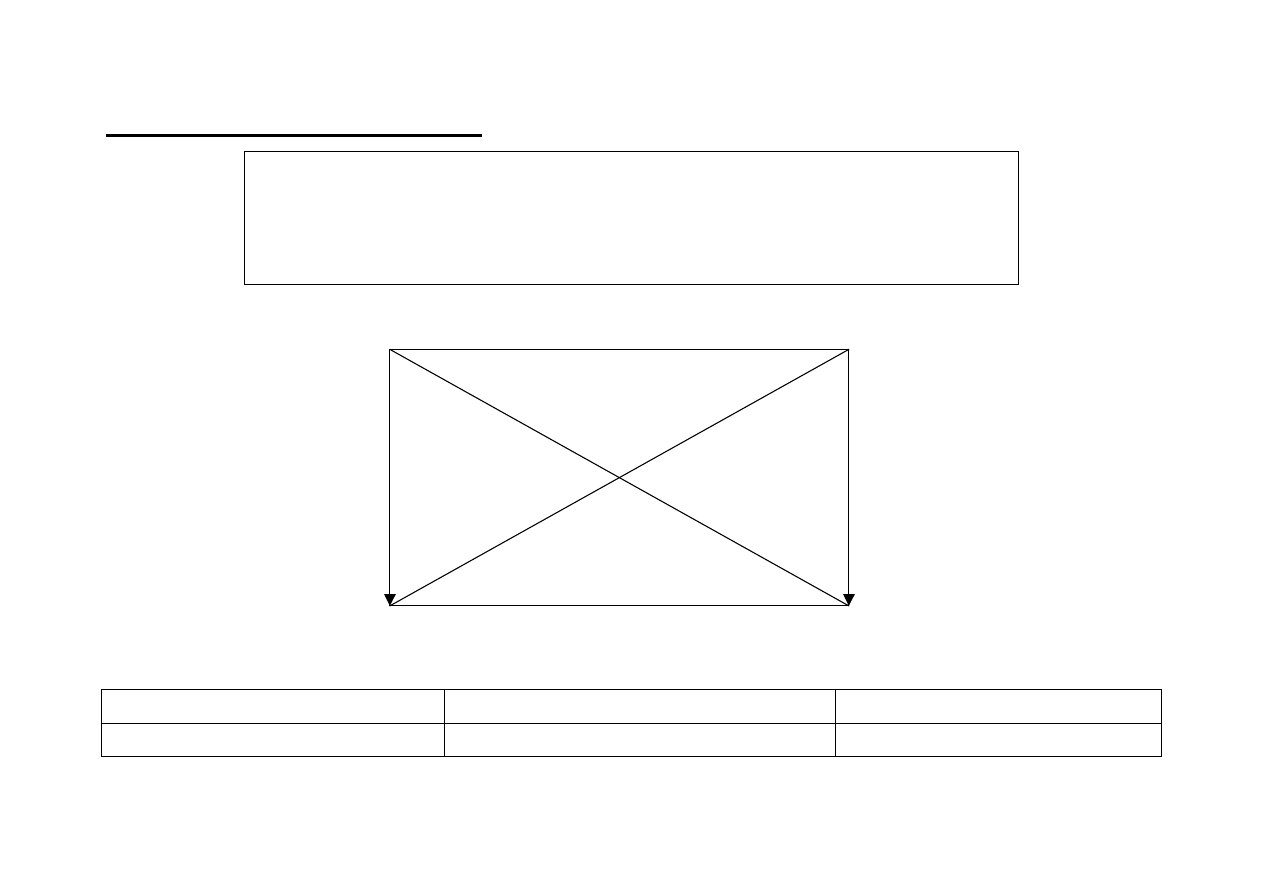
sprzeczne

sprzeczne

SaP

SoP

SiP

SeP

przeciwne

podprzeciwne

podporządkowane

podporządkowane

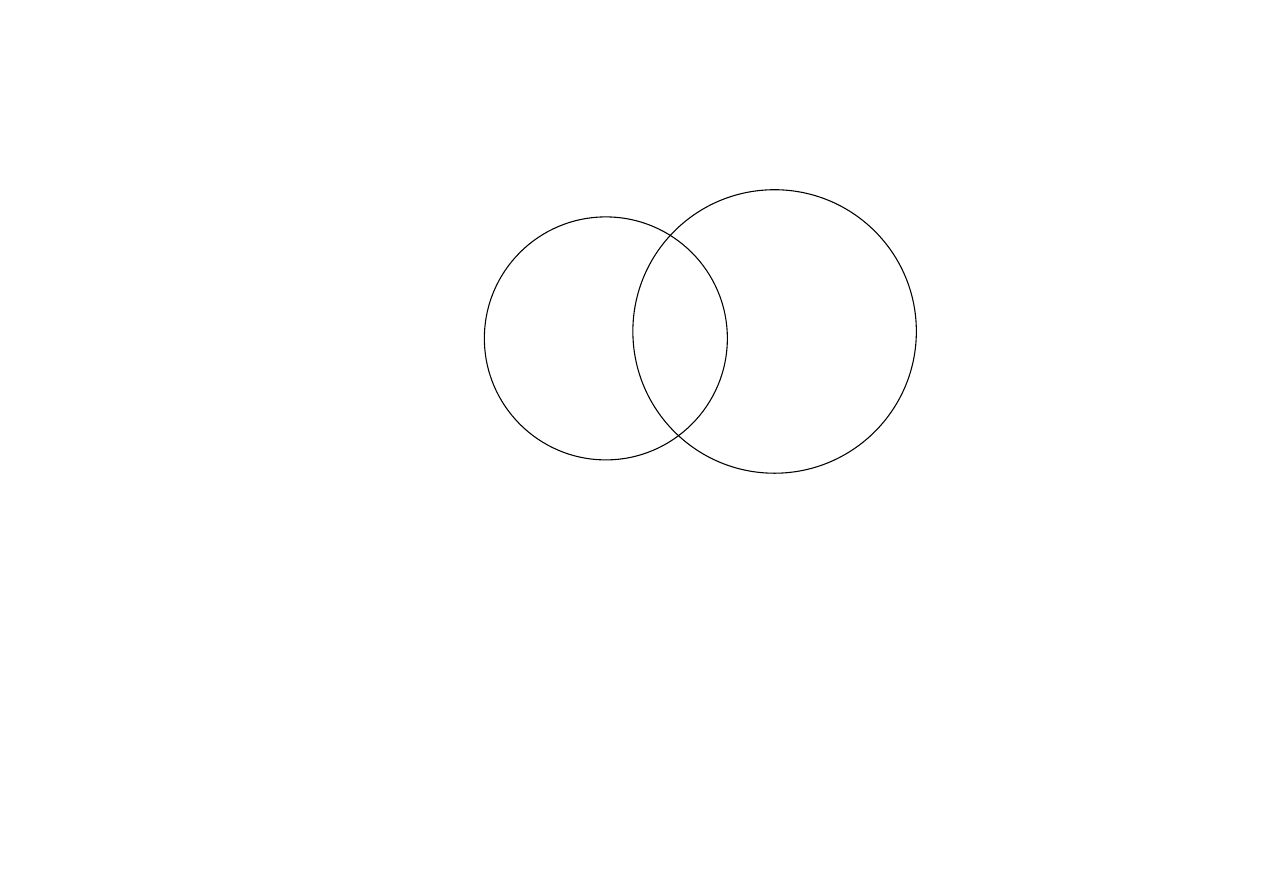
Piotr Łukowski, Wykład dla studentów prawa

8

S

- zakres nazwy S

P

- zakres nazwy P

I - obiekty S, które są P
II - obiekty S, które nie są P
III - obiekty P, które nie są S

S

P

I

II

III

Piotr Łukowski, Wykład dla studentów prawa

9

Zadanie Wykaż, że:

(SaP

∧

Ex(S))

→

¬

SeP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy krasnal ma czapkę i jakiś

krasnal istnieje (krasnale istnieją), to nieprawdą jest, że żaden krasnal nie ma czapki.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

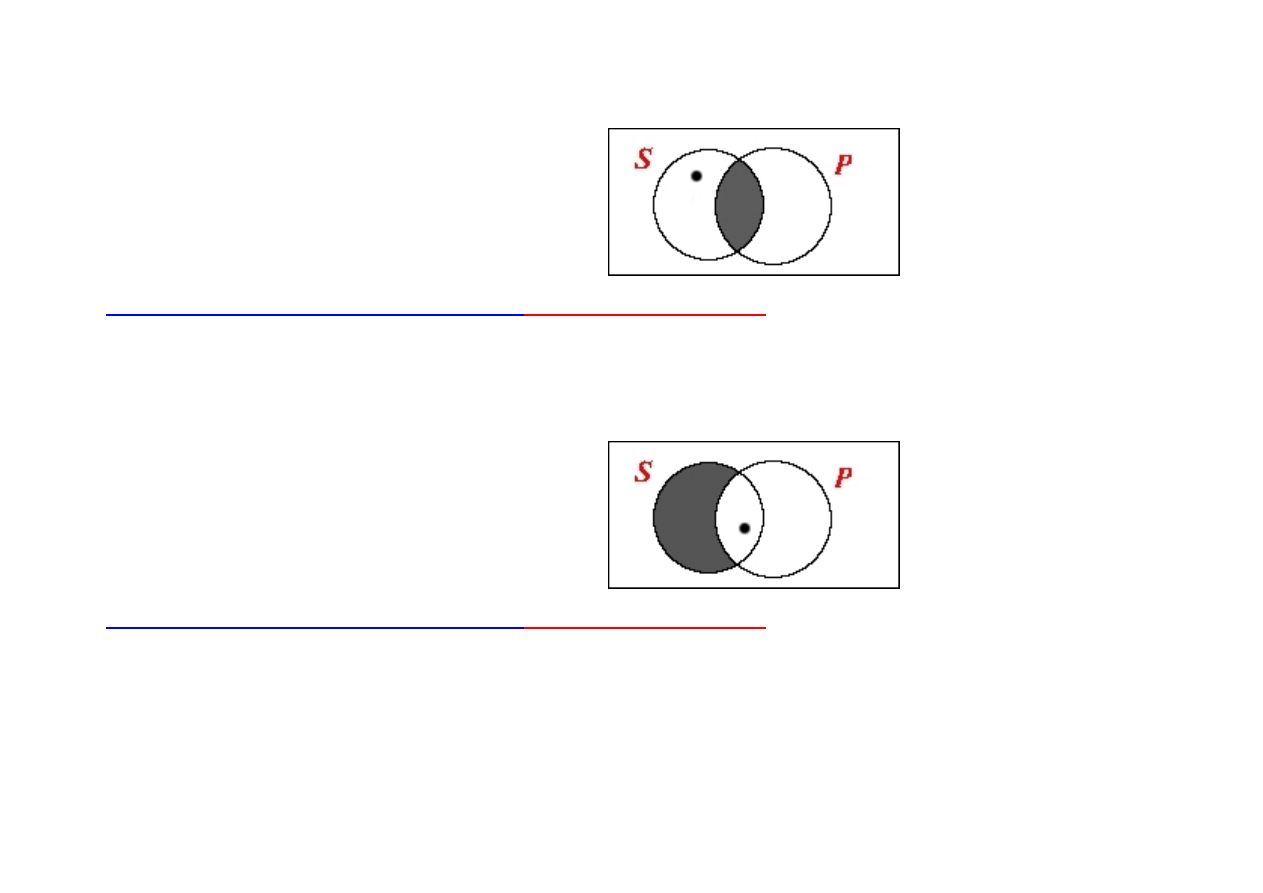
(SeP

∧

Ex(S))

→

¬

SaP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli żaden krasnal nie ma pistoletu i

jakiś krasnal istnieje (krasnale istnieją), to nieprawdą jest, że każdy krasnal ma pistolet.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

Piotr Łukowski, Wykład dla studentów prawa

10

(

¬

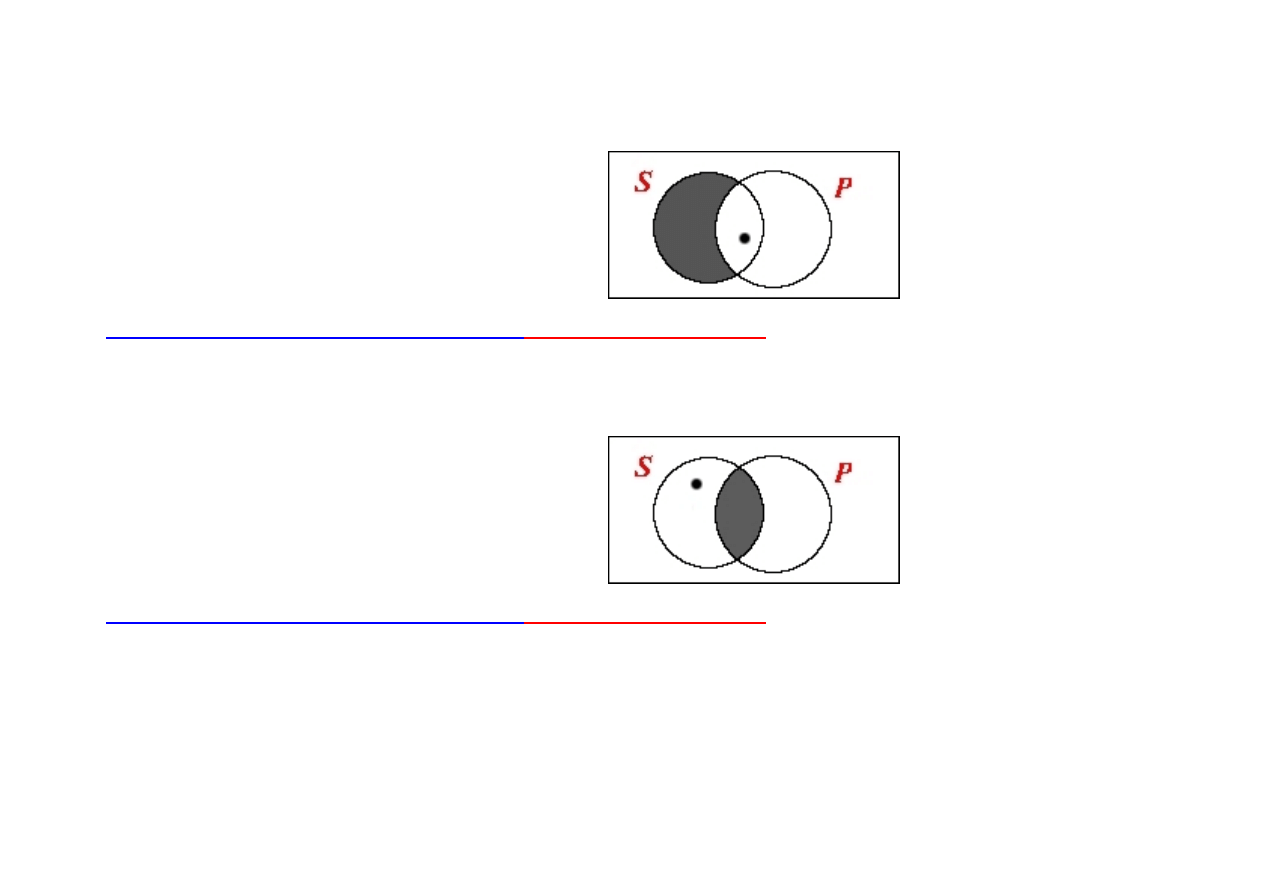
SiP

∧

Ex(S))

→

SoP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli nieprawdą jest, że pewien krasnal

ma chorobę weneryczną i jakiś krasnal istnieje (krasnale istnieją), to pewien krasnal nie ma choroby
wenerycznej.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

(

¬

SoP

∧

Ex(S))

→

SiP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli nieprawdą jest, że pewien krasnal

nie ma narzeczonej i jakiś krasnal istnieje (krasnale istnieją), to pewien krasnal ma narzeczoną.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

Piotr Łukowski, Wykład dla studentów prawa

11

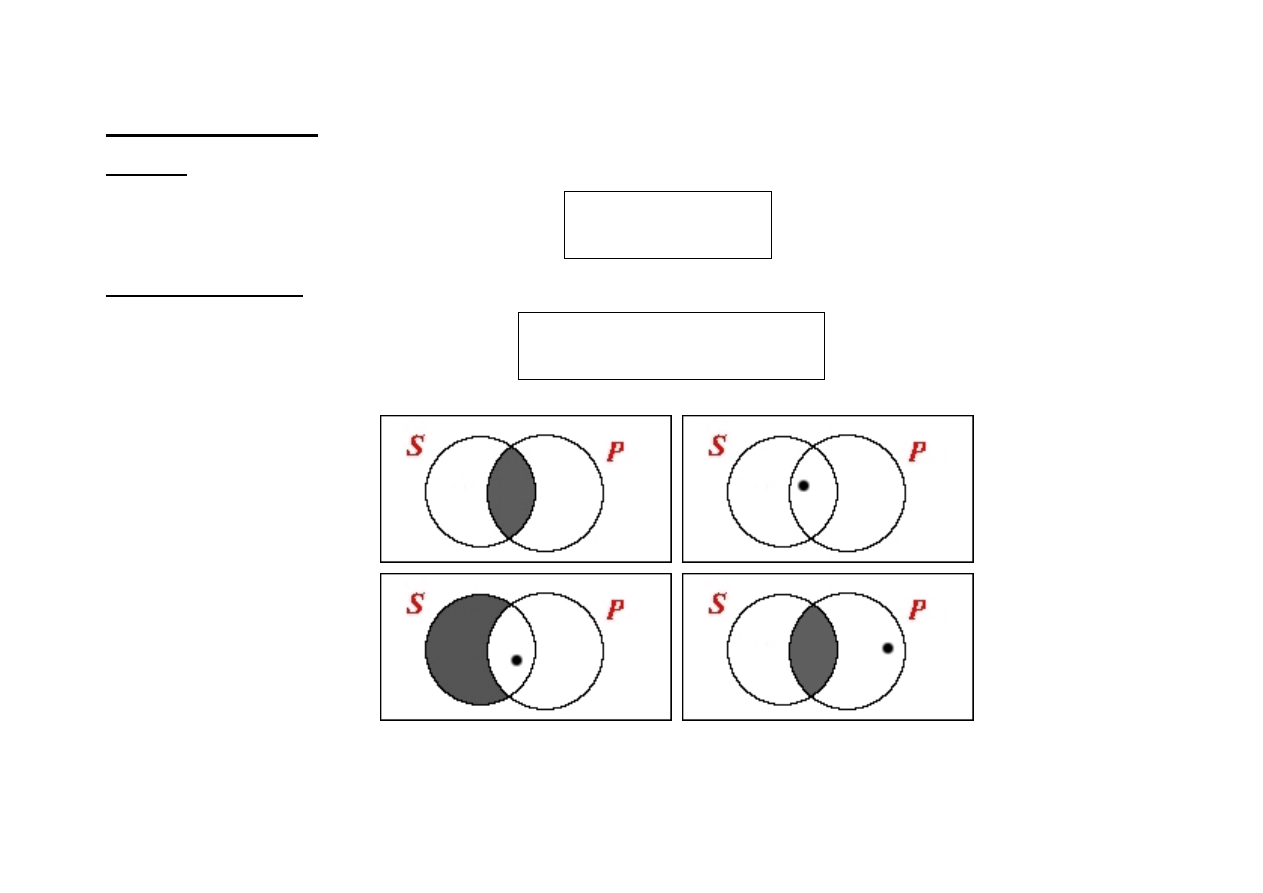
(SaP

∧

Ex(S))

→

SiP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli każdy krasnal ma czapkę i jakiś

krasnal istnieje (krasnale istnieją), to pewien krasnal ma czapkę.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

(SeP

∧

Ex(S))

→

SoP

Przykład potwierdzaj

ą

cy (weryfikuj

ą

cy)

(nie ma mocy dowodu)

: jeśli żaden krasnal nie ma narzeczonej

i jakiś krasnal istnieje (krasnale istnieją), to pewien krasnal nie ma narzeczonej.

[nazwa „krasnal” jest tu zastosowana celowo - dlaczego?]

Piotr Łukowski, Wykład dla studentów prawa

12

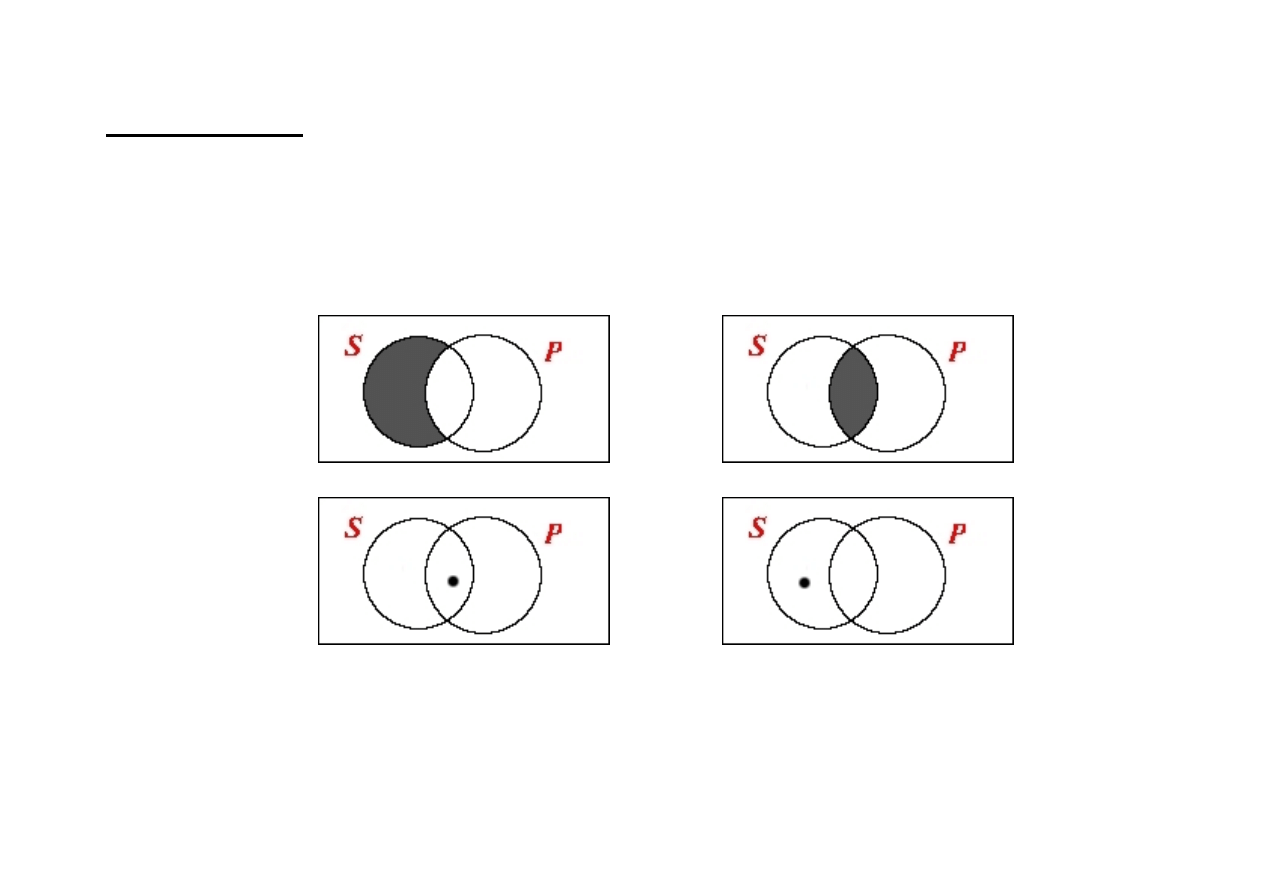
Prawa konwersji

(konwersja to przestawienie podmiotu i orzecznika)

prostej

SeP

↔

PeS

1

SiP

↔

PiS

z ograniczeniem

(SaP

∧

Ex(S))

→

PiS

2

(SeP

∧

Ex(P))

→

PoS

1

2

Piotr Łukowski, Wykład dla studentów prawa

13

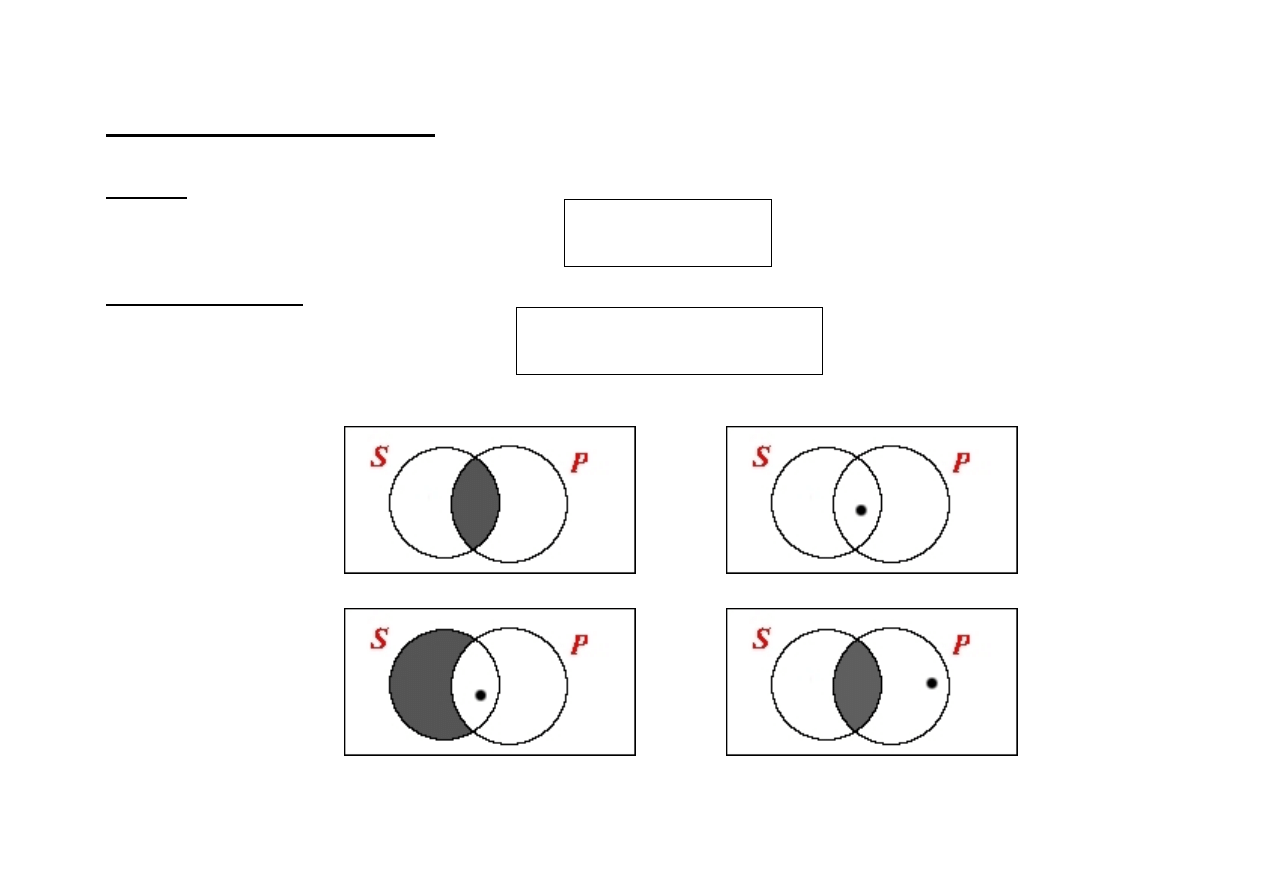
Prawa obwersji

(obwersja to zanegowanie orzecznika i zmiana jako

ś

ci zdania)

(1) SaP

↔

Se-P (2) SeP

↔

Sa-P (3) SiP

↔

So-P (4) SoP

↔

Si-P

(1)

(2)

(3)

(4)

Piotr Łukowski, Wykład dla studentów prawa

14

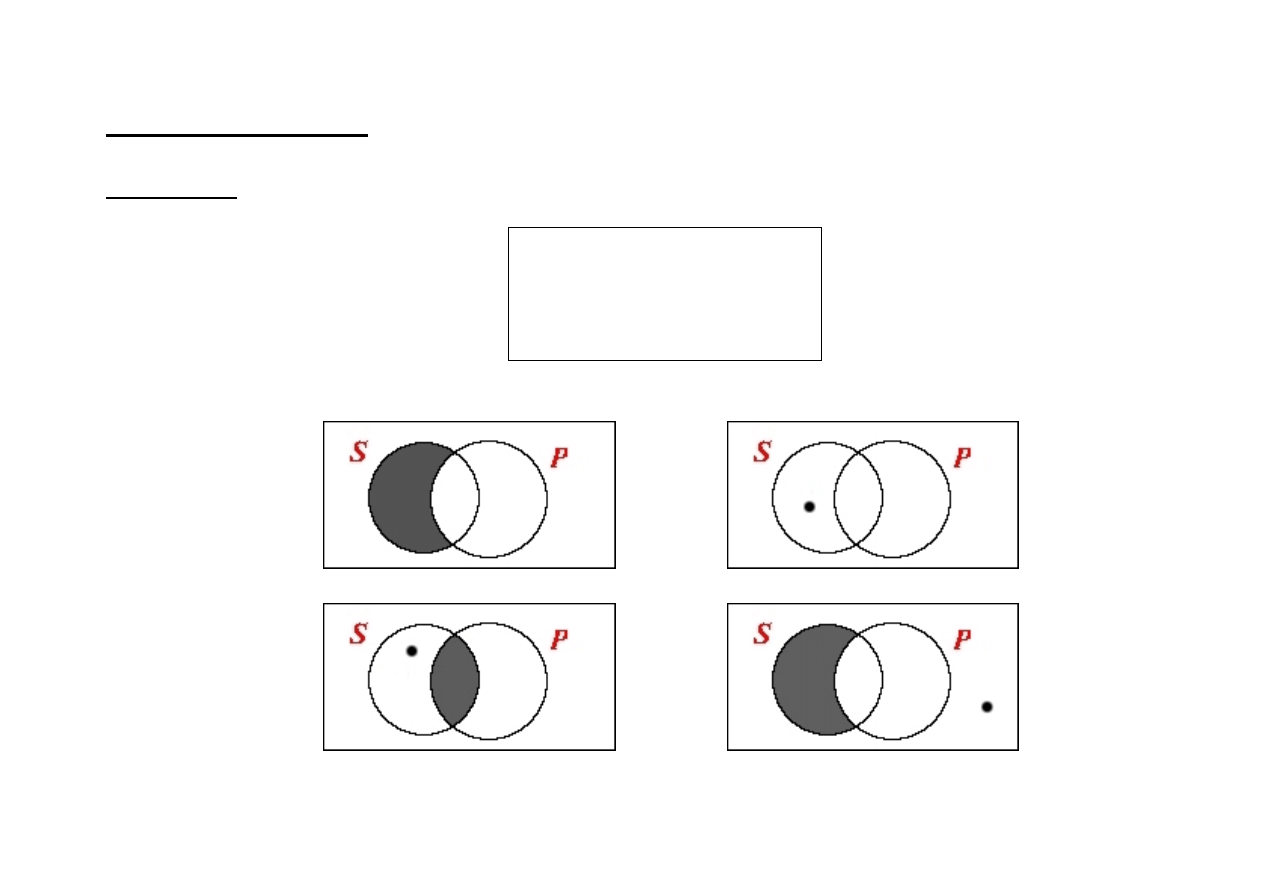
Prawa obwersji konwersji

(obwersja zastosowana do prawej strony prawa konwersji)

prostej

SeP

↔

Pa-S

1

SiP

↔

Po-S

z ograniczeniem

(SaP

∧

Ex(S))

→

Po-S

2

(SeP

∧

Ex(P))

→

Pi-S

1

2

Piotr Łukowski, Wykład dla studentów prawa

15

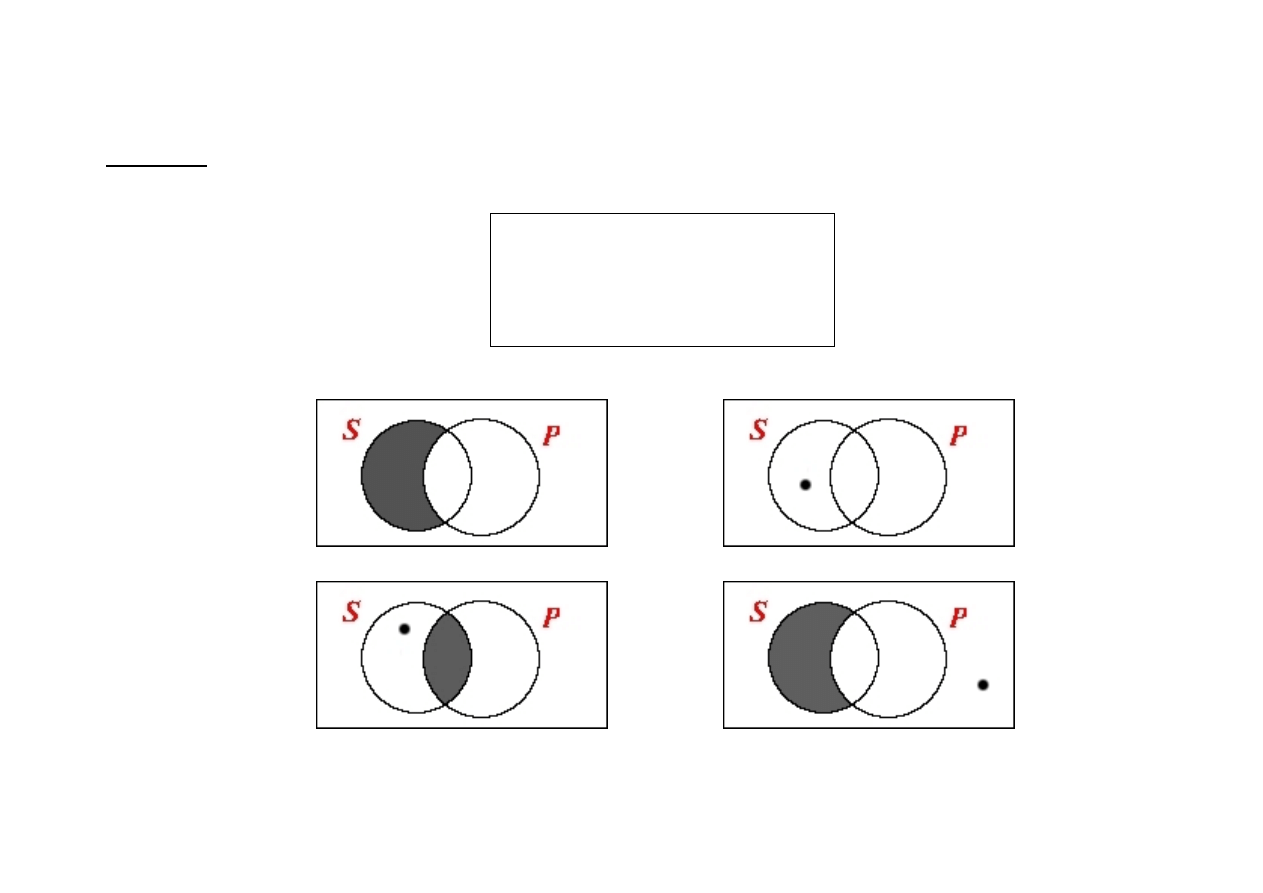
Prawa kontrapozycji

cz

ęś

ciowej

(kontrapozycja cz

ęś

ciowa = konwersja + zmiana jako

ś

ci + negacja orzecznika)

1

SaP

↔

-PeS

2

SoP

↔

-PiS

3

(SeP

∧

Ex(S))

→

-PiS

4

(SaP

∧

Ex(-P))

→

-SoP

1

2

3

4

Piotr Łukowski, Wykład dla studentów prawa

16

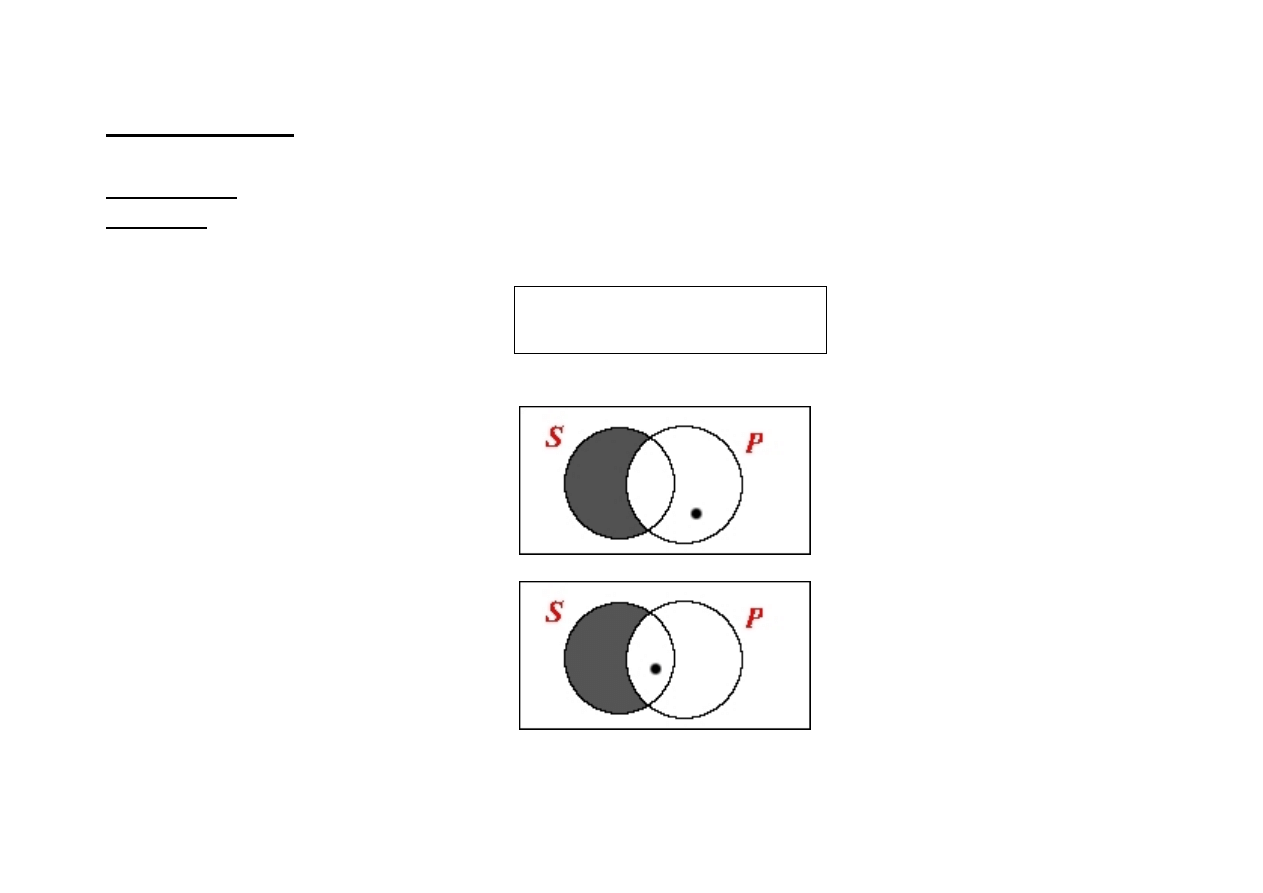
zupełnej

(kontrapozycja zupełna = konwersja+ negacja orzecznika + negacja podmiotu)

1

SaP

↔

-Pa-S

2

SoP

↔

-Po-S

3

(SeP

∧

Ex(S))

→

-Po-S

4

(SaP

∧

Ex(-P))

→

-Si-P

1

2

3

4

Piotr Łukowski, Wykład dla studentów prawa

17

Prawa inwersji

cz

ęś

ciowej

(inwersja cz

ęś

ciowa = negacja podmiotu + zmiana jako

ś

ci + zmiana ilo

ś

ci)

zupełnej (negacja podmiotu + negacja orzecznika + zmiana ilo

ś

ci)

1

(SeP

∧

Ex(P))

→

-SiP

2

(SeP

∧

Ex(P))

→

-So-P

1

2

Piotr Łukowski, Wykład dla studentów prawa

18

Tryby sylogistyczne

Forma zdania kategorycznego, to funkcja zdaniowa zbudowana z jednej ze stałych „a”, „e”, „i”,
„o” i ze zmiennych nazwowych.

Trybem sylogistycznym nazywamy schemat wnioskowania spełniający dwa warunki:

1. Wstępują w nim dwie przesłanki będące formami zdania kategorycznego i ewentualnie

przesłanka o niepustości jakiegoś terminu. Wiosek jest też formą zdania kategorycznego.

2. Wstępują w nim trzy terminy, przy czym podmiot wniosku występuje w jednej

przesłance, a orzecznik wniosku występuje w drugiej przesłance. Termin występujący w obu
przesłankach nie występuje we wniosku - jest on nazywany terminem średnim.

Mamy więc cztery możliwe figury trybów sylogistycznych:

I

II

III

IV

M P

P M

M P

P M

S M

S M

M S

M S

S P

S P

S P

S P

Piotr Łukowski, Wykład dla studentów prawa

19

Poprawne tryby sylogistyczne

MaP

MeP

MaP

SaM

MeP

SaM

MaP

MeP

SaM

Ex(S)

SaM

Ex(S)

SiM

SiM

figura

I

SaP

SiP

SeP

SoP

SiP

SoP

PeM

PaM

PeM

SaM

PaM

SeM

PeM

PaM

SaM

Ex(S)

SeM

Ex(S)

SiM

SoM

figura

II

SeP

SoP

SeP

SoP

SoP

SoP

MaP

MeP

MaS

MiP

MaP

MaS

MoP

MeP

Ex(M)

MaS

MiS

Ex(M)

MaS

MiS

figura

III

SiP

SiP

SiP

SoP

SoP

SoP

PaM

PaM

PeM

MaS

PaM

MeS

PiM

MaS

PeM

Ex(P)

MeS

Ex(S)

MaS

Ex(M)

MiS

figura

IV

SiP

SeP

SoP

SiP

SoP

SoP

Piotr Łukowski, Wykład dla studentów prawa

20

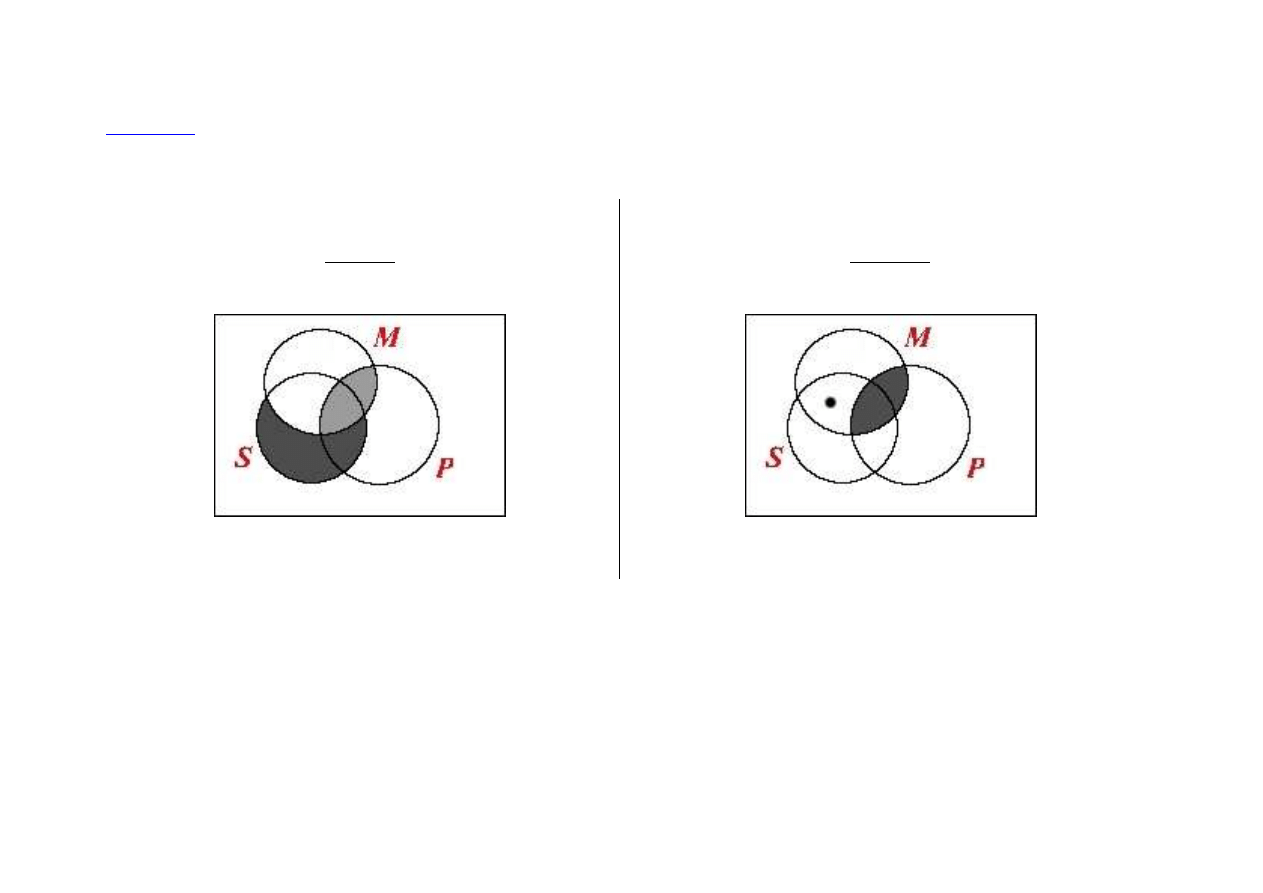
Zadanie. Sprawdź niezawodność następujących trybów sylogistycznych:

MeP

SaM

SeP

PeM

SiM
SoP

niezawodny

niezawodny

Piotr Łukowski, Wykład dla studentów prawa

21

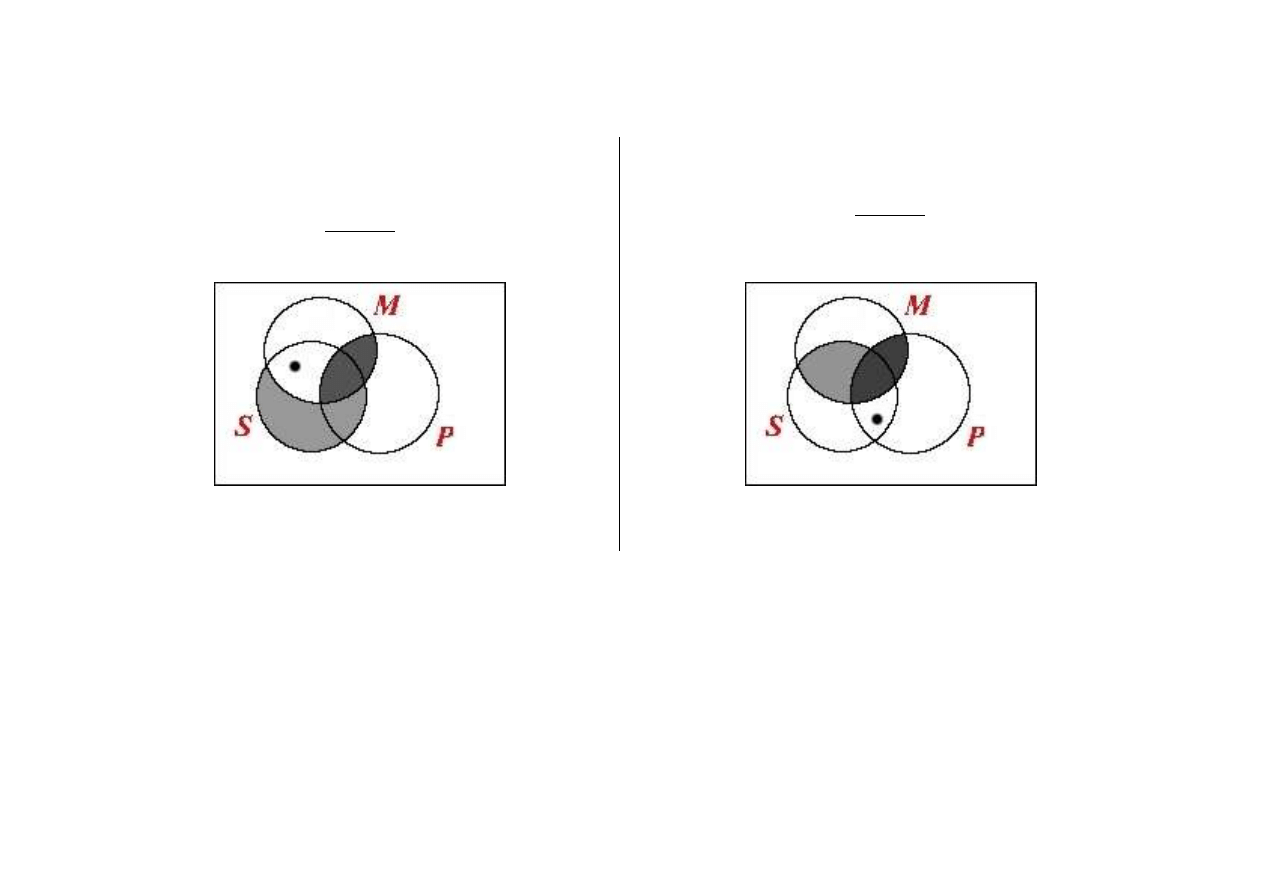
PeM

SaM

Ex(S)

SoP

PeM

MeS

SeP

niezawodny

zawodny

Piotr Łukowski, Wykład dla studentów prawa

22

Dotyczy wszelkich rozumowań, nie tylko trybów sylogistycznych:

Rozumowanie jest poprawne, gdy nie jest w nim popełniony, ani błąd formalny (jest
poprawne logicznie), ani materialny (jest poprawne treściowo).

Błędem materialnym jest wykorzystanie w rozumowaniu przesłanki fałszywej, czyli
wzięcie jakiejś przesłanki fałszywej za prawdziwą.

Błędem formalnym jest zastosowanie zawodnego (niededukcyjnego) schematu
wnioskowania. Wówczas, wniosek nie wynika logicznie z przesłanek, ani na mocy
klasycznego rachunku zdań, ani na mocy klasycznego rachunku kwantyfikatorów, ani
na mocy klasycznego rachunku nazw.

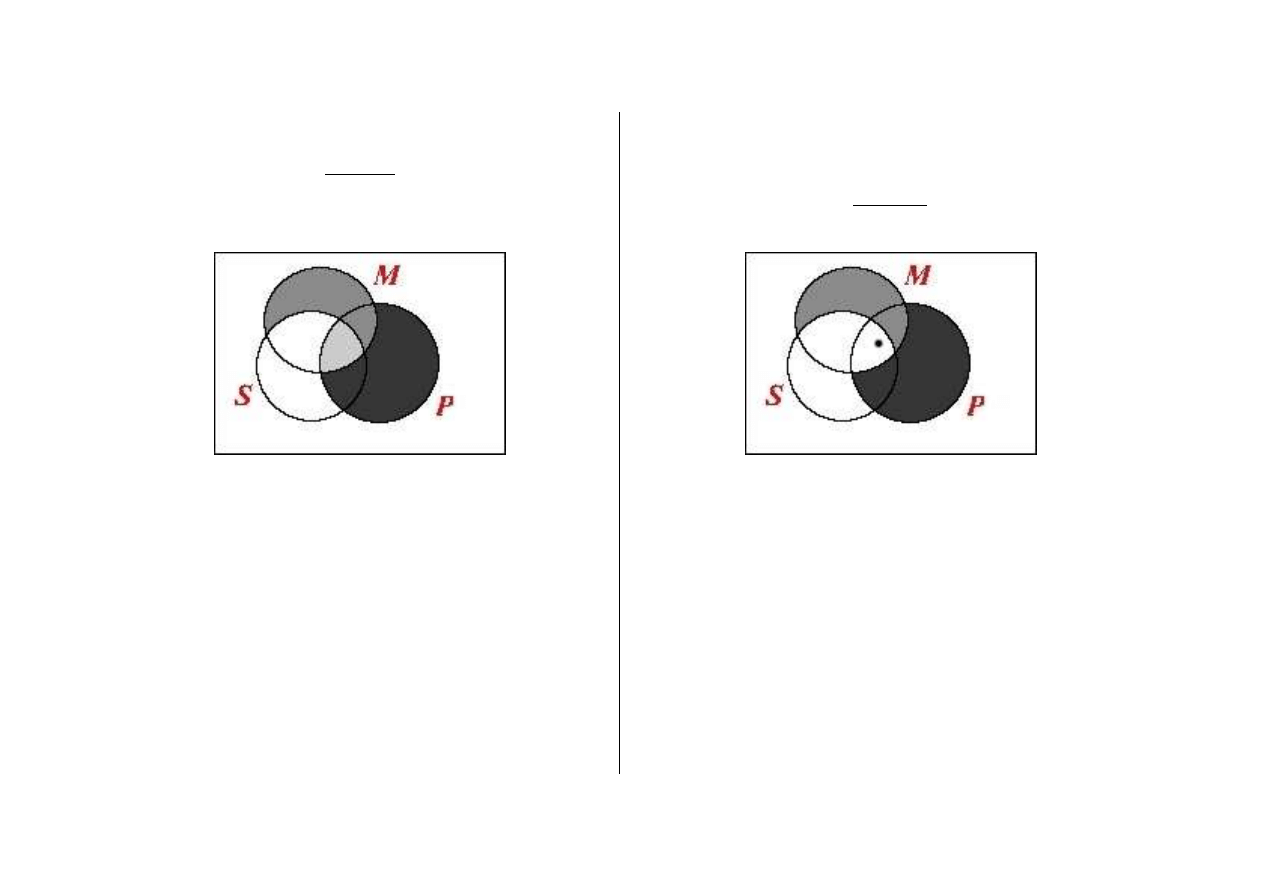
Piotr Łukowski, Wykład dla studentów prawa

23

PaM

MaS

SiP

PaM

MaS

Ex(P)

SiP

zawodny

Brak zało

ż

enia niepusto

ś

ci P - np. je

ś

li ka

ż

dy pegaz

(P) ma skrzydła umo

ż

liwiaj

ą

ce latanie (M), i ka

ż

da

istota maj

ą

ca skrzydła umo

ż

liwiaj

ą

ce latanie (M) mo

ż

e

lata

ć

(S), to i tak nie wynika z tego,

ż

e pewna istota

lataj

ą

ca jest pegazem.

Rozumowanie niepoprawne cho

ć

zastosowane do

prawdziwych przesłanek, bo niededukcyjne (z powodu
popełnienia bł

ę

du formalnego).

niezawodny

Istnienie

zało

ż

enia

niepusto

ś

ci

P

gwarantuje

niezawodno

ść

trybu - nawet rozumowanie dotycz

ą

ce

pegazów jest wnioskowaniem logicznym: je

ś

li ka

ż

dy

pegaz (P) ma skrzydła umo

ż

liwiaj

ą

ce latanie (M), i ka

ż

da

istota maj

ą

ca skrzydła umo

ż

liwiaj

ą

ce latanie (M) mo

ż

e

lata

ć

(S) i pegaz istnieje, to pewna istota lataj

ą

ca jest

pegazem.

Rozumowanie dedukcyjne cho

ć

niepoprawne, z powodu

popełnienia bł

ę

du materialnego, czyli wykorzystania

przesłanki fałszywej.

Piotr Łukowski, Wykład dla studentów prawa

24

Relacje

Definicja pary uporządkowanej

<a,b> = {{a},{a,b}}.

Wprost z definicji pary uporządkowanej wynika, że

•

<a,b>

≠

<b,a > (bo przecież {{a},{a,b}}

≠

{{b},{a,b}}).

•

<a,b> = <c,d > wtw a = c i b = d.

Definicja trójki uporządkowanej

<a,b,c> = <<a,b>,c>.

Definicja n-tki uporządkowanej

<a

1

,...,a

n

> = <<a

1

,...,a

n-1

>,a

n

>.

Z definicji n-tki uporządkowanej wynika, że

•

<a,b,c> = <<a,b>,c> = <{{a},{a,b}},c> = {{{{a},{a,b}}},{{{a},{a,b}},c}}.

•

<a

1

,...,a

n

> = <b

1

,...,b

n

> wtw a

1

= b

1

, ..., a

n

= b

n

.

Piotr Łukowski, Wykład dla studentów prawa

25

Zdanie stwierdzające zachodzenie relacji R między obiektami a i b ma postać (różne notacje):

aRb

(a pozostaje z b w relacji R) (a jest w relacji R z b)

R(a,b)

<a,b>

∈

∈

∈

∈

R

(para uporządkowana <a,b> należy do (jest w) relacji R)

Notacja druga i trzecia umożliwiają wyrażenie relacji więcej niż dwuczłonowej:

R(a,b,c), R(a

1

,...,a

n

)

<a,b,c>

∈

∈

∈

∈

R, <a

1

,...,a

n

>

∈

∈

∈

∈

R

Piotr Łukowski, Wykład dla studentów prawa

26

Definicja nieformalna relacji
Relacją nazywamy związek zachodzący pomiędzy przedmiotami określonego typu.

[dość kiepska definicja, bo jak na jej podstawie mówić np. o sumie relacji?]

Definicja relacji
Relacją nazywamy podzbiór iloczynu kartezjańskiego zbiorów. Relacja jest n-argumentowa jeśli
jest podzbiorem iloczynu kartezjańskiego n zbiorów.

[dobra definicja]

Zatem
Relacja dwuczłonowa, to zbiór par uporządkowanych,
relacja trójczłonowa, to zbiór trójek uporządkowanych,
relacja czteroczłonowa, to zbiór czwórek uporządkowanych,
itd.
relacja n-członowa, to zbiór n-tek uporządkowanych.

Piotr Łukowski, Wykład dla studentów prawa

27

Przykład 1:
Jeśli L jest zbiorem [wszystkich] ludzi, to iloczyn kartezjański L

x

L jest zbiorem [wszystkich

możliwych] par uporządkowanych ludzi.

Wśród tych par są np. takie, że na pierwszym miejscu znajduje się człowiek posiadający
dziecko, a na drugim to właśnie dziecko. Wszystkie te i tylko te pary tworzą relację „bycia
rodzicem”:

aR

1

b wtw a jest rodzicem b.

relacja bycia rodzicem = {<a,b>

∈

L

x

L: <a,b>

∈

R

1

}

gdzie

R

1

⊆

L

x

L.

Dlatego poprawna definicja relacji mówi „tylko” o tym, że relacja jest [jakimś] podzbiorem
iloczynu kartezjańskiego pewnych zbiorów. To zaś jaką jest relacją zależy od tego jakim jest
podzbiorem. Ma tu miejsce definicyjne utożsamienie bycia konkretnym podzbiorem iloczynu
kartezjańskiego z treściowo rozumianym byciem jakąś konkretną relacją.

Piotr Łukowski, Wykład dla studentów prawa

28

Przykład 2:

•

Relacją dwuczłonową R

1

jest „x jest rodzicem y-ka”. Zatem, jeśli a jest rodzicem b, to aR

1

b.

•

Relacją trójczłonową R

2

jest „x jest rodzicem y-ka w chwili z”. Zatem, jeśli a jest rodzicem b w

przedziale czasu do którego należy chwila t, to R

2

(a,b,t).

•

Przykładową relację pięcioczłonową R

3

tworzą wszystkie takie piątki uporządkowane

<a,b,c,d,e>, w których
a jest dla c i d w przedziale czasu, do którego należy chwila e rodzicem płci żeńskiej,
b jest dla c i d w przedziale czasu, do którego należy chwila e rodzicem płci męskiej
(czyli, c i d są dziećmi a i b w przedziale czasu, do którego należy chwila e).

Piotr Łukowski, Wykład dla studentów prawa

29

Dla relacji dwuczłonowych jest sens mówić o dziedzinie i przeciwdziedzinie relacji.

Dziedzina relacji R:

D

R

= {x: <x,y>

∈

R}

czyli

x

∈

D

R

wtw

∃

y xRy.

Przeciwdziedzina relacji R:

D

R

−−−−

= {y: <x,y>

∈

R}.

czyli

y

∈

D

R

wtw

∃

x xRy.

Pole relacji R:

P

R

= D

R

∪

D

R

−

.

Piotr Łukowski, Wykład dla studentów prawa

30

Przykład 3:

Dziedziną relacji R

1

jest zbiór wszystkich ludzi, którzy są rodzicem dla przynajmniej jednego

dziecka.
Przeciwdziedziną relacji R

1

jest zbiór wszystkich ludzi, dla których ktoś jest rodzicem.

Pytania do przykładu 3:

•

W jakiej chwili ktoś jest, a w jakiej ktoś nie jest rodzicem?

•

W jakiej chwili ktoś ma rodzica?

•

Czy przeciwdziedzina relacji R

1

jest równa zbiorowi wszystkich ludzi? Których ludzi?

Czy tylko tych, żyjących?

•

Czy pole relacji R

1

jest równe przeciwdziedzinie tej relacji?

•

W jakim sensie ktoś jest rodzicem? W sensie biologicznym, czy w świetle prawa?

Odpowiedzi na te pytania zależą, od tego jak zdefiniowana jest relacja R

1

, czyli od tego, które

konkretnie pary uporządkowane ją tworzą, a więc i od tego jak określony jest L - zbiór
wszystkich ludzi.

Niestety, zazwyczaj poprzestajemy na niedookreśleniach.

Piotr Łukowski, Wykład dla studentów prawa

31

Rodzaje relacji:

Niech R

⊆

Z

x

Z.

Relacją pustą jest:

R =

∅

(żadna para uporządkowana nie jest w relacji R)

Relacją pełną w Z jest:

R =

Z

x

Z

(każda para uporządkowana jest w relacji R)

Konwersem relacji R (relacją odwrotną do R) jest:

R

-1

= {<x,y>: <y,x>

∈

R}

Ograniczeniem relacji R w dziedzinie do zbioru A jest:

R

D|A

= {<x,y>: x

∈

A

∧

<x,y>

∈

R}

Ograniczeniem relacji R w przeciwdziedzinie do zbioru A jest: R

D-|A

= {<x,y>: y

∈

A

∧

<x,y>

∈

R}

Ograniczeniem relacji R w polu do zbioru A jest:

R

P|A

= {<x,y>: x

∈

A

∧

y

∈

A

∧

<x,y>

∈

R}

Iloczynem relacji R i S jest:

R

∩

S = {<x,y>: <x,y>

∈

R

∧

<x,y>

∈

S}

Sumą relacji R i S jest:

R

∪

S = {<x,y>: <x,y>

∈

R

∨

<x,y>

∈

S}

Iloczynem względnym relacji R i S jest:

R

•

S = {<x,z>:

∃

y (<x,y>

∈

R

∧

<y,z>

∈

S)}

R jest relacją lewostronnie jednoznaczną (R

L!

) jeśli:

∀

x,y,z ((<x,z>

∈

R

∧

<y,z>

∈

R)

→

x = y)

R jest relacją prawostronnie jednoznaczną (R

P!

) jeśli:

∀

x,y,z ((<x,y>

∈

R

∧

<x,z>

∈

R)

→

y = z)

R jest relacją jednoznaczną (R

!

) jeśli R jest lewostronnie jednoznaczną i R jest prawostronnie jednoznaczną.

Piotr Łukowski, Wykład dla studentów prawa

32

Przykład 4:

♠

Pustą relacją jest „x jest ojcem x”.

♠

Pełną relacją jest „x jest przodkiem y lub x nie jest przodkiem y”.

♠

Konwersem relacji „x jest mężem y” jest relacja „y jest żoną x” (także „x jest żoną y” ☺ ).

♠

Ograniczeniem relacji „x jest rodzicem y” w dziedzinie do zbioru kobiet jest „x jest matką y”.

♠

Ograniczeniem relacji „x jest rodzicem y” w przeciwdziedzinie do zbioru osób płci żeńskiej

jest relacja „x jest rodzicem y”, gdzie y jest córką x-a (nie „x jest córką y”, bo to byłby konwers
tej relacji).

♠

Relację „x jest rodzicem y” można ograniczyć w polu do zbioru osób zameldowanych w

mieście Łodzi.

♠

Iloczynem relacji „x jest ojcem y” i „x jest młodszy od y” jest relacja pusta.

♠

Sumą relacji „x jest ojcem y” i „x jest matką y” jest relacja „x jest rodzicem y”.

♠

Iloczynem względnym relacji „x jest matką y” i „y jest żoną z” jest relacja ... „x jest „kochaną

mamusią” z”.

♠

Relacja „x jest matką y” jest lewostronnie jednoznaczna.

♠

Relacja „x jest wicewojewodą y” jest prawostronnie jednoznaczna.

♠

Relacja „x jest wojewodą y” jest jednoznaczna.

Piotr Łukowski, Wykład dla studentów prawa

33

Rodzaje relacji (c.d.):

Niech R

⊆

Z

x

Z.

R jest zwrotna w Z

wtw

∀

x

∈

Z xRx

R jest przeciwzwrotna w Z

wtw

∀

x

∈

Z

¬

(xRx)

R jest symetryczna w Z

wtw

∀

x,y

∈

Z (xRy

→

yRx)

R jest przeciwsymetryczna w Z

wtw

∀

x,y

∈

Z (xRy

→

¬

(yRx))

R jest na wpół (słabo) przeciwsymetryczna w Z

wtw

∀

x,y

∈

Z ((xRy

∧

yRx)

→

x = y)

*

R jest przechodnia (tranzytywna) w Z

wtw

∀

x,y,z

∈

Z ((xRy

∧

yRz)

→

xRz)

R jest przeciwprzechodnia (przeciwtranzytywna) w Z

wtw

∀

x,y,z

∈

Z ((xRy

∧

yRz)

→

¬

(xRz))

R jest spójna w Z

wtw

∀

x,y

∈

Z (xRy

∨

yRx

∨

x = y)

* tradycyjną nazwą tej relacji jest „słabo antysymetryczna”

R jest relacją równoważności na Z wtw R jest zwrotna, symetryczna i przechodnia

R jest relacją porządkującą zbiór Z wtw R jest przeciwsymetryczna, przechodnia i spójna w Z.

R jest relacją częściowo porządkującą zbiór Z wtw R jest zwrotna, słabo przeciwsymetryczna i przechodnia w Z.

R jest relacją liniowo porządkującą zbiór Z wtw R jest częściowo porządkująca zbiór Z oraz jest spójna w Z.

Piotr Łukowski, Wykład dla studentów prawa

34

Przykład 5:

♠

Relacją zwrotną na zbiorze ludzi jest „x jest tego samego wzrostu co y”.

♠

Relacją symetryczną na zbiorze ludzi jest „x jest małżonkiem y”.

♠

Relacją przeciwsymetryczną na zbiorze ludzi jest „x jest żoną y”.

♠

Relacją słabo przeciwsymetryczną na zbiorze mizantropów-egoistów jest „x kocha y”. ☺

♠

Relacją słabo przeciwsymetryczną na zbiorze liczb jest „x

≤

y”.

♠

Relacją przechodnią na zbiorze ludzi jest „x jest przodkiem y”.

♠

Relacją przeciwprzechodnią na zbiorze ludzi jest „x jest synem y”.

♠

Relacją spójną na zbiorze liczb naturalnych jest „rok urodzenia x jest wcześniejszy niż rok

urodzenia y”.

Piotr Łukowski, Wykład dla studentów prawa

35

Uwaga oczywista 1:

Relacja, która nie jest symetryczna nie musi być przeciwsymetryczna, np. „x szanuje y”.
Relacja, która nie jest, ani symetryczna, ani przeciwsymetryczna nie musi być słabo przeciwsymetryczna.

Bywają relacje, które nie są ani symetryczne, ani przeciwsymetryczne, ani słabo przeciwsymetryczne.
Przykładem takiej relacji jest „x kocha y” określona na zbiorze ludzi.

Uwaga oczywista 2:

Relacja, która nie jest przechodnia nie musi być przeciwprzechodnia.

Bywają relacje, które nie są ani przechodnie, ani przeciwprzechodnie. Przykładem takiej relacji jest „x jest
krewnym y” określona na zbiorze ludzi.

Gor

ą

ca pro

ś

ba

:

Nie twórzmy relacji nonsymetrycznych, jako takich, które miałyby nie być, ani symetrycznymi, ani
przeciwsymetrycznymi, czy też relacji nontranzytywnych, które miałyby nie być, ani tranzytywnymi, ani
przeciwtranzytywnymi.

Tak jak nie tworzymy „równoległoboków samych” (choć takie pomysły istnieją tu i

ówdzie), które miałyby być tymi, które nie są, ani rombami, ani prostokątami. ☺

Skoro o człowieku nie

powie się, ani że jest parzysty, ani że jest nieparzysty, to nie znaczy, że trzeba mówić, że jest nonparzysty -
po prostu tych określeń nie używa się mówiąc o ludziach. ☺

Piotr Łukowski, Wykład dla studentów prawa

36

Przykład 6: Relacją równoważności na zbiorze uczniów szkół podstawowych jest „x jest
uczniem tej samej klasy szkoły podstawowej co y”.

Relacja równoważności na zbiorze Z jest podstawą podziału logicznego zbioru Z, na którym jest
określona. Człony tego podziału nazywają się klasami abstrakcji.

Klasę abstrakcji danej relacji równoważności R tworzą wszystkie te obiekty, które są ze sobą w
relacji R:

[a]

R

= {b

∈

Z: aRb}.

a jest reprezentantem swojej klasy abstrakcji. Dowolny element z danej klasy abstrakcji może
być jej reprezentantem.

Wracając do przykładu: relacja równoważności przynależności do tej samej klasy szkoły podstawowej
określona na zbiorze uczniów wszystkich szkół podstawowych jest relacją, która dzieli zbiór uczniów
wszystkich szkół podstawowych na klasy abstrakcji będące klasami tych szkół. Każdy uczeń danej klasy jest
reprezentantem klasy abstrakcji tożsamej z tą klasą. Naturalnie, wspomniana relacja może być określona na
zbiorze wszystkich uczniów jednej konkretnej szkoły podstawowej. Wówczas, dzieli ona na klasy abstrakcji
uczniów jedynie tej szkoły.

Inną relacją równoważności jest:
- relacja „x pozostaje na tym samym gospodarstwie domowym co y” określona na zbiorze obywateli RP.
- relacja „x jest rówieśnikiem y” określona na zbiorze ludzi.
- relacja „x jest sztućcem z tego samego kompletu co y” określona na zbiorze sztućców.

Piotr Łukowski, Wykład dla studentów prawa

37

♠

Relacją porządkującą (porządkującą liniowo) zbiór jest „x jest długiem hipotecznym

wpisanym do księgi wieczystej [nie] wcześniej niż dług y”. Istotnie, jest to relacja
przeciwsymetryczna, przechodnia i spójna w zbiorze długów hipotecznych danej księgi
wieczystej.

♠

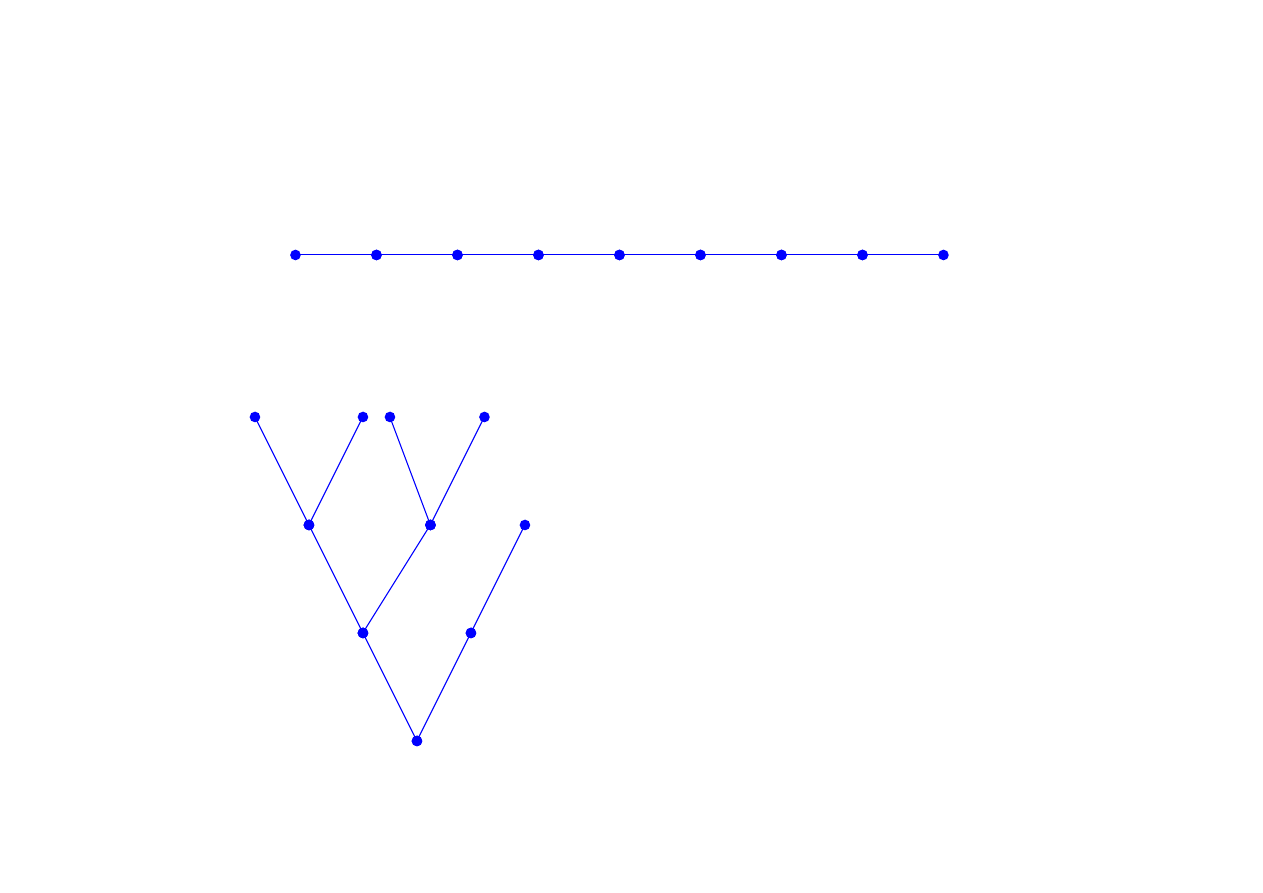
Drzewo genealogiczne reprezentuje relację porządkującą nieliniowo:

porz

ą

dek liniowy

Relacja „x

≤

y” jest zwrotna, słabo

przeciwsymetryczna i przechodnia w
zbiorze punktów diagramu. Porządkuje
więc ten zbiór zgodnie z symboliką kresek:
punkt x połączony kreską z punktem y, jest
w relacji „x

≤

y”, jeśli x leży niżej niż y.

porz

ą

dek cz

ęś

ciowy (nie jest porz

ą

dkiem liniowym)