Piotr Łukowski, Wykład dla studentów prawa

1

Logiczne podstawy prawoznawstwa

Piotr Łukowski

Piotr Łukowski, Wykład dla studentów prawa

2

WYKŁAD 7

zdanie

wynikanie

wynikanie logiczne

Piotr Łukowski, Wykład dla studentów prawa

3

Definicja wynikania

Zdanie W wynika logicznie ze zdania Z, jeśli implikacja

Z

→

W

jest zdaniem prawdziwym na mocy związku jaki zachodzi między tym o czym orzeka
zdanie W a tym o czym orzeka zdanie Z.

Z nazywamy racją, a W następstwem.

Z definicji wynikania wnioskujemy, iż istnieją różne rodzaje wynikania W z Z w
zależności od rodzaju związku będącego podstawą prawdziwości implikacji Z

→

W.

Piotr Łukowski, Wykład dla studentów prawa

4

Związek zachodzący między Z i W, będący podstawą prawdziwości może być:

- przyczynowo-skutkowy (ze względu na wiedzę o rzeczywistości)

Jeśli zaleję herbatę zimną wodą, to jej nie zaparzę.

- strukturalny (w sensie czasu lub przestrzeni)

Jeśli wczoraj był poniedziałek, to jutro jest środa. (także analityczny)
Jeśli obraz a wisi nad obrazem b, to obraz b wisi pod obrazem a. (także analityczny)
Jeśli stoję twarzą na północ, to po prawej ręce mam wschód.

- tetyczny (ze względu na obowiązywanie pewnych norm)

Jeśli w sklepie płacę za towar, to część mojej zapłaty jest przeznaczona na podatek.

- analityczny (ze względu na sens słów - węższe rozumienie analityczności)

Jeśli ta figura jest kwadratem, to [ta figura] ma cztery boki równe.

- logiczny (gdy Z

→

W jest prawdą logiczną)

Jeśli Jan jest łysym adwokatem, to Jan jest adwokatem.
(Jeśli Jan jest łysy i Jan jest adwokatem, to Jan jest adwokatem.)

W ka

ż

dym powy

ż

szym przykładzie, pierwsze podkre

ś

lenie oznacza Z (racj

ę

) drugie za

ś

W (nast

ę

pstwo).

Piotr Łukowski, Wykład dla studentów prawa

5

Jeśli implikacja Z

→

W jest oczywista, wówczas wypowiedź prezentująca

rozumowanie „W wynika z Z na mocy Z

→

W” zwykle pomija tę implikację i ma

uproszczoną postać „W wynika z Z” (każdy bowiem wie, że Z

→

W).

Ta ukryta, bo niewypowiedziana na mocy oczywistości przesłanka Z

→

W nazywana

jest przesłanką entymematyczną, zaś wnioskowanie w którym występuje przesłanka
entymematyczna jest nazywane wnioskowaniem entymematycznym.

Przykład:
Zamiast mówić
„Każdy syn jest młodszy od swojego ojca. Jan jest synem Marka, więc Jan jest młodszy od
Marka”
powiemy
„Jan jest synem Marka, więc Jan jest młodszy od Marka”
(„Jan jest młodszy od Marka, bo jest jego synem”).

Uwaga:
Wnioskowania entymematyczne są bardzo powszechne w mowie potocznej. Należy jednak
pamiętać, że niekiedy oczywistość przesłanki entymematycznej Z

→

W jest złudzeniem (np.

„każda część jest mniejsza od całości” - „jeśli a jest częścią b, to a jest mniejsze od b”), a wtedy
wnioskowanie może być błędne.

Piotr Łukowski, Wykład dla studentów prawa

6

Definicja wynikania logicznego

1. Zdanie W wynika logicznie ze zdania Z, wtedy i tylko wtedy, gdy implikacja

Z

→

W

jest prawdą logiczną. Symbolicznie

Z

|

−

W

.

Z to przesłanka (założenie), zaś W to wniosek.

2. Zdanie W wynika logicznie ze zdań Z

1

,...,Z

n

(ze zbioru zdań {Z

1

,...,Z

n

}) wtedy i tylko

wtedy, gdy implikacja

(Z

1

∧

...

∧

Z

n

)

→

Z

jest prawdą logiczną. Symbolicznie

{Z

1

,...,Z

n

}

|

−

W

.

Z

1

,...,Z

n

to przesłanki (założenia), zaś W to wniosek.

3.

Zbiór zdań {W

1

,...,W

k

} wynika logicznie ze zbioru zdań {Z

1

,...,Z

n

} wtedy i tylko

wtedy, gdy implikacja

(Z

1

∧

...

∧

Z

n

)

→

(W

1

∨

...

∨

W

k

)

jest prawdą logiczną. Symbolicznie

{Z

1

,...,Z

n

}

|

−

{W

1

,...,W

k

}

.

Piotr Łukowski, Wykład dla studentów prawa

7

Wnioskowanie dedukcyjne (dedukcja) to wnioskowanie w którym wniosek wynika
logicznie z przesłanek.

Wnioskowanie niezawodne to takie, które od prawdziwych przesłanek zawsze
prowadzi do prawdziwych wniosków. Dedukcja jest wnioskowaniem niezawodnym.

Piotr Łukowski, Wykład dla studentów prawa

8

Zadanie 1. Czy zdanie „Ulice są mokre” wynika logicznie ze zdania „Deszcz pada”?

p - Deszcz pada
q - Ulice są mokre

Zatem, czy p

→

q jest tautologią?

p

→

q

0

- założenie dowodu nie wprost

1 0

Schemat ten nie jest tautologią, gdyż istnieje podstawienie przy którym staje się on zdaniem
fałszywym:

p/ 1, q/0

(deszcz pada a mimo to ulice nie są mokre,

np. z powodu ich zadaszenia - konstrukcja możliwego świata)

Zatem zdanie q nie wynika ze zdania p (oczywiście!).

Uwaga: W świecie, w którym żadna ulica nie jest zadaszona, zdanie „Ulice są mokre” wynika ze
zdania „Deszcz pada”. Nie jest to jednak wynikanie logiczne, lecz wynikanie przyczynowo-
skutkowe, ustalone na mocy wiedzy o świecie.

Piotr Łukowski, Wykład dla studentów prawa

9

Zadanie 2. Czy zdanie „Ulice są mokre” wynika logicznie ze zdania „Jeśli deszcz pada, to ulice
są mokre”?

p - Deszcz pada
q - Ulice są mokre

Zatem, czy (p

→

q)

→

q jest tautologią?

(p

→

q)

→

q

1

0

- założenie dowodu nie wprost

2

1

0

3

0

- przepisujemy wartość q

4

0

Schemat (p

→

q)

→

q nie jest tautologią, gdyż istnieje podstawienie przy którym staje się on

zdaniem fałszywym: p/0, q/0. Zatem, zdanie q nie wynika logicznie ze zdania p

→

q

(oczywiście!). Zdanie „Ulice są mokre” nie wynika logicznie ze zdania wyrażającego jedynie
zależność tego, że ulice są mokre od tego, że deszcz pada. Sam związek nie wystarcza, bo w
ś

wiecie bez zadaszonych ulic związek ten jest prawdziwy zawsze, a więc i wtedy, gdy deszcz

nie pada.

Piotr Łukowski, Wykład dla studentów prawa

10

Zadanie 3. Czy zdanie „Ulice są mokre” wynika logicznie ze zdań „Deszcz pada” oraz „Jeśli
deszcz pada, to ulice są mokre”?

p - Deszcz pada
q - Ulice są mokre

Zatem, czy (p

∧

(p

→

q))

→

q jest tautologią?

(p

∧

(p

→

q))

→

q

1

0

- założenie dowodu nie wprost

2

1

0

3

1

1

4

1

0

- przepisujemy wartości p i q

5

0

- sprzeczność

Schemat (p

∧

(p

→

q))

→

q jest tautologią, gdyż nie istnieje podstawienie przy którym staje się on zdaniem

fałszywym. Zatem, zdanie q wynika logicznie ze zbioru zdań {p, p

→

q}.

Symbolicznie:

{p, p

→

q} |

−

q.

Jest to reguła odrywania (Modus Ponens).

p, p

→

q

q

(inny zapis)

Piotr Łukowski, Wykład dla studentów prawa

11

Zadanie 4. Czy zdanie „Nieprawda, że deszcz pada” wynika logicznie ze zdań „Nieprawda, że
ulice są mokre” oraz „Jeśli deszcz pada, to ulice są mokre”?

p - Deszcz pada
q - Ulice są mokre

Zatem, czy (

¬

q

∧

(p

→

q))

→

¬

p jest tautologią?

(

¬

q

∧

(p

→

q))

→

¬

p

1

0

- założenie dowodu nie wprost

2

1

0

3

1

1

1

4

0

5

1

0

- przepisujemy wartości p i q

6

0

- sprzeczność

Schemat (

¬

q

∧

(p

→

q))

→

¬

p jest tautologią, gdyż nie istnieje podstawienie przy którym staje się on

zdaniem fałszywym. Zatem, zdanie

¬

p wynika logicznie ze zbioru zdań {

¬

q, p

→

q}. Symbolicznie:

{

¬

q, p

→

q} |

−

¬

p.

Jest to reguła Modus Tollens.

¬

q, p

→

q

¬

p

(inny zapis)

Piotr Łukowski, Wykład dla studentów prawa

12

Zadanie 5. Czy zdanie „Jestem w czytelni” wynika logicznie ze zdań „Jestem w czytelni lub w
katalogach” oraz „Nieprawda, że jestem w katalogach”?

p - Jestem w czytelni
q - Jestem w katalogach

Zatem, czy ((p

∨

q)

∧

¬

q)

→

p jest tautologią?

((p

∨

q)

∧

¬

q)

→

p

1

0

- założenie dowodu nie wprost

2

1

0

3

1

1

4

0

5

0 0

- przepisujemy wartości p i q

6

0

- sprzeczność

Schemat ((p

∨

q)

∧

¬

q)

→

p jest tautologią, gdyż nie istnieje podstawienie przy którym staje się on zdaniem

fałszywym. Zatem, zdanie p wynika logicznie ze zbioru zdań {p

∨

q,

¬

q}. Symbolicznie:

{(p

∨

q),

¬

q} |

−

p.

Jest to reguła odłączania alternatywy.

p

∨

q,

¬

q

p

∨

q,

¬

p

p

(inny zapis)

q

(także)

Piotr Łukowski, Wykład dla studentów prawa

13

Zadanie 6. Czy zdanie „Jan ma tysiąc dolarów lub Jan ma tysiąc złotych” wynika logicznie ze
zdania „Jan ma tysiąc dolarów”?

p - Jan ma tysiąc dolarów
q - Jan ma tysiąc złotych

Zatem, czy p

→

(p

∨

q) jest tautologią?

p

→

(p

∨

q)

1

0

- założenie dowodu nie wprost

2

1

0

3

1

- przepisujemy wartość p

4

1

- sprzeczność

Schemat p

→

(p

∨

q) jest tautologią, gdyż nie istnieje podstawienie przy którym staje się on

zdaniem fałszywym. Zatem, zdanie p wynika logicznie ze zbioru zdań {(p

∨

q),

¬

q}.

Symbolicznie:

{p} |

−

p

∨

q (p |

−

p

∨

q).

Jest to reguła dołączania alternatywy.

p

q

p

∨

q

(inny zapis)

p

∨

q

(także)

Piotr Łukowski, Wykład dla studentów prawa

14

Zadanie 7. Czy zdanie „Jan jest złodziejem i mordercą” wynika logicznie ze zdania „Jan jest
złodziejem”?

p - Jan jest złodziejem
q - Jan jest mordercą

Zatem, czy p

→

(p

∧

q) jest tautologią?

p

→

(p

∧

q)

1

0

- założenie dowodu nie wprost

2

1

0

3

1

- przepisujemy wartość p

4

0

Schemat p

→

(p

∧

q) nie jest tautologią, gdyż istnieje podstawienie przy którym staje się on

zdaniem fałszywym: p/1, q/0 (świat, w którym Jan jest złodziejem i nie jest mordercą). Zatem,
zdanie p

∧

q nie wynika logicznie ze zdania p.

Piotr Łukowski, Wykład dla studentów prawa

15

Zadanie 8. Czy zdanie „Jan jest złodziejem” wynika logicznie ze zdania „Jan jest złodziejem i
mordercą”?

p - Jan jest złodziejem
q - Jan jest mordercą

Zatem, czy (p

∧

q)

→

p jest tautologią?

( p

∧

q)

→

p

1

0

- założenie dowodu nie wprost

2

1

0

3

0

- przepisujemy wartość p

4

0

- sprzeczność

Schemat (p

∧

q)

→

p jest tautologią, gdyż nie istnieje podstawienie przy którym staje się on

zdaniem fałszywym. Zatem, zdanie p wynika logicznie ze zdania p

∧

q:

reguła odłączania koniunkcji:

{p

∧

q} |

−

p (p

∧

q |

−

p).

p

∧

q

p

∧

q

p

(inny zapis)

q

(także)

Piotr Łukowski, Wykład dla studentów prawa

16

Zadanie 9. Czy zdanie „Jan jest złodziejem i mordercą” wynika logicznie ze zdań „Jan jest
złodziejem” i „Jan jest mordercą”?

p - Jan jest złodziejem
q - Jan jest mordercą

Zatem, czy (p

∧

q)

→

p

∧

q jest tautologią? Oczywiście, że TAK.

Zatem, zdanie p

∧

q wynika logicznie ze zbioru zdań {p, q}:

reguła dołączania koniunkcji:

{p, q} |

−

p

∧

q.

p, q

p

∧

q

(inny zapis)

Fakt ten można dowodzić w oparciu o sylogizm hipotetyczny bezkoniunkcyjny:

p

→

(q

→

(p

∧

q)).

Piotr Łukowski, Wykład dla studentów prawa

17

Zadanie 10. Niżej przypomniany dowcip z PRL-u jest dowodem na to, że posługujemy się
logiką (rozumiemy logikę), bez względu na to, czy logikę lubimy, czy nie ☺

Student kupił książkę do logiki i przed księgarnią spotkał kolegę ze szkoły podstawowej, który obecnie jest milicjantem.

M(ilicjant): Co to za książka?

S(tudent): Do logiki.

M: Co to jest logika?

S: To nauka o poprawnym myśleniu.

M: Jakie myślenie jest poprawne?

S: Wyjaśnię ci na przykładzie. Masz akwarium?

M: Tak.

S: Skoro masz akwarium, to lubisz rybki.

M: Tak!

S: Skoro lubisz rybki, to lubisz wypić.

M: Tak!

S: Skoro lubisz wypić, to lubisz dziewczyny.

M: Zgadza się! Fantastyczna jest ta logika! Też kupię tę książkę!

Gdy milicjant wrócił na komendę z książką do logiki, kolega milicjant pyta go

M2: Co to za książka?

M: Do logiki.

M2: Co to jest logika?

M: To nauka o poprawnym myśleniu.

M2: Jakie myślenie jest poprawne?

M: Wyjaśnię ci na przykładzie. Masz akwarium?

M2: Nie.

M: To ty jesteś gejem!

Piotr Łukowski, Wykład dla studentów prawa

18

Analiza logiczna dowcipu:

p - M ma akwarium; q - M lubi rybki; s - M lubi wypić; r - M lubi dziewczyny

A. Czy zdanie r wynika logicznie ze zbioru zdań {p, p

→

q, q

→

s, s

→

r}? TAK, bo:

(p

∧

(p

→

q)

∧

(q

→

s)

∧

(s

→

r))

→

r

1

0

- założenie dowodu nie wprost

2

1

1

1

1

0 - patrz przypis

3

1

0

- przepisujemy wartości p i r

4

1

5

1

- przepisujemy wartość q

6

1

7

1

- przepisujemy wartość s

8

0

- sprzeczność

B. Czy zdanie

¬

r wynika logicznie ze zbioru zdań {

¬

p, p

→

q, q

→

s, s

→

r}? NIE, bo:

(

¬

p

∧

(p

→

q)

∧

(q

→

s)

∧

(s

→

r))

→

¬

r

1

0

- założenie dowodu nie wprost

2

1

1

1

1

0 - patrz przypis

3

0

1

4

0

1

- przepisujemy wartości p i r

5

0

0

0

0

- przypisujemy wartość fałszu zdaniom q i s

Podstawienie obalające: p/0, q/0, s/0, r/1.

Piotr Łukowski, Wykład dla studentów prawa

19

Niezbędny komentarz do powyższej analizy.

Oczywiście, to tylko dowcip, więc nie każde ze zdań p

→

q, q

→

s, s

→

r musi być

uznane za prawdziwe!

Ponadto, ma tu miejsce błąd ekwiwokacji:
zamiast jednego zdania q, powinny być dwa różne zdania q

1

oraz q

2

- w innym

znaczeniu lubi się rybki, hodując je w akwarium, w innym zaś, gdy się je traktuje jako
zakąskę.

Piotr Łukowski, Wykład dla studentów prawa

20

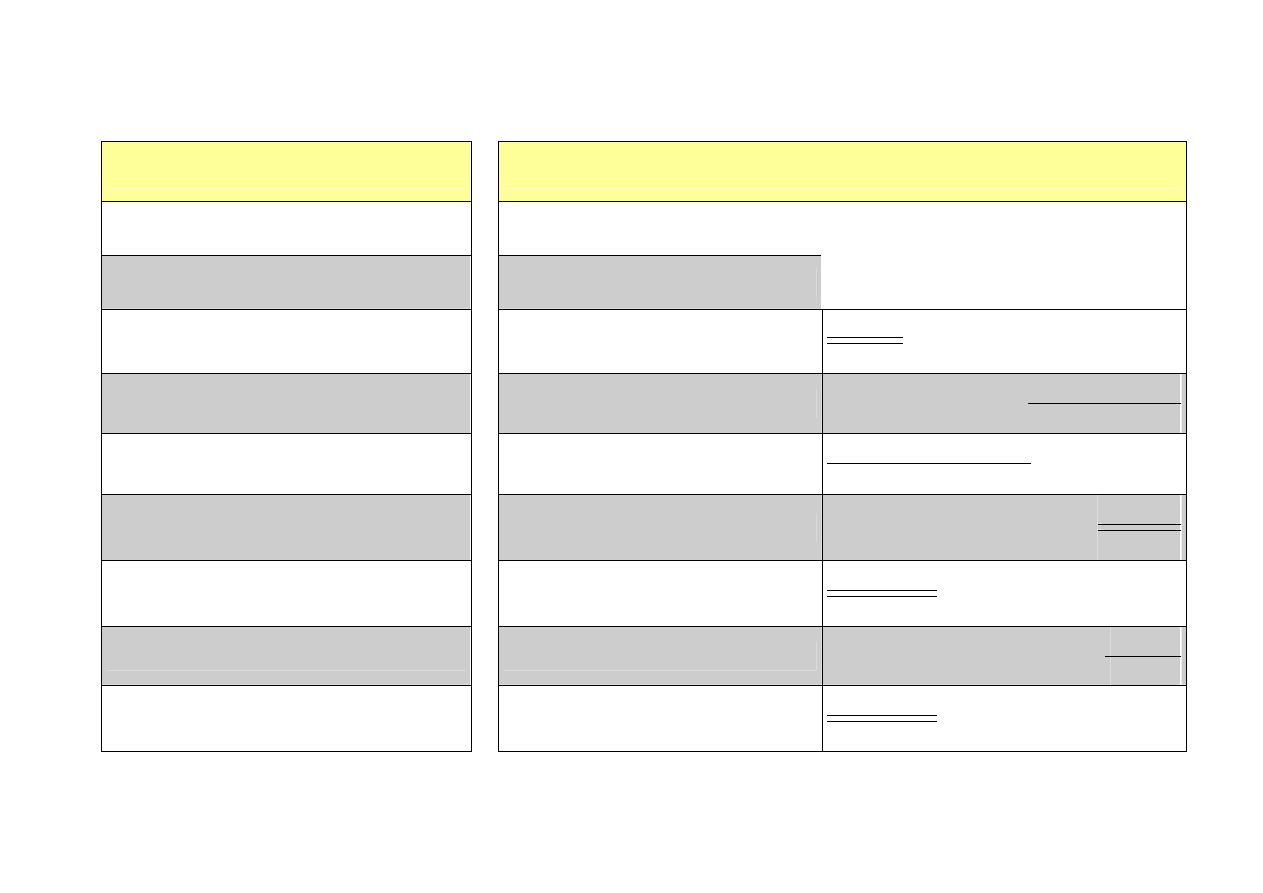
tautologie KRZ

reguły KRZ

p

∨

¬

p

∅

|

−

p

∨

¬

p

¬

(p

∧

¬

p)

∅

|

−

¬

(p

∧

¬

p)

prawdy logiczne zawsze można

dodać do przesłanek*

p

↔

¬¬

p

p |

−

|

¬¬

p

p

¬¬

p

((p

→

q)

∧

(q

→

p))

→

(p

↔

q)

{p

→

q, q

→

p} |

−

p

↔

q

p

→

q, q

→

p

p

↔

q

(p

↔

q)

→

((p

→

q)

∧

(q

→

p))

{p

↔

q} |

−

(p

→

q)

∧

(q

→

p)

p

↔

q

(p

→

q)

∧

(q

→

p)

(p

→

q)

↔

(q

∧

¬

p)

p

→

q |

−

| q

∧

¬

p

p

→

q

q

∧

¬

p

(p

→

q)

↔

(

¬

q

→

¬

p)

p

→

q |

−

|

¬

q

→

¬

p

p

→

q

¬

q

→

¬

p

p

→

(

¬

p

→

q)

{p,

¬

p} |

−

q

p,

¬

p

q

¬

(p

∨

q)

↔

(

¬

p

∧

¬

q)

¬

(p

∨

q) |

−

|

¬

p

∧

¬

q

¬

(p

∨

q)

¬

p

∧

¬

q

Piotr Łukowski, Wykład dla studentów prawa

21

¬

(p

∧

q)

↔

(

¬

p

∨

¬

q)

¬

(p

∧

q) |

−

|

¬

p

∨

¬

q

¬

(p

∧

q)

¬

p

∨

¬

q

¬

(p

→

q)

↔

(p

∧

¬

q)

¬

(p

→

q) |

−

| p

∧

¬

q

¬

(p

→

q)

p

∧

¬

q

((p

→

q)

∧

(q

→

s)

∧

p)

→

s

{p

→

q, q

→

s, p} |

−

s

p

→

q, q

→

s, p

s

((p

→

q)

∧

(q

→

s))

→

(

¬

s

→

¬

p)

{p

→

q, q

→

s,

¬

s} |

−

¬

p

p

→

q, q

→

s,

¬

s

¬

p

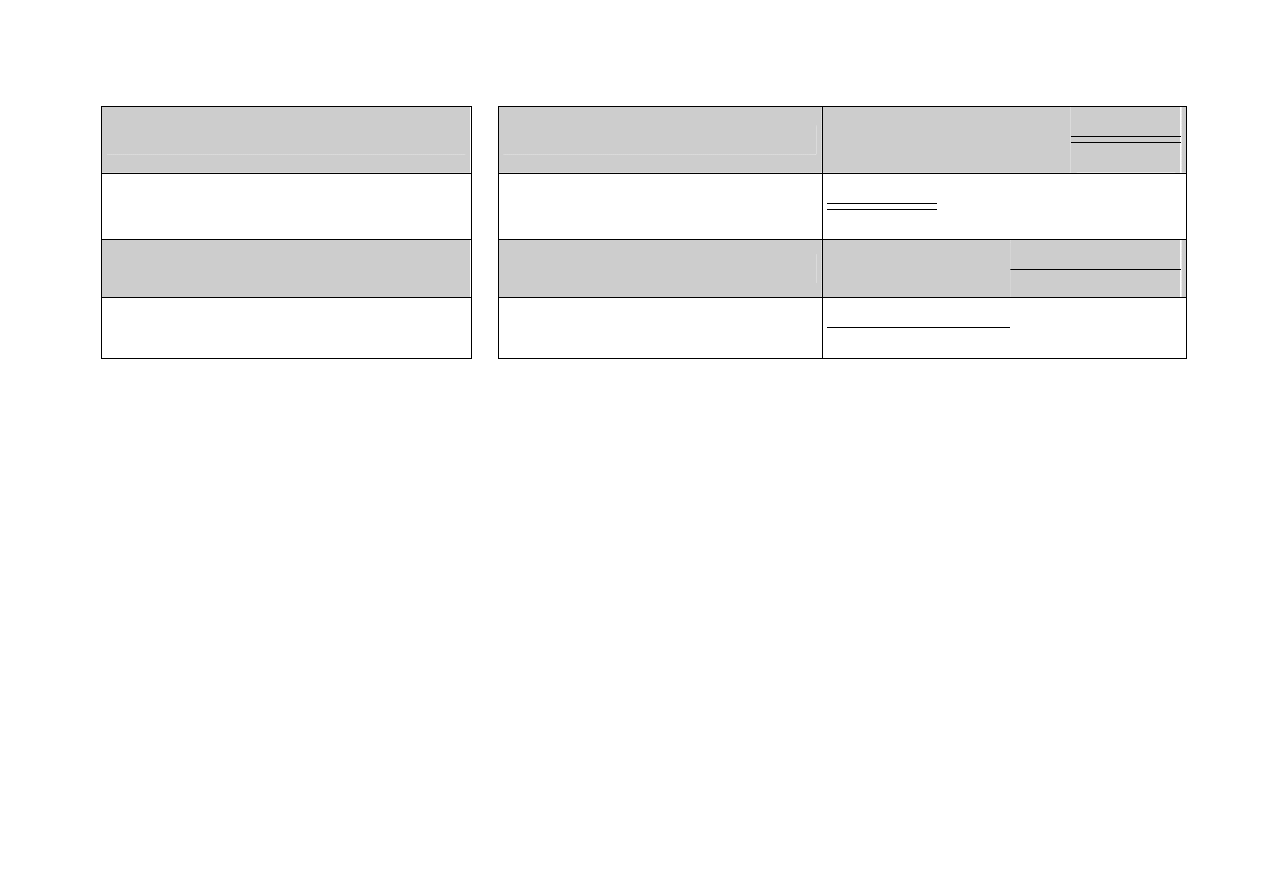
W powyższej tabeli podwójna kreska w ułamku wyrażającym regułę oznacza, że ułamek ten wyraża dwie
reguły: w jednej licznik jest przesłanką, a mianownik wnioskiem, w drugiej mianownik jest przesłanką, a
licznik wnioskiem.

Piotr Łukowski, Wykład dla studentów prawa

22

Wnioskowanie KRZ jest monotoniczne, tzn.

jeśli X

⊆

Y i X |

−

p, to Y |

−

p.

*Wniosek
Zatem, w szczególności, jeśli jakieś zdanie wynika ze zbioru pustego, to wynika z
każdego zbioru przesłanek, bo zbiór pusty zawiera się w każdym zbiorze przesłanek.

Wynikania logiczne oparte na wielu logikach formalnych, w tym logice klasycznej, są
monotoniczne, tzn. poszerzenie zbioru przesłanek o nowe przesłanki poszerza dotychczasowy
zbiór wniosków (konsekwencji). Fakt ten odróżnia te wynikania od „zwykłego” rozumowania
człowieka, które jest niemonotoniczne.

zbiór przesłanek

wniosek

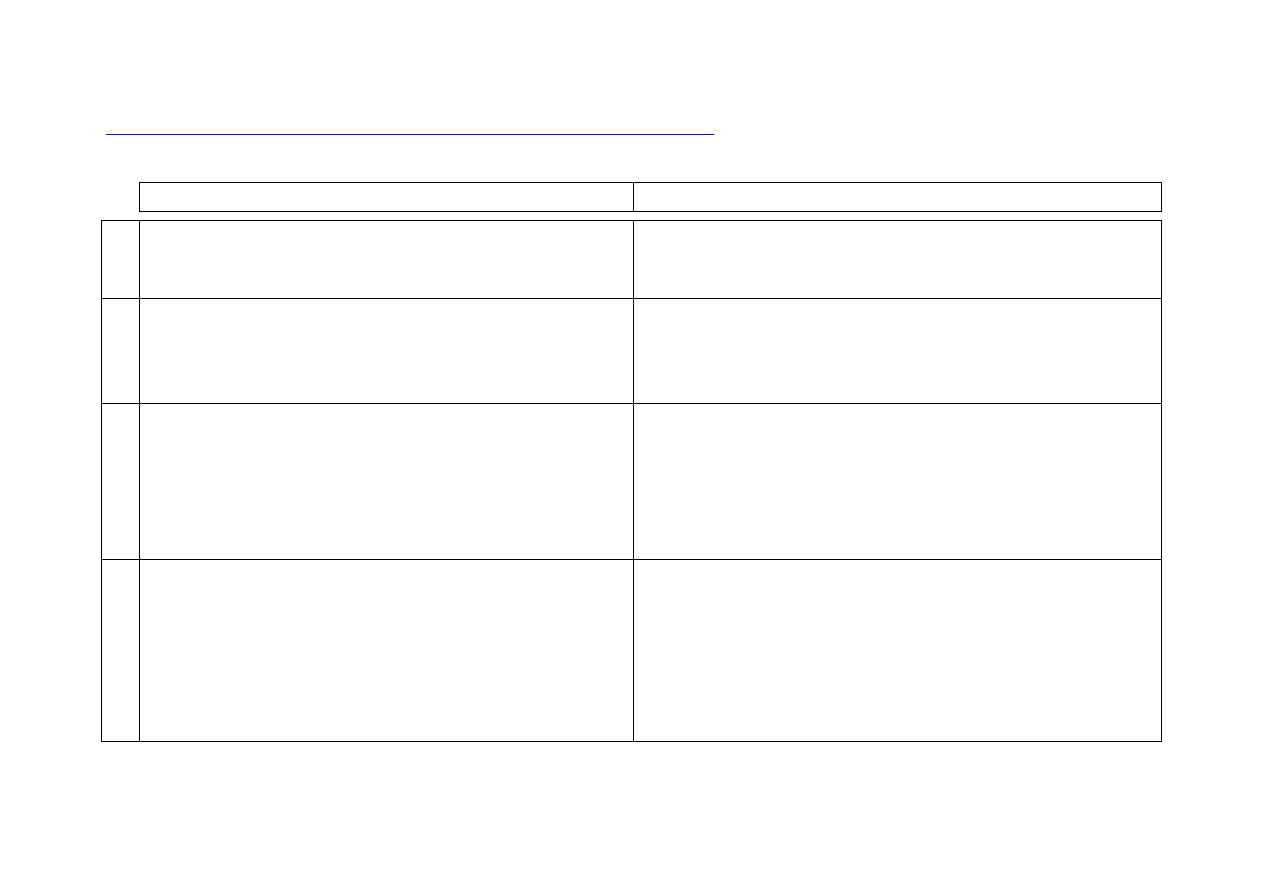
Piotr Łukowski, Wykład dla studentów prawa

23

Przykład na niemonotoniczność ludzkiego rozumowania:

poszerzanie zbioru przesłanek

zmiana zbioru konkluzji

I.

z1 - O godzinie t mam spotkanie w kawiarni x z
osobą y.

w1 - O odpowiedniej godzinie muszę się odpowiednio
ubrać, wyjść z domu o odpowiedniej godzinie i pójść do
kawiarni x.

II.

z1 - O godzinie t mam spotkanie w kawiarni x z
osobą y.
z2 - (przed wyjściem z domu) Termometr wskazuje
niską temperaturę.

w1 - O odpowiedniej godzinie muszę się odpowiednio
ubrać, wyjść z domu o odpowiedniej godzinie i pójść do
kawiarni x.
w2 - Musze się cieplej ubrać.

III.

z1 - O godzinie t mam spotkanie w kawiarni x z
osobą y.
z2 - (przed wyjściem z domu) Termometr wskazuje
niską temperaturę.
z3 - (przed wyjściem z domu) Zaczął padać deszcz.

w1 - O odpowiedniej godzinie muszę się odpowiednio
ubrać, wyjść z domu o odpowiedniej godzinie i pójść do
kawiarni x.
w2 - Muszę się cieplej ubrać.
w3 - Muszę zabrać parasol.

Do tego miejsca rozumowanie jest monotoniczne.

IV.

z1 - O godzinie t mam spotkanie w kawiarni x z
osobą y.
z2 - (przed wyjściem z domu) Termometr wskazuje
niską temperaturę.
z3 - (przed wyjściem z domu) Zaczął padać deszcz.
z4 - (miałem rozmowę telefoniczną z osobą z) Osoba
y miała wypadek samochodowy i leży w szpitalu.

w4 - Moje spotkanie o godzinie t w kawiarni x z osobą y
nie odbędzie się.

Zatem, wnioski w1-w3 przestają być ważne -
rozumowanie przestaje być monotoniczne.

Piotr Łukowski, Wykład dla studentów prawa

24

Zadanie 11.
Wykażemy, że świat nie jest Absolutem.

Jeśli bowiem świat byłby Absolutem, to jeśli byłby

ponadto stworzony, to musiałby sam się stworzyć.

Lecz to ostatnie oznaczałoby, że świat ma

początek.

Jednak wówczas świat nie może być wieczny.

Z drugiej strony jasne jest, że Absolut

nie może nie być wieczny.

Ponadto, jeśli świat istnieje, to musiał mieć kiedyś początek.

Jeśli,

natomiast, nie istnieje, to tym bardziej nie może być Absolutem.

p - świat jest Absolutem
p

1

- świat jest stworzony

p

2

- świat sam się stworzył

p

3

- świat ma początek

p

4

- świat jest wieczny

p

5

- świat istnieje

{

p

→

(p

1

→

p

2

)

,

p

2

→

p

3

, p

3

→

¬

p

4

,

p

→

p

4

,

p

5

→

p

3

,

¬

p

5

→

¬

p

}

|

−

¬

p

Piotr Łukowski, Wykład dla studentów prawa

25

{

p

→

(p

1

→

p

2

)

,

p

2

→

p

3

, p

3

→

¬

p

4

,

p

→

p

4

,

p

5

→

p

3

,

¬

p

5

→

¬

p

}

|

−

¬

p

(p

→

(p

1

→

p

2

))

∧

(p

2

→

p

3

)

∧

(p

3

→

¬

p

4

)

∧

(p

→

p

4

)

∧

(p

5

→

p

3

)

∧

(

¬

p

5

→

¬

p

))

→

¬

p

0

1

1

1

1

1

1

0

1

1

1

1

1

1

0

0

1

1

1

1

1

0

Przesłanki pierwsza i druga nie są wykorzystane w analizie. Zatem, wniosek

¬

p wynika

logicznie także ze zbioru mniejszego, czyli z

{p

3

→

¬

p

4

,

p

→

p

4

,

p

5

→

p

3

,

¬

p

5

→

¬

p

}.

Piotr Łukowski, Wykład dla studentów prawa

26

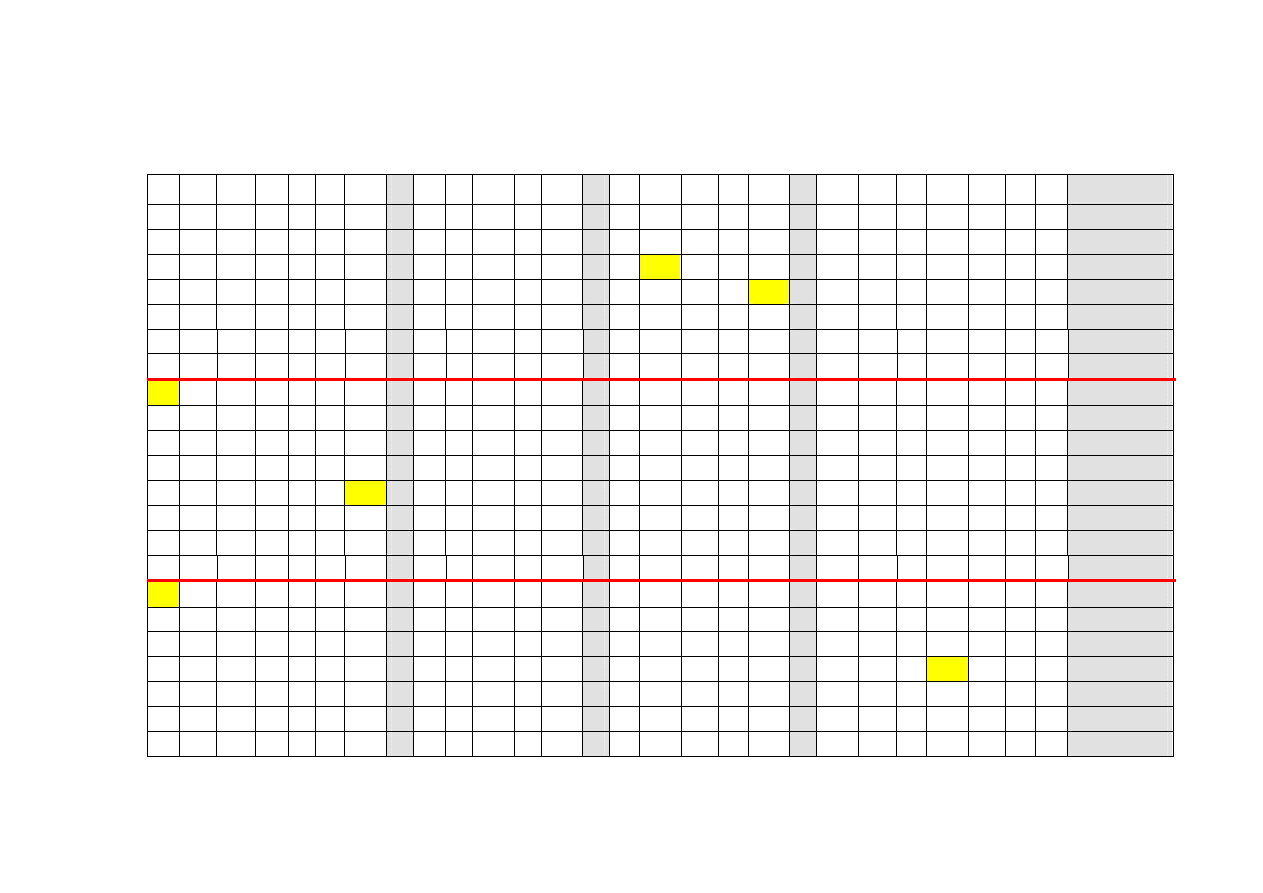
Zadanie 12.
Wykażemy, że następujący zbiór zdań tworzy wypowiedź sprzeczną:

„Jeśli świat jest wieczny, to nie ma początku lub końca.

Z drugiej strony, świat jest wieczny lub

ma zarazem początek i koniec.

Nie jest prawdą, że stworzoność świata implikuje to że nie ma on

początku.

Ponadto, świat nie jest stworzony, o ile założymy, że jest wieczny wtedy i tylko

wtedy, gdy nie ma końca.”

p

1

- świat jest wieczny

p

2

- świat ma początek

p

3

- świat ma koniec

p

4

- świat jest stworzony

{

p

1

→

(

¬

p

2

∨

¬

p

3

)

,

p

1

∨

(p

2

∧

p

3

)

,

¬

(p

4

→

¬

p

2

),

(p

1

↔

¬

p

3

)

→

¬

p

4

}

Piotr Łukowski, Wykład dla studentów prawa

27

{

p

1

→

(

¬

p

2

∨

¬

p

3

)

,

p

1

∨

(p

2

∧

p

3

)

,

¬

(p

4

→

¬

p

2

),

(p

1

↔

¬

p

3

)

→

¬

p

4

}

p

1

→

(

¬

p

2

∨

¬

p

3

)

∧

p

1

∨

(p

2

∧

p

3

)

∧

¬

(p

4

→

¬

p

2

)

∧

(p

1

↔

¬

p

3

)

→

¬

p

4

1

1

1

1

0

1

0

1

1

1

1

0

0

0

1

zał.1

1

1

1

1

0

1

0

1

1

0

zał.2

0

1

0

0

0

0

0

Piotr Łukowski, Wykład dla studentów prawa

28

Nie istnieje podstawienie, przy którym wszystkie cztery formuły zamienią się w zdania
prawdziwe. Nie jest więc możliwe, aby wszystkie cztery zdania były jednocześnie prawdziwe.
Oznacza to, że tekst jest sprzeczny.

Piotr Łukowski, Wykład dla studentów prawa

29

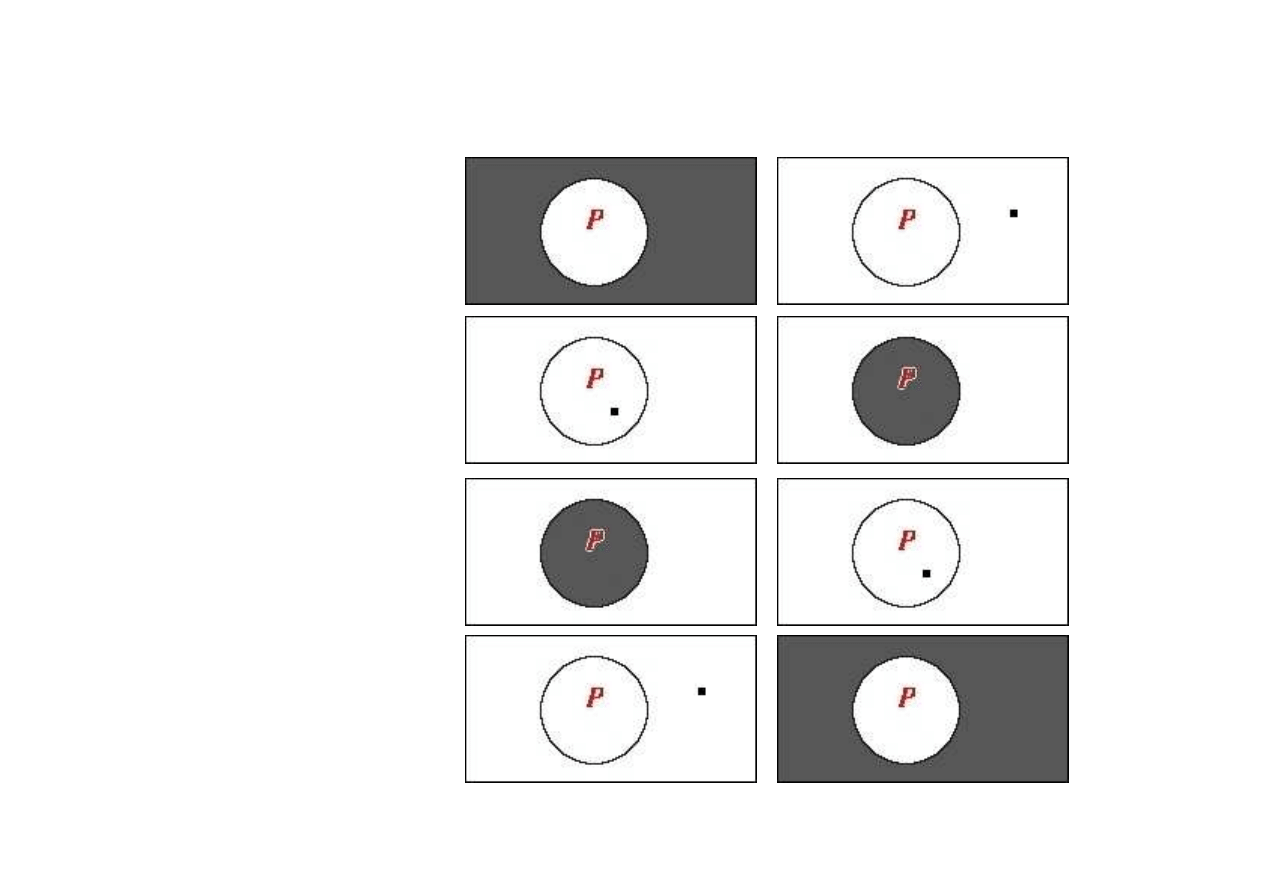
Elementy Klasycznej Logiki Kwantyfikatorów

x, y, z - zmienne nazwowe

∀

- kwantyfikator ogólny „dla każdego...”

∃

- kwantyfikator szczegółowy „dla pewnego...”, „istnieje... takie, że...”

P(x), Q(y) - formuły jednej zmiennej (wyrażają własności)
P(x,y), Q(y,z) - formuły dwóch zmiennych (wyrażają relacje, związki)
P(x,y,x), Q(y,z,x) - formuły trzech zmiennych (wyrażają relacje, związki)

„

∀

x P(x)” czytamy „dla każdego x, P(x)”

„

∃

x P(x)” czytamy „dla pewnego x, P(x)” lub „istnieje x takie, że P(x)”

∀

x P(x)

↔

{x: P(x)} = Dz

(Dz - dziedzina rozważań)

¬∀

x P(x)

↔

{x: P(x)}

≠

Dz

∃

x P(x)

↔

{x: P(x)}

≠

∅

¬∃

x P(x)

↔

{x: P(x)} =

∅

∀

x

¬

P(x)

↔

{x:

¬

P(x)} = Dz

∃

x

¬

P(x)

↔

{x:

¬

P(x)}

≠

∅

Piotr Łukowski, Wykład dla studentów prawa

30

zdanie prawdziwe

zdanie fałszywe

∀

x P(x)

∃

x P(x)

∀

x

¬

P(x)

∃

x

¬

P(x)

Piotr Łukowski, Wykład dla studentów prawa

31

Objaśnienie.
Czarna kropka na diagramie oznacza niepustość zbioru, do którego należy.
Szare wypełnienie oznacza pustość zbioru wypełnionego tym kolorem.

Negacja zdań skwantyfikowanych:

¬∀

x P(x)

↔

∃

x

¬

P(x)

¬∃

x P(x)

↔

∀

x

¬

P(x)

Zatem,

∀

x P(x)

↔

¬∃

x

¬

P(x)

∃

x P(x)

↔

¬∀

x

¬

P(x)

Piotr Łukowski, Wykład dla studentów prawa

32

Zadanie: Jak brzmi zaprzeczenie zdania:

1. Każdy adwokat kiedyś obroni jakiegoś oskarżonego.

2. śaden prokurator nie wycofa nigdy żadnego aktu oskarżenia.

3. Pewien sędzia wydał kiedyś [jakiś] niesprawiedliwy wyrok.

1.

∀

x

∈

A

∃

y

∈

T

∃

z

∈

Os Obr(x,y,z)

¬∀

x

∈

A

∃

y

∈

T

∃

z

∈

Os Obr(x,y,z)

↔

∃

x

∈

A

∀

y

∈

T

∀

z

∈

Os

¬

Obr(x,y,z)

Odp: Pewien adwokat nigdy nie obroni żadnego oskarżonego.

2.

∀

x

∈

Pr

∀

y

∈

T

∀

z

∈

Akt

¬

W(x,y,z)

¬∀

x

∈

Pr

∀

y

∈

T

∀

z

∈

Akt

¬

W(x,y,z)

↔

∃

x

∈

Pr

∃

y

∈

T

∃

z

∈

Akt W(x,y,z)

Odp: Pewien prokurator kiedyś wycofa jakiś akt oskarżenia.

3.

∃

x

∈

A

∃

y

∈

T

∃

z

∈

NW Wyd(x,y,z)

¬∃

x

∈

A

∃

y

∈

T

∃

z

∈

NW Wyd(x,y,z)

↔

∀

x

∈

A

∀

y

∈

T

∀

z

∈

NW

¬

Wyd(x,y,z)

Odp: śaden sędzia nigdy nie wydał [żadnego] niesprawiedliwego wyroku.