MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

1

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

4.1. Wiadomości podstawowe

W niniejszym rozdziale zapoznamy się z wyznaczaniem sił przekrojowych w płaskich układach

prętowych pominąwszy kratownice płaskie omówione w rozdziale 3. Omówimy więc rozwiązywanie belek i
ram płaskich. Z definicją belki i ramy płaskiej zapoznaliśmy się w rozdziale 1. W rozdziale tym poznaliśmy
także rodzaje podpór tych układów prętowych oraz ich analizę kinematyczną. W rozdziale 2 poznaliśmy siły
bierne czyli reakcje działające na poszczególnych typach podpór oraz sposoby ich wyznaczania czyli analizę
statyczną.

4.2. Obciążenia belek i ram płaskich

Pierwszym typem obciążenia działającego na belkę lub ramę płaską jest siła skupiona nazywana dalej

po prostu siłą. Działania na siłach zostały omówione w rozdziale 2. Jednostką siły w układzie SI jest Niuton
[N]. Tutaj będziemy się posługiwali jej wielokrotnością czyli kN. Przykładem siły działającej na belkę lub
ramę płaską jest reakcja.

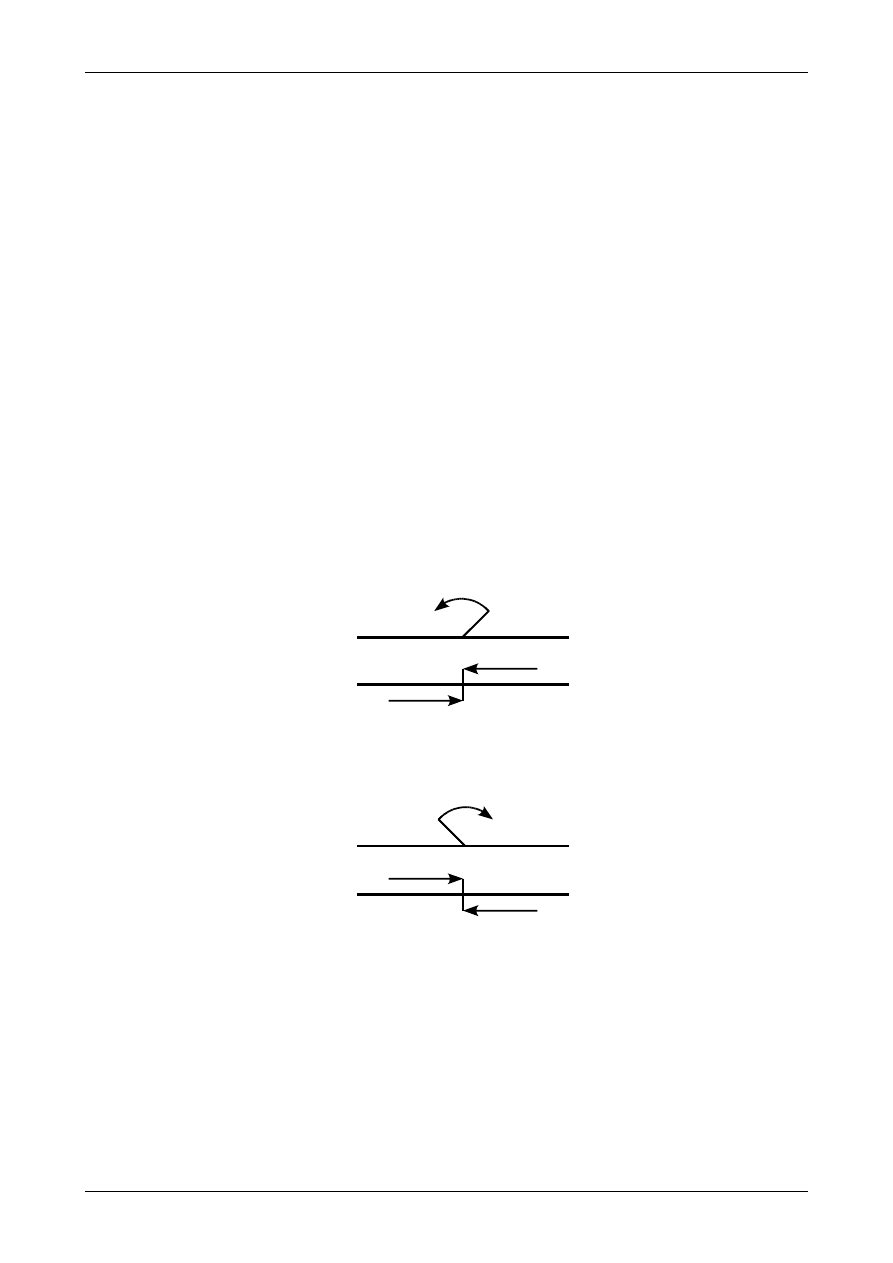
Drugim rodzajem obciążenia działającego na belkę lub ramę płaską jest moment skupiony.

Statycznie odpowiada on parze sił, którą omówiliśmy w rozdziale 2. Para ta jest przyłożona w tym samym
punkcie co moment skupiony. Obciążenie to przedstawia rysunek 4.1. i 4.2. Jak więc widać siła wypadkowa
z takiego obciążenia wynosi zero natomiast wartość momentu pary sił względem dowolnego punktu jest
stała i równa się wartości momentu skupionego. Jednostką tego obciążenia w układzie SI jest Nm. Tutaj
będziemy się posługiwali wielokrotnością czyli kNm.

M

P

P

a)

b)

Rys. 4.1. Moment skupiony przeciwny do ruchu wskazówek zegara. a) wektor momentu skupionego, b) statycznie

równoważna para sił

a)

P

P

b)

M

Rys. 4.2. Moment skupiony zgodny z ruchem wskazówek zegara. a) wektor momentu skupionego, b) statycznie

równoważna para sił

Trzecim, i ostatnim rodzajem, obciążenia działającego na belkę lub ramę płaską jest obciążenie

ciągłe. W przeciwieństwie do obciążeń przedstawionych powyżej, które były przyłożone w ściśle
określonym punkcie belki lub ramy płaskiej, obciążenie ciągłe jest rozłożone na długości pewnego
przedziału. Jednostką tego typu obciążenia w układzie SI jest N/m. Tutaj będziemy się posługiwali
wielokrotnością czyli kN/m.

Pierwsze z nich obciążenie ciągłe równomiernie rozłożone prostopadłe do osi pręta jest

najczęściej występującym obciążeniem ciągłym w belkach i ramach płaskich. Charakteryzuje ono się tym,
że jego wartość na długości całego przedziału jest stała.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

2

Drugi typ obciążenia ciągłego omawianego w niniejszym opracowaniu to obciążenie ciągłe liniowe

prostopadłe do osi pręta. Charakteryzuje ono się tym, że zmienia się ono liniowo na długości przedziału, w
którym działa. Obciążenie to będzie więc liniową funkcją zmiennej x, która oznacza nam współrzędną
punktu na długości pręta, w którym wyznaczamy wartość obciążenia ciągłego liniowego.

W przypadku belek i rygli ram płaskich, czyli prętów, które są poziome, będziemy rozpatrywali

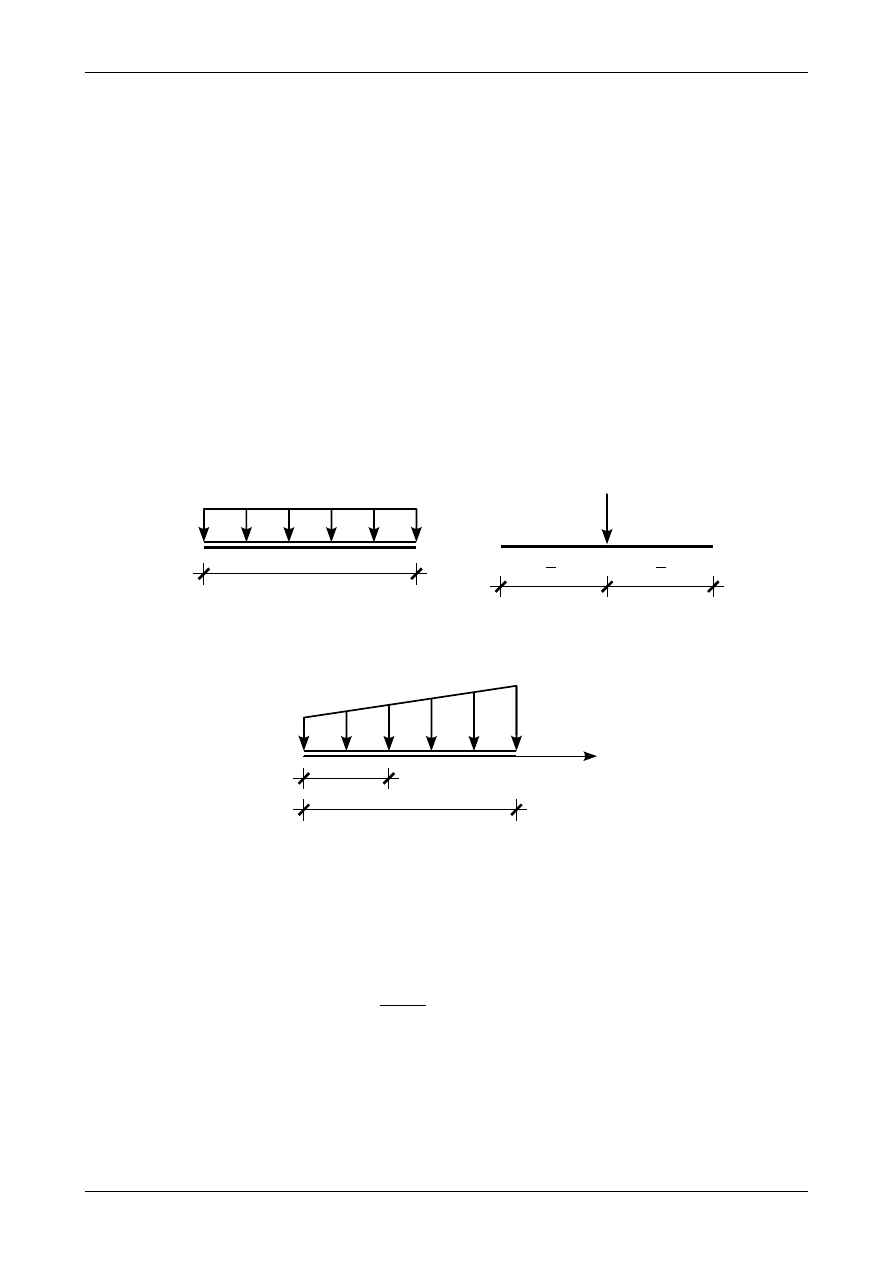
obciążenia ciągłe pionowe. Obciążenia te są prostopadłe do osi pręta. Rysunek 4.3 przedstawia obciążenie
ciągłe równomiernie rozłożone działające na pręcie belki lub rygla ramy płaskiej. Jak widać ma ono postać
prostokąta. Jako dodatnie będziemy przyjmowali obciążenie działające w dół. Obciążenie to możemy
zastąpić statycznie równoważną siłą wypadkową. Jeżeli obciążenie ciągłe równomiernie rozłożone działa w
przedziale o długości L to wartość siły wypadkowej z tego obciążenia równa się polu prostokąta, czyli
wynosi

W

=

q

⋅

L

.

(4.1)

Położenie siły wypadkowej przedstawia rysunek 4.3 b). Jeżeli obciążenie q działałoby do góry, czyli byłoby
ujemne, to oczywiście także i siła wypadkowa W działałaby do góry.

a)

q

W

L

L
2

L
2

b)

Rys. 4.3. Obciążenie ciągłe równomiernie rozłożone. a) oznaczenie obciążenia, b) statycznie równoważna siła

wypadkowa

q

1

L

q

2

X

x

q(x)

Rys. 4.4. Obciążenie ciągłe liniowe

Rysunek 4.4 przedstawia pręt belki lub rygla ramy płaskiej z obciążeniem ciągłym liniowym. Z osią

pręta pokrywa się oś X, której początek znajduje się w lewym końcu przedziału. Jak więc widać obciążenie
ciągłe liniowe jest funkcją liniową zależną od zmiennej x. Funkcja ta ma postać

q



x



=

q

2

−

q

1

L

⋅

x



q

1

.

(4.2)

Do funkcji (4.2) wartości q

1

oraz q

2

podstawiamy oczywiście z odpowiednim znakiem. Jeżeli q

1

lub q

2

działa

w dół to z plusem jeżeli do góry to z minusem.

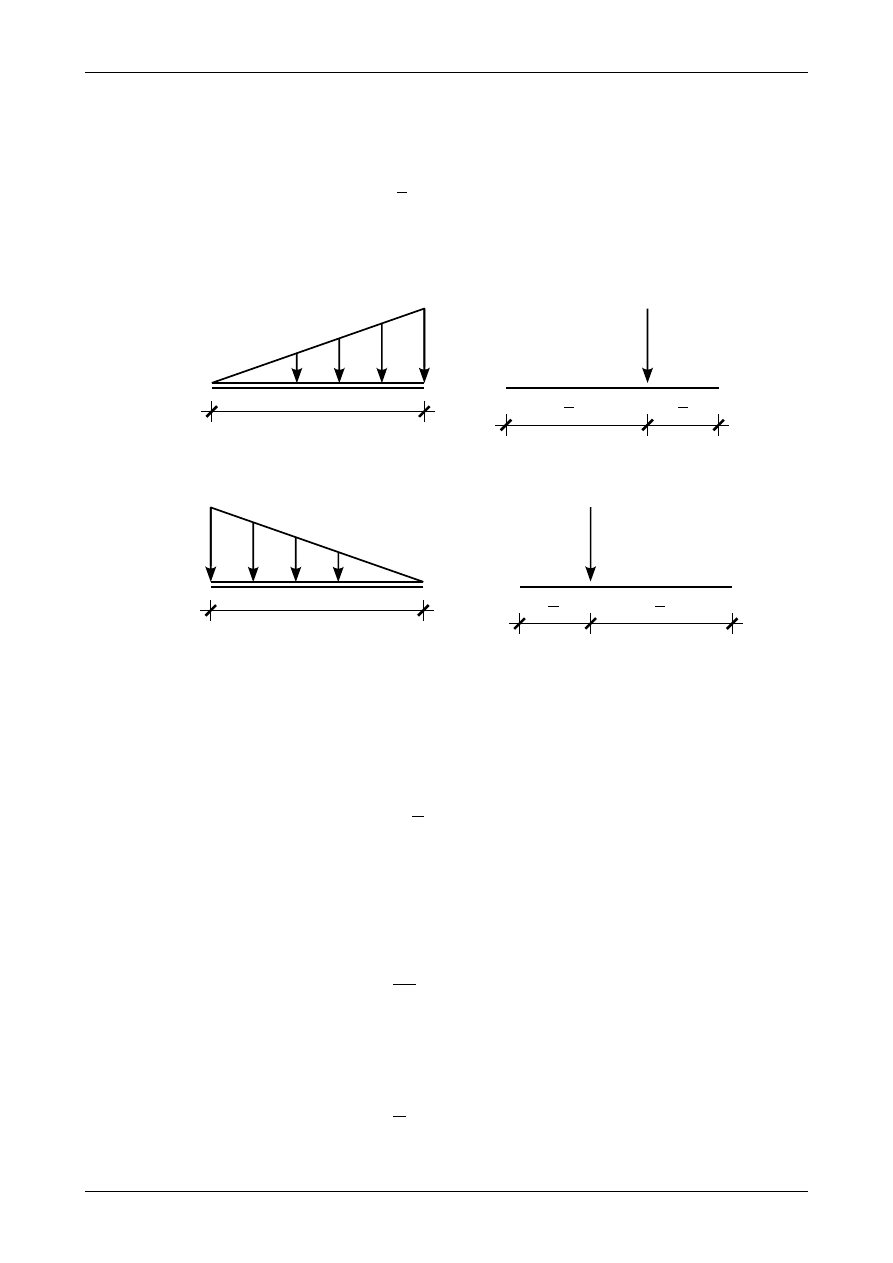
Najprostszym przypadkiem obciążenia liniowego jest obciążenie ciągłe trójkątne. Jak widać na

rysunkach 4.5 i 4.6 ma ono formę trójkąta prostokątnego. Obciążenie to może rosnąć lub maleć począwszy
od lewego końca przedziału. Możemy je zastąpić statycznie równoważną siłą wypadkową. Jeżeli obciążenie

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

3

ciągłe trójkątne działa w przedziale o długości L to wartość siły wypadkowej z tego obciążenia równa się
polu trójkąta prostokątnego, czyli wynosi

W

=

1
2

⋅q⋅L

.

(4.3)

Położenie siły wypadkowej przedstawiają rysunki 4.5 b) i 4.6 b).

L

q

L
3

2

3

⋅L

W

a)

b)

Rys. 4.5. Obciążenie ciągłe trójkątne. a) oznaczenie obciążenia, b) statycznie równoważna siła wypadkowa

L

q

L
3

2

3

⋅L

W

a)

b)

Rys. 4.6. Obciążenie ciągłe trójkątne. a) oznaczenie obciążenia, b) statycznie równoważna siła wypadkowa

W przypadku obciążenia ciągłego trójkątnego rosnącego przedstawionego na rysunku 4.7 postać

funkcji liniowej otrzymamy podstawiając do (4.2) q

1

równe zero natomiast q

2

równe q. Otrzymamy więc

funkcję liniową w postaci

q



x



=

q
L

⋅

x

.

(4.4)

W przypadku obciążenia ciągłego trójkątnego malejącego przedstawionego na rysunku 4.8 postać

funkcji liniowej otrzymamy podstawiając do (4.2) q

1

równe q natomiast q

2

równe zero. Otrzymamy więc

funkcję liniową w postaci

q



x



=−

q

L

⋅xq

,

(4.5)

którą możemy zapisać jako

q



x



=

q
L

⋅



L

−

x



.

(4.6)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

4

L

q

X

x

q(x)

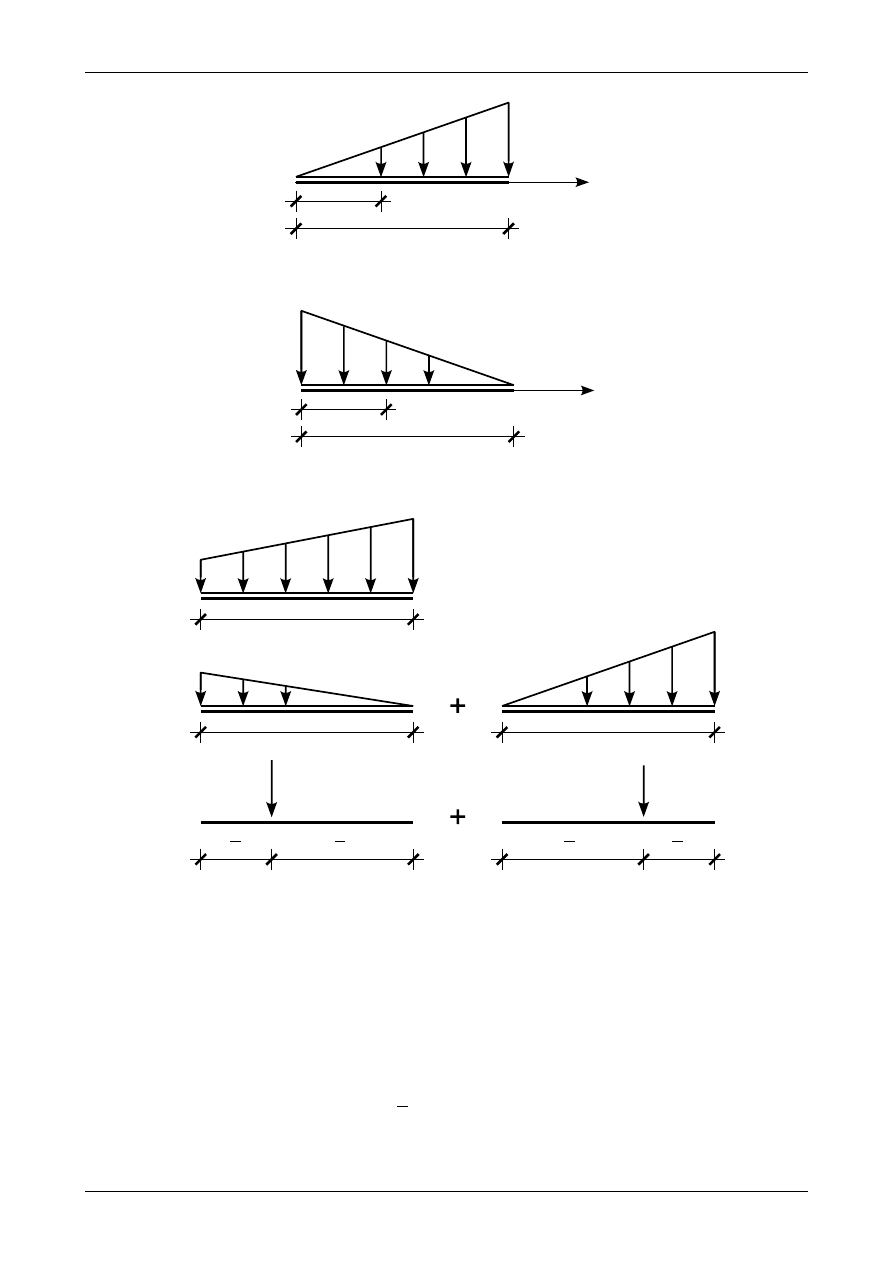
Rys. 4.7. Obciążenie ciągłe trójkątne rosnące

L

q

X

x

q(x)

Rys. 4.8. Obciążenie ciągłe trójkątne malejące

q

1

L

q

2

q

1

L

L

q

2

a)

b)

c)

W

1

W

2

L
3

2

3⋅

L

L
3

2

3⋅

L

Rys. 4.9. Obciążenie ciągłe liniowe. a) oznaczenie obciążenia, b) składowe obciążenia ciągłe trójkątne, c) statycznie

równoważne siły wypadkowe

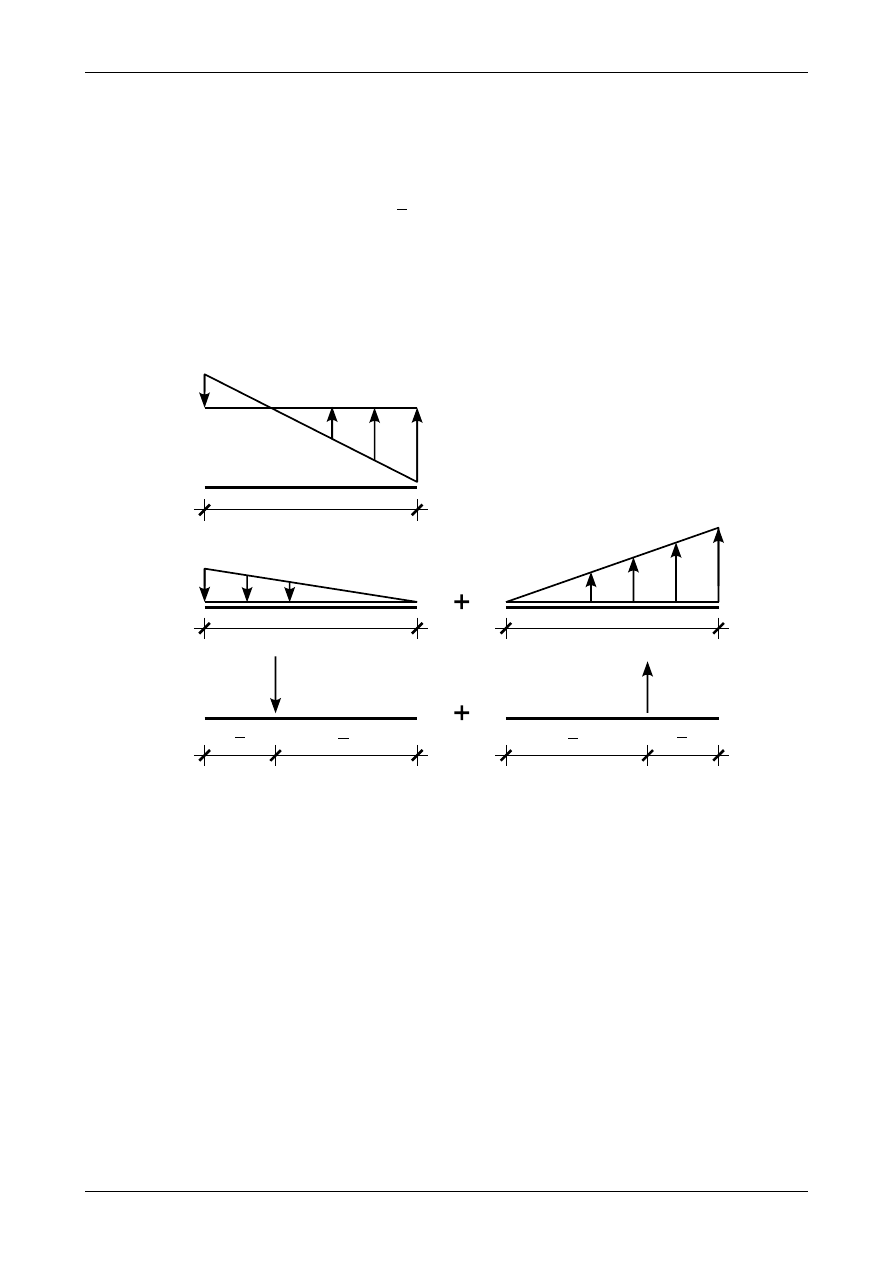
Dowolne obciążenie liniowe możemy także zastąpić statycznie równoważną siłą wypadkową. W tym

celu obciążenie to zastępujemy dwoma obciążeniami ciągłymi trójkątnymi. Rysunek 4.9 przedstawia
dowolne obciążenie ciągłe liniowe, w którym q

1

oraz q

2

działają w dół czyli są dodatnie. Pierwsze

obciążenie ciągłe trójkątne powstaje poprzez połączenie wartości q

1

z lewej strony z zerem z prawej strony.

Wypadkowa z tego obciążenia ma wartość

W

1

=

1
2

⋅

q

1

⋅

L

.

(4.7)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

5

Położenie tej siły wypadkowej przedstawia rysunek 4.9 c). Drugie obciążenie ciągłe trójkątne powstaje
poprzez połączenie wartości q

2

z prawej strony z zerem z lewej strony. Wypadkowa z tego obciążenia ma

wartość

W

2

=

1
2

⋅q

2

⋅L

.

(4.8)

Położenie tej siły wypadkowej przedstawia rysunek 4.9 c). Jeżeli wartości obciążenia ciągłego liniowego q

1

oraz q

2

byłyby ujemne czyli obciążenie to działałoby do góry to obie wypadkowe W

1

oraz W

2

działałyby

także do góry.

q

1

L

q

2

q

1

L

L

q

2

a)

b)

c)

W

1

W

2

L
3

2

3⋅

L

L
3

2

3⋅

L

Rys. 4.10. Obciążenie ciągłe liniowe przewinięte. a) oznaczenie obciążenia, b) składowe obciążenia ciągłe trójkątne, c)

statycznie równoważne siły wypadkowe

Rysunek 4.10 przedstawia obciążenie ciągłe liniowe przewinięte. Jak widać wartości tego obciążenia

na obu końcach przedziału mają różne znaki. Rozkład tego obciążenia ciągłego na dwa obciążenia ciągłe
trójkątne przedstawia rysunek 4.10 b). Statycznie równoważne siły wypadkowe przedstawia natomiast
rysunek 4.10 c). Siły wypadkowe W

1

oraz W

2

wyznaczymy ze wzorów (4.7) i (4.8).

W przypadku słupów ram płaskich będziemy rozpatrywać tylko obciążenie ciągłe równomiernie

rozłożone dwóch typów.

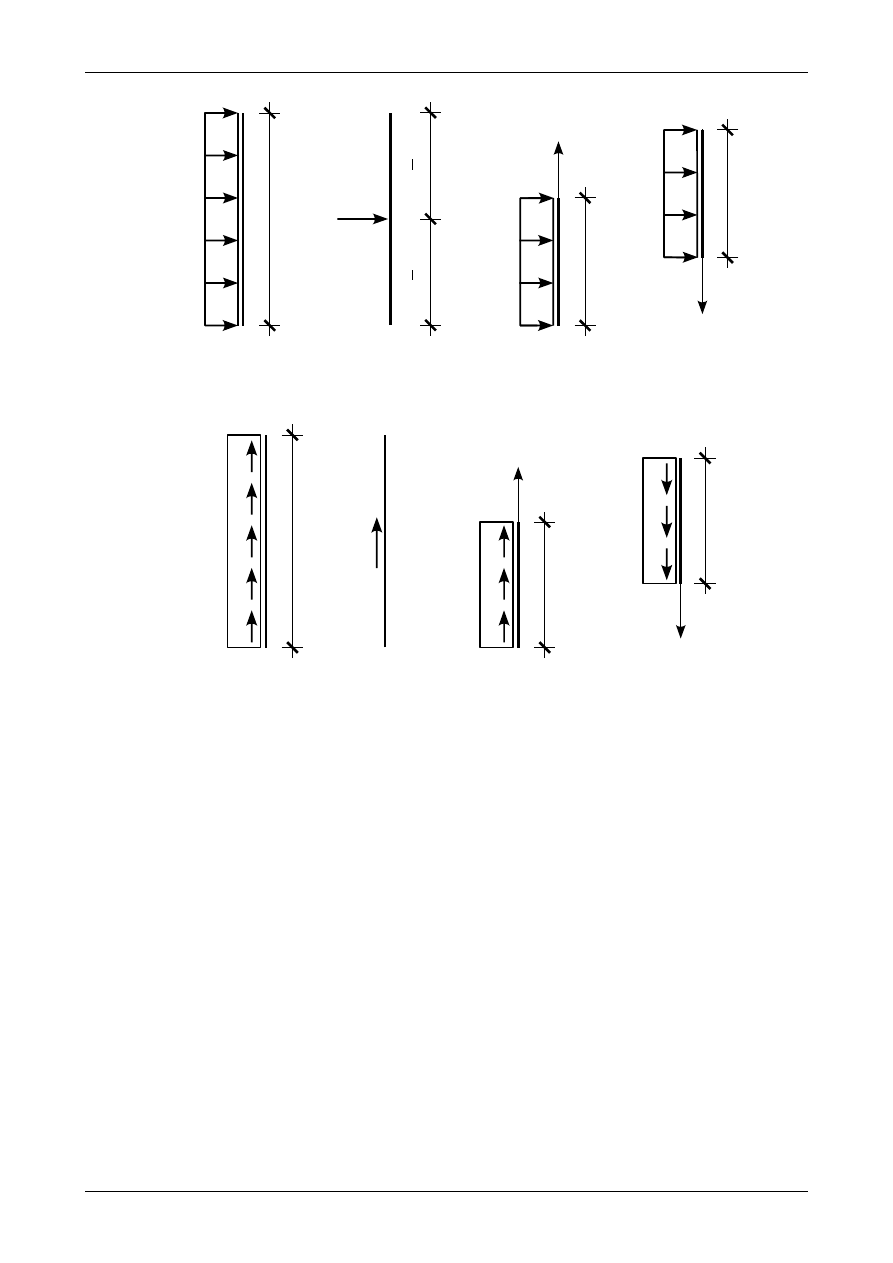
Pierwszym z nich będzie obciążenie ciągłe równomiernie rozłożone prostopadłe do osi słupa. Będzie

to obciążenie takie samo jak w przypadku belek i rygli ram płaskich omówione powyżej. Rysunek 4.11
przedstawia ten typ obciążenia ciągłego działającego na słup. Jak widać na rysunku 4.11 b) obciążenie to
możemy zastąpić siłą wypadkową, której wartość wyznaczymy ze wzoru (4.1). Siła ta ma zwrot taki sam jak
zwrot obciążenia q. Zasada znakowania obciążenia ciągłego równomiernie rozłożonego będzie taka sama jak
dla belek i rygli ram płaskich. Musimy jednak precyzyjnie określić dolną część pręta. W przypadku słupów
rozpatrywanych w niniejszym opracowaniu oraz dołączonych przykładach dolną część słupa
przyjmiemy po jego prawej stronie. Obciążenie q przedstawione na rysunku 4.11 będzie obciążeniem
działającym w dół. Będziemy więc traktować je jako dodatnie.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

6

a)

q

W

L

L

2

L

2

b)

c)

q

x

X

d)

q

x

X

Rys. 4.11. Obciążenie ciągłe równomiernie rozłożone prostopadłe do osi słupa. a) schemat obciążenia. b) siła

wypadkowa, c) dodatnie obciążenie q, d) dodatnie obciążenie q.

a)

h

W

L

b)

c)

h

x

X

d)

h

x

X

Rys. 4.12. Obciążenie ciągłe równomiernie rozłożone równoległe do osi słupa. a) schemat obciążenia. b) siła

wypadkowa, c) dodatnie obciążenie h, d) dodatnie obciążenie h.

Drugim typem obciążenia ciągłego równomiernie rozłożonego będzie obciążenie równoległe do osi

słupa. Rysunek 4.12 przedstawia ten typ obciążenia ciągłego działającego na słup. Jak widać na rysunku
4.12 b) obciążenie to możemy zastąpić siłą wypadkową, której wartość wyznaczymy ze wzoru

W

=

h

⋅

L

.

(4.9)

Siła ta ma zwrot taki sam jak zwrot obciążenia h. W obliczeniach nie ma jednak znaczenia punkt przyłożenia
tej siły. Będzie ona przyłożona w dowolnym punkcie przedziału, w którym działa obciążenie ciągłe
równomiernie rozłożone równoległe do osi słupa. Dodatnie obciążenie ciągłe h będzie miało zwrot zgodny
ze zwrotem osi X związanej ze słupem. Rysunki 4.12 c) i d) przedstawiają więc dodatnie obciążenie h.

Pozostało nam do omówienia obciążenie ciągłe działające na pręcie ukośnym ramy płaskiej. W

niniejszym opracowaniu będziemy przyjmować tylko obciążenie ciągłe równomiernie rozłożone.

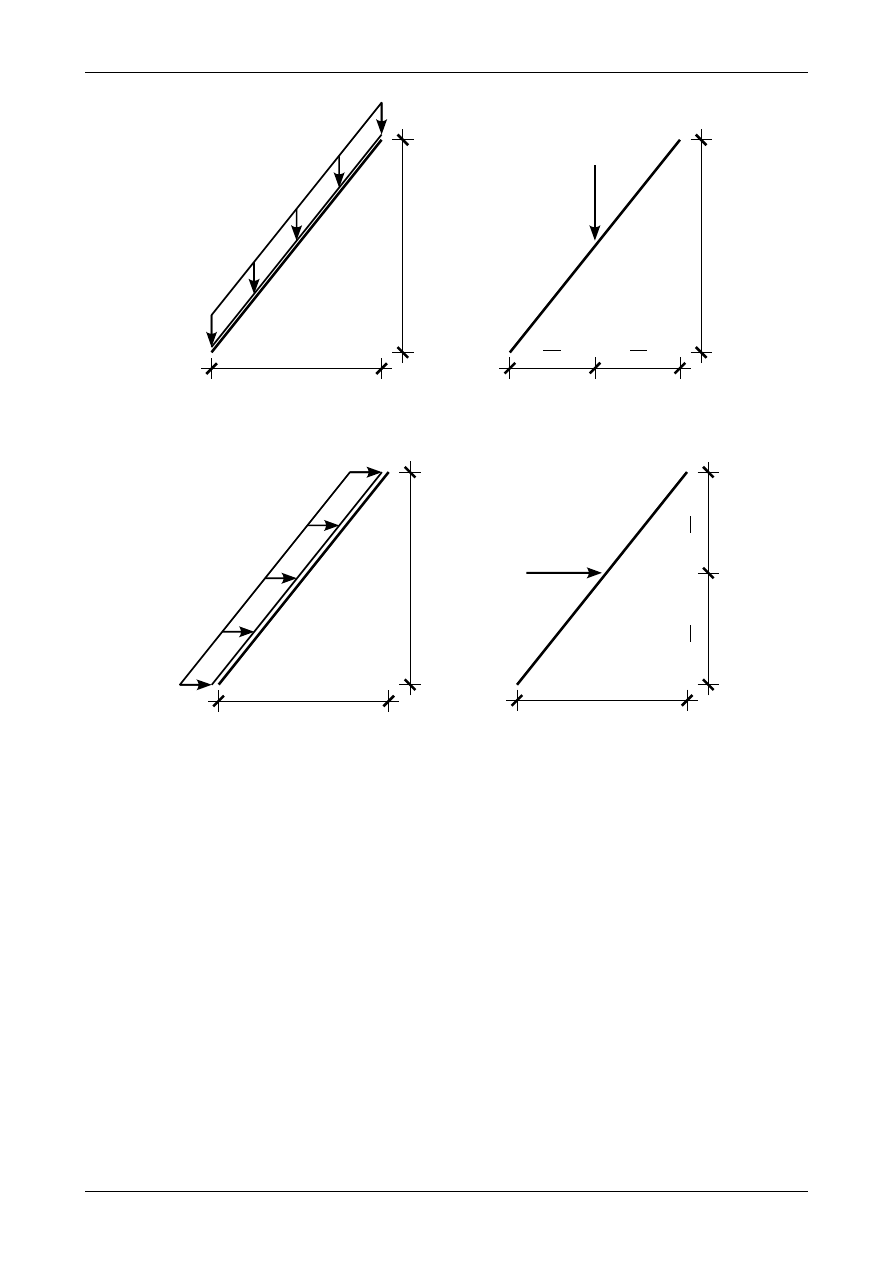
Pierwszy rodzaj tego obciążenia ciągłego to obciążenie ciągłe równomiernie rozłożone na długości

pręta ukośnego. Przedstawiają je rysunki 4.13 a) i 4.14 a). Obciążenie to możemy zastąpić statycznie
równoważną siłą wypadkową o wartości

W

=

p

⋅

L

.

(4.10)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

7

p

L

X

L

Y

- L

-

W

L

Y

- L

-

L

X

2

L

X

2

a)

b)

Rys. 4.13. Pionowe obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego. a) schemat obciążenia, b)

siła wypadkowa

p

L

X

L

Y

- L

-

W

- L

-

a)

b)

L

X

L

Y

2

L

Y

2

Rys. 4.14. Poziome obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego. a) schemat obciążenia, b)

siła wypadkowa

Położenie siły wypadkowej przedstawiają rysunki 4.13 b) i 4.14 b). Jak widać siła wypadkowa działa w
połowie rzutu poziomego lub pionowego pręta ukośnego.

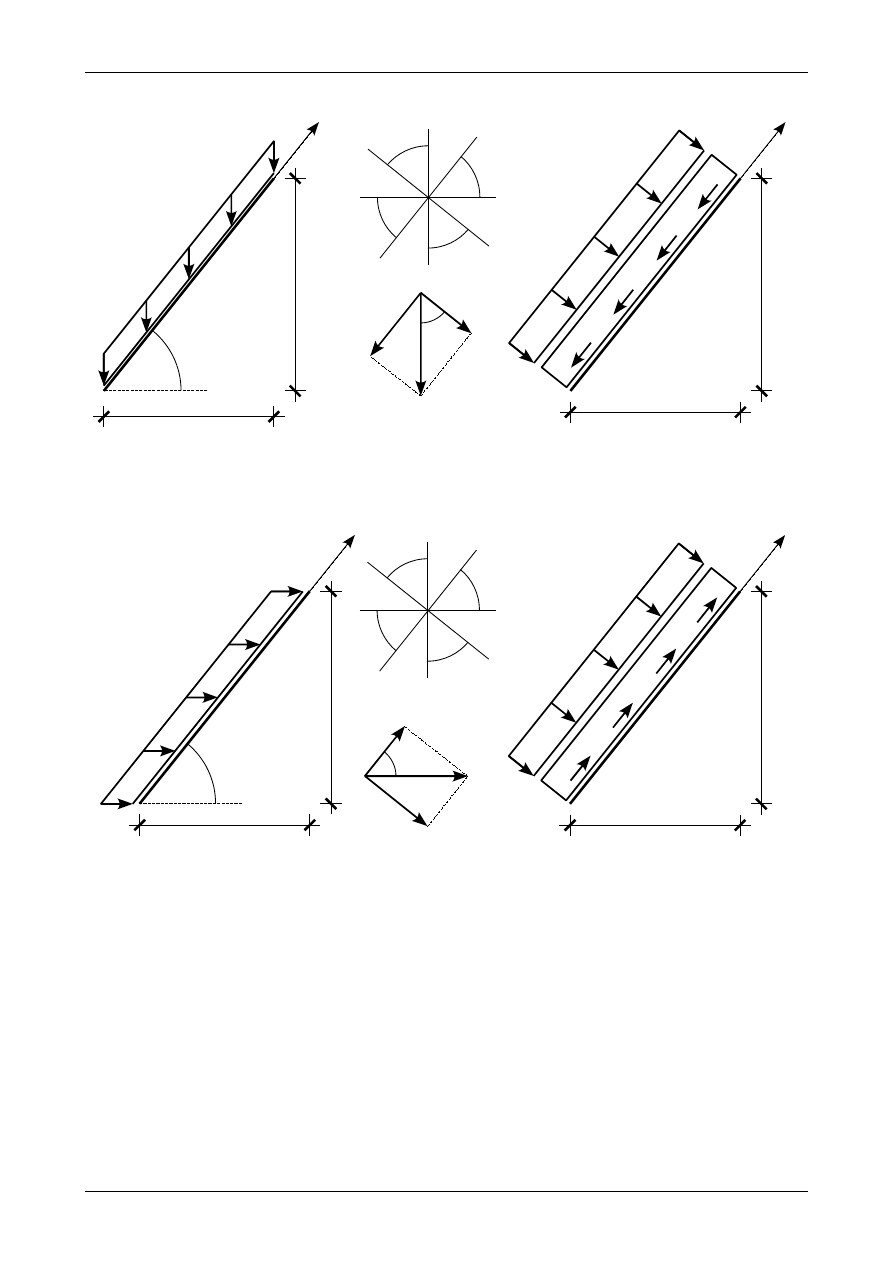
Obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego możemy rozłożyć na dwie

składowe: prostopadłą i równoległą do osi tego pręta. Zgodnie z rysunkiem 4.15 wartość bezwzględna
obciążenia ciągłego równomiernie rozłożonego prostopadłego do osi tego pręta wynosi

∣

q

∣

=

∣

p

∣

⋅

cos







.

(4.11)

Natomiast wartość bezwzględna obciążenia ciągłego równomiernie rozłożonego równoległego do osi tego
pręta wynosi

∣

h

∣

=

∣

p

∣

⋅sin







.

(4.12)

We wzorach (4.11) i (4.12)

α

oznacza kąt nachylenia pręta ukośnego do poziomu.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

8

p

- x

-

X

- x

-

X

α

α

α

α

α

α

p

q

h

q

h

x

⋅cos







x

⋅cos







x⋅

sin







x⋅

sin







Rys. 4.15. Rozkład pionowego obciążenia ciągłego równomiernie rozłożonego na długości pręta ukośnego na składową

prostopadłą i równoległą do osi tego pręta

X

- x

-

X

α

α

α

α

α

p

q

h

q

h

p

- x

-

α

x

⋅cos







x⋅

sin







x

⋅cos







x⋅

sin







Rys. 4.16. Rozkład poziomego obciążenia ciągłego równomiernie rozłożonego na długości pręta ukośnego na składową

prostopadłą i równoległą do osi tego pręta

Znak poszczególnych obciążeń ciągłych ustalamy, na postawie znanych już zasad znakowania,

indywidualnie w każdym przypadku położenia pręta ukośnego oraz działającego na niego obciążenia
ciągłego p. Na rysunku 4.15 obciążenie ciągłe q jest dodatnie natomiast obciążenie ciągłe h jest ujemne. Na
rysunku 4.16 oba obciążenia ciągłe q i h są dodatnie.

Drugim rodzajem obciążenia ciągłego działającego na pręt ukośny jest obciążenie ciągłe

równomiernie rozłożone na rzut poziomy lub pionowy pręta ukośnego. Rysunek 4.17 a) przedstawia
pionowe obciążenie ciągłe rozłożone na długości rzutu poziomego pręta ukośnego. Zgodnie z nim siła
wypadkowa z tego obciążenia wynosi

W

=

p

⋅

L

X

,

(4.13)

Dr inż. Janusz Dębiński

Zaoczni

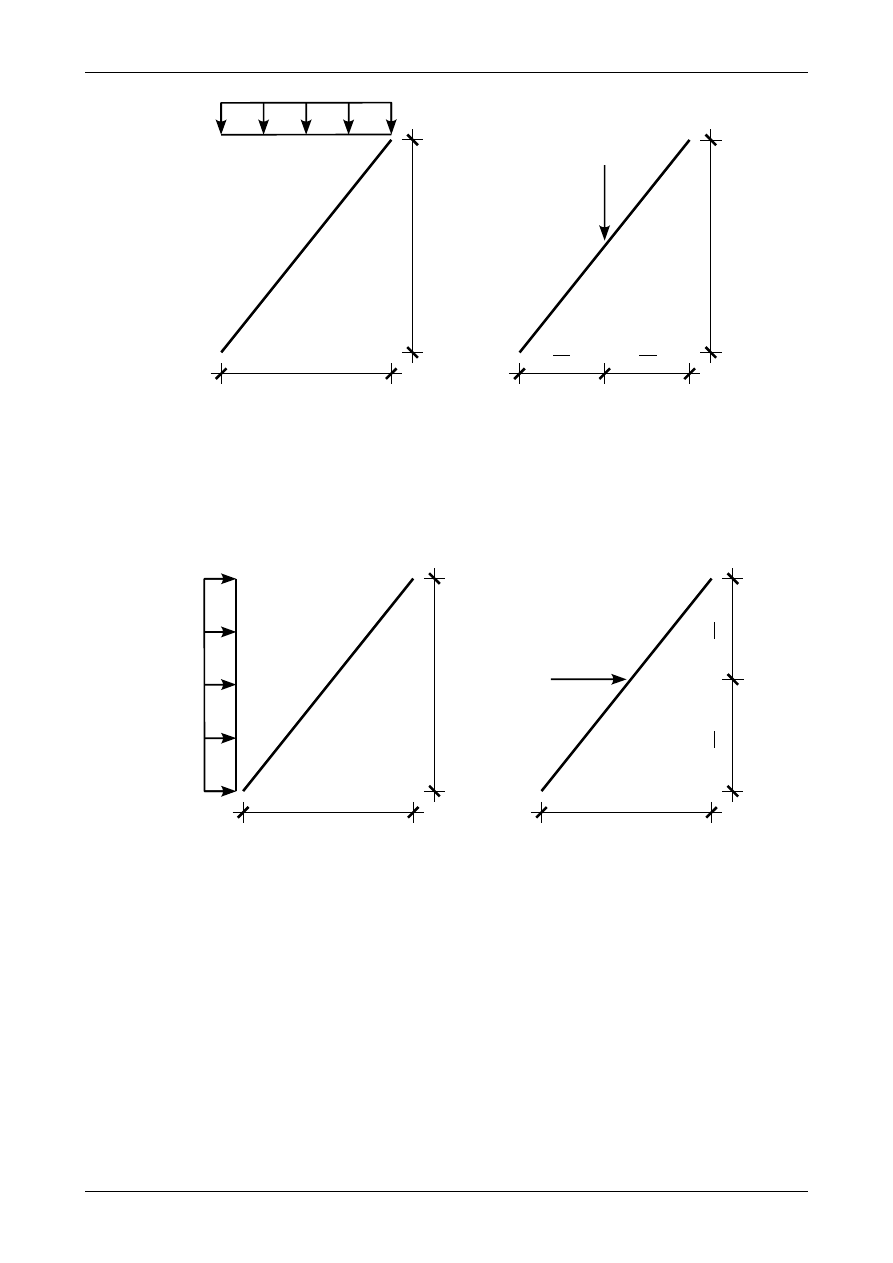
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

9

p

L

X

L

Y

- L

-

W

L

Y

- L

-

L

X

2

L

X

2

a)

b)

Rys. 4.17. Pionowe obciążenie ciągłe równomiernie rozłożone na długości rzutu poziomego pręta ukośnego. a) schemat

obciążenia, b) siła wypadkowa

w którym L

X

oznacza długość rzutu poziomego tego pręta ukośnego. Położenie siły wypadkowej

przedstawia rysunek 4.17 b). Jak widać siła wypadkowa działa w połowie rzutu poziomego tego pręta
ukośnego.

p

L

X

L

Y

- L

-

W

- L

-

a)

b)

L

X

L

Y

2

L

Y

2

Rys. 4.18. Poziome obciążenie ciągłe równomiernie rozłożone na długości rzutu pionowego pręta ukośnego. a) schemat

obciążenia, b) siła wypadkowa

Rysunek 4.18 a) przedstawia poziome obciążenie ciągłe rozłożone na długości rzutu pionowego pręta

ukośnego. Zgodnie z nim siła wypadkowa z tego obciążenia wynosi

W

= p⋅L

Y

.

(4.14)

Położenie siły wypadkowej przedstawia rysunek 4.18 b). Jak widać siła wypadkowa działa w połowie
rzutu pionowego tego pręta ukośnego.

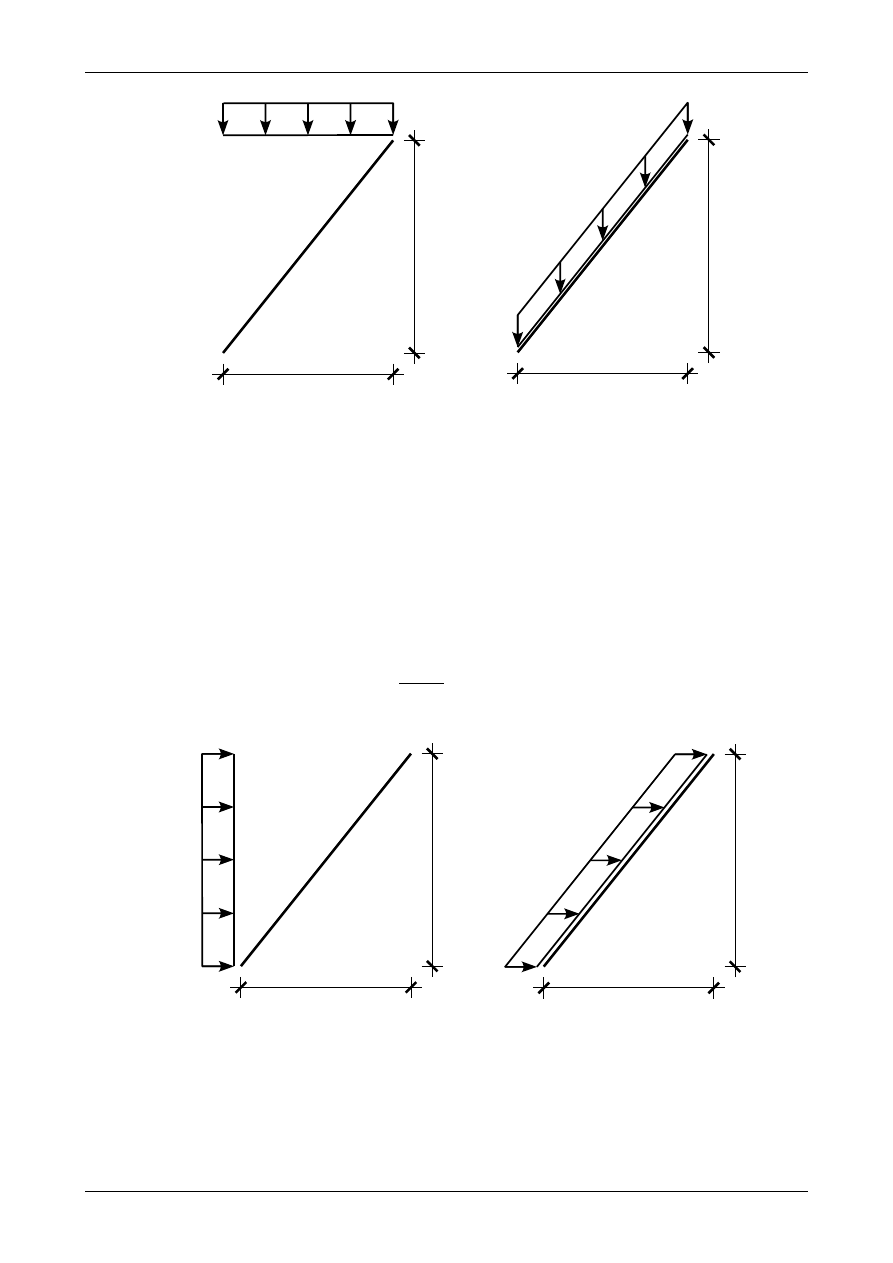
Obciążenie ciągłe równomiernie rozłożone na długości rzutu pręta ukośnego będziemy zastępowali

statycznie równoważnym obciążeniem ciągłym równomiernie rozłożonym na długości tego pręta. Rysunek
4.19 a) przedstawia pionowe obciążenie ciągłe równomiernie rozłożone na długości rzutu poziomego pręta
ukośnego natomiast rysunek 4.19 b) statycznie równoważne obciążenie ciągłe rozłożone na długości tego
pręta ukośnego.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

10

p

L

X

L

Y

- L

-

a)

p'

L

X

L

Y

- L

-

b)

Rys. 4.19. Pionowe obciążenie ciągłe równomiernie rozłożone na długości rzutu poziomego pręta ukośnego. a) schemat

obciążenia. b) statycznie równoważne obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego

Siły wypadkowe z obu obciążeń muszą być sobie równe. Możemy więc zapisać

∣

p

∣

⋅

L

X

=

∣

p '

∣

⋅

L

.

(4.15)

Wartość bezwzględna zastępczego pionowego obciążenia ciągłego równomiernie rozłożonego na długości
pręta ukośnego wynosi więc

∣

p'

∣

=

∣

p

∣

⋅L

X

L

.

(4.16)

p

L

X

L

Y

- L

-

a)

p'

L

X

L

Y

- L

-

b)

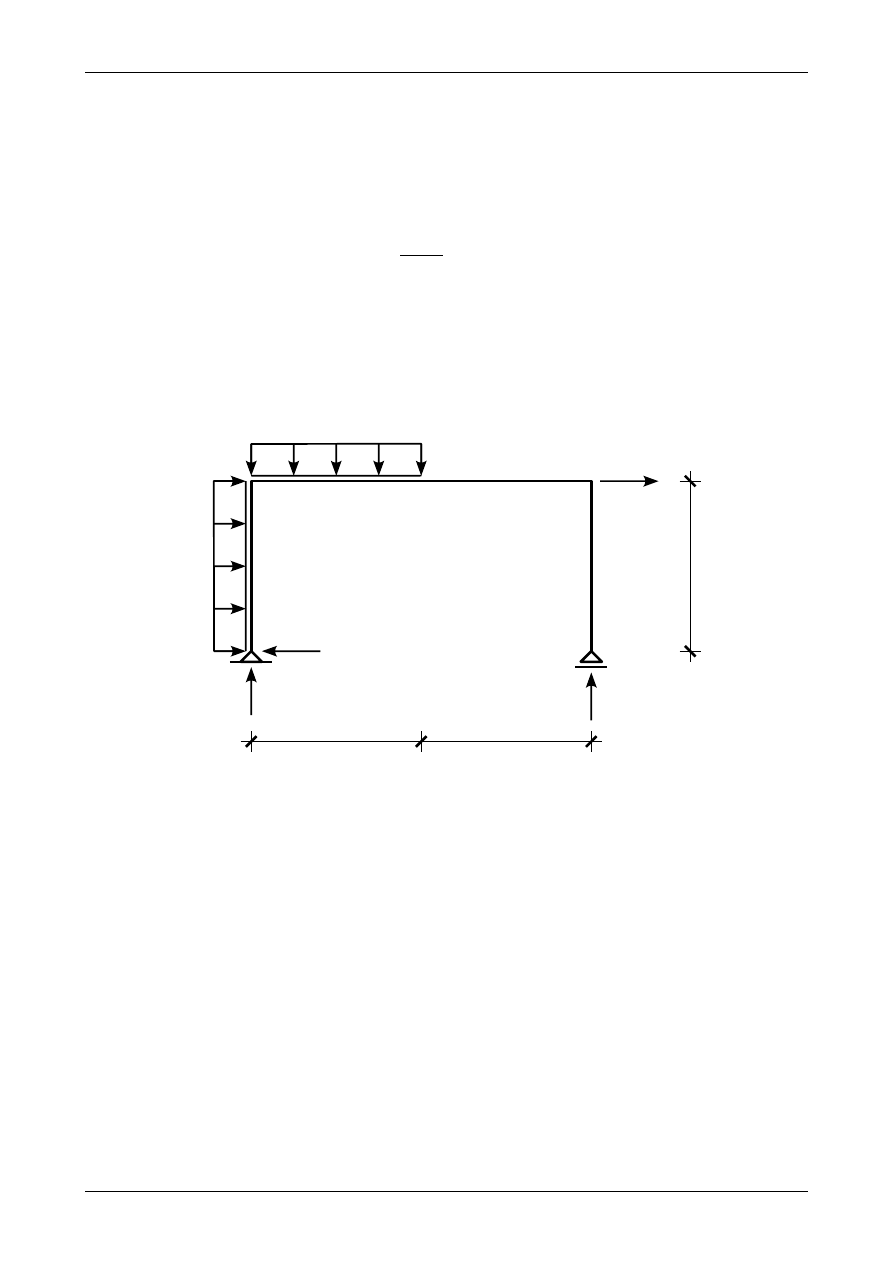
Rys. 4.20. Poziome obciążenie ciągłe równomiernie rozłożone na długości rzutu pionowego pręta ukośnego. a) schemat

obciążenia. b) statycznie równoważne obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego

Rysunek 4.20 a) przedstawia poziome obciążenie ciągłe równomiernie rozłożone na długości rzutu

pionowego pręta ukośnego natomiast rysunek 4.20 b) statycznie równoważne obciążenie ciągłe
równomiernie rozłożone na długości tego pręta ukośnego. Siły wypadkowe z obu obciążeń muszą być sobie
równe. Możemy więc zapisać

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

11

∣

p

∣

⋅L

Y

=

∣

p'

∣

⋅L

.

(4.17)

Wartość bezwzględna zastępczego poziomego obciążenia ciągłego równomiernie rozłożonego na długości
pręta ukośnego wynosi więc

∣

p '

∣

=

∣

p

∣

⋅L

Y

L

.

(4.18)

4.3. Siły przekrojowe

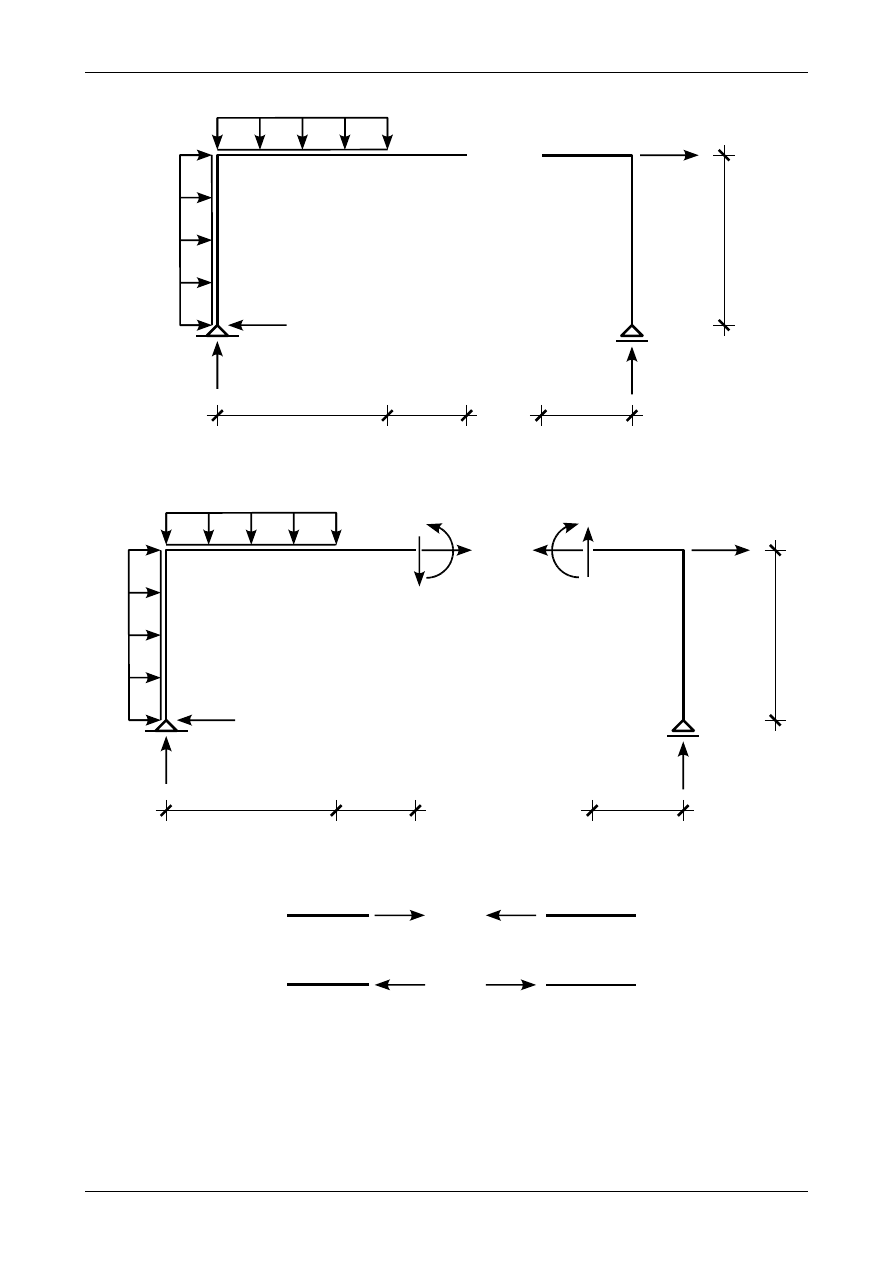
Rysunek 4.21 przedstawia przykładową ramę płaską, w której siły czynne i bierne (reakcje) znajdują

się w równowadze.

8,0 kN/m

2,

0

kN

/m

2,0

2,0

2,

0

[m]

12,0 kN/m

9,0 kN

7,0 kN

8,0 kN/m

Rys. 4.21. Siły czynne i bierne działające na ramę płaską będące w równowadze

Przetnijmy ramę płaską w dowolnym miejscu. Otrzymamy w ten sposób dwie części ramy

przedstawione na rysunku 4.22. Jak łatwo sprawdzić obie części nie znajdują się w równowadze. Aby
równowaga była zachowana w przekroju pręta w miejscu przecięcia ramy płaskiej muszą działać dodatkowe
siły. Siły te nazywamy siłami przekrojowymi. Siły przekrojowe przedstawia rysunek 4.23. Jak widać siły
przekrojowe są funkcjami zależnymi od zmiennej x, która określa nam położenie miejsca, w którym
je wyznaczamy. W przypadku płaskich układów prętowych w przekroju pręta działają trzy siły przekrjowe.

Pierwszą siła przekrojową jest siła normalna N, którą poznaliśmy już przy okazji kratownic płaskich.

Jak wiadomo jest ona dodatnia, jeżeli powoduje rozciągnięcie (wydłużenie) pręta. Dodatnią i ujemną
siłę normalną przedstawia rysunek 4.24.

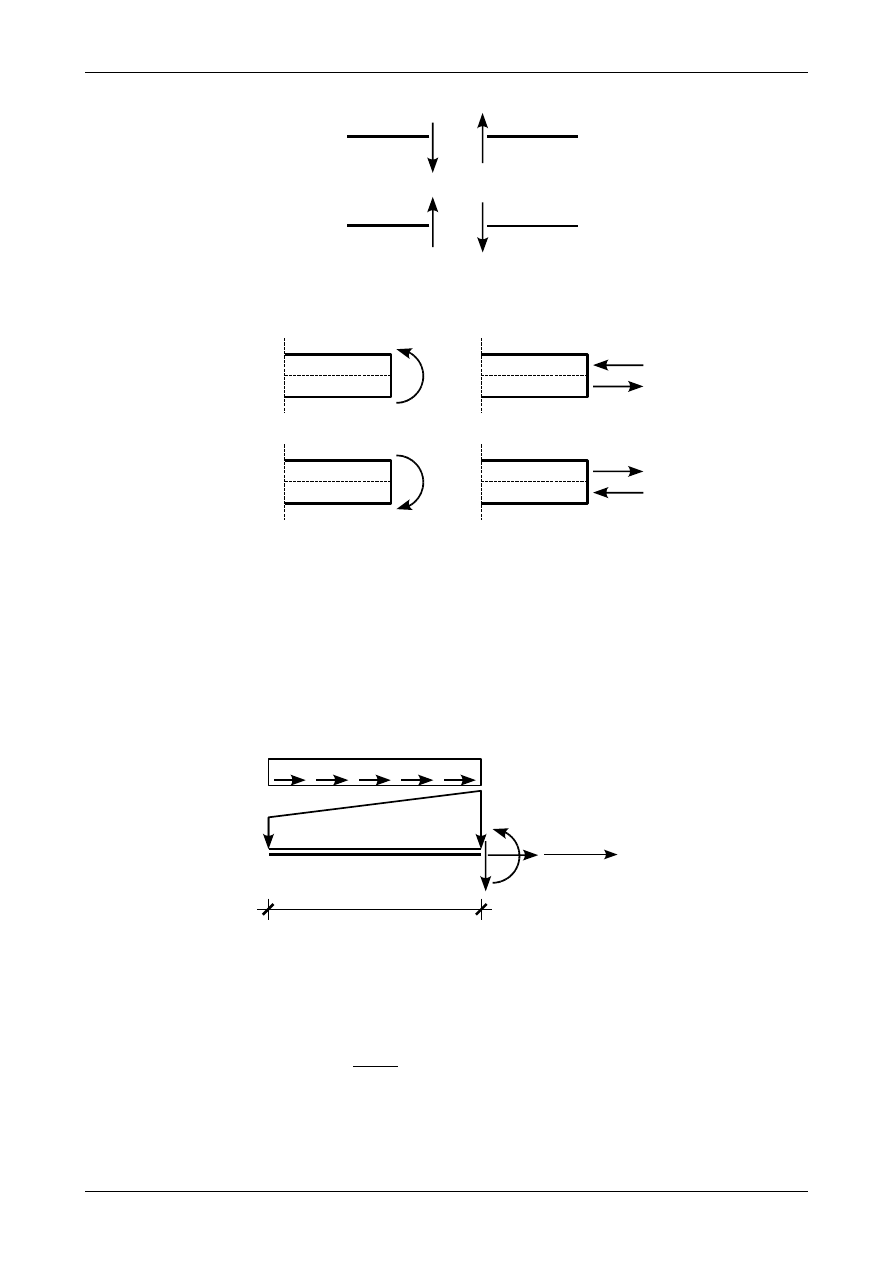
Drugą siłą przekrojową jest siła poprzeczna nazywana niekiedy siłą tnącą. W niniejszym

opracowaniu będziemy używali nazwy siła poprzeczna. Siła poprzeczna będzie dodatnia, jeżeli będzie
kręciła odciętą częścią pręta zgodnie z ruchem wskazówek zegara. Punktem obrotu będzie przeciwny
koniec części pręta. Rysunek 4.25 przedstawia dodatnią i ujemną siłę poprzeczną.

Ostatnią siłą przekrojową jest moment zginający, który rozumiemy jako moment pary sił. Jedna z

tych sił powoduje rozciąganie części przekroju pręta druga natomiast powoduje ściskanie pozostałej części
przekroju pręta. Moment zginający, który rozciąga dolną i górną część przekroju pręta przedstawia rysunek
4.26.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

12

8,0 kN/m

2,

0

kN

/m

2,0

x

12,0 kN/m

7,0 kN/m

2,0-x

2,

0

[m]

9,0 kN/m

8,0 kN/m

Rys. 4.22. Dwie części przeciętej ramy płaskiej

8,0 kN/m

2,

0

kN

/m

2,0

x

12,0 kN/m

7,0 kN/m

2,0-x

2,

0

[m]

9,0 kN/m

8,0 kN/m

N(x)

N(x)

T(x)

T(x)

M(x)

M(x)

Rys. 4.23. Siły przekrojowe

N

N

N

N

a)

b)

Rys. 4.24. Siła normalna. a) dodatnia, b) ujemna

Jako dodatni moment zginający będziemy przyjmowali moment, który rozciąga dolną część przekroju

pręta. W przypadku prętów pionowych będziemy przyjmować, że dolna część pręta jest jego prawą częścią.
Znaków momentu zginającego nie będziemy pisali na wykresie. Przyjmiemy tylko, że wykresy funkcji
momentu zginającego będziemy rysowali po stronie rozciąganej.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

13

T

a)

b)

T

T

T

Rys. 4.25. Siła poprzeczna. a) dodatnia, b) ujemna

M

M

S

S

S

S

a)

b)

Rys. 4.26. Moment zginający. a) rozciągający dolną część przekroju pręta, b) rozciągający górną część przekroju pręta

4.4. Równania różniczkowe równowagi

Okazuje się, że pomiędzy: funkcjami obciążenia ciągłego q i h oraz funkcjami siły normalnej,

poprzecznej i momentu zginającego istnieją pewne zależności nazywane różniczkowymi równaniami
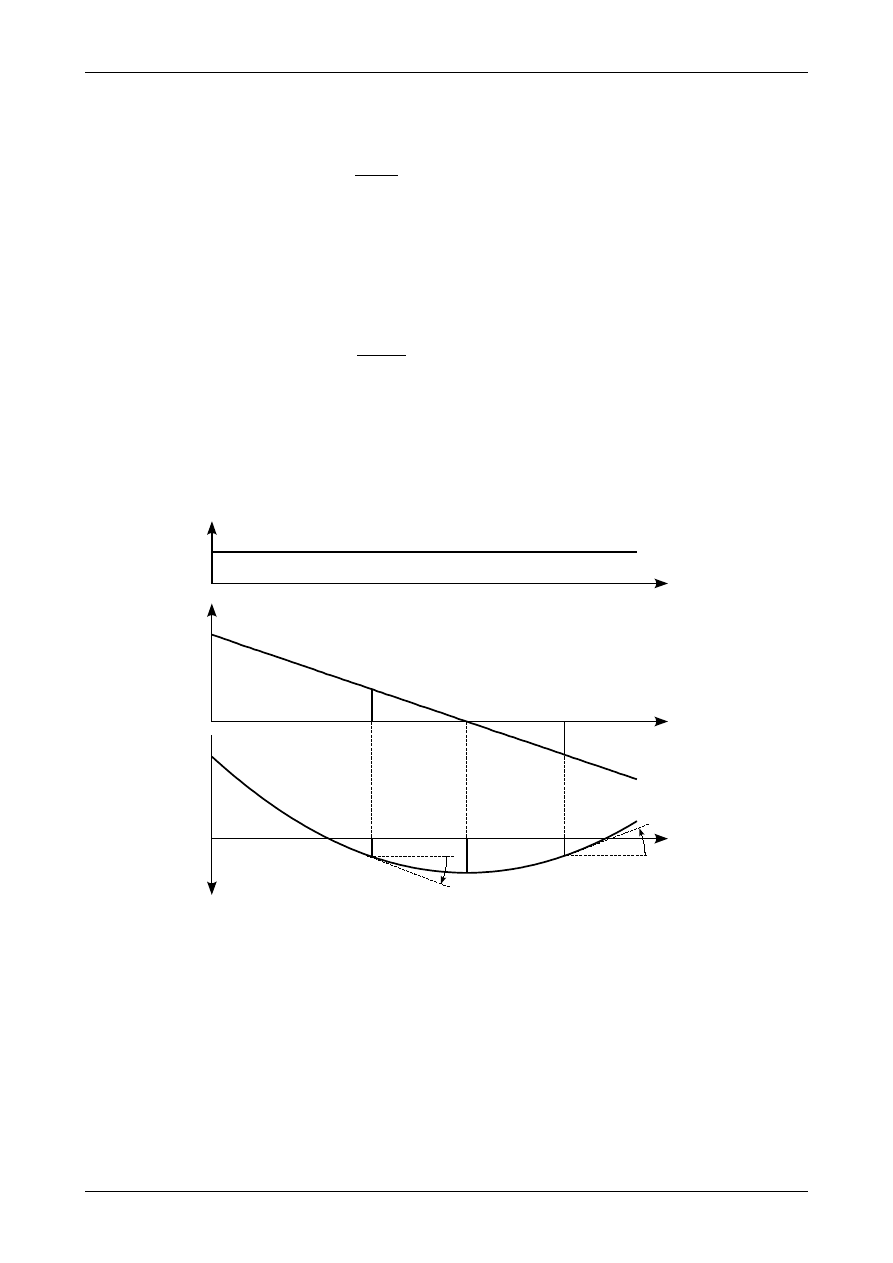
równowagi. Równań tych jest trzy. Rysunek 4.27 przedstawia część pręta, w którym oś X zwrócona jest w
prawą stronę, obciążoną obciążeniem ciągłym prostopadłym i równoległym do osi pręta. Oba obciążenia są
dodatnie.

q(x)

h(x)

X

N(x)

T(x)

M(x)

x

Rys. 4.27. Oś pręta zwrócona w prawą stronę

Pierwsze równanie różniczkowe równowagi ma postać

dN



x



dx

=−

h



x



(4.19)

i opisuje zależność pomiędzy funkcją obciążenia ciągłego równoległego do osi pręta a siłą normalną w tym
pręcie.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

14

Drugie równanie różniczkowe równowagi ma postać

dT



x



dx

=−q



x



(4.20)

i opisuje zależność pomiędzy funkcją obciążenia ciągłego prostopadłego do osi pręta a siłą poprzeczną w
tym pręcie.

Trzecie równanie różniczkowe równowagi ma postać

dM



x



dx

=T



x



(4.21)

i opisuje zależność pomiędzy funkcją momentu zginającego a funkcją siły poprzecznej w tym pręcie.

Jak więc widać pochodną funkcji momentu zginającego jest funkcja siły poprzecznej natomiast

pochodną funkcji siły poprzecznej jest minus funkcja obciążenia ciągłego.

T(x)

M(x)

X

X

O

1

α

1

α

2

T

1

T

2

M

EXT

M

1

q(x)

X

q=const.

M

2

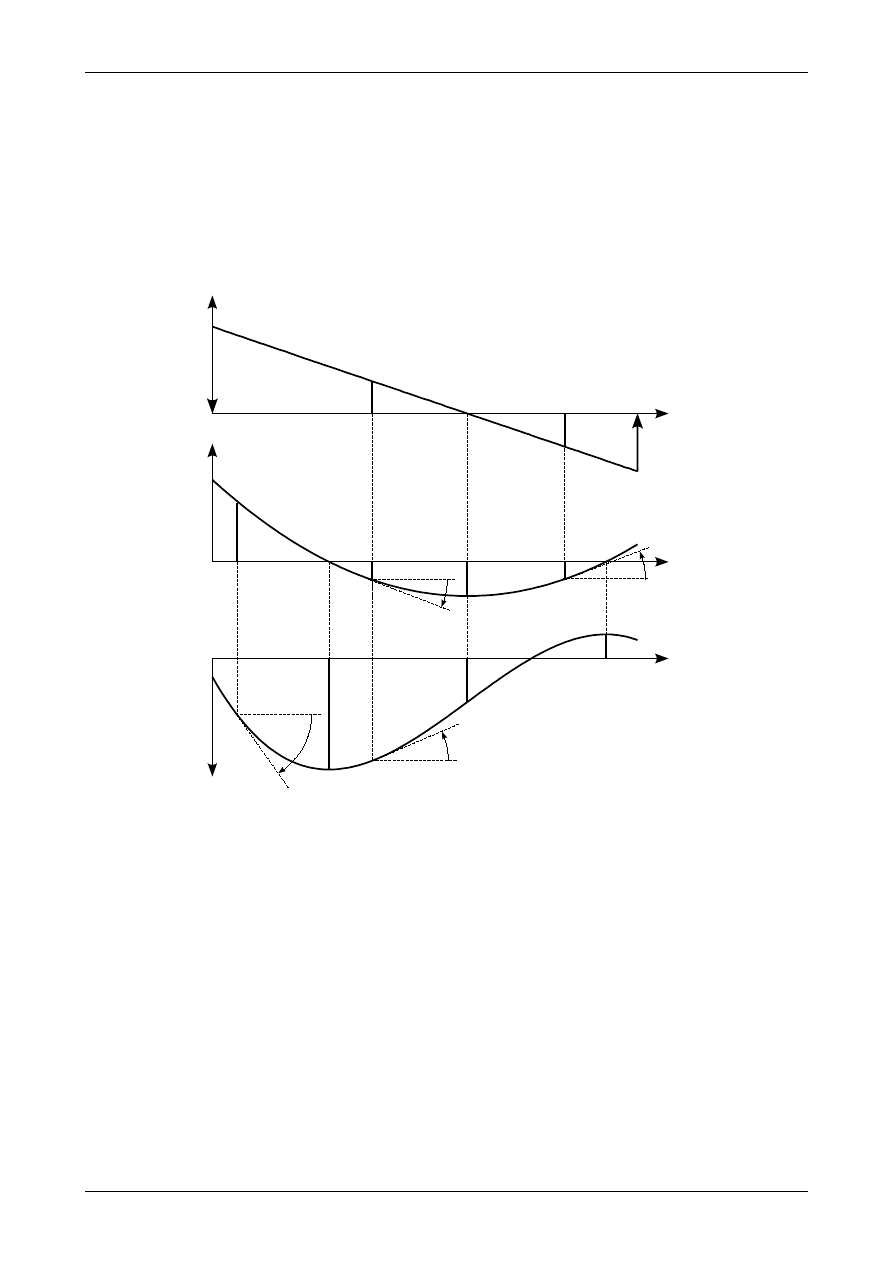
Rys. 4.28. Wykresy obciążenia ciągłego, siły poprzecznej i momentu zginającego

Rysunek 4.28 przedstawia przykładowe wykresy obciążenia ciągłego prostopadłego do osi pręta, siły

poprzecznej i momentu zginającego spełniające równania (4.20) i (4.21). Zwrot osi M(x) jest w dół,
ponieważ dodatni moment rozciąga dolną część przekroju pręta. W miejscu, w którym siła poprzeczna
posiada miejsce zerowe (punkt O

1

) moment zginający będzie miał ekstremum. Jest to zgodne z warunkiem

koniecznym istnienia ekstremum funkcji. Zgodnie z interpretacją pochodnej funkcji w punkcie wartość
tangensa kąta nachylenia stycznej do funkcji momentu zginającego

α

1

wynosi

tg





1



=

T

1

.

(4.22)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

15

Wartość tangensa kąta nachylenia stycznej do funkcji momentu zginającego

α

2

wynosi

tg





2



=T

2

.

(4.23)

Kąt

α

1

jest dodatni, ponieważ kręci on od osi X do osi M(x) natomiast kąt

α

2

jest ujemny, ponieważ kręci on

od osi M(x) do osi X.

q(x)

T(x)

M(x)

X

X

X

O

1

O

2

O

3

α

1

α

2

q

1

q

2

T

EXT

M

EXT1

M

EXT2

T

3

α

3

T

1

α

4

T

2

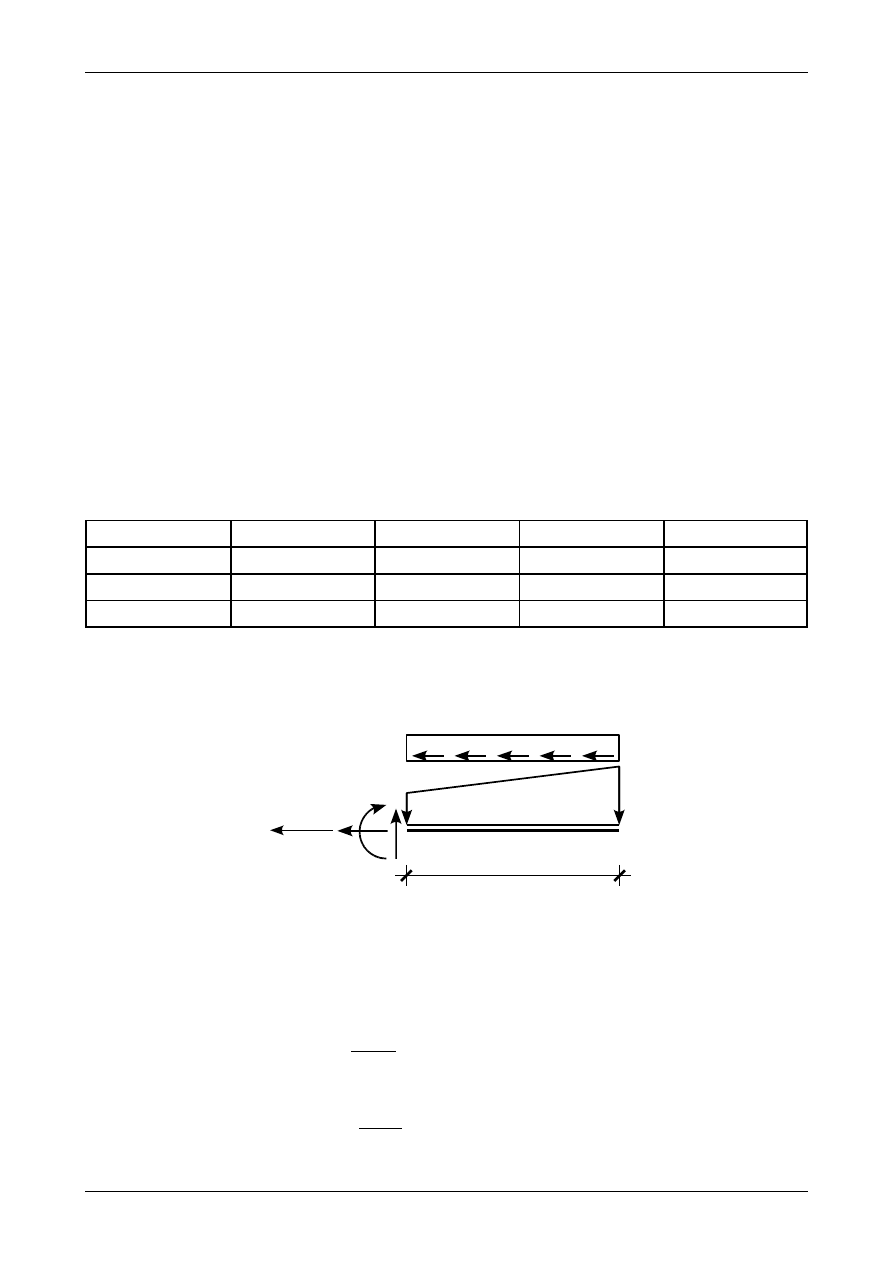
Rys. 4.29. Wykresy obciążenia ciągłego, siły poprzecznej i momentu zginającego

Rysunek 4.29 przedstawia przykładowe wykresy obciążenia ciągłego prostopadłego do osi pręta, siły

poprzecznej i momentu zginającego spełniające równania (4.20) i (4.21). W miejscu, w którym funkcja
obciążenia ciągłego posiada miejsce zerowe (punkt O

1

) siła poprzeczna będzie miała ekstremum. W miejscu,

w którym funkcja siły poprzecznej posiada miejsce zerowe (punkty O

2

oraz O

3

) funkcja momentu

zginającego będzie miała ekstrema. Wartość tangensa kąta nachylenia stycznej do funkcji siły poprzecznej

α

1

wynosi

tg





1



=−q

1

.

(4.24)

Wartość tangensa kąta nachylenia stycznej do funkcji siły poprzecznej

α

2

wynosi

tg





2



=−q

2

.

(4.25)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

16

Wartość tangensa kąta nachylenia stycznej do funkcji momentu zginającego

α

3

wynosi

tg





3



=T

3

.

(4.26)

Wartość tangensa kąta nachylenia stycznej do funkcji momentu zginającego

α

4

wynosi

tg





4



=T

4

.

(4.27)

Kąt

α

1

jest ujemny, ponieważ kręci on od osi T(x) do osi X natomiast kąt

α

2

jest dodatni, ponieważ kręci on

od osi X do osi T(x). Kąt

α

3

jest dodatni, ponieważ kręci on od osi X do osi M(x) natomiast kąt

α

4

jest

ujemny, ponieważ kręci on od osi M(x) do osi X.

W niniejszym opracowaniu rozważamy obciążenia ciągłe prostopadłe do osi pręta zerowe, stałe oraz

liniowe. Tabela 1 przedstawia postacie funkcji siły poprzecznej oraz momentu zginającego w zależności od
postaci obciążenia ciągłego.

Tabela 1. Funkcje siły poprzecznej oraz momentu zginającego w zależności od funkcji obciążenia ciągłego.

Funkcja

Przypadek 1

Przypadek 2

Przypadek 3

Przypadek 4

q(x)

0

0

const. (≠0)

liniowa

T(x)

0

const. (≠0)

liniowa

kwadratowa

M(X)

const. (≠0)

liniowa

kwadratowa

wielomian 3 stopnia

Opisane powyżej różniczkowe równania równowagi będą najczęściej stosowane. Jednak nie zawsze

oś X musi być zwrócona w prawo. Rysunek 4.30 przedstawia sytuację, kiedy oś X jest zwrócona w lewo.

q(x)

h(x)

X

N(x)

T(x)

M(x)

x

Rys. 4.30. Oś pręta zwrócona w lewą stronę

Równania różniczkowe równowagi w przypadku pręta, w którym oś X jest zwrócona w lewą stroną

będą miały następującą postać

dN



x



dx

=−

h



x



,

(4.28)

dT



x



dx

=q



x



,

(4.29)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

17

dM



x



dx

=−T



x



.

(4.30)

4.5. Metoda ogólna wyznaczania funkcji sił przekrojowych

Metoda ogólna wyznaczania funkcji sił przekrojowych polega na przecięciu belki lub ramy płaskiej w

dowolnym punkcie przedziału w odległości x od jednego z jego końców i rozpatrywaniu równowagi
wszystkich sił działających na odciętą część. Punktami granicznymi przedziałów są: punkty przyłożenia sił
skupionych (sił czynnych i reakcji), punkty przyłożenia momentów skupionych, punkty, w których zaczyna
się i kończy obciążenie ciągłe.

Siłę normalną wyznacza się z równania sumy rzutów wszystkich sił działających na odciętą

część belki lub ramy płaskiej na kierunek tej siły.

Siłę poprzeczną wyznacza się z równania sumy rzutów wszystkich sił działających na odciętą

część belki lub ramy płaskiej na kierunek tej siły.

Moment zginający wyznacza się z równania sumy momentów wszystkich sił działających na

odciętą część belki lub ramy płaskiej względem punktu, w którym wyznaczamy moment zginający.

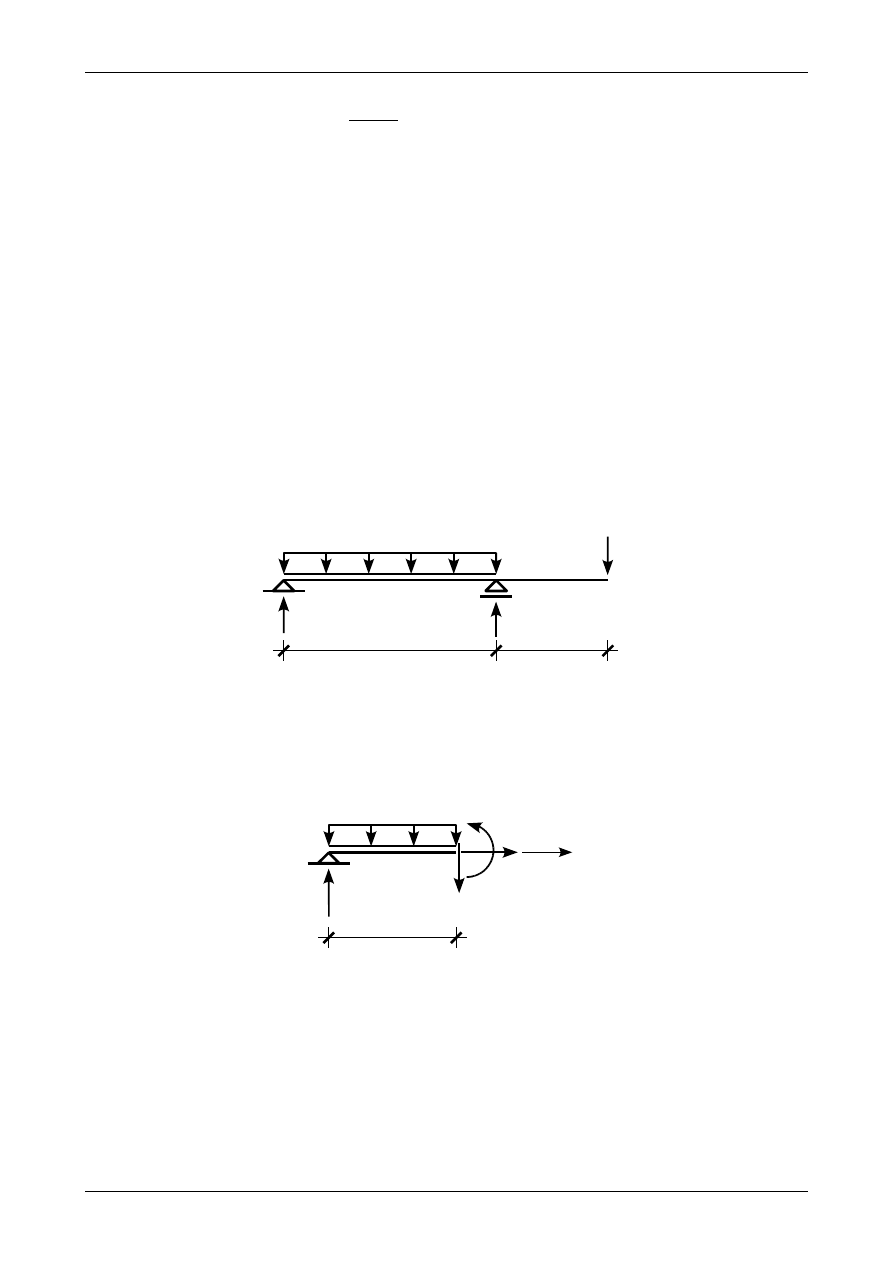
Rysunek 4.31 przedstawia przykładową belkę z działającymi na nią siłami czynnymi i biernymi

(reakcjami) będącymi w równowadze. Belkę dzielimy na dwa przedziały AB i BC.

q

P

A

B

C

V

A

V

B

a

b

Rys. 4.31. Belka

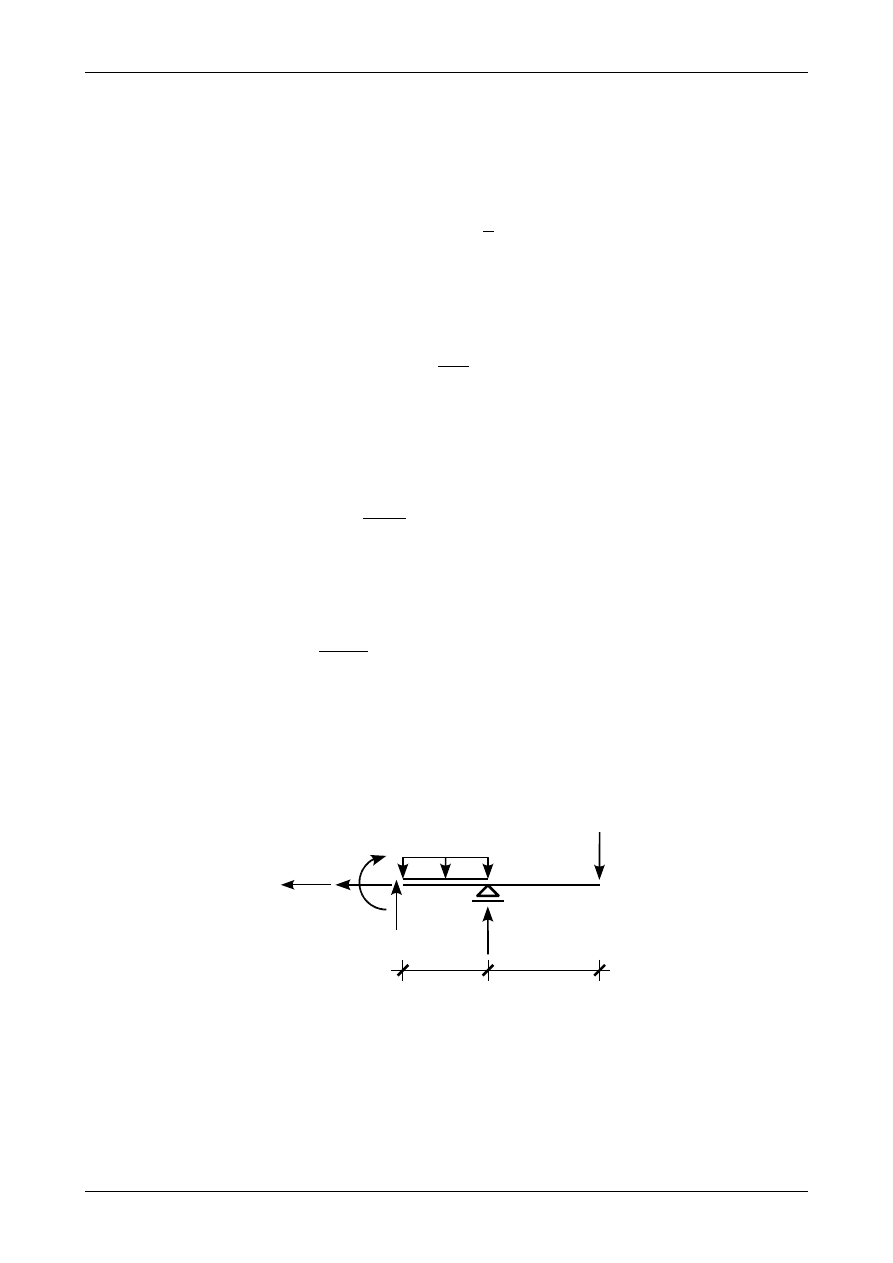
Aby wyznaczyć siły przekrojowe w przedziale AB przecinamy belkę w dowolnym punkcie tego

przedziału. Odciętą lewą część belki z osią X skierowaną w prawą stronę przedstawia rysunek 4.32.

q

A

V

A

x

M(x)

X

N(x)

T(x)

Rys. 4.32. Odcięta lewa część belki w przedziale AB

Jak widać na rysunku 4.32 siła normalna w przedziale AB wynosi zero. Siłę poprzeczną w przedziale

AB wyznaczymy z równania równowagi

 T

=

T



x



−

V

A



q

⋅

x

=

0

.

(4.31)

Ostatecznie funkcja siły poprzecznej w przedziale AB ma postać

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

18

T



x



=

V

A

−

q

⋅

x

.

(4.32)

Funkcję momentu zginającego w przedziale AB wyznaczymy z równania równowagi

 M

=−

M



x





V

A

⋅

x

−

q

⋅

x

⋅

x

2

=

0

.

(4.33)

Ostatecznie funkcje momentu zginającego w przedziale AB ma postać

M



x



=V

A

⋅x−

q

⋅x

2

2

.

(4.34)

Drugie różniczkowe równanie równowagi (4.20) w przypadku części belki na rysunku 4.32 będzie

miało postać

dT



x



dx

=−

q

.

(4.35)

Trzecie różniczkowe równanie równowagi (4.21) będzie miało postać

dM



x



dx

=V

A

−q⋅x=T



x



.

(4.36)

Jak więc widać funkcje siły poprzecznej (4.32) i momentu zginającego (4.34) spełniają różniczkowe
równania równowagi.

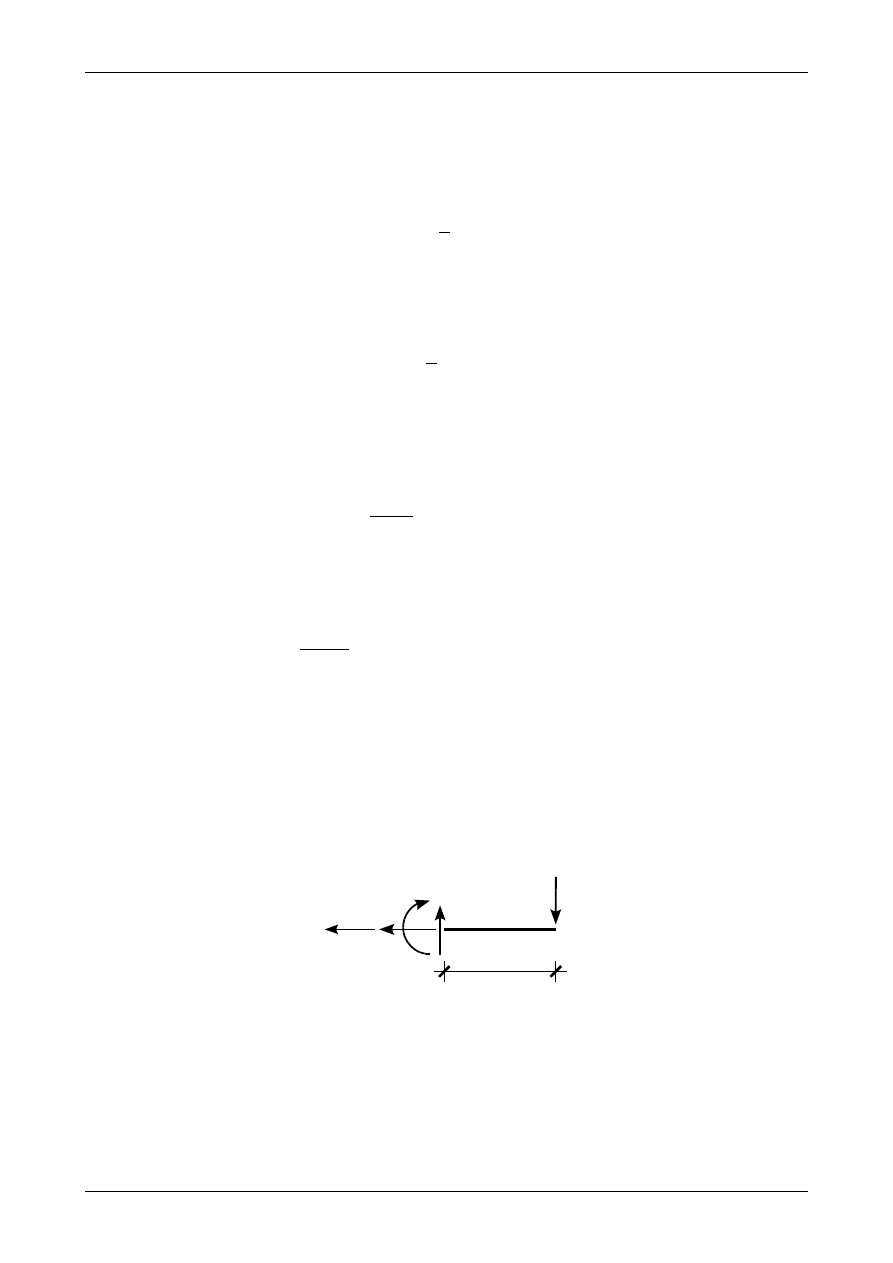
Siły przekrojowe w przedziale AB możemy wyznaczyć także rozpatrując równowagę prawej części

belki przedstawionej na rysunku 4.33. Oś X jest w tym przypadku zwrócona w lewo.

q

P

B

C

V

B

x

b

X

M(x)

N(x)

T(x)

Rys. 4.33. Odcięta prawa część belki w przedziale AB

Siłę poprzeczną w przedziale AB wyznaczymy z równania równowagi

 T =T



x



V

B

−q⋅x−P=0

.

(4.37)

Ostatecznie funkcja siły poprzecznej w przedziale AB ma postać

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

19

T



x



=−V

B

q⋅xP

.

(4.38)

Funkcję momentu zginającego w przedziale AB wyznaczymy z równania równowagi

 M =M



x



−V

B

⋅xq⋅x⋅

x

2

P⋅



x

b



=0

.

(4.39)

Ostatecznie funkcje momentu zginającego w przedziale AB ma postać

M



x



=V

B

⋅x−q⋅x⋅

x

2

−P⋅



x

b



.

(4.40)

Drugie różniczkowe równanie równowagi (4.29) w przypadku części belki na rysunku 4.33 będzie

miało postać

dT



x



dx

=q

.

(4.41)

Trzecie różniczkowe równanie równowagi (4.30) będzie miało postać

dM



x



dx

=V

B

−q⋅x−P=−T



x



.

(4.42)

Jak więc widać funkcje siły poprzecznej (4.38) i momentu zginającego (4.40) spełniają różniczkowe
równania równowagi dla pręta, w którym oś X jest skierowana w lewo.

Pomimo, że postacie funkcji siły poprzecznej i momentu zginającego dla obu części belki są różne ich

wykresy muszą być identyczne.

Rysunek 4.34 przedstawia odciętą prawą część belki w przedziale BC. Rozpatrywanie lewej części

belki jest nieefektywne, ponieważ na tą część działa dużo więcej sił i łatwiej o pomyłkę.

P

C

x

X

M(x)

N(x)

T(x)

Rys. 4.34. Odcięta prawa część belki w przedziale BC

Jak widać na rysunku 4.34 siła normalna w przedziale BC wynosi zero. Siłę poprzeczną w przedziale

BC wyznaczymy z równania równowagi

 T=T



x



−P =0

.

(4.43)

Dr inż. Janusz Dębiński

Zaoczni

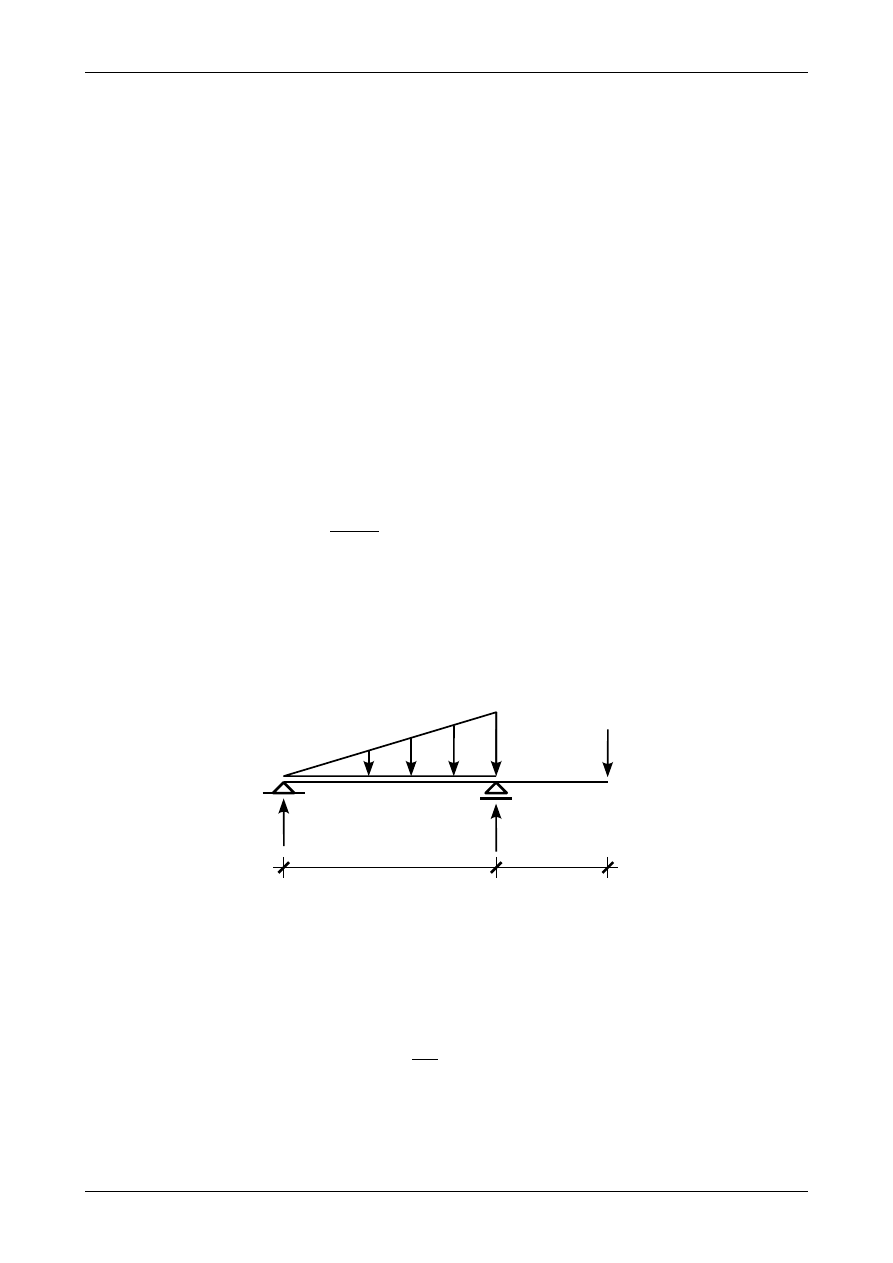
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

20

Ostatecznie funkcja siły poprzecznej w przedziale BC ma postać

T



x



=P

.

(4.44)

Funkcję momentu zginającego w przedziale BC wyznaczymy z równania równowagi

 M =M



x



P⋅x=0

.

(4.45)

Ostatecznie funkcje momentu zginającego w przedziale AB ma postać

M



x



=−P⋅x

.

(4.46)

Drugie różniczkowe równanie równowagi wynosi w przedziale BC zero. Natomiast trzecie równanie

ma postać

dM



x



dx

=−P=−T



x



.

(4.47)

Jak więc widać funkcja momentu zginającego (4.46) spełnia różniczkowe równanie równowagi dla pręta, w
którym oś X jest skierowana w lewo.

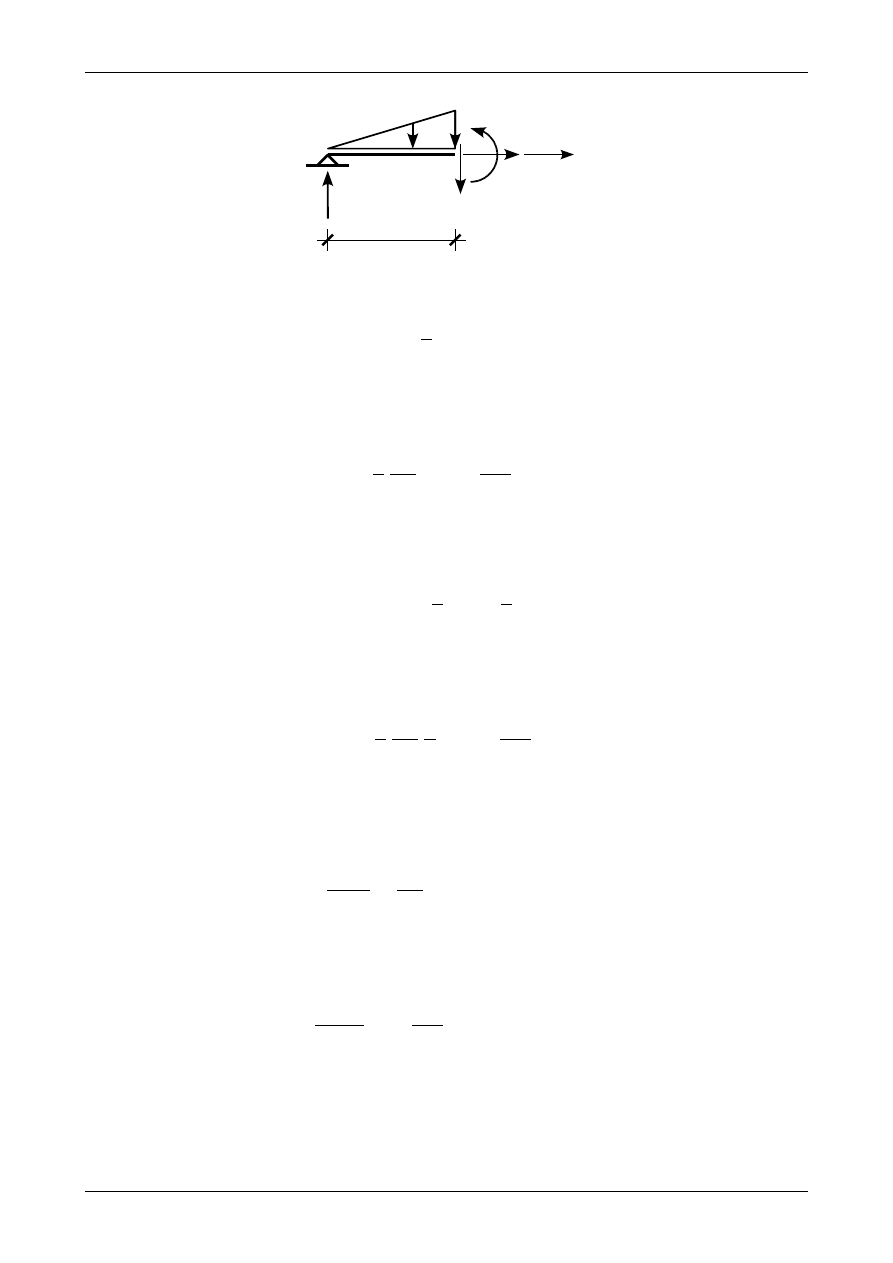
Rysunek 4.35 przedstawia belkę z obciążeniem ciągłym trójkątnym rosnącym. Wszystkie siły

działające na tę belkę znajdują się w równowadze.

q

P

A

B

C

V

A

V

B

a

b

Rys. 4.35. Belka obciążeniem ciągłym trójkątnym rosnącym

Chcąc wyznaczyć funkcje siły poprzecznej i momentu zginającego w przedziale AB będziemy

rozpatrywać równowagę lewej części przedstawionej na rysunku 4.36. Funkcja obciążenia ciągłego, zgodnie
z (4.4), będzie miała postać

q



x



=

q

⋅x
a

.

(4.48)

Siłę poprzeczną w tym przedziale wyznaczymy z równania równowagi

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

21

A

V

A

x

q(x)

M(x)

X

N(x)

T(x)

Rys. 4.36. Lewa część belki w przedziale AB

 T=T



x



−V

A



1

2

⋅q



x



⋅x=0

.

(4.49)

Funkcja siły poprzecznej będzie miała ostatecznie postać.

T



x



=V

A

−

1
2

⋅

q

⋅x
a

⋅x=V

A

−

q

⋅x

2

2

⋅a

.

(4.50)

Funkcję momentu zginającego w przedziale AB wyznaczymy z równania równowagi

 M =−M



x



V

A

⋅x−

1
2

⋅q



x



⋅x⋅

x
3

=0

.

(4.51)

Ostatecznie funkcja momentu zginającego będzie miała postać.

M



x



=V

A

⋅x−

1
2

⋅

q

⋅x

a

⋅

x

3

=V

A

⋅x−

q

⋅x

3

6

⋅a

.

(4.52)

Drugie różniczkowe równanie równowagi (4.20) w przypadku części belki na rysunku 4.36 będzie

miało postać

dT



x



dx

=−

q

⋅x

a

=−q



x



.

(4.53)

Trzecie różniczkowe równanie równowagi (4.21) będzie miało postać

dM



x



dx

=V

A

−

q

⋅x

2

2

⋅a

=T



x



.

(4.54)

Jak więc widać funkcje siły poprzecznej (4.50) i momentu zginającego (4.52) spełniają różniczkowe
równania równowagi.

Rysunek 4.37 przedstawia belkę z obciążeniem ciągłym trójkątnym malejącym. Wszystkie siły

działające na tę belkę znajdują się w równowadze.

Dr inż. Janusz Dębiński

Zaoczni

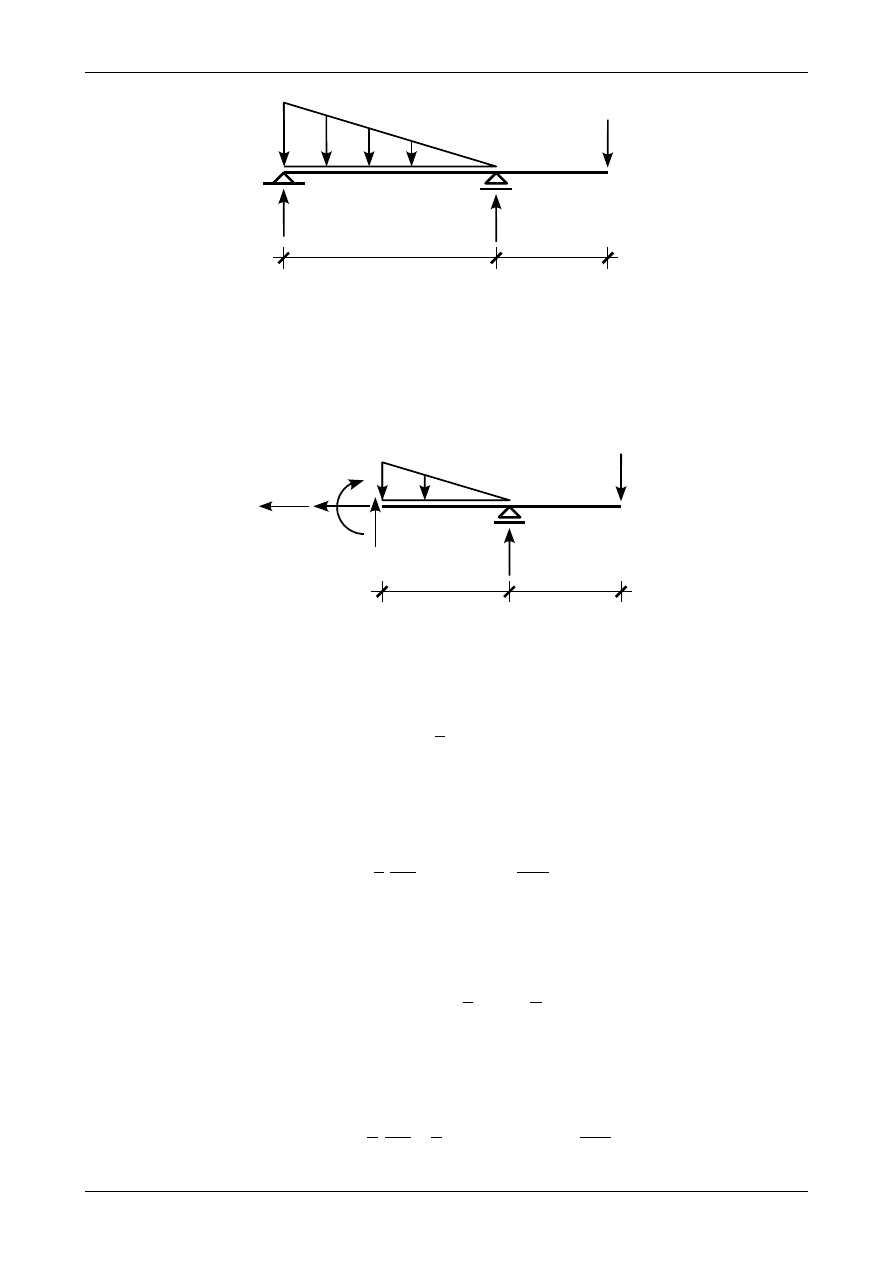
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

22

q

P

A

B

C

V

A

V

B

a

b

Rys. 4.37. Belka obciążeniem ciągłym trójkątnym malejącym

Chcąc wyznaczyć funkcje siły poprzecznej i momentu zginającego w przedziale AB będziemy

rozpatrywać równowagę prawej części przedstawionej na rysunku 4.38. W ten sposób unikniemy obciążenia
ciągłego będącego trapezem w lewej części tej belki. Funkcję obciążenia ciągłego wyznaczymy ze wzoru
(4.48).

q(x)

P

B

C

V

B

x

b

X

M(x)

N(x)

T(x)

Rys. 4.38. Prawa część belki w przedziale AB

Siłę poprzeczną w tym przedziale wyznaczymy z równania równowagi

 T =T



x



V

B

−P −

1
2

⋅q



x



⋅x=0

.

(4.55)

Funkcja siły poprzecznej będzie miała ostatecznie postać.

T



x



=−V

B

P

1
2

⋅

q

⋅x

a

⋅x=−V

B

P

q

⋅x

2

2

⋅a

.

(4.56)

Funkcję momentu zginającego w przedziale AB wyznaczymy z równania równowagi

 M =M



x



−V

B

⋅xP⋅



x

b





1
2

⋅q



x



⋅x⋅

x

3

=0

.

(4.57)

Ostatecznie funkcja momentu zginającego będzie miała postać.

M



x



=V

B

⋅x−P⋅



x

b



−

1
2

⋅

q

⋅x
a

⋅x⋅

x
3

=V

B

⋅x−P⋅



x

b



−

q

⋅x

3

6

⋅a

.

(4.58)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

23

Drugie różniczkowe równanie równowagi (4.29) w przypadku części belki na rysunku 4.38 będzie

miało postać

dT



x



dx

=

q

⋅x

a

=q



x



.

(4.59)

Trzecie różniczkowe równanie równowagi (4.30) będzie miało postać

dM



x



dx

=V

B

−P−

q

⋅x

2

2

⋅a

=−T



x



.

(4.60)

Jak więc widać funkcje siły poprzecznej (4.56) i momentu zginającego (4.58) spełniają różniczkowe
równania równowagi dla pręta, w którym oś X jest skierowana w lewo.

h

X

M(x)

N(x)

T(x)

q

A

V

A

H

A

M

A

x

Rys. 4.39. Część słupa ramy płaskiej

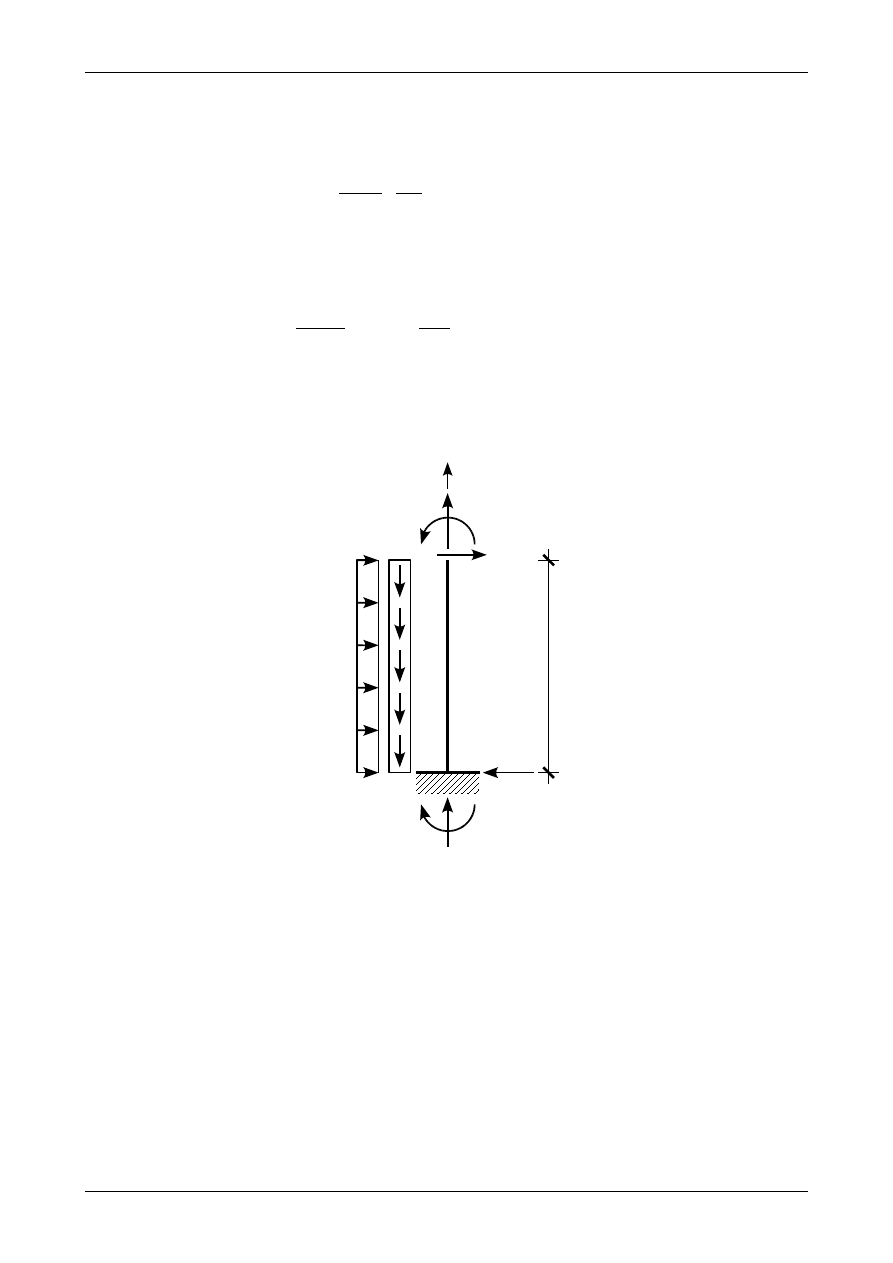
Rysunek 4.39 przedstawia wyciętą część słupa ramy płaskiej. Jako dolną część pręta przyjmiemy jego

prawą część. Na słup działają obciążenia ciągłe równomiernie rozłożone prostopadłe i równoległe do osi
słupa. Obciążenia te wynoszą

q



x



=

q

,

(4.61)

h



x



=−h

.

(4.62)

Funkcję siły normalnej w słupie wyznaczymy z równania równowagi

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

24

 N =N



x



V

A

−h⋅x=0

.

(4.63)

Funkcja ta ma ostatecznie postać

N



x



=−V

A

h⋅x

.

(4.64)

Funkcję siły poprzecznej w słupie wyznaczymy z równania równowagi

 T =T



x



−H

A

q⋅x=0

.

(4.65)

Funkcja ta ma ostatecznie postać

T



x



=H

A

−q⋅x

.

(4.66)

Funkcję momentu zginającego w słupie wyznaczymy z równania równowagi

 M =−M



x



H

A

⋅x−q⋅x⋅

x

2

M

A

=0

.

(4.67)

Ostatecznie funkcja momentu zginającego ma postać

M



x



=H

A

⋅x−

q

⋅x

2

2

M

A

.

(4.68)

Pierwsze różniczkowe równanie równowagi ma postać

dN



x



dx

=h=−h



x



.

(4.69)

Drugie różniczkowe równanie równowagi ma postać

dT



x



dx

=−q=−q



x



.

(4.70)

Trzecie różniczkowe równanie równowagi ma postać

dM



x



dx

=H

A

−q⋅x=T



x



.

(4.71)

Dr inż. Janusz Dębiński

Zaoczni

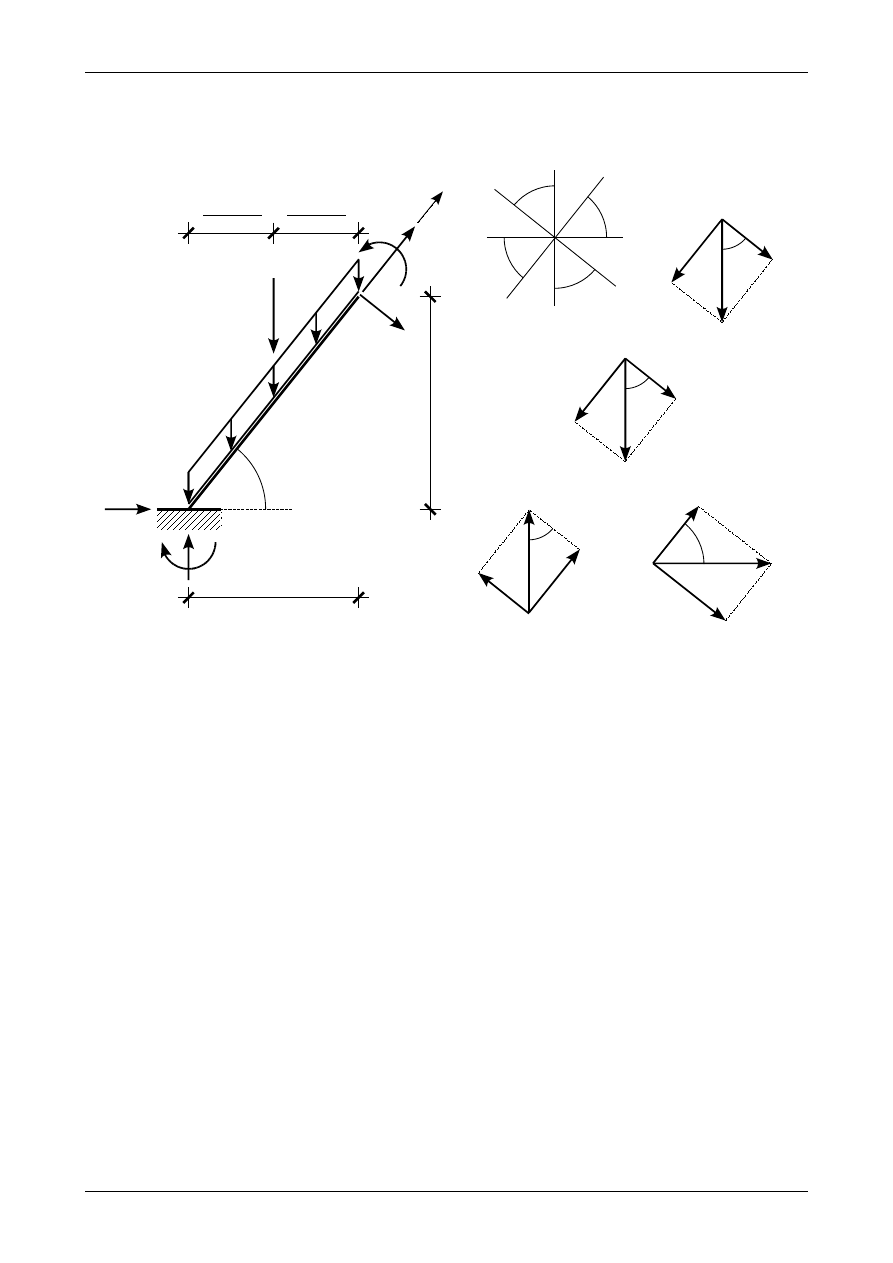
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

25

Jak więc widać funkcje siły normalnej (4.64), siły poprzecznej (4.66) i momentu zginającego (4.68)
spełniają różniczkowe równania równowagi.

p

- x

-

X

α

α

α

α

α

α

p

q

h

x

⋅cos







x⋅

sin







V

A

H

A

M

A

α

V

A

H

A

α

M

(x

)

N(

x)

T(

x)

W

x

⋅cos







2

x

⋅cos







2

α

W

Rys. 4.40. Pręt ukośny z pionowym obciążeniem ciągłym równomiernie rozłożonym na długości pręta

Rysunek 4.40 przedstawia pręt ukośny z pionowym obciążeniem ciągłym równomiernie rozłożonym

na długości tego pręta. Obciążenie to możemy rozłożyć na obciążenie prostopadłe i równoległe do osi pręta
ukośnego. Zgodnie z rysunkiem 4.40 obciążenia te wynoszą

q



x



=

q

=

p

⋅

cos







,

(4.72)

h



x



=h=− p⋅sin







.

(4.73)

Siła wypadkowa z obciążenia ciągłego p wynosi

W

=

p

⋅

x

.

(4.74)

Funkcję siły normalnej w pręcie ukośnym wyznaczymy z równania równowagi

 N

=

N



x





V

A

⋅

sin









H

A

⋅

cos







−

W

⋅

sin







=

0

.

(4.75)

Ostatecznie funkcja siły normalnej będzie miała postać

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

26

N



x



=−V

A

⋅sin







−H

A

⋅cos







 p⋅x⋅sin







.

(4.76)

Funkcję siły poprzecznej w pręcie ukośnym wyznaczymy z równania równowagi

 T =T



x



−V

A

⋅cos







H

A

⋅sin







W⋅cos







=0

.

(4.77)

Ostatecznie funkcja siły poprzecznej będzie miała postać

T



x



=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅cos







.

(4.78)

Funkcję momentu zginającego w pręcie ukośnym wyznaczymy z równania równowagi

 M =−M



x



V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−W⋅

x

⋅cos







2

M

A

=0

.

(4.79)

Ostatecznie funkcja momentu zginającego będzie miała postać

M



x



=V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−

p

⋅x

2

⋅cos







2

M

A

.

(4.80)

Pierwsze różniczkowe równanie równowagi ma postać

dN



x



dx

= p⋅sin







=−h



x



.

(4.81)

Drugie różniczkowe równanie równowagi ma postać

dT



x



dx

=−p⋅cos







=−q



x



.

(4.82)

Trzecie różniczkowe równanie równowagi ma postać

dM



x



dx

=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅cos







=T



x



.

(4.83)

Jak więc widać funkcje siły normalnej (4.76), siły poprzecznej (4.78) i momentu zginającego (4.80)
spełniają różniczkowe równania równowagi.

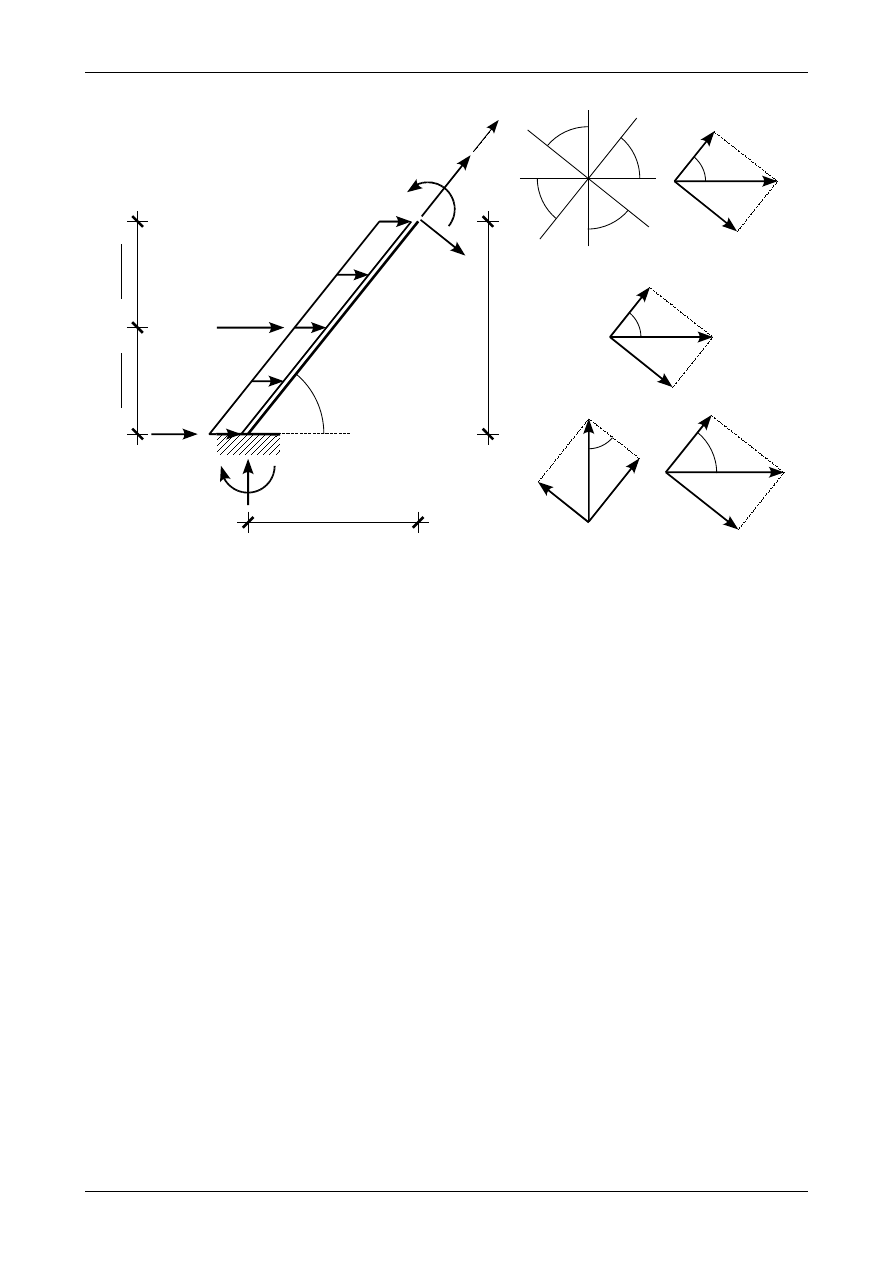
Rysunek 4.41 przedstawia pręt ukośny z poziomym obciążeniem ciągłym równomiernie rozłożonym

na długości tego pręta. Obciążenie to możemy rozłożyć na obciążenie prostopadłe i równoległe do osi pręta
ukośnego. Zgodnie z rysunkiem 4.41 obciążenia te wynoszą

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

27

X

α

α

α

α

α

p

q

h

p

- x

-

α

x

⋅cos







x⋅

sin







V

A

H

A

M

A

M

(x

)

N(

x)

T(

x)

W

α

V

A

H

A

α

x⋅

sin







2

x⋅

sin







2

α

W

Rys. 4.41. Pręt ukośny z poziomym obciążeniem ciągłym równomiernie rozłożonym na długości pręta

q



x



=q= p⋅sin







,

(4.84)

h



x



=h= p⋅cos







.

(4.85)

Siła wypadkowa z obciążenia ciągłego p wynosi

W

=

p

⋅

x

.

(4.86)

Funkcję siły normalnej w pręcie ukośnym wyznaczymy z równania równowagi

 N =N



x



V

A

⋅sin







H

A

⋅cos







W⋅cos







=0

.

(4.87)

Ostatecznie funkcja siły normalnej będzie miała postać

N



x



=−V

A

⋅sin







−H

A

⋅cos







− p⋅x⋅cos







.

(4.88)

Funkcję siły poprzecznej w pręcie ukośnym wyznaczymy z równania równowagi

 T =T



x



−V

A

⋅cos







H

A

⋅sin







W⋅sin







=0

.

(4.89)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

28

Ostatecznie funkcja siły poprzecznej będzie miała postać

T



x



=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅sin







.

(4.90)

Funkcję momentu zginającego w pręcie ukośnym wyznaczymy z równania równowagi

 M =−M



x



V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−W⋅

x

⋅sin







2

M

A

=0

.

(4.91)

Ostatecznie funkcja momentu zginającego będzie miała postać

M



x



=V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−

p

⋅x

2

⋅sin







2

M

A

.

(4.92)

Pierwsze różniczkowe równanie równowagi ma postać

dN



x



dx

=− p⋅cos







=−h



x



.

(4.93)

Drugie różniczkowe równanie równowagi ma postać

dT



x



dx

=−p⋅sin







=−q



x



.

(4.94)

Trzecie różniczkowe równanie równowagi ma postać

dM



x



dx

=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅sin







=T



x



.

(4.95)

Jak więc widać funkcje siły normalnej (4.88), siły poprzecznej (4.90) i momentu zginającego (4.92)
spełniają różniczkowe równania równowagi.

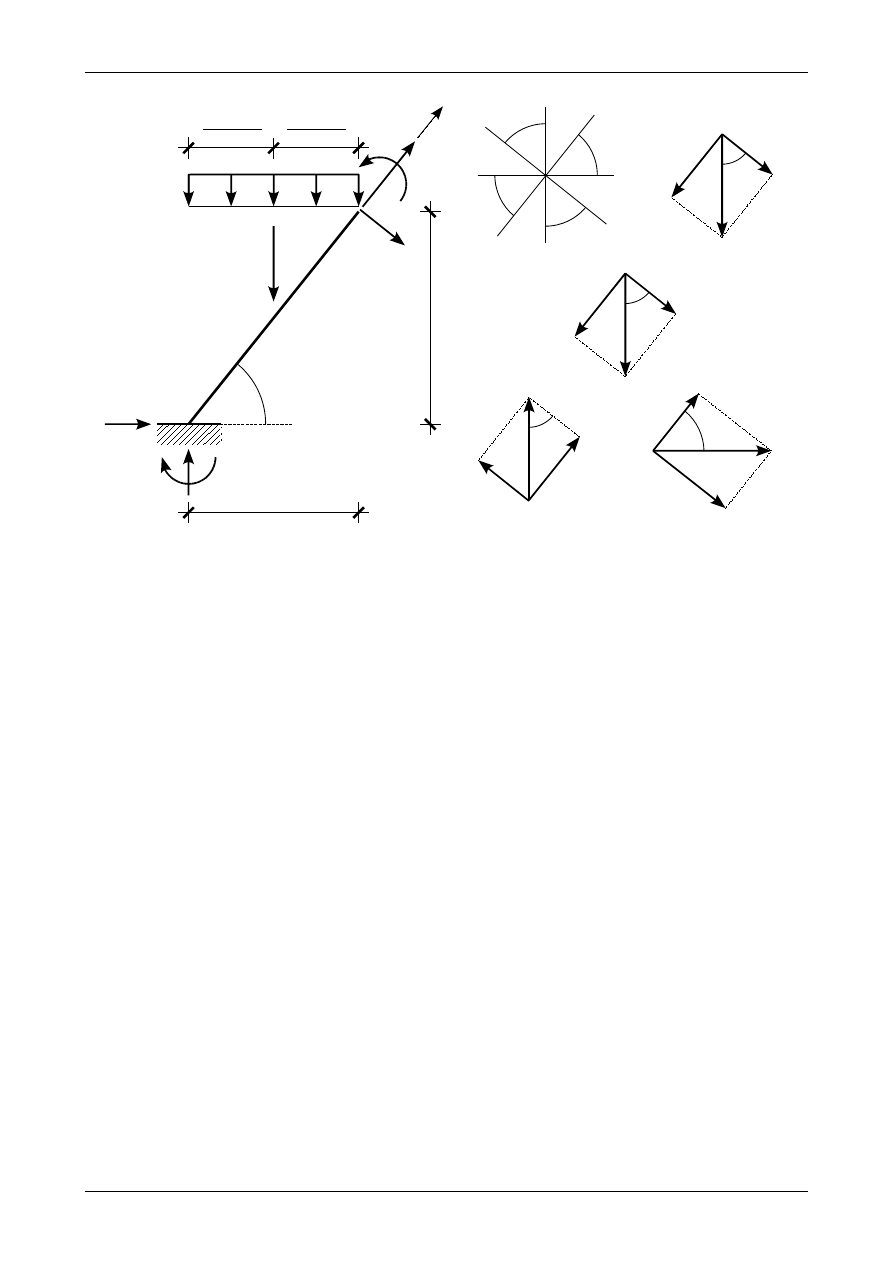
Rysunek 4.42 przedstawia pręt ukośny z pionowym obciążeniem ciągłym równomiernie rozłożonym

na długości rzutu poziomego tego pręta. Zastępcze obciążenie ciągłe równomiernie rozłożone na długości
pręta ukośnego wyznaczymy porównując siły wypadkowe z obu typów obciążenia ciągłego. Otrzymamy
zależność

p

⋅

x

⋅

cos







=

p '

⋅

x

,

(4.96)

w którym z lewej strony mamy siłę wypadkową z obciążenia ciągłego rozłożonego na długości rzutu pręta, z
prawej natomiast siłę wypadkową z zastępczego obciążenia ciągłego rozłożonego na długości pręta
ukośnego.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

29

p

- x

-

X

α

α

α

α

α

α

p'

q

h

x

⋅cos







x⋅

sin







V

A

H

A

M

A

α

V

A

H

A

α

M

(x

)

N(

x)

T(

x)

W

x

⋅cos







2

x

⋅cos







2

α

W

Rys. 4.42. Pręt ukośny z pionowym obciążeniem ciągłym równomiernie rozłożonym na długości rzutu poziomego pręta

Ostatecznie zastępcze obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego wynosi

p '

= p⋅cos







,

(4.97)

Zastępcze obciążenie ciągłe p' możemy rozłożyć na obciążenie prostopadłe i równoległe do osi pręta

ukośnego. Zgodnie z rysunkiem 4.42 oraz uwzględniając zależność (4.97) obciążenia te wynoszą

q



x



=q= p'⋅cos







= p⋅cos

2







,

(4.98)

h



x



=h=− p'⋅sin







=− p⋅sin







⋅cos







.

(4.99)

Siła wypadkowa z obciążenia ciągłego p wynosi

W

= p⋅x⋅cos







.

(4.100)

Funkcję siły normalnej w pręcie ukośnym wyznaczymy z równania równowagi

 N =N



x



V

A

⋅sin







H

A

⋅cos







−W⋅sin







=0

.

(4.101)

Ostatecznie funkcja siły normalnej będzie miała postać

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

30

N



x



=−V

A

⋅sin







−H

A

⋅cos







 p⋅x⋅sin







⋅cos







.

(4.102)

Funkcję siły poprzecznej w pręcie ukośnym wyznaczymy z równania równowagi

 T =T



x



−V

A

⋅cos







H

A

⋅sin







W⋅cos







=0

.

(4.103)

Ostatecznie funkcja siły poprzecznej będzie miała postać

T



x



=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅cos

2







.

(4.104)

Funkcję momentu zginającego w pręcie ukośnym wyznaczymy z równania równowagi

 M =−M



x



V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−W⋅

x

⋅cos







2

M

A

=0

.

(4.105)

Ostatecznie funkcja momentu zginającego będzie miała postać

M



x



=V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−

p

⋅x

2

⋅cos

2







2

M

A

.

(4.106)

Pierwsze różniczkowe równanie równowagi ma postać

dN



x



dx

= p⋅sin







⋅cos







=−h



x



.

(4.107)

Drugie różniczkowe równanie równowagi ma postać

dT



x



dx

=−p⋅cos

2







=−q



x



.

(4.108)

Trzecie różniczkowe równanie równowagi ma postać

dM



x



dx

=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅cos

2







=T



x



.

(4.109)

Jak więc widać funkcje siły normalnej (4.102), siły poprzecznej (4.104) i momentu zginającego (4.106)
spełniają różniczkowe równania równowagi.

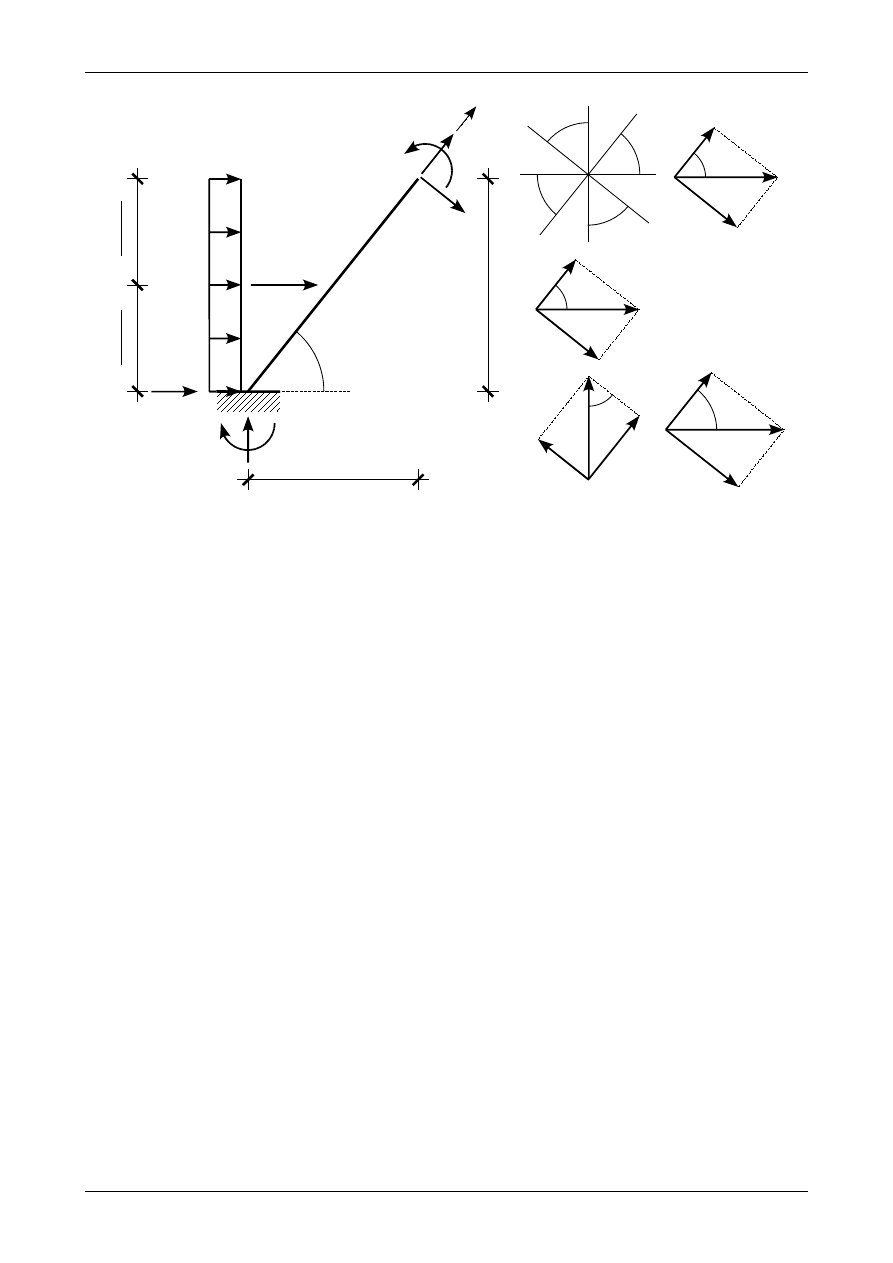
Rysunek 4.43 przedstawia pręt ukośny z poziomym obciążeniem ciągłym równomiernie rozłożonym

na długości rzutu pionowego tego pręta. Zastępcze obciążenie ciągłe równomiernie rozłożone na długości
pręta ukośnego wyznaczymy porównując siły wypadkowe z obu typów obciążenia ciągłego. Otrzymamy
zależność

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

31

X

α

α

α

α

α

p'

q

h

p

- x

-

α

x

⋅cos







x⋅

sin







V

A

H

A

M

A

M

(x

)

N(

x)

T(

x)

W

α

V

A

H

A

α

x⋅

sin







2

x⋅

sin







2

α

W

Rys. 4.43. Pręt ukośny z poziomym obciążeniem ciągłym równomiernie rozłożonym na długości rzutu pionowego pręta

p

⋅x⋅sin







= p'⋅x

,

(4.110)

w którym z lewej strony mamy siłę wypadkową z obciążenia ciągłego rozłożonego na długości rzutu pręta, z
prawej natomiast siłę wypadkową z zastępczego obciążenia ciągłego rozłożonego na długości pręta ukoś-
nego. Ostatecznie zastępcze obciążenie ciągłe równomiernie rozłożone na długości pręta ukośnego wynosi

p'

= p⋅sin







,

(4.111)

Zastępcze obciążenie ciągłe p' możemy rozłożyć na obciążenie prostopadłe i równoległe do osi pręta

ukośnego. Zgodnie z rysunkiem 4.42 oraz uwzględniając zależność (4.111) obciążenia te wynoszą

q



x



=q= p'⋅sin







= p⋅sin

2







,

(4.112)

h



x



=h= p'⋅cos







= p⋅sin







⋅cos







.

(4.113)

Siła wypadkowa z obciążenia ciągłego p wynosi

W

= p⋅x⋅sin







.

(4.114)

Funkcję siły normalnej w pręcie ukośnym wyznaczymy z równania równowagi

 N =N



x



V

A

⋅sin







H

A

⋅cos







W⋅cos







=0

.

(4.115)

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

32

Ostatecznie funkcja siły normalnej będzie miała postać

N



x



=−V

A

⋅sin







−H

A

⋅cos







− p⋅x⋅sin







⋅cos







.

(4.116)

Funkcję siły poprzecznej w pręcie ukośnym wyznaczymy z równania równowagi

 T =T



x



−V

A

⋅cos







H

A

⋅sin







W⋅sin







=0

.

(4.117)

Ostatecznie funkcja siły poprzecznej będzie miała postać

T



x



=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅sin

2







.

(4.118)

Funkcję momentu zginającego w pręcie ukośnym wyznaczymy z równania równowagi

 M =−M



x



V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−W⋅

x

⋅sin







2

M

A

=0

.

(4.119)

Ostatecznie funkcja momentu zginającego będzie miała postać

M



x



=V

A

⋅x⋅cos







−H

A

⋅x⋅sin







−

p

⋅x

2

⋅sin

2







2

M

A

.

(4.120)

Pierwsze różniczkowe równanie równowagi ma postać

dN



x



dx

=− p⋅sin







⋅cos







=−h



x



.

(4.121)

Drugie różniczkowe równanie równowagi ma postać

dT



x



dx

=−p⋅sin

2







=−q



x



.

(4.122)

Trzecie różniczkowe równanie równowagi ma postać

dM



x



dx

=V

A

⋅cos







−H

A

⋅sin







− p⋅x⋅sin

2







=T



x



.

(4.123)

Jak więc widać funkcje siły normalnej (4.116), siły poprzecznej (4.118) i momentu zginającego (4.120)
spełniają różniczkowe równania równowagi.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

33

Zastosowanie metody ogólnej do wyznaczania wykresów sił przekrojowych w belkach i ramach

płaskich zostanie przedstawione na załączonych do niniejszego opracowania przykładów.

4.6. Metoda punktów charakterystycznych

Oprócz metody ogólnej wyznaczania sił przekrojowych istnieje metoda punktów charakterystycz-

nych. Metoda ta opiera się na wyznaczeniu wartości sił przekrojowych tylko w pewnych
charakterystycznych punktach poszczególnych przedziałów belki lub ramy płaskiej. Liczba tych punktów
musi być taka, aby jednoznacznie narysować wykresy, które reprezentują funkcje siły poprzecznej i
momentu zginającego, a których postać jest uzależniona od różniczkowych równań równowagi.

Aby jednoznacznie narysować wykres funkcji stałej potrzebujemy jednej wartości tej funkcji w

dowolnym punkcie przedziału.

Aby jednoznacznie narysować wykres funkcji liniowej potrzebujemy wartości tej funkcji w dwóch

punktach. Będą to punkty znajdujące się na obu końcach przedziału.

Aby jednoznacznie narysować wykres funkcji kwadratowej potrzebujemy wartości w trzech punktach.

Punktami tymi będą: dwa punkty znajdujące się na obu końcach przedziału oraz jeden punkt znajdujący się
wewnątrz przedziału. W przypadku funkcji kwadratowej będącej wykresem momentu zginającego wartość
w trzecim punkcie da się zastąpić właściwością wynikającą z różniczkowych równań równowagi.

Aby jednoznacznie narysować wykres funkcji będącej wykresem wielomianu trzeciego stopnia

potrzebujemy wartości w czterech punktach. Punktami tymi będą: dwa punkty znajdujące się na obu
końcach przedziału oraz dwa punkty znajdujące się wewnątrz przedziału. W przypadku funkcji sześciennej
będącej wykresem momentu zginającego wartości w trzecim i czwartym punkcie da się zastąpić
właściwością wynikającą z różniczkowych równań równowagi.

Wartości sił przekrojowych w punktach charakterystycznych wyznacza się rozpatrując równowagę

odciętej w takim punkcie belki lub ramy płaskiej.

4.7. Metoda punktów charakterystycznych w belkach

Belkę złożoną dzielimy na belki proste. Następnie każdą belkę prostą dzielimy na poszczególne

przedziały. Punktami granicznymi przedziałów są: punkty przyłożenia sił skupionych (sił czynnych i
reakcji), punkty przyłożenia momentów skupionych, punkty, w których zaczyna się i kończy obciążenie
ciągłe (równomiernie rozłożone i liniowe).

Rysowanie wykresu siły poprzecznej zaczynamy od punktu zero na lewym końcu belki. Poruszając się

następnie w prawo rysujemy wykres. Musimy jednak przestrzegać kilka zasad:

•

Jeżeli w dowolnym przedziale nie działa obciążenie ciągłe to siła poprzeczna ma stałą wartość w
tym przedziale.

•

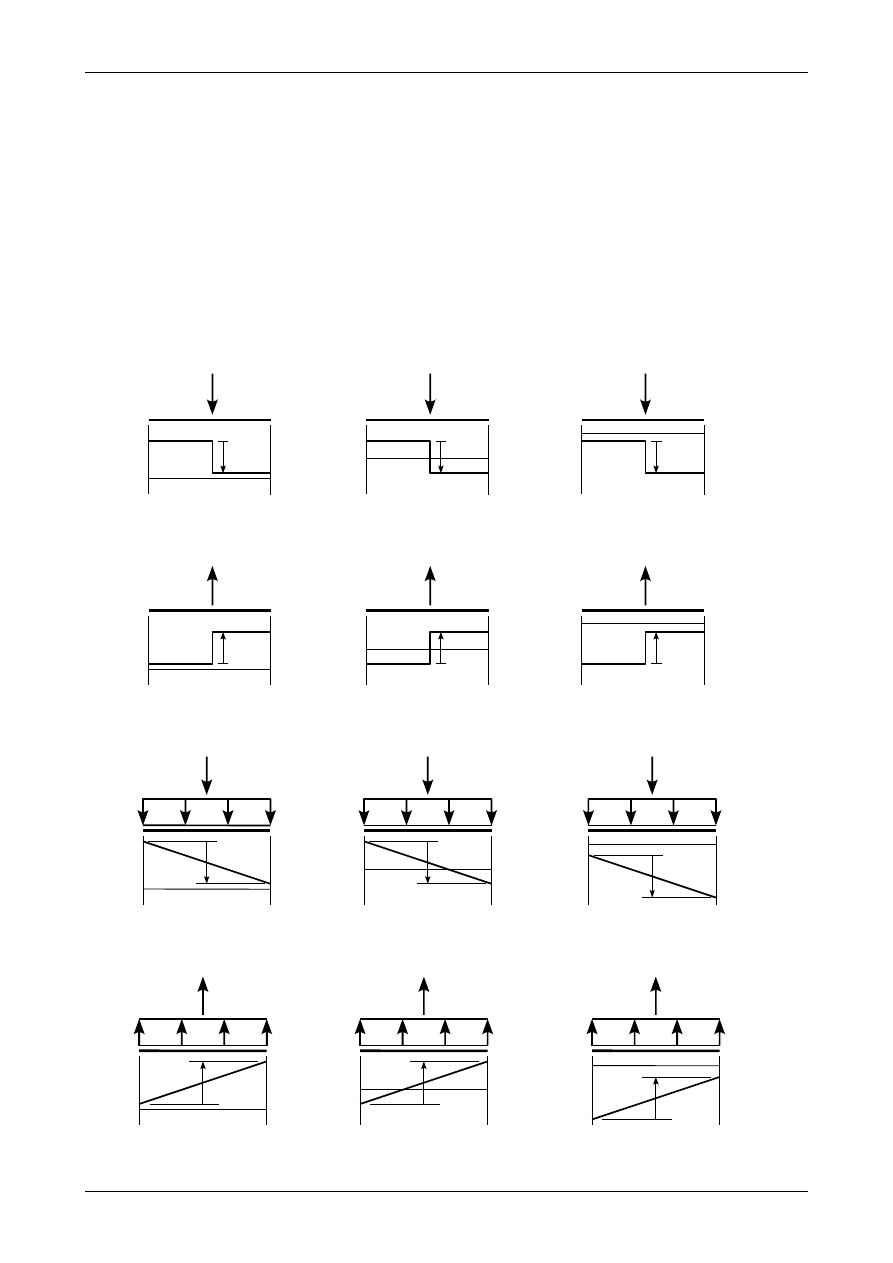
Jeżeli w dowolnym punkcie belki działa siła skupiona (siła czynna lub reakcja) w dół to siła
poprzeczna skokowo maleje o wartość siły. Przedstawia to rysunek 4.44.

•

Jeżeli w dowolnym punkcie belki działa siła skupiona (siła czynna lub reakcja) do góry to siła
poprzeczna skokowo rośnie o wartość siły. Przedstawia to rysunek 4.45.

•

Moment skupiony oraz przegub rzeczywisty, w którym nie działa żadna pionowa siła czynna nie
wpływają na wartość siły poprzecznej.

•

Jeżeli w przedziale działa obciążenie ciągłe równomiernie rozłożone q działające w dół to siła
poprzeczna maleje liniowo. Różnica pomiędzy lewym a prawym końcem równa się sile wypadkowej
z obciążenia ciągłego. Przedstawia to rysunek 4.46.

•

Jeżeli w przedziale działa obciążenie ciągłe równomiernie rozłożone q działające do góry to siła
poprzeczna rośnie liniowo. Różnica pomiędzy lewym a prawym końcem równa się sile wypadkowej
z obciążenia ciągłego. Przedstawia to rysunek 4.47.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

34

•

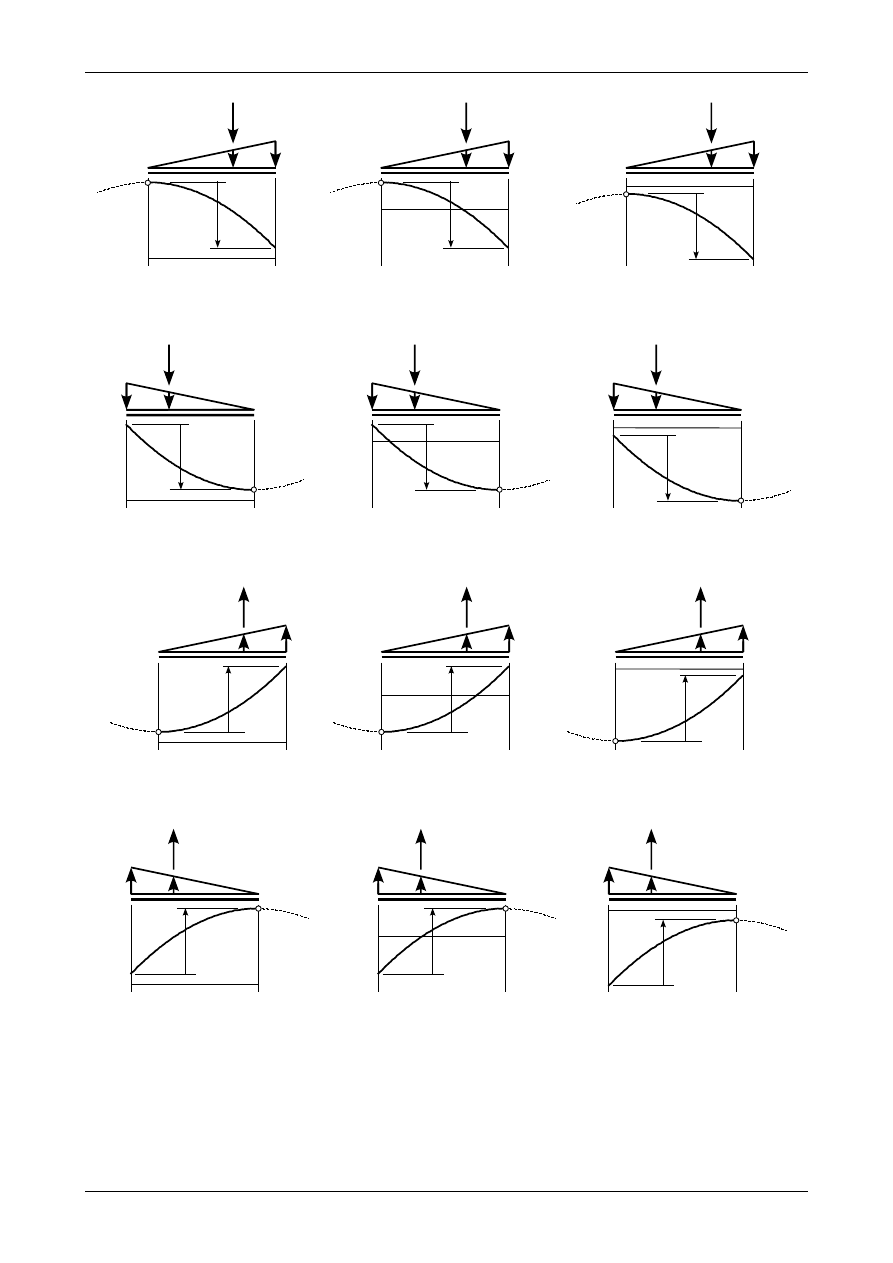
Jeżeli w przedziale działa obciążenie trójkątne w dół to siła poprzeczna parabolicznie maleje.
Przedstawiają to rysunki 4.48 i 4.49. Różnica pomiędzy lewym a prawym końcem równa się sile
wypadkowej z obciążenia ciągłego. Krzywizna tej paraboli jest uzależniona od położenia jego
ekstremum, które znajduje się w punkcie, w którym obciążenie trójkątne ma wartość zero. Jest to
punkt E na rysunkach 4.48 i 4.49. Na rysunkach tych znajduje się także część paraboli poza
przedziałem.

•

Jeżeli w przedziale działa obciążenie trójkątne do góry to siła poprzeczna parabolicznie rośnie.
Przedstawiają to rysunki 4.50 i 4.51. Różnica pomiędzy lewym a prawym końcem równa się sile
wypadkowej z obciążenia ciągłego. Krzywizna tej paraboli jest uzależniona od położenia jego
ekstremum, które znajduje się w punkcie, w którym obciążenie trójkątne ma wartość zero. Jest to
punkt E na rysunkach 4.50 i 4.51. Na rysunkach tych znajduje się także część paraboli poza
przedziałem.

T(x)

P

P

T(x)

P

P

T(x)

P

P

Rys. 4.44. Wykres siły poprzecznej w punkcie działania siły w dół

T(x)

P

P

T(x)

P

P

T(x)

P

P

Rys. 4.45. Wykres siły poprzecznej w punkcie działania siły do góry

T(x)

W

q

W

T(x)

W

q

W

T(x)

W

q

W

Rys. 4.46. Wykres siły poprzecznej w przedziale z obciążeniem ciągłym równomiernie rozłożonym w dół

T(x)

W

q

W

T(x)

W

q

W

T(x)

W

q

W

Rys. 4.47. Wykres siły poprzecznej w przedziale z obciążeniem ciągłym równomiernie rozłożonym do góry

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

35

T(x)

W

q

W

E

T(x)

W

q

W

E

T(x)

W

q

W

E

Rys. 4.48. Wykres siły poprzecznej w przedziale z obciążeniem trójkątnym w dół

T(x)

W

q

W

E

T(x)

W

q

W

E

T(x)

W

q

W

E

Rys. 4.49. Wykres siły poprzecznej w przedziale z obciążeniem trójkątnym w dół

T(x)

W

q

W

E

T(x)

W

q

W

E

T(x)

W

q

W

E

Rys. 4.50. Wykres siły poprzecznej w przedziale z obciążeniem trójkątnym do góry

T(x)

W

q

W

E

T(x)

W

q

W

E

T(x)

W

q

W

E

Rys. 4.51. Wykres siły poprzecznej w przedziale z obciążeniem trójkątnym do góry

Jeżeli liniowa lub paraboliczna siła poprzeczna w przedziale posiada na obu końcach wartości

przeciwnych znaków oznacza to, że w przedziale tym będzie ona miała miejsce zerowe. Musimy określić
jego położenie, ponieważ w tym punkcie moment zginający będzie miał ekstremalną wartość.

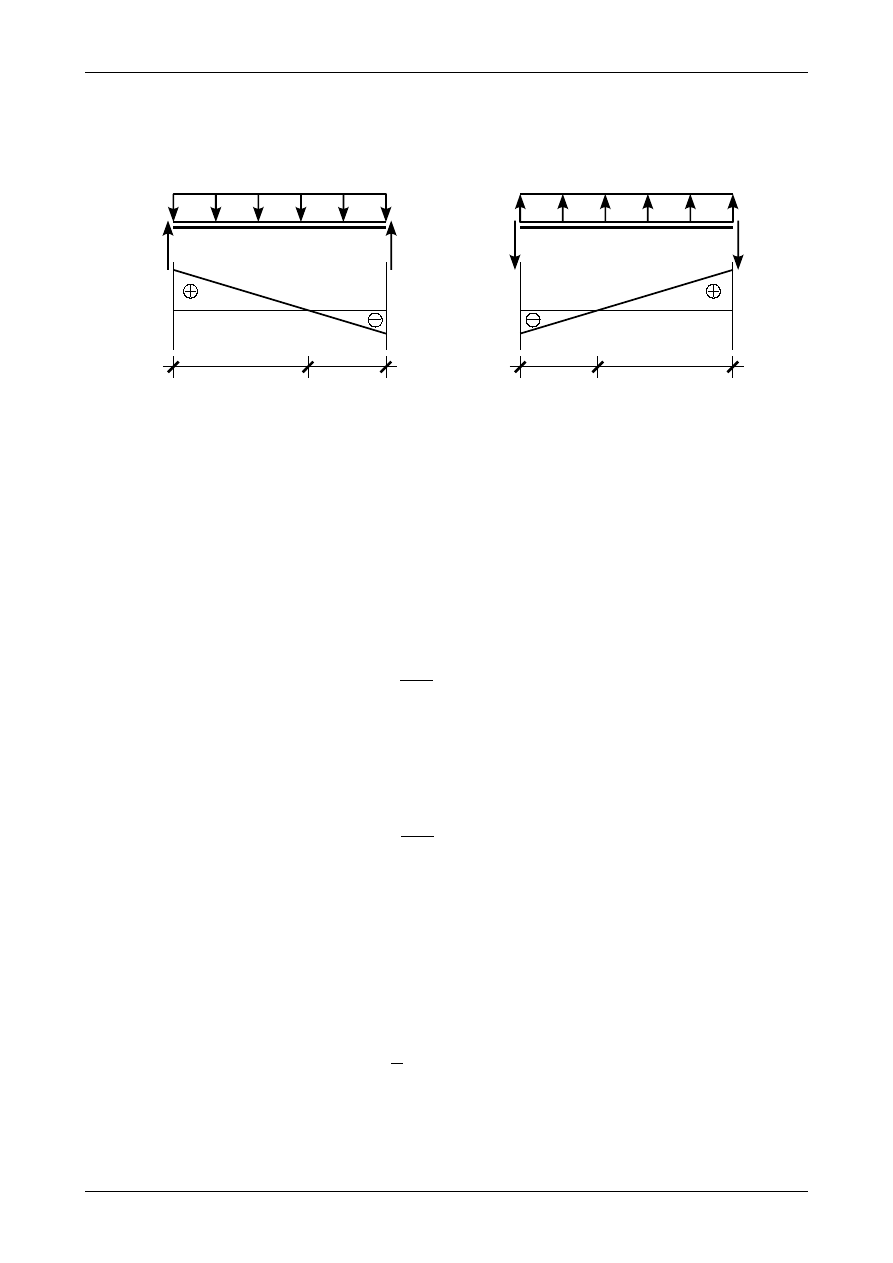
Jeżeli w przedziale działa obciążenie ciągłe równomiernie rozłożone w dół to siła poprzeczna na

lewym końcu jest dodatnia a na prawym ujemna. Przedstawia to rysunek 4.52 a). Jeżeli w przedziale działa

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

36

obciążenie ciągłe równomiernie rozłożone do góry to siła poprzeczna na lewym końcu jest ujemna a na
prawym dodatnia. Przedstawia to rysunek 4.52 b).

T(x)

T(x)

T

(L)

T

(P)

T

(L)

T

(P)

T

(L)

T

(P)

T

(L)

T

(P)

x

L

x

P

x

L

x

P

q

q

a)

b)

Rys. 4.52. Miejsca zerowe wykresu siły poprzecznej w przedziale z obciążeniem ciągłym równomiernie rozłożonym

Miejsce zerowe będzie się znajdowało w odległości x

L

takiej, aby siła wypadkowa z obciążenia

ciągłego q równała się wartości siły poprzecznej T

(L)

. Możemy więc napisać

∣

T

 L

∣

=

∣

q

∣

⋅

x

L

.

(4.124)

Ostatecznie więc odległość miejsca zerowego siły poprzecznej w przedziale, w którym działa obciążenie
ciągłe równomiernie rozłożone, od lewego końca będzie wynosiła

x

L

=

∣

T



L



∣

∣

q

∣

.

(4.125)

Natomiast odległość miejsca zerowego siły poprzecznej w przedziale, w którym działa obciążenie ciągłe
równomiernie rozłożone, od prawego końca będzie wynosiła

x

P

=

∣

T



P



∣

∣

q

∣

.

(4.126)

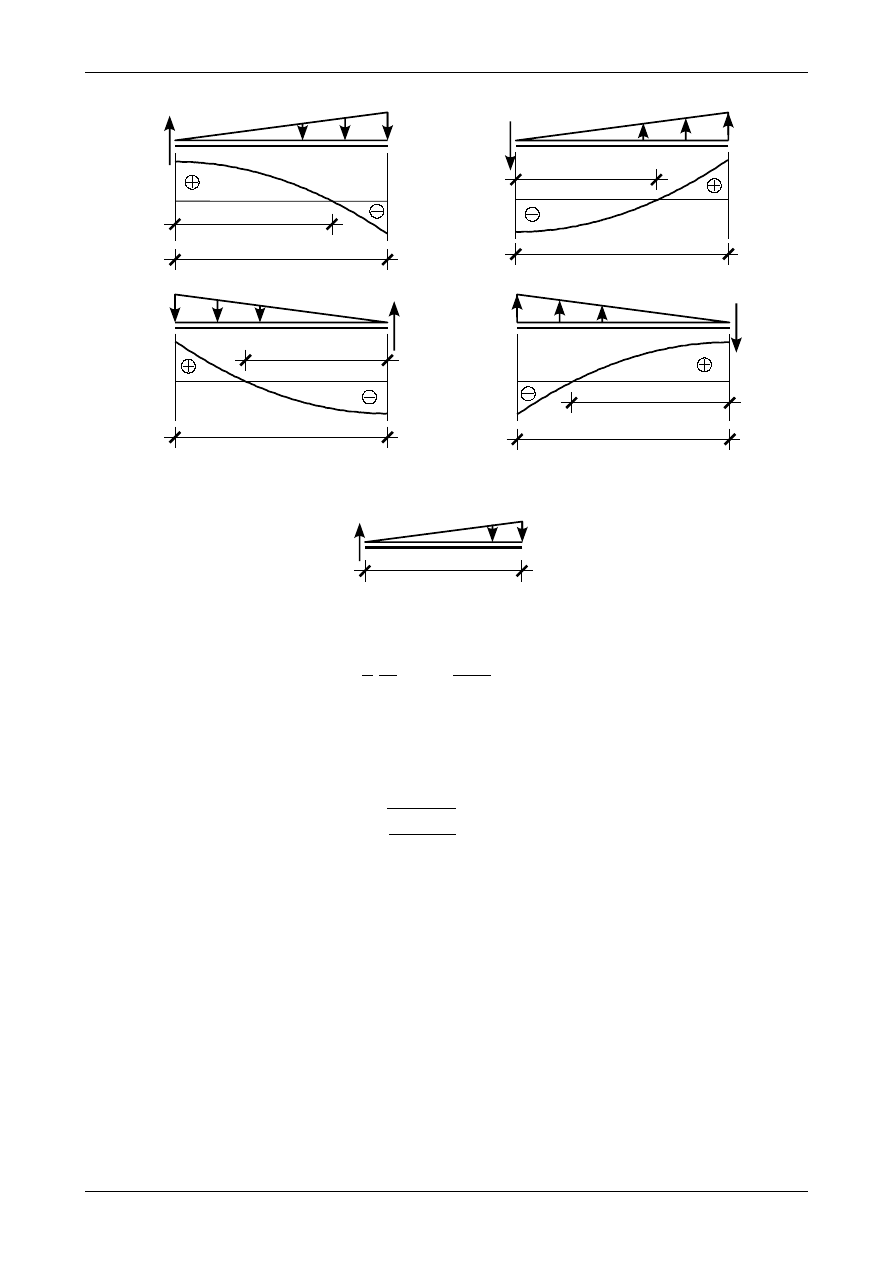
W przypadku przedziału z obciążeniem trójkątnym będziemy określali tylko odległość miejsca

zerowego od punktu, w którym obciążenie to przyjmuje wartość zero. Rysunek 4.53 przedstawia wszystkie
możliwe przypadki występowania miejsca zerowego. Miejsce zerowe będzie się znajdowało w odległości x

0

od punktu, w którym obciążenie trójkątne ma wartość zero, takim aby siła wypadkowa z obciążenia
trójkątnego równała się wartości siły poprzecznej T

(K)

, w tym punkcie. Zgodnie z rysunkiem 4.53 możemy

więc napisać

∣

T

 K 

∣

=

1
2

⋅

q



x

0



⋅

x

0

.

(4.127)

Wstawiając funkcję obciążenia trójkątnego (4.4) otrzymamy

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

37

T(x)

T

(K)

T

(K)

x

0

q

a)

T(x)

T

(K)

T

(K)

x

0

q

b)

T(x)

T

(K)

T

(K)

x

0

q

c)

T(x)

T

(K)

T

(K)

x

0

q

d)

L

L

L

L

Rys. 4.53. Miejsca zerowe wykresu siły poprzecznej w przedziale z obciążeniem trójkątnym

T

(K)

x

0

q(x

0

)

Rys. 4.54. Miejsce zerowe siły poprzecznej

∣

T



K



∣

=

1
2

⋅

∣

q

∣

L

⋅x

0

⋅x

0

=

∣

q

∣

⋅x

0

2

2

⋅L

.

(4.128)

We wzorze (4.128) L oznacza długość przedziału, w którym działa obciążenie trójkątne. Ostatecznie
możemy więc zapisać odległość x

0

jako

x

0

=



2

⋅

∣

T

 K 

∣

⋅

L

∣

q

∣

.

(4.129)

Mając narysowany wykres siły poprzecznej możemy przystąpić do rysowania wykresu momentu

zginającego. Będziemy go rysować na podstawie wartości obliczonych w charakterystycznych punktach.
Wartości momentu zginającego będziemy wyznaczać rozpatrując równowagę odciętej części belki. Musimy
przestrzegać następujących warunków:

•

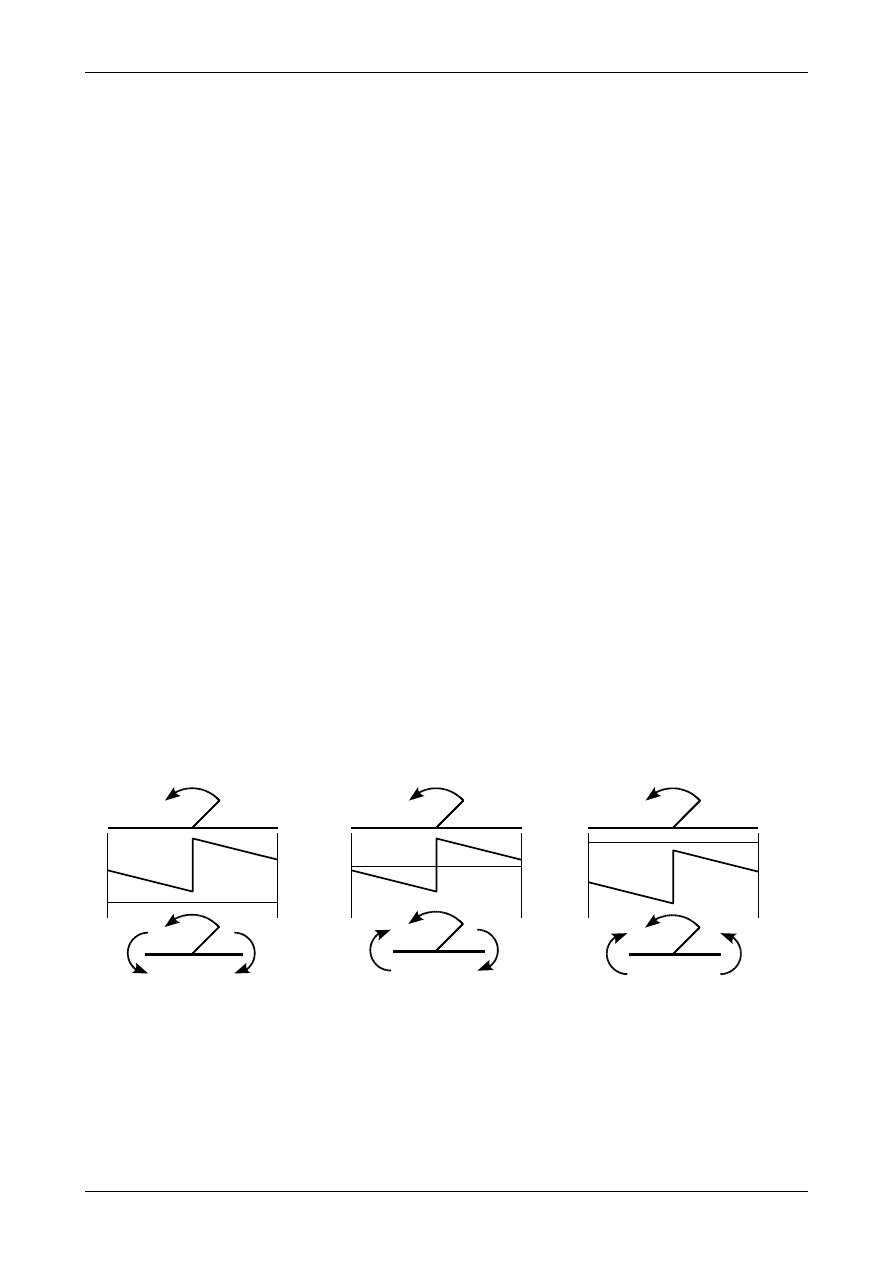
W większości przypadków wykres momentu zginającego w belce jest ciągły. Jedynym obciążeniem
powodującym nieciągłość tego wykresu jest moment skupiony. Wartość bezwzględna tego skoku
jest równa wartości momentu skupionego. Kierunek tego skoku uzależniony jest od kierunku
momentu skupionego. Przedstawiają to rysunki 4.55 i 4.56. Na rysunkach tych narysowana jest
także równowaga w otoczeniu punktu przyłożenia momentu skupionego.

•

Jeżeli w pewnym przedziale belki nie działa żadne obciążenie ciągłe to wykres momentu jest
funkcją liniową. Wystarczy więc wyznaczyć wartości momentu zginającego na początku i końcu
tego przedziału. Jeżeli siła poprzeczna będzie dodatnia liniowy moment zginający będzie malejący,
natomiast jeżeli siła poprzeczna będzie ujemna to będzie on rosnący. Przykładowe wykresy
przedstawiają rysunki 4.57 i 4.58.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

38

•

Jeżeli w pewnym przedziale belki działa obciążenie ciągłe równomiernie rozłożone to wykres
momentu zginającego jest parabolą. Ponadto siła poprzeczna posiada w tym przedziale miejsce
zerowe. Aby jednoznacznie narysować wykres momentu zginającego należy wyznaczyć wartości
momentu zginającego w trzech punktach: na początku i na końcu przedziału oraz w miejscu
zerowym siły poprzecznej. „Brzuszek” takiej paraboli jest skierowany w tą samą stronę co
obciążenie ciągłe równomiernie rozłożone. Przykładowe wykresy przedstawiają rysunki 4.59 i 4.60.

•

Jeżeli w pewnym przedziale belki działa obciążenie ciągłe równomiernie rozłożone oraz siła
poprzeczna nie posiada w tym przedziale miejsca zerowego (czyli jest w całym przedziale dodatnia
lub ujemna) to wykres momentu zginającego jest także parabolą ale aby ją jednoznacznie narysować
wystarczy wyznaczyć wartości momentu zginającego tylko w dwóch punktach: na początku i na
końcu przedziału. Trzeci punkt wykresu stanowi „brzuszek” paraboli, który jest skierowany w tą
samą stronę co obciążenie ciągłe równomiernie rozłożone. Jeżeli siła poprzeczna będzie dodatnia
parabola momentu zginającego będzie malejąca, natomiast jeżeli siła poprzeczna będzie ujemna to
będzie ona rosnąca. Przykładowe wykresy przedstawiają rysunki 4.61, 4.62, 4.63 i 4.64.

•

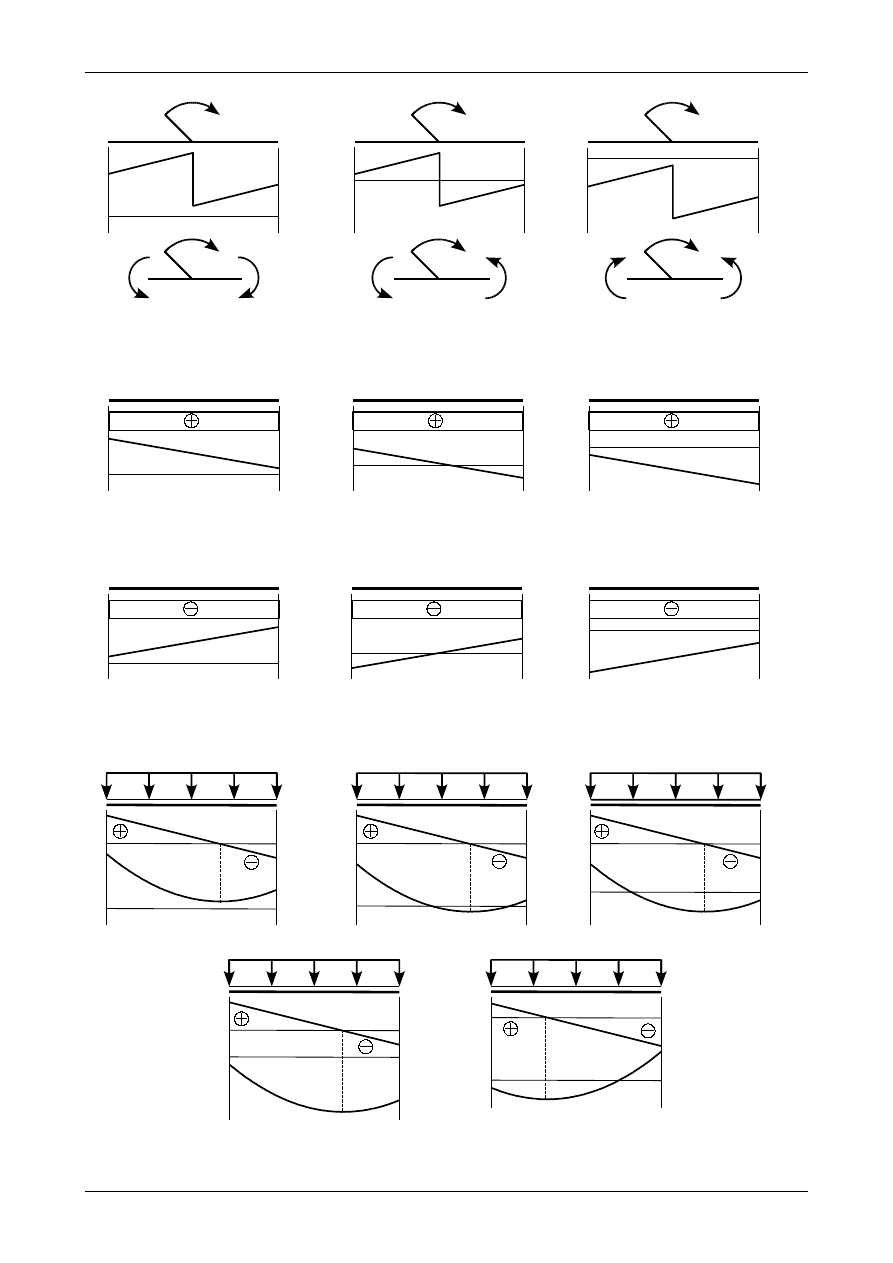
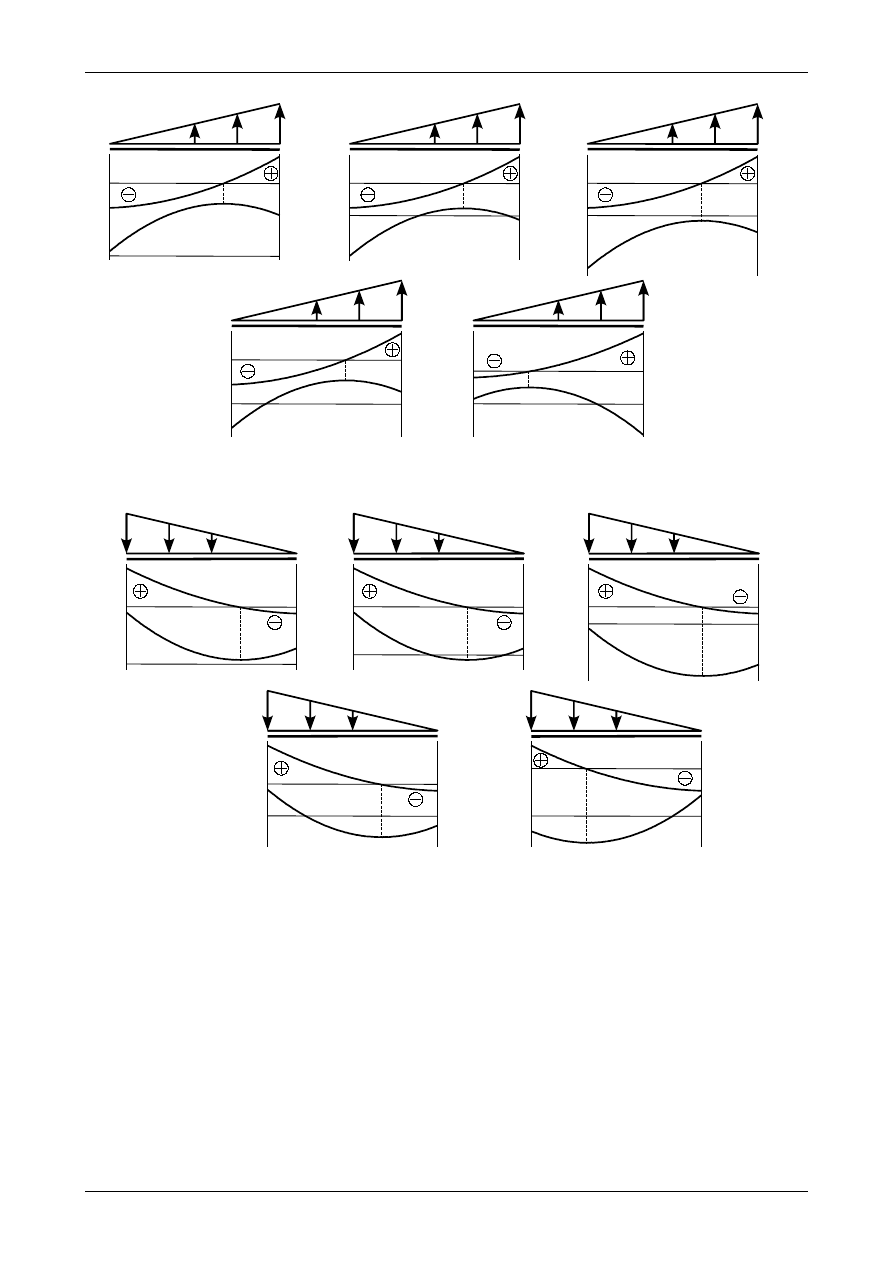
Jeżeli w pewnym przedziale belki działa obciążenie trójkątne to wykres momentu zginającego jest
funkcją trzeciego stopnia. Ponadto siła poprzeczna posiada w tym przedziale miejsce zerowe. Aby
jednoznacznie narysować wykres momentu zginającego należy wyznaczyć wartości momentu
zginającego tylko w trzech punktach: na początku i na końcu przedziału oraz w miejscu zerowym
siły poprzecznej. Czwartym punktem tej funkcji będzie „brzuszek”, który jest skierowany w tą samą
stronę co obciążenie trójkątne. Przykładowe wykresy przedstawiają rysunki 4.65, 4.66, 4.67 i 4.68.

•

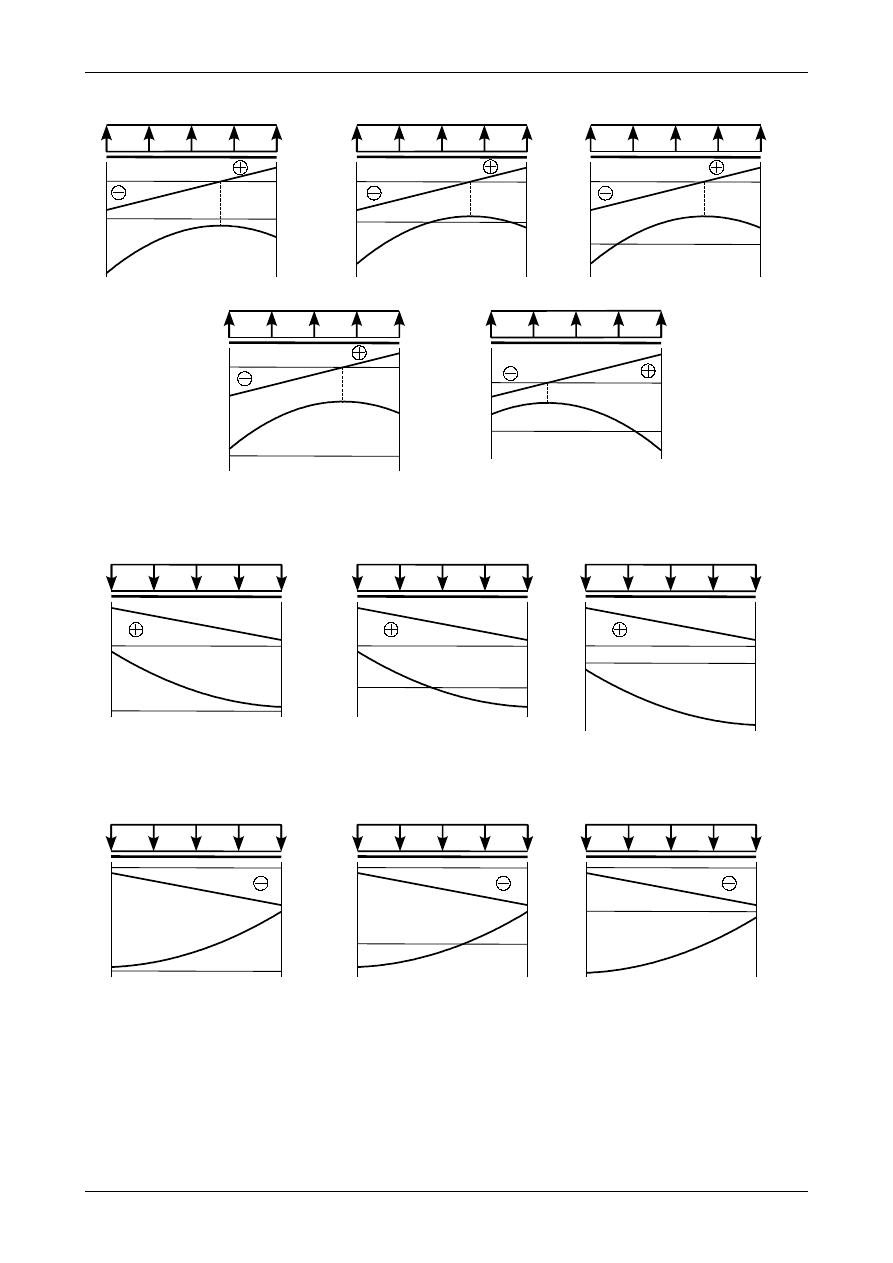
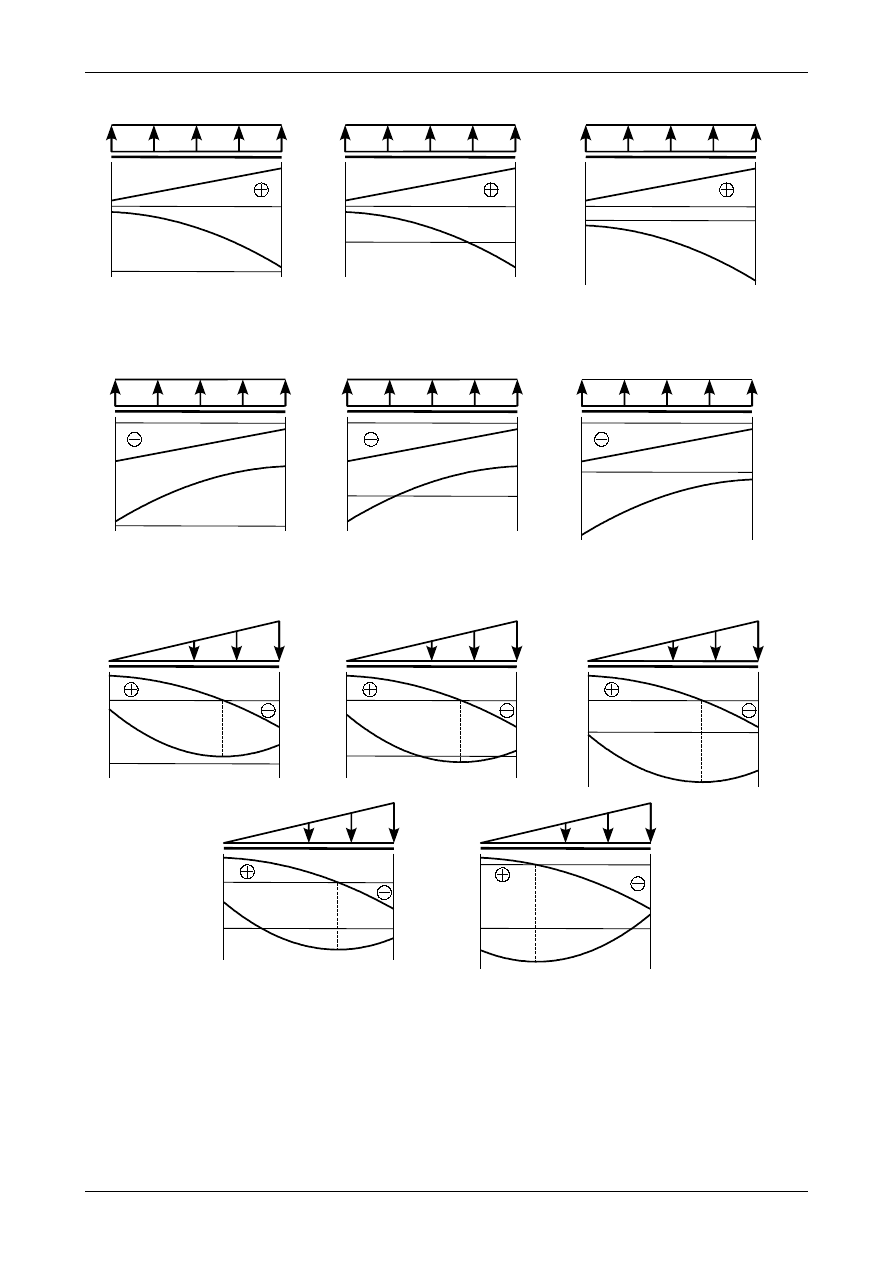
Jeżeli w pewnym przedziale belki działa obciążenie trójkątne oraz siła poprzeczna nie posiada w
tym przedziale miejsca zerowego (czyli jest w całym przedziale dodatnia lub ujemna) to wykres
momentu jest także funkcją trzeciego stopnia ale aby go jednoznacznie narysować należy
wyznaczyć wartości momentu zginającego tylko w dwóch punktach: na początku i na końcu
przedziału. Cały wykres musi się mieścić pomiędzy wartościami momentu zginającego na obu
końcach przedziału. Pozostałymi dwoma punktami tej funkcji będzie „brzuszek”, który jest
skierowany w tą samą stronę co obciążenie trójkątne. Jeżeli siła poprzeczna będzie dodatnia wykres
momentu zginającego będzie malejący, natomiast jeżeli siła poprzeczna będzie ujemna to będzie on
rosnący. Przykładowe wykresy przedstawiają rysunki od 4.69 do 4.76.

Przykłady zastosowania tej metody w praktyce znajdują się w zadaniach dołączonych do niniejszego

opracowania.

M

a)

M(x)

M

M

(L)

M

(P)

M

(P)

=M+M

(L)

M

b)

M(x)

M

M

(L)

M

(P)

M

(P)

=M-M

(L)

M

c)

M(x)

M

M

(L)

M

(P)

M

(P)

=M

(L)

-M

Rys. 4.55. Skok wykresy momentu zginającego

4.8. Metoda punktów charakterystycznych w ramach płaskich

Ramę płaską dzielimy na poszczególne przedziały. Punktami granicznymi przedziałów są: węzły ramy

płaskiej, punkty przyłożenia sił skupionych (sił czynnych i reakcji), punkty przyłożenia momentów skupio-
nych, punkty, w których zaczyna się i kończy obciążenie ciągłe (równoległe i prostopadłe do osi pręta) oraz
miejsca, w których znajdują się przeguby rzeczywiste.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

39

M

M(x)

M

M

(L)

M

(P)

M

(P)

=M

(L)

-M

M

M(x)

M

M

(L)

M

(P)

M

(P)

=M-M

(L)

M

M(x)

M

M

(L)

M

(P)

M

(P)

=M+M

(L)

a)

b)

c)

Rys. 4.56. Skok wykresy momentu zginającego

a)

M(x)

T(x)

q=0

b)

M(x)

T(x)

q=0

c)

M(x)

T(x)

q=0

Rys. 4.57. Liniowe wykresy momentu zginającego

M(x)

T(x)

q=0

M(x)

T(x)

q=0

M(x)

T(x)

q=0

a)

b)

c)

Rys. 4.58. Liniowe wykresy momentu zginającego

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

T(x)

q

M(x)

d)

T(x)

q

M(x)

e)

Rys. 4.59. Paraboliczne wykresy momentu zginającego z ekstremum

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

40

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

T(x)

q

M(x)

d)

T(x)

q

M(x)

e)

Rys. 4.60. Paraboliczne wykresy momentu zginającego z ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

b)

Rys. 4.61. Paraboliczne wykresy momentu zginającego bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.62. Paraboliczne wykresy momentu zginającego bez ekstremum

Wartości siły normalnej i poprzecznej oraz momentu zginającego w dowolnym przedziale ramy

płaskiej będziemy wyznaczali rozpatrując równowagę odciętej części ramy płaskiej. Liczba punktów, w
których będziemy wyznaczali wartości poszczególnych sił przekrojowych będzie uzależniona od postaci
funkcji opisującej daną siłę przekrojową. Postać ta zależy, jak wiadomo, od różniczkowych równań
równowagi (4.19), (4.20) i (4.21).

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

41

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.63. Paraboliczne wykresy momentu zginającego bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.64. Paraboliczne wykresy momentu zginającego bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

b)

T(x)

q

M(x)

d)

T(x)

q

M(x)

e)

Rys. 4.65. Momenty zginające będące wielomianem trzeciego stopnia z ekstremum

Aby narysować wykres siły normalnej w ramie płaskiej będziemy musieli przestrzegać następujących

warunków:

•

Jeżeli w dowolnym przedziale nie działa żadne obciążenie ciągłe to siła normalna jest funkcją stałą.
Aby ją narysować wystarczy wyznaczyć jej wartość w dowolnym punkcie danego przedziału.

•

Jeżeli w dowolnym przedziale działa tylko obciążenie ciągłe równomiernie rozłożone prostopadłe
do osi pręta to siła normalna jest także funkcją stałą.

Dr inż. Janusz Dębiński

Zaoczni

MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

42

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

T(x)

q

M(x)

d)

T(x)

q

M(x)

e)

Rys. 4.66. Momenty zginające będące wielomianem trzeciego stopnia z ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

T(x)

q

M(x)

d)

T(x)

q

M(x)

e)

Rys. 4.67. Momenty zginające będące wielomianem trzeciego stopnia z ekstremum

•

Moment skupiony oraz siła działająca prostopadłe do osi pręta nie wpływają na zmianę wartości siły
normalnej.

•

Jeżeli w pręcie ukośnym działa siła, która nie jest prostopadła do osi tego pręta to będzie ona
powodowała skok siły normalnej. Wartość bezwzględna tego skoku równa się składowej tej siły
równoległej do osi pręta ukośnego. Sytuację taką przedstawia rysunek 4.77.

•

Jeżeli w przedziale działa obciążenie ciągłe równomiernie rozłożone równoległe do osi pręta to siła
normalna jest funkcją liniową. Aby ją jednoznacznie narysować wystarczy wyznaczyć jej wartości
na obu końcach przedziału.

•

Jeżeli w pręcie ukośnym działa obciążenie ciągłe równomiernie rozłożone na długości pręta lub na
długości jego rzutu poziomego lub pionowego to siła normalna jest funkcją liniową. Aby ją
jednoznacznie narysować wystarczy wyznaczyć jej wartości na obu końcach przedziału.

Dr inż. Janusz Dębiński

Zaoczni

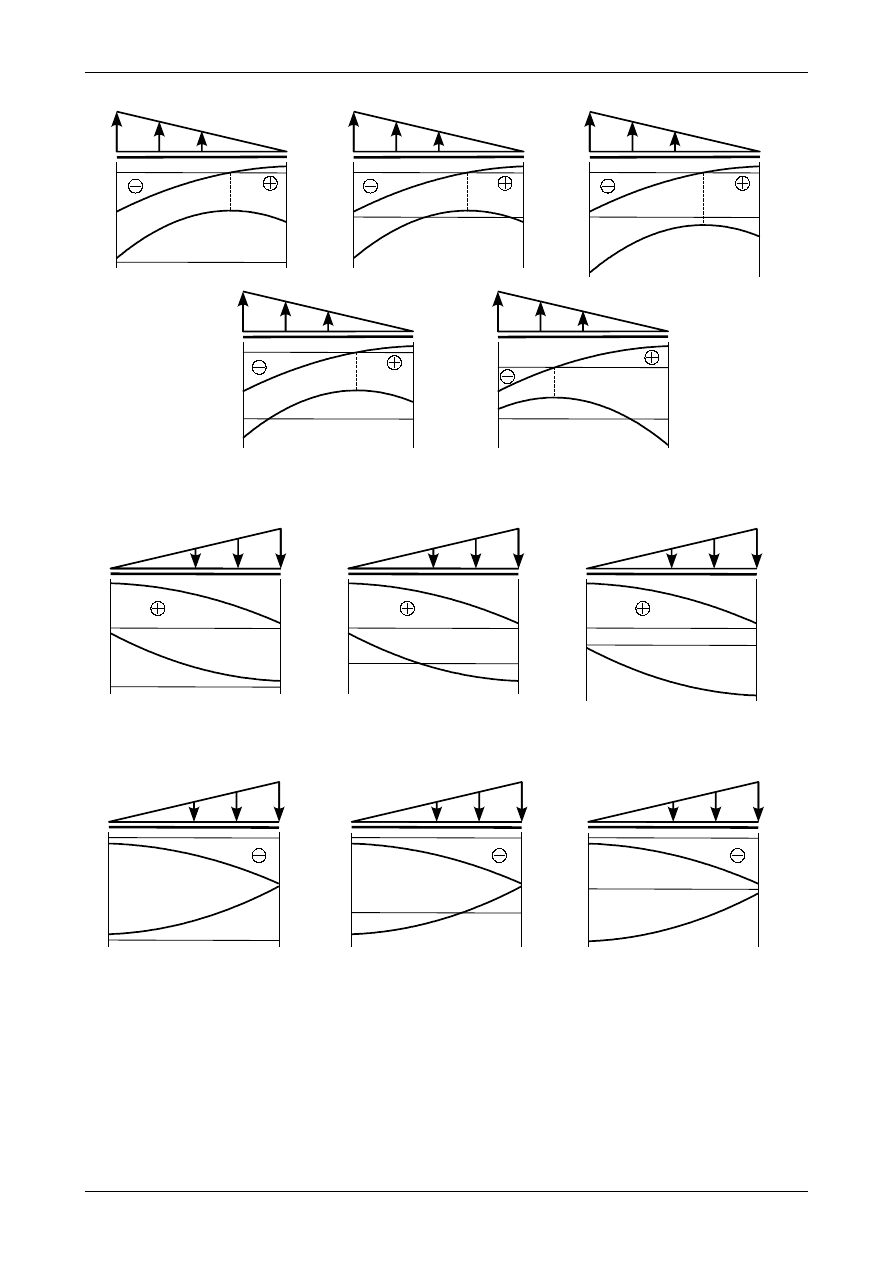
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

43

T(x)

q

a)

M(x)

T(x)

q

b)

M(x)

T(x)

q

c)

M(x)

T(x)

q

d)

M(x)

T(x)

q

M(x)

e)

Rys. 4.68. Momenty zginające będące wielomianem trzeciego stopnia z ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.69. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.70. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

Aby narysować wykres siły poprzecznej w ramie płaskiej będziemy musieli przestrzegać

następujących warunków:

•

Jeżeli w dowolnym przedziale nie działa żadne obciążenie ciągłe to siła poprzeczna jest funkcją
stałą. Aby ją narysować wystarczy wyznaczyć jej wartość w dowolnym punkcie danego przedziału.

•

Jeżeli w dowolnym przedziale działa tylko obciążenie ciągłe równomiernie rozłożone równoległe do
osi pręta to siła poprzeczna jest także funkcją stałą.

Dr inż. Janusz Dębiński

Zaoczni

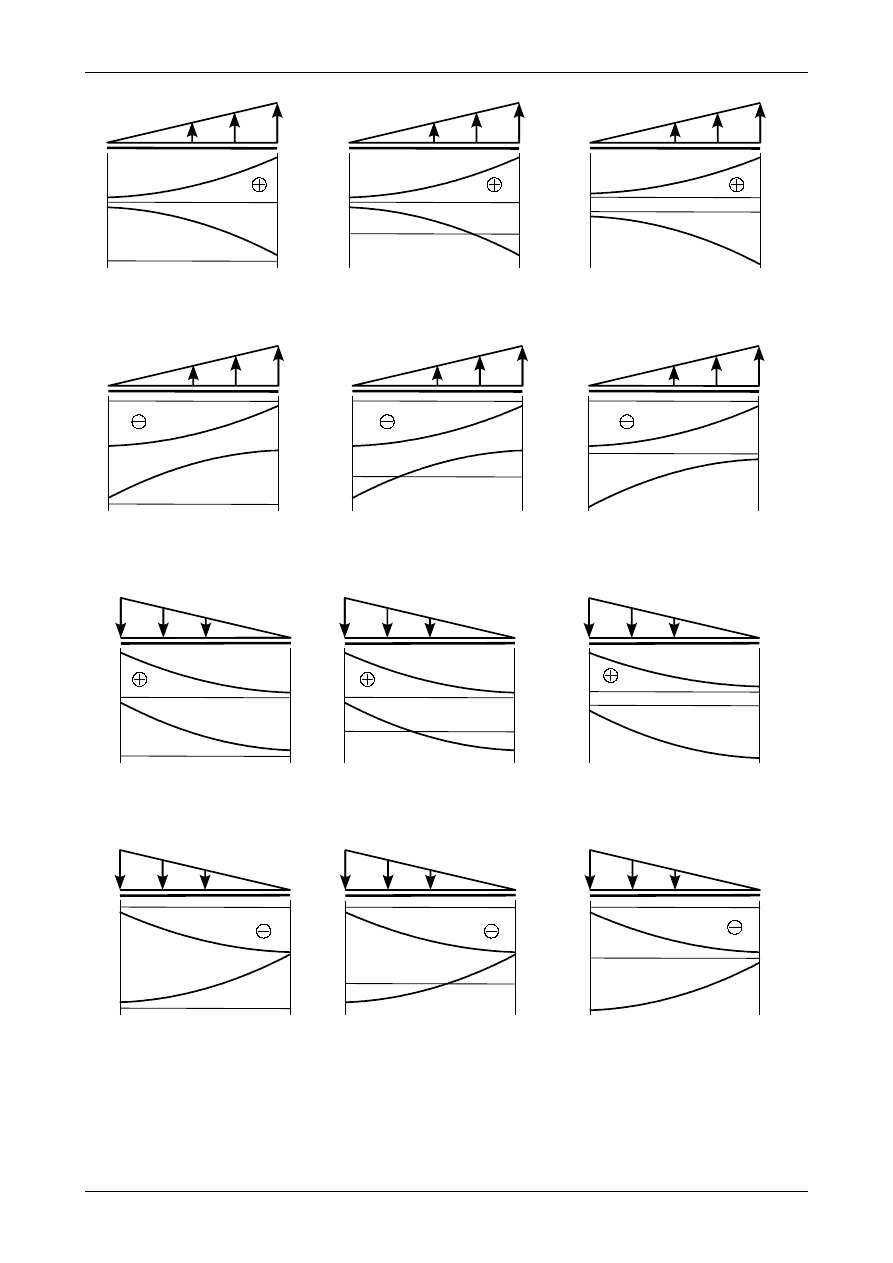
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

44

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.71. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.72. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.73. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.74. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

•

Jeżeli w dowolnym punkcie pręta poziomego lub pionowego działa siła prostopadła do osi tego
pręta to powoduje ona skok siły poprzecznej. Wartość bezwzględna tego skoku równa się wartości
tej siły.

Dr inż. Janusz Dębiński

Zaoczni

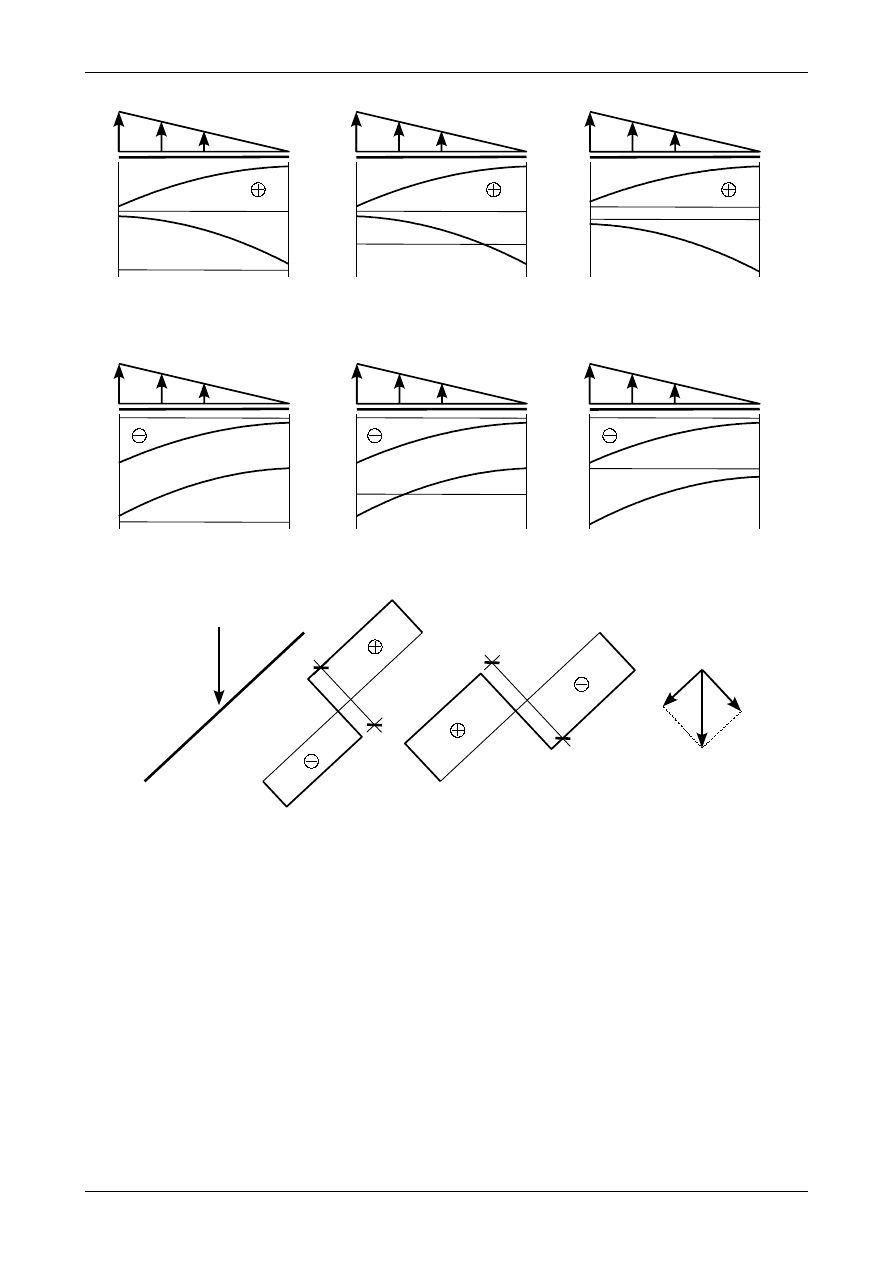
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

45

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.75. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

T(x)

q

M(x)

a)

T(x)

q

M(x)

b)

T(x)

q

M(x)

c)

Rys. 4.76. Momenty zginające będące wielomianem trzeciego stopnia bez ekstremum

P

P

P

T

P

N

P

T

P

N

T(

x)

N(

x)

Rys. 4.77. Skok siły normalnej i poprzecznej w pręcie ukośnym w punkcie działania siły P

•

Jeżeli w pręcie ukośnym działa siła, która nie jest równoległa do osi tego pręta to będzie ona
powodowała skok siły poprzecznej. Wartość bezwzględna tego skoku równa się składowej tej siły
prostopadłej do osi pręta ukośnego. Sytuację taką przedstawia rysunek 4.77.

•

Moment skupiony działający w dowolnym punkcie ramy płaskiej nie wpływa na zmianę wartości
siły poprzecznej.

•

Jeżeli w poziomym i pionowym pręcie działa obciążenie ciągłe równomiernie rozłożone prostopadłe
do osi tego pręta to siła poprzeczna będzie funkcją liniową. Aby ją jednoznacznie narysować należy
wyznaczyć jej wartości na obu końcach przedziału. Możemy tutaj zastosować zasady takie same jak
dla belek.

•

Jeżeli w pręcie ukośnym działa obciążenie ciągłe równomiernie rozłożone na długości pręta lub na
długości jego rzutu poziomego lub pionowego to siła poprzeczna jest także funkcją liniową. Aby ją
jednoznacznie narysować wystarczy wyznaczyć jej wartości na obu końcach przedziału.

Dr inż. Janusz Dębiński

Zaoczni

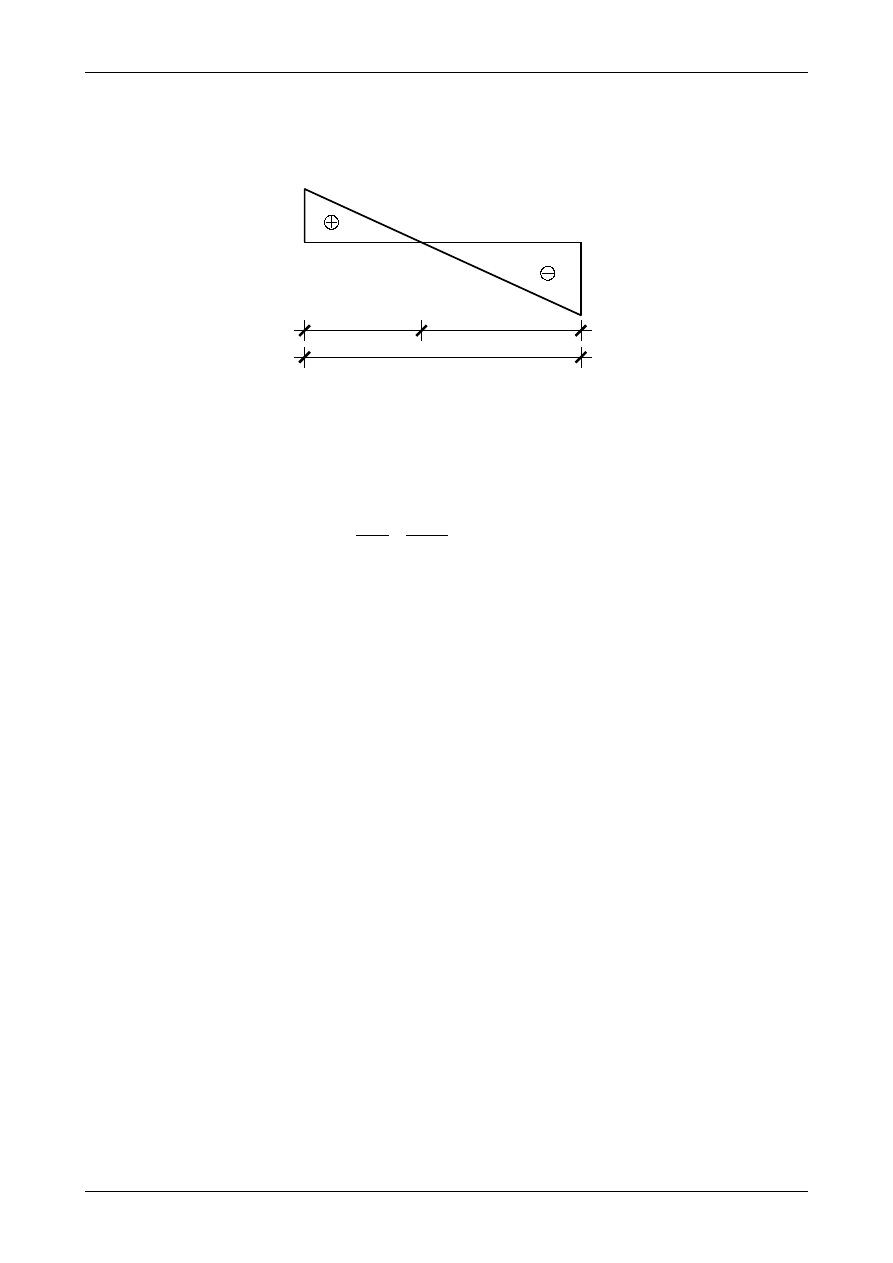
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

46

Jeżeli liniowa funkcja siły poprzecznej ma na obu końcach przedziału wartości różnych znaków

będzie ona miała w tym przedziale miejsce zerowe. Rysunek 4.78 przedstawia taki wykres siły poprzecznej
w przedziale o długości L.

L

L-x

0

x

0

T(x)

T

(L)

T

(P)

Rys. 4.78. Liniowy wykres siły poprzecznej z miejscem zerowym

Zgodnie z tym rysunkiem odległość miejsca zerowego od lewego końca przedziału możemy wyznaczyć z
twierdzenia Talesa. Odpowiednia proporcja na postać

∣

T

 L

∣

x

0

=

∣

T

P 

∣

L

−

x

0

.

(4.130)

Z równania (4.130) możemy wyznaczyć odległość x

o

.

Aby narysować wykres momentu zginającego w ramie płaskiej będziemy musieli przestrzegać

następujących warunków:

•

Jeżeli w dowolnym punkcie ramy płaskiej działa moment skupiony to powoduje on skok momentu
zginającego. Wartość bezwzględna tego skoku jest równa wartości momentu skupionego. Kierunek
tego skoku uzależniony jest od kierunku momentu skupionego.

•

Jeżeli w dowolnym przedziale nie działa żadne obciążenie ciągłe to wykres momentu jest funkcją
liniową. Wystarczy więc wyznaczyć wartości momentu zginającego na początku i końcu tego
przedziału.

•

Jeżeli w dowolnym przedziale działa tylko obciążenie ciągłe równomiernie rozłożone równoległe do
osi pręta to wykres momentu jest funkcją liniową. Wystarczy więc wyznaczyć wartości momentu
zginającego na początku i końcu tego przedziału.

•

Jeżeli w pręcie pionowym lub poziomym działa obciążenie ciągłe równomiernie rozłożone
prostopadłe do osi tego pręta to wykres momentu zginającego jest parabolą. Ponadto siła poprzeczna
posiada w tym przedziale miejsce zerowe. Aby jednoznacznie narysować wykres momentu
zginającego należy wyznaczyć wartości momentu zginającego w trzech punktach: na początku i na
końcu przedziału oraz w miejscu zerowym siły poprzecznej. „Brzuszek” takiej paraboli jest
skierowany w tą samą stronę co obciążenie ciągłe.

•

Jeżeli w pręcie pionowym lub poziomym działa obciążenie ciągłe równomiernie rozłożone
prostopadłe do osi tego pręta oraz siła poprzeczna nie posiada w tym przedziale miejsca zerowego
(czyli jest w całym przedziale dodatnia lub ujemna) to wykres momentu zginającego jest także
parabolą ale aby ją jednoznacznie narysować wystarczy wyznaczyć wartości momentu zginającego
tylko w dwóch punktach: na początku i na końcu przedziału Trzeci punkt wykresu stanowi
„brzuszek” paraboli, który jest skierowany w tą samą stronę co obciążenie ciągłe równomiernie
rozłożone.

•

Jeżeli w przedziale pręta ukośnego działa obciążenie ciągłe równomiernie rozłożone na długości
tego pręta lub na długości jego rzutu poziomego lub pionowego to wykres momentu zginającego jest

Dr inż. Janusz Dębiński

Zaoczni

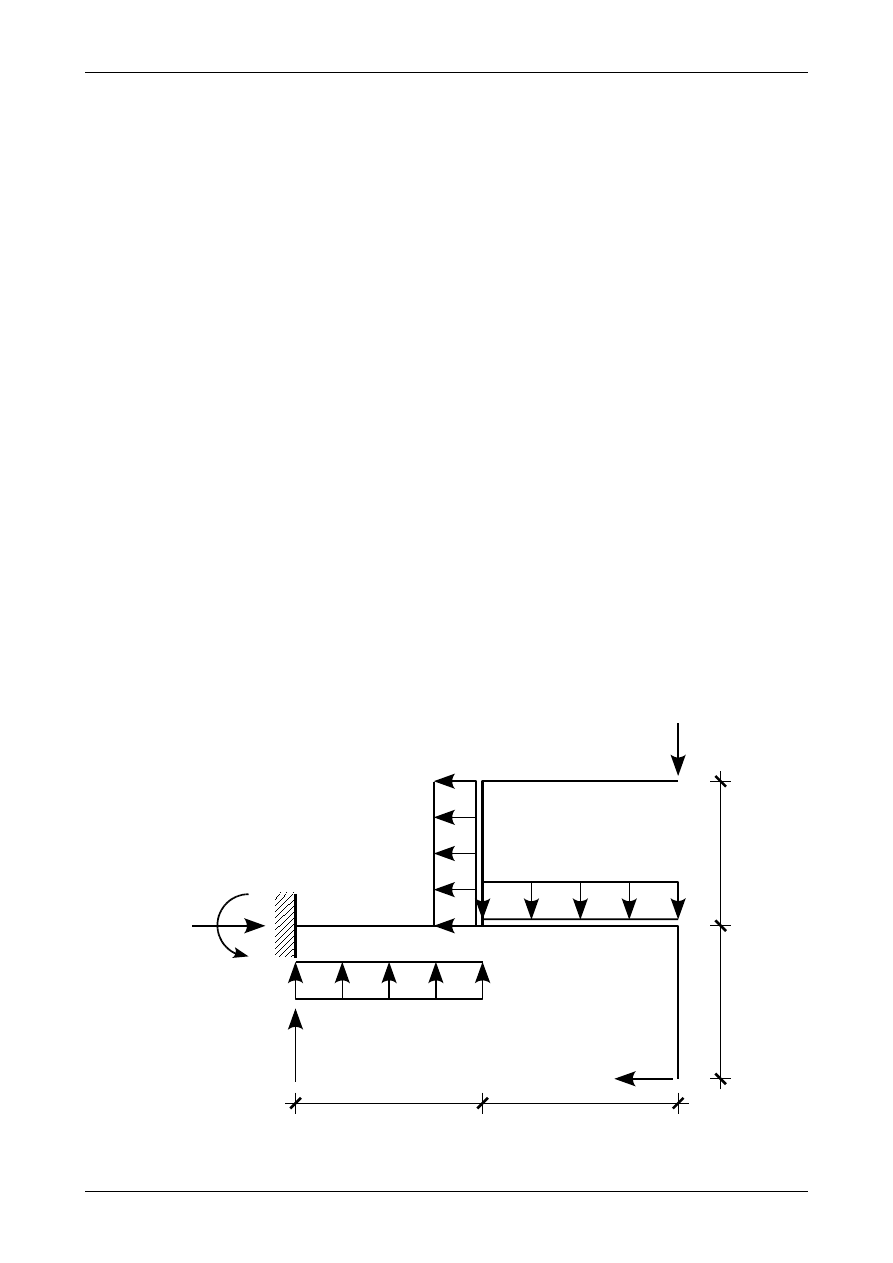
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

47

parabolą. Ponadto siła poprzeczna posiada w tym przedziale miejsce zerowe. Aby jednoznacznie
narysować wykres momentu zginającego należy wyznaczyć wartości momentu zginającego w trzech
punktach: na początku i na końcu przedziału oraz w miejscu zerowym siły poprzecznej. „Brzuszek”
takiej paraboli jest skierowany w tą samą stronę co obciążenie ciągłe.

•

Jeżeli w przedziale pręta ukośnego działa obciążenie ciągłe równomiernie rozłożone na długości
tego pręta lub na długości jego rzutu poziomego lub pionowego oraz siła poprzeczna nie posiada w
tym przedziale miejsca zerowego (czyli jest w całym przedziale dodatnia lub ujemna) to wykres
momentu zginającego jest także parabolą ale aby ją jednoznacznie narysować wystarczy wyznaczyć
wartości momentu zginającego tylko w dwóch punktach: na początku i na końcu przedziału Trzeci
punkt wykresu stanowi „brzuszek” paraboli, który jest skierowany w tą samą stronę co obciążenie
ciągłe równomiernie rozłożone.

Przykłady zastosowania tej metody w praktyce znajdują się w zadaniach dołączonych do niniejszego

opracowania.

4.9 Równowaga sił w węzłach ramy płaskiej

W celu sprawdzenia poprawności wykonania wykresów siły normalnej, poprzecznej i momentu

zginającego należy sprawdzić równowagę węzłów ramy. W tym celu wycinamy dany węzeł i z wykresów
sił przekrojowych odczytujemy wartości oraz zwroty odpowiednich sił przekrojowych (zgodnie z zasadami
znakowania). Siły te przykładamy w odpowiednich prętach ramy płaskiej. Następnie sprawdzamy, czy
spełnione są równania równowagi: sumy rzutów wszystkich sił na oś poziomą X, pionową Y oraz równanie
sumy momentów wszystkich sił względem punktu węzła. Należy pamiętać o sile skupionej oraz momencie
skupionym, które są przyłożone w punkcie węzła ramy płaskiej. Ponieważ długość prętów dochodzących do
węzła wynosi zero nie uwzględniamy przy sprawdzeniu równowagi węzła obciążeń ciągłych działających na
prętach dochodzących do węzła.

Rysunek 4.79 przedstawia przykładową ramę płaską z prętami ortogonalnymi (prostopadłymi do

siebie).

7,6 kN

6,2 kN

3,8 kN/m

5,2 kN/m

4,

3

kN

/m

A

B

C

D

E

F

2,2

2,3

1,

8

1,

7

4,9 kN

13,51 kN

55,84 kNm

[m]

Rys. 4.79. Ortogonalna rama płaska

Dr inż. Janusz Dębiński

Zaoczni

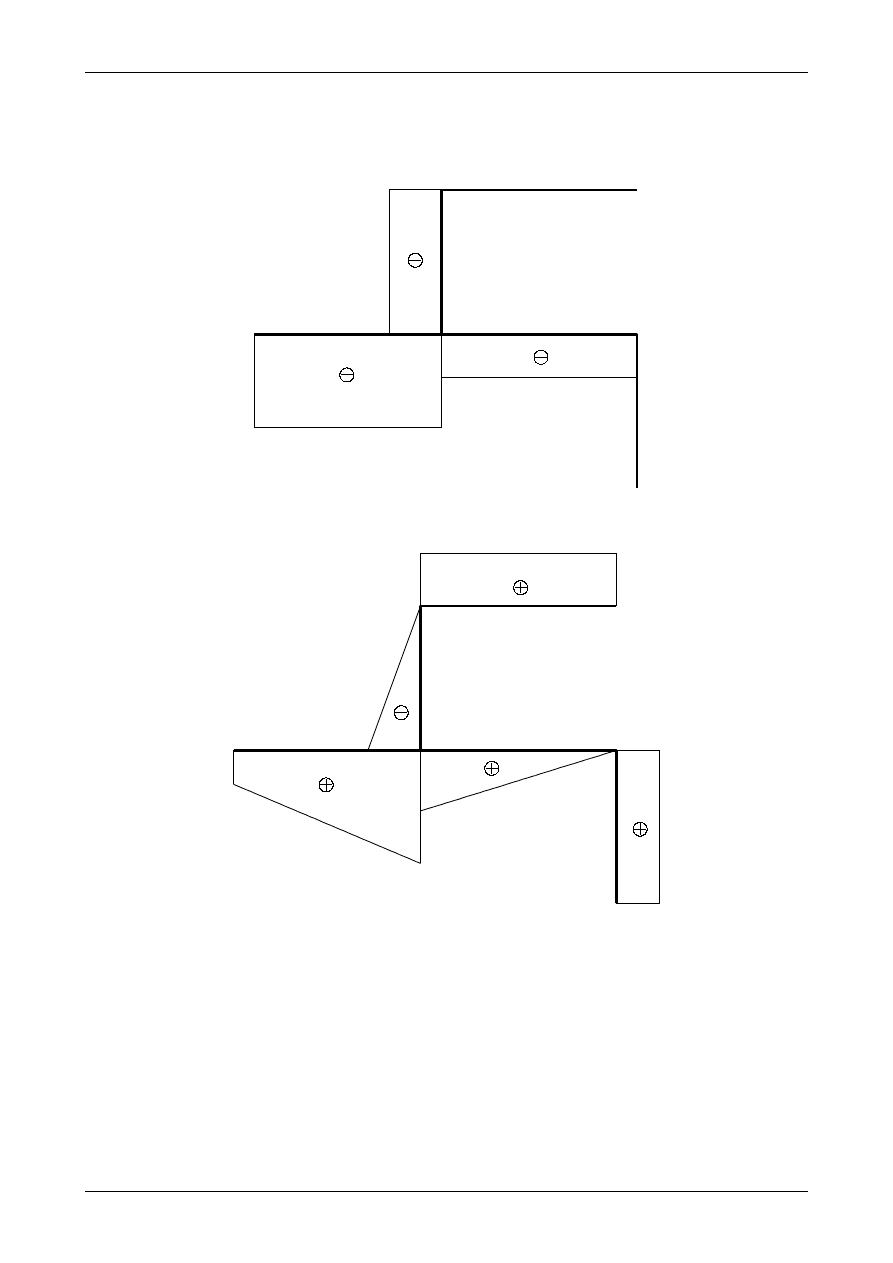
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

48

Rysunki 4.80, 4.81 i 4.82 przedstawiają wykresy siły normalnej, poprzecznej i momentu zginającego

dla tej ramy wspornikowej. Sprawdzenie równowagi we wszystkich węzłach dokonamy tylko na podstawie
tych wykresów.

N [kN]

6,2

13,51

7,

6

0,0

Rys. 4.80. Wykres siły normalnej

T [kN]

6,

2

7,6

0,0

7,31

0,

0

8,

74

16

,3

4

4,

9

Rys. 4.81. Wykres siły poprzecznej

Rysunek 4.83 przedstawia siły przekrojowe działające w węźle B ramy płaskiej przedstawionej na

rysunku 4.79. Jak widać siły te znajdują się w równowadze.

Rysunek 4.84 przedstawia siły przekrojowe działające w węźle E ramy płaskiej przedstawionej na

rysunku 4.79. Jak widać siły te znajdują się w równowadze.

Rysunek 4.85 przedstawia siły przekrojowe działające w węźle C ramy płaskiej przedstawionej na

rysunku 4.79. Jak widać siły te znajdują się w równowadze.

Rysunek 4.86 przedstawia siły przekrojowe oraz reakcje działające w węźle F czyli w utwierdzeniu

ramy płaskiej przedstawionej na rysunku 4.79. Jak widać wszystkie te siły znajdują się w równowadze.

Dr inż. Janusz Dębiński

Zaoczni

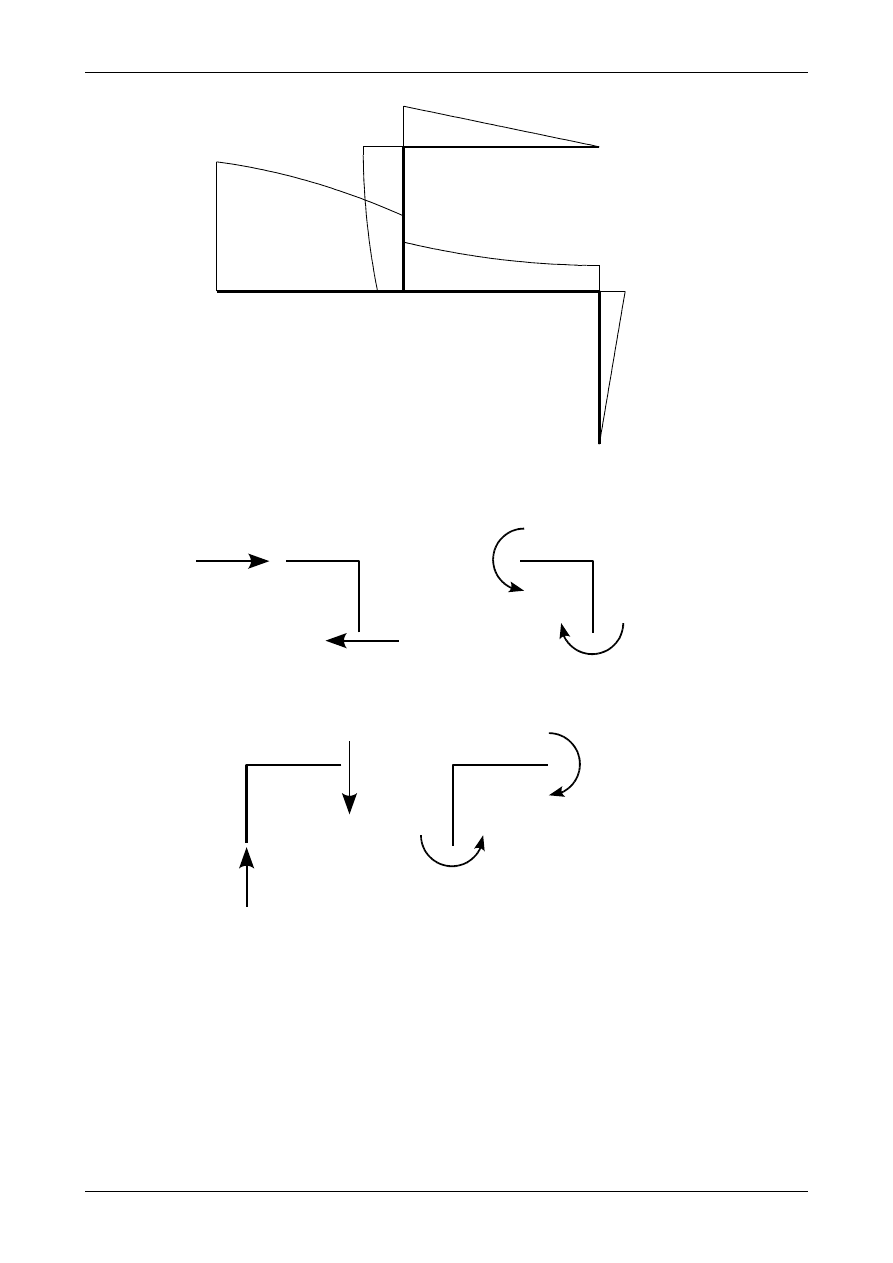
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

49

M [kNm]

0,0

21

,2

1

11,16

11

,1

6

0,

0

17

,4

8

17,48

32

,4

8

11,27

55

,8

4

Rys. 4.82. Wykres momentu zginającego

6,2 kN

11,16 kNm

6,2 kN

11,16 kNm

B

B

Rys. 4.83. Równowaga węzła B

7,6 kN

7,6 kN

17,48 kNm

17,48 kNm

E

E

Rys. 4.84. Równowaga węzła E

Rysunek 4.87 przedstawia przykładową ramę trójprzegubową z prętem ukośnym. Rysunki 4.88, 4.89 i

4.90 przedstawiają wykresy siły normalnej, poprzecznej i momentu zginającego dla tej ramy.

W przypadku równowagi węzła B w pierwszej kolejności należy sprawdzić równowagę całego pręta

ukośnego. Rysunek 4.91 przedstawia siły działające na wycięty pręt ukośny. Z równania sumy momentów
wszystkich sił działających na pręt ukośny względem punktu A sprawdzimy poprawność obliczenia siły
poprzecznej w pręcie ukośnym w węźle B, której wartość odczytana z wykresu siły poprzecznej na rysunku
4.89 wynosi -12,02 kN. Robimy tak, ponieważ podczas wyznaczania wartości siły normalnej i poprzecznej
w pręcie ukośnym można pomylić sinus z kosinusem, a funkcje te nie wchodzą do równania
sprawdzającego.

Dr inż. Janusz Dębiński

Zaoczni

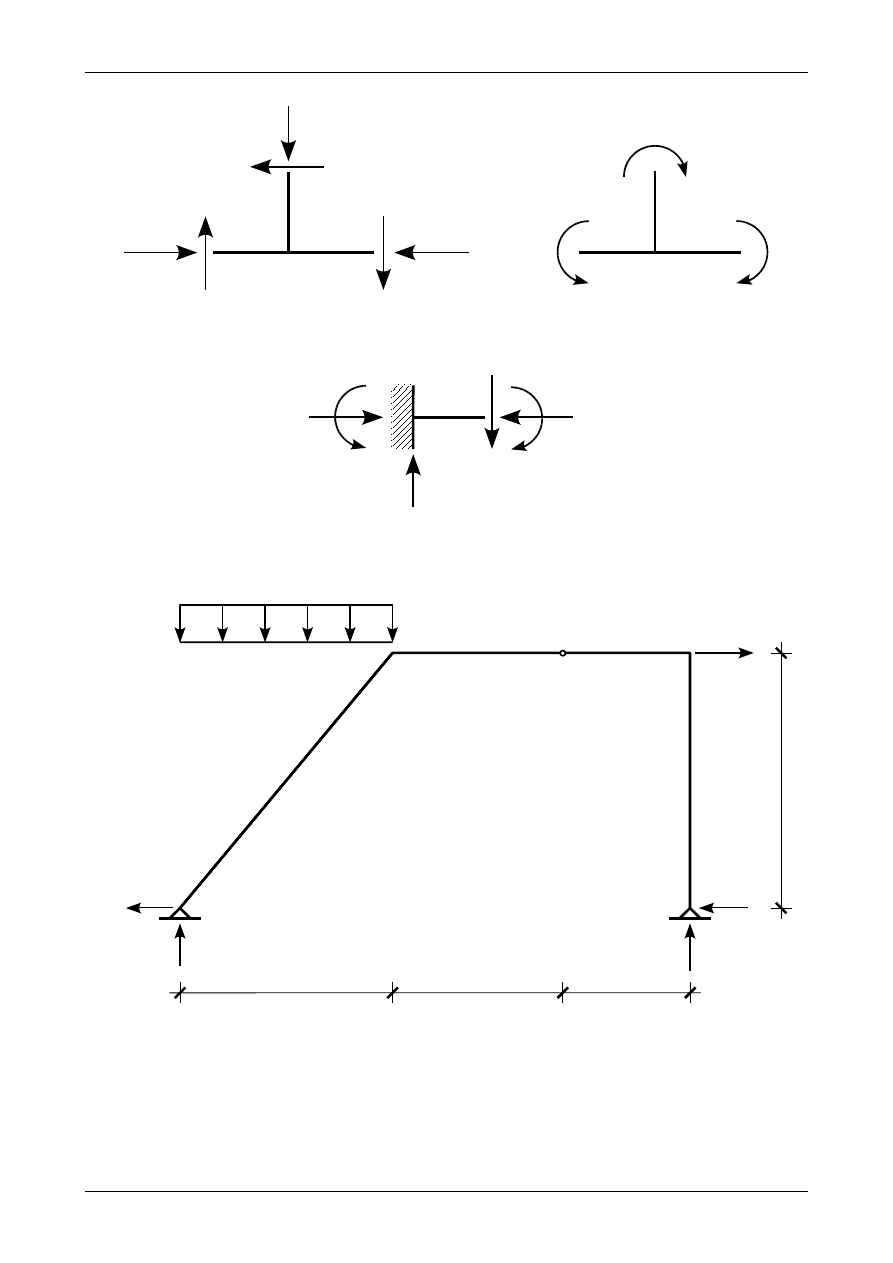
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

50

C

C

7,6 kN

6,2 kN

13,51 kN

7,31 kN

8,74 kN

16,34 kN

11,27 kNm

21,21 kNm

32,48 kNm

Rys. 4.85. Równowaga węzła C

F

4,9 kN

13,51 kN

55,84 kNm

13,51 kN

4,9 kN

55,84 kNm

Rys. 4.86. Równowaga utwierdzenia F

18,0 kN/m

A

B

C

D

E

5,0

4,0

3,0

6,

0

28,0 kN

11,63 kN

57,25 kN

32,75 kN

16,38 kN

Rys. 4.87. Rama trójprzegubowa z prętem ukośnym

Po tym sprawdzeniu możemy sprawdzić równowagę sił działających w węźle B. Rysunek 4.92

przedstawia wszystkie siły działające w tym węźle. Siły: normalną i poprzeczną sprawdzimy z równania
sumy rzutów wszystkich sił na oś poziomą X i pionową Y. Momenty zginające sprawdzimy z równania sumy
momentów względem punktu B.

Dr inż. Janusz Dębiński

Zaoczni

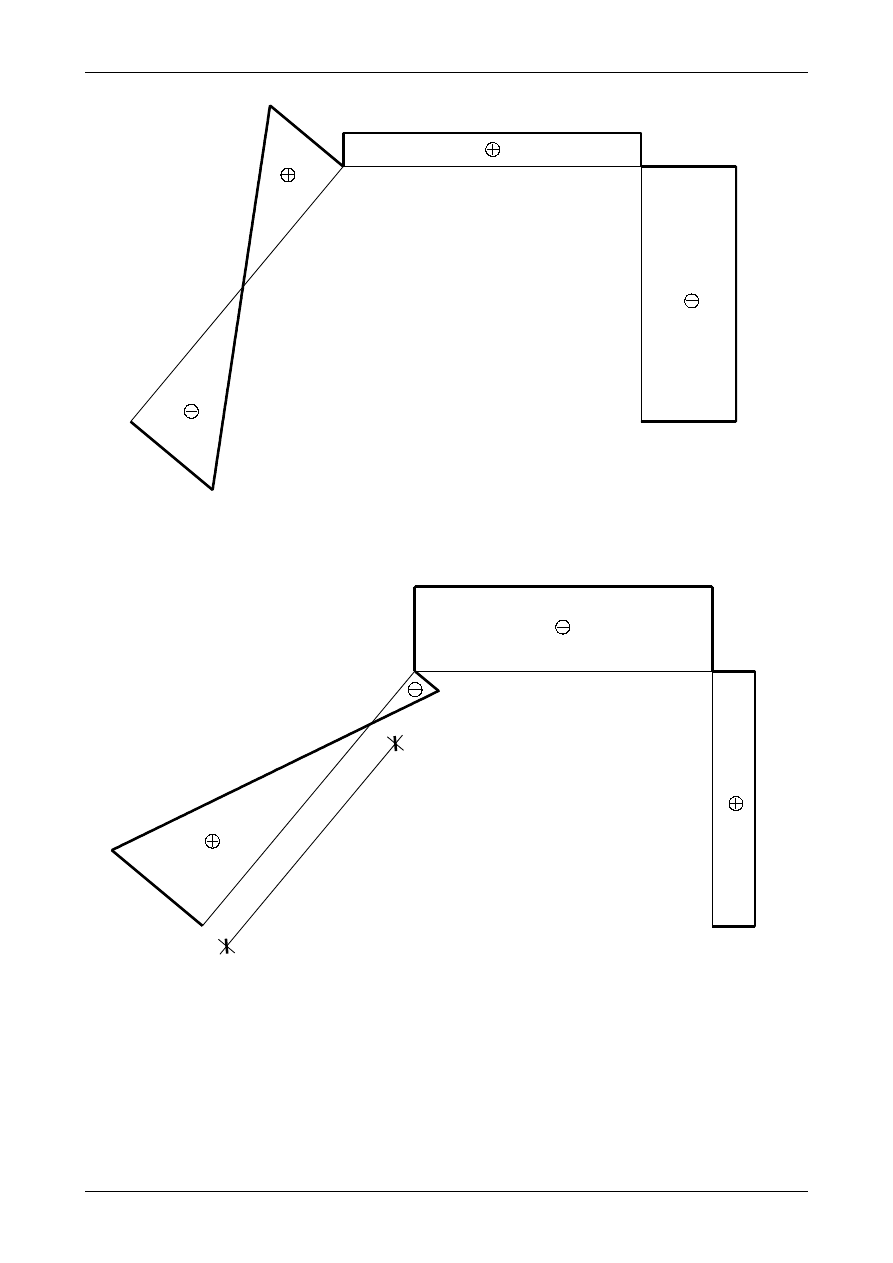
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

51

N [kN]

36,5

3

32,6

0

11,63

32

,7

5

Rys. 4.88. Wykres siły normalnej

T [kN]

45,5

9

12,0

2

32,75

16

,3

8

6,

18

Rys. 4.89. Wykres siły poprzecznej

4.10. Przykładowe wykresy sił przekrojowych w belkach

Rysunek 4.93 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki wspornikowej

obciążonej momentem skupionym na wolnym końcu.

Rysunek 4.94 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki wspornikowej

obciążonej siłą P na wolnym końcu.

Dr inż. Janusz Dębiński

Zaoczni

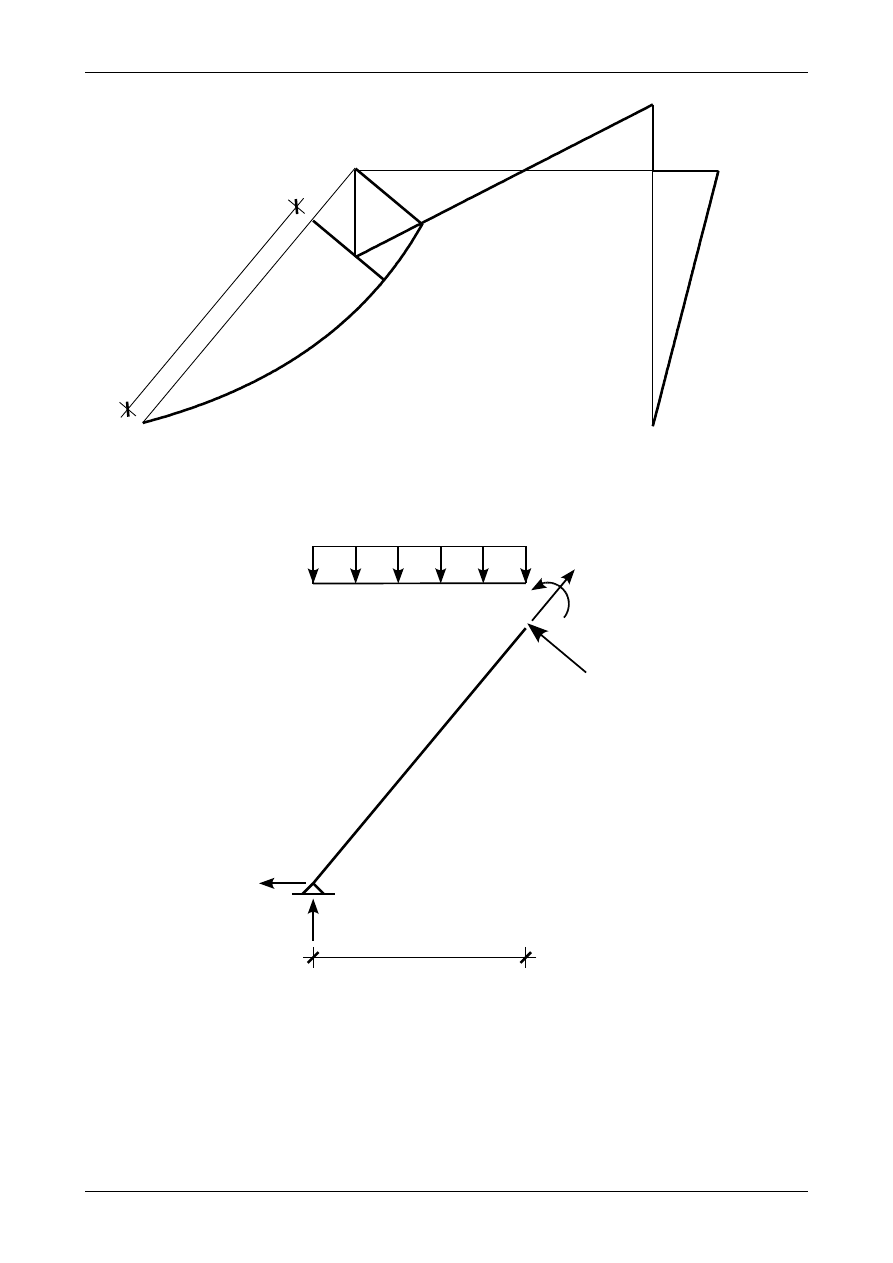
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

52

M [kNm]

0,0

131

,0

13

1,0

0,0

98

,2

8

98,28

6,

18

140

,9

Rys. 4.90. Wykres momentu zginającego

18,0 kN/m

A

5,0

11,63 kN

57,25 kN

32

,6

0

kN

12,0

2 k

N

131,0 kNm

- 7

,8

1

-

Rys. 4.91. Siły działające na pręt ukośny

Rysunek 4.95 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki wspornikowej z

obciążeniem ciągłym równomiernie rozłożonym q.

Rysunek 4.96 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki swobodnie

podpartej obciążonej momentem skupionym w dowolnym punkcie tej belki. Na rysunku tym jest
przedstawiona także równowaga momentów zginających i skupionego w otoczeniu punktu przyłożenia tego
ostatniego.

Dr inż. Janusz Dębiński

Zaoczni

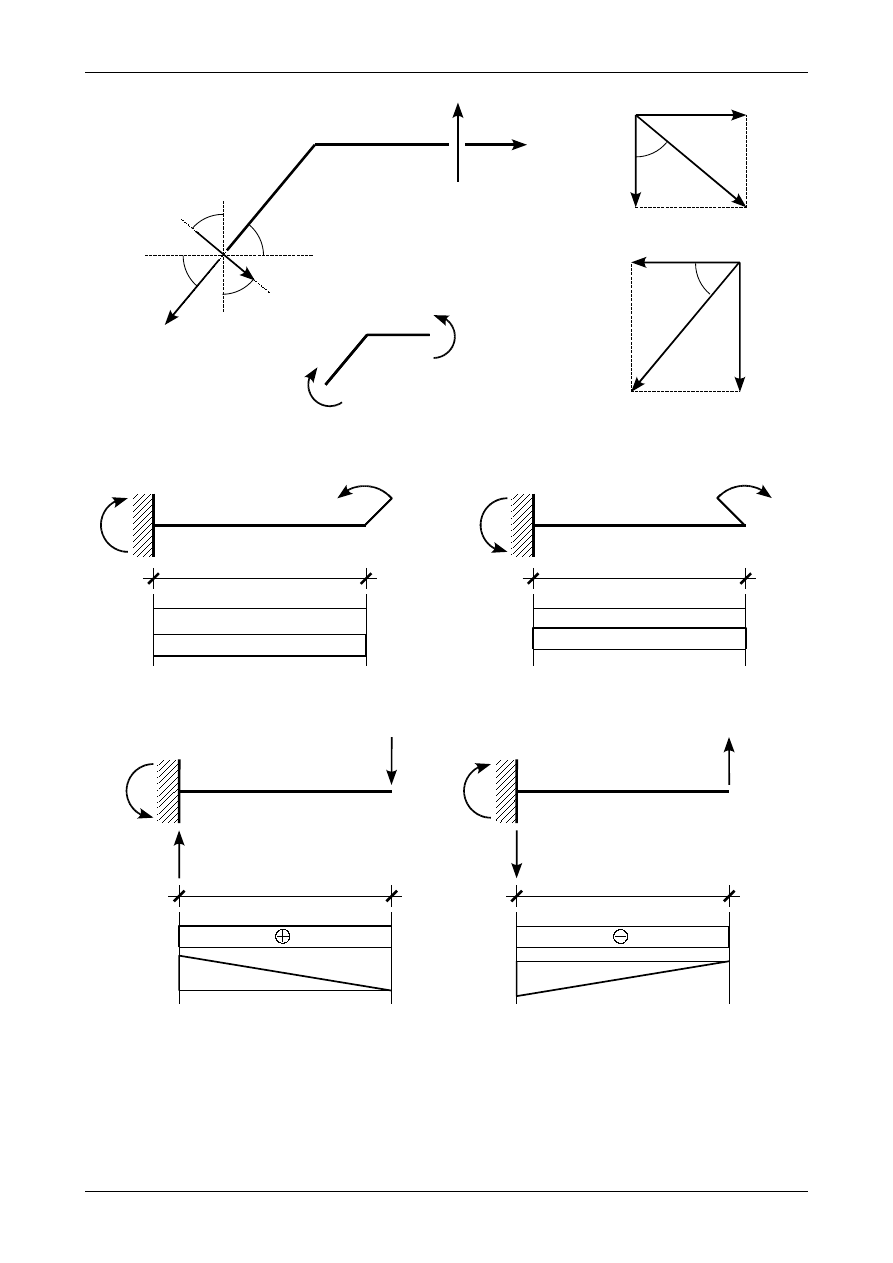
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

53

α

α

α

α

11,63 kN

32,75 kN

12,0

2 k

N

32

,6

k

N

α

12,0

2 k

N

α

32

,6

k

N

131,0 kNm

131,0 kNm

B

B

Rys. 4.92. Siły działające w węźle B

M

L

M

T(x)

M(x)

0

M

M

L

M

T(x)

M(x)

0

M

Rys. 4.93. Wykresy sił przekrojowych dla belki wspornikowej obciążonej momentem skupionym

L

T(x)

M(x)

P

P

P

⋅L

P

P

⋅L

L

T(x)

M(x)

P

P

P

⋅L

P

P

⋅L

Rys. 4.94. Wykresy sił przekrojowych dla belki wspornikowej obciążonej siłą na końcu

Rysunek 4.97 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki swobodnie

podpartej obciążonej siłą skupioną w dowolnym punkcie tej belki. Rysunek 4.98 przedstawia wykresy siły
poprzecznej i momentu zginającego dla belki swobodnie podpartej obciążonej siłą skupioną w połowie
rozpiętości tej belki.

Dr inż. Janusz Dębiński

Zaoczni

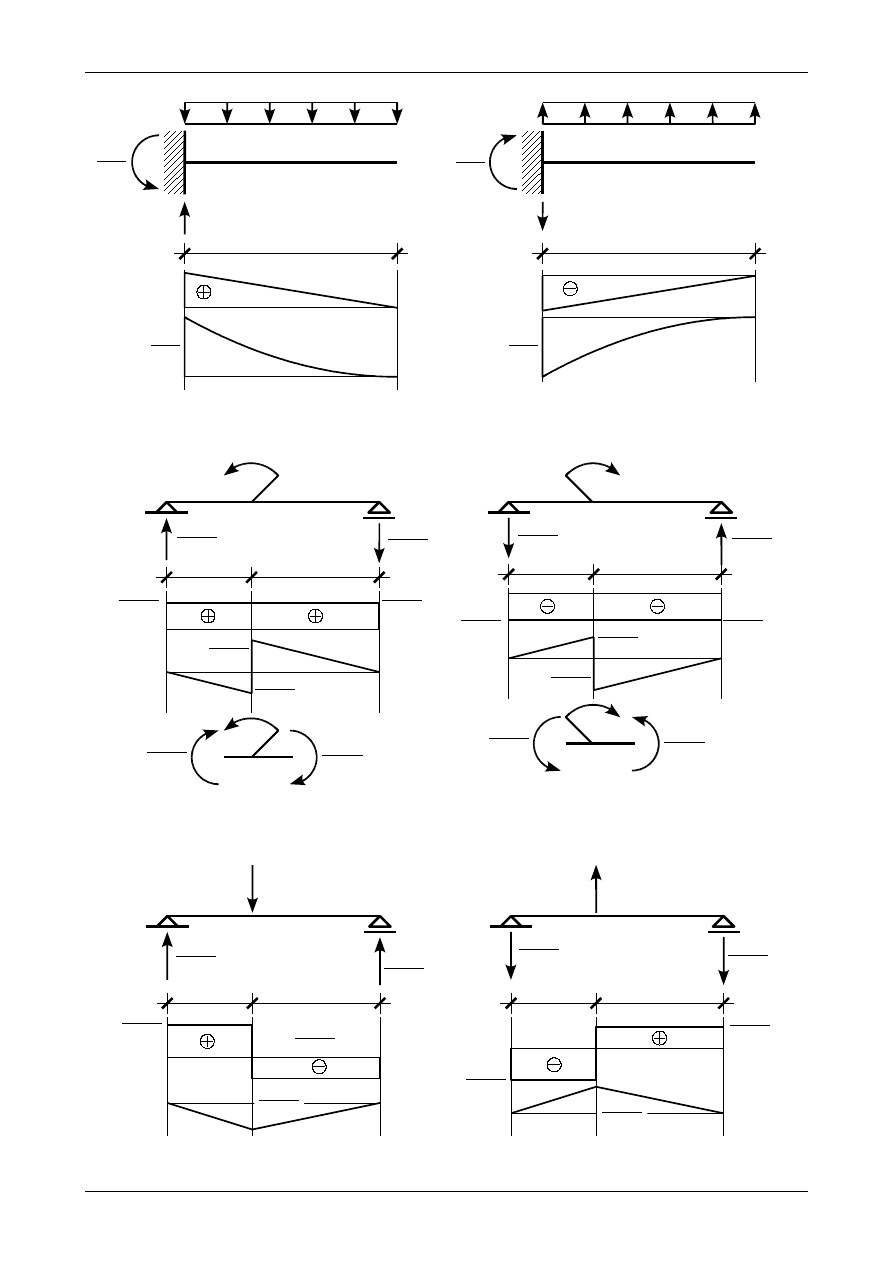
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

54

L

T(x)

M(x)

q

⋅L

q

⋅L

2

2

q

q

⋅L

q

⋅L

2

2

L

T(x)

M(x)

q

⋅L

q

⋅L

2

2

q

q

⋅L

q

⋅L

2

2

Rys. 4.95. Wykresy sił przekrojowych dla belki wspornikowej z obciążeniem ciągłym q

a

b

M

M



a

b



M



a

b



T(x)

M(x)

M



a

b



M



a

b



M

⋅a



a

b



M

⋅b



a

b



M

M

⋅a



a

b



M

⋅b



a

b



a

b

M

M



a

b



M



a

b



T(x)

M(x)

M



a

b



M



a

b



M

⋅a



a

b



M

⋅b



a

b



M

M

⋅a



a

b



M

⋅b



a

b



Rys. 4.96. Wykresy sił przekrojowych dla belki swobodnie podpartej obciążonej momentem skupionym

a

b

T(x)

M(x)

P

⋅a



a

b



P

⋅b



a

b



P

P

⋅b



a

b



P

⋅a



a

b



P

⋅a⋅b



a

b



a

b

T(x)

M(x)

P

⋅a



a

b



P

⋅b



a

b



P

P

⋅b



a

b



P

⋅a



a

b



P

⋅a⋅b



a

b



Rys. 4.97. Wykresy sił przekrojowych dla belki swobodnie podpartej obciążonej siłą w dowolnym punkcie

Dr inż. Janusz Dębiński

Zaoczni

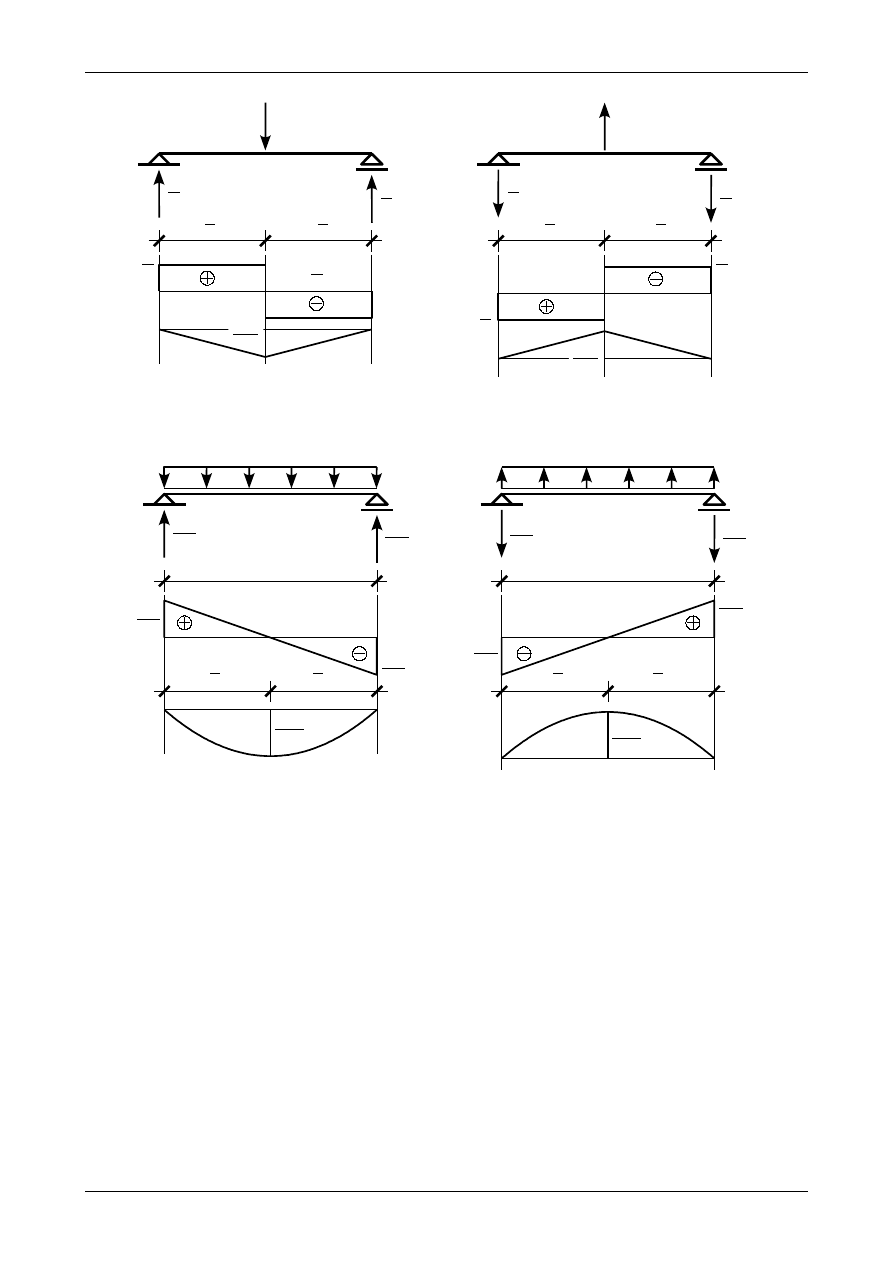
MO

4. SIŁY PRZEKROJOWE W BELKACH I RAMACH PŁASKICH

55

T(x)

M(x)

P

L
2

L
2

P

2

P

2

P

2

P

2

P

⋅L

4

T(x)

M(x)

P

L
2

L
2

P

2

P

2

P

2

P

2

P

⋅L

4

Rys. 4.98. Wykresy sił przekrojowych dla belki swobodnie podpartej obciążonej siłą w połowie rozpiętości

T(x)

M(x)

L

q

q

⋅L
2

q

⋅L
2

L
2

L
2

q

⋅L
2

q

⋅L
2

q

⋅L

2

8

T(x)

L

q

q

⋅L
2

q

⋅L
2

L
2

L
2

q

⋅L
2

q

⋅L
2

q

⋅L

2

8

M(x)

Rys. 4.99. Wykresy sił przekrojowych dla belki swobodnie podpartej z obciążeniem ciągłym q

Rysunek 4.99 przedstawia wykresy siły poprzecznej i momentu zginającego dla belki swobodnie

podpartej z obciążeniem ciągłym równomiernie rozłożonym q. Wartość ekstremalnego momentu
zginającego dla tej belki jest jedną z częściej używanych wartości do projektowania.

Dr inż. Janusz Dębiński

Zaoczni