METODA NEWTONA

Metoda ta służy do obliczenia przybliżonej wartości pierwiastka równania f(x) = 0 przy założeniu, że w przedziale <a;b>, w którym znajduje się pierwiastek, funkcja f(x) ma na końcach różne znaki oraz znak pierwszej i drugiej pochodnej jest stały.

W metodzie tej z tego końca przedziału <a;b>, w którym funkcja f(x) ma ten sam znak co f ”(x) prowadzimy styczną do wykresu funkcji y = f(x) i punkt x₁, w którym ta styczna przecina oś OX przyjmujemy za pierwsze przybliżenie szukanego pierwiastka  Oczywiście f(x₁) ma ten sam znak co rzędna punktu, z którego wyprowadzona była styczna. Jeżeli otrzymane przybliżenie jest za mało dokładne, to z punktu o współrzędnych (x₁, f(x₁)) prowadzimy następną styczną. Punkt x₂ przecięcia tej stycznej z osią OX jest drugim przybliżeniem pierwiastka. W ten sposób otrzymujemy kolejne wyrazy ciągu przybliżeń

x₁, x₂, ..., x_n zbieżnego monotonicznie do 

Na rysunku pokazano geometryczną interpretację metody Newtona dla przypadku, gdy zarówno pierwsza, jak i druga pochodna funkcji f(x) są dodatnie na rozpatrywanym przedziale.

Styczną prowadzimy z punktu B₀ (bowiem f '(b) > 0 i f ”(b-) > 0). Jej równanie ma postać y - f(b) = f '(b)(x - b).

Przyjmując y = 0, otrzymamy x₁ = b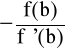

.

Wykażemy , że x₁ leży bliżej  niż b. Korzystają ze wzoru Taylora mamy

f( = f(b) + f '(b)(  -b) + 0.5f ”(c )( -b)², gdzie c
(;b). Ponieważ f()=0, więc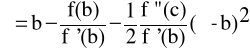

i wobec x₁ = b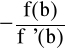

mamy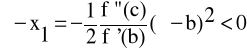

gdyż przy przyjętych założeniach f ”(c ) > 0 i f '(b) > 0. Stąd x₁ > , a ponieważ z x₁ - b =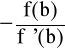
<0
więc x₁<b.

Z twierdzenia Lagrange'a mamy f(x₁) - f() = f '(c₁)(x₁- ) przy czym c₁
( ,x₁). Ponieważ f() = 0 i f '(c₁) > 0, więc f(x₁) > 0, a stąd wynika, że styczna poprowadzona w punkcie B₁(x₁, f(x₁)) będzie miała identyczne własności co styczna poprowadzona w punkcie B₀. Z równania drugiej stycznej

y - f(x₁) = f '(x₁)(x-x₁) otrzymamy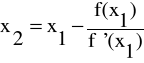
co pozwala na podanie wzoru rekurencyjnego opisującego kolejne wyrazy ciągu przybliżeń

.

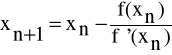
Tak jak w poprzednich metodach, ciąg przybliżeń jest ciągiem malejącym
ograniczonym z dołu (<x_n), a więc zbieżnym. Przechodząc do granicy w równości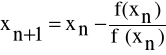
dla
mamy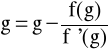
czyli f(g) = 0, a więc g = .

Program typu m-plik służący do obliczania wartości pierwiastka z metody Newtona.

Wzór funkcji:
x³ + 3 x² - 9 x - 2 = 0

Punkt startowy: x = 4

x=input(`punkt startowy x = `);

p=1;

while abs(p)>=0.001

p=(x^3+3*x^2-9*x-2)/(3*x^2+6*x-9);

x=x-p;

end;

x

Grzegorz Brożek

Gr. 9 Rok II ImiR

Sprawozdanie z przedmiotu:

Metody numeryczne i statystyka dla inżynierów

Obliczanie wartości

pochodnej przy pomocy funkcji

programu MATLAB

f(x₁)

f(b)

f(x)

f(a)

0

B₁

B₀

b

a

x₁



x₂

x