Postawienie problemu
Za przedmiot modelowania obrałam cenę notebooka firmy Asus. Naszą zmienną objaśnianą ![]()
będzie cena laptopa.
Przyjmuję, że model w projekcie będzie modelem jednowymiarowym. Ogólna postać modelu jednowymiarowego jest następująca:
![]()
gdzie:
![]()
- zmienna objaśniana (regresant, zmienna endogeniczna),
![]()
- postać analityczna modelu,
![]()
- zmienne objaśniające (regresowy, zmienne egzogeniczne),
![]()
- składnik losowy.
Wybór zmiennych objaśniających
Zmienne objaśniane:
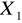
- Prędkość procesora- [GHz];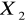
- Częstotliwość FSB - [MHz];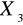
- Pamięć ram- [MB];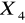
- Dysk twardy- [GB];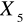
- Matryca- [Cale];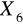
- Waga- [kg];
Tabela 1. przedstawia wartości poszczególnych zmiennych dla 30 obserwacji.
Lp. |
Nazwa |
Cena |
Procesor |
Częstotliwość FSB |
Pamięć ram |
Dysk twardy |
Matryca |
Waga |
1 |
Asus EEE 904HD |
589 |
0,90 |
353 |
1024 |
80 |
8,9 |
1,40 |
2 |
Asus Eee 900 |
688 |
0,90 |
353 |
1024 |
120 |
8,9 |
0,99 |
3 |
Asus EPC-1000HD |
898 |
0,90 |
353 |
1024 |
120 |
8,9 |
1,40 |
4 |
Asus Eee PC 1201HA |
1009 |
1,30 |
533 |
1024 |
250 |
12,1 |
1,40 |
5 |
Asus 1008HA-PIK032X |
1109 |
1,33 |
667 |
1024 |
160 |
10,1 |
1,10 |
6 |
Asus 1101HA-BLK038M |
1119 |
1,33 |
533 |
1024 |
250 |
11,6 |
1,40 |
7 |
Asus Eee 1101HA |
1180 |
1,33 |
533 |
1024 |
160 |
11,6 |
1,38 |
8 |
Asus1005HA-BLK135X |
1189 |
1,33 |
533 |
1024 |
160 |
10,1 |
1,27 |
9 |
Asus EeePC 1008HA |
1429 |
1,60 |
667 |
2048 |
200 |
10,1 |
1,10 |
10 |
Asus Eee 1005HA |
1469 |
1,60 |
667 |
2048 |
250 |
10,0 |
1,27 |
11 |
Asus Eee PC 1201HA |
1479 |
1,60 |
667 |
2048 |
250 |
12,1 |
1,40 |
12 |
Asus Eee l 1008HA-N280 |
1506 |
1,66 |
667 |
1024 |
250 |
10,1 |
1,10 |
13 |
Asus Eee PC |
1589 |
1,60 |
533 |
1024 |
250 |
10,1 |
1,27 |
14 |
Asus PRO5DIJ-SX221 |
1768 |
1,80 |
667 |
2048 |
320 |
15,6 |
2,60 |
15 |
Asus K50IJ-SX036 |
1889 |
1,80 |
667 |
2048 |
250 |
15,6 |
2,60 |
16 |
Asus X58LE-EX137X |
1899 |
2,00 |
800 |
2048 |
250 |
16,6 |
2,88 |
17 |
Asus K50IN - SX034C |
2089 |
2,00 |
800 |
3071 |
320 |
15,6 |
2,60 |
18 |
Asus K50IJ |
2249 |
2,10 |
667 |
2048 |
500 |
16,6 |
2,60 |
19 |
Asus K50IN-SX126E |
2426 |
2,10 |
667 |
2048 |
250 |
15,6 |
2,60 |
20 |
Asus K70IJ |
2505 |
2,10 |
667 |
2048 |
320 |
17,3 |
3,12 |
21 |
Asus K70IC - TY010 |
2729 |
2,10 |
800 |
4096 |
320 |
17,3 |
2,80 |
22 |
Asus UL50VG-XX023 |
3069 |
2,10 |
800 |
2048 |
250 |
15,6 |
2,30 |
23 |
Asus N71VG-TY023V |
3289 |
2,20 |
1066 |
2048 |
320 |
17,3 |
2,63 |
24 |
AsusN731GE- TY03B |
3299 |
2,20 |
800 |
2048 |
320 |
17,3 |
3,20 |
25 |
Asus N61VG |
3390 |
2,20 |
1066 |
2048 |
500 |
15,6 |
2,71 |
26 |
Asus N71VN-TY015 |
3769 |
2,53 |
1066 |
4096 |
500 |
17,3 |
3,40 |
27 |
Asus M60J |
4099 |
2,80 |
1066 |
4096 |
320 |
15,6 |
3,30 |
28 |
Asus N71VN-P8700 |
4294 |
2,80 |
800 |
4096 |
1000 |
17,3 |
3,67 |
29 |
Asus M60J-720QM |
4589 |
2,80 |
1066 |
4096 |
320 |
15,6 |
3,30 |
30 |
Asus N90 |
4889 |
2,80 |
1066 |
4096 |
640 |
18,4 |
4,20 |
Tabela 1. Dane dotyczące poszczególnych zmiennych
Dane dotyczące modeli notebooków dla poszczególnych zmiennych ![]()
oraz dane dotyczące zmiennej objaśnianej ![]()
pochodzą ze stron internetowych sklepów komputerowych. Na podstawie zaczerpniętych informacji dokonałam wyborów średnich cen rynkowych danych modeli laptopów.
2.1. Eliminacja zmiennych quasi-stałych
Odchylenie standardowe jest bezwzględną miara rozrzutu zmiennej względem średniej. Odchylenie standardowe mówi nam, o ile średnio poszczególne wartości zmiennej różnią się od średniej.
Współczynnik zmienności ![]()
jest względna miarą rozrzutu wartości zmiennej, i mówi nam, czy jest to rozproszenie duże czy małe w stosunku do średniej.
Jeżeli ![]()
to zmienna charakteryzuje się małą zmiennością i tą zmienną traktujemy jako quasi- stałą. Taką zmienną eliminuje się z modelu.
2.1.1. Obliczenia (eliminacja zmiennych quasi-stałych)
|
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
Śr. |
2249,80000 |
1,86033 |
719,66667 |
2150,36667 |
306,66667 |
13,82667 |
2,23300 |
S |
1205,73829 |
0,55308 |
213,20527 |
1101,26813 |
176,49048 |
3,19697 |
0,92147 |
V |
0,53593 |
0,29730 |
0,29626 |
0,51213 |
0,57551 |
0,23122 |
0,41266 |
Tabela 2. Średnia, odchylenie standardowe, współczynnik zmienności dla poszczególnych zmiennych kandydujących na zmienne objaśniające
Poszczególne wartości zmiennej ![]()
różnią się od średniej 1,86033 wynoszącej średnio o 0,55308. Dla zmiennej ![]()
wartości różnią się od średniej 719,6666667 wynoszącej średnio o 213,20527. Kolejno wartości zmiennej ![]()
różnią się od średniej wynoszącej 2150,366667 średnio o 1101,26813. Z kolei wartości zmiennej ![]()
różnią się od średniej wynoszącej 306,66667 średnio o 176,490478. Natomiast dla zmiennej ![]()
wartości różnią się od średniej wynoszącej 13,82667 średnio o 3,19697. Dla ostatniej ze zmiennych - zmiennej ![]()
- wartości różnią się od średniej wynoszącej 2,233 średnio o 0,92147.
W rozważanym przykładzie żadną ze zmiennych nie uznaję za quasi-stałą (a co za tym idzie, żadnej ze zmiennych nie eliminujemy), gdyż zmienne ![]()
charakteryzują się dużą zmiennością a ich współczynniki zmienności są większe od wartości 0,1.
Wnioskuję zatem, że wszystkie wcześniej przyjęte zmienne ![]()
są zmiennymi objaśniającymi.
2.2. Analiza współczynników korelacji
2.2.1. Obliczenie współczynników korelacji
Dla współczynników korelacji ![]()
tworzymy macierz ![]()
.
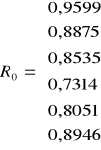
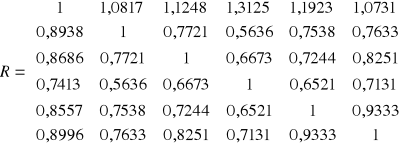
Dla współczynników korelacji ![]()
tworzymy macierz ![]()
.
2.2.2. Ustalenie wartości krytycznej współczynnika korelacji
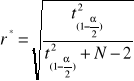
gdzie:
![]()
- poziom istotności, ![]()
,
![]()
- liczba obserwacji, ![]()
,
![]()
- wartość statystyki t-Studenta dla zadanego poziomu istotności ![]()
oraz dla ![]()
stopni swobody,
![]()
- liczba stopni swobody.
![]()
![]()
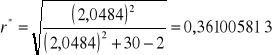
Badam kolejno wszystkie potencjalne zmienne objaśniające w celu wyeliminowania tych zmiennych, które są słabo skorelowane z ![]()
. Korzystam przy tym z warunku:
![]()
W przypadku możemy powiedzieć, że silna korelacja jest w przedziałach ![]()
.
Zestaw potencjalnych zmiennych objaśniających:
|
|
|
|
|
|
Do modelu wybraliśmy zmienną
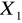
gdyż jest najsilniej skorelowana z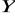
:eliminujemy zmienne
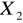
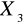
,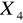
,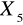
,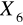
gdyż są one zbyt silnie skorelowane ze zmienną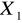
:Szacowanie liniowej zależności ceny notebooka od prędkości procesora
|
|
|
|
|
|
|
|
|
|
|
|
Ostatecznie do modelu trafia tylko jedna zmienna - ![]()
( jest nią prędkość procesora ). Zmienne ![]()
, ![]()
, ![]()
, ![]()
zostały wyeliminowane, gdyż są zbyt silnie skorelowane z![]()
.
Zależność zmiennej objaśnianej ![]()
od zmiennej objaśniającej ![]()
( czyli zależność ceny notebooka od prędkości procesora ) przedstawia wykres 1.
Wykres 1. Wykres zależności zmiennej ![]()
od zmiennej ![]()
z linią trendu o typie liniowym
Z wykresu można odczytać, że występuje bardzo silna korelacja dodatnia co oznacza, że wzrost prędkości procesora towarzyszy wzrost ceny notebooka.
Na wykresie 1 przedstawiony jest trend typu liniowego, opisany równaniem:
![]()
Oraz współczynnik determinacji ![]()
wynoszący ![]()
.
Zakładam model postaci:
![]()
,
gdzie zmienna ![]()
to przyjęta do naszego modelu ekonometrycznego zmienna objaśniająca ![]()
(w dalszych obliczeniach oznaczana po prostu jako zmienna ![]()
).
![]()
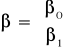
Obliczam macierz ![]()
:
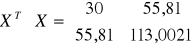
Wyznacznik macierzy ![]()
:
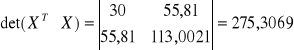
Macierz dopełnień algebraicznych:
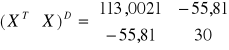
Macierz odwrotna:
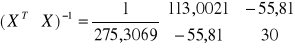
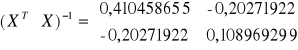
Obliczam macierz ![]()
:
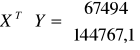
Obliczamy macierz ![]()
:
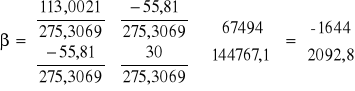
Model ma postać:
![]()
Interpretacja otrzymanego modelu:
Jednostkowy wzrost prędkości procesora spowoduje wzrost ceny o ok. ![]()
. Można powiedzieć zatem, że wzrost prędkości o 1 GHz spowoduje wzrost ceny o około 2092,80 zł.
5.1. Współczynnik determinacji
Współczynnik determinacji oblicza się ze wzoru:
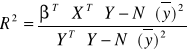
Wartość ![]()
jest liczbą z przedziału ![]()
. Bliskie jedności ![]()
wskazują na dobre, natomiast bliskie zera na złe dopasowanie modelu do danych empirycznych.
Współczynnik determinacji mówi, jaka część całkowitej zmienności zmiennej ![]()
jest wyjaśniona przez model.
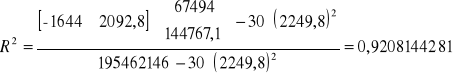
Wyznaczony model w 92,08 % wyjaśnia zmienność kształtowania się przeciętnej ceny notebooka. Ukazuje nam iż dopasowanie modelu w tym przypadku jest dobre.
5.2. Weryfikacja statystyczna modelu
![]()
Wartości cen przewidywane przez model różnią się od zaobserwowanych średnio o 351,20 zł. Są to błędy średnie co do wielkości, o czym świadczy współczynnik zmienności równy około 15,61 %.
Macierz wariancji i kowariancji estymatorów parametrów:
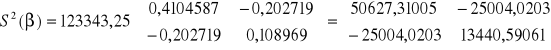
Średnie błędy szacunku parametrów ![]()
(błędy bezwzględne):
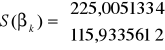
Błąd oszacowania parametru ![]()
wynosi 225,0051334 natomiast błąd oszacowania parametru ![]()
wynosi 115,9335612.
Średni błąd względny szacunku k-tego parametru:
Dla parametru ![]()
: 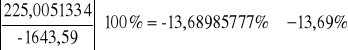
Dla parametru ![]()
: 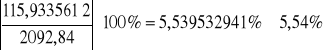
Zapisujemy model w postaci:
![]()
(225,0051334) (115,9335612)
(-13,69%) (5,54%)
Interpretacja błędów w modelu:
Parametr ![]()
jest wyznaczony z błędem 225,0051334 natomiast parametr ![]()
z błędem 115,9335612. Dokładniej wyznaczony jest parametr ![]()
, gdyż jego błąd względny jest mniejszy od błędu względnego parametru ![]()
.
5.3. Testowanie hipotez o statystycznej istotności parametrów strukturalnych modelu
Dla danych dotyczących ceny telefonu komórkowego zależnego od liczby pikseli aparatu cyfrowego oraz poziomu istotności ![]()
model ma postać:
![]()
(225,0051334) (115,9335612)
5.3.1. Stawianie hipotez dla parametrów ![]()
Hipotezy dla parametru ![]()
:
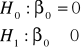
Hipotezy dla parametru ![]()
:
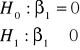
5.3.2. Wartość statystyki testowej oraz obszary krytyczne
Statystyka testowa:
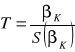
Statystyka ta ma rozkład t-Studenta o N-K-1 stopniach swobody.
Wartość krytyczna statystyki t-Studenta dla ![]()
oraz ![]()
stopni swobody:
![]()
Wartość statystyki testowej oraz obszary krytyczne dla parametru ![]()
:
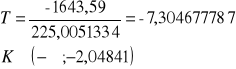
Wartość statystyki testowej oraz obszary krytyczne dla parametru ![]()
:
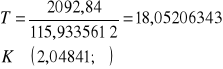
Interpretacja:
Dla parametru ![]()
i ![]()
wartość statystyki testowej należy do obszaru krytycznego, dlatego w obu przypadkach odrzucamy hipotezy zerowe, uznając za prawdziwe hipotezy alternatywne. W szczególności oznacza to, że prędkość procesora notebooków firmy Asus ma pozytywny wpływ na cenę komputera.
5.4. Przedziały ufności dla parametrów modelu
Przedział ufności dla parametru ![]()
na poziomie istotności ![]()
ma postać:
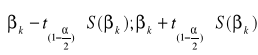
gdzie:
![]()
- jest kwartylem rzędu ![]()
rozkładu t-Studenta o ![]()
stopniach swobody.
Dla danych dotyczących ceny notebooka zależnego od prędkości procesora oraz poziomu istotności ![]()
model ma postać:
![]()
(225,0051334) (115,9335612)
![]()
Dla parametru ![]()
:
![]()
Dla parametru ![]()
:
![]()
Interpretacja:
Z prawdopodobieństwem 0,95 współczynnik ![]()
należy do przedziału: ![]()
, a ![]()
.
W szczególności dla parametru ![]()
oznacza to, że jednostkowy wzrost prędkości procesora w notebooku może spowodować wzrost ceny komputera.
Wnioski:
Na podstawie uzyskanego modelu ekonometrycznego możemy stwierdzić, że cena notebooka jest zależna od prędkości jego procesora i wzrost prędkości niesie za sobą wzrost ceny komputera..
Podsumowując możemy stwierdzić, że obliczenie dokonane w naszym modelu ekonometrycznym obarczone są niewielkim błędem i mogą być uznane za wiarygodne
9
Wyszukiwarka
Podobne podstrony:
ASUS Notebook seria L3
projekt o narkomanii(1)
!!! ETAPY CYKLU PROJEKTU !!!id 455 ppt
Wykład 3 Dokumentacja projektowa i STWiOR
Projekt nr 1piątek
Projet metoda projektu
34 Zasady projektowania strefy wjazdowej do wsi
PROJEKTOWANIE ERGONOMICZNE
Wykorzystanie modelu procesow w projektowaniu systemow informatycznych
Narzedzia wspomagajace zarzadzanie projektem
Zarządzanie projektami 3
Metody Projektowania 2
BYT 109 D faza projektowania
p 43 ZASADY PROJEKTOWANIA I KSZTAŁTOWANIA FUNDAMENTÓW POD MASZYNY
więcej podobnych podstron