Gr.24A	Wykonali: Herbuś Mariusz Miśta Tomasz		Laboratorium z mechaniki ogólnej
Ćw. nr 5	Rozwiązywanie równań dynamicznych metodą numeryczną.
Ocena		Data	Podpis

1.Cel ćwiczenia

Celem ćwiczenia było wykreślenie wykresów prędkości i przemieszczenia w funkcji czasu dla ciała spadającego z pewnej wysokości i dla ciała rzuconego pionowo do góry z pewną prędkością .

2. Rysunek .

- βv

mg

m=5 kg

g=10 m/s² x

β=10,5

t=15s

Δ=0,01s

3. Równanie ruchu .

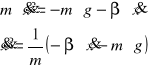
3. Schemat blokowy programu kreślącego wykresy prędkości i przemieszczenia ciała rzuconego do góry z prędkością początkową równą 15 m/s. 1

1e6 -15

50 5 15 0 0 15

con ‾ Att Int Int lim Plot

a1 a2 a3 a5 a6 x

2

-15

10,5 0 15

Gai Rel Plot

Δ=0,01 a4 a7 v

t=15

TIME

4. Program

a1=CON [No Inputs]

Constant value : 5.00000E+1

a2=ATT [-a1-a4]

Attenuation : 5.00000

a3=INT [a2]

Initial value : 1.50000E+1

a4=GAI [a3]

Gain : 1.05000E+1

a5=INT [a3]

Initial value : 0.000000

a6=LIM [a5]

Minimum : 0.000000

Maximum : 1.00000E+6

a7=REL [a3 , 0.000000 , 0.000000 , a5]

Compare value : 0.000000

t=TIME[No Inputs]

Time step DELTA : 1.00000E-2

End time : 1.50000E+1

v=PLOT[a7]

PLOT number : 2.00000

Minimum :-1.50000E+1

Maximum :1.50000E+1

x=PLOT[a6]

PLOT number : 1.00000

Minimum :-1.50000E+1

Maximum : 1.50000E+1

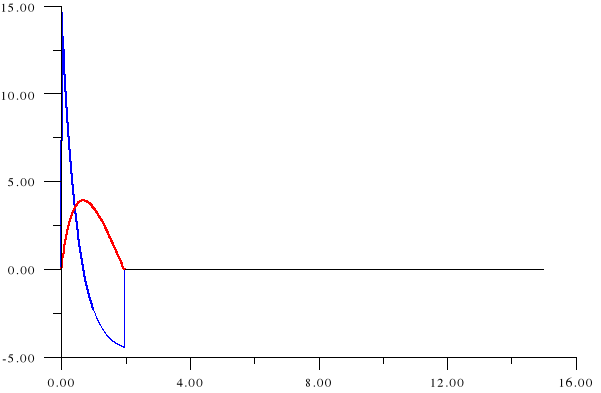
5. Wykres prędkości i przemieszczenia ciała rzuconego do góry z prędkością początkową równą 15 m/s.

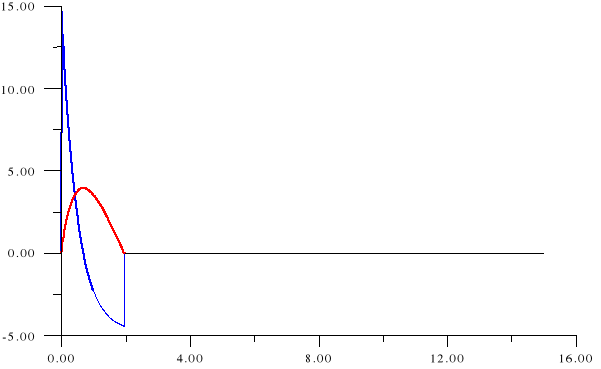
v[m/s]

x[m]

prędkość

przemieszczenie

czas[s]

6. Schemat blokowy programu kreślącego wykresy prędkości i przemieszczenia ciała

puszczonego z wysokości x(0)=55m. 1

1e6 -60

50 5 0 55 0 60

con ‾ Att Int Int lim Plot

a1 a2 a3 a5 a6 x

2

-60

10,5 0 60

Gai Rel Plot

a4 a7 v

7. Program

a1=CON [No Inputs]

Constant value : 5.00000E+1

a2=ATT [-a1-a4]

Attenuation : 5.00000

a3=INT [a2]

Initial value : 0.000000

a4=GAI [a3]

Gain : 1.05000E+1

a5=INT [a3]

Initial value : 5.50000E+1

a6=LIM [a5]

Minimum : 0.000000

Maximum : 1.00000E+6

a7=REL [a3 , 0.000000 , 0.000000 , a5]

Compare value : 0.000000

t=TIME[No Inputs]

Time step DELTA : 1.00000E-2

End time : 1.50000E+1

v=PLOT[a7]

PLOT number : 2.00000

Minimum :-6.00000E+1

Maximum : 6.00000E+1

x=PLOT[a6]

PLOT number : 1.00000

Minimum :-6.00000E+1

Maximum : 6.00000E+1

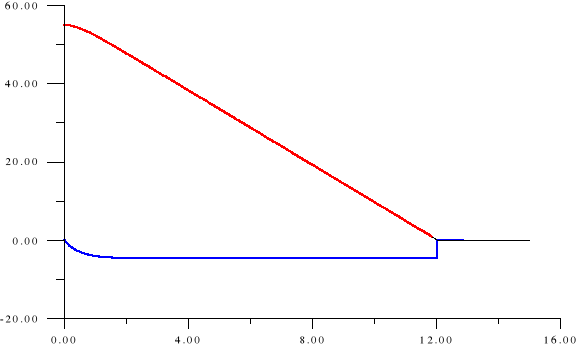
8. Wykres prędkości i przemieszczenia ciała puszczonego z wysokości x(0)=55m.

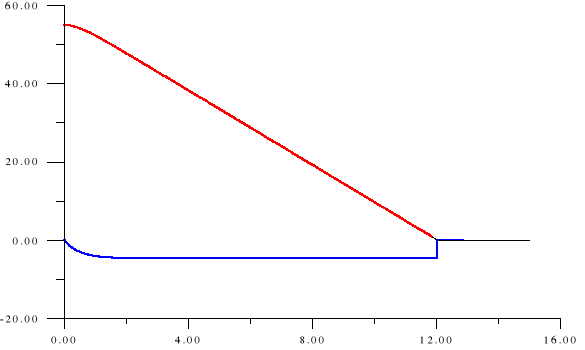
v[m/s]

x[m]

prędkość

przemieszczenie

czas[s]

9. Wnioski:

Na podstawie wykresu możemy określić na jaką wysokość wzniesie się ciało o określonej masie nadając mu określoną prędkość początkową. Możemy równięż po jakim czasie ciało powróci do punktu z którego zostało wyrzucone .

Na podstawie drugiego wykresu możemy się dowiedzieć jaką maksymalną prędkość osiągnie ciało spadając z określonej wysokości.