ROZDZIAŁ 2.

ROZKŁADY TEORETYCZNE WYKORZYSTYWANE

WE WNIOSKOWANIU STATYSTYCZNYM

2.1. Zmienne losowe i ich rozkłady

Zmienna losowa to dowolna funkcja X: →R określona na zbiorze zdarzeń elementarnych  i przyjmująca wartości w zbiorze liczb rzeczywistych R.

Intuicyjnie można powiedzieć, że jest to taka zmienna, która w wyniku doświadczenia realizuje różne wartości liczbowe z określonym prawdopodobieństwem.

Wartości, jakie mogą przyjmować zmienne losowe, nazywamy realizacjami zmiennej losowej.

Jeżeli przy tym znany jest zbiór wszystkich możliwych realizacji zmiennej losowej i prawdopodobieństwa przyjęcia tych realizacji przez tą zmienną, to mówimy, że znany jest rozkład zmiennej losowej.

Rozkład zmiennej losowej może być przedstawiony w postaci szeregu, wykresu lub funkcji, opisującej zależność między wartościami zmiennej losowej, a odpowiadającymi im prawdopodobieństwami.

Można wyróżnić dwie klasy zmiennych losowych, a mianowicie zmienne losowe skokowe (dyskretne) i zmienne losowe ciągłe.

Zmienna losowa typu skokowego może przyjmować skończoną lub nieskończoną, ale przeliczalną liczbę wartości z odpowiednimi prawdopodobieństwami (tzw. punktów skokowych x₁,x₂,x₃,…,x_k realizowanych z prawdopodobieństwem p₁,p₂,p₃,…,p_k nazywanym skokami).

Zmienna losowa X jest typu ciągłego, jeśli jej możliwe warianty tworzą przedział ze zbioru liczb rzeczywistych.

Podstawowe charakterystyki rozkładu zmiennej losowej to:

1. Funkcja prawdopodobieństwa - określająca rozkład prawdopodobieństwa zmiennej losowej.

Dla zmiennej typu skokowego:

(2.1)

(2.2)

. (2.3)

Z kolei dla zmiennej losowej ciągłej podaje się tzw. funkcję gęstości prawdopodobieństwa spełniającą warunki:

. (2.4)

Funkcja ta ma następujące własności:

(2.5)

(2.6)

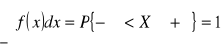
. (2.7)

2. Dystrybuanta - określająca prawdopodobieństwo tego, że zmienna losowa X przyjmie wartość mniejszą od określonej liczby x. Oznaczamy ją jako F(x).

Dla zmiennej losowej skokowej:

(2.8)

Natomiast dla zmiennej losowej ciągłej:

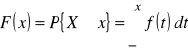
(2.9)

Własności dystrybuanty:

• jest funkcją niemalejącą, lewostronnie ciągłą,
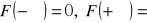
  1,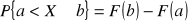

• 
  ,

• dla zmiennej losowej ciągłej, funkcja dystrybuanty jest ciągła i jej pochodną jest funkcja gęstości:
  .

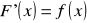
Podstawowe charakterystyki liczbowe rozkładu zmiennej losowej czyli parametry tego rozkładu to:

1. Wartość oczekiwana zmiennej losowej X:

• dla zmiennej losowej skokowej:

(2.10)

• dla zmiennej losowej ciągłej:

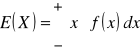
. (2.11)

Wartość oczekiwana nazywana jest również nadzieją matematyczną zmiennej losowej.

1. Wariancja zmiennej losowej X:

• dla zmiennej losowej skokowej:

, (2.12)

• dla zmiennej losowej ciągłej:

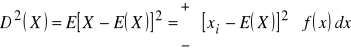
. (2.13)

Przykład 2.1

Rozkład prawdopodobieństwa liczby wypadków powstających w ciągu dnia roboczego jest następujący:

Liczba wypadków	0	1	2	3	4	5
Prawdopodobieństwo wystąpienia wypadku	0,02	0,18	0,28	0,25	0,20	0,07

Źródło: dane umowne.

a) określ zmienną losową X,

b) wykreśl funkcję rozkładu prawdopodobieństwa zmiennej losowej X,

c) wyznacz jej dystrybuantę,

d) oblicz: oraz ,

e) ustal wartość oczekiwaną i wariancję zmiennej losowej X.

Rozwiązanie:

ad a) Zmienna losowa X - liczba wypadków w ciągu dnia roboczego.

ad b) Obrazem graficznym rozkładu prawdopodobieństwa zmiennej losowej X jest następujący wykres:

ad c) Dystrybuantą zmiennej losowej X w ogólnym przypadku jest funkcja
określona wzorem:

.

Dla zmiennej losowej skokowej : , stąd mamy:

	0	1	2	3	4	5
	0,02	0,18	0,28	0,25	0,20	0,07	—
	0	0,02	0,20	0,48	0,73	0,93	1,00

Sporządzamy wykres dystrybuanty

ad d) Wykorzystamy tu następujące własności dystrybuanty:

ad e) Dla zmiennej losowej skokowej wartość oczekiwaną definiujemy wzorem:

 ,

a wariancję:

.

Wygodniej jednak skorzystać ze wzoru:

,

gdzie: .

Mamy więc:

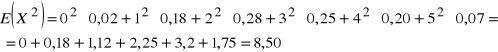
= 8,50 - 2,64² = 8,50 - 6,9696 = 1,5304

Przykład 2.2

Dana jest zmienna losowa o następującej funkcji gęstości:

a) przedstaw postać analityczną funkcji gęstości znajdując najpierw stałą c,

b) przedstaw w postaci analitycznej dystrybuantę ,

c) oblicz: ,

d) oblicz i
.

Rozwiązanie:

ad a) Stałą c  wyznaczamy korzystając z własności: .

Ponieważ zmienna losowa X jest określona w przedziale (5,15), więc wystarczy rozwiązać:

,

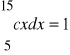
stąd

,

,

,

.

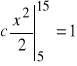
Postać analityczna wyraża się wzorem:

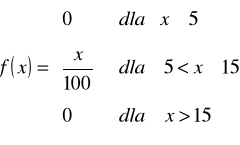
ad b) Dystrybuantę zmiennej losowej ciągłej wyraża się wzorem:

,

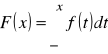
a więc

dla

,

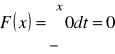
dla

,

,

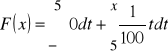
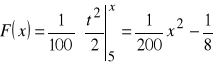
dla

,

.

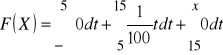
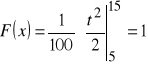
Z tych obliczeń wynika, że:

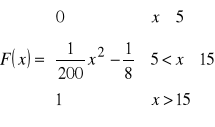
ad c)

Prawdopodobieństwo tego, że zmienna losowa X przyjmie wartości:

- większe od 7 wynosi ;

- nie większe od 10 wynosi ;

- nie mniejsze od 8 a mniejsze od 15 wynosi .

ad d)

Wygodniej jest jednak skorzystać ze wzoru :

= 62,5 - 5,41² = 33,23

2.2. Rozkład normalny

Rozkład normalny odgrywa podstawową rolę w statystyce matematycznej. Jest to rozkład zmiennej losowej ciągłej, przy czym zmienna ta przyjmuje wartości z przedziału

(- ∞; + ∞ ).

Funkcja gęstości zmiennej losowej X o rozkładzie normalnym ma postać:

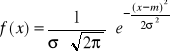
, (2.14)

gdzie:

m - wartość oczekiwana,

- wariancja.

Wartość oczekiwana i wariancja są podstawowymi parametrami rozkładu normalnego, stąd też zmienną losową o tym rozkładzie z reguły zapisujemy X~ N(m,σ).

Jest to rozkład symetryczny względem parametru m, stąd też w rozkładzie tym
(gdzie:
- trzeci moment standaryzowany). Ponadto w rozkładzie normalnym czwarty moment standaryzowany
.

Obrazem graficznym funkcji gęstości rozkładu normalnego jest tzw. krzywa Gaussa (rys.1).

Wartość maksymalną funkcja f(x) osiąga w punkcie
dla x = m, przy czym im
jest większe tym bardziej krzywa ta jest spłaszczona.

Zmienną losową X~ N(m, σ) można sprowadzić do zmiennej losowej Z~ N(0, 1), o której mówimy, że ma rozkład normalny standaryzowany, za pomocą następującego wzoru:

. (2.15)

Rys.1. Funkcja gęstości rozkładu normalnego dla m =10 oraz
,
i

Źródło: Opracowanie własne.

Przekształcenie to jest niezbędne, jeśli chcemy posługiwać się przy obliczaniu prawdo-podobieństwa, że zmienna losowa X przyjmie wartość należącą do przedziału [a, b] z „gotowych” opracowanych tablic dystrybuanty rozkładu normalnego standaryzowanego.

Funkcję dystrybuanty rozkładu normalnego standaryzowanego przedstawiliśmy na rys. 2.

Rys.2. Funkcja dystrybuanty rozkładu normalnego standaryzowanego

Źródło: Opracowanie własne.

Przykład 2.1

Zysk przedsiębiorstwa ma rozkład normalny z parametrami m = 100 tys. zł. oraz
= 10 tys. zł.

Oblicz prawdopodobieństwo tego, że przedsiębiorstwo osiągnie zysk powyżej 120 tys. zł.

Rozwiązanie:

Korzystając ze wzoru (2.15) zamieniamy zmienną losową X na zmienną losową standaryzowaną Z. Otrzymujemy:

Z tablic dystrybuanty rozkładu normalnego standaryzowanego odczytujemy, że:

Stąd

Odpowiedź:

Prawdopodobieństwo osiągnięcia przez przedsiębiorstwo zysku powyżej 120 tys. zł. wynosi tylko 0,0228.

2.3. Rozkład χ² (chi-kwadrat)

Zmienna losowa U² będąca ciągiem niezależnych zmiennych losowych o rozkładzie N(0, 1) w postaci:

(2.16)

ma rozkład χ² o k stopniach swobody.

Liczba k jest parametrem tego rozkładu i oznacza liczbę niezależnych składników sumy tworzącej zmienną o tym rozkładzie. Jest to jedyny parametr tego rozkładu, przy czym k musi być przynajmniej równy jedności.

Rozkład χ² jest określony w przedziale <0, +∞). Im k jest większe, tym rozkład staje się bardziej zbliżony do rozkładu normalnego.

Okazuje się, że jeżeli zmienna losowa U ² ma rozkład χ² o k stopniach swobody, przy czym k → ∞, to dystrybuanta zmiennej losowej
jest szybko zbieżna do dystrybuanty rozkładu normalnego N(
1).

Wartość oczekiwana zmiennej losowej o rozkładzie χ² wynosi E(U²) = k, zaś jej wariancja D²(U²) = 2k.

Obrazem graficznym funkcji gęstości rozkładu χ² jest krzywa pokazana na rys. 3.

Istnieją dwa rodzaje opracowanych tablic rozkładu χ². W praktycznych zastosowaniach statystyki matematycznej wykorzystywany jest taki rodzaj tablic, że dla różnych wartości parametru k, podana jest taka liczba rzeczywista, dla której prawdopodobieństwo przyjęcia przez zmienną losową wartości większej od tej liczby jest równe z góry ustalonej liczbie .

Rys.3. Funkcja gęstości rozkładu
dla k=1, 10 i 15 stopni swobody

Źródło: Opracowanie własne.

2.4. Rozkład t-Studenta

Rozkład t-Studenta jest rozkładem zmiennej losowej ciągłej, która może przyjmować wartości z przedziału (-∞; +∞).

Mówimy, że zmienna losowa
, gdzie Z jest zmienną losową o rozkładzie N(0, 1), a U² jest zmienną losową o rozkładzie χ² i k stopniach swobody, ma rozkład t-Studenta o k stopniach swobody.

Funkcja gęstości rozkładu t-Studenta ma postać zbliżoną do funkcji gęstości rozkładu normalnego, z tym tylko, że krzywa jest bardziej spłaszczona i przy ‌‌|t |→ ∞ rzędne krzywej wolniej zbliżają się do osi odciętych niż funkcji gęstości rozkładu normalnego.

Rozkład t-Studenta jest rozkładem symetrycznym względem punktu t = 0.

Okazuje się przy tym, że przy k → ∞ rozkład t-Studenta dąży do rozkładu normalnego. Istnieją gotowe tablice tego rozkładu w dwóch wersjach. Pierwsza wersja to tablice dystrybuanty. Druga natomiast, zdecydowanie częściej wykorzystywana w praktyce, to tablice podające dla różnych  takie wartości
, że przy danej liczbie stopni swobody k spełniona jest relacja
.

Graficznie funkcję gęstości rozkładu t-Studenta przedstawiono na rys. 4.

Rys.4. Funkcja gęstości rozkładu t-Studenta dla k=1, 3 i 10 stopni swobody

Źródło: Opracowanie własne.

2.5. Rozkład F Fishera - Snedecora

Jest to rozkład często spotykany w zagadnieniach statystyki matematycznej dotyczących wnioskowania w analizie wariancji i rachunku korelacji.

Zmienna losowa F zdefiniowana wzorem:

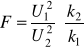
, (2.17)

gdzie
i
są dwiema niezależnymi zmiennymi losowymi o rozkładzie χ²
i odpowiednio k₁ i k₂ stopniach swobody nazywana jest zmienną losową o rozkładzie F Fishera - Snedecora o k₁ i k₂ stopniach swobody. Przyjmuje się przy tym, że
>
, stąd zmienna przyjmuje wartości nie mniejsze od jedności.

Istnieją gotowe tablice rozkładu F, które zbudowane są w ten sposób, że dla różnych  i różnych kombinacji stopni swobody zamieszczone są takie wartości F_ , że spełniona jest zależność:

. (2.18)

Rozkład ten został opracowany przez G. Snedecora, który na cześć Fishera nazwał go rozkładem F. Graficznie funkcję gęstości tego rozkładu przedstawiono na rys. 5.

Rys.5. Funkcja gęstości rozkładu F Fishera - Snedecora dla różnej liczby stopni swobody

Źródło: Opracowanie własne.

22

---