P O L I T E C H N I K A Ś W I Ę T O K R Z Y S K A LABORATORIUM AUTOMATYKI
Ćwiczenie nr: 2		Temat : WYZNACZENIE ODPOWIEDZI SKOKOWEJ UKŁADU BĘDĄCEGO POŁĄCZENIEM SZEREGOWYCH CZŁONÓW CAŁKUJĄCEGO I OSCYLACYJNEGO
1999/2000 Rok akadem.	V Semestr.		32B Grupa.	Tor Piotr Purtak Michał Nazwisko i imię studenta	99-12-12 Data.	Ocena.

1. Wstęp teoretyczny.

1. Element całkujący.

Elementem całkującym nazywamy obiekt dynamiczny opisany równaniem różniczkowym w postaci:

gdzie k oznacza współczynnik wzmocnienia określony jako stosunek pochodnej odpowiedzi do wymuszenia w stanie ustalonym. Stosując odpowiednie przekształcenia otrzymujemy transmitancję:

oraz odpowiedź jednostkową h(t) = k ^. t, przedstawiona na rysunku poniżej.

Odpowiedź jednostkowa elementu całkującego

2. Element oscylacyjny.

Równanie różniczkowe opisujące zachowanie się elementu oscylacyjnego ma postać:

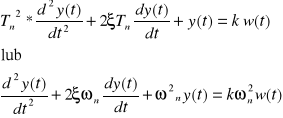
gdzie:

k - współczynnik wzmocnienia w stanie ustalonym,

pulsacja drgań własnych nietłumionych - naturalna,

względny / zredukowany / współczynnik tłumienia ,

Dokonując transformacji Laplace”a powyższego równania obliczamy transmitancją operatorową :

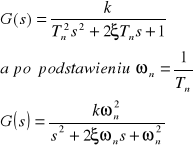
Charakterystykę jednostkową rozpatrywanego elementu określa zależność:

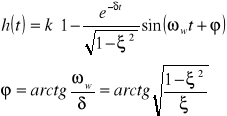
Rys. Odpowiedź jednostkowa elementu oscylacyjnego.

3. Połączenie szeregowe.

2. Przebieg ćwiczenia.

Wyznaczyć odpowiedź skokową układu będącego połączeniem szeregowym członów :

• całkującego (Tc=1[s])

• oscylacyjnego II rzędu (k =1; T = 0,1 [s]; ξ = 0,1)

Równania różniczkowe i transmitancje członów;

• całkującego

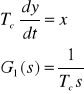
• oscylacyjnego II rzędu;

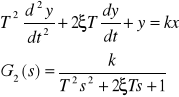
Transmitancja zastępcza dla połączenia szeregowego:

Po przekształceniu i podaniu równania przekształceniu odwrotnemu LAPLACE”A otrzymuje równanie różniczkowe:

po podstawieniu wartości;

y(t)

t

α

tgα = k

Rys. 1.1. Oznaczenie elementu całkującego na schematach blokowych.

---