Model elementarny
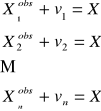
X- wartość estymowana, szukana
Wynikiem są estymatory - wartość przeciętna, odchylenie standardowe
Propagacja błędów
Przykład1.
Z jaką dokładnością należy pomierzyć długości a i b , działki w kształcie prostokąta, aby dokładność powierzchni wynosiła mp=0,20m.
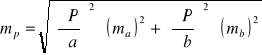
Dane
A = 20 m
B = 30 m
Zakładam, że :
ma=mb=m
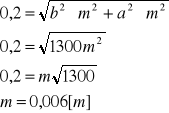
Przykład2.
Wysokość punktu wyznaczoną metodą trygonometryczną, opisaną wzorem
Hp=HA+i+d*sin (d- odległość wzdłuż celowej)
lub
Hp=HA+i+D*tg (D - odległość pozioma)
Obliczyć błąd :
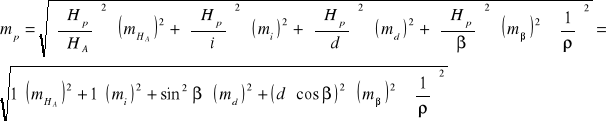
lub
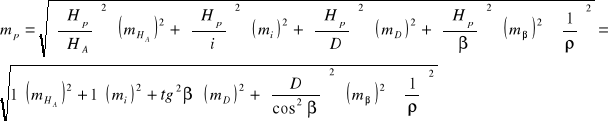
Pamiętać o „ro” !!!
Jak przyjmowane są wagi w zadaniach wyrównawczych?
![]()
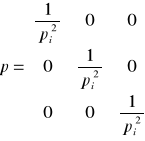
Aproksymacja mnk - metodą najmniejszych kwadratów. Objaśnić zadanie wyrównawcze i algorytm metody mnk w zadaniu aproksymacji wyników pomiarów płyty fundamentowej.
Przykład.
Dane h1, h2, h3, h4
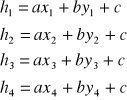
Układ równań poprawek:
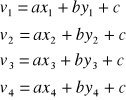
Objaśnić układ r-nań, co wyznaczamy, błędy, macierz kowariancji
![]()
=> metoda mnk
![]()
=> metoda mnk z wagami
![]()
=> metoda mnk macierzowa
Metoda parametryczna:
Przykład.
Napisać układ równań poprawek dla sieci niwelacyjnej jak na szkicu:
W jaki sposób dokonuje się kontroli obliczeń w metodzie parametrycznej?
Wielkości wyrównane (obliczone) == Wielkości pomierzone wyrównane
Sprawdzamy dokładność obliczeń
Dokładność - miejsca po przecinku
Napisać równania obserwacyjne dla zadania:
Pomierzono : , , d13
Znamy : współrzędne pkt 1 i 2 (X,Y)
Wzory ogólne będą podane.
Aby wyznaczyć współrzędne punktu 3 (X3,Y3) - rysunek powyżej - pomierzono g023, 1=49g964, d13=199.970 m. Znamy współrzędne punktu 1 (100,00; 200,00) i 2 (300,00 ; 200,00).
Wyznaczyć przybliżone wartości wielkości potrzebnych do rozwiązania zadania.
Wskazówka : Przyjąć sobie X3, Y3 i obliczyć jeszcze raz , , d13.
Macierz kowariancji obliczona jest ze wzoru:
![]()
Jak jest wykorzystywane i co oznacza :
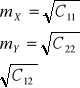
Co jest wynikiem wyrównania metoda pośredniczącą (parametryczną) ?
Mnk - metoda parametryczna
Na równaniach błędów ( lub równania obserwacyjne)
Równania te rozwiązujemy równaniami normalnymi.
Błąd położenia punktu. Wyjaśnić graficznie. Czym się różni od elipsy błędu?
![]()
![]()
Wprowadzamy jeszcze długości półosi a i b oraz kąt
Metoda warunkowa. Co jest dane, co jest wynikiem, kiedy jest stosowana?
![]()
-> warunek
Podobieństwa i różnice metody parametrycznej i warunkowej.
Podobieństwa:
- ![]()
- rozwiązujemy równania normalne
- określa wartość niewiadomych i ich błędy
Różnice:
- ilość równań ( ilość obserwacji a ilość warunków)
Pojęcie defektu sieci.
Defekt wewnętrzny - np. są kąty, ale nie ma długości boków, przez co jest nieskończona ilość podobnych trójkątów; dw = 1
Defekt zewnętrzny - czy trójkąt na płaszczyźnie XY może się przesuwać; dz=3
f=n-r+dz+dw
f =3-6+3+1=1
f - liczba równań (warunków)
n - liczba obserwacji
r - liczba niewiadomych
Jeden warunek ( suma kątów równa 200 g)
Przykład.
f= 7-8+0+3=2
dwa warunki:
sin= … -> dla pierwszego trójkąta
sin= … -> dla drugiego trójkąta
Defekt sieci - występuje, gdy w zbiorze danych do wyrównania obserwacji w danej sieci, brakuje pewnej liczby wielkości geometrycznych niezbędnych do wyznaczenia położenia jej punktów w przyjętym układzie współrzędnych. Defekt charakteryzujemy poprzez podanie liczby oraz rodzaju brakujących wielkości geometrycznych. Rozróżniamy defekt zewnętrzny (lokalizacyjny) dz i wewnętrzny dw. Całkowity defekt d = dz + dw.
Defekt zewnętrzny - występuje, gdy w zbiorze obserwacji wykonanych w danej sieci brak jest wielkości geometrycznych pozwalających unieruchomić tę sieć w przyjętym układzie współrzędnych, bez nakładu jakichkolwiek ograniczeń na jej elementy wewnętrzne. Jest to wiec liczba stopni swobody ruchu (przesunięcia, obroty) tej sieci w przestrzeni zgodnej z jej wymiarem.
Defekt wewnętrzny - występuje, gdy w zbiorze obserwacji wykonanych w danej sieci brak jest wielkości geometrycznych niezbędnych do uzyskania wyznaczalności wzajemnego położenia jej punktów. Gdy w zbiorze obserwacji brak jest elementu liniowego (długości) to taki defekt wewnętrzny nazywamy defektem skali.
W zagadnieniu wyrównawczym utworzono dwa równania:
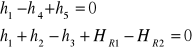
Jak obliczyć wyrazy wolne?
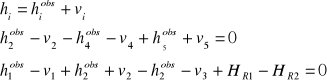
v2- v4+ v5+ (![]()
)=0
v1+ v2- v3 (![]()
)=0
(w nawiasie wyrazy wolne)
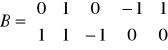
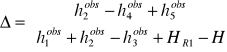
Wyrównanie odporne ( na błędy grube)
Podać algorytm rozwiązania:
l1= 21.20 -3
l2= 21.22 -1
l3= 21.23 0
l4= 21.27 +4
Ustalenie odchyłki dopuszczalnej - przedział z odchyłką dopuszczalną, czyli średnia arytmetyczna plus/minus odchyłka dopuszczalna
Metoda I
Odrzucamy obserwacje z przekroczoną odchyłką i liczymy dla tego przypadku od nowa tylko dla dwóch obserwacji
Metoda II
Dla przedziału z nie przekroczoną odchyłką stosujemy wagę p = 1
Dla obserwacji z przekroczoną odchyłką inną wagę.
p1 l1=0.66*l1
p2 l2=1*l2
p3 l3=1*l3
p4 l4=0.33*l4
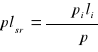
Wyszukiwarka
Podobne podstrony:
Z Obliczenia dla sieci kątowej, Geodezja i Kartografia, Rachunek Wyrównawczy
Sieci płaskie, Geodezja i Kartografia, Rachunek Wyrównawczy
Obliczenia na liczbach przybliżonych, Geodezja i Kartografia, Rachunek Wyrównawczy
Rachunek wyrównawczy TERMIN II
Ćw. 1 Zastosowanie form rachunkowych Hausbrandta, Geodezja i Kartografia, Rachunek Wyrównawczy
S 7 Równania obserwacji 3, Geodezja i Kartografia, Rachunek Wyrównawczy
Wyrównanie parametryczne - metoda macierzowa, Geodezja i Kartografia, Rachunek Wyrównawczy
Słowniczek ważniejszych terminów z RW, Geodezja, Rachunek wyrównawczy, Materiały egzamin
Exam RW[1], Studia, 3 semestr, Rachunek Wyrównawczy, egzamin
Z 3, ZESTAW EGZAMINACYJNY Z RACHUNKU WYRÓWNAWCZEGO semestr II zestaw nr 2
Z 4P, ZESTAW EGZAMINACYJNY Z RACHUNKU WYRÓWNAWCZEGO semestr II zestaw nr 2
Z 3, ZESTAW EGZAMINACYJNY Z RACHUNKU WYRÓWNAWCZEGO semestr II zestaw nr 2
Z 4P, ZESTAW EGZAMINACYJNY Z RACHUNKU WYRÓWNAWCZEGO semestr II zestaw nr 2
Wagi i błędności, Geodezja i Kartografia, Rachunek Wyrównawczy
zad 2 pierwiastek krakowianowy, rachunek wyrównawczy(1), prace domowe
Wyrównania korelat, Geodezja i Kartografia, Rachunek Wyrównawczy
Z 5P, ZESTAW EGZAMINACYJNY Z RACHUNKU WYRÓWNAWCZEGO semestr II zestaw nr 2
Ściaga RW, Geodezja i Kartografia, Rachunek Wyrównawczy
więcej podobnych podstron