Zespół nr 3	Piotr Bielówka & Krzysztof Lis	Ćw. 61/62
Wydział FiTJ	Drgania i fale elektromagnetyczne. Drgania relaksacyjne	Data oddania:
Pracownia fizyczna	Data wykonania:	Ocena:

1. ) Cel ćwiczenia :

Celem tego ćwiczenia jest zapoznanie się z drganiami elektrycznymi i ze zjawiskiem rezonansu. Podczas ćwiczenia należy się także zapoznać ze zjawiskiem drgań relaksacyjnych.

2. ) Wprowadzenie :

Idealny obwód elektryczny złożony z idealnego kondensatora o pojemności C , oraz z cewki o indukcyjności L , ma własności podobne do prostego oscylatora harmonicznego. Drgania takiego obwodu trwałyby nieskończenie długo. Matematycznie możemy to zjawisko opisać za pomocą prawa Ohma:

zatem :

Po przekształceniach otrzymamy wynik, którym jest funkcja : i=i₀ sin (ω₀ t + ϕ )

W rzeczywistości , każdy układ elektryczny posiada opór rzeczywisty R, który sprawia że badane drgania obwodu zanikają. Takie drgania nazywamy drganiami tłumionymi.

Za pomocą prawa Ohma możemy zapisać:

zatem :

Rozwiązaniem jest funkcja:

gdzie:
,
,

Włączenie w obwód RLC źródła siły elektromotorycznej spowoduje, że drgania stają się ponownie niegasnące. Zdolność absorbowania energii dostarczanej przez źródło siły elektromotorycznej zależy od badanego obwodu i od samego źródło SEM. Wielkością decydująca o przekazywaniu energii od źródła do obwodu jest częstotliwość. Jeżeli częstotliwość zmian SEM jest równa częstotliwości drgań idealnego obwodu LC , to amplituda drgań wymuszonych jest największa. Taki przypadek nazywamy rezonansem.

Matematyczny opis zjawiska drgań wymuszonych dla szeregowego układu RLC ma postać:

czyli :

Rozwiązaniem jest funkcja:

i=i₀ sin (Ωt + α) gdzie: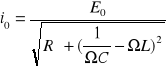

Zauważamy, że dla ω² LC=1 impedancja układu jest najmniejsza , czyli amplituda osiągnie maksimum.

Matematyczny opis układu równoległego RLC ma postać:

i=i₀ sin (Ωt + α) gdzie: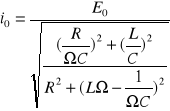

Widzimy, że dla ω LC=1 nastąpi zjawisko rezonansu.

Drganiami relaksacyjnymi nazywamy drgania periodyczne zmiany napięcia w określonych przedziałach wartości, zachodzące wzdłuż dwóch krzywych wykładniczych, nie są więc to drgania harmoniczne. Przykładem drgań relaksacyjnych są tz. Drgania piłokształtne, w naszym przypadku okres drgań wynosi: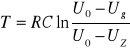

3. Opracowanie wyników :

a.) Opór urządzeń zewnętrznych

Aby obliczyć stałą czasową τ należy skorzystać ze wzoru :

U=U_Max(1-exp(-t/τ))

Po czasie t =τ U = U_Max(1-0,37) = 0,63U_Max

Po wykonaniu serii 10 pomiarów przy różnych wartościach L i R otrzymaliśmy , za pomocą wzoru :

R_x = τ / L -R

średnią wartość oporu urządzeń zewnętrznych podczas badania obwodu RL równą: R₁=125,77 ± 63,7 [Ω] , a opór wewnętrzny układu do badania dwójnika RC wyniósł R₂=104,45±97 [Ω]

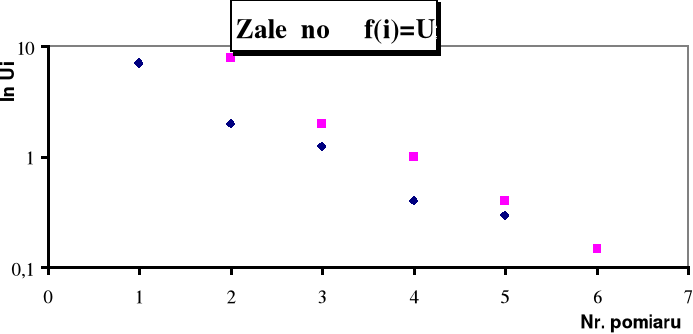
b.) drgania tłumione :

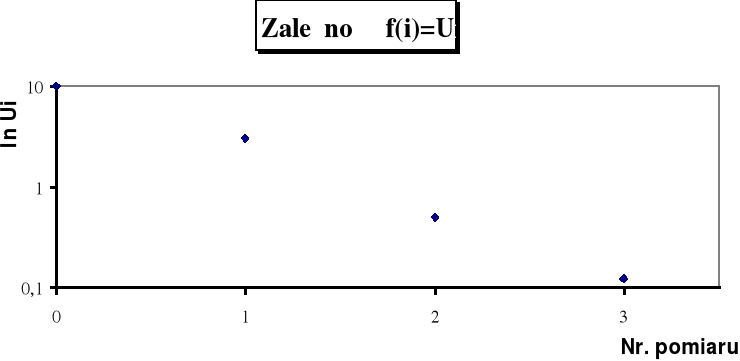
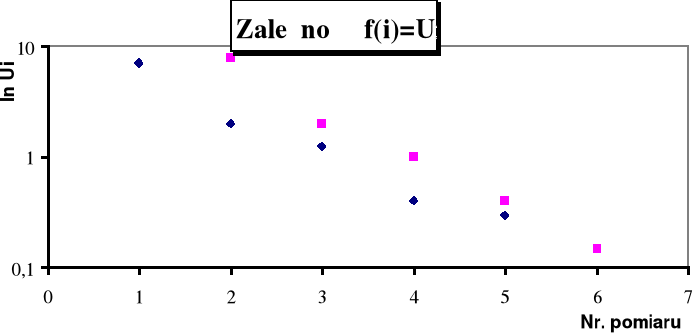
Logarytmiczną zależność pomiędzy kolejnymi maksymami napięcia w układzie RLC a współczynnikiem tłumienia β przedstawiają wykresy.

Wartość współczynnika tłumienia β można wyznaczyć z β= 2a/T ,

gdzie :

a—współczynnik nachylenia prostej f(i) = ln(U_i) ,

T—częstość kołowa

Wartości współczynników wynoszą: a₁=0,79 T₁=4545,5 [rad/s] zatem β₁=0,340*10^-3 a₂=0,95 T₂=5555,6 [rad/s] β₂=0,342*10^-3

a₃=1,5 T₃=8000 [rad/s] β₃=0,375*10^-3

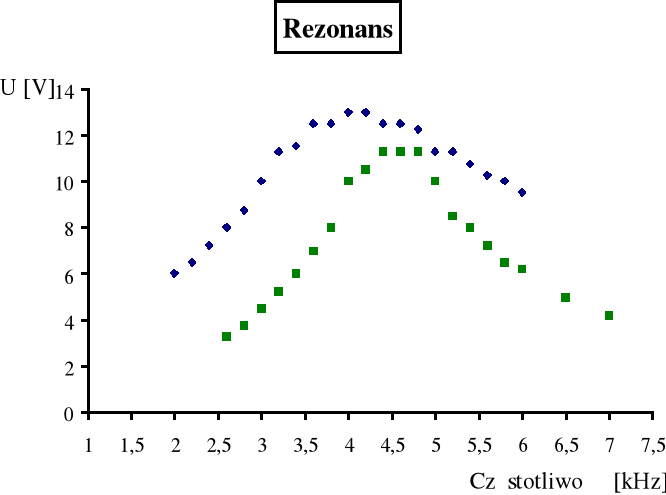
c.) Badanie rezonansu:

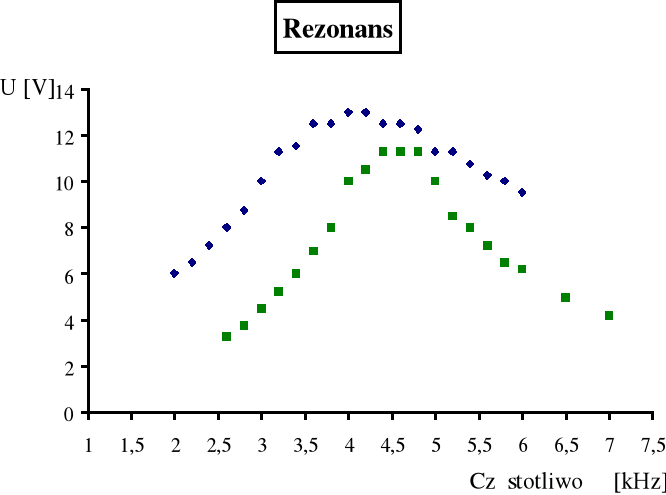
Na podstawie doświadczenia możemy stwierdzić że rezonans zaszedł w pierwszym przypadku przy częstotliwości 4 kHz a w drugim przy 4,6 kHz .

---