Wydział WNiG	Łukasz Kut Łukasz Mizera Artur Badzioch		Rok II		Grupa 2		Zespół 4
	Temat: Wyznaczanie bezwymiarowego współczynnika liniowego						Nr ćwiczenia 1
Data wykonania	Data oddania 24.05.2005	Zwrot do popr.		Data oddania		Data zaliczenia	Ocena

1. Cel ćwiczenia

Celem ćwiczenia jest wyznaczenie bezwymiarowego współczynnika oporu liniowego przy przepływie powietrza przez prostoosiową rurę o stałym przekroju.

2. Wstęp teoretyczny

Twierdzenie π Buckinghama analizy wymiarowej mówi , że strata ciśnienia przy przepływie płynu przez rurę jest funkcją prędkości średniej v , średnicy przewodu D , długości przewodu L , chropowatości ( bezwzględnej k lub względnej ε) ścianek przewodu, lepkości μ i gęstości ρ płynu .

Funkcję tę można zapisać w postaci bezwymiarowej

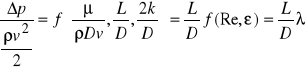
W powyższej zależności występują wielkości bezwymiarowe:

Liczba Reynoldsa

Chropowatość względna

Współczynnik oporu liniowego

Współczynnik (przy przepływach laminarnych) λ nie zależy od chropowatości i jest równy

Przy przepływach turbulentnych w przewodach gładkich (ε = 0 ) współczynnik λ dla

< Re <
ze wzrostem liczby Reynoldsa maleje i w tym przedziale wynosi

wzór Blasiusa

W przewodach chropowatych podczas przepływu turbulentnego współczynnik
jest w ogólności funkcją liczby Reynoldsa

Dla mniejszych liczb Reynoldsa współczynnik
zależy zarówno od Re jak i od

Natomiast przy dużych liczbach Reynoldsa
zależy tylko od chropowatości względnej i jest równy

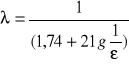
straty ciśnienia wyliczany ze wzoru Darcy`ego-Weisbacha

Pomiędzy stratą ciśnienia a prędkością przepływu przy ruchu laminarnym zachodzi zależność liniowa.

Przy ruchu turbulentnym obowiązuje zależność kwadratowa.

Na podstawie wyżej wymienionych wzorów mamy zależność:

3. Tabele pomiarowo-obliczeniowe

d₁ = 13 mm - średnica żółtej rurki

d₁ = 13 mm - średnica szarej rurki

t_s = 22ºC - temp. powietrza w środowisku suchym

t_m = 13,5ºC - temp. powietrza w środowisku wilgotnym

p = 990hPa = 741mmHg - ciśnienie powietrza

ρ = 1,16 kg/m³ - gęstość powietrza odczytana z nomogramu dla t_s, t_m i p

υ = 0,0000157 m²/s - lepkość powietrza odczytana z funkcji t_m i p

S₁ = 0,000134 m² - pole przekroju żółtej rurki

S₂ = 0,000452 m² - pole przekroju szarej rurki

Tab.1. Rurka o średnicy d=13 mm (rurka żółta)

Lp.	h [m]	p[Pa]			Re		ln( )	ln(Re)
1	0,004	39,24	5,845	1,733	1434,968	0,0446	7,269	-3,110
2	0,009	88,29	8,769	2,600	2152,866	0,0297	7,675	-3,516
3	0,01	98,10	9,242	2,740	2268,790	0,0282	7,727	-3,568
4	0,009	88,29	8,768	2,599	2152,038	0,0297	7,674	-3,515
5	0,002	19,62	4,133	1,225	1014,331	0,0631	6,922	-2,763
6	0,001	9,81	2,923	0,867	717,898	0,0891	6,576	-2,417
7	0,031	304,11	16,273	4,824	3994,395	0,0397	8,293	-3,226
8	0,043	421,83	19,165	5,682	4704,841	0,0382	8,456	-3,264
9	0,059	578,79	22,450	6,656	5511,338	0,0367	8,615	-3,305
10	0,076	745,56	25,479	7,554	6254,904	0,0355	8,741	-3,337
11	0,09	882,90	27,727	8,220	6806,369	0,0348	8,826	-3,358
12	0,107	1049,67	30,232	8,963	7421,592	0,0340	8,912	-3,380

Tab.2. Rurka o średnicy 24mm (rurka szara)

Lp.	l[m]	p[Pa]			Re		ln(Re)	ln( )
1	0,002	7,848	2,959	0,877	726,178	0,0881	6,588	-2,429
2	0,004	15,696	4,185	1,241	1027,580	0,0623	6,935	-2,776
3	0,004	15,696	4,185	1,241	1027,580	0,623	6,935	-2,776
4	0,005	19,62	4,679	1,387	1148,471	0,0557	7,046	-2,887
5	0,005	19,62	4,679	1,387	1148,471	0,0557	7,046	-2,887
6	0,006	23,544	5,126	1,520	1258,599	0,0509	7,138	-2,979
7	0,015	58,86	8,129	2,410	1995,541	0,0320	7,599	-3,440
8	0,018	70,632	8,878	2,632	2179,363	0,0294	7,687	-3,528
9	0,023	90,252	10,036	2,975	2463,376	0,0449	7,809	-3,104
10	0,030	117,72	11,462	3,398	28,13,631	0,0434	7,942	-3,138
11	0,039	153,036	13,068	3,874	3207,771	0,0420	8,073	-3,170
12	0,031	121,644	11,651	3,454	2860,000	0,0432	7,959	-3,142

gdzie:

Δ p- spadek ciśnienia,

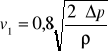
dla rurki o średnicy 24
bo

- liczba Reynoldsa,

gdy Re < 2300 jest to przepływ laminarny wówczas:

gdy Re > 2300 jest to przepływ turbulentny wówczas:
- wzór Blasiusa

dla d=13mm dla d=24mm

,

gdzie
gdzie
,

4. Wnioski

Przy przepływach laminarnych współczynnik λ nie zależy od chropowatości, wynosi
i maleje wraz ze wzrostem Re. Zaś przy przepływach turbulentnych (ε=0) współczynnik λ oblicza się z wzoru Blasiusa
, lecz nie maleje ze wzrostem Re tak szybko jak w poprzednim przypadku.

1