Zestawnieniem nazywamy grupę utworzoną ze wszystkich lub z części jakichkolwiek n-przedmiotów lub zdarzeń zwanych elementarnymi (wariacje,permutacje,kombinacje) Wariacje-jest to takie zestawienie które spełnia dwa następujące warunki:każde obejmuje r spośród n-elementów przy czym elementy te muszą być niejednakowe.Wśród tych zestawień są tylko zest rożniące się tylko zest elementów.

Permutacje-jest to takie zest które każde obejmuje n-danych i niejednakowych elementów.Tworzona jest na całym zbiorze.Elementy te różnią się od siebie tylko porządkiem.

Kombinacja-obejmuje r spośród n-elementów i nie ma wśród niej zest które różnią się porządkiem el.

Zdarzenia(proste,złożone)jeżeli zajście zdarzenia E2 jest wynikiem E1 to mówimy że E1 pociąga za sobą E2.

Zd pewne-jest to zd które zawsze zachodzi jeśli zachodzi zdarzenie pociągające je za sobą

Zd niemożliwe-zd które nie może zajść chociaż jest zdarzenie które mogłoby je wywołać

Zd przeciwne-zd prz zd E nazywamy zd polegające na tym że zd E nie zachodzi

Zd wykluczające-są nimi takie zd które żadne 2 nie mogą zajśc równocześn

Zd niezależne-to takie zd dla których zajście jednego z nich nie ma wpływu na wystąpienie jakiegokolwiek innego.

Suma zdarzeń-nazywamy zd polegające na tym że zachodzi przynajmnie jedno ze zdarzeń wchodzących w skład sumy Es=E1+E2+...+En

Iloczyn zdarzeń-nazywamy zd polegające na tym ze zachodzą wszystkie zd wchodzące w jego skład Ej=E1*E2*...*En

Jeżeli zd Es jest równe sumie zd wzajemnie się wykluczających a więc zajście zd Es jest równoważne zajściu jednego ze zdarzeń od E1doEn to wówczas mówimy że zd Es rozkłada się na zd odE1doEn.Jeżeli suma zdarzeń od E1doEn jest zd pewnym tzn. że jedno z nich zawsze zachodzi to wówczas mówimy że zdarzenia te tworzą pełną grupę zd. W tej grupie wszystkie zd muszą być pewne.Jeśli przy zajściu zd E° rozkładającego się na n-zd E1,E2doEn może zajść zd E którym się interesujemy i zd to rozkłada się na E1,E2doEm przy czym m<n to mówimy że zajściu zd E sprzyja m-zd.

Prwdp zdarzeń jeśli zd E° rozkłada się na n-wykluczających sie i jednakowo możliwych zd spośród których m-sprzyja pojawieniu się iinteresującego nas zd E to prwdp zd E nazywamy stosunek liczby zd sprzyjających do liczby zd P(E)=m/n [0≤P(E)≤1]

Prwdp całkowite P(E)= ΣP(Ei)*P(E/Ei)

Wzór Bayesa P(Ei/E)=[P(Ei)*P(E/Ei)]/ [ΣP(Ei)*P(E/Ei)] służy do wyznaczania prwpdp zajścia przyczyny zd E czyli zajścia jednego z wykluczających się zdarzeń towarzyszących zd E(zakładając że zd E zaszło)

Zm losowa jeśłi każdemu z wykluczających się zd E1,E2,..,En tworzących pełną liczbę zd przyporządkujemy pewną liczbęR to zbiór tych liczb stanowi funkcję rzeczywistą określoną na tym zbiorze którą nazywamy zmienną losową (X,Y,Z, Ω). Zd polegające na tym że zmienna losowa X przybierze wartość x (liczba przyporządkowana zd Ek) jest równoważne zd polegającemu na tym że w wyniku jakiegoś doświadczenia gry lub innego przypadku pojawia się zd Ea należące do pełnej gr zd wobec tego że prwdp zd są równe to P(Ek)=P(X=x) każdej więc wartości zm. Losowej przyporządkowane jest określone prwdp czyli może przyjmować rózne wartości z różnymi prwdp.

Zm losową skokową nazywamy taką zm która ma skończony lub przeliczalny zbiór wartości a więc może przybrać tylko niektóre wartości głownie liczby N. Rozkład rozkładem zm l skok nazywamy przyporządkowanie każdej waartości zm.los jej prwpdp P(X=x1)pi;Σpi=1 Dystrybuanta jeśli x jest pewną l R to prwdp zd że zm los X przybierze wartość mniejszą od x jest również funkca X.Jest to dystrybunata: F(x)=P(X<x) [0≤F(x)≤1]

Rozkład zero-jed nazywa się nim taki rzokład wartości w którym zm może przybierać tylko wartości x1=1,x2=2.Wielkości mogą przybierać wartości równe p;q=1-p.

roz dwumianowy wzór Bernulliego P(x=k)=C p^k(1-p)^(n-k) służy do wyznacznia prwdp k-krotnego wystp pewnego zd E w n-niezależnych i powtarzających się doświadczeniach jeśli znane jest prwdp p zajścia tego zd w poscz. doś. [X=k od0 do n] dystrybuanta: F(k)=P(X>k)=ΣC p^k(1-p)^(n-k)

Zmienna losowa X jest ciągła, jeżeli jej dystrybuanta F_X jest ciągła. Jest to równoważne ze stwierdzeniem, że P(X=a)=0 dla dowolnej liczby a∈R.

Funkcją rozkladu zm los c nazywamy prwdp tego zd że zm los X przyjmie wartości spełniające nierówność x1<X<x2. Funkcja rozkładu zm l c jest przyrostem dystrybuanty tej zmiennej którą określa się dla zm l c w ten sam sposób jak dla zm l skok F(x)=P(X<x). Jeśli dystr. Zm l c ma poch. W pkt. X to ta poch nazywa się gęstością prwdp zm l c w pkt x: f(x)=F(x);F(x)=∫f(t)dt. Funkcje rozkładu z m l c P(x1<X<x2)= ∫f(t)dx. Zm l X jest w danym przedziale ciągła jeśli w tym przedziale gęstośc prwdp F=(x) istnieje i jest ciągła względem X z wyjątkiem l.pkt.

Rozkład Poissona- P(X=k)=[(n-p)^k)/k!*e^-ep {n>20,p≤0,2} (należy do praw małych liczb)Rozkłady jednostajny f(x)={0 dla x<a;1/(b-a) dla a ≤x≤b;0 dla x>b; F(x)={0 dla x≤a;(x-a)/(b-a) dla a<x≤b;0 dla x>b; E(x)=∫x/ (b-a)*dx=(a+b)/2 E(x²)=∫x²/(b-a)*dx=(b²+ab+a²)/3 wykładniczy f(x)={0 dla x<0;λe^-λx dla x ≥0 gdzie λ>0 Gamma f(x)={0 dla x≤0;a^p/Г(p)*x^p-1*e^-ax dla x>0 Г-funkcja gamma Eulera Г(p)=∫x^p-1*e^-x* dx E(x)=∫x*a^p/Г(p)*x^p-1*e^-ax...=p/a V(x)=E(x²)-(E(x))²=∫x²*a^p/Г(p)*x^p-1*e^-ax*dx-p²/a²=p/a² normalny f(x)=1/(√2π*σ)*e^-(x-m)² gdzie σ>0 m∈R E(x)=1/2√π*σ^m∫xexp(-(x-m)²/(2σ²))dx=m V(x)= E(x-m)²=σ² m=0 σ=1 ϕ(x)=1/2π∫e^(-u²)/2*du dla x≥0 F(x)=0,5+ϕ(x) dla x≥0 F(x)=0,5-ϕ(x) dla x<0

Miary wlk. Centralnych- najbardziej pożyteczą wlk. Związaną ze zbiorem danych jest jego wartość średnia czyli arytmetyczna.Jeśli ciag obserwowanych wartości oznaczymy przez x1,x2...xn to wartość średnią z próby x określamy: x=1/nΣxi tw. o prwdp. całkowitym P[A]=P[A∩B1]+P[A∩Bi]+...+ P[A∩Bn]=ΣP[A∩Bi] każdy składnik parzystej sumy może być na mocy równości przedstawiony w postaci P[A\Bi]P[Bi], a zatem P[A]=ΣP[A\Bi]P[Bi]. Prwdp. warunkowe prwdp zajścia zd A, kiedy wiadomo, że zachodzi zd B. Odpowiada to sytuacji, gdy zd B już zaszło. Prwdp. warunkowe zapisujemy P(A|B) i czytamy "prwdp. zd A pod warunkiem zajścia zd B". Brzegowa funkcja masy prwdp px(X)=P[X=x]=Σpx(x,yi) Fx(x)=P(X≤x)=ΣPx(Xi)=Σxi≤xΣyi*px,y(xi,yi)=Fx,y(x,∞) funkcję tą znajduje się sumując wartości łączne funkcji po wszystkich wartościach pominiętej zmiennej rzeczywistego ruch X Wartość przeciętna (centralna,średnia,oczekiwana,nadzieja mat.) E(x)-Jeśli X jest zm. los. typu skokowego i rodzina określona wielościami X={x1,x2... przy czym prwdp. wyst. P(xk)=P(X=Xk) i nast. szereg Σ(Xk)p(Xk) jest zbieżny to wlk centralna jest definiowana jako E(x)=ΣXkP(Xk). Sumowanie po k rozciągnięte po xk do dziedziny-jeśli X to zm los ciągła i zbieżna jest całka ∫|x|f(x)dx to E(x)=∫xfxdx. Odchylenie przecietne Op(x)=Σ|Xk-E(x)|p(xi) dla zm los skokowej Op(x)=∫x-E(x)f(x)dx miare rozrzutu dopuszcza mediana dowolnego rzędu parzystego oznaczenia. Mediana kwanty-medianą zm los X1 definiujemy jako prwdp ze wielkosc P({wX(w)≤x12})≥½ P{wix(w)≥x12}≥½ ⇒∫f(x)dx=½. Jeśli poszukujemy mediany z funkcji gestości ∫e^-x*dx=½ czyli 1-exp(-x½)=½ [x½=ln2] Mediana nie musi być zm los. Zapis mediany przy pomocy dystrybuanty F(x½)≤½≤F(x½t) F(x½)=½ Kwantyl zm los kwantylem rzędu „p” gdzie p zawiera się w granicach 0<p<1 o dystrybuancie F nazywamy liczbę xp taką że dystrybuanta x≤p F(xp)≤p≤F(xp+) F(xp)=p Kwantyl to taka wlk która dzieli pole prwdp pod funkcję gęstości. Statystyka ma się zajmować masowymi zjawiskami losowymi wyst. w technice przyrodzie. podchodzi do problemu opisowo. Estymacja szacowanie wartości parametrów pewnych cech el. populacj Weryfikacja hipotez stat. -poszukiwanie odp czy opis do danej populacji jest właściwy czy nie-. Cała rozważaną zbiorowość która jest obszarem zainteresowaa w stat. nazywamy populacją generalną. Elementy populacji są do siebie podobne pod względem badanej cechy, ale nie są identyczne. Np.badanie ludzi pod względem wzrostu. Grupa zbiór wylosowany z populacji . Zbiór wszystkich możliwych prób nazywamy przestrzenią losową-próbą losowa. Mówiąc że populacja generalna ma rozkład Px to cechą? el. populacji jest zmienna losowa X o rozkładzie px. Dystrybuantę F zm los γ nazywamy dyst. chuj wie jaką. Oznaczając kolejne wartości w zaobserwowanej próbcex1,x2,x3..,xn możemy zapisać funkcję F(x)=1/nCavd?{i:xi<i≤x,i=1,2,n} cavd A-licznośc zbioru par. Fe-r-s-dystrybuanta empiryczna przyporządkowanie kolejnym wartościom cechy statystycznej (zmiennej) odpowiadających im częstości skumulowanych (względnie liczebności skumulowanych).. Dyst. teoretyczna- ma charakter dyst. rozkładu ciągłego a dyst. empiryczna zm los skokowej. Np. empiryczna wartość jest definiowana γn=1/n* Σxi wariacje empiryczne S²=1/n*Σ(x1-x2)² moment empiryczny rzędu R mr=1/n*Σxi Jeśli wielkości x1,x2 są niezależnymi o jednakowych dystrybuantach F natomiast F1 jest dyst. empiryczną to P({ω:lim sup (Fn(x,ω)-F(x)=0})=1 Rozkładem dn-kwadrat o „n” stopniach swobody nazywamy rozkład prwdp. sumy kwadratów m niezależnych zm los o rozkładach N(0,1)

Zad

W firmie produkuje się telewizory na trzech maszynach A1 A2 A3 których produkcja wynosi odpowiednio 25% 35% 40%calej produkcji. Maszyny wytwarzają odpowiednio 5% 4% 2% braków. Obliczyć:

a) prawdopodobieństwo ze wyprodukowała je maszyna A1

b) prawdopodobieństwo tego ze jest ona brakiem

c) prawdopodobieństwo tego ze ona nie jest brakiem

d) prawdopodobieństwo warunkowe ze wyprodukowała je maszyna A1 jeśli stwierdzono ze jest ona brakiem

P(A₁)=25/100; P(A₂)=35/100; P(A₃)=40/100

P(D/A₁)=95/100; P(B/A₁)=5/100; P(D/A₂)=96/100; P(B/A₂)=4/100

P(D/A₃)=98/100; P(B/A₃)=2/100;

ad a) P(A1)=25/100

ad b) P(B)=P(B/A1)*P(A1)+P(B/A2)*P(A2)+P(B/A3)*P(A3)

ad c) P(C)= P(D/A1)*P(D1)+P(D/A2)*P(D2)+P(D/A3)*P(D3)

ad d)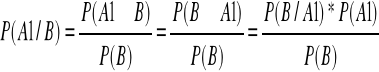
wzór Bayesa

Zad.

Rozkład prawdopodobieństw zmiennej losowej X jest dany w postaci tabeli

x	-1	0	1	2	4	8
P(X=x)	0,15	0,2	0,2	0,5	0,1	0,05

Postac rozkładu zmiennej losowej x²

y=x²

i

Zad

Sporządź w tym samym układzie współrzędnych wykresy gęstości zmiennej losowej o rozkładach normalnych N(0,1) N(0,2) N(0,3)

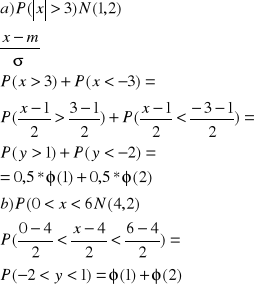
Zad

Zmienna losowa X ma następujący rozkład prawdopodobieństw P(X=-1)=1/4 P(X=2)=3/4 zrobić układ prawdopodobieństw zmiennej losowej y=2x+1

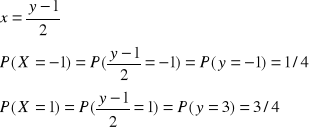
Zad.

Na loterii jest 1000 losów z następującymi wygranymi 1los wygrywa 500zl, 10 losow wygrywa po 100 zł, 50 po 20zł i 100 po 5zł

Jakie jest prawdopodobieństwo ze osoba kupujaca jeden los wygra co najmniej 20zł

A-zd. Polegające na wylosowaniu za 500

P(A)=1/1000

B-zd. Polegające na wylosowaniu za 100

P(B)=10/1000

C-zd. Polegające na wylosowaniu za 20

P(C)=50/100

D- prawdopodobieństwo że osoba wygra co najmniej 20zł

P(D)=P(A)+P(B)+P(C)

Zad.

W pewnym przedsiębiorstwie 96% wyprodukowanych .. jest dobrych. Wśród 100 sztuk dobrych wyrobow 75 jest pierwszego gatunku. Znalesc prawdopodobieństwo tego ze pewna sztuka jest pierwszego gatunku

P(D)=96/100-dobre; P(W)=4/100-wadliwe

P(I/D)=75/100; P(II/D)=25/100

P(I)=P(I/D)*P(D)=75/100*96/100=7200/10000=0.72

Zad.

Obliczyc prawdopodobieństwo tego ze przypadkowo wybrany element jest pierwszego gatunkijesli wiadomo ze 5%wszystkich elem. stanowia braki a 70% niewybrukowanych elementow jest 1 gatunku

P(D)=95/100-dobre; P(B)=5/100-wadliwe

P(I/D)=70/100; P(II/D)=30/100

P(I)=P(I/D)*P(D)=70/100*95/100=

Zad.

W pewnych określonych warunkach prawdopodobieństwo znalezienia przez kontrolera pasażera jadącego na gape jest rowne ½. Obliczyć prawdopodobieństwo zdarzenia A polegającego na znalezieniu w określonych warunkach co najmniej jednego gapowicza przez 10 pracujących niezależnie od siebie kontrolerow

P=1/2 prawdopodobieństwo znalezienia gapowicza

n=10 liczba kontrolerów

q=1-1/2=1/2 prawdop. Nie znalezienia pasażera bez biletu

k- liczba pasażerów bez biletu

k>=1

)

P(A)=P(1)+P(2)+P(3)+…+P(10)

K=0 zd przeciwne do A

P(A)= 1-P(A')

Zad.

Prawdopodobieństwo trafienia w cel w jednym strzale jest równe 1/5 Niech X5 oznacza liczbę strzałow celnych w wykonanej serii 5 niezależnych strzałow

Znalesc rozklad zmiennej losowej X5 Obliczyć prawdopodobieństwo tego ze liczba strzałow celnych będzie nie mniejsza niż 2

p=1/5 prawdopodobieństwo trafienia w cel

n=5 liczba strzałów

q=4/5 prawdopodobieństwo nie trafienia

k>=0- liczba trafien

P(X0)=(5/0)*(1/5)⁰*(4/5)⁵ symbol Newtona!!!!

P(X1)=(5/1)*(1/5)¹*(4/5)⁴ symbol Newtona!!!!

P(X2)=(5/2)*(1/5)²*(4/5)³ symbol Newtona!!!!

P(X3)=(5/3)*(1/5)³*(4/5)² symbol Newtona!!!!

P(X4)=(5/4)*(1/5)⁴*(4/5)¹ symbol Newtona!!!!

P(X5)=(5/5)*(1/5)⁵*(4/5)⁰ symbol Newtona!!!!

A - zd polegające na tym ze liczba strzałów celnych będzie nie mniejsza niż 2

P(a)= P(X2)+ P(X3)+P(X4)+P(X5)

Zad

Po mieście jeździ przeciętnie 1000 samochodów. Prawdopodobieństwo wezwania pogotowia technicznego w ciągu doby przez jeden samochód jest równe 0,002. Obliczyć prawdopodobieństwo wezwania pogotowia przez którykolwiek z samochodów zakładając ze są zdarzeniami niezależnymi.

P=0,002 prawd. Wezwania pogotowia technicznego

n=1000 liczba samochodów

q=0,998 prawd nie wezwania pogotowia technicznego

k>=1

A-zdarzenie polegające na wezwaniu pogotowia technicznego

K=0

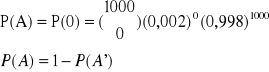
Zad

Prawdopod. trafienia w ruchomy cel przy jednym strzale jest równa 2/3. Pięć osób strzela niezależnie od jednego ruchomego celu. Jakie jest prawd. że cel zostanie trafiony.

P=2/3 prawdop. trafienia w cel

n=5 liczba osób

q=1/2 prawdop. nie trafienia w cel

k≥1 A-zdarzenie polegające na trafieniu w cel

P(A)=P(1)+P(2)+...+P(5)

A′-zd. przeciwne do zdarzenia A

k=0 P(A′ )=P(0)=(
) * (
)⁰ * (
)⁵

P(A)=1-P(A′ )

Zad

W magazynie są ubrania z trzech krawieckich firm A1, A2, A3, przy czym wiadomo, że z firmy A1 pochodzi 50% ubrań, z A2- 30%, a z A3-20%. Ze względu na jakość produkcja w poszczególnych firmach kształtuje się następująco:

Firma A1 produkuje 80%- ubrań I gatunku, 20%- II gatunku

Firma A2 produkuje 70%- I gatunek, 30%- II gatunek

Firma A3 produkuje 60%- I gatunek, 40%- II gatunek

W sposób przypadkowy wzięto ubranie z magazynu. Obliczyć prawdop. tego, że pochodzi ono z firmy A1; prawdop. tego, że jest ono I gatunku; prawdop. warunkowe tego, że pochodzi z firmy A1 jeśli stwierdzono, że jest ono I gatunku

P(A)=50/100

P(I)=P(I/A1)*A+P(I/A2)*A2+P(I/A3)*A3

P(A1/I)=
=

Zad

Robotnik obsługuje 4 jednakowe automaty funkcjonujące niezależnie od siebie. Prawd. że w ciągu godziny automat będzie wymagał interwencji robotnika wynosi 0,9. Obliczyć prawdop. tego że w ciągu godziny:

a) żaden z automatów nie będzie wymagał interwencji

b)dokładnie jeden automat będzie wymagał interwencji

c) liczba automatów wymagających interwencji będzie nie większa od 2

d) znaleźć najbardziej prawd. liczbę automatów wymagających interwencji w ciągu doby.

n=4 liczba automatów

p=0,9 prawd. że automat będzie wymagał interw.

q=0,1 prawd. że automat nie będzie wymagał interw

a) k=0 P(A)=(
)*(0,9)⁰*(0,1)⁴

b)k=1 P(B)=(
)*(0,9)¹*(0,1)³

c)k≤2 P(C)=P(A)+P(B)+ (
)*(0,9)²*(0,1)²

d) (n+1)*P - wzór na najbardziej prawd. Liczbę

5*0,9=4,5 4 automaty

Zad

prawdop. Nie popełnienia przez wykładowcę błędu na wykładzie jest równe ½. Obliczyć prawd. Zdarzenia A, polegającego na popełnieniu przez wykładowcę przynajmniej jednego błędu w czasie semestru (15 wykładów). Zakładamy, że popełnienie błędów na różnych wykładach są zdarzeniami niezależnymi

p=1/2 prawd. Popełnienia błędu przez wykładowcę

n=15 liczba wykładów

q=1-(1/2)=1/2 prawd. Nie popełnienia błędu przez wykładowcę

k liczba popełnionych błędów

k =1 A-zd. Polegające na popełnieniu błędu przez wykładowcę

P(A)=P(1)+P(2)+P(3)+...+P(15)

P(A)=(
)*(1/2)¹*(1/2)^15-1+...

A'- zdarzenie przeciwne do zdarzenia A

k=0

P(A')=P(0)= (
)*(1/2)⁰*(1/2)¹⁵=1*1*(1/2)¹⁵

P(A)=1-P(A')

---