1.Całka podwójna w prostokącie
Na płaszczyźnie OXY dany jest prostokąt P określony nierównościami

P: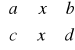
Dana jest też funkcja z = f(x,y) ograniczona i określona w tym prostokącie
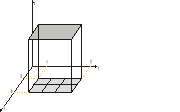
Prostokąt P dzielimy na n-prostokątów częściowych, które oznaczamy przez Pi
![]()
a) określamy średnicę podziału ∂i - jest to największa odległość dwóch punktów należących do prostokąta Pi
![]()
b) w każdym z prostokątów Pi dobieramy punkt pośredni Ai (xi,yi) oraz wyznaczamy wartość funkcji w punkcie pośrednim f(xi,yi)
następnie tworzymy sumę Sn=
c) czynności te powtarzamy wiele razy tworząc ciąg .... prostokąta P, taki , że średnica δn →0 jeśli n →0
Def. Jeśli ciąg sum całkowitych Sn ma tę samą granicę przy każdym normalnym podziale prostokąta P i jeżeli granica ta nie zależy od wyboru punktów pośrednich Ai to granicę tę nazywamy całką podwójną funkcji f(x,y) w prostokącie P i oznaczamy
![]()
ją :
Czyli 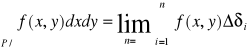
2.Całka podwójna w obszarze normalnym
Podział nazywamy normalnym jeżeli Δn → 0 gdy n → ∞
Def. Jeżeli dla każdego dowolnego normalnego ciągu podziału istnieje granica właściwa
![]()
![]()
Jeśli istnieje ta granica, to jest całką podwójną.
Tw. Z = f(x,y) jest całkowalne w P<=>kiedy f(x,y) będzie ciągła za wyjątkiem punktu zbieżnego do zera.
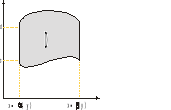
Def. Obszarem normalnym względem OX nazywamy obszar D spełniający nierówność
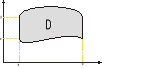
D: 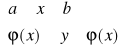
C = inf ϕ(x) d:sup ϕ(x)
x∈<a,b> x∈<a,b>
f (x,y) = 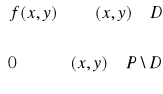
P: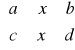
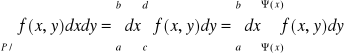
Def. Obszarem normalnym względem OY nazywamy obszar D spełniający warunek:
D: D: 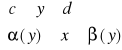
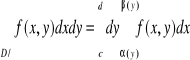
3. Interpretacja geometryczna całki podwójnych
Niech f(x,y) = k
![]()
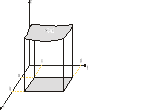
f (x,y)≥0
![]()
P: 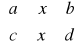
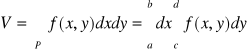
![]()
![]()
![]()
![]()
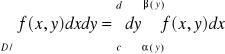
![]()
Wyszukiwarka
Podobne podstrony:
15, studia, studia, matematyka, całki i szeregi
28, studia, studia, matematyka, całki i szeregi
12 , studia, studia, matematyka, całki i szeregi
7 8 9, studia, studia, matematyka, całki i szeregi
20, studia, studia, matematyka, całki i szeregi
16a, studia, studia, matematyka, całki i szeregi
25, studia, studia, matematyka, całki i szeregi
4-6, studia, studia, matematyka, całki i szeregi
19, studia, studia, matematyka, całki i szeregi
17, studia, studia, matematyka, całki i szeregi
24, studia, studia, matematyka, całki i szeregi
Całki, Ekonomia- studia, matematyka
calki wzory na egzam, Studia, Matematyka wyższa ;p
6643194-sciaga-calki, Studia, Matematyka, Analiza Matematyczna
Analiza matematyczna egzamin I (lato) calki teoria, Wykłady - Studia matematyczno-informatyczne
Całki funkcji zespolonej, Politechnika Lubelska, Studia, Studia, Sprawozdania, studia, Matematyka, M
więcej podobnych podstron