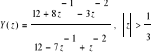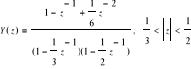Teoria sygnałów, laboratorium - ćwiczenie 7

Przykładowe pytania z zakresu siódmego ćwiczenia:

Zalecana literatura to:

[2]: ćw. 3 - w szczególności rozdziały 1.1, i 1.2

[5]: rozdz. 6.3 (str.230-236)

Dodatek zawarty w pliku „Odwrotne_przeksztalcenie_z.doc”

1. Podaj definicję transformaty „z”.

2. Co to jest obszar zbieżności transformaty „z”?

3. Jakie są zastosowania transformaty „z”? Czy ułatwia ona jakieś obliczenia związane z cyfrowym przetwarzaniem sygnałów?

4. Jakie cechy musi spełniać dowolna transformata, aby była użyteczna z punktu widzenia cyfrowego przetwarzania sygnałów?

5. Policz transformatę „z” dla sygnału delta (d[n]) oraz skok jednostkowy (u[n]). Pamiętaj o podaniu obszaru zbieżności.

6. Czy jeżeli dla pewnego ciągu suma definicyjna jego transformaty „z” nie jest zbieżna (lub nie jesteśmy pewni czy jest zbieżna), to można podać transformatę „z” tylko w postaci tej sumy?

7. Podaj definicję odwrotnej transformaty „z” (wzór całkowy!).

8. Jakie są sposoby obliczania odwrotnej transformaty „z”? Podaj krótką charakterystykę każdej z metod wraz z założeniami kiedy ją można stosować.

9. Wyznacz transformaty „z” dla poniższych ciągów:

a)
b)

10. Wyznacz odwrotne transformaty „z” dla poniższych funkcji określonych w dziedzinie „z”:

a)
b)

11. Udowodnij twierdzenie o liniowości transformaty „z”.

12. Udowodnij twierdzenie o transformacie „z” ciągu z przesuniętym indeksem.

13. Udowodnij twierdzenie o transformacie „z” ciągu pomnożonego przez stałą podniesioną do potęgi -n.

14. Udowodnij twierdzenie o transformacie „z” splotu dwóch sygnałów.

15. *Udowodnij twierdzenie Parseval'a w sformułowaniu dla przekształcenia „z”.

16. Wyprowadź zależność pomiędzy transmitancją „z” i równaniem różnicowym.

17. Wyznacz transmitancję w dziedzinie „z” dla systemów opisanych następującymi równaniami różnicowymi:

1. y[n]=2x[n]

2. y[n]-5y[n-2]=5x[n]+3x[n-1]

3. y[n]=0.5(x[n-1]+x[n])

18. Wyznacz odwrotną transformatę „z” dla poniższych funkcji korzystając z metody rozkładu na ułamki proste.

1. 
   

2. 
   

19. Sprawdź wyniki z poprzedniego ćwiczenia korzystając z instrukcji residuez MatLab'a.

20. Znajdź odwrotną transformatę „z” dla poniższych funkcji zarówno korzystając z metody rozkładu na ułamki proste, jak i podziału wielomianów:

1. 
   

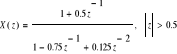
21. Sprawdź wyniki swoich obliczeń z poprzedniego punktu korzystając z instrukcji impz MatLab'a.

22. Uzasadnij korzystając (m.in.) z tabel 1 i 2, związek miedzy biegunami transmitancji i stabilnością systemu.

23. Mając określony system jak można określić obszar zbieżności jego transmitancji „z”? Jakie cechy musi posiadać ten system, by tak sformułowane zadanie miało sens?

24. Ile i jak położonych biegunów oraz miejsc zerowych ma system opisany następującym równaniem różnicowym:

y[n]=2x[n]-x[n-1]+x[n-2] ?

Teoria sygnałów, laboratorium - ćwiczenie 7

1

1