Ćwiczenia 3 - 11-
Przykład 11
Wyznaczyć prędkość i przyspieszenie punktu, oraz promień krzywizny toru punktu, jeżeli równania ruchu punktu mają postać.
![]()
![]()
![]()
(11.1)
Rozwiązanie
składowe prędkości: ![]()
![]()
![]()
(11.2)
prędkość: ![]()
![]()
składowe przyspieszenia:![]()
; ![]()
; ![]()
przyspieszenie:![]()
przyspieszenie styczne do toru: 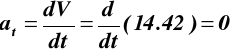
przyspieszenie normalne do toru punktu 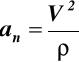
przyśpieszenie 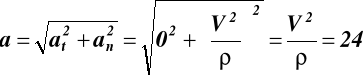
stąd

Przykład 12
Lot rakiety (rys.12.1) na początkowym pionowym odcinku toru jest śledzony za pomocą urządzenia radarowego. Wyznaczyć analityczną zależność prędkości i przyspieszenia rakiety od funkcji * kąta namiaru oraz wartość prędkości i przyspieszenia rakiety dla t = 4 s. Dane b = 200 m, * = 0.004t3.
z
VC
C
zC
*
0 x
Rys.12.1
b
Rozwiązanie - 12-
równanie toru rakiety: ![]()
(12.1)
prędkość: 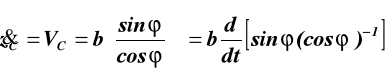

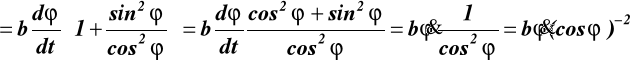
![]()
(12.2)
przyśpieszenie: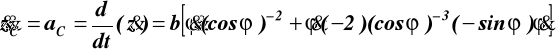
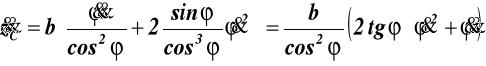
(12.3)
![]()
; ![]()
; ![]()
dla t = 4 s z (12.1) ![]()
z (12.2) 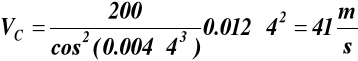
z (12.3) 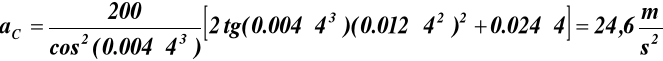
Przykład 13
Punkt A porusza się po okręgu koła o promieniu r = 1.2 m, ze stałą co wartości prędkością. Promień wodzący 0A tego punktu (rys.13.1) wykonuje przy tym
n = 258 obr/min. Należy wyznaczyć przyspieszenie punktu A.
V
A
an *
0
r Rys.13.1
Rozwiązanie
równanie ruchu punktu na torze: ![]()
prędkość 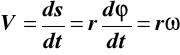
- 13 -
w naszym przypadku V = const. czyli ω = const.
wstawka: jeśli n jest ilością obrotów na jednostkę czasu to:
![]()
gdzie t jest czasem w którym określamy kąt *
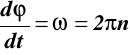
jeżeli n ma miano obr/min a chcemy ω mieć w rad/sek to
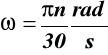
w naszym przypadku ω = cons. ponieważ n jest stałe
przyspieszenie styczne: 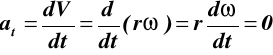
przyśpieszenie normalne: 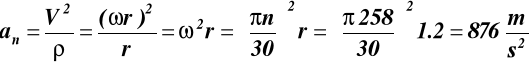
wartość przyśpieszenia: 
Przykład 14
Punkt A zaczyna poruszać się po okręgu koła o promieniu r = 0.4 m ze stałym przyśpieszeniem stycznym at = 2 m/s2. W chwili początkowej prędkość punktu była równa zeru. Należy wyznaczyć, po jakim czasie przyśpieszenie normalne stanie się liczbowo równe przyśpieszeniu stycznemu.
Rozwiązanie
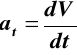
; ![]()
; 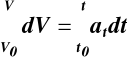
; ponieważ at = const.
to: ![]()
stąd ![]()
(14.1)
dla ![]()
; ![]()
podstawiając do (14.1) mamy: ![]()
przyśpieszenie normalne 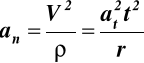
(14.2)
gdy ![]()
wtedy ![]()
uwzględniając (14.2) otrzymujemy 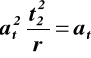
; stąd 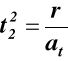
; 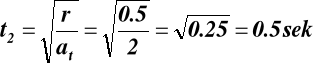
Wyszukiwarka
Podobne podstrony:
mechanika budowli ćwiczenia (11 04 2010 r )
Mechanika - Kinematyka, cwiczeniakinematyka2, ćwiczenia 2
Mechanika - Kinematyka, cwiczeniakinematyka4
Mechanika - Kinematyka, cwiczeniakinematyka5, Ćwiczenie 5
Mechanika - Dynamika, cwiczeniadynamika11, Ćwiczenie 11
Fizjologia Cwiczenia 11 id 1743 Nieznany
Biologia Cwiczenia 11 id 87709 Nieznany (2)
cwiczenie 11
sprawko z ćwiczenia 11, Farmacja, II rok farmacji, I semstr, fizyczna, Fizyczna, Sprawozdania z fizy
Patomorfologia cwiczenia ,11,11
Mechanika gruntów Ćwiczenie 5 Sprawozdanie 3
MIKROEKONOMIA ĆWICZENIA 5 (11 12 2011)
cwiczenie 11 id 125145 Nieznany
Mechanika gruntów - Ćwiczenie 1 - Sprawozdanie 1, Budownictwo S1, Semestr III, Mechanika gruntów, La
więcej podobnych podstron