Miary położenia i tendencji centralnej.

1. Wartość średnia

- średnia arytmetyczna
, średnia ważona :
,
dla cechy ciągłej
gdzie
- środek przedziału

2. Dominanta - dla cechy ciągłej :

X_D - dolna granica klasy, w której znajduje się dominanta

n_D - liczebność przedziału dominanty

n_D-1 - liczebność przedziału poprzedzającego przedział dominanty

i_D - rozpiętość przedziału dominanty

3. Mediana (wartość środkowa, kwartyl drugi) M_e próbki x₁, x₂, ... , x_n

Dla cechy ciągłej

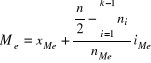
4. Kwartyl pierwszy (dla cechy ciągłej)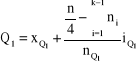
,

4. Kwartyl trzeci (dla cechy ciągłej)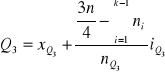

X_Me, X_{Q 1}, X_{Q 3} - dolne granice przedziałów, w których znajdują się mediana i kwartyle

i_Me, i_Q1 , i_Q3 - rozpiętość przedziału mediany, kwartyla pierwszego i trzeciego

n_Me, n_Q1, n_Q3 - liczebność przedziału mediany, kwartyla pierwszego i kwartyla trzeciego

n - ogólna liczebność populacji.

Miary rozproszenia

1. Rozstęp R = x_max - x_min

2. Wariancja
, jeśli dany szereg rozdzielczy

3. Odchylenie standardowe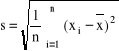
, jeśli dany szereg rozdzielczy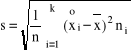

4. Współczynnik zmienności

Miary asymetrii

1. Trzeci moment centralny
, jeśli dany szereg rozdzielczy

2. Współczynnik asymetrii

3. Współczynnik skośności

Miary koncentracji

1. Moment centralny czwartego rzędu:
jeśli dany szereg rozdzielczy

2. Standaryzowany moment centralny (współczynnik spłaszczenia )

3. Kurtoza = współczynnik spłaszczenia - 3

Dystrybuanta

• Dystrybuanta empiryczna

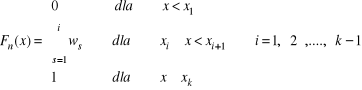
F(x) = P(X ≤ x),
,

Zmienna losowa

Dystrybuanta zmiennej losowej ciągłej

- wartość oczekiwana

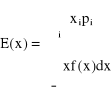
- Wariancja zmiennej losowej X

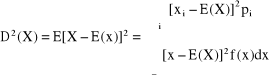
Rozkład dwumianowy

Rozkład Poissona

Rozkład prostokątny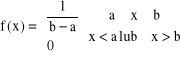

Rozkład normalny

Rozkład średniej arytmetycznej z próby dla populacji normalnej N(m,
)

Rozkład t-Studenta.
,

Rozkład różnicy średnich z prób z populacji o znanym odch. stand. σ (
-
)
.

Rozkład różnicy średnich (
-
) z prób pochodzących z dwóch populacji normalnych o nieznanym odchyleniu standardowym
,
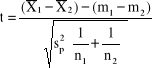
, df = n₁ + n₂ -2

Zmienna losowa standaryzowana. Niech X będzie zmienną losową o wartości oczekiwanej E(X) i odchyleniu standardowym D(X). Zmienną losową standaryzowaną U jest:

Przedział ufności dla średniej m w populacji normalnej ze znanym odchyleniem standardowym.

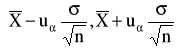
Przedział ufności dla średniej m w populacji normalnej z nieznanym odchyleniem standardowym.

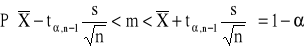
Przedział ufności dla wariancji σ² w populacji normalnej (dla małych prób)

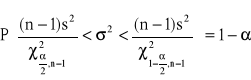
Przedział ufności dla odchylenia standardowego w populacji normalnej (dla dużych prób).

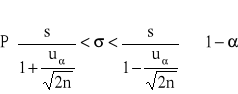
Przedział ufności dla wskaźnika struktury w populacji normalnej.

Minimalna liczebność próby.

Dla populacji o rozkładzie normalnym ze znanym odchyleniem standardowym.

Dla populacji o rozkładzie normalnym ze nieznanym odchyleniem standardowym

Testy statystyczne.

Test istotności dla średniej z populacji o znanym odchyleniu standardowym.

Sprawdzeniem hipotezy jest statystyka
,.

Test istotności dla średniej z populacji o nieznanym odchyleniu standardowym.

Sprawdzeniem hipotezy jest statystyka
.o rozkładzie t_Studenta dla n-1 stopni swobody

Test istotności dla dwóch średniej z populacji o znanym odchyleniu standardowym.

Sprawdzeniem hipotezy jest statystyka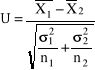
.

Test istotności dla dwóch średniej z populacji o nieznanym odchyleniu standardowym - test t Studenta

Sprawdzeniem hipotezy jest statystyka t dla n₁+n₂-2 stopni swobody

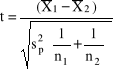
, gdzie

Test istotności dla wariancji. Sprawdzeniem hipotezy jest statystyka

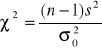
o rozkładzie chi-kwadrat o n -1 stopniach swobody

Test istotności dla dwóch wariancji. Sprawdzeniem hipotezy jest statystyka

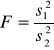
o rozkładzie F Snedecora o n₁-1 i n₂-1 stopniach swobody.

Test dla wskaźnika struktury. Sprawdzeniem hipotezy jest statystyka

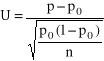
Test dla dwóch wskaźników struktury. Sprawdzeniem hipotezy jest statystyka

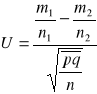
, gdzie
,

Test chi-kwadrat (zgodności)
Do weryfikacji hipotezy zerowej wykorzystuje się statystykę

o rozkładzie chi -kwadrat z r-k-1 stopniami swobody

Dla zmiennej losowej skokowej

Dla zmiennej losowej ciągłej

Dla zmiennej losowej ciągłej

Dla zmiennej losowej skokowej