Twierdzenie o środkowych boków trójkąta
Środkową boku trójkąta nazywamy odcinek łączący wierzchołek trójkąta ze środkiem przeciwległego boku
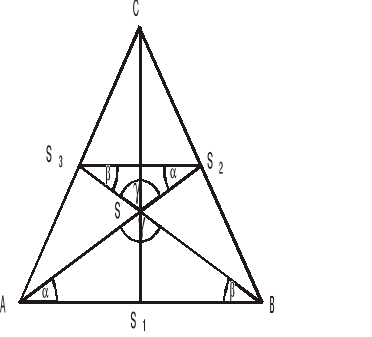
W dowolnym trójkącie, środkowe boków, przecinają się w jednym punkcie zwanym środkiem ciężkości trójkąta w stosunku 2:1 licząc od wierzchołka trójkąta.
Założenie:
Dany jest dowolny trójkąt ABC
![]()
środkowe boków w trójkącie ABC
Teza:
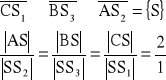
Dowód:
Łączymy odcinkiem punkty ![]()
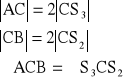
(wynika to z cechy podobieństwa trójkątów bok kąt bok ![]()
)
zatem ![]()
![]()
jest równoległe do ![]()
oraz ![]()
=2![]()
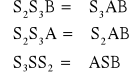
![]()
Stąd wynika, że ![]()
![]()
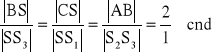
Wyszukiwarka
Podobne podstrony:
ftryg, materialy, Matematyka, matematyka - dowody
TM36, materialy, Matematyka, matematyka - dowody
tm29, materialy, Matematyka, matematyka - dowody
zadanie6, materialy, Matematyka, matematyka - dowody
tm16, materialy, Matematyka, matematyka - dowody
tm4-2, materialy, Matematyka, matematyka - dowody
tm3, materialy, Matematyka, matematyka - dowody
zadanie18, materialy, Matematyka, matematyka - dowody
tm35ciagi, materialy, Matematyka, matematyka - dowody
Iloczynkartezjaski, materialy, Matematyka, matematyka - dowody
tm5, materialy, Matematyka, matematyka - dowody
PROSTA, materialy, Matematyka, matematyka - dowody
tm4, materialy, Matematyka, matematyka - dowody
tm2Twierdzeniecosinusw, materialy, Matematyka, matematyka - dowody
TM31Wartbezwzgl, materialy, Matematyka, matematyka - dowody
kombinatorykaTM41, materialy, Matematyka, matematyka - dowody
ZadanieTM20, materialy, Matematyka, matematyka - dowody
ZBIORY, materialy, Matematyka, matematyka - dowody
TRYGONOMETRIA1, materialy, Matematyka, matematyka - dowody
więcej podobnych podstron