2.Metody i techniki wyznaczanie różnic wysokości. ( Geodezja I - Ząbek)

Rodzaje niwelacji :

-Niwelacja geometryczna - (błąd średni podwójnej niwelacji 1-10mm/km) polega na wyznaczeniu niwelatorem różnicy wysokości pomiędzy dwoma punktami przez celowanie wzdłuż poziomej linii celowej do pionowo ustawionych łat niwelacyjnych.

- Niwelacja trygonometryczna - (błąd średni podwójnej niwelacji 1-10cm/km) polega na wyznaczeniu teodolitami różnicy wysokości między dwoma punktami A i B z zależności trygonometrycznej zachodzącej w trójkącie prostokątnym. Mierzymy odległość poziomą d między punktami A i B oraz kąt α nachylenia odcinka AB (kąt pionowy). Obliczamy h=d*tgα.

- Niwelacja barometryczna - (dokładność 1-3m) - polega na pomiarze wartości ciśnienia atmosferycznego na tych dwóch punktach, między którymi wyznaczamy różnicę wysokości za pomocą barometrów rtęciowych lub aneroidów. Wiadomo, że ciśnienie atmosferyczne maleje o 1 hPa przy zwiększeniu wysokości o 8-9m (1000hPa = 750 mm Hg).

- Niwelacja tachimetryczna

-Niwelacja powierzchniowa (niwelacja siatkowa, niwelacja profilami, niwelacja punktów rozproszonych)

Podział niwelacji geometrycznej:

- Niwelacja precyzyjna - (błąd średni podwójnej niwelacji 0,5-2mm/km). Wykonywana dla wyznaczenia wysokości stałych punktów z bardzo dużą dokładnościa. Punkty te tworzą precyzyjna sieć niwelacyjną zwana podstawową osnową wysokościową, która jest oparciem osnowy szczegółowej.

- Niwelacja techniczna reperów - (błąd średni podwójnej niwelacji 2-5mm/km). Wykonywana dla wyznaczenia wysokości szeregu stałych punktów (reperów). Punkty te tworzą sieć niwelacyjną zwaną szczegółową osnową wysokościową, która stanowi zagęszczenie osnowy podstawowej i jest jednocześnie oparciem dla osnowy pomiarowej.

- Niwelacja techniczna - (błąd średni podwójnej niwelacji 5-10mm/km). Wykonywana dla wyznaczenia pomiarowej osnowy wysokościowej, która stanowi zagęszczenie osnowy szczegółowej i służy do takich celów technicznych. Jak wyznaczanie przekrojów terenu lub jego rzeźby.

Metody niwelacji geometrycznej:

- Niwelacja w przód

- Niwelacja ze środka

3.Techniki pomiarów sytuacyjno-wysokościowych i opracowania rzeźby terenu (G-4).

BEZPOŚREDNIE POMIARY SYTUACYJNE

 Metody:

- Metoda domiarów prostokątnych

 

1. Metoda domiarów prostokątnych polega na pomiarze rzędnej i odciętej mierzonego punktu sytuacyjnego względem linii, na którą rzutujemy dany punkt.
Metoda ta zalecana jest do stosowania w terenach zainwestowanych, charakteryzujących się nieznaczną różnicą poziomów między linią pomiarową a punktem sytuacyjnym.

2.Przy pomiarze metodą domiarów prostokątnych należy linie łączące punkty osnów tyczyć, dzieląc je na odcinki o długości 50-100 m, zależnie od grupy dokładnościowej mierzonych szczegółów terenowych.

3.Sposób i warunki tyczenia linii podaje tabela I.

Tabela I

Sposób tyczenia linii łączących punkty osnów (linie pomiarowe)	Grupa dokładnościowa szczegółów terenowych
		I   i   II	III
		długość linii do tyczenia
węgielnicą dwupryzmatyczną lub w dowolny sposób	do 150 m	do 200 m
lornetką	do 300 m	do 500 m
teodolitem	ponad 300 m	ponad 500 m
maksymalna długość odcinków po przetyczeniu	około 50 m	około 100 m

 .

   Przy stosowaniu metody domiarów prostokątnych długości rzędnych oraz dokładność pomiaru mierzonych rzędnych i odciętych zależą od grupy dokładnościowej szczegółów terenowych.

Warunki pomiaru podano w tabeli II.

Tabela II

Wymagania	Grupa dokładnościowa szczegółów terenowych
		I	II	III
sprzęt do wyznaczenia prostopadłej	węgielnica dwupryzmatyczna
dopuszczalne rzędne	25 m	50 m	70 m
dokładność pomiaru	0.05 m	0.05 m	0.10 m

 

Metoda biegunowa

 

1. Metoda biegunowa polega na pomiarze odległości od stanowiska instrumentu do punktu celowania oraz pomiarze kierunku na ten punkt,

2. Pomiar szczegółów metodą biegunową wykonywać należy ze stanowisk instrumentu, którymi w zasadzie powinny być punkty osnowy szczegółowej i pomiarowej.

3. Szczegóły terenowe II i III grupy dokładnościowej mierzyć można ze stanowisk obieranych na punktach sytuacyjnych I grupy dokładnościowej, w szczególności na zastabilizowanych lub zamarkowanych punktach załamania granic, które zostały uprzednio pomierzone wraz z elementami kontrolnymi.

 

1. Pomiar szczegółów terenowych metodą biegunową może być wykonywany z zastosowaniem następujących sposobów pomiaru odległości:

a) optycznie - przy czym rozróżnia się pomiar tachimetryczny, dalmierczy oraz stolikowy,

b) elektrooptycznie - tzw. pomiar dokładny,

c) bezpośrednio

2. Pomiar tachimetryczny wykonuje się przy użyciu zwykłych tachimetrów nitkowych lub redukcyjnych diagramowych.

3. Pomiar dalmierczy wykonuje się przy użyciu dalmierzy dwuobrazowych.

4. Pomiar stolikowy wykonuje się przy użyciu kierownic autoredukcyjnych, stolika topograficznego z centrownikiem oraz łat niwelacyjnych.

5. Pomiar elektrooptyczny wykonuje się przy użyciu dalmierzy elektromagnetycznych.

6. Bezpośredni pomiar odległości stosowany w szczególnych przypadkach wykonuje się przymiarem wstęgowym.

 

1. Metoda biegunowa, przy zastosowaniu pomiaru odległości dalmierzami, odpowiada pod względem dokładności metodzie domiarów prostokątnych.

2. Metodę biegunową, przy zastosowaniu bezpośredniego pomiaru odległości, stosować należy w ograniczonym zakresie, przy minimalnej ilości mierzonych punktów sytuacyjnych, szczególnie przy pomiarach uzupełniających.

  

 

Metoda przedłużeń konturów sytuacyjnych

 

1. Metodę przedłużeń konturów sytuacyjnych na linie pomiarowe można stosować na terenach łatwo dostępnych do bezpośredniego pomiaru odległości.

2. Stosowanie tej metody zalecane jest szczególnie w odniesieniu do pomiaru budynków i budowli oraz granic, a także przy wykonywaniu wszelkich pomiarów uzupełniających.

3. Przy pomiarze szczegółów terenowych metodą przedłużeń należy zachować następujące warunki:

a) linia konturu powinna być przedłużona do przecięcia się z linią pomiarową,

b) stosunek długości przedłużenia do długości odcinka przedłużonego nie może być większy niż 2:1,

c) kąt pomiędzy linią przedłużenia a linią pomiarową powinien być większy od 45^o (50^g) mniejszy od 135^o (150^g),

4. Linia pomiarowa, na którą przedłuża się mierzone kontury sytuacyjne, powinna być przetyczona zgodnie z warunkami ustalonymi w § 27 p.3.

5. W przypadku nie zachowania warunków ujętych w ust.3 należy dokonać pomiaru elementów kontrolnych.

 

Metoda wcięć kątowych, liniowych i kątowo-liniowych

 

   Dobór jednego ze sposobów wykonywania pomiaru metodą wcięć uzależniony jest od usytuowania szczegółów terenowych względem punktów osnowy pomiarowej lub linii pomiarowych oraz od rodzaju terenu mającego wpływ ma stopień trudności pomiaru.

 

   Warunki geometryczne elementów wyznaczających wcięciem położenie punktów charakterystycznych szczegółu terenowego powinny być tak dobrane, aby zachowane były kryteria dokładnościowe w poszczególnych grupach szczegółów terenowych a ponadto spełnione następujące wymagania:

a) pomierzony co najmniej jeden element nadliczbowy wcięcia przy wyznaczaniu punktów pojedynczych,

b) dokonany pomiar odległości między wciętymi punktami określającymi szczegół terenowy.

 

1. Wcięcie kątowe polega na wyznaczeniu położenia punktu na podstawie pomierzonych kątów w stosunku do punktów o znanym położeniu.

2. Wcięcie liniowe polega na wyznaczeniu położenia punktu na podstawie pomierzonych odległości między wyznaczanym punktem, a punktami o znanym położeniu.

3. Wcięcie kątowo - liniowe jest to takie wcięcie, w którym dla określenia położenia punktu podlegają pomiarowi kierunki i odległości.

 

Inne metody pomiaru szczegółów terenowych

 

   Przy pomiarze szczegółów terenowych można stosować - w sposób łączny - podane uprzednio lub inne metody, pod warunkiem zachowania wymagań dokładnościowych ustalonych dla poszczególnych grup szczegółów terenowych.

 

BEZPOŚREDNIE POMIARY RZEŹBY TERENU

 

Pomiar rzeźby terenu może być wykonany metodą:

- niwelacji powierzchniowej,

- niwelacji tachimetrycznej.

Wybór metody uzależniony jest od wymagań dokładnościowych i warunków terenowych.

 

Niwelacja powierzchniowa może być wykonana:

- sposobem niwelacji siatkowej,

- sposobem niwelacji profilów,

- sposobem niwelacji punktów rozproszonych,

- połączeniem wyżej wymienionych sposobów.

Metody:

 

N i w e l a c j a   p o w i e r z c h n i o w a:

-Niwelacja siatkowa

 

W celu wykonania niwelacji siatkowej należy w pierwszej kolejności w terenie założyć siatkę.
Budowę siatki przeprowadza się w dwóch etapach:

- wyznaczenie figury (figur) podstawowych

- wyznaczenie figur zapełniających.

 

1. Przy doborze wielkości i kształt figur podstawowych należy kierować się następującymi zasadami:

a) w każdej figurze podstawowej powinna być zawarta całkowita ilość figur zapełniających (oczek siatki),

b) wielkość figury podstawowej i jej kształt uzależnione są od wielkości obiektu podlegającego pomiarowi, od celu dla którego wykonywana jest niwelacja, od rzeźby terenu i skali mapy.

2. Wierzchołki figur podstawowych należy wyznaczyć w terenie w oparciu o istniejące punkty poziomej osnowy geodezyjnej, za pomocą metod i sprzętu pozwalających na uzyskanie średnich błędów nie przekraczających 0,50 m oraz zamarkować je palikami osadzonymi równo z powierzchnią terenu.

3. Jeżeli w pobliżu wierzchołków figury podstawowej brak jest punktów osnowy wysokościowej, wówczas przy jednym z nich należy założyć reper roboczy.

4. W celu określenia wysokości reperów roboczych oraz wierzchołków figur podstawowych należy zaniwelować je w nawiązaniu do punktów istniejącej wysokościowej osnowy geodezyjnej wg zasad podanych w §§ 83-87.

 

1. Rozwinięciem figury podstawowej są figury zapełniające. Ich kształt i wielkość pozostają w ścisłym związku z czynnikami warunkującymi wielkość i kształt figury podstawowej.

2. Przy ustalaniu wielkości figur zapełniających należy kierować się zasadą, aby powierzchnia terenu objęta jedną figurą była zbliżona do płaszczyzny, a długość boku nie przekraczała 100 metrów.

3. Charakterystyczne punkty rzeźby terenu położone wewnątrz figur zapełniających wyznacza się jako punkty dodatkowe.

4. Wierzchołki figur zapełniających w zależności od potrzeb markuje się palikami osadzonymi równo z powierzchnią terenu.

 

Niwelację wierzchołków figur zapełniających należy wykonać w nawiązaniu do istniejących punktów wysokościowej osnowy geodezyjnej, założonych reperów roboczych lub wierzchołków figur podstawowych, z zachowaniem następujących wymagań:

a) ciągi niwelacyjne powinny być dowiązane obustronnie,

b) długości celowych nie powinny przekraczać 80 m,

c) na danym stanowisku należy zaniwelować w pierwszej kolejności punkty nawiązania wysokości, następnie pozostałe wierzchołki figur zapełniających i punkty dodatkowe,

d) niwelację ciągów należy wykonać dwukrotnie.

 

Dopuszczalna odchyłka różnicy wysokości przy dwukrotnej niwelacji ciągu służącego do określenia wysokości wierzchołków figur zapełniających nie powinna przekraczać wielkości obliczonej ze wzoru:

  mm

gdzie: L - długość ciągu w km.

W warunkach wyjątkowo niekorzystnych (bagna, torfowiska itp.) dopuszcza się zwiększenie odchyłki o 50 %.

 

-Niwelacja profilami

 

W celu wykonania niwelacji terenu profilami podłużnymi i poprzecznymi należy założyć wzajemnie powiązane ze sobą ciągi pomiarowej osnowy poziomej i wysokościowej.

 

1. Profil podłużny należy założyć wzdłuż osi mierzonego obiektu natomiast profile poprzeczne, prostopadle do niej.
   Kierunek profilu poprzecznego wyznacza się przy użyciu węgielnicy lub instrumentu zaopatrzonego w koło poziome.

2. Odległość między profilami poprzecznymi nie powinny przekraczać 100 m, a odległości między sąsiednimi pikietami na profilu podłużnym powinny być dostosowane do charakteru terenu i nie mogą przekraczać 50 m.

3. Przy wykonywaniu pomiaru dla celów specjalnych odległości podane w ust.2 mogą być zmienione.

 

-Niwelacja punktów rozproszonych

 

Pomiar wysokościowy metodą punktów rozproszonych wykonuje się w oparciu o istniejącą lub nowo założoną poziomą i wysokościową osnowę geodezyjną.

 

1. Jako stanowiska niwelatora należy wykorzystywać przede wszystkim punkty poziomej osnowy geodezyjnej.

2. Jeśli dla mierzonego terenu istnieje mapa sytuacyjna, stanowiskami niwelatora mogą być także te punkty, których położenie zostało na mapie zidentyfikowane.

3. Jedli pomiar wykonywany jest jako uzupełnienie pomiaru rzeźby opracowanej metodami fotogrametrycznymi, miejsca stanowisk niwelatora i pikiet można obierać na charakterystycznych punktach sytuacji terenowej, których położenie da się jednoznacznie odczytać na zdjęciach, fotoszkicach lub na punktach, których położenie wyznaczone zostało metodą bezpośrednią.

4. Odległość między sąsiednimi stanowiskami niwelatora nie powinna przekraczać 200 m.

5. Stanowiska niwelatora markuje się palikami wbitymi równo z powierzchnią terenu.

6. Dla każdego stanowiska niwelatora należy określić rzędną wysokości.

7. Długości celowych do punktów terenowych (pikiet) nie powinny przekraczać 100 m. W terenach rolnych i leśnych dopuszcza się wydłużenie celowych do 150 m.

 

1. Na każdym stanowisku należy określić:

a) numer stanowiska,

b) wysokość osi poziomej niwelatora z dokładnością do 0,01 m nad znakiem markującym punkt,

c) kierunki orientujące na dwa sąsiednie stanowiska, bądź na punkty sytuacyjne dające się ustalić na mapie,

d) odczyt na kole poziomym oraz odczyt na łacie dla każdej pikiety.

2. Pikiety powinny być wyznaczone w takiej ilości, która zapewnia wierne odtworzenie rzeźby terenu. Odległość między nimi nie powinna być większa od 50 m.

 

N i w e l a c j a   t a c h i m e t r y c z n a

 

1. Określenie położenia i wysokości charakterystycznych punktów rzeźby terenu przy pomiarze tachimetrycznym wykonuje się sposobem punktów rozproszonych z założonych stanowisk tachimetrycznych przy użyciu tachimetrów nitkowych lub autoredukcyjnych.

2. Położenie punktów (sytuacyjne i wysokościowe) określone metodą pomiaru tachimetrycznego powinno charakteryzować się następującymi dokładnościami:

a) przy określeniu wysokości punktów względem osnowy wysokościowej - 0,05 m,

b) przy określeniu położenia poziomego szczegółów terenowych względem poziomej osnowy geodezyjnej - 0,50.

 

1. Pomiar tachimetryczny należy wykonać w oparciu o punkty istniejącej poziomej i wysokościowej osnowy geodezyjnej, zagęszczonej w miarę potrzeby ciągami tachimetrycznymi.

2. Średni błąd poziomego położenia punktu ciągu tachimetrycznego nie powinien przekraczać 0,50 m.

3. Wysokości stanowisk ciągów tachimetrycznych należy określać z dokładnością nie mniejszą niż 0,15 m względem punktów osnowy wysokościowej.

 

1. Przy wyborze stanowisk tachimetrycznych należy się kierować zasadami podanymi w § 96 ust. 1-4.

2. Punkty ciągów tachimetrycznych należy markować palikami wbitymi równo z powierzchnią terenu.

3. Dopuszczalne długości celowych do punktów terenowych (pikiet) nie powinny przekraczać 100 m. Na terenach rolnych i leśnych dopuszcza się wydłużenie celowych do 250 m.

 

1. Długości boków ciągów tachimetrycznych należy mierzyć dwukrotnie w obu kierunkach, przy czym błąd względny nie powinien przekraczać:

- dla terenów zurbanizowanych 1 : 3 000,

- dla terenów rolnych i leśnych 1 : 1 500.

2. Średni błąd pomiaru kąta poziomego nie powinien przekraczać:

- dla terenów zurbanizowanych 30" (90^cc),

- dla terenów rolnych i leśnych 60" (180^cc).

3. Dopuszczalny błąd wysokości w ciągach określa się:

a) przy pomiarze różnic wysokości stanowisk metodą niwelacji geometrycznej, wg wzoru:

  m

gdzie: L - długość ciągu w km,

b) przy pomiarze różnic wysokości stanowisk metodą tachimetryczną, wg wzoru:

  m

gdzie: n - ilość stanowisk tachimetru.

 

Przed przystąpieniem do pomiaru należy wyznaczyć (sprawdzić) stałe dalmierza:

a) stałą mnożenia,

b) stałą dodawania.

 

   Na każdym stanowisku tachimetrycznym należy:

a) przed przystąpieniem do pomiaru pikiet wyznaczyć i zapisać w dzienniku:

- wysokość osi obrotu lunety z dokładnością 0,01 m,

- kierunki orientujące na dwa sąsiednie stanowiska lub na punkty sytuacyjne dające się ustalić na mapie,

- miejsce zera na kole pionowym,

- położenie koła przy którym ma być wykonany pomiar pikiet.

b) przy pomiarze pikiet pomierzyć i zarejestrować elementy pozwalające określić:

- kierunek,

- odległość,

- przewyższenie.

 

1. Przy wyborze pikiet należy dążyć do tego, aby były one obierane odpowiednio do konfiguracji terenu, tj. na wszystkich punktach charakterystycznych i w takiej liczbie, która gwarantuje wierne odtworzenie rzeźby terenu.

2. Wzajemne odległości pikiet na terenach o równomiernych spadkach nie powinny być większe od 50 m, a na terenach rolnych i leśnych 100 m.

FOTOGRAMETRYCZNE POMIARY SYTUACYJNE I WYSOKOŚCIOWE (w to już się wgłębiać nie będę, jak cos to instrukcja G-4)

4. Poprawki i redukcje obserwacji geodezyjnych:

Z zakresu `geodezyjnych pomiarów szczegółowych':

• na średni poziom pomiaru
  

• na poziom instrumentu
  

• na poziom lustra
  

• na poziom odniesienia
  

Poprawka odwzorowawcza:

• Redukcja długości na płaszczyznę GK

• Redukcja kątów na płaszczyznę GK

Poprawka odwzorowawcza - odwzorowanie GK modyfikowane (Mo = 0,999923)

• redukcja długości

• redukcja kąta

• POPRAWKI

• instrumentalne:

• stała dodawania dalmierza i pryzmatów zwrotnych (k)

Wywołana różnicą między centrem geometrycznym dalmierza, a jego centrem elektronicznym. Trzeba ją wprowadzić, żeby zmierzona odległość była faktycznie odległością między punktami.

• częstotliwości

Zmiana częstotliwości wzorcowej od jej wartości nominalnej. λ=v/f - więc zmiana częstotliwości f zmienia „przymiar” λ. Na skutek starzenia się kryształów kwarcu. Istotna w starych instrumentach. Nie jest duża, ważna tylko w precyzyjnych pomiarach.

• fazomierza

• ze względu na warunki atmosferyczne:

• atmosferyczna

Zmieniają się warunki atmosferyczne-> zmienia się współczynnik załamania-> zmienia się prędkość fali-> błędny pomiar odległości. Zjawisko podłużnej refrakcji atmosferycznej.

Wyznaczamy współczynnik załamania (np. przy użyciu wzorów Barella i Searsa dla fal optycznych)

Poprawka atmosferyczna:

n₀ - wartość współczynnika załamania odpowiadająca przeciętnym (standardowym) warunkom meteorologicznym, przy użyciu których dany model dalmierza wyznacza długość,

n - wartość współczynnika załamania odpowiadająca panującym warunkom meteorologicznym.

• częstotliwości

Zmienia się temperatura-> zmienia się częstotliwość drgań-> zmienia się długość fali wzorcowej („przymiar”).

• refrakcyjna

Niejednorodność atmosfery powoduje zakrzywienie toru fali pomiarowej - biegnie ona po łuku (tzw. krzywa refrakcji), a nie po prostej. Zmianie ulegają obserwowane odległości i kąty pionowe.

Odległość: mierzona jest długość łuku, a nie cięciwa, która jest interesującą nas odległością. Jest to jednak na tyle mała różnica, że na ogół nie trzeba tego uwzględniać.

s-cięciwa, s^r- łuk, k- współczynnik refrakcji.

Kąty: wyjaśnia rysunek.

Z zakresu `geodezji wyższej':

• REDUKCJE GEOMETRYCZNE

• Redukcje obserwacji geodezyjnych na płaszczyznę odniesienia (z elipsoidy odniesienia na płaszczyznę):

• Redukcje długości r = S - s (S- długość na płaszczyźnie, s- na elipsoidzie)

- w odwzorowaniu Gaussa-Krugera

więc

Po scałkowaniu, przyjmując R = R_m - średni promień krzywizny środkowego punktu linii, otrzymamy w przybliżeniu:

)

Długość S na płaszczyźnie w odwzorowaniu G-K jest zawsze większa lub co najwyżej równa długości na elipsoidzie S
(tylko na południku osiowym, gdy y=0, S=s). W miarę oddalania się od południka osiowego, redukcje rosną.

- w odwzorowaniu UTM

Zniekształcenia w UTM mają bardziej złożony charakter, ponieważ występuje zmienność skali na południku osiowym.

- w odwzorowaniu quasi-stereograficznym

Zniekształcenia układają się w okręgi rosnące w miarę oddalania się od punktu głównego.

Np. układ 1965: m=0.9998+68.15·d²·10^-10

(0.9998-skala dla punktu głównego, d- odległość od punktu głównego[km])

Niech będzie dany na elipsoidzie punkt P o współrzędnych (B, L) oraz w bliskim „różniczkowym” jego otoczeniu drugi punkt Q odległy o ds. Punkty te odwzorują się na płaszczyźnie w odpowiednie punkty P' oraz Q', zaś łuk PQ o długości ds w odpowiadający łuk P'Q' o długości dS. Elementarną skalę liniową definiujemy stosunkiem m = dS/ds. W odwzorowaniach wiernokątnych jest ona niezależna od azymutu łuku PQ i wyraża się funkcją położenia np. we współrzędnych geodezyjnych (B,L) lub odwzorowawczych (x, y).

- redukcje kierunków

[Bardziej jako dopełnienie tematu, bo kto wie, czy nie zahaczą o to]

Wiernokątność odwzorowania odnosi się do kątów miedzy liniami krzywymi. Na płaszczyźnie chcemy jednak mierzyć kąty między cięciwami tych krzywych, zaś odpowiedniki azymutów pomiędzy kierunkami równoległymi do południka osiowego i cięciwami odpowiednich krzywych.

δ - kąty, jakie tworzy cięciwa z łukiem krzywej boku trójkąta na płaszczyźnie = redukcje kierunków.

Wzór przybliżony:

t, γ - zbieżność południków (kąt jaki tworzy równoległa do południka osiowego przesunięta przez punkt P z obrazem południka tego punktu) odpowiednio na elipsoidzie i płaszczyźnie.

Kąty kierunkowe w P₁' P₂' wyrażone są przez azymuty , zbieżności południków na płaszczyźnie i redukcje kierunków:

α₁₂=A₁₂-γ₁-δ₁₂ α₂₁=A₂₁-γ₂-δ₂₁

7. Błędy występujące w instrumentach geodezyjnych.

TEODOLIT

1. Niedokładne ustawienie osi instrumentu w pionie - wówczas os instrumentu tworzy niewielki kąt z pionem, a oś instrumentu nie przechodzi przez zenit. Bład ten wynika z niedokłądego spełnienia warunku prostopadłości libeli głównej do osi pionowej instrumentu.

2. Bład inklinacji - oś obrotu lunety nie tworzy kąta prostego z osią obrotu instrumentu, lecz kąt 90 + i, którego wpływ na pomiar kierunku wyraza wzór ε=itgh. Istotny gdy cel jest połozony wysoko. (eliminowana w pomiarze w dwóch położeniach lunety). Wybieramy punkt możliwie wysoko i przy zablokowanym kole poziomym opuszczamy go na poziom terenu. To samo w drugim połżeniu. Punkty powinny się pokrywać - jeśli nie przeprowadzamy rektyfikację

3. Błąd kolimacji - jeśli os celowa nie jest prostopadła do osi obrotu lunety, to wówczas podczas obrotu lunety zakresla ona stożek obrotowy i mówimy wówczas, ze występuje bład kolimacji. Rektyfikacja - wybieramy dobrze widoczny cel (mniej więcej w płaszcz. poziomej żeby wyeliminować wpływ błędu inklinacji) i celujemy do niego w dwóch położeniach lunety. Róznica midzy odczytami powinna wynosci ok. 180 (w granicach błedu celowania i odczytu). Ewentualna odchyłak jest podwojonym błedem kolimacji

4. Mimośrodowe osadzenie lunety - os celowa nie przecina się z osią pionowa instrumentu (max. Kilka milimetrów) wiekszy dla krótkich celowych, dla długich celowych bliski zeru. Celując do punktu w dwóch położeniach lunety kierunki zostaną pomierzone z błędem mimośrodu (za każdym razem będzie on miał przeciwny znak). Średnia arytmetyczna pomiaru eliminuje wpływ mimośrodu osi celowej.

5. Ekscentryczność alidady - jeżeli os obrotu alidady nie przechodzi przez środek nimbus lecz jest osadzona względem niego ekscentrycznie. Jest największy dla kata 90. Usunąć się go nie da ale można łatwo wyeliminować - pomiar w dwóch położeniach lunety (średnia arytmetyczna)

6. Błąd podziału koła

7. Błąd indeksu koła pionowego - odchylenie każdego indeksu od poprawnego odczytu (błąd położenia miejsc zera), eliminacja przy pomiarze kata w dwóch położeniach lunety.

8. Bład ustawienia siatki celowniczej - poziomujemy teodolit i celujemy na sznurek zawieszonego pionu. Jeżeli nie pokrywaja się pierścien siatki celowniczej nalezyodpowiednio skręcić srubkami. Usuwamy przez dwukrotny pomiar lub przez celowania zawsze srodkiem siatki

NIWELATOR

Pod względem konstrukcji niwelatory nożna podzielić na;

a) niwelatory libelowe - poziome położenie osi celowej jest realizowane za pomocą libeli niwelacyjnej umieszczonej na lunecie. Środkowe położenia pęcherzyka libeli niwelacyjnej uzyskuje się dzięki śrubie elewacyjnej zmieniającej położenie osi celowej w płaszczyźnie pionowej w zakresie małego kata pionowego. Niwelator libelowy bez śruby elewacyjnej jest nazywany niwelatorem głuchym.

b) niwelatory samopoziomujące - oś celowa ustawia ale w poziomie automatycznie w pewnych granicach pochylenia lunety. Poziomowanie to jest realizowane automatycznie z wysoką precyzją za pomocą urządzenia zwanego kompensatorem lub stabilizatorem.

Obracając lunetę kilkakrotnie wokół osi głównej instrumentu stwierdzamy czy układ osiowy działa prawidłowo, ta znaczy czy oś obrotu nie jest zatarta.

Jeżeli niwelator jest wyposażony w krąg poziomy, należy sprawdzić błąd paralaksy runu.

Sprawdzenie i rektyfikacja niwelatorów libelowych

1) płaszczyzna P, styczna do libeli sferycznej w jej punkcie głównym, powinna być pozioma,

2) oś pionowa VV musi być prostopadła do płaszczyzny P, - Po starannym spoziomowaniu niwelatora w oparciu o zrektyfikowaną libelę sferyczna oś główna niwelatora VV będzie zajmować pionowe położenie.

3) kreska pionowa siatki celowniczej powinna leżeć w płaszczyźnie kolimacyjnej niwelatora,

4) oś libeli niwelacyjnej LL powinna być równoległa do osi celowej,

Ad 3. Niwelator ustawiamy na statywie i starannie poziomujemy w oparciu o zrektyfikowane libele. Na wysokości osi celowej wybieramy dobrze widoczny punkt. Celujemy poziomą nitką krzyża kresek na obrany punkt, ustawiając go w lewym skrajnym położeniu w polu widzenia. Zaciskamy śruby zaciskowe alidady. Śrubą ruchu leniwego alidady przesuwamy cel wzdłuż poziomej nitki krzyża kresek. Jeżeli punkt nie zejdzie z poziomej nitki krzyża kresek warunek jest spełniony. W przeciwnym przypadku należy krzyż zrektyfikować.

Ad 4. Metoda polowa sprawdzania warunku c l.

Sprawdzany niwelator ustawiamy w terenie i starannie poziomujemy.

W odległości około 40 m ustawiany dwie łaty w punktach A i B. Ze stanowiska S₁ - po środku łat, wyznaczamy różnicę wysokości (a₁ - b₁) nie obarczoną ewentualnym wpływem błędu nierównoległości osi c i l. Następnie ustawiamy niwelator w punkcie S₂ - (klasycznie-8m od łaty bliższej i 32m do łaty dalszej). Celując do łaty ustawionej nad punktem B, wykonujemy odczyt b₂. Znając różnicę (a₁ - b₁) wyliczamy odczyt a₂, nie obarczony błędem nierównoległości osi c i l.

Sprawdzenie i rektyfikacja niwelatorów samopoziomujących

W zakresie warunków geometrycznych, które powinien spełniać niwelator samopoziomujący:

1) płaszczyzna głównej libelli sferycznej P musi być prostopadła do osi pionowej instrumentu VV,

2) oś celowa niwelatora, ustawiona w poziomie za pomocą kompensatora, powinna być rzeczywiście pozioma w zakresie działania kompensatora,

Ad l. Podczas obrotu niwelatora wokół osi VV pęcherzyk libeli sferycznej musi zachować symetryczne położenie w stosunku do podziału naniesionego na czaszy libeli. w przeciwnym razie libelę należy zrektyfikować za pomocą trzech śrub rektyfikacyjnych według powszechnie znanej metody,

Ad 2, Sprawdzenie warunku osi celowej wykonujemy jak sprawdzenie warunku 4 niwelatora libellowego.

Dalmierze elektroniczne

1. Błąd stały

2. Błąd częstotliwości wzorcowej - powstają jeżeli co najmniej jeden ze składników instrumentu odpowiedzialny za generowanie fali mierzącej działa niepoprawnie - gdy oscylator się zestarzeje lub kiedy termostat nie utrzymuje temperatury we właściwym zakresie

3. Błąd cykliczny - wywołany niedoskonałością urządzenia mierzącego fazę lub niedużą deformacją mierzonego sygnału, na przykład błąd ten może być wywołany niedoskonałą modulacją fali nośnej (różnica w modulacji amplitud pojawia się w postaci błędu okresowego, którego znak i wielkość zależy od pozycji różnicy na osi poziomej)

4. Inne błedy - dalmierze dawnego typu, gdzie dalmierz był montowany na teodolicie - nierównoległość osi dalmierza i osi celowej teodolitu.

7. Błędy występujące w instrumentach geodezyjnych (niwelatorach, teodolitach i dalmierzach).

Teodolit

Sprawdzenie i rektyfikacja teodolitu obejmuje trzy grupy czynności

1. usunięcie uszkodzeń mechanicznych

2. konserwację elementów optycznych,

3. rektyfikację warunków geometrycznych,

Do rektyfikacji warunków geometrycznych teodolitu można przystąpić po uprzednim usunięciu uszkodzeń mechanicznych i należytej konserwacji elementów optycznych. Wpływ pewnych błędów można wprawdzie eliminować drogę odpowiednich metod pomiaru (najczęściej przez pomiar w dwóch położeniach lunety), ale ogólnie dąży się do tego, aby drogą rektyfikacji eliminować stwierdzone błędy instrumentalne, sprowadzające ich niekorzystny wpływ praktycznie do zera.

Uszkodzenia mechaniczne

Przed przystąpieniem do konserwacji elementów optycznych i rektyfikacji warunków geometrycznych należy stwierdzić i ewentualnie usunąć uszkodzenia mechaniczne instrumentu, spodarki i statywu.

Przyczyny powstawania uszkodzeń mechanicznych są różne. Najczęściej ulega uszkodzeniu instrument podczas transportu lub niewłaściwej obsługi. Dokręcania zacisków i śrub bez wyczucia prowadzi do uszkodzenia poszczególnych elementów tych urządzeń. Szkodliwa naciski na mechanizmy śrubowe, mikroskopy, libele, lunetę itp., na przykład podczas wyjmowania lub wkładania instrumentu do skrzynki, są także bardzo często przyczynę uszkodzeń. Poniżej omówimy przegląd teodolitu w aspekcie jego uszkodzeń mechanicznych.

Po wyjęciu instrumentu ze skrzynki należy ustawić go na stabilnym podłożu i dokonać szczegółowego przeglądu wszystkich części mechanizmów zaciskowych, śrub ruchu leniwego, zamocowania libel itp. Wszystkie śruby i pokrętła, na przykład okularu lunety i mikroskopu odczytowego, powinny obracać się ruchem płynnym na całej swej długości. Obracając alidadę kilkakrotnie wokół osi głównej instrumentu stwierdzamy, czy układ osiowy działa prawidłowo- to znaczy czy oś obrotu nie jest zatarta.

Obracając lunetę w płaszczyźnie pionowej, badamy jej prawidłowy obrót w łożyskach osi obrotu.

Stwierdzone przez geodetę uszkodzenia lub usterki mechaniczne powinny być usunięte w odpowiednim zakładzie mechanicznym. Zmianę lub uzupełnienie smarów wykonuje mechanik precyzyjny. Geodeta może tylko wyregulować śruby ruchu leniwego w przypadku, gdy mechanizm śrubowy nie jest uszkodzony i samo jego rozwiązanie przewiduje regulację śruby bez jej demontażu.

W dalszej kolejności należy wyjąć Instrument ze spodarki i sprawdzić jej poszczególna elementy. Trzymając spodarkę w jednej ręce sprawdzamy drugą, czy śruby poziomujące obracają się ruchem płynnym na całej długości śruby, Sprawdzamy także, czy siła potrzebna do obrotu jest taka sama dla wszystkich trzech śrub. Ewentualna różnice usuwany przez odpowiednie wyregulowanie śruby

Sprawdzenie statywu polega na kontroli właściwego połączenia części drewnianych i metalowych. Zauważone luzy usuwamy, dokręcając śruby specjalnym kluczem. Należy, także sprawdzać, czy okucia w dolnej części nóg nią są poluzowane. W przypadku stwierdzenia luzów należy dokręcić odpowiednie wkręty. Śruby motylkowe, służące do unieruchomienia połówek nóg po ustaleniu określonej wysokości statywu, powinny pewnie dociskać okucia elementów drewnianych. W przypadku stwierdzenia zerowania gwintu śrub motylkowych statyw jest niesprawny. Uszkodzone śruby należy wymienić.

Sprawdzenie systemu odczytowego

Po przeglądzie i ewentualnej konserwacji elementów mechanicznych i optycznych teodolitu należy sprawdzić, czy system odczytowy jest wolny od dwóch podstawowych błędów: błędy paralaksy i błędu runu.

Jednomiejscowy system odczytowy

Klasycznym przykładem jednomiejscowego systemu odczytowego jest mikroskop skalowy

W układzie optycznym systemu jednoodczytowego teodolitu mogę wystąpić następująca błędy:'

1. błąd paralaksy systemu odczytowego,

2. błąd runu,

Błąd paralaksy systemu odczytowego

Definicja: Błąd paralaksy systemu odczytowego występuje wówczas, gdy obraz limbusa (kreski wskaźnikowej) nie tworzy się w płaszczyźnie skali. Obraz limbusa i obraz skali, oglądane od strony okularu systemu odczytowego, nie są wtedy jednocześnie jednakowo ostre.

Wykrywanie: Ruchem obrotowy soczewki okularowej systemu odczytowego nastawiamy obraz skali na ostrość. Nieostry będzie obraz limbusa (kreski wskaźnikowej),

Błąd runu

Definicja: Błąd runu występuje wówczas, gdy wielkość obrazu jednej działki opisu kręgu jest różna od długości skali.

Wykrywanie: Lewę kreskę skali pokrywany z początkiem skali oczekując pokrycia kraski prawej z końcem skali. Jeżeli na końcu skali nie ma pokrycia kresek, występuje błąd runu. W niektórych teodolitach skala jest przedłużona na obydwu końcach o jedne działkę. W takim przypadku ustawiamy lewę kreskę opisaną (obraz kręgu) na środku lewego dodatkowego interwału skali (bisekcja), oczekując symetrycznego położenia prawej kreski opisanej. Metoda bisekcji wykrywania błędu runu jest dokładniejsza od sposobu polegającego na pokrywaniu kresek.

Dla usunięcia obu błędów należy teodolit oddać do zakładu specjalistycznego.

Dwumiejscowy system odczytowy

Dwumiejscowy system odczytowy jest zastosowany w teodolitach precyzyjnych (na przykład Theo 010) wyposażonych w mikrometr optyczny, który działa na zasadzie dwóch par klinów optycznych lub dwóch płytek płaskorównoległych.

Błąd paralaksy systemu odczytowego

W dwumiejscowym systemie odczytowym występują dwa rodzaje błędu paralaksy:

• paralaksa pomiędzy dwoma obrazami podziału kręgu A i B,

• paralaksa pomiędzy obrazami podziału (A i B) a obrazem mikrometru.

Błąd paralaksy pomiędzy dwoma obrazami podziału kręgu A i B występuje wówczas, gdy obraz części A nie tworzy się w płaszczyźnie części B. Obrazy kresek górnych i dolnych nie są jednocześnie jednakowo ostre.

Błąd paralaksy pomiędzy obrazem podziału kręgu A i B a obrazem mikrometru powstaje wówczas,- gdy obraz podziału kręgu (A i B) nie tworzy się w płaszczyźnie skali. Obraz podziału kręgu (A i B) i obraz mikrometru nie są jednocześnie jednakowo ostre

Błąd runu

W dwumiejscowym systemie odczytowym występuję dwa rodzaje błędu runu:

• błąd runu pomiędzy dwoma obrazami podziału kręgu A i B,

• błąd runu pomiędzy obrazem podziału kręgu (a i B) a mikrometrem.

Błąd runu pomiędzy dwoma obrazami podziału kręgu A i B występuje wówczas, gdy wielkość obrazu interwału a nie odpowiada długości obrazu interwału b.

Błąd runu pomiędzy obrazem podziału kręgu a mikrometrem występuje wówczas, gdy wielkość obrazu połowy jednej działki a lub b nie odpowiada pełnemu zakresowi skali mikrometru. Sprawdzany to w ten sposób, że przy zerowym odczycie na mikrometrze i. koincydencji dowolnej pary kresek pokrętłem mikrometru doprowadzamy sąsiednie kreski do koincydencji. Nadmiar lub niedobór na podziałce mikrometru jest wielkością błędu runu..

Dla usunięcia błędów należy teodolit oddać do zakładu specjalistycznego.

Warunki geometryczne

Każdy teodolit musi spełniać następujące zasadnicze warunki geometryczne:

1. os główne instrumentu, identyczna z osie obrotu alidady, powinna być pionowa l przechodzić przez punkt terenu, nad którym jest ustawiony teodolit,

2. osie libel alidadowych powinny być prostopadłe do osi głównej teodolitu,

3. oś obrotu lunety powinna być prostopadła do osi głównej teodolitu i przy spoziomowanym instrumencie musi zajmować położenie poziome,

4. oś celowa lunety musi być prostopadła do poziomej osi obrotu lunety.

Inne warunki, dotyczące na przykład płytki ogniskowej, libeli kolimacyjnej lub kręgów Hz i V, będę omówione w odpowiednich rozdziałach dotyczących poszczególnych błędów instrumentalnych. Niektóre warunki geometryczne, omówione niżej bardziej szczegółowo, będę sprawdzana i rektyfikowane w oparciu o kolimator. W takich przypadkach zakładamy, że kolimator ten jest w pełni sprawny i został przed rektyfikacją także sprawdzony metodami podanymi

Warunek libel

W ramach tego warunku należy sprawdzić i zrektyfikować wszystkie libele umieszczone na alidadzie, oprócz libeli kolimacyjnej i ewentualnie libeli na lunecie, którą rektyfikujemy przy usuwaniu błędu miejsca zera. Libele na alidadzie sprawdzamy w zależności od sposobu umieszczenia ich na alidadzie. Na rysunku przedstawiono schematycznie cztery najczęściej spotykane przypadki umieszczania libel na alidadzie,

Przypadki umieszczenia libel na alidadzie:

1. jedna libela rurkowa

2. libela rurkowa i sferyczna

3. dwie libele rurkowe,

4. jedna libela sferyczna

1. Przypadek a. pojedynczej libeli rurkowe rektyfikujemy według powszechnie znanej metody.

2. Przypadek b: libelę rurkową rektyfikujemy jak w przypadku a. W oparciu o zrektyfikowaną libelę rurkową sprowadzamy oś główną instrumentu do położenia pionowego. Tymi samym płaszczyzna alidady będzie pozioma. Pęcherzyk libeli sferycznej umieszczonej na tej płaszczyźnie powinien leżeć w punkcie głównym libeli. Ewentualne wychylenie usuwamy śrubkami rektyfikacyjnymi libeli sferycznej (cały błąd).

3. Przypadek c: postępujemy analogicznie jak w przypadku b, rektyfikując najpierw jedna z libel rurkowych. Drugą libelę rurkowa rektyfikujemy jak libelę sferyczne w przypadku b,

4. Przypadek d: trudność polega na wykryciu kierunku maksymalnego odchylenia pęcherzyka. Czynności rektyfikacji należy, dlatego wielokrotnie powtarzać metodę kolejnych przybliżeń.

Może się zdarzyć, że podczas rektyfikacji libel stwierdzi się niemożność ustawienia płaszczyzny alidady w poziomie wyznaczonym przez obrót alidady i środkowym położeniu pęcherzyka. Przy pozornie rektyfikowanej libeli będą takie położenia alidady, przy których pęcherzyk wyjdzie z położenia środkowego. Przypadek taki może wystąpić w teodolicie z układem osiowym na łożysku kulkowym bez koszyczka (kulki luzem).

Podczas oddzielania części górnej alidady od dolnej, na przykład dla zmiany smaru w systemie osiowym, można zgubić jedną z kulek. Jeżeli kulka zastępcza ma nieco wyższa średnicę od pozostałych, płaszczyzna alidady nie będzie mogła zajmować położenia poziomego przy jej obrocie. Należy wówczas powtórnie zdemontować alidadę, śrubą mikrometryczna pomierzyć średnice wszystkich kulek i tą niewłaściwą zastępie kulką o odpowiedniej średnicy.

Warunek siatki kresek

Prostopadłość kresek poziomych i pionowych jest zapewniona fabrycznie, przy takim założeniu warunek siatki kresek brzmi: kreska pozioma siatki powinna być prostopadła do osi głównej teodolitu

Sprawdzenie. Teodolit ustawiamy na statywie i starannie poziomujemy w oparciu o zrektyfikowane libele. Na wysokości osi celowej wybieramy dobrze widoczny punkt. Celujemy poziomą nitką krzyża kresek na obrany punkt, ustawiając go w lewym skrajnym położeniu w polu widzenia. Zaciskamy śruby zaciskowe alidady i lunety. Śrubą ruchu leniwego alidady przesuwamy cel wzdłuż poziomej nitki krzyża kresek. Jeżeli punkt nie zejdzie z poziomej nitki krzyża kresek warunek jest spełniony. W przeciwnym przypadku należy krzyż zrektyfikować.

Rektyfikacja. Odkręcamy osłonę przy okularze lunety. Po zdjęciu osłony będą widoczne śruby rektyfikacyjne płytki ogniskowej, jak na rysunku.

Należy lekko zwolnić śruby (1) sprzęgające obudowę płytki ogniskowej z tubusem lunety. Obracamy płytkę ogniskową o połowę kąta wychylenia poziomej nitki krzyża od punktu celu. Następnie czynności sprawdzające wykonujemy ponownie i ewentualne wychylenie poziomej nitki krzyża korygujemy o połowę wychylenia. Czynności te wykonujemy do momentu uzyskania zadowalających efektów. Następnie należy stopniowo (np. po pół obrotu) dokręcać kolejno wszystkie cztery śruby do oporu. Realizację warunku sprawdzamy po niezależnym wycelowaniu na dobrze widoczny punkt.

Błąd kolimacji

Definicja. Błąd kolimacji występuje, gdy oś celowa nie jest prostopadła do poziomej osi obrotu instrumentu

Wykrywanie. Po sprawdzeniu i rektyfikacji warunków podanych wyżej, celujemy do wyraźnego punktu na wysokości osi celowej. Wykonujemy odczyt kręgu Hz, przekładamy lunetę przez zenit i celując w II położeniu lunety na punkt robimy drugi odczyt Hz.
Przykładowo otrzymano (np. dla teodolitu T-6)

I = 12^g26^c

II= 212^g34^c

2k= 08^c

k= 04^c

Otrzymane odczyty poprawiamy o błąd kolimacji

I + K = 12^g30^c

II - K = 212^g30^c

II - I = 200^g00^c

Odczyty z obydwu położeń powinny różnić się o 200^g lub 180°.

Usuwanie. Leniwką alidady (ruchu poziomego lunety) nastawiamy na mikroskopie skalowym odczyt uśredniony (np. z II położenia lunety) Hz =212^g 30^c. Wtedy kreska pionowa siatki teodolitu zejdzie z punktu celu. Pionową kreskę krzyża należy wprowadzić na cel śrubami rektyfikacyjnymi krzyża. Do usuwania błędu kolimacji służą cztery śruby (2) (rys. nr 2). Parę pionowych śrub lekko zwalniany, a ruchem śrub poziomych doprowadzamy kreskę pionowe siatki teodolitu do pokrycia z celem. Po uzyskaniu pokrycia i dokręceniu wszystkich śrub (2) do oporu, należy powtórnie wyznaczyć błąd kolimacji i ewentualnie praktycznie uchwytne wielkości tego błędu usuwać metodę kolejnych przybliżeń.

Błąd inklinacji

Definicja. Błąd inklinacji występuje, wówczas, gdy oś obrotu lunety nie jest prostopadła do osi głównej teodolitu.

Wykrywanie: Obieramy wyraźny punkt położony na pewnej wysokości, pod którym ustawiamy podziałkę milimetrową. W pierwszym położeniu lunety celujemy do punktu, po czym obniżany lunetę i celując kreskę pionowa do podziałki wykonujemy odczyt. Tę sarnę czynność powtarzamy przy drugim położeniu lunety. Przykładowo otrzymano:

I = 42,2 mm

II = 47,0 mm.
2i = 4,8 mm

i= 2,4 mm

Odczyt średni, wolny od błędu inklinacji, wynosi w naszym przypadku

O_śr = 44,6 mm

Usuwanie błędu inklinacji polega na zmianie położenia poziomej osi obrotu lunety. W teodolitach starego typu regulacjo taka jest możliwa dzięki specjalnej konstrukcji łożyska osi poziomej. W teodolitach optycznych zmiana położenia osi obrotu lunety odbywa się przez podniesienie lub obniżenie łożyska osi umieszczonego od strony zacisku lunety. Zmiana położenia łożyska jest możliwa po zwolnieniu odpowiednich wkrętów. Oś obrotu lunety będzie prostopadła do osi głównej teodolitu, gdy kreska pionowa siatki pokryje się z odczytam średnim. W naszym przypadku O_śr = 44,6 mm,

Błąd miejsca zera

Definicja: Błąd miejsca zera (indeksu) występuje, gdy przy poziomej osi celowej lunety i środkowym położeniu pęcherzyka libeli kręgu pionowego (kolimacyjnej) odczyt V≠100⁹ lub V≠ 300^g (dla podziału zenitalnego kręgu).

Wykrywanie. Po starannym spoziomowaniu teodolitu celujemy na dobrze widoczny punkt znajdujący się na horyzoncie, wykonując odczyty kręgu V w I i II położeniu lunety (O_L i O_P) Przy każdym odczycie leniwką libeli kolimacyjnej doprowadzamy jej pęcherzyk do położenia środkowego.

Określamy błąd indeksu oraz odczyt kręgu V () pozbawiony wpływu tego błędu

Usuwanie: Leniwką libeli kolimacyjnej nastawiamy odczyt wolny od błędu indeksu, czyli . Podczas tej czynności pęcherzyk libeli kolimacyjnej wyjdzie z położenia środkowego. Pęcherzyk libeli kolimacyjnej doprowadzamy ponownie do położenia środkowego za pomocą śrub rektyfikacyjnych libeli kolimacyjnej.

W przypadku teodolitu z dwumiejscowym systemem odczytowym, na przykład Theo 010, usuwanie błędu miejsca zera przebiega następująco: pokrętłem mikrometru nastawić odczyt (końcówkę). Zburzoną podczas powyższej czynności koincydencję obrazów podziału głównego należy powtórnie zrealizować za pomocą leniwki libeli kolimacyjne. Wychylenie pęcherzyka libeli kolimacyjnej usunąć śrubkami rektyfikacyjnymi libeli,

W teodolitach z automatycznym wskaźnikiem odczytu kręgu pionowego (bez libeli kolimacyjnej) usuwanie błędu indeksu odbywa się w zależności od rozwiązania samego teodolitu albo przez zmianę położenia osi celowej lub 'regulację wahadła. W teodolicie Theo 020 nastawia się odczyt bezbłędny (V) leniwkę lunety, wówczas oś celowa wychodzi z celu.

Poprawę położenie osi celowej realizuje się śrubami (2) siatki celowniczej. W teodolicie DAHLTA 010 A błąd indeksu usuwa się metodą regulacji wahadła, zaopatrzonego w odpowiednia pierścienie rektyfikacyjne.

Sprawdzenia pionu optycznego

W przypadku pionu optycznego wbudowanego na stała w alidadę; teodolitu, mamy do czynienia tylko z dolną osią celowa. Oś celowa takiego pionu optycznego jest wyznaczona przez środek znaczka celowniczego S i środek optyczny obiektywu O. Oś celowa jest załamana w pryzmacie P pod kątem prostym.

Plon optyczny w alidadzie musi spełniać następująca warunki

1) pionowa część osi celowej plonu optycznego powinna podczas obrotu alidady wokół osi głównej teodolitu o 360° przebijać-dowolna płaszczyzn; prostopadłą do osi pionu w jednym punkcie;

2) płaszczyzna pozioma wyznaczona przez zrektyfikowane libele alidadowe teodolitu musi być prostopadła do pionowej części osi celowej plonu optycznego.

Ad 1.Instrument ustawiamy na stabilnym statywie. Na podłodze kładziemy kartkę, papieru, na której zaznaczamy ślad punktu S. Po obrocie alidady o 180° i otrzymaniu drugiego śladu punktu S' wyznaczamy środek odcinka S-S'. Rektyfikację pionu przeprowadzany różnie, zależnie od konstrukcji elementów plonu optycznego. Jeżeli przy okularze pionu są widoczne śrubki rektyfikacyjna, znaczek S naprowadzamy na środek odcinka S-S' tymi śrubkami. W przypadku gdy znaczek celowniczy jest na stałe zamontowany w części okularowej, błąd pionu optycznego usuwamy ruchem pryzmatu P (np. w T-6 i T-30). W tym celu za pomocą klucza dwupunktowego odkręcany i zdejmujemy dwie osłony A. Na rysunku pokazano dla przejrzystości tylko jedną z nich. W otworach znajdują się śruby unieruchamiające pryzmat P. Po zwolnieniu tych śrub za pomocą śrubokrętu można pryzmat ustawić tak, aby obraz znaczka celowniczego pokrył się za środkiem odcinka S-S'.

Przy zrektyfikowanym pionie optycznym pionowa część osi calowej pionu powinna być identyczna z osie główna teodolitu.

Ad 2. Realizacje tego warunku polega na sprawdzeniu i rektyfikacji libel alidadowych.

Niwelator

Pod względem konstrukcji niwelatory nożna podzielić na;

a) niwelatory libelowe,

b) niwelatory samopoziomujące.

Ad a.

W niwelatorze libelowym poziome położenie osi celowej jest realizowane za pomocą libeli niwelacyjnej umieszczonej na lunecie. Środkowe położenia pęcherzyka libeli niwelacyjnej uzyskuje się dzięki śrubie elewacyjnej. zmieniającej położenie osi celowej w płaszczyźnie pionowej w zakresie małego kata pionowego. Niwelator libelowy bez śruby elewacyjnej jest nazywany niwelatorem głuchy.

Ad b.

W niwelatorze samopoziomującym, zwanym także automatycznym, oś celowa ustawia ale w poziomie automatycznie w pewnych granicach pochylenia lunety. Poziomowanie, to jest realizowana automatycznie z wysoką precyzję za pomocą urządzenia zwanego kompensatorem lub stabilizatorem.

Przed przystąpieniem do rektyfikacji warunków geometrycznych niwelatora należy usunąć ewentualne uszkodzenia mechaniczne i w razie potrzeby przeprowadzić konserwację elementów optycznych.

W ramach kontroli części mechanicznych należy sprawdzić statyw, spodarkę i elementy mechaniczne niwelatora. Po wyjęciu niwelatora ze skrzynki należy ustawić go na stabilnym podłożu i dokonać szczegółowego przeglądu wszystkich części mechanizmów zaciskowych, śruby ruchu leniwego, śruby elewacyjnej, zamocowania libel itp. Wszystkie śruby i pokrętła - na przykład okularu lunety i mikroskopu odczytowego kręgu poziomego - powinny obracać się ruchem płynnym na całej swej długości. Obracając lunetę kilkakrotnie wokół osi głównej instrumentu stwierdzamy czy układ osiowy działa prawidłowo, ta znaczy czy oś obrotu nie jest zatarta.

Stwierdzane przez geodetę uszkodzenia lub usterki mechaniczne niwelatora powinny być usunięte w odpowiednim zakładzie mechanicznym. Zmiana lub uzupełnienia smarów jest wykonywana przez mechanika precyzyjnego

Geodetę noże tylko wyregulować śruby ruchu leniwego w przypadku, gdy mechanizm śrubowy nie jest uszkodzony, a samo.jego rozwiązanie przewiduje regulację śruby bez jej demontażu.

W dalszej kolejności należy sprawdzić śruby poziomujące niwelatora, czy obracają się ruchem płynnym na całej swej długości. Jeżeli spodarka jest wyposażona w płytkę sprężynowa, należy także sprawdzić jej stan.

Jeżeli niwelator jest wyposażony w krąg poziomy, należy sprawdzić błąd paralaksy runu.

Kolejnym etapem jest sprawdzenie warunków geometrycznych niwelatora.

Sprawdzenie i rektyfikacja niwelatorów libelowych

Niwelator libelowy, którego schemat pokazano na rysunku powinien-spełniać następujące warunki geometryczne:

1) płaszczyzna P, styczna do libeli sferycznej w jej punkcie głównym, powinna być pozioma,

2) oś pionowa VV musi być prostopadła do płaszczyzny P,

3) kreska pionowa siatki celowniczej powinna leżeć w płaszczyźnie kolimacyjnej niwelatora,

4) oś libeli niwelacyjnej LL powinna być równoległa do osi celowej,

Sprawdzenie i rektyfikację niwelatora wykonujemy w kolejności warunków podanych powyżej-

Ad.1. Libele sferyczne sprawdzamy i rektyfikujemy według znanych metod

Ad 2. Po starannym spoziomowaniu niwelatora w oparciu o zrektyfikowaną libelę sferyczna oś główna niwelatora VV będzie zajmować pionowe położenie. Przy pionowy położeniu osi głównej VV niwelatora można przystąpić do sprawdzania dalszych warunków.

Ad 3. Niwelator ustawiamy na statywie i starannie poziomujemy w oparciu o zrektyfikowane libele. Na wysokości osi celowej wybieramy dobrze widoczny punkt. Celujemy poziomą nitką krzyża kresek na obrany punkt, ustawiając go w lewym skrajnym położeniu w polu widzenia. Zaciskamy śruby zaciskowe alidady. Śrubą ruchu leniwego alidady przesuwamy cel wzdłuż poziomej nitki krzyża kresek. Jeżeli punkt nie zejdzie z poziomej nitki krzyża kresek warunek jest spełniony. W przeciwnym przypadku należy krzyż zrektyfikować.

Rektyfikacja. Odkręcamy osłonę przy okularze lunety. Po zdjęciu osłony będą widoczne śruby rektyfikacyjne płytki ogniskowej, jak na rysunku.

Należy lekko zwolnić śruby (1) sprzęgające obudowę płytki ogniskowej z tubusem lunety. Obracamy płytkę ogniskową o połowę kąta wychylenia poziomej nitki krzyża od punktu celu. Następnie czynności sprawdzające wykonujemy ponownie i ewentualne wychylenie poziomej nitki krzyża korygujemy o połowę wychylenia. Czynności te wykonujemy do momentu uzyskania zadowalających efektów. Następnie należy stopniowo (np. po pół obrotu) dokręcać kolejno wszystkie cztery śruby do oporu. Realizację warunku sprawdzamy po niezależnym wycelowaniu na dobrze widoczny punkt.

Wzajemna prostopadłość kresek siatki celowniczej jest we współczesnych instrumentach zapewniona fabrycznie,

Ad 4. Metoda polowa sprawdzania warunku c l.

Sprawdzany niwelator ustawiamy w terenie i starannie poziomujemy.

W odległości około 40 u ustawiany dwie łaty w punktach A i B (rys). Ze stanowiska S₁ wyznaczamy różnicę wysokości (a₁ - b₁) nieobarczoną ewentualnym wpływem błędu nierównoległości osi c i l. Następnie ustawiamy niwelator w punkcie S₂ celując do łaty ustawionej nad punktem B, wykonujemy odczyt b₂. Znając różnicę (a₁ - b₁) wyliczamy odczyt a₂, nieobarczony błędem nierównoległości osi c i l.

Rektyfikacja: Śrubą elewacyjną naprowadzamy poziomą nitkę krzyża kresek na odczyt a₂., doprowadzając w ten sposób oś celową do poziomu. Libela niwelacyjna wyjdzie z górowania. Śrubkami rektyfikacyjnymi libeli niwelacyjnej doprowadzamy ją do górowania. Uzyskujemy w ten sposób równoległość osi c i l.

Po wykonaniu rektyfikacji instrument należy poddać ponownemu sprawdzeniu warunku równoległości osi c i l. Ewentualne odchylenia należy skorygować.

Sprawdzenie i rektyfikacja niwelatorów samopoziomujących

Przed sprawdzeniem warunków geometrycznych niwelatora samopoziomującego należy usunąć ewentualne uszkodzenie mechaniczne oraz dokonać przeglądu optyki.

W zakresie warunków geometrycznych ograniczymy się do dwóch podstawowych warunków, które powinien spełniać niwelator samopoziomujący

1) płaszczyzna głównej libeli sferycznej P musi być prostopadła do osi pionowej instrumentu VV,

2) oś celowa niwelatora, ustawiona w poziomie za pomoce kompensatora, powinna być rzeczywiście pozioma w zakresie działania kompensatora,

Ad l. Podczas obrotu niwelatora wokół osi VV pęcherzyk libeli sferycznej musi zachować symetryczne położenie w stosunku do podziału naniesionego na czaszy libeli. w przeciwnym razie libelę należy zrektyfikować za pomocą trzech śrub rektyfikacyjnych według powszechnie znanej metody,

Ad 2, Sprawdzenie warunku osi celowej wykonujemy jak sprawdzenie warunku 4 niwelatora libelowego.

Rektyfikacja: poziomą nitkę krzyża kresek przesuwamy na obliczony odczyt a₂, za pomocą śrub rektyfikacyjnych krzyża kresek. Naprawę tego warunku wykonujemy poprzez przesuwanie krzyża nitek prawie we wszystkich powszechnie używanych niwelatorach samopoziomujących, z wyjątkiem niwelatorów firmy Filotecnica oraz GK 1-A i GK 1-AC firny Kern, a także niwelatora NA2 firmy Wild,

• obracając płytkę wejściowe w niwelatorach firmy Filotecnica,

• przesuwając jeden z elementów optycznych kompensatora - w GK 1-A i GK 1-AC.

• zmieniając współczynnik kompensacji, na przykład w niwelatorze NA 2.

Zrektyfikowany niwelator należy skontrolować, czy przy spoziomowanej libeli sferycznej kompensator działa prawidłowo.

Przed przystąpieniem do realizacji warunku drugiego należy sprawdzić prawidłowe działanie wahadła, to znaczy czy nie jest ono uszkodzone lub nie opiera się o jeden z amortyzatorów. Niwelator ustawiamy na trwałym podłożu. Po starannym spoziomowaniu niwelatora ze pomocą zrektyfikowanej libeli sferycznej kompensator powinien zajęć pozycję swobodnego zawieszenia. Sprawdzamy to stukając lekko w obudowę niwelatora. Wówczas obraz siatki celowniczej niwelatora, oglądany przez okular, powinien drgać.

Sprawdzenie i rektyfikacja niwelatora precyzyjnego

Niwelator precyzyjny charakteryzuje;

• wyższa dokładność libel, zwłaszcza libeli niwelacyjnej,

• dokładniejszy skok gwintu śrub poziomujących,

• lepsza optyka lunety,

• cieńsze kreski siatki celowniczej, których kształt umożliwia symetryczne ich ustawianie względem znaczka na łacie,

• dokładniejszy sposób odczytywania podziału łaty.

Podziały łat stosowanych w niwelacji precyzyjnej są także dostosowane do przedstawionych wyżej wymogów. Na białym tle specjalnej taśmy inwarowej niepodlegającej wpływom temperatury i wilgotności, umieszczonej-w drewnianej oprawie łaty, naniesiony jest podwójny podział kreskowy o grubości kresek 1 mm. Na łatach firm Carl-Zeiss-Jena i Kern podział jest półcentymetrowy, a na łatach firmy Wild naniesiony jest podział centymetrowy. Dwa niezależne podziały na każdej łacie przesunięte są względem siebie o 2.5 mm, w podziale półcentymetrowym lub o 5 mm w podziale centymetrowym. Numeracja podziału naniesiona jest na drewnianej części łaty i składa się z dwóch niezależnych opisów różnych o pewną stałą wartość. Na łatach firmy Zeiss-Jena różnica pomiędzy odczytem wynosi 606500 zaś podziały łat firmy Wild różnię się o 301550.

Przesunięcie podziałów na taśmie inwarowej oraz stała różnica opisów łaty stwarzają możliwość dokonania dwóch niezależnych odczytów przy jednym wycelowaniu. Zmienia się tylko położenie siatki celowniczej, co uzyskuje się ruchem pokrętła mikrometru.

W zależności od sposobu realizacji poziomego położenia osi celowej niwelatory precyzyjne mogę być libelowe lub samopoziomujące. Niezależnie- jednak od powyższego rozwiązania zasada odczytywania podziału łaty jest analogiczna.

Przed obiektywem lunety niwelatora precyzyjnego umieszczona.jest płytka płaskorównoległa P, połączona z mikrometrem M (rys). Obrót mikrometru powoduje zmianę położenia płytki, co w efekcie daje pozorne przesunięcie osi celowe; w płaszczyźnie pionowej. Liniowa wielkość tego przesunięcia (np. x) jest odczytywana na mikrometrze,-

Przykłady odczytu, -

1. Łata firmy Zeiss Jena z podziałem półcentymetrowym:

odczyt z łaty- 19.7 m/20

odczyt z mikrometru 0.034 m/20

O = 19.734 m/20 w podziale łaty
po podzieleniu przez 20, O = • 0.9867 w podziale metr.

2. Łata firmy Wild z podziałem centymetrowym

odczyt z łaty 1.48

odczyt z mikrometru 653

O = 1.48653 m

Precyzyjny niwelator libelowy

Sprawdzenie i ewentualna rektyfikacja libelowego niwelatora precyzyjnego obejmuje następujące czynności;

1. Sprawdzenie libel alidadowych zapewniających pionowe położenie osi głównej (obrotu) niwelatora.

2. Sprawdzenie i realizacja warunku równoległości osi celowej c do osi libeli niwelacyjnej l.

3. Sprawdzenie i ewentualne usuniecie wichrowatości osi celowej c i osi libeli niwelacyjnej l.

4. Badanie stałości osi celowej niwelatora,

Ad. l. Libele alidadowe sprawdzamy i rektyfikujemy według znanych zasad

Ad, 2. Warunek równoległości osi celowej c do osi libeli niwelacyjnej można sprawdzić i realizować metodą polową

Firma Carl-Zeisa Jena zaleca wprowadzić do korygowanego odczytu poprawkę k ze względu na krzywiznę Ziemi i zjawisko refrakcji. Dla szerokości geograficznej 50 i k = 0,13 łączna poprawka k wyraża się wzorem

gdzie; k - łączna poprawka ze względu na krzywiznę Ziemi i zjawisko refrakcji,

Realizacja warunku c||l odbywa ale następująco: na mikrometrze nastawiamy końcowe część odczytu a₂. czyli 63. Podczas tej czynności kreska celownicza przesunie się względem znaczka na łacie. Położenie symetryczne znaczka opisanego (w naszyć przykładzie) 38,1 i kreski celowniczej uzyskamy powtórnie ruchem śruby elewacyjnej niwelatora. Po tej czynności oś celowa zajmie położenie poziome, natomiast pęcherzyk libeli niwelacyjnej wychyli się, Doprowadzany go do położenia środkowego pionowymi wkrętami rektyfikacyjnymi (1) libeli niwelacyjnej.

Firma Wild pomija przy realizacji tego warunku poprawkę k, natomiast proponuje ustawiać rektyfikowany niwelator nad punktem S, w odległości 1/10 AB i koryguje z tego tytułu odczyt a₂ o 1/10 wyznaczonego błędu.

Ad. 3. Często zdarzę się, że mino realizacji warunku równoległości osi c i l nie są one w przestrzeni równoległe lecz skrzyżowane pod pewnym kątem. Błąd ten nazywa się wichrowatością osi celowej i osi libeli niwelacyjnej. Zjawisko wichrowatości przedstawiono na rysunku.

Widzimy, ze w takim przypadku rzuty osi c i l na płaszczyznę pionowe (YZ) są równoległe, czyli c||l. Natomiast rzuty tych osi na płaszczyznę poziome (xy) nie są wzajemnie równoległe, czyli c nierównoległe do l.

Ślady osi celowej i osi libeli niwelacyjnej na płaszczyźnie poziomej przecinają się i tworzę kąt .

Aby wykryć wichrowatość osi celowej l osi. libeli, należy niwelator ustawić w stosunku do dowolnego punktu, na przykład łaty niwelacyjnej tak, jak na rysunku

Dwie śruby poziomujące, np. (2), (3) wyznaczają prostą równoległa do osi celowej. Po spoziomowaniu instrumentu pęcherzyk libeli niwelacyjnej zajmie położenie środkowe. Następnie. pokręcając śruba poziomująca (l), przechylany niwelator względem prostej wyznaczonej przez śruby (2-3) i wtedy oś główna wychyli się w płaszczyźnie pionowej o pewien kąt. W przypadku występowania błędu wichrowatości osi, c i l pęcherzyk wyjdzie z położenia środkowego. Śrubą poziomującą (l) wykonujemy obroty w przeciwnym kierunku i wtedy zaobserwujemy ruch pęcherzyka libeli także w przeciwnym kierunku, W wyniku tych czynności zostało stwierdzone zjawisko wichrowatości. Wychylania niwelatora można także zaobserwować po uprzednia wycelowaniu środkiem siatki kresek niwelatora do podziałki na łacie.

Błąd ten usuwany w ten sposób, że przy wychylonej osi głównej niwelatora sprowadzamy pęcherzyk libeli niwelacyjnej do położenia środkowego poziomymi wkrętami rektyfikacyjnymi (2) libeli niwelacyjnej. Czynność powyższą dla kontroli powtarzamy. Po usunięciu błędu wichrowatości należy jeszcze raz sprawdzić warunek c||l podana w punkcie 2, ponieważ podczas usuwania wichrowatości zwolniono lekko wkręty pionowe

Ad. 4. Z definicji osi celowej wynika, że jest to prosta wyznaczona przez środek optyczny obiektywu i środek- siatki krasek płytki ogniskowej. Wiadomo jednak, że prosta ta przechodzi także przez środek optyczny soczewki ogniskującej, która jest elementem ruchomym w układzie optycznym lunety niwelatora. Zmienne położenie soczewki ogniskującej może spowodować niestałość osi celowej, wpływając bezpośrednio na odczyt. Zjawisko to może mieć uchwytny wpływ na wyniki pomiaru, w związku z czym niwelator precyzyjny należy przebadać dla przekonania się, czy odpowiada on swoim założonym wymaganiom.

Badanie stałości osi celowej niwelatora precyzyjnego można przeprowadzić bazie polowej.

Dalmierz elektromagnetyczny
Stosując w pomiarach odległości dalmierze elektromagnetyczne musimy uwzględniać wpływy błędów przypadkowych i systematycznych, które obciążają wyniki tych pomiarów. Ogólnie można powiedzieć, że błędy te związane są z samym dalmierzem oraz z wpływem środowiska na sygnał pomiarowy. Te ostatnie zostały omówione na poprzednim wykładzie.

Wyróżnić można następujące błędy instrumentalne:

• Błąd przypadkowy

• Błąd systematyczny niezależny od odległości

• Błąd systematyczny zależny liniowo od odległości

• Błąd systematyczny zależny nieliniowo od odległości

• Błąd cykliczny

• Błąd zależny od temperatury

• Błąd zależny od czasu

• Błąd zależny od napięcia zasilania

Charakterystyka błędów przypadkowych i systematycznych niezwiązanych z instrumentem:

• Błędy centrowania instrumentu i reflektora nad lub pod znakami pomiarowymi

• Błąd poziomowania dalmierza i lustra

• Błąd wycelowania:
  a) dalmierza na lustro
  b) lustra w kierunku dalmierza

• Błąd popełniany przy pomiarach nasadką dalmierczą

• Błąd pomiaru temperatury, ciśnienia i wilgotności na drodze sygnału pomiarowego

• Błąd pomiaru lub zaniechania wprowadzenia którejś z poprawek do długości

• Błędy wynikające z odbicia sygnałów pomiarowych od obiektów będących w tle reflektora

• Błędy wywołane turbulencją atmosferyczną

• Błąd zależny od czasu pomiaru i związany z różną ilością pomiarów przejść fazowych

Celem komparacji jest wyznaczenie błędów systematycznych pochodzenia instrumentalnego, które mogą być wyeliminowane z pomiarów poprzez wprowadzenie do nich poprawek wyznaczonych w procesie komparacji.

W praktyce wyznacza się trzy rodzaje poprawek:
1. Poprawkę stałej dodawania k
2. Poprawkę ze względu na zmianę częstotliwości wzorcowej od jej wartości nominalnej
3. Poprawkę ze względu na błąd cykliczny, która może występować tylko w dalmierzach fazowych

Ad.1 Poprawka stałej dodawania k
Ogólny wzór na obliczenie odległości pomierzonej dalmierzem wygląda następująco:

Stała k łączy ze sobą wpływ różnicy między centrem mechanicznym dalmierza, a jego centrem elektronicznym. Najczęściej wartość stałej k wyznacza się na krótkim odcinku poprzez porównanie odległości pomierzonej i długości wyznaczonej inną metodą, zazwyczaj o rząd dokładniejszą. Odcinek, na którym wykonywane są pomiary powinien mieć około 5-10 metrów. Wartość stałej dodawania obliczamy wówczas ze wzoru:

Pewniejszym sposobem wyznaczenia stałej k jest pomiar odległości 2-3 odcinków o długościach różniących się o 1-2 metry. Najlepiej, jeżeli są to np. odcinki odpowiednio w odległości 10,12 i 15 metrów od instrumentu.

Jeżeli nie znamy długości odcinka z dokładnością o rząd wyższą możemy zastosować inną metodę wyznaczania stałej k. Polega ona na pomiarze długości odcinka AB, na który wtycza się dodatkowo punkt C. Przedstawione to zostało na rysunku obok.

Rys.1 Sposób wykonania bazy pomiarowej

Mierzymy w dwóch kierunkach odcinki AC, CB i AB. Możemy wówczas zapisać prostą zależność łączącą wyniki pomiarów i stałą k dalmierza:

(AC+k)+(CB+k)=AB+k

Z czego po uproszczeniu otrzymujemy wzór na stałą dodawania k:

k=AB-(AC+CB)

 

Ad.2 Wyznaczenie błędu cyklicznego

Błąd cykliczny wynika z tzw. sprzężeń pasożytniczych występujących między częścią nadawczą a częścią odbiorczą dalmierza. Na sygnał powracający nałożony jest niejako sygnał zakłócający o tej samej częstotliwości. Błąd cykliczny pojawia się także w elektrycznym przesuwniku fazy.
Wartość błędu cyklicznego określamy w następujący sposób. Tworzymy bazę AB, na którą wytyczamy punkt C. Odcinek CB powinien być równy lub trochę dłuższy od połowy długości „przymiaru” podstawowego? dalmierza. Odcinek ten należy podzielić na dziesięć równych

części, których długość równa jest
. Pomiary dalmiercze na tej bazie wykonujemy tylko na podstawowej częstotliwości wzorcowej. Obliczamy odchyłki długości pomierzonych od ich nominalnych wartości określonych z o rząd większą dokładnością. Jeżeli odchyłki te dla wszystkich długości są podobne to wartość ta jest stałą dodawania k dalmierza a błąd cykliczny nie występuje. Wówczas, gdy odchyłki są różne rysujemy wykres, na którym przedstawiamy zmiany. Na poniższym rysunku znajduje się przykład takiego wykresu. Służy on do określania poprawek długości dla różnych długości z tytułu błędu cyklicznego.

Rys.3 Wykres będący wynikiem wyznaczenia poprawek z tytułu błędu cyklicznego

Ad.3 Błąd zmiany częstotliwości

Pod wpływem różnych czynników, głównie jednak na skutek starzenia się kwarcu, częstotliwość wzorcowa dalmierza ulega zmianie. Powoduje to zmianę skali mierzonych nim długości. Możemy to zapisać następująco:

gdzie:
-zmiana częstotliwości wzorcowej

-częstotliwość wzorcowa nominalna(znana jest z metryki)

-częstotliwość wzorcowa w czasie pomiaru

W procesie komparacji chodzi, zatem o wyznaczenie wartości Δf. Wykonuje się to poprzez porównanie aktualnej częstotliwości wzorcowej dalmierza f_wp z częstotliwością wytwarzaną przez odpowiedni generator. Tego rodzaju bezpośredni pomiar wykonuje się w laboratoriach odpowiednich instytucji. Komparację częstotliwości można realizować także w warunkach polowych przez porównanie aktualnej jej wartości z tzw. krajowym wzorcem częstotliwości fal radiowych emitowanych regularnie przez niektóre radiostacje. Poprawkę z tytułu zmian częstotliwości podaje Polskie Radio codziennie o 12:00.

Obowiązujące przepisy nakładają na użytkowników dalmierzy obowiązek ich okresowej kontroli. W jej wyniku dalmierz uzyskuje tzw. Metrykę. Do wykonywania kontroli, którą nazywamy komparacją dalmierza zostały upoważnione w Polsce Instytut Geodezji i Kartografii w Warszawie oraz kilka instytucji, które założyły i utrzymują tzw. Komparatory polowe. Komparatory polowe są to zbiory punktów zastabilizowanych w terenie w linii prostej w postaci postumentów betonowych., których trzon osadzony jest poniżej poziomu zamarzania gruntu. Długości baz takich komparatorów osiągają wartość 1,5 kilometra, a długości odcinków zawarte w tym zakresie wahają się od kilku do kilkunastu metrów. Odcinki komparatorów są wyznaczane i znane z dokładnością o rząd większą niż posiadają badane na nich instrumenty.

8.Zjawiska wywołujące błędy pomiarowe towarzyszące pomiarom bezpośrednim

• zakrzywienie ziemi

• refrakcja

• wibracja powietrza

• refrakcja różnicowa

• temperatura, wilgotność, ciśnienie, gęstość

• refrakcja boczna

• jednostronne oświetlenie sygnałów o kształcie cylindrycznym

• wpływ słońca na pęcherzyk libelli

• silne wiatry

• odległość od celu i tło sygnału zmniejszające zasięg widoczności

• przeszkody pomiędzy sygnałem a teodolitem, obcinające część wiązki promieni

• osiadania statywu i sprzętu pomiarowego w czasie pomiaru

Pomiary bezpośrednie są najprostsze - polegają wprost na porównaniu danej wielkości z odpowiednią miarą wzorcową np. pomiar wymiarów ciała za pomocą linijki, suwmiarki, śruby mikrometrycznej itp., pomiar czasu trwania jakiegoś procesu przy użyciu stopera, pomiar natężenia prądu amperomierzem.

Różnicę pomiędzy wynikiem pomiaru, a rzeczywistą wartością mierzonej wielkości nazywamy błędem pomiaru. Błędy pomiarów tradycyjnie dzielimy na grube (omyłki), przypadkowe oraz systematyczne.

Błędy grube powstają zwykle na skutek nieuwagi lub niestaranności obserwatora przy odczytywaniu lub zapisywaniu wyników lub w wyniku nagłej zmiany warunków pomiaru (np. wstrząsy). Jeśli mamy serię pomiarów wyniki obarczone błędem grubym są łatwe do wykrycia i usunięcia.

Błędy systematyczne wynikają z niedoskonałości przyrządów i metod pomiarowych. Można je redukować stosując bardziej doskonałe i precyzyjne metody i przyrządy, jednak całkowite wyeliminowanie błędów systematycznych jest niemożliwe. Rozpoznane błędy systematyczne należy uwzględniać poprzez wprowadzenie odpowiednich poprawek do wyniku, np. kiedy ważymy na wadze, której wskazanie bez obciążenia wynosi m₀ zamiast 0 to m₀ jest błędem systematycznym, który należy odjąć od wyniku ważenia, innym typowym przykładem jest poprawka na opór wewnętrzny woltomierza przy pomiarze napięcia .

Z błędami przypadkowymi mamy do czynienia zawsze. Wynikają one z różnych przypadkowych i nie dających się uwzględnić czynników (np. wahania temperatury, lub ruch powietrza w pobliżu przyrządu pomiarowego). Inną przyczyną może być niezgodność przyjętego modelu z obiektem mierzonym - np. gdy mamy zmierzyć średnicę pręta, zakładamy milcząco, że jest on idealnym walcem, co nie jest prawdą. O istnieniu błędów przypadkowych świadczy niepowtarzalność wyników pomiaru jednej i tej samej wielkości. Błędy przypadkowe redukuje się poprzez wielokrotne powtarzanie pomiaru - zachodzi wówczas częściowa kompensacja przypadkowych zawyżających i zaniżających odchyłek wyniku.

9.Mapy do celów projektowych i do celów prawnych.

Mapa co celów prawnych:

* Mapa do celów prawnych jest dokumentem, na podstawie którego notariusz może dokonywać umów.

* Mapa ta często powstaje po zakończeniu inwestycji.

* Na podstawie mapy prawnej dochodzi do podpisania dokumentu upoważniającego inwestora do wejścia w inwestycje, czasami nadaje się jej w umowie numer.

Mapa w swej treści powinna zawierać:

1.granice nieruchomości-istniejące i projektowane,

2.granice działek,

3.numery według ewidencji gruntów i budynków,

4.nazwy i numery ksiąg wieczystych, Zbiorów dokumentów lub ksiąg hipotecznych

5.miary czołowe,

6.nazwy ulic i numery porządkowe nieruchomości,

7.numery ewidencyjne i oznaczenia ksiąg wieczystych dla nieruchomości sąsiednich,

8.budynki i ogrodzenia trwałe,

9.oznaczenia klas i użytków dla gruntów rolnych.

Opracowuje się ją:

1.w skali mapy zasadniczej lub mapy ewidencji gruntów;

2.w formatach odpowiadających wielokrotności arkusza A-4,

3. W dwóch kolorach; czarnym dla treści istniejącej, czerwonym dla elementów projektowanych,

4.stosując znaki konwencjonalne określone w instrukcji K-1.

Mapa do celów projektowych:

Treść mapy do celów projektowych powinna zawierać elementy stanowiące treść mapy zasadniczej oraz aktualne informacje o wszystkich danych ewidencyjnych odnoszących się zarówno do obszaru projektowanego terenu inwestycji, jak i do obszaru otaczającego ten teren w pasie co najmniej 30 metrów. Sporządzana jest przez jednostki wykonawstwa geodezyjnego. Zazwyczaj mapę taką wykonuje się w skali 1:500

10.Klasyfikacja osnów realizacyjnych oraz osnów budowlano-montażowych.

Osnowa realizacyjna jest to osnowa geodezyjna przeznaczona do wykonywania pomiarów realizacyjnych

Osnowę realizacyjną poziomą i wysokościową dzieli się na:

1) podstawową - Podstawowa osnowa realizacyjna służy do powiązania tyczonego obiektu z otaczającym go terenem i jego uzbrojeniem, wyznaczenia szczegółowej osnowy realizacyjnej oraz w miarę możliwości - do bezpośredniego wykonywania pomiarów realizacyjnych.
Podstawowa osnowa realizacyjna powinna być nawiązana geodezyjnie do punktów wcześniej nałożonych w sposób umożliwiający prawidłowe określenie nowych punktów w państwowym układzie współrzędnych lub wysokości

2) szczegółową - Szczegółowa osnowa realizacyjna służy do bezpośredniego oparcia pomiarów realizacyjnych

a) Osnowa podstawowa- osnowa realizacyjna

b)Osnowa szczegółowa- osnowa budowlano- montażowa

(często zakładane niezależnie )

Pod względem geometrii osnowy realizacyjne dzieli się na :

• Osnowy dowolnego kształtu” swobodne”- punkty położone w większości na zewnątrz obszaru obiektu z sygnalizacją ziemną, wieżową albo ścienną służą do zapewnienia możliwości tyczenia przy wykorzystaniu grupy wielu punktów z użyciem tachimetru z odpowiednim oprogramowaniem

• Sieci regularne-punkty nie ułożone w układzie regularnym, jednak ściśle powiązane z układem osi komunikacyjnych i montażowych obsługiwanego obiektu, wymagające tyczenia szczegółowego, w celu uproszczenia późniejszych prac życzeniowych

• Sieci regularne- punkty rozmieszczone regularnie w układzie prostokątnym, stabilizowane znakami ziemnymi z płytkami trasowania, wymagającej tyczenia szczegółowego

• Układ linii pomiarowych (baz)-zbiór linii pomiarowych, których końce lub przecięcia powiązane są układem obserwacji kątowo-liniowej sieci powierzchniowej, wymagającej tyczenia szczegółowego

• Osnowy liniowe (wydłużone)-konstrukcja geometryczna wyraźnie wydłużona np. ciąg poligonowy

Osnowa budowlano-montażowa:

1) osnowa w układzie lokalnym powiązana z punktami osiowymi

2) osnowa dowiązana do osnowy państwowej

13.Badanie geometrii układu torowego oraz ustroju suwnicy.

Budowa i podział suwnic:

1. suwnice bramowe (portalowe) charakteryzują się tym że konstrukcja nośna w kształcie bramy porusza się po torze ułożonym bezpośrednio na podłożu, a ładunek przenoszony jest w przestrzeni miedzy szynami i na wysokość portalu. Suwnice te stosuje się głównie w rozległych składowiskach surowców, nabrzeżach portowych, na miejscach montażu dużych i ciężkich konstrukcji

2. suwnice półportalowe -ze względu na różnicę wysokości szyn toru jezdnego stosuje się głównie jako przyścienne. Jedna szyna ułożona jest bezpośrednio na podłożu, druga natomiast - połozona - wyżej - spoczywa na ścianie lub na belkach ułożonych na wspornikach słupów. Ten sposób rozwiązania stosuje się w hutach i rozległych halach.

3. Suwnice wspornikowe- to takie których obie szyny umieszczone są na wspornikach ściennych. Stosowane SA do nie wielkich ciężarów

4. suwnice pomostowe (mostowe) - sa najbardziej rozpowszechnione, stosowane na wolno stojących estakadach lub halach, gdzie wykorzystuje się konstrukcje nośną hali. Szyny takiej suwnicy są na specjalnych belkach podsuwnicowych , które podparte są na wspornikach słupow konstrukcyjnych

Podstawowe wymagania geometryczne w stosunku do toru suwnicy:

Do prawidłowej pracy suwnicy niezbędne jest aby:

• szyny toru stanowiły elementy prostoliniowe

• toki szyn były oddalone od siebie w płaszczyźnie poziomej i pionowej o wielkości ustalone w projekcie suwnicy

• szyny i belki ułożone były w odpowiednich odległościach od elementow konstrukcji nosnej hali lub estakady oraz innych urządzeń , szczególnie elektrycznych

• część toczna szyny miała określony wymiar i ułożenie przestrzenne(nachylenie)

wartości dopuszczalnych odchyłek od badanych parametrów geometrycznych:

- różnica miedzy rzeczywistym i teoretycznym rozstawem osi szyn dla torów suwnicy-rostaw nominalny

- odchyłki od prostoliniowości

- przechyłka (różnica poziomów głowek szyn)

- pochylenie podłużne szyn

- przesunięcie główek szyn na styku (poziome i pionowe)

Aby prawidłowo dokonać inwentaryzacji toru należy określić:

• początek i koniec toru

• miejsca podparcia szyn i punkty miedzy nimi

• styki szyn

• miejsca wyraźnych wyboczeń i obniżeń szyn

16. Metody wyznaczania przemieszczeń obiektu inżynierskiego. (mam nadzieje ze to o takie metody chodziło) - żywcem z ksiazki Prószka i opracowan pytan do egzaminu

Metoda obliczania przemieszczeń - ciąg przetworzeń wyników pomiarów obejmujący:

• sprawdzenie poprawności materiału obserwacyjnego i wprowadzenie ewentualnych korekt;

• znalezienie bazy odniesienia i zdefiniowanie układu dniesienia;

• obliczenie w tym układzie składowych wektorów przemieszczeń punktów kontrolowanego obiektu i ich charakterystyk dokładnościowych;

• ocenę istotności przemieszczeń;

Dla różnych metod mamy do czynienia różnymi sposobami realizacji wymienionych etapów.

Metoda różnic obserwacji (metoda różnicowa)- metoda obliczania przemieszczeń punktów na podstawie różnic odpowiadających sobie obserwacji w dwu pomiarach okresowych.

Metoda różnic obserwacji:

- dla każdej obserwacji w (t) musi istnieć odpowiednik w (t');

- musi być zachowana struktura sieci kontrolnej - te same punkty (fizycznie) oraz ten sam układ wiążących je operacji;

- zalecana jest także zbliżona dokładność pomiarów w (t) i (t');

Metodę tę można stosować po wybudowaniu obiektu, gdy teren wokół jest uporządkowany. W czasie budowy metoda ta nie powinna być wykorzystywana, gdyż punkty mogą łatwo ulec zniszczeniu lub przesunięciu.

Metoda różnic współrzędnych - metoda obliczania przemieszczeń punktów na podstawie różnic między współrzędnymi tych punktów wyznaczonymi w tym samym układzie odniesienia, odrębnie na podstawie każdego z dwu pomiarów okresowych.

Metoda różnic współrzędnych

- wyrównaniu podlegają oddzielnie obserwacje z pomiaru (t') i (t), dopiero na ich podstawie obliczamy przemieszczenia;

- nie jest konieczne dokładne odtworzenie geometrii sieci w (t') i (t);

Metoda wyrównania łącznego - metoda obliczania przemieszczeń punktów w jednym procesie wyrównawczym na podstawie wyników dwu bądź więcej pomiarów okresowych.

18. Precyzyjne techniki pomiarowe w tzw. pomiarach względnych

19. Projektowanie tras komunikacyjnych w ujęciu geodezyjnym, krzywe przejściowe.

Geodezyjne opracowanie projektu trasy komunikacyjnej jest to zespół czynności, mających na celu określenie danych geodezyjnych, potrzebnych do wyznaczenia w terenie położenia projektowanej osi trasy i innych elementów trasy, w stosunku do osnowy geodezyjnej.

Danymi geodezyjnymi będą zarówno współrzędne x, y, wysokość H oraz odpowiednie długości d i kąty α od punktów osnowy do punktów wyznaczanych, położonych na odcinkach prostoliniowych i krzywoliniowych trasy.

W celu zlokalizowania w terenie osi trasy, trzeba ją opracować w układzie współrzędnych mapy, na której wykonano projekt. Przy uzyskiwaniu danych geodezyjnych stosuje się metodę analityczno - graficzną. Punkty osnowy geodezyjnej są podstawą wyznaczenia w terenie punktów projektowych i one mają współrzędne obliczone analitycznie. Niektóre punkty projektu również określa się analitycznie, jednak większość punktów projektowych określa się graficznie. Graficznie określa się też niektóre miary liniowe, z kolei miary kątowe określa się analitycznie, ze względu na zbyt małą dokładność metody graficznej.

Dokładność obliczeń w geodezyjnym opracowaniu projektów jest zależna od dokładności wyznaczania w terenie poszczególnych elementów opracowania - w praktyce dokładności obliczeń są regulowane instrukcjami GUGiKu lub instrukcjami i przepisami resortowymi.

Końcowym efektem geodezyjnego opracowania projektu trasy jest szkic dokumentacyjny projektu, który jest podstawą wyznaczenia w terenie przebiegu osi trasy. Zawiera on oś trasy, punkty osnowy geodezyjnej oraz wszystkie wymiary i miary potrzebne do wytyczenia trasy. Sposób zapisu miar na szkicu wyznacza metodę tyczenia trasy w terenie.

Do wyznaczenia w terenie poszczególnych punktów projektu trasy stosuje się metody:

• prostokątną

• biegunową

• wcięć liniowych

• wcięć kątowych w przód

• przecięcia prostych

Do kontroli wyznaczenia w terenie poszczególnych punktów projektu powinno się stosować dwie różne metody.

Krzywe przejściowe.

Zadaniem krzywych przejściowych jest stopniowe przeprowadzanie pojazdu z prostej w łuk i na odwrót lub też z jednego łuku w inny. Gdyby nie stosować krzywej przejściowej, to działanie siły odśrodkowej spowoduje boczne uderzenie pojazdu przy wjeździe z prostej na łuk.

Ze względu na warunki dynamiczne ruchu największe zastosowanie na trasach znalazły klotoida (trasy drogowe) i parabola stopnia trzeciego (trasy kolejowe). W mniejszym zakresie, na skrzyżowaniach i węzłach miejskich oraz przy zjazdach z autostrad, stosuje się takie krzywe jak: lemniskata, sinusoida, elipsa, parabola stopnia drugiego, spirala logarytmiczna, łuki koszowe czy krzywa Pawłowicza.

24. UKŁADY WSPÓŁRZĘDNYCH PŁASKICH

Układ współrzędnych 2000 (2000 r)

Dla opracowań katastralnych i przy opracowaniu mapy zasadniczej w skali 1:5 000 i skalach większych stosuje się odwzorowanie Gaussa-Krügera tworzące cztery układy współrzędnych płaskich prostokątnych, oznaczone symbolami: "2000/15", "2000/18", "2000/21" i  "2000/24",  w systemie GRS-80.

Współrzędne płaskie prostokątne x, y są obliczane w odwzorowaniu Gaussa-Krügera w pasach trzystopniowych o południkach osiowych:15°, 18°, 21°, 24°. Pasy ponumerowane są: 5, 6, 7, 8 (rys.13). Współczynnik zmiany skali równa się 0,999923 w południku osiowym.

Początkiem układu współrzędnych w danym pasie odwzorowania jest punkt przecięcia się obrazu południka osiowego z obrazem równika. Przy określaniu współrzędnych -  współrzędna x pozostaje nie zmieniona, a do współrzędnej y w zależności od południka osiowego dodaje się np. 5 500 000 m przy południku Lo = 15°, Pierwsza cyfra współrzędnej y oznacza numer pasa odwzorowania.

Najważniejsze cechy:

• elipsoida GRS-80

• odwzorowanie Gaussa-Krügera

• cztery 3-stopniowe pasy odwzorowawcze dla południków 15°, 18°, 21°, 24°

• skala m0 = 0.999923,

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

• obowiązuje od 8.08.2000 r

• dla mapy zasadniczej

Układ ten realizuje kompromis w rozłożeniu zniekształceń liniowych; od -7,7 cm/km na południku środkowym strefy do maksymalnie około +7 cm/km na brzegu strefy.

Układ współrzędnych 1992 (2000 r)

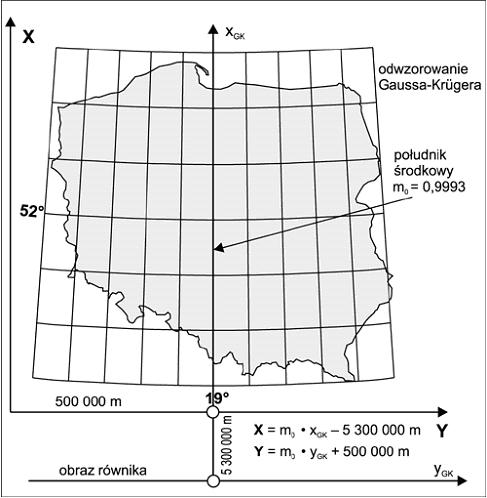
Dla map topograficznych w skali 1:10 000 i mniejszych stosuje się jeden układ dla całego kraju"1992/19" (rys. poniżej ), w systemie GRS 80.

Najważniejsze cechy:

• elipsoida: GRS-80

• odwzorowanie: Gaussa-Krügera

• jeden pas odwzorowawczy dla całej Polski L0 = 19°

• skala m0 = 0.9993,

• X = x - 5 300 000 m, Y = y + 500 000 m

• obowiązuje od 8.08.2000 r

• dla map w skalach 1:10 000 i mniejszych

Dla wyznaczania wysokości w systemie odniesień przestrzennych "1992" stosuje się system wysokości normalnych "Kronsztad 86", w którym zostały określone wysokości punktów podstawowej i szczegółowej osnowy geodezyjnej kraju.

Ze względu na znaczne zniekształcenia liniowe układ nie jest rekomendowany do wielkoskalowych opracowań kartograficznych.

Układ współrzędnych GUGIK 80 (1980 r)

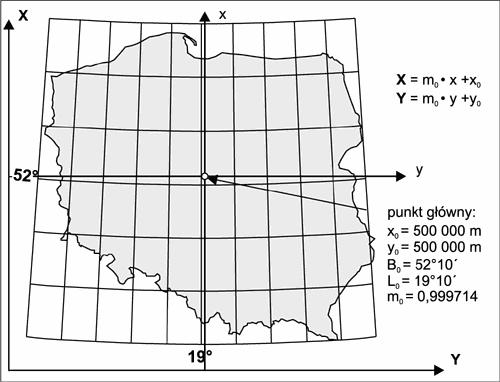
Najważniejsze cechy:

• elipsoida: Krasowskiego

• punkt przyłożenia: Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry ( A = 121°40'38.79'')

• odwzorowanie quasi-stereograficzne (Roussilhe'a)

• punkt główny: B = 52°10?, L = 19°10?;

• m0 = 3499/3500, r0 = 215 km

• X0 = 500 000, Y0 = 500 000

Układ współrzędnych 1965 (1965 r)

Układ współrzędnych "1965" wprowadzony został do opracowań kartograficznych przeznaczonych dla potrzeb gospodarczych w roku 1968

Rozporządzeniem Rady Ministrów z dnia 8 sierpnia 2000 r. w sprawie państwowego systemu odniesień przestrzennych układ "1965", oraz lokalne układy współrzędnych mogą być stosowane do dnia 31 grudnia 2009 r.

Najważniejsze cechy

• 
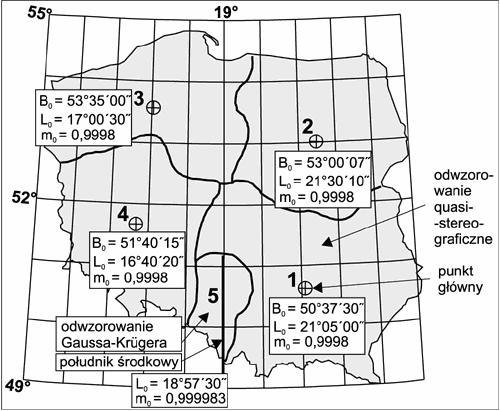
  elipsoida: Krasowskiego

• punkt przyłożenia:  Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry (A = 121°40'38.79'')

• 5 stref odwzorowawczych:

• w strefach I - IV odwzorowanie quasi-stereograficzne (Roussilhe'a),

• w strefie V odwzorowanie Gaussa-Krügera

• w strefach I - IV skala m0 = 0.9998, r0 = 178.7 km

Mapy sporządzone w państwowym układzie współrzędnych płaskich prostokątnych "1965" nie posiadają siatki kartograficznej. Sporządzone są one w prostokątnym podziale arkuszowym.

układ współrzędnych 1942 (1952 r)

Wprowadzony na podstawie uchwały Prezydium Rządu w 1953 r. w sprawie założenia jednolitej państwowej sieci geodezyjnej i opracowania mapy podstawowej państwa. Uchwała ta zobowiązywała do opracowania i wydania mapy topograficznej w skali 1:25 000 (mapa ta została wykonana dla całego kraju w ciągu 6 lat). Kolejna uchwała Prezydium Rządu, podjęta w 1955 r., zobowiązywała do opracowania mapy topograficznej w skali 1:10 000.

Najważniejsze cehy:

• elipsoida: Krasowskiego

• punkt przyłożenia: Pułkowo (B = 59°46'18.55'', L = 30°19'42.09'')

• azymut orientacji: Pułkowo - Bugry (A = 121°40'38.79'')

• odwzorowanie: Gaussa-Krügera

• dwa 6-stopniowe pasy odwzorowawcze dla południków 15°, 21°

• skala m0 = 1

• X = x, Y = y + (3 500 000, 4 500 000) m

• cztery 3-stopniowe pasy odwzorowawcze dla południków środkowych 15°, 18°, 21°, 24°

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

Przy pomiarach wysokościowych przyjmujemy geoidę Kronsztadzką (teoretyczny poziom Morza Bałtyckiego w Kronsztadzie).

W państwowym układzie współrzędnych płaskich prostokątnych "1942" opracowane zostały mapy topograficzne w skalach 1:25 000, 1:50 000, 1:100 000, 1:200 000, 1:500 000.

Mapy te sporządzone są w odwzorowaniu Gaussa-Krügera. Jest to równokątne poprzeczne odwzorowanie elipsoidy obrotowej na pobocznice walca, przy czym środkowy południk obszaru, zwany też południkiem osiowym, odtwarza się wiernie.

Mapy topograficzne sporządzone w układzie współrzędnych płaskich prostokątnych 1942 mają siatkę kartograficzną i siatkę kilometrową. Arkusze map topograficznych są sporządzane w podziale na sekcje trapezowo-elipsoidalne, przy czym linie podziału pokrywają się z obrazami równoleżników i południków.

Układ współrzędnych Borowa Góra (1920 r)

Opracowany przez Wojskowy Instytut Geograficzny (WIG) w 1936 roku. Obowiązywał do lat 50-tych, do momentu wprowadzenia układu "1942".

 Najważniejsze cechy:

• elipsoida: Bessela

• punkt przyłożenia: Borowa Góra (B = 52°28'32.85'', L = 21°02'12.12'')

• azymut orientacji: Borowa Góra - Modlin (A = 261°53'15.90'')

• odwzorowanie: Roussilhe'a

• skala m0 = 1

• pięć 2-stopniowych pasów odwzorowawczych dla południków: 17° , 19° , 21° ,23° ,25°

• X = x - 5 280 000 m, Y = y + 90 000 m

Modyfikacja odwzorowania z 1920 r

• cztery 3-stopniowe pasy odwzorowawcze dla południków środkowych 15°, 18°, 21°, 24°

• skala m0 = 0.999935

• X = x, Y = y + (5 500 000, 6 500 000, 7 500 000, 8 500 000) m

• od roku 1949 skala m0 = 1

Wysokości dynamiczne pkt P otrzymujemy dzieląc ujemną wartość różnicy potencjału W_P w pkt P i W_O na geoidzie przez wartość przyspieszenia normalnego na szerokości B=45⁰

H^d_P =(-W_P-W_O)/γ₀⁴⁵

Wykorzystuje się do wyrażenia innych poprawek w innych systemach wysokości.

Wys. dynam. i popr. dynam. są wyznaczane ściśle na podstawie pomierzonych różnic wysokości i przyspieszenia siły ciężkości. Poprawki dynamiczne nie mają żadnej interpretacji geometrycznej. Bardzo ważną właściwością tych wysokości jest to, że pkt. położone na tej samej powierzchni ekwipotencjalnej mają taką samą wys. dynam. System wys. dynam. nie uwzględnia nierówności powierzchni ekwipotencjalnych

Zastosowanie: technika, budownictwo wodne, projekty na bardzo dużych obszarach (gdzie wymagana jest duża dokładność projektowania spadków)

SYSTEMY WYSOKOŚCI

Wysokości otometryczne jest to odległość pkt. fizycznej pow. Ziemi od geoidy mierzona wzdłuż linii pionu (posiada interpretację geometryczną ).

Wys. ortometryczna.

H=C/g, gdzie C=(W_O-W_P)

C - liczba wyrażająca pracę w polu potencjalnym;

g - przeciętna wartość przyspieszenia siły ciężkości wzdłuż linii pionu.

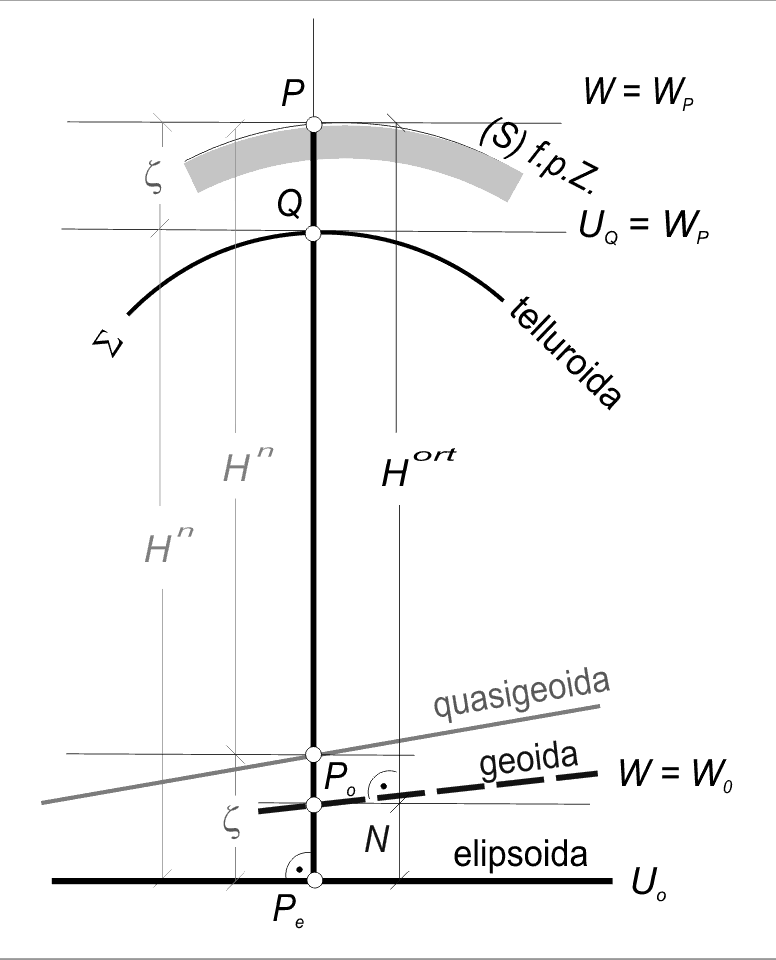
Wysokość normalna Mołodeńskiego:

Wysokość geometryczna telluroidy (odległość telluroidy od elipsoidy)

Telluroida (podejście wprowadzone przez Hirvonena) to pewien obraz (przybliżenie) fizycznej powierzchni Ziemi, gdzie dla dwóch punktów na linii pionu pola normalnego (lub normalnej) potencjał normalny w punkcie Q jest taki sam jak potencjał rzeczywisty w punkcie P

1. Wysokości normalne nie maja jasnej interpretacji geometrycznej.

Wyrażają one co prawda odległości pomiędzy geoida i telluroida lub quasigeoida i punktem na fizycznej powierzchni Ziemi, ale zarówno qusigeoida jak i telluroida to powierzchnie `wtórne' w stosunku do wysokości normalnych (nie można ich zdefiniować bez znajomości wysokości normalnych!!!).

2. Quasigeoida nie jest powierzchnia ekwipotencjalna potencjału normalnego, a wiec nie można jej traktować jako powierzchni odniesienia wysokości normalnych w takim samym sensie jak traktuje sie geoide dla wysokości ortometrycznych! Ponadto quasigeoida jest

powierzchnia nieciągła (teoretycznie może leżeć na „dwóch poziomach” dla tych samych współrzędnych np. w przypadku urwiska; taka sytuacja w przypadku geoidy nigdy nie może mieć miejsca!!!).

3. Wysokości i poprawki normalne wyznacza sie bez jakichkolwiek założeń co do rozkładu gęstości warstw przypowierzchniowych skorupy ziemskiej.

4.Punkty leżące na tej samej powierzchni ekwipotencjalnej maja różne

wysokości normalne.

5. Wysokości normalne nadają się do rozwiązywania zagadnień związanych z wyznaczaniem figury Ziemi wg koncepcji Mołodenskiego.

6. Na terenach nizinnych i płaskich różnice wysokości normalnych i ortometrycznych są niewielkie (w Polsce wahają się od 0cm na północy do kilku centymetrów w Tatrach).

7. System wysokości normalnych jest obowiązującym systemem wysokości w Polsce!

Określenie wysokości

Problem określenia wysokości jest odrębnym problemem, wymagającym znajomości odstępów geoidy od elipsoidy WGS84 w danym rejonie. Dokładna mapa takich odstępów zwana mapą geoidy została dla obszaru Polski opracowana w Centrum Badań Kosmicznych PAN przez prof. Adama Łyszkowicza .

Posiadając mapę geoidy (w zapisie cyfrowym) można określić odstęp geoidy w dowolnym, o znanych współrzędnych punkcie z dokładnością lepszą od 5 cm. Wówczas:
H = h + N,
lub
h = H - N, gdzie:
H - wysokość nad elipsoidą WGS84,
H - wysokość określana jako wysokość nad powierzchnią morza.

Na obszarze Polski odstępy elipsoidy satelitarnej WGS84 od geoidy sięgają od 26 m do 43 m.

25 Metody pomiarów inwentaryzacyjnych kominów i konstrukcji wieżowych.

1.Metoda trygonometryczna (różnicowa)-polega na pomiarze kierunków do punktów kontrolnych, rozmieszczonych na rożnych poziomach badanego obiektu. Z obserwacji wykonanych na poszczególnych stanowiskach należy określić wielkości różnic kątowych odpowiadających wyznaczanym wychyleniom osi komina, przyjmując za kierunek odniesienia średnią wartość kierunków na poziom zerowy(wylicza się różnicę pomiędzy kier.średnim poziomów wyższych a kier. średnim na poziom zerowy). Kolejny etapem jest zamiana wartości kątowej wychyleń na liniowe. Określamy dokładność wychyleń poprzecznych korzystając z wzoru Gaussa na błąd średni funkcji wyliczając pochodne cząstkowe po kolejnych zmiennych. Zaleca się przed pomiarem wyznaczyć błąd pomiaru kierunku.

2.Metoda bezpośredniego rzutowania-w tej metodzie pomiary kątowe zastąpiono pomiarami liniowymi. Stosuje się tutaj płaszczyznę kolimacyjną teodolitu do przerzutowania poszczególnych kierunków z punktu badanego na stała bazę (łata niwelacyjna umieszczona poziomo i prostopadle do osi celowej).Ważne jest aby instrument był dobrze wypoziomowany w płaszczyźnie prostopadłej do celowej. Po każdorazowym wycelowaniu na badany punkt opuszczamy lunetę i odczytujemy z łaty (założony błąd odczytu 1mm). Podobnie ja wcześniej wyliczamy wartości średnie, obliczamy różnice względem poziomu zero, żeby otrzymać wychylenia zrzutowane na łatę. Z tw.Talesa skalujemy wyliczone wcześniej wychylenia, aby uzyskać wychylenia odniesione do obiektu. Dokładność określamy podobnie wykorzystując wzór Gaussa.

3.Metoda wcięć kątowych-polega na wykonaniu obserwacji kątowych z wzajemnie widocznych stanowisk obserwacyjnych w celu wyznaczenia wsp. badanych punktów osi komina na podstawie których oblicza się wychylenia punktów osi linii pionu przechodzącej przez punkt odniesienia. Obs. analogiczne jak w met.trygonometrycznej. Wyliczamy średnie wartości do osi. Dla każdego stanowiska zestawia się kąty między kierunkami na sąsiednie stanowisko i kierunkami do osi.

Zaleca się przed pomiarem wyznaczyć błąd pomiaru kierunku (kąta).

4.Metoda projekcji laserowej-odmiana metody trygonometrycznej. Osnowa pomiarowa w tej metodzie musi być założona z jednej strony badanego obiektu, aby umożliwić jednoczesną obserwację punktów na zasygnalizowanych poziomach ze wszystkich stanowisk. Na środkowym stan. Ustawia się teodolit laserowy( rola instrumentu mierzącego i wskazującego poziom obs. pozostałym 2 teodolitom). Ze wszystkich stanowisk wykonuje się obserwacje na obie tworzące komina na poziomie zasygnalizowanym przez światło lasera. Metoda stosowana, gdy nie można wyodrębnić poszczególnych poziomów obs. Opracowanie wyników takie samo jak w met.tryg.

5.Metoda fotogrametryczna-zalety: obserwacje wykonywane w krótkim czasie, wyznaczenie wychyleń wszystkich punktów obiektu, zdjęcia są wolne od błędów osobowych, powtórzenie pomiaru może być dokonane przez inną osobę. Zdjęcia muszą być wykonane jednocześnie, z co najmniej z 2 stanowisk. Istotnym czynnikiem jest dokładne spoziomowanie kamery. Opracowanie następuje na stereokomparatorze (pomiar wsp. tłowych na wybranych punktach). Oblicza się wychylenia poprzeczne w skali zdjęcia. Rzeczywiste otrzymuję się mnożąc te wartości przez skalę zdjęcia. Dalej postępuje się podobnie jak w met.tryg. lub rzutowania.

26. Techniki laserowe w pomiarach deformacji.

Geodezyjne systemy pomiarowe do celów przemysłowych określane są najczęściej skrótem IMS (Industrial measurement system) lub RMS (Remote measurement system). Główna ideą systemów jest zastosowanie dalmierza o odpowiednio dużej mocy laserowej wiązki. Systemy te oparte są na metodzie wcięć kątowych. Przy typowych wymiarach badanego obiektu w granicach 10-15 m dokładność tych systemów jest z reguły nie mniejsza niż 0.1-0.3 mm dla minimalnej zaś długości celowych wynoszącej ok. 1 m , może sięgać 0.03-0.07 mm.

Dzięki odpowiedniemu oprogramowaniu systemy pomiarowe wykorzystujące metodę wcięć mogą wyznaczać współrzędne punktów w czasie rzeczywistym co umożliwia zastosowanie ich do sterowania procesem ustawiania lub montażu różnych elementów.

Znacznie większe możliwości dają systemy wyposażone w zautomatyzowane tachimetry (serwomotory) które umożliwiają zdalne naprowadzanie, ogniskowanie lunety. Dobre narzędzie do badania permanentnych zmian położeń punktów o znanych w przybliżeniu współrzędnych.

Systemy RMS stosowane są najczęściej w działach przemysłu

Wśród technik laserowych można wyróżnić:

• Trakery

• Skanery ręczne

• Wskaźniki laserowe

• Interferometry

Traker jest urządzeniem pomiarowym wyposażonym w kodery obrotowe i laserowy mechanizm pomiaru odległości, które działają w ramach układu sterowania w pętli zamkniętej oraz umożliwiają śledzenie i pomiar przestrzennego położenia retrorefleksyjnej kostki i kul. Trakery laserowe bardzo dobrze nadają się do pomiaru części dużych, znajdujących się w trudnodostępnych miejscach lub po prostu zbyt dużych do dokładnego zmierzenia w inny sposób. Trakery znajdują szerokie zastosowanie w branżach takich, jak aeronautyka, budowa okrętów i łodzi podwodnych, budownictwo, wydobycie ropy naftowej, energia jądrowa, infrastruktura itp. Posiada on zasięg opisany średnicą o wartości 110m (361ft) oraz pozwala osiągnąć dokładność przestrzenną na poziomie 0.049mm (0.002”) w odległości 10m (33ft).

Tracker Absolutny to przenośny system pomiarowy wykorzystujący wiązkę laserową do dokładnych pomiarów i kontroli w sferycznej przestrzeni pomiarowej do 160 m [525 ft]. Tracker Absolutny może gromadzić współrzędne 3D na trzy sposoby: poprzez podążanie za niewielką kulą lustrzaną, zwaną również reflektorem, poprzez śledzenie ręcznej, „obrotowej”, dotykowej sondy bezprzewodowej Leica T-Probe lub poprzez śledzenie bezdotykowego skanera laserowego wysokiej szybkości Leica T-Scan. Metoda pomiarowa będzie zależeć od zastosowania.

Skanowanie laserowe oznacza, że powierzchnie lub formy 3D są omiatane wiązką lasera o układzie pionowym lub siatkowym w celu dokonania pomiarów i przetworzenia danych pomiarowych albo wygenerowania obrazu 3D. Zeskanowane dane można zapisywać w wielu formatach plików w celu dalszej manipulacji i analizy względem pierwotnych modeli itp.

Skaner laserowy to określenie urządzenia prowadzącego wiązkę lasera. Istnieją laserowe głowice skanujące, które można zamontować na ramionach pomiarowych lub tradycyjnych urządzeniach współrzędnościowych w celu dokumentowania niewielkich obiektów, a także skanery laserowe mogące zarejestrować dane np. całego budynku. Skanowanie laserowe szczególnie dobrze sprawdza się w inżynierii odwrotnej oraz w sytuacjach niedostępności oryginalnych rysunków lub specyfikacji.

27. Zastosowania technik hybrydowych w pomiarach przemieszczeń.

Techniki GPS należą obecnie do najdokładniejszych, najszybszych i ekonomicznych metod wyznaczania współrzędnych punktów sieci geodezyjnych zarówno państwowych jak i lokalnych, wykorzystywanych dla potrzeb geodezji inżynieryjnej, obiektów hydrotechnicznych i zakładów przemysłowych.

Wysokości wyznaczane z pomiarów satelitarnych nie są równoznaczne z wysokościami uzyskanymi z klasycznej niwelacji geometrycznej. Lecz dokładność jaką aktualnie można osiągnąć przy prawidłowo zaplanowanych sesjach pomiarowych (odchylenie standardowe) mniejsze niż 3 mm (błąd średni składowych wektora do 10 km) pozwala stosować tą technologię do monitoringu.

Należy podkreślić, że wyznaczanie współrzędnych punktów do analizy przemieszczeń i odkształceń powinno być wykonywane przede wszystkim metodami statycznymi.

Zalety

1. Brak konieczności wzajemnej widoczności punktów

2. Praktyczna niezależność od czasu (pory roku, pory dnia i nocy) oraz warunków atmosferycznych pomiaru

3. Pełna automatyzacja procesu wykonywania obserwacji

4. Wysoka dokładność pomiaru

5. Praktyczna niezależność dokładności od odległości pomiędzy punktami (w zakresie odległości do ok. 10 km)

6. Możliwość wykonywania pomiarów ciągłych

7. Możliwość otrzymywania wyników pomiarów w czasie zbliżonym do rzeczywistego

Wymagania

1. Odkryty horyzont (powyżej ok. 10 stopni)

2. Specjalistyczny i kosztowny sprzęt (odbiorniki geodezyjne GPS, precyzyjne anteny)

3. Odpowiednio długie sesje obserwacyjne w pomiarach statycznych

4. Konieczność transmisji danych (kablowa, radiowa, itp.) w pomiarach w czasie rzeczywistym

5. Specjalistyczne oprogramowanie

Uwarunkowania precyzyjnych pomiarów GPS

1. Zastosowanie precyzyjnego sprzętu pomiarowego (odbiorniki geodezyjne, anteny precyzyjne)

2. Ograniczenie odległości pomiędzy punktami do ok. 10 km

3. Odpowiednia długość sesji pomiarowych

4. Dobra geometria satelitów (DOP)

5. Rozwiązanie nieoznaczoności fazowych

6. Estymacja korekt troposferycznych

7. Minimalizacja efektu wielotorowości

8. Redundancja pomiarów

Podsumowanie

1. Zalety techniki GPS (brak wizur, wysoka dokładność, automatyzacja pomiaru) powodują coraz powszechniejsze jej stosowanie w pomiarach deformacji obiektów inżynierskich.

2. Uzyskanie wysokich dokładności pomiarów wymaga zastosowania zaawansowanych procedur eliminacji lub ograniczenia wpływu podstawowych źródeł błędów pomiarowych.

Możliwość pełnej automatyzacji procesu pomiarowego i obliczeniowego predysponuje technikę GPS do automatycznych systemów kontrolno-pomiarowych.

28. Fotografia cyfrowa w badaniach przemieszczeń i pomiarach kształtu obiektów inżynierskich

Kamery cyfrowe mają wyższą rozdzielczość radiometryczną niż analogowe co daję lepszą rozróżnialność szczegółów, zarówno w jasnych jak i w ciemnych partiach obrazu. Dodatkową zaletą jest dostępność obrazu zaraz po jego wykonaniu. Kamera cyfrowa używana w zastosowaniach fotogrametrii z bliska to kamera CCD.

Fotogrametria jest szczególnie przydatna i dobrze przystosowana do badań odkształceń ze względu na kilka ważnych korzystnych własności:

• wykonanie pomiaru dla obiektów trudno dostępnych

• rejestracja pomiaru w ciągu kilku sekund, a nawet po uprzednim przygotowaniu w ułamku sekundy

• możliwości jednoczesnego rejestrowania wielu punktów rozmieszczonych na płaszczyźnie lub w przestrzeni

• obiektywność dokumentów pomiarowych, czyli zdjęć, odtwarzających konkretny stan, który może być rozpatrywany i mierzony wielokrotnie przez różnych obserwatorów w dowolnym czasie

Wykorzystanie precyzyjnych pomiarów okresowych lub inwentaryzacyjnych do wyznaczania przemieszczeń lub odchyleń od wzorca polega na analitycznym określaniu współrzędnych punktów kontrolowanych i porównaniu ich ze współrzędnymi stanu pierwotnego lub współrzędnymi wzorca. Stosuję się do tego celu metodę dwuobrazową lub wieloobrazową i określa zazwyczaj składowe przemieszczeń przestrzennych (lub odchyleń)

Zastosowanie metod fotogrametrycznych dla pomiaru i kontroli różnych zadań przemysłowych i inżynierskich jest ogólnie zwane fotogrametrią przemysłową

Główne zastosowania obejmują budownictwo, inżynierię lądową, lotnictwo, górnictwo, konstrukcję pojazdów i maszyn mechanicznych, budowę statków.

We wszystkich tych dziedzinach fotogrametryczne metody dostarczają danych dla planowania, produkcji, testowania, monitorowania, reperacji i rekonstrukcji.

Obiekty mierzone metodami fotogrametrycznymi mogą być stałe, płynne i gazowe, a także zjawiska w ruchu…

Zalety metod fotogrametrycznych w porównaniu do innych

• pomiary wykonywane z dala od obiektu

• rejestracja pomiaru bardzo szybka, zależy tylko od systemu rejestrującego

• pomiary mogą być wykonane w niebezpiecznych środowiskach

• obrazy dostarczają permanentnej rejestracji która może być powtórnie pomierzona w późniejszym czasie

• system rejestrujący nie wymaga tak stabilnych platform, jak w przypadku systemów geodezyjnych

• dokładności osiągają 1/100000 wymiaru obiektu, przy zachowaniu odpowiednich warunków. Przy użyciu konwencjonalnych systemów rejestrujących można uzyskać dokładność rzędu 1/20000

Każde zadanie wymaga stosownego projektu pomiaru obejmującego optymalizację osnowy, liczby i geometrii zdjęć, metody przetworzenia, w celu zabezpieczenia wymagań dokładnościowych oraz formatu wyznaczonych danych

Zastosowanie fotogrametrii cyfrowej dotyczy głównie wyznaczenia:

- kształtu obiektów lub ich części

- deformacji lub przemieszczeń obiektów w jednym, dwóch lub trzech kierunkach w funkcji czasu, w trakcie ich eksploatacji

Przykłady zastosowań przemysłowych

- przemysł lotniczy

- przemysł samochodowy

Metoda fotogrametrii naziemnej

Wyznaczanie przemieszczeń w płaszczyźnie poziomej i pionowej.

Zaletą tej metody jest:

• synchroniczna rejestracja położenia dowolnej liczby punktów kontrolowanych na jednym fotogramie;

• szybkość pomiarów;

• możliwość wykorzystania archiwalnych zdjęć do ich konfrontowania z aktualnymi fotogramami;

• fotograficzną rejestrację i dokumentację postępu prac ziemnych, betonowych, budowlanych itp.

Klasycznymi sposobami fotogrametrii analitycznej wyznaczane są współrzędne przestrzenne X, Y i H, a następnie na podstawie wyników kolejnych serii zdjęć wartości przemieszczeń w czasie.

30.Lokalizacja urządzeń podziemnych technikami pośrednimi.

INSTRUKCJA G-4.4

Zakres pomiarów:

1/ przewody kanalizacyjne, rurowe i kable,

2/ podłączenia,

3/ kanały zbiorcze przewodów podziemnych,

4/ miejsca przejść przewodów podziemnych w naziemne,

5/ nisze, szyby, włazy, zdroje uliczne, studnie i studzienki, boczne wejścia kanałowe, zsypy śniegowe, wpusty uliczne i podwórzowe, znaki drogowe podświetlane, skrzynki kablowe, szafki kablowe,

6/ hydranty, zasuwy, zawory itp.,

7/ stacje ujęcia i uzdatniania wody, przepompownie, zbiorniki wody, oczyszczalnie i przepompownie ścieków kanalizacyjnych, przepompownie i stacje wymienników sieci cieplnej, stacje redukcyjno- pomiarowe sieci gazowych, stacje zbiorników gazowych, stacje przetłaczania i uzdatniania gazu, mieszalnie gazów, stacje transformatorowe, stacje zasilania, stacje rozdzielcze, centrale telefoniczne itd.

8/ urządzenia specjalne np. rurociągi naftowe.

Prace terenowe:

1. Wyznaczanie położenia przewodów zakrytych przy geodezyjnej inwentaryzacji uzbrojenia terenu należy wykonać wykrywaczem elektronicznym, wykorzystując informacje dotyczące przebiegu przewodów, a mianowicie:

1/ istniejące materiały i dokumenty jak:

- mapy branżowe i szkice powykonawcze przedstawiające przebieg sieci wraz z uzbrojeniem przewodów,

- rysunki i szkice uzbrojenia,

- projekty techniczne sieci,

- przekroje podłużne projektowanych sieci przewodów,

2/ elementy naziemne uzbrojenia przewodów podziemnych,

3/ słupki i tabliczki wskaźnikowe sygnalizujące oś trasy lub zmianę kierunku przewodu,

4/ odkrywki terenowe,

5/ informacje mieszkańców lub właścicieli terenów, na których znajdują się przewody podziemne,

6/ zasady projektowania i budowy sieci uzbrojenia podziemnego oraz znajomość odpowiednich norm technicznych.

Opis stosowanego przez nas na ćwiczeniach wykrywacza:

GEOPILOT S - elektromagnetyczny lokalizator - wykrywacz kabli i rurociągów podziemnych. Wykrywa kable elektroenergetyczne, kable telefoniczne, kable sterownicze, przewody wodne, przewody gazowe, przewody centralnego ogrzewania i inne przewody metalowe. Można nim wykrywać również rurociągi niemetalowe ale tylko wówczas, jeżeli wprowadzimy do nich przewodnik elektryczny np. drut, elektrolit itp. Przy pomocy wykrywacza GEOPILOT można wyznaczyć trasę ciągu oraz głębokość jego położenia. GEOPILOT pracuje metodą indukcyjną - (bez konieczności włączania kablami sygnału do wykrywanego przewodu) lub galwaniczną (przy której sygnał generatora włączamy kablami przyłączeniowymi do lokalizowanego przewodu).

Komplet składa się z nadajnika i odbiornika. Nadajnik jest wmontowany w walizkę, która jest zarazem pojemnikiem na odbiornik i akcesoria (kable przyłączeniowe, słuchawki).

W trakcie wykrywania, przy zbliżaniu się do przewodu odbiornik daje coraz głośniejszy sygnał akustyczny, natomiast nad samym przewodem następuje wyciszenie (minimum) sygnału, po czym po przekroczeniu osi przewodu sygnał znów staje się mocniejszy. Ten minimalny sygnał występuje nad osią przewodu z dokładnością kilku centymetrów.

Gniazda podłączenia galwanicznego, wyłącznik nadajnika oraz przełącznik redukcji mocy nadajnika znajdują się na zewnątrz walizki, co jest bardzo wygodne podczas pracy.

Dane techniczne:

-można nim wyznaczać trasę oraz głębokość położenia przewodu;
-metoda pracy indukcyjna lub galwaniczna;
-sposób identyfikacji na minimum sygnału;
-rodzaj sygnału ciągły lub pulsujący;
-odbiór sygnału słuchawkami ;
-częstotliwość sygnału roboczego 55.4 kHz;
-moc nadajnika od 0.1 do 0.2 W regulowana skokowo;
-maksymalna głębokość lokalizacji 8 m;

33. Charakterystyki dokładności stosowane w analizach geodezyjnych sieci inżynieryjnych.

O-1

Miarę dokładności szczegółowej osnowy II klasy jest średni błąd położenia punktu po wyrównaniu, który powinien być mniejszy od 0,05 m.

Miarą dokładności szczegółowej osnowy III klasy jest średni błąd położenia punktu po wyrównaniu, który powinien być mniejszy od 0,10 m.

Miarę dokładności podstawowej. osnowy wysokościowej I klasy jest średni błąd niwelacji po wyrównaniu, który powinien być mniejszy od ......... 1,0 mm/km.

Miarą dokładności podstawowej osnowy wysokościowej II klasy jest średni błąd niwelacji po wyrównaniu, który powinien być mniejszy od....... 2,0 mm/km.

Miarą dokładności szczegółowej osnowy wysokościowej III klasy jest średni błąd niwelacji po wyrównaniu, który powinien być mniejszy od ....... 4,0 mm/km.

Miarą dokładności szczegółowej osnowy wysokościowej IV klasy jest średni błąd niwelacji po wyrównaniu który powinien być mniejszy od ....... 10 mm/km.

Miarą dokładności osnowy pomiarowej jest średni błąd:

- niwelacji po wyrównaniu który powinien być mniejszy od ....... 20 mm/km,

- określenia wysokości punktu mniejszy od .................. 10 cm.

G - 1 Osnowa pozioma

Dokładność położenia punktów poszczególnych klas charakteryzują błędy średnie po wyrównaniu:

Klasa	Przeciętny błąd względny długości boku	Błąd położenia punktu względem punktów nawiązania
I	md : d ≤ 5
II		mp ≤ 0,05 m
III		mp ≤ 0,10 m

Błędy średnie należy obliczać przy założeniu bezbłędności punktów nawiązania. Wszystkie punkty osnowy podstawowej i szczegółowej powinny posiadać współrzędne obliczone w państwowym układzie współrzędnych oraz być zaklasyfikowane do jednej z tych klas.

G-2 Osnowa wysokościowa

Dokładność osnowy danego rodzaju i klasy charakteryzuje ogólnie średni błąd pomiaru niwelacji, po wyrównaniu (m_o).

Rodzaj osnowy	Klasa	mo [mm/km]
Podstawowa	I II	±1,0 ±2,0
Szczegółowa	III IV	±4 ±10
Pomiarowa	V	±20

Osnowy realizacyjne (na podstawie m.in. normy ISO 4463-1 - nie sądzę, żeby było potrzeba aż tylu szczegółów, ale w razie czego)

Jako główne kryterium oceny dokładności poziomej osnowy realizacyjnej przyjmuje się błąd średni po wyrównaniu długości najsłabiej wyznaczonego boku. Określa on wzajemne położenie sąsiadujących punktów osnowy, co jest bardzo istotne dla wykonanego tyczenia szczegółowego. Natomiast pomocniczymi kryteriami dokładnościowymi są:

- średnie błędy boków wyrównanej sieci,

- średnie błędy kątów wyrównanej sieci,

- średnie błędy kierunków wyrównanej sieci,

- średnie błędy podłużne i poprzeczne punktów,

- parametry geometryczne elips błędów średnich położenia punktów

Jako kryterium dokładności wysokości osnowy realizacyjnej przyjmuje się błąd średni niwelacji po wyrównaniu wyrażony w mm na 1 km linii niwelacyjnej. Pomocnicze kryterium to błąd średni wysokości punktów po wyrównaniu.

Norma PN-ISO 4463-1 wprowadza kryteria akceptacji, czyli dopuszczalne odchylenia dla długości kątów i wysokości. Kryteria te odnoszą się do pomiarów powykonawczych, które mają na celu sprawdzenie zgodności zakończonego etapu budowy z odchyłką dopuszczalną.

Osnowa pierwszego rzędu powinna podlegać akceptacji w dwóch etapach. Pierwszym z nich jest porównanie zmierzonych odległości i kątów z otrzymanymi ze współrzędnych wyrównanych. Różnica nie powinna przekraczać:

dla odległości przy minimum 4 mm dla kątów (w gradach) L - odległość w metrach między punktami pierwszego rzędu dla kątów - krótsza z dwóch odległości określających kąt

Drugi etap to porównanie odległości i kątów otrzymanych na podstawie podanych współrzędnych z tymi, które uzyskano z pomiaru powykonawczego. Różnica nie powinna przekraczać:

dla odległości przy minimum 8 mm dla kątów (w gradach) L - odległość w metrach między punktami pierwszego rzędu dla kątów - krótsza z dwóch odległości określających kąt

Punkty drugiego rzędu również powinny podlegać akceptacji w dwóch etapach. W pierwszym etapie w stosunku do kluczowych punktów pierwszego rzędu. W drugim etapie w stosunku do innych kontrolowanych punktów drugiego rzędu. Dopuszczalne odchylenia w pierwszym i drugim etapie to:

dla odległości do 7 m: ± 4 mm dla odległości większych niż 7 m: dla kątów (w gradach) L - odległość w metrach między punktami dla kątów - krótsza z dwóch odległości określających kąt

Punkty szczegółowe, tak samo jak punkty osnowy wyższego rzędu powinny podlegać akceptacji w dwóch etapach. Etap pierwszy to obliczenie różnicy w stosunku do punktu drugiego rzędu, natomiast etapem drugim jest sprawdzenie odchyleń dopuszczalnych w stosunku do innych punktów szczegółowych w tej samej części obiektu budowlanego. Dopuszczalne odchylenia oblicza się tak samo w obu etapach, i wynoszą one:

dla odległości do 4 m: ± 2K1 mm dla odległości większych niż 4 m: L - odległość w metrach między punktami K1 - stała

34. Nawiązywanie sieci do punktów o danej błędności (np. o danych elipsach błędu średniego).

Zakładana osnowa jest o tej samej dokładności co osnowa państwowa- współrzędne osnowy realizacyjnej obliczamy uwzględniając dokładność punktów nawiązania (m_p; m_x, m_y; A, B, φ). W tym wypadku osnowa zagęszczająca uwzględnia błędy osnowy wyższego rzędu. A więc dokładność nawiązania ma wpływ na dokładność wewnętrzną punktów osnowy realizacyjnej. Osnowę realizacyjną wyrównuje się metodą najmniejszych kwadratów . W przypadku, gdy dokładność osnowy realizacyjnej przewyższa dokładność osnowy nawiązania, osnowę realizacyjną wyrównuje się z odrzuceniem bezbłędności punktów nawiązania.

(Wydaje mi się, że to tylko o to chodzi w odpowiedzi na pytanie. Przynajmniej tylko tyle było napisane w wykładach Kowalskiego)

35. Zagadnienie niezawodności wewnętrznej sieci geodezyjnej.

Do wykrywania obserwacji obarczonych błędem grubym, czyli tzw. obserwacji odstających, konieczne jest występowanie w sieci nadliczbowości obserwacji, zapewniającej nadmiar informacyjny układu ze względu na wyznaczane parametry. Ogólnie rzecz biorąc, im większy jest ten nadmiar i im bardziej równomiernie rozłożony w strukturze sieci, tym większa jest szansa wykrycia obserwacji odstających. Na tej właśnie relacji oparte jest pojęcie niezawodności sieci.

Poziom niezawodności sieci jest tym wyższy, im mniejsze jest prawdopodobieństwo niewykrycia obserwacji odstającej i tym samum dopuszczenia jej do udziału w procesie wyznaczania niewiadomych, a wskutek tego - do zniekształcenia ich wartości.

Poziom niezawodności wewnętrznej sieci jest tym wyższy, im wyższy jest stopień kontrolowalności obserwacji w tej sieci.

Wzajemna kontrolowalność wynika z faktu, iż w przypadku występowania nadliczbowości obserwacji w sieci, wchodzą on ze sobą w związki pozwalające wyznaczyć wartość danej obserwacji na podstawie wartości innych obserwacji. Niespełnienie tych związków wykraczające poza granice wynikające z określonej dokładności pomiaru daje nam informację (sygnał) o zaistnieniu nieprawidłowości w wynikach pomiaru (pojedynczy błąd gruby, kilka błędów grubych).

Można wyróżnić następującą gradację poziomów niezawodności wewnętrznej:

1. układ obserwacyjny nie daje sygnału o wystąpieniu błędu grubego (brak obserwacji nadliczbowych), np. wiszący ciąg niwelacyjny;

2. układ daje sygnał o wystąpieniu błędu grubego, ale nie pozwala go zlokalizować (zbyt mała liczba obserwacji nadliczbowych), np. obwodnica niwelacyjna;

3. układ daje sygnał o wystąpieniu błędu grubego i pozwala go zlokalizować (dostateczna liczba obserwacji nadliczbowych), np. obwodnica niwelacyjna uzupełniona ciągami przewiązującymi.

Możemy mieć do czynienia z niezawodnością w szerszym zakresie, tj. gdy brane są pod uwagę wszystkie elementy procesu wyznaczania punktów sieci (tj. odpowiednie kwalifikacje personelu, instrumenty pomiarowe z atestami-okresowo kontrolowane, procedury pomiaru zawierające mechanizmy autokontroli, możliwości wprowadzania korekt z tytułu zaburzających wpływów warunków atmosferycznych, konstrukcje pomiarowe umożliwiające kontrolę poprawności obserwacji) i z niezawodnością w węższym sensie, tj. gdy ograniczamy się do elementów dających się modelować w sposób ścisły, takich jak struktura sieci i jej charakterystyki dokładnościowe. Lokując rozważania w tym zawężonym zakresie można stwierdzić, iż jednym z ważnych czynników, które należy brać pod uwagę w projektowaniu przedsięwzięcia pomiarowego, jest odpowiednie ukształtowanie struktury sieci, tj. takie, które zapewniłoby odpowiedni poziom wzajemnej kontrolowalności obserwacji, podnosząc przez to skuteczność procedur wykrywania błędów grubych. Przydatne do tego celu są wskaźniki niezawodności wewnętrznej sieci, uzyskane ze wzoru

,
,
i=1,…,n (indeks obserwacji)

gdzie:
-macierz niezawodności oznaczana tez symbolem R

A - macierz współczynników w standaryzowanym układzie równań obserwacyjnych (obserwacje nieskorelowane)

S - macierz współczynników w warunkach definiujących układ odniesienia dla pozycji lub przemieszczeń

W pomiarach przemieszczeń za poprawnie, punktu widzenia niezawodności, zaprojektowaną siec kontrolną uważa się taką sieć, w której:

, i= 1,…,n (indeks obserwacji)

W geodezyjnym wyznaczaniu przemieszczeń podstawą do podjęcia identyfikacji układu odniesienia dla wyznaczonych przemieszczeń jest przeprowadzenie, w procesie wyrównania wstępnego, diagnostyki błędów grubych w obserwacjach, zakończonej wyeliminowaniem obserwacji odstających (tj. obarczonych tymi błędami). Oprócz odpowiedniego zaprojektowania samej metody identyfikacyjnej należy pamiętać o konieczności weryfikacji poprawności jej wyniku na etapie finalnego obliczania przemieszczeń. W przypadku zastosowania układu elastycznego będzie to sprawdzenie istotności przemieszczeń na punktach odniesienia. Potwierdzeniem identyfikacji będzie nieistotność tych przemieszczeń. W przypadku zaś zastosowania układu sztywnego będzie to sprawdzenie wartości estymatora współczynnika wariancji (
), tj. globalnego wskaźnika zgodności obserwacji z przyjętym modelem wyrównawczym. O poprawności identyfikacji świadczyć tutaj będzie nieprzekroczenie przez ten wskaźnik ustalonej dlań wartości krytycznej. Nawet i w tej sytuacji zalecane jest także sprawdzenie wartości poprawek zunifikowanych.

43

---