
1.Potencjał grawitacyjny i potencjał siły ciężkości – definicja i własności dla pola ciężkościowego rzeczywistego i
normalnego, wielkości charakteryzujące pole.
Potencjał grawitacyjny jest funkcją odpowiadającą sile grawitacji wywołanej przez masę w postaci
Własności potencjału grawitacyjnego:
Liniami sił grawitacyjnych są krzywe wzdłuż których działają siły
(F), powierzchnią prostopadłą do tych linii jest tzw.
Powierzchnia pozioma. Masy znajdujące się na powierzchni
poziomej pozostają w pozycji równowagi. Powierzchnia pozioma nosi nazwę powierzchni ekwipotencjalnej co wyraża się
równaniem (V= const). Praca przy przesunięciu ciała po powierzchni ekwipotencjalnej jest równa 0. Poruszanie się po
powierzchni ekwipotencjalnej nie wymaga pracy przeciwko sile grawitacji.
3. Odstęp powierzchni ekwipotencjalnej jest odwrotnie proporcjonalny do siły
Równanie Laplace’a spełnione jest na zewnątrz
masy , natomiast wewnątrz masy spełnione jest równanie Poissona.
Na siłę ciężkości składa się siła przyciągania i siła odśrodkowa.
V(A)- potencjał grawitacyjny w pkt A
u(A)- potencjał odśrodkowy
U- potencjał normalny dominujący
T – potencjał zakłócający
q- stosunek siły odśrodkowej do siły ciężkości
Normalne pole Ziemi pozwala na wydzielenie z ziemskiego pola ciężkościowego części podstawowej (dominującej) i
posługiwanie się jedynie różnicami między wartościami naturalnymi (rzeczywistymi) i normalnymi. Zadanie określenia
kształtu bryły (podstawowe równanie geodezji) będzie się sprowadzało do badania odstępów od powierzchni modelu
zwanego normalnym polem ciężkości. Pole normalne można uważać za pole potencjalne idealnego ciała fizycznego
zastępującego ziemię rzeczywistą i nazywano ziemią normalną.
- masa elipsoidy =masa Ziemi

- nasz model obraca się z taką samą prędkością kątową co nasza Ziemia
- osie obrotu pokrywają się ze sobą lub odchylenie osi jest zaniedbywalne
2. Charakterystyka podstawowego równania geodezji fizycznej.
UP – potencjał normalny w pkt
TP – potencjał zakłócający
Korzystając z zależności Brunsa [9], łączącej potencjał zakłócający T i odstęp N geoidy od elipsoidy można
przedstawić anomalię grawimetryczną na geoidzie w postaci tzw. podstawowego równania grawimetrii

3. Dane jest podstawowe równanie geodezji fizycznej. Wyprowadź jego przybliżoną postać dla Ziemi kulistej.
R- średni promień Ziemi
g
- zaburzenia grawimetryczne

4. Redukcje i anomalie grawimetryczne i ich wykorzystanie do badania figury Ziemi
Pomierzonych w różnych punktach na fizycznej figurze Ziemi przyspieszeń sił ciężkości nie można ze sobą
bezpośrednio porównywać. Podobnie jak wyniki geometrycznych pomiarów geodezyjnych należałoby je zredukować
na wybraną powierzchnię odniesienia. W przypadku przyspieszenia siły ciężkości tą powierzchnią jest powierzchnia
geoidy (W=W
0
).
Zredukowane na powierzchnię przyspieszenie wykorzystuje się do interpretacji własności pola siły ciężkości
lub do badania pola figury Ziemi.
W myśl koncepcji Stokesa do badania figury Ziemi wykorzystuje się tylko te redukcje przyspieszenia, które nie
deformują geoidy tzn., nie zmieniają położenia geoidy w przestrzeni, nie zmieniają jej masy i położenia środka
ciężkości.
Geoida powinna być zredukowana, tzn. cała masa Ziemi powinna być skupiona pod powierzchnią Ziemi.
Precyzyjne spełnienie tych dwóch warunków jest praktycznie niemożliwe, ale istnieją redukcje, które tylko w
minimalnym stopniu deformują geoidę i takie będą nam potrzebne do badania figury Ziemi.
W myśl koncepcji Stokesa anomalię grawimetryczną wyraża następujący wzór:
0
0
0
Rg
g
g
A
g
0
g
- wartość przyspieszenia na geoidzie (potrafimy zmierzyć na fizycznej powierzchni Ziemi
0
g
=g+Rg,
0
- wartość przyspieszenia na elipsoidzie poziomej,
g – przyspieszenie pomierzone,
Rg – sposób obliczania tej redukcji definiuje rodzaj i wartość anomalii
a) REDUKCJA I ANOMALIA WOLNOPOWIETRZNA ORAZ FAYE’A
Własności i zastosowanie redukcji wolnopowietznej:
-nie uwzględnia mas na drodze redukcji,
- powoduje „wgniecenie” tych mas pod powierzchnię odniesienia (geoidy), (równomierne
rozciągnięcie warstwy (H, s) na powierzchni geoidy tak aby H0®0 a gęstość takiej warstwy
wynosiła s0= sH ),- spełnia warunki koncepcji Stokesa,
- minimalnie deformuje geoidę (np. dla HmaxPolska - DN < 20cm)
Do wzoru drugiego: zazwyczaj stosujemy tylko część: H a 2
Do wzoru trzeciego: 0,3086 jest takie samo na tym samym równoleżniku (gradient normalny).
Redukcja Faye’a:
, gdzie RT= wpływ nierówności terenu na przyspieszenie
Własności i zastosowanie anomalii wolnopowietrznej:
- wykorzystywane do wyznaczania figury Ziemi (N) zgodnie z koncepcją Stokesa lub
obliczania odchylenia linii pionu,
- anomalie obliczane są często na drodze interpolacji anomalii Bouguere’a (mapy
grawimetryczne)
b) REDUKCJA I ANOMALIA BOUGUERE’A
Redukcja i anomalia Bouguere’a wyraża grawitacyjny wpływ warstwy o znanej grubości (H) i gęstości (s) na punkt
znajdujący się na tej warstwie.

Własności i interpretacja redukcji Bouguere’a:
- usunięcie warstwy powoduje znaczną deformację geoidy (np. dla HmaxPolska ® DN < 47 m)
przez co nie nadaje się do badania figury Ziemi,
- w badaniach geofizycznych – usunięcie warstwy umożliwia badania głębszych warstw,
- w badaniach geologicznych – wykrywanie gęstości (mas) zakłócających (Ds=s’-s)
- stosowana tam łącznie z redukcją wolnopowietrzną tzw. redukcja Bouguere’a-Younga.
- masy zakłócające w RBY zostają „wtłoczone” pod powierzchnię odniesienia (np. geoidę) a zredukowane tak
przyspieszenie może być porównane z przyspieszeniem normalnym.
Anomalie AgB umożliwiają wyodrębnienie tzw. tła regionalnego na podstawie którego można dokonywać
ilościowej interpretacji rozkładu gęstości tj. głębokości i rozmiarów ciała zaburzającego.
Anomalie AgB wykorzystuje się do interpolacji anomalii Agwp lub AgF .
Anomalia Bouguere’a-Younga: Rg
BY
= Rg
wp
+ R
B
Na podstawie map anomalii Bouguere’a można byłoby wyinterpolować i obliczyć wartości anomalii
wolnopowietrznej w następujący sposób:
1. Odczytać w danym rejonie wartości Ag
B.
2. Obliczyć anomalię wolnopowietrzną na podstawie anomalii Bouguere’a.
3. Wyinterpolować wartości anomalii wolnopowietrznej między punktami
.
c) REDUKCJA POINCAREGO-PREYA
Redukcja Poincarego-Preya. Etapy redukcji:
- wygładzenie terenu wokół stanowiska pomiaru przyspieszenia (RT),
- usunięcie przyciągania płyty (RgB),
- zredukowanie przyspieszenia na przyjęty poziom odniesienia (Rgwp),
- przywrócenie przyciągania płyty (RgB),
- odtworzenie zróżnicowanej rzeźby terenu (R’T).
Całość tej złożonej redukcji przedstawia ogólnie wzór [33] lub w postaci do obliczeń [34].
Własności i interpretacja redukcji Poincarego-Preya:
- umożliwia obliczenie przyspieszenia w miejscu niedostępnym dla jego bezpośredniego
pomiaru,
- nie regularyzuje geoidy – nie jest przydatna dla potrzeb wyznaczenia jej kształtu,
- wykorzystywana do obliczania poprawek grawimetrycznych w systemach niwelacyjnych,
oraz opracowania pomiarów grawimetrycznych wykonanych w kopalniach, szybach
wiertniczych i na morzu.

5. Redukcja Poincarego- Preya i jej zastosowanie w geodezji
Rg
PP
=R
T
+ Rg
B
+ Rg
wp
+Rg
B
+R
T
’
=(0,3086-0,0838σ)*H+ R
T
’
+ R
T
[mGal]
normalny gradient przysp. siły ciężkości
wysokość ortometryczna
2* Rg
B
gęstość skorupy Ziemi=2,44g/cm
3
Rg
PP
-
redukcja grawimetryczna Poincarego- Preya. Efektem redukcji ma być przyspieszenie siły ciężkości, które
pomierzylibyśmy ,,zanurzywszy” przyrząd pomiarowy w masach skorupy ziemskiej na wysokość równą wysokości nad
poziomem morza.
R
T
- regularyzacja terenu →POPRAWKA TOPOGRAFICZNA (liczona w temacie 1)
.
Określa ona wpływ przyciągania
otaczających mas, wyrównuje teren do wysokości punktu w którym jest pomiar
Rg
B
- usunięcie wpływu warstw.
Rg
B
=-2πGσH=-0,0419σH [mGal]→REDUKCJA GRAWIMETRYCZNA BOUGERA. Usuwa
całą warstwę terenu pod punktem w którym jest pomiar
Rg
wp
- redukcja na spód warstw.
Rg
wp
=0,3085*H [mGal]→ REDUKCJA GRAWIMETRYCZNA WOLNOPOWIETRZNA.
Redukuje pomiary ze względu na wysokość pomiaru (redukcja na geoide)
Rg
B
- redukcja na górę→ REDUKCJA GRAWIMETRYCZNA BOUGERA. Przywracanie mas ziemi, które są teraz nad
punktem.
R
T
’
- redukcja na rzeźbę terenu→ POPRAWKA TOPOGRAFICZNA (nie była liczona w temacie 1). Przywraca pofałdowania
terenu.
R
T
=
R
T
’
=
sk=n (ilość sektorów);
st=k (ilość stref)
Redukcja ta nie regularyzuje geoidy i nie jest przydatna w badaniu figury Ziemi. Służy do obliczania wartości przyspieszenia w
punkcie niedostępnym dla pomiaru grawimetrycznego. Jest wykorzystywana do obliczenia poprawek grawimetrycznych w
systemach wysokościowych. Ponadto wykorzystuje się ją w grawimetrii górniczej (szyby kopalniane i szyby wiertnicze) i w
pomiarach grawimetrycznych na morzach i oceanach (pomiary podwodne).

6.wyznaczenie odstępu geoidy od elipsoidy metodą grawimetryczną-
założenia metody grawimetrycznej. Zależności niezbędne do wyznaczenia
odstępu.
Odstęp geoidy od elipsoidy wynika z podstawowego równania geodezji fizycznej. Dla
sferycznej powierzchni ekwipotencjalnej i dowolnego stanowiska, na podstawie:
Można wyprowadzić wzór na odstęp w funkcji anomalii grawimetrycznej tzw. wzór Stokesa.
Gdzie: gdzie: R – promień sfery,
- promień wodzący stanowiska centrum masy bryły
(geoidy),
-odległość sferyczna stanowiska od elementu powierzchni ds.
Założenia do wzoru Stokesa :
1. Anomalie dotyczące geoidy zregularyzowanej, tzn. pozbawionej masy ponad poziomem
morza,
2. Geoida i elipsoida powinny mieć ten sam środek ciężkości.
3. Geoida i elipsoida powinny obejmować całą masę Ziemi.
4. (2) i (3) oznacza, że objętości obu brył muszą być jednakowe.
5. Geoida i elipsoida muszą mieć tą samą oś obrotu.
6. (W
0
=U
0
).
7. Suma przyrostów odstępów na całej powierzchni powinna być równa zeru.
Spełnienie wszystkich ww. warunków jest niemożliwe dlatego opracowano kilka koncepcji
wyznaczania odstępu przy niezachowaniu niektórych warunków.
Odstęp dla poszczególnych warunków
1.( W
0
U
0
Pozostałe warunki spełnione) Gdy warunek równości potencjałów rzeczywistego i
normalnego nie zostanie spełniony wtedy wg. koncepcji Pizzettiego odstęp wyraża się
wzorem :
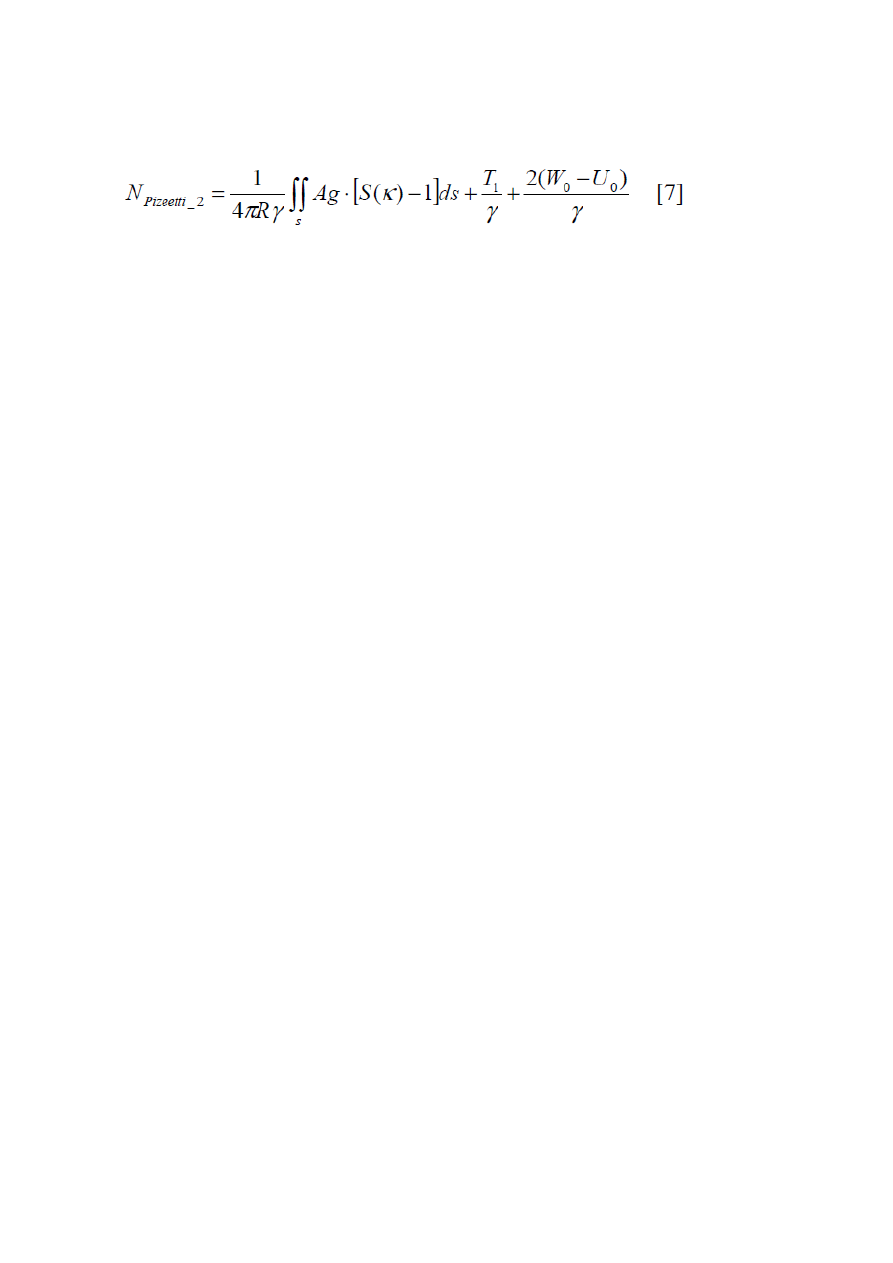
2. W
0
U
0
, różne środki mas i różne masy geoidy i elipsoidy (T
1
)- Piezzetti. –reszta spełnione
Wprowadzenie w miejsce funkcji Stokesa funkcję Helmerta prowadzi do kolejnej postaci wzoru na
odstęp. Wzór ten przedstawiony jest w postaci funkcji współrzędnych azymutalnych. Jest to nadal
postać dla Ziemi kulistej, czyli jest ona przybliżona. Aby zwiększyć dokładność wprowadza się
poprawkę ze względu na elipsoidalny kształt Ziemi i elipsoidalny rozkład przyspieszenia normalnego.
Wartość tej poprawki jest rzędu maksymalnie 20 cm.
7. Postulaty jakie musi spełniać system wysokości
1) Precyzyjne wyznaczenie wysokości wymaga uwzględnienia własności pola ciężkości Ziemi.
2) Wybór systemu wysokości powinien uwzględniać:
Wyznaczone wysokości powinny być niezależne od trasy ciągu niwelacyjnego.
Wysokości punktów nie powinny być zależne od czynników, określonych w sposób
przybliżony np. rozkładu masy, topografii
Poprawki przenoszące przewyższenie do określonego systemu powinny być na tyle
małe, aby ich nie uwzględniać przy niwelacji o niższej dokładności.
W przewyższeniu, w danym systemie wysokościowym, należy wydzielić część
geometryczną, pochodzącą z bezpośredniego pomiaru i część geoidalną- tzw. p
oprawkę niwelacyjną
Wysokości punktów na tej samej powierzchni ekwipotencjalnej powinny być jak
najbliższe sobie.

8. Postulaty jakie musi spełniać system wysokości.
Precyzyjne wyznaczenie wysokości wymaga uwzględnienia własności pola ciężkościowego
Ziemi. Wybór systemu wysokościowego powinien uwzględniać:
1) Wyznaczane wysokości powinny być niezależne od trasy ciągu niwelacyjnego;
2) Wysokości punktów nie powinny być zależne od czynników wyznaczanych w sposób
przybliżony np. rozkład masy;
3) Poprawki przenoszące przewyższenia do określonego systemu powinny być na tyle
małe aby ich nie uwzględniać w niwelacji o niższej dokładności;
4) W przewyższeniu w danym systemie wysokości należy wydzielić część geometryczną
pochodzącą z bezpośredniego pomiaru i część geoidalną tzw. poprawkę niwelacyjną;
5) Wysokości punktów na tej samej powierzchni ekwipotencjalnej powinny być jak
najbliższe siebie.
9. Rola wartości geopotencjalnej w definiowaniu wysokości
Wartość geopotencjalna jest to "miernik wysokości"
To praca przeciwko sile ciężkości jaką należy wykonać przenosząc masę 1kg z powierzchni geoidy do
pkt P. Jest ona uniwersalnym miernikiem wysokości.
Ten parametr wykorzystuje się w definicji wysokości. Jeśli przez wysokość chcemy rozumieć drogę
wzdłuż kierunku gradientu pola W między powierzchniami
0
W
i
P
W
, tzn. najkrótszą drogę, na jakiej
wykonano pracę określoną przez liczbę geopotencjalną, to należy tę ostatnią podzielić przez siłę (a
dla jednostkowej masy przez przyspieszenie siły) właściwą dla drogi O – P wzdłuż linii pionu. Sposób
wyznaczenia przyspieszenia reprezentatywnego dla drogi O – P określa tzw. system wysokości, czyli
system geodezyjnych pomiarów wysokościowych. Jeżeli określimy przeciętną wartość rzeczywistego
przyspieszenia
g
wzdłuż linii pionu od geoidy do punktu P przez średnią wartość całki
P
dh
g
H
g
0
1
(1),
to wysokość
g
C
H
ort
będziemy nazywać wysokością ortometryczną punktu, równą długości
odcinka linii pionu (krzywej) od geoidy do punktu P. Praktyczne wyznaczenie przeciętnej wartości
g
według wzoru (1) jest niemożliwe bez hipotetycznego przyjęcia rozkładu gęstości mas Ziemi wzdłuż
linii pionu na odcinku O – P.
Dzieląc C przez tzw. przyspieszenie normalne
45
0
obliczone dla pewnego modelu rozkładu
masy w globie ziemskim (na poziomie morza i dla szerokości geograficznej 45
0
), otrzymamy tzw.
wysokości dynamiczne
45
0
C
H
dyn
, charakteryzujące się tym, że punkty wybranej powierzchni
poziomej mają takie same wysokości dynamiczne. Wysokości te mają zatem istotne znaczenie w
inżynierii, m. in. dla projektów wodnych na dużych obszarach.

Jednostka wart. geopotencjalnej 10m/s2= 1 kGal/m
-
różnica wartości potencjału między powierzchnią zerową a pow.
przechodzącą przez P
Cp- wart. geopotencjalna pkt P
Podzielenie Cp przez γk=10m/s2--> przyspieszenie, daje nam
odstęp Z powierzchni zwany wysokością. Jedną z tych pow. jest
pow. zerowa, którą przyjmujemy za poziom morza.

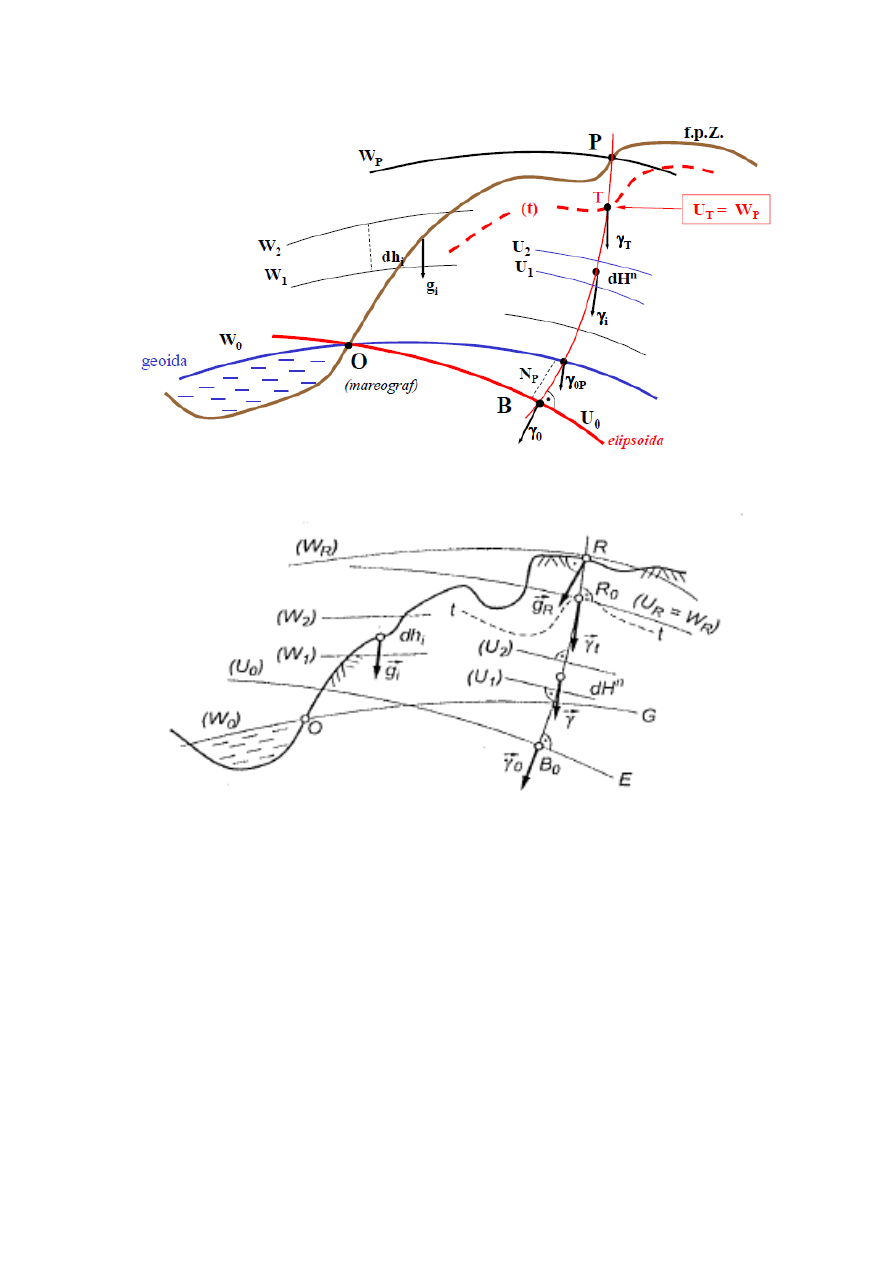
10. Definicja i znaczenie telluroidy oraz quasi-geoidy w systemie wysokości normalnych.
Telluroida – bryła, w geodezji, powierzchnia, będąca aproksymacją powierzchni Ziemi w systemie
geometrycznych wysokości normalnych Michaiła Mołodenskiego, utworzoną przez punkty, w których
normalny potencjał siły ciężkości jest równy potencjałowi rzeczywistemu (naturalnemu) punktów na
powierzchni Ziemi, leżących na tych samych normalnych liniach pionu, co punkty telluroidy, przy
czym
odstępy
telluroidy
od
powierzchni
Ziemi
są
praktycznie
równe
wysokościom quasigeoidy nad elipsoidą odniesienia.
Quasigeoida (również jako quasi-geoida) – teoretyczna powierzchnia aproksymująca swobodny
poziom mórz i oceanów w systemie wysokości normalnych. Praktyczna generalizacja geoidy,
stanowiąca powierzchnię pomocniczą przy określaniu modelu Ziemi.
Powierzchnia opracowana i zdefiniowana po raz pierwszy w latach 50. XX w. przez rosyjskiego
uczonego Michaiła S. Mołodieńskiego (1909-1991) w związku nieokreślonym kształtem geoidy w
przypadku gdy nie jest znany rozkład gęstości i położenie mas leżących na zewnątrz geoidy. W
przeciwieństwie do geoidy, quasigeoida nie jest powierzchnią ekwipotencjalną – można ją
jednoznacznie wyznaczyć.
Na obszarze mórz quasigeoida Mołodieńskiego pokrywa się z geoidą. Na obszarach lądów odstępy w
stosunku do geoidy nie przekraczają dwóch metrów – quasigeoida przebiega nad geoidą. W
przypadku obszarów równinnych, odstępy w stosunku do geoidy nie przekraczają kilku centymetrów.
W Polsce, na obszarach lądowych położonych do 750 m n.p.m., przedmiotowy odstęp mieści się w
granicach 1-3 cm, dla obszarów położonych wyżej – mieści się w granicach 5 do 10 cm.
Wartość wysokości normalnej mierzymy od quasi-geoidy
Wysokość normalna – iloraz liczby geopotencjalnej (różnica potencjału geoidy i potencjału
powierzchni przechodzącej przez punkt) przez przeciętną wartość przyspieszenia normalnego wzdłuż
linii pionu pola normalnego siły ciężkości.
Tę samą wartość liczby geopotencjalnej można przedstawić jako różnicę potencjałów elipsoidy
ekwipotencjalnej (U
0
= W
0
) oraz potencjału normalnego U
Q
w takim punkcie Q linii pionu pola
normalnego, w którym tenże potencjał jest równy potencjałowi rzeczywistemu W
P
na fizycznej
powierzchni ziemi w punkcie P: C = U
0
–U
Q
. Punkt Q leży na telluroidzie, której odległość od elipsoidy
ekwipotencjalnej jest równa wysokości normalnej H
n
. Wynika z tego, że wysokość normalna jest
jednocześnie wysokością geometryczną telluroidy (odległością telluroidy od elipsoidy).
Ścisłe wyznaczenie wysokości normalnych możemy otrzymać poprzez całkowanie wzoru na
przyspieszenie normalne dla wysokości h ponad elipsoidą. Dzięki procesowi iteracyjnemu możemy
dokładnie wyznaczyć wysokość normalną. Przybliżoną wysokość normalną otrzymujemy z różnicy
wysokości normalnych. Różnica ta jest sumą poprawki normalnej (wyznaczanej z przeciętnej
przyspieszenia normalnego na elipsoidzie dla średniej szerokości i średniej wysokości) i sumy
pomierzonych różnic wysokości.
11. Związek wysokości elipsoidalnej i normalnej i jego zastosowanie w geodezji.
Wysokość normalna H punktu P jest to różnica potencjałów siły ciężkości W0-WP na powierzchni
geoidy (W0) oraz w danym punkcie (WP), czyli wartość geopotencjalna CP podzielona przez średnią
wartość przyspieszenia siły ciężkości , mierzonego wzdłuż linii pionu normalnego pola siły ciężkości.
Uwzględniając, że : CP=W0-WP otrzymamy: H=Cp. Wysokość normalną interpretuje się też jako
odległość danego punktu od guasigeoidy mierzoną wzdłuż normalnej linii pionu.
Wysokość elipsoidalna h, czyli odległość pomiędzy danym punktem P a powierzchnią elipsoidy
odniesienia. Wysokość ta jest dodatnia dla punktów leżących ponad elipsoidą. Odstęp N geoidy od
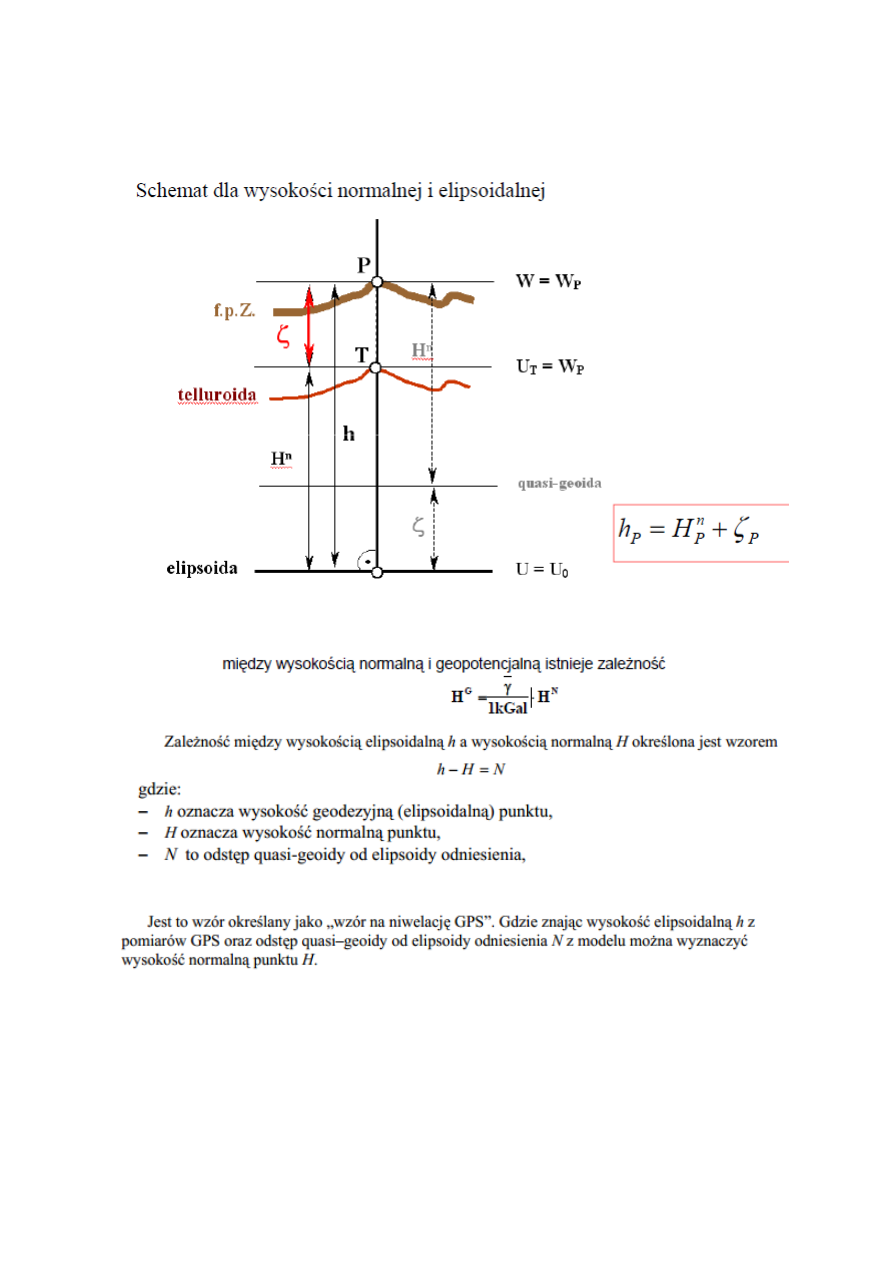
elipsoidy zależy od poziomego położenia punktu, określonego współrzędnymi B, L i wyraża się
wzorem: N=h-H.

12. Zamiana wysokości między różnymi systemami wysokościowymi na przykładzie dwóch
wybranych systemów.
Wyróżniamy 3 główne systemy wysokościowe:
1. System wysokości dynamicznych, gdzie wysokość punktu P nad geoidą wyrażona jest wzorem:
gdzie:
- liczba geopotencjalna
- wartość przyspieszenia normalnego siły ciężkości dla szerokości B = 45
2. System wysokości ortometrycznych, gdzie wysokość punktu P nad geoidą wyrażona jest wzorem:
gdzie:
- liczba geopotencjalna
- przeciętna wartość rzeczywistego przyspieszenia siły ciężkości
3. System wysokości normalnych, gdzie wysokość punktu P nad quasigeoidą wyrażona jest wzorem:
gdzie:
- liczba geopotencjalna
– przeciętna wartość normalnego przyspieszenia siły ciężkości
Wspólną wartością łączącą 3 systemy wysokościowe jest liczba geopotencjalna
(jednostka:
potencjału) lub
(specjalna jedno.: jednostka geopotencjalna) , wyrażająca różnicę
potencjałów
W pomiędzy geoidą, a pewną powierzchnią ekwipotencjalną przechodzącą przez punkt P.
Wykorzystując zależność różnych systemów wysokości od liczby geopotencjalnej
, mamy:
1.
gdzie:
- odpowiednie przyspieszenie siły ciężkości
2.
3. Przykład zamiany dla systemu wysokości normalnych i wysokości dynamicznych:
Z normalnej na dynamiczną:
Z dynamicznej na normalną:

13. Odstęp quasi-geoidy od geoidy – wielkości niezbędne do jego wyznaczenia, znaczenie
składników wzoru na odstęp.
Wielkości niezbędne do wyznaczenia odstępu (temat 4):
1. Współrzędne geodezyjne (szerokość ϕ i długość geograficzna λ),
2. Wysokości normalne punktów
,
3. Wartości przyspieszenia siły ciężkości g,
4. Gradient pionowy przyspieszenia siły ciężkości G,
5. Wartości poprawki topograficznej R
T
,
6. Wartości gęstości wierzchniej warstwy skorupy ziemskiej σ
I składnik:
1. Ma on największy wpływ na wartość wyznaczanego odstępu quasigeoidy od geoidy. Dla Ag
B
rzędu 10
2
mGal (obszary górskie) oraz dla przyspieszenia γ przeciętnego normalnego rzędu 10
6
mGal składnik ten osiągnie wielkość ok 10cm. Na obszarach nizinnych jego wielkość będzie
zdecydowanie mniejsza (do 1cm). Stąd w wielu przypadkach wartość ta jest wystarczająca a
pozostałe składniki wzoru pomija się.
2. Ze względu na niewielką wartość ułamka
wysokość ortometryczną w tym składniku
zastępuje się wysokością normalną lub po prostu przybliżoną wysokością.
II składnik:
1. wartość drugiego składnika będzie miała znaczenie jedynie na obszarach górskich, wynika to z
różnicy gradientu normalnego I rzeczywistego (Γ-G), który na tym obszarze może osiągać
wartość 0,1 mGal. Zatem przy wysokości rzędu 500-1000 m składnik ten będzie rzędu 1-5 cm.
III składnik:
1. Ostatni składnik wzoru na obszarze Polski osiąga wartości nie większe niż 0,02mm, a więc jest
do pominięcia.
Wnioski:
Dla obszaru Polski najczęściej odstęp quasi-geoidy od geoidy oblicza się na podstawie I składnika
(anomalii Bouguera). Na obszarach górskich należałoby uwzględnić II składnik wzoru po uprzednim
wyznaczeniu rzeczywistego gradientu przyspieszenia siły ciężkości.
14. Na czym polega niwelacja astronomiczno-geodezyjna i astronomiczno-
grawimetryczna
Odstępy geoidy/quasi-geoidy od elipsoidy są niezbędne do:
- wyznaczenia kształtu bryły Ziemi,
- redukcji obserwacji geodezyjnych na powierzchnię odniesienia (elipsoidę),
- integracji niwelacji klasycznej i satelitarnej.
Wyznaczenie przyrostów odstępów geoidy/quasi-geoidy od elipsoidy jest możliwe za pomocą
odpowiedniego opracowania pomiarów astronomicznych, geodezyjnych (w tym satelitarnych)
i grawimetrycznych.
NIWELACJA ASTRONOMICZNO-GEODEZYJNA
Niwelacja astronomiczna
(astronomiczno-geodezyjna) polega na wyznaczaniu przyrostów
odstępów (dN) na podstawie znanych składowych (
,
) względnego odchylenia linii pionu (
) w
punktach wybranego profilu i w kierunku określonym azymutem (
).
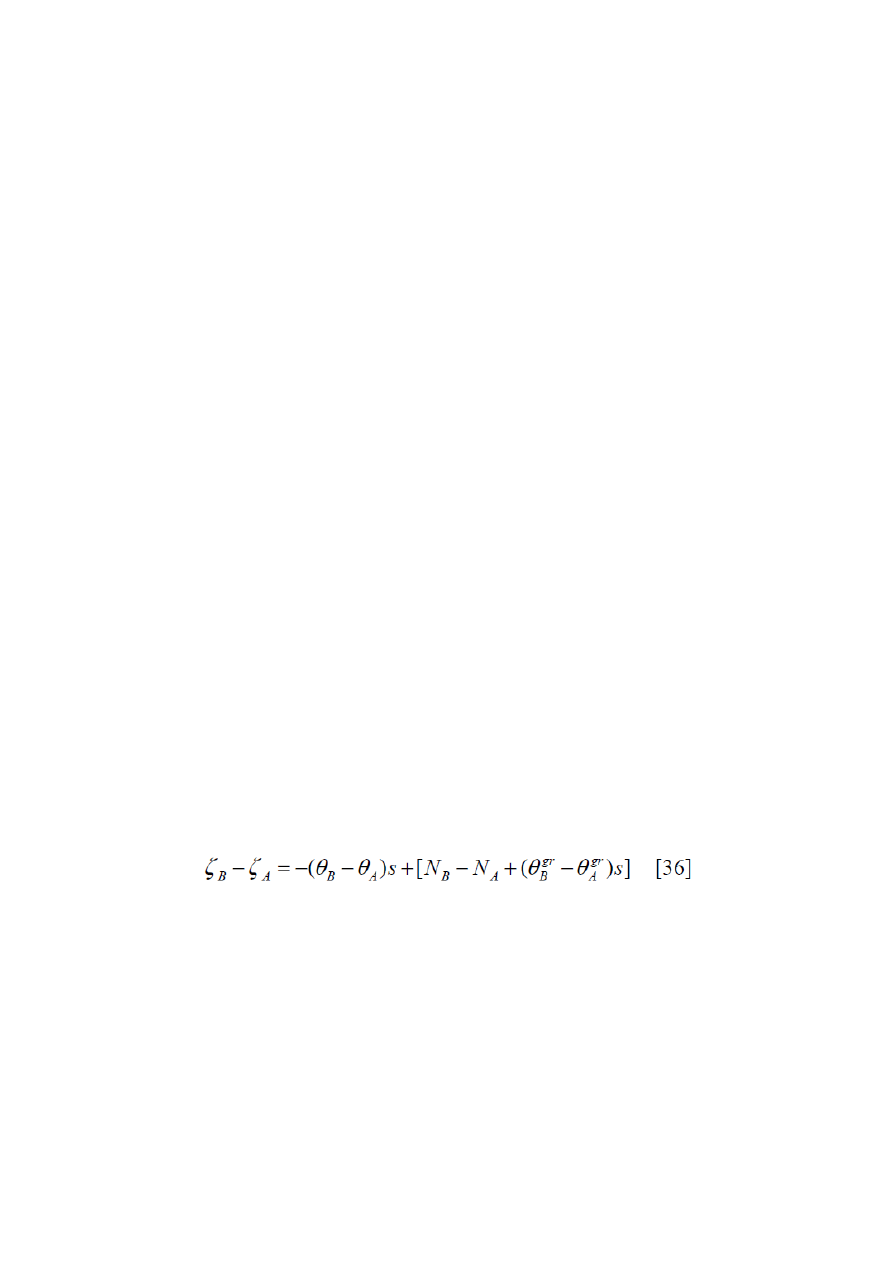
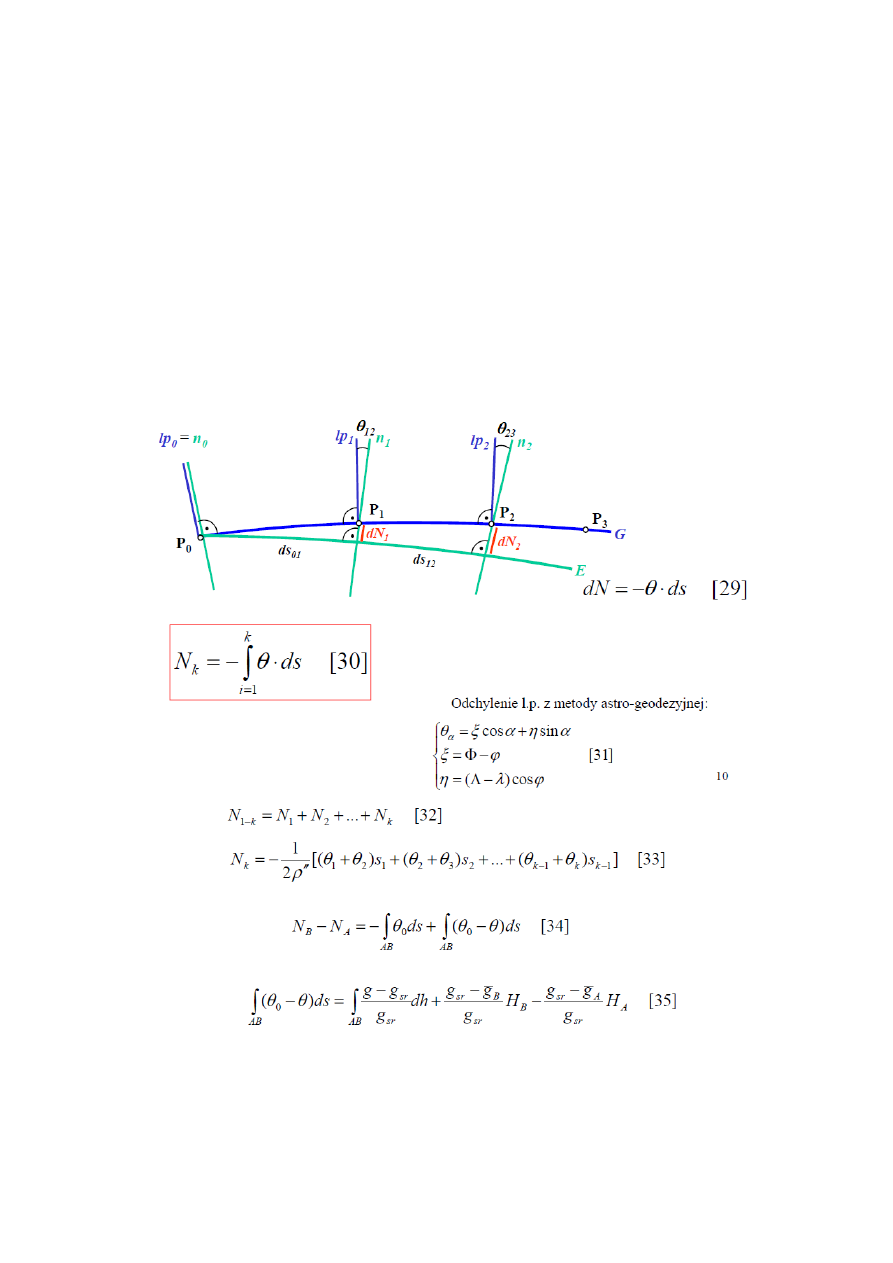
Rysunek: w P
0
punkcie początkowym pewnego profilu powierzchnia geoidy pokrywa się z
powierzchnią elipsoidy. Stąd odstęp między ww. powierzchniami jest zerowy a linia pionu pokrywa
się z normalną do elipsoidy. W kolejnym punkcie P
1
omawianego profilu odległym od P o niewielka
odległość ds
01
nachylenie obu powierzchni zmienia się a w związku z tym odchylenie linii pionu od
normalnej wzrasta do wartości
12
wobec tego na drodze ds. nastąpił przyrost odstępu dN
1
. Na
drodze od P
1
do P
2
nastąpił podobny przyrost odchylenia do wartości
23
i odpowiedni przyrost
odstępu do wartości dN
2
. Przyrosty odstępów dN są w ścisłym związku z odpowiadającymi im
przyrostami odchylenia
na drodze s, zgodnie z wzorem [29], przy czym znak „_” określa kierunek
wzrastania odstępu. A zatem wysokość punktu końcowego K tego profilu nad elipsoidą będzie można
obliczyć po scałkowaniu zależności [29] czyli wzorem [30]. W praktyce nie można zrealizować tego
wzoru ze względu na zmienną wartość odchylenia linii pionu na danym odcinku. Zmienność tą nie da
się opisać jakąś zależnością funkcyjną co wyklucza całkowanie analityczne. Stąd istnieje konieczność
podziału profilu na krótkie odcinki i sumowaniu przyrostów odstępów na każdym z nich (całkowanie
numeryczne).
Wartości odchylenia linii pionu oblicza się w kolejnych punktach profilu z metody astro-
geodezyjnej, czyli na podstawie znanych współrzędnych F,L-astronomicznych i j,l- geodezyjnych
zgodnie z wzorami [31].
Zgodnie z powyższym odstęp w punkcie końcowym będzie równy sumie odstępów
obliczonych na poszczególnych punktach profilu A-B na f.p.Z. wg wzoru [32], przy czym do obliczenia
każdego z nich wykorzystuje się średnie odchylenie wyznaczone na sąsiednich punktach [33]. Przy
założeniu liniowej zmiany odchylenia na kolejnych odcinkach (i;i+1) przyjmuje się graniczne długości
odcinków:
S < 20km na obszarach nizinnych
S < 3-5km na obszarach górskich.
Obliczenie odstępu dla odchyleń pionu znanych na fizycznej powierzchni Ziemi (punkty P0,...PK
znajdują się na f.p.Z.) należy uwzględnić dodatkowo zmianę krzywizny powierzchni
ekwipotencjalnych geopa z f.p.Z. (qfpZ ¹ qgeoida = q0) w porównaniu z geoidą (drugi składnik wzoru
[34]). Składnik ten można obliczyć na podstawie odpowiedniego rozpoznania grawimetrycznego
zgodnie z zależnością [35], gdzie: gsr – średnie przyspieszenie w kolejnych punktach profilu A-B, „g z
kreską” – przyspieszenie przeciętne w połowie wysokości (zredukowane redukcją Poincarego-Preya),
H – wysokości punktów nad geoidą.
Warto przypomnieć, że geopem – nazywamy powierzchnię ekwipotencjalną potencjału
rzeczywistego ciężkościowego na poziomie dowolnego punktu, geopem na poziomie morza jest
geoida.
NIWELACJA ASTRONOMICZNO-GRAWIMETRYCZNA
Ten rodzaj niwelacji wykorzystuje zarówno pomiary astronomiczno-geodezyjne (jak poprzednio
omawiana niwelacja) jak i odchylenia wyznaczone metodą Veniga-Meinesza z map anomalii
grawimetrycznych oraz odstępy określone metodą Stokesa (metoda grawimetryczna badania figury
Ziemi). Ogólny wzór realizujący niwelację astronomiczno- grawimetryczną ma postać [36], gdzie:
B
,
A
– undulacja quasi-geoidy w punktach A i B,
B
,
A
– astronomiczne odchylenie linii pionu,
N
A
,N
B
– undulacja geoidy w punktach A i B (metoda grawimetryczna Stokesa),
B
gr
,
A
gr
– grawimetryczne odchylenie linii pionu z map anomalii grawimetrycznych (Venig-
Meinesz),
S – odległość między punktami A i B.
Metoda niwelacji astronomiczno-grawimetrycznej umożliwia ograniczenie liczby punktów, w których
wykonuje się obserwacje astronomiczne do wyznaczenia astronomicznego odchylenia linii pionu.

15. Wyjaśnić wpływ zjawiska pływowego na pomiar przewyższenia i przyspieszenia sił
ciężkości (rysunek z komentarzem)
Wychylenie linii pionu wywołane przyciąganiem Słońca i Księżyca zilustrowano na rys. Wektor
ciężkości ziemskiej w punkcie P oznaczono przez g. Przyciąganie Słońca i Księżyca generuje niewielki
wektor przyciągana grawitacyjnego
g
SK
. Wektor ten działa na kierunku określonym kątem
zenitalnym z
SK
. Suma wektorów g i
g
SK
jest równa wektorowi g
SK
wychylonemu od pierwotnego
kierunku o niewielki kąt
. Wartość tego kąta łatwo można obliczyć na podstawie g i
g
SK
[22]. Z kolei
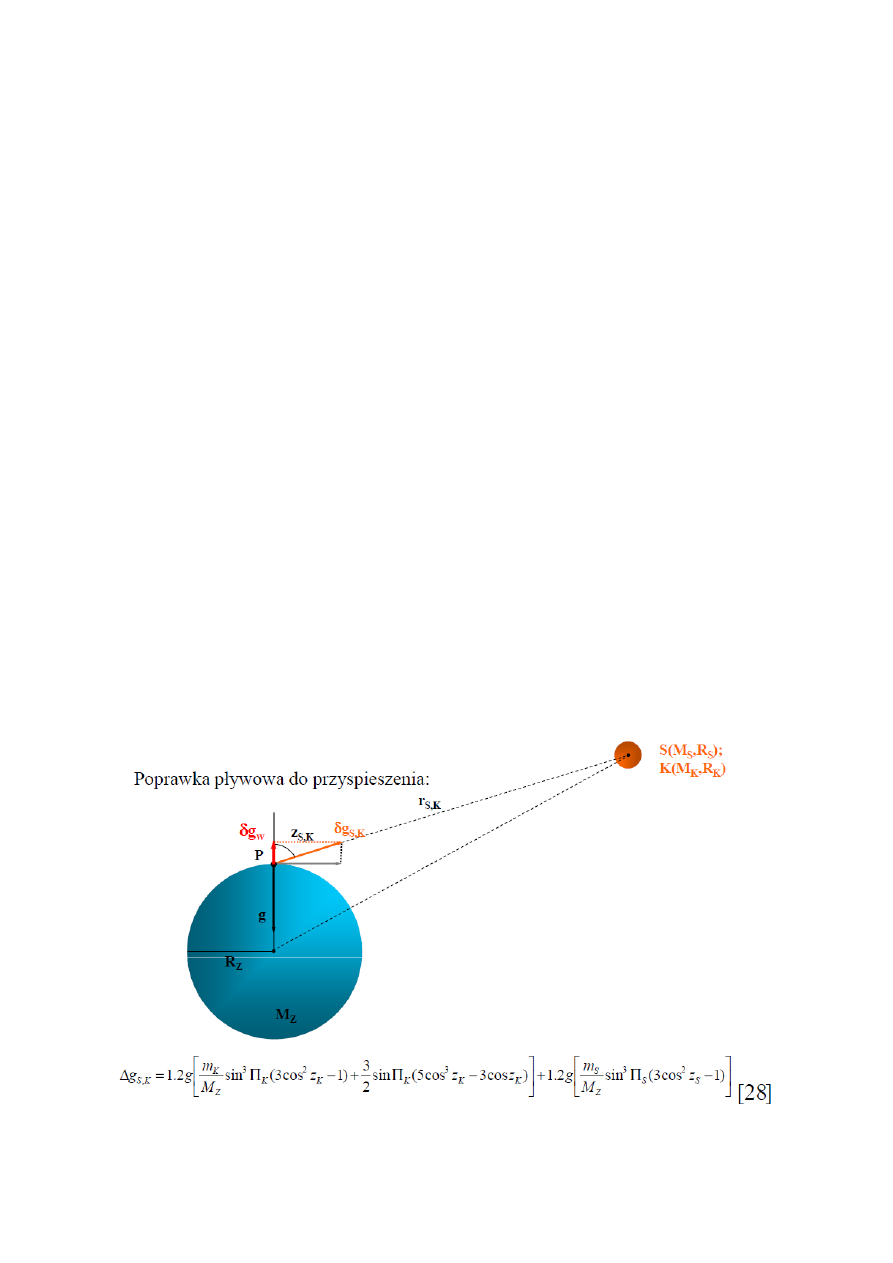
grawitacyjne przyciąganie Słońca albo Księżyca można obliczyć znając masy i rozmiary obu ciał oraz
ich odległości i kierunek działania tego przyciągania [23]. Ostatecznie kierunek linii pionu czyli
kierunek wektora ciężkości po uwzględnieniu przyciągania obu ciał niebieskich musi jeszcze
uwzględniać różne położenie obu ciał względem punktu P. Jest to realizowane dla kierunku danego
azymutu A i azymutu Słońca oraz Księżyca w danym momencie. Wartość wychylenia linii pionu
jest
wychyleniem linii w płaszczyźnie azymutu A [24].
Niektóre wielkości wzoru [24] są stałe stąd można je obliczyć, podać w postaci
współczynników i w ten sposób uprościć wzór [25]. Zmiennymi pozostają współrzędne Słońca i
Księżyca (azymut, kąt zenitalny) oraz azymut kierunku na powierzchni Ziemi (A). Współrzędne są
zmienne w czasie, co oznacza, że ich wartość należy obliczyć na określony moment. Wymaga to
znajomości tego momentu (czas) ale również informacji o wyjściowym położeniu obu ciał. To drugie
znajdziemy w Roczniku Astronomicznym w funkcji współrzędnych równikowych godzinnych.
Konieczne zatem będzie powiązanie tych współrzędnych z układem horyzontalnym (z, A - trójkąt
paralaktyczny).
Wychylenie linii pionu wpływa na orientację (spoziomowanie) np. niwelatora wykonującego
pomiar niwelacji precyzyjnej. Inne spoziomowanie generuje inne mierzone przewyższenia a zatem
inne wyniki niwelacji. W związku z tym wyniki pomiarów niwelacyjnych należałoby odnieść do
warunków pomiaru niezależnych od zmiennego wpływu Słońca i Księżyca. Wychylenie linii pionu o
kąt
powoduje przyrost wysokości proporcjonalnie do s. W związku z tym
h czyli tzw. poprawka
pływowa wyniesie [26].
Elastyczne własności skorupy Ziemi sprawiają, że teoretycznie obliczony przyrost wysokości jest
rekompensowany zgodnie ze współczynnikiem elastyczności
. W Polsce przyjmuje się jego wartość
równą 0.8. Zatem poprawka pływowa do wyników niwelacji oblicza się ostatecznie z wzoru [27].
Warto zauważyć, że dla takiego samego położenia wpływa Księżyca jest dwukrotnie większy
niż wpływa Słońca.
Ze względu na czas wykonywania pomiaru odcinka niwelacyjnego (długość odcinków,
niwelacja "tam i z powrotem") poprawkę wprowadza się tylko do przewyższenia na kierunku "tam" i
"z powrotem", czyli dla średniego położenia Słońca i Księżyca w czasie pomiaru w każdym z ww.
kierunków. Potrzebne są zatem założenia co do czasu pomiaru a także zmienności azymutu odcinka
niwelacyjnego. Czas pomiaru dla danego kierunku nie powinien być większy niż 2.5
h
,
<15
.

Zjawisko przyciągania Słońca i Księżyca wpływa na wartość pomiaru przyspieszenia
ciężkościowego na powierzchni Ziemi. Tym razem interesuje nas składowa pionowa
g
w
wektora
przyciągania
g
SK
. Zwrot wektora
g
w
będzie przeciwny do wektora ciężkości a zatem przyciąganie
ww. ciał niebieskich będzie zmniejszać mierzone przyspieszenie. Wartość
g
w
podobnie jak
poprzednio zależy od położenia obu ciał względem punktu pomiaru przyspieszenia na powierzchni
Ziemi. Zamiast azymutu nieistotnego na kierunku pionowym ważna jest wartość paralaksy
obu ciał.
Wzór [28] służy do obliczenia przyrostu przyspieszenia wynikającego przez grawitacyjne
oddziaływanie Słońca i Księżyca. Pozwala on obliczyć poprawkę z dokładnością poprawki 0.01 mGal.
Pierwsza jego część związana z wpływem Księżyca osiąga maksymalne wartości rzędu 165 mGal,
druga - wpływ Słońca - to maksymalnie 76 mGal. Na pomiar przyspieszenia na f.p.Z. wpływają
również inne planety. Wpływ ten jest jednak znikomy i nie przekracza w sumie 0.01 mGal.
Obserwacje pływów dostarczają cennych informacji nt. pola ciężkościowego Ziemi i budowy
oraz własności skorupy Ziemi. Stąd wykonuje się je permanentnie stacjach pływowych za pomocą
grawimetrów stacjonarnych (pływowych).

16. Zjawiska wykorzystywane do pomiaru przyspieszenia siły ciężkości.
–
zjawisko swobodnego spadku ciała w polu siły ciężkości
Pomiary balistyczne – wykorzystujące realizację równania drogi przebytej w polu siły
ciężkości ruchem jednostajnie przyspieszonym (spadek próbnika) lub/i jednostajnie
opóźnionym (podrzut i spadek próbnika w próżni).
–
zjawisko wahadła fizycznego,
Pomiary wahadłowe – wykorzystujące obserwacje zależności okresu swobodnego ruchu
wahadła od przyspieszenia siły ciężkości w miejscu pomiaru. W aparacie notuje się interwał
czasu między kolejnymi przejściami przez położenie równowagi lub od jednego skrajnego
położenia do drugiego.
–
zjawisko równoważenia siły ciężkości siłą sprężystości ciała stałego, gazu
–
zjawiska naprężenia struny (drgania)
Obserwacje częstotliwości drgań własnych obciążonej metalowej struny, związanej
funkcyjnie z wartością przyspieszenia siły ciężkości.
–
zjawiska przemieszczenia się naładowanych cząstek w polu elektrycznym
DOCZYTAĆ!!!!!!!!!!!!!!

Pomiary grawimetryczne
dzielimy na:
pomiary absolutne (bezwzględne) – w wyniku których uzyskujemy pełną wartość
przyspieszenia siły ciężkości g w miejscu obserwacji. Do tych wyznaczeń możemy użyć tylko
metod dynamicznych. Chcąc uzyskać wyniki z dostateczną dokładnością konieczne jest
wykonywanie wielogodzinnych cyklów obserwacyjnych oraz stosowanie bardzo
zaawansowanych instrumentów.
pomiary względne – dostarczające przyrostu przyspieszenia siły ciężkości ∆g między
stanowiskami instrumentu. Niegdyś do tych pomiarów używało się aparatów wahadłowych
obecnie stosuje się prawie wyłącznie grawimetry statyczne.
Rejestruje się zmiany długości
lub skręcenia nici (czyli deformację sprężyny pomiarowej) lub kąta nachylenia systemu
pomiarowego.
Ze względu na sposób pomiaru i konstrukcję elementu czujnikowego grawimetru dzieli się
metody pomiarów przyspieszenia siły ciężkości na dwie grupy:
pomiary dynamiczne (obserwacje ruchu ciała w polu siły ciężkości)
i pomiary statyczne (obserwacje stanu równowagi masy czujnika grawitacyjnego, na którą
działa zarówno siła ciężkości, jak i siła ją kompensująca, wzorcowa, dokładnie określana
mechanicznie lub elektronicznie). Do dynamicznych metod pomiarów grawimetrycznych
zalicza się:
Metody statyczne pomiarów grawimetrycznych polegają na doprowadzaniu masy próbnej M
umieszczonej w systemie pomiarowym do stanu równowagi za pomocą wzorcowanej siły
kompensującej F. Równanie równowagi spełnione w tym momencie w grawimetrze
statycznym przez jego system ma postać znaną z mechaniki:
Siła kompensująca może być wytwarzana przez deformację skręcanej nici, wydłużanie
(skracanie) sprężyny, a także przez siłę elektromotoryczną, działającą na przewodnik pod
napięciem elektrycznym w polu magnetycznym.

17. Definicja punktu grawimetrycznego, sieci grawimetrycznej i poziomu odniesienia
grawimetrycznego. Jak obecnie realizowany jest poziom odniesienia grawimetrycznego.
Punkt grawimetryczny – punkt sieci grawimetrycznej trwale zastabilizowany lub zaznaczony
na powierzchni Ziemi, w którym wyznaczono wartość przyspieszenia siły ciężkości lub jego
gradientu.
Sieć grawimetryczna – ustabilizowany zbiór punktów grawimetrycznych na danym terenie,
dla których w wyniku opracowania pomiarów grawimetrycznych określono przyspieszenie
siły ciężkości w odniesieniu do danej epoki.
Poziom odniesienia grawimetrycznego – miejsce gdzie pierwotnie wyznaczono wartość
przyśpieszenia, do tego punktu należało się odnieść. poziom grawimetryczny sieci IGSN71
jest określony przez 10 absolutnych pomiarów g na 8 stacjach grawimetrycznych, zaś cała sieć
składa się z 1854 punktów. IGNS71-system punktów odniesienia, w tej chwili okresowo co 2
lata kalibracja przyrządów pomiarowych.
Grawimetryczny poziom odniesienia, jest ustalony na podstawie absolutnych pomiarów
przyspieszenia siły ciężkości.

18. Zjawiska wykorzystane do pomiaru przyśpieszenia siły ciężkości
Do wyznaczania wartości przyspieszenia ciężkościowego wykorzystuje się kilka zjawisk fizycznych:
swobodny spadek ciała, ruch wahadła, precesja giroskopu, drganie struny, zakrzywienie powierzchni
wirującej cieczy, deformacja ciał sprężystych, ruch przewodnika lub naładowanych cząstek w polu
magnesu stałego i inne.
Wszystkie zjawiska wykorzystywane do wyznaczenia przyspieszenia lub jego gradientu można
podzielić na:
*statyczne
- polegające na równoważeniu siły ciężkości siłą sprężystości ciała lub siłami pola
magnetycznego,
obserwacje stanu równowagi masy czujnika grawitacyjnego, na którą działa zarówno siła
ciężkości, jak i siła ją kompensująca, wzorcowa, dokładnie określana mechanicznie lub elektronicznie
*dynamiczne
-
obserwacje ruchu ciała w polu siły ciężkości;
swobodny spadek ciała, wahanie wahadła,
drganie struny.
Z kolei wyznaczenia przyspieszenia można podzielić na:
*absolutne - celem jest wyznaczenie wartości p.s.c. w danym punkcie.
Do tych wyznaczeń możemy
użyć tylko metod dynamicznych. Chcąc uzyskać wyniki z dostateczną dokładnością konieczne jest wykonywanie
wielogodzinnych cyklów obserwacyjnych oraz stosowanie bardzo zaawansowanych instrumentów.
*względne - celem jest wyznaczenie różnicy przyspieszeń między punktami na podstawie pomiarów
p.s.c. na punktach.
Dostarczające one przyrostu przyspieszenia siły ciężkości Δg między stanowiskami
instrumentu. Niegdyś do tych pomiarów używało się aparatów wahadłowych obecnie stosuje się prawie
wyłącznie grawimetry statyczne
Do dynamicznych metod pomiarów grawimetrycznych zalicza się:
Pomiary wahadłowe – wykorzystujące obserwacje zależności okresu swobodnego ruchu wahadła od
przyspieszenia siły ciężkości w miejscu pomiaru. W aparacie notuje się interwał czasu między kolejnymi
przejściami przez położenie równowagi lub od jednego skrajnego położenia do drugiego.
Pomiary balistyczne – wykorzystujące realizację równania drogi przebytej w polu siły ciężkości ruchem
jednostajnie przyspieszonym (spadek próbnika) lub/i jednostajnie opóźnionym (podrzut i spadek próbnika w
próżni).
Obserwacje częstotliwości drgań własnych obciążonej metalowej struny, związanej funkcyjnie z wartością
przyspieszenia siły ciężkości.
Metody statyczne pomiarów grawimetrycznych polegają na doprowadzaniu masy próbnej M umieszczonej w
systemie pomiarowym do stanu równowagi za pomocą wzorcowanej siły kompensującej F. Równanie
równowagi spełnione w tym momencie w grawimetrze statycznym przez jego system ma postać znaną z
mechaniki Mg+f=0
Siła kompensująca może być wytwarzana przez deformację skręcanej nici, wydłużanie (skracanie) sprężyny, a
także przez siłę elektromotoryczną, działającą na przewodnik pod napięciem elektrycznym w polu
magnetycznym.
Inny sposób podziału obserwacji grawimetrycznych to wyróżnienie pomiarów absolutnych (bezwzględnych) i
względnych (różnicowych). Bezpośrednie pomiary wartości drugich pochodnych potencjału siły ciężkości są
wyznaczeniami bezwzględnymi, natomiast pomiary absolutne natężenia siły ciężkości służą do określania pełnej
wartości wektora przyspieszenia siły ciężkości g. Ponieważ wymiar przyspieszenia liniowego zawiera w sobie
zarówno długość, jak i czas, dlatego określenie natężenia tej siły wymaga pomiaru wartości tych dwóch
wielkości. Wymogowi temu odpowiadają tylko metody dynamiczne. Aparatura pomiarowa musi zatem
posiadać wzorzec długości (dalmierz, interferometr) i czasu (zegar). Ze względu na ograniczenie rozmiarów
aparatury zarówno koniecznością transportu, jak i możliwościami zapewnienia dużej stabilności warunków
zewnętrznych (ciśnienie, wilgotność i temperatura powietrza, izolacja od mikrosejsm), odcinek obserwacji
ruchu próbnika w aparacie balistycznym nie przekracza 1 m, a interwał czasu – 1 s.
Grawimetryczne pomiary względne służą do określania różnic (przyrostów) natężenia siły ciężkości Dg między
stanowiskami obserwacyjnymi. Wyznacza się przy tym zmiany wskazań tego samego przyrządu (grawimetru) na
punkcie wyjściowym ciągu (bazowym, oporowym) i na punkcie pomiarowym, na którym określa się wartość
przyspieszenia. Rejestruje się za pomocą odpowiedniego systemu odczytowego grawimetru statycznego

zmiany długości lub skręcenia nici (czyli deformację sprężyny pomiarowej) lub kąta nachylenia systemu
pomiarowego. Natomiast obsługa grawimetru względnego dynamicznego może polegać na rejestracji czasu
(okresu) drgań wahadła lub częstotliwości drgań struny.
19. Definicja punktu grawimetrycznego, sieci grawimetrycznej i poziomu odniesienia grawimetrycznego.
Punkt grawimetryczny
- fizyczny, trwale zastabilizowany lub oznaczony punkt na powierzchni (lub
pod powierzchnią) Ziemi, na którym wyznaczono drogą pomiarów grawimetrycznych wartość
przyspieszenia s.c.(lub jego gradientu)
Sieć grawimetryczna - usystematyzowany zbiór punktów w terenie, dla których w wyniku
opracowania pomiarów grawimetrycznych określono przyspieszenie siły ciężkości odniesione do
przyjętej epoki.
Poziom odniesienia grawimetrycznego
- umownie przyjęta wartość przyspieszenia s.c.
-
w tzw. punkcie Helmerta w Poczdamie (system Poczdamski, 1909),
-
IGSN-71, 10 punktów (International Gravity Standardization Net 1971) (poprawka –14mGal),
-
Ustalony na podstawie okresowych kampanii kalibracyjnych grawimetrów absolutnych
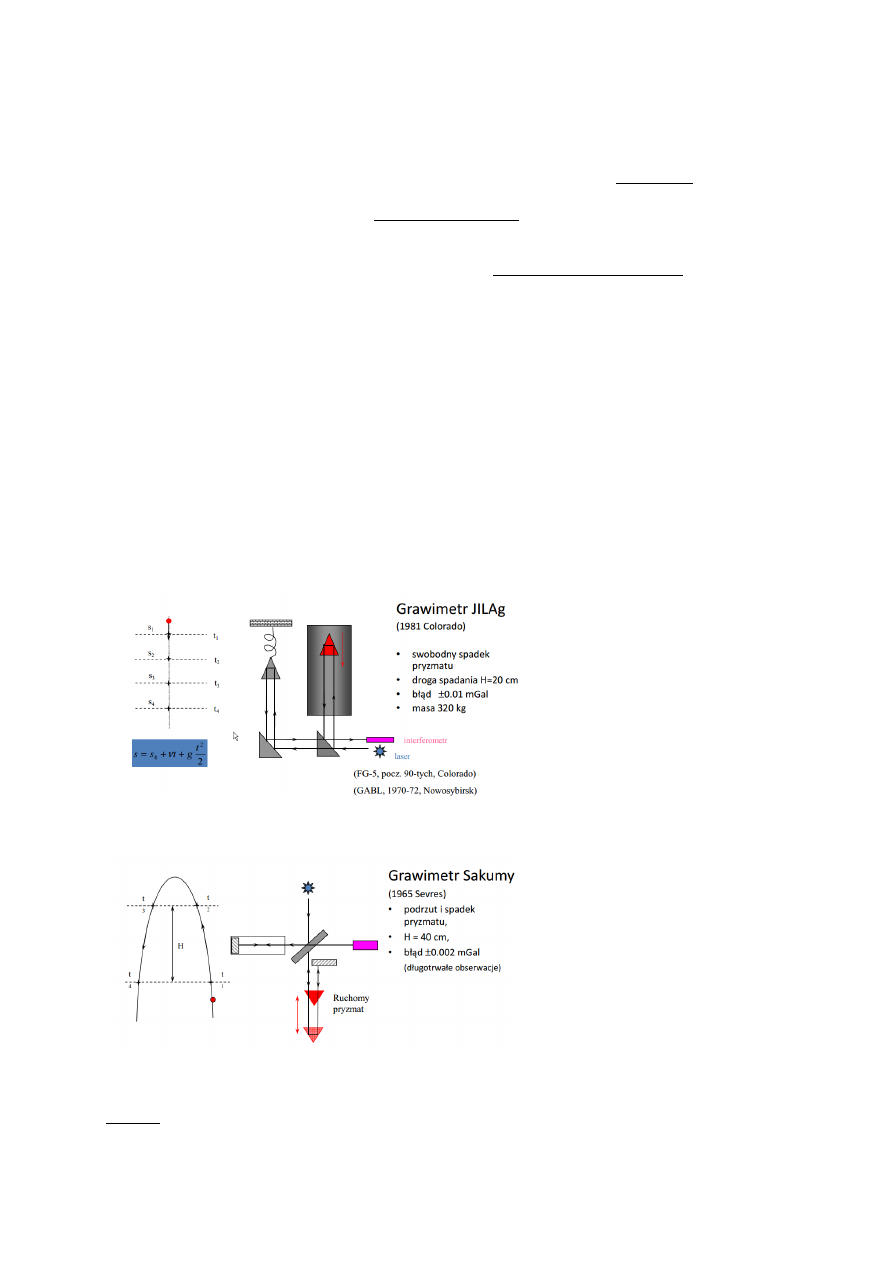
20. Zasada działania grawimetru balistycznego oraz statycznego (rodzaje błędów, eliminacja
niekorzystnych zjawisk występujących podczas pomiaru).
Grawimetr jest to urządzenie stosowane powszechnie do pomiarów przyśpieszenia siły ciężkości.
Rozróżniamy wiele typów grawimetrów np. grawimetry balistyczne. Poszczególne konstrukcje grawimetrów
balistycznych wykorzystujących spadek ciała różni sposób ruchu (spadek lub podrzut i spadek), długość drogi
(s), liczba detektorów a także sposób wykorzystania (stacjonarny lub przenośny), masa, błąd wyznaczenia
przyspieszenia. Idea pomiarów tym przyrządem na przykładzie grawimetru balistycznego JILAg sprowadza się
do wyznaczenia wartości przyspieszenia ziemskiego w danym punkcie (wyznaczenia dynamiczne, absolutne).
Grawimetr składa się z próżniowej rury, w której na pewnym podnośniku umieszczony jest pryzmat wraz z
kilkoma detektorami ruchu, źródła światła laserowego i interferometru oraz zespołu pryzmatów
skierowujących część promienia świetlnego do interferometru. Pryzmat w rurze jest podnoszony na pewną
wysokość po czym spada swobodnie. Promień światła ze źródła jest rozdzielany i pokonuje dwie drogi: jedna o
stałej długości (przez zespół pryzmatów), druga zmienna przez spadający pryzmat. Długość tej drogi jest zależna
od położenia przemieszczającego się w polu siły ciężkości pryzmatu. Pryzmat porusza się ruchem jednostajnie
przyspieszonym z przyspieszeniem równym przyspieszeniu siły ciężkości (g). Ruch pryzmatu kontrolowany jest
przez rejestrację momentu (t) przejścia przez kolejne detektory rozmieszczone w znanych odległościach (s).
Identyfikację promienia świetlnego realizowany jest interferometr. Podstawowym równaniem opisującym ruch
pryzmatu jest równanie drogi (s) w ruchu jednostajnie przyspieszonym, ze znanymi wartościami czasu (t),
prędkości początkowej (V0), drogi początkowej (s0). Należy podkreślić, że obserwacje tego rodzaju
grawimetrami balistycznymi realizowane są w sposób automatyczny, w wielogodzinnych sesjach, dzięki czemu
uzyskuje się dużą liczbę wyznaczeń. Grawimetry balistyczne ze względu na swoją konstrukcję i dużą masę
dobrze sprawdzają się jako urządzenia stacjonarne, służące np. do badania pływów na punktach stacji
pływowych. Obecnie coraz częściej wykorzystuje się w pomiarach są grawimetry balistyczne przewoźne,
montowane na kilkudniowe pomiary na danym punkcie podstawowej osnowy grawimetrycznej.
Inne wykorzystywane grawimetry balistyczne :
Grawimetr FG-5, Grawimetr polski ZZG (PW)
Czynniki, które niekorzystnie wpływają na dokładność wyznaczenia przyspieszenia:
zjawiska pochodzenia zewnętrznego takie jak:
– opór pozostałości powietrza w rurze próżniowej,
– wpływ pola magnetycznego i elektrycznego Ziemi,
– wpływ mikrosejsmy podłoża,
– wahania grawimetru na skutek podrzutu/upadku,
oraz niedoskonałości konstrukcji grawimetru:
– obroty i wahania podrzucanego/spadającego pryzmatu,
– nachylenie promienia świetlnego,
– opóźnienia sygnału świetlnego.
Biorąc pod uwagę potrzebę wyznaczenia precyzyjnego przyspieszenia (ważne np. w badaniu zjawisk
geodynamicznych) powyższe czynniki muszą być eliminowane lub ich wpływ powinien być w znacznym stopniu
osłabiany.
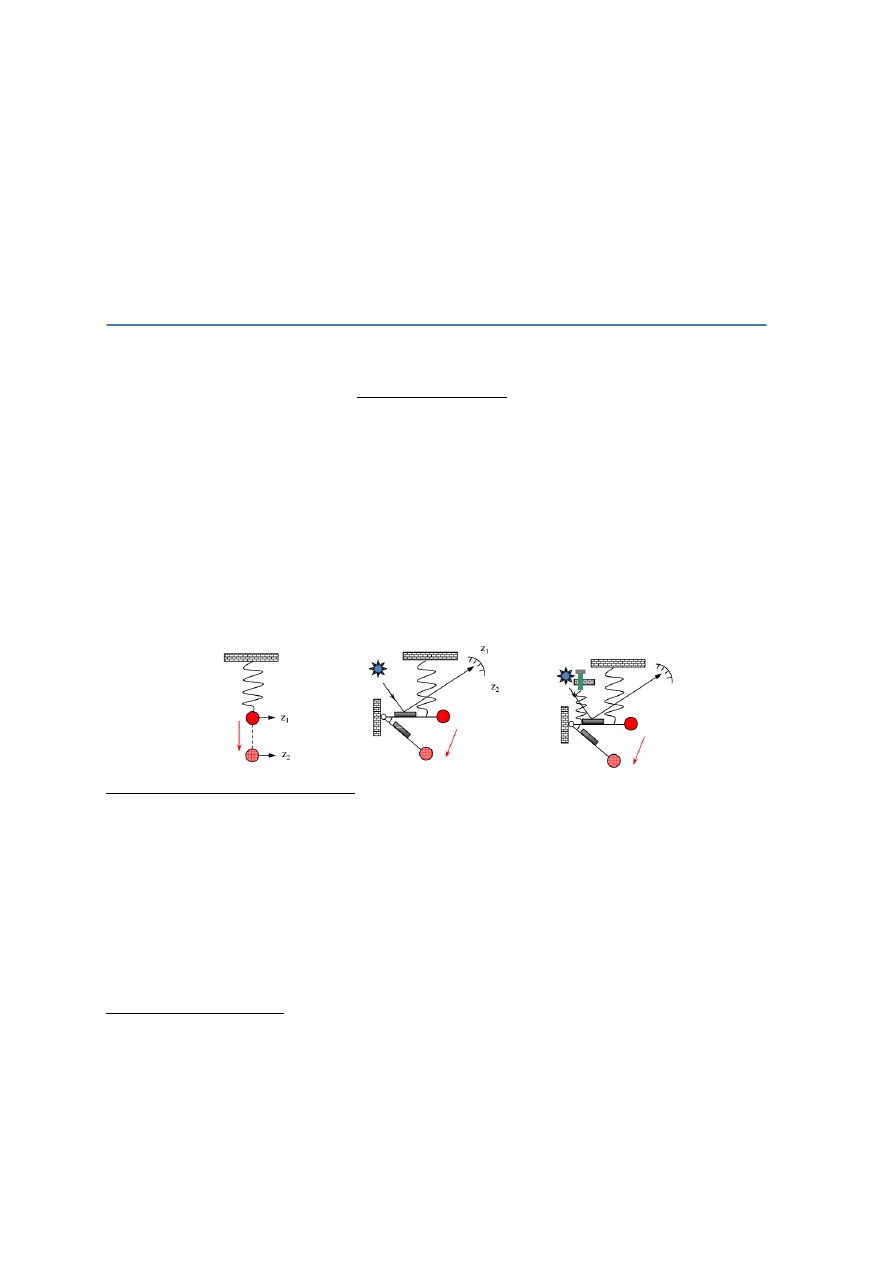
W pomiarach względnych przyspieszenia ciężkościowego wykorzystuje się zjawisko równoważenia siły
ciężkości np. siłą sprężystości wybranego ciała lub siłami pola magnetycznego. Taki rodzaj pomiarów
nazywamy statycznymi. Zasadę działania grawimetru statycznego ilustrują 3 schematy. Na pierwszym
przedstawiono pewną masę próbną zaczepioną na sprężynie, przymocowanej do stabilnej obudowy.
Zgodnie z prawem powszechnego ciążenia na masę tą działa siła ciężkości ziemskiej powodująca
przesuniecie do środka masy Ziemi. Jednocześnie na masę tą działa siła sprężystości sprężyny skierowana
przeciwnie. Masa osiąga równowagę w momencie równowagi obu sił tj równowagi obu przyspieszeń (dla
stałej masy). Na odpowiedniej skali obserwuje się wychylenie "z" masy próbnej tzw. wskazanie grawimetru.
Jest ono proporcjonalne do wartości przyspieszenia w danym punkcie. Podobne obserwacje realizowane są
na drugim punkcie pomiarowym. Różnica wskazań z obu punktów wymnożona przez pewien współczynnik
proporcjonalności "K" jest różnicą przyspieszenia ciężkościowego ∆g między oboma punktami [7].
Konstrukcja grawimetru wg. pierwszego schematu jest uzupełniona o odpowiedni moduł odczytowy
poprawiający precyzję wskazań (promień świetlny, wychylenie masy) oraz dodatkowy układ stabilizujący
poprawiający czułość grawimetru (dodatkowa sprężyna), jak to pokazano na następnych
dwóch rysunkach.
Charakterystyka grawimetru statycznego
–typ czynnika równoważącego (ciała sprężystego):
grawimetry gazowe, kwarcowe lub metalowe i grawimetry nadprzewodnikowe.
-rejestracja: optyczna, automatyczna,
–czułość grawimetru – zdolność rozdzielcza
–zakres grawimetru - dokładność, zakres mierzonego przyspieszenia
–kalibracja- Bez ustalenia współczynnika kalibracji nie jest możliwe korzystanie z grawimetru i wyznaczanie
różnic przyspieszenia.
na bazach kalibracyjnych ,przez nachylenie, obciążenie i zbliżenie
– wyznaczanie stałej grawimetru,
–chód (dryft) grawimetru- czyli zmiana jego własności pomiarowych w czasie
Błędy pomiarów statycznych:
–dryft grawimetru (obliczenie i wprowadzenie poprawki )
–wpływ przyciągania atmosfery (poprawka obliczona na podstawie H n.p.m),
–wpływ przyciągania Słońca i Księżyca (odpowiednia poprawka „lunosolarna”),
–efekt baryczny i adiabatyczny (próżnia i hermetyzacja – eliminacja prawie całkowita)
–wpływ pola magnetycznego Ziemi (tylko dla metalowych)
(jednakowa orientacja grawimetru w czasie pomiarów)

20. Zasada działania grawimetru strunowego i nadprzewodnikowego- zastosowanie
Do metod dynamicznych pomiaru przyspieszenia można zaliczyć pomiary grawimetrem strunowym. Zasada
jego działania oparta jest na pomiarze częstotliwości drgania pionowo zawieszonej struny, obciążone masą
próbną. Struna jest naciągnięta między dwoma stabilnymi i masywnymi elementami obudowy. Rejestracji
podlega częstotliowość, realizowana w odpowiednim w obwodzie elektrycznym zaopatrzonym w licznik. Za
pomocą takiego urządzenia wyznacza się różnicę przyspieszenia miedzy dwoma punktami. Przyrost
przyspieszenia między punktami A i B jest proporcjonalny do przyrostu rejestrowanej częstotliwości ∆f
między tymi punktami zgodnie z wzorem. Grawimetry strunowe charakteryzują się niższą dokładnością
wyznaczeń od innych grawimetrów służących do pomiarów względnych. Mają jednak dwie ważne zalety,
polegającą na prostej konstrukcji i prostym układzie pomiarowym oraz na mniejszym wpływie
niekorzystnych zewnętrznych czynników. Stąd znalazły zastosowanie w pomiarach niewymagających dużej
precyzji, gdzie nie można byłoby zastosować innych konstrukcji np. w grawimetrii morskiej, lotniczej lub np.
do pomiaru przyspieszenia na Księżycu.
Zasada działania grawimetru nadprzewodnikowego oparta jest o zjawisko nadprzewodności metali w
niskich temperaturach (ok. 6K). Zmiana siły mechanicznej podtrzymującej element pomiarowy w położeniu
równowagi na siłę pola magnetycznego. Element pomiarowy (sfera) wykonany z nadprzewodnika i
umieszczony w stałym polu magnetycznym, lewituje miedzy dwoma magnesami. Zmiana położenia sfery
wywołuje zmianę pojemności elektrycznej między sferą a magnesami i jest rekompensowana przez
sprzężony układ elektromagnetyczny, który przesuwa sferę w położenie wyjściowe.
Grawimetr nadprzewodnikowy charakteryzuje się następującymi własnościami:
- konstruowany jest w wersji stacjonarnej (obserwatoria pływowe) i przenośna (15kg), (1995)
- posiada zaniedbywalny dryft,
- nie wymaga kalibracji,
- wymaga częstej (co 7 dni) wymiany układu chłodzenia (ciekły hel)
- wysoka powtarzalność pomiaru 0.0001 mGal.
Pomiary przyspieszenia wykonane grawimetrami statycznymi obarczone są szeregiem błędów wynikających
z czynników zewnętrznych (otoczenia) lub wewnętrznych (budowa grawimetru).
Do połowy lat 90. wykorzystywano grawimetry nadprzewodnikowe jako instrumenty stacjonarne tylko do
rejestracji pływowych zmian siły ciężkości i wpływu ruchu biegunów Ziemi na grawitację.
od 1995 r. produkuje się precyzyjne, przenośne grawimetry nadprzewodnikowe. W grawimetry tego typu
wyposażone są liczące się na świecie obserwatoria pływowe. W 1997 r. zainstalowano taki grawimetr do
monitorowania pływów ziemskich w obserwatorium satelitarno-geodynamicznym w Wettzell (Niemcy)

23. Podobieństwa i różnice między geoidą a quasi-geoidą
PODOBIEŃSTWA:
- aproksymacja poziomu mórz i oceanów,
- na obszarze mórz przebiegają tak samo,
- powierzchnie teoretyczne .
RÓŻNICE:
- QG – wyznaczona na podstawie wysokości normalnych,
- QG – na lądach przebiega nad geoidą,
- QG – nie jest powierzchnią ekwipotencjalną (można ją jednoznacznie wyznaczyć),
- G – jest powierzchnią ekwipotencjalną,
- QG – powierzchnia odniesienia dla wysokości normalnych,
- G – powierzchnia odniesienia dla wysokości ortometrycznych.

Pytanie 24: Wyjaśnić na czym polega wpływ mas topograficznych na mierzoną wartość
przyspieszenia siły ciężkości (rysunek + komentarz)
To jedyna sensowna rzecz, którą znalazłem :/
Pytanie 25: Obliczyć redukcję grawimetryczną i anomalię grawimetryczną jeśli dane są:
Każdą anomalię grawimetryczną można obliczyć ze wzoru:
Rodzaj anomalii zależy wyłącznie od rodzaju zastosowanej redukcji. Przyspieszenie normalne na
elipsoidzie GRS 80 może być podane, ale równie dobrze może być obliczone ze wzoru:
Redukcja wolnopowietrzna
Anomalia wolnopowietrzna:
Redukcja Fay’a
Stanowi sumę redukcji wolnopowietrznej i poprawki topograficznej

Poprawka topograficzna
Ewentualne wzory na tą poprawkę
sk – to liczba stref, na które został podzielony obszar wokół punktu
Redukcja Bouguera
Anomalia Bouguera
Redukcja Poincarego-Preya
Redukcję tę można również zapisać pomijając redukcje terenowe (poprawki topograficzne)

Zad. 26 Jakie dane są potrzebne i jakie oblczenie należy wykonac w celu wyznaczenia:
a) składowe odchylenia linii pionu w strefie centralnej metodą grawimetryczną
Bezpośrednio do obliczenia składowych odchylenia linii pionu potrzebne są wartości anomalii
wolnopowietrznej na czterech punktach rozmieszczonych południkowo i równoleżnikowo w
odległości nie większej niż 5 km, musimy znać promień strefy centralnej oraz odległości między
punktami na podstawie których wykonujemy obliczenia.
Pośrednio potrzebne są:
- do obliczenia anomalii wolnopowietrznej - wartość anomalii Bouguera i anomalii wysokości
- do obliczenia anomalii Bouguera – pomierzona wartość przyspieszenia siły ciężkości, wysokość
punktu, gęstość mas ziemi, przyspieszenie normalne na elipsoidzie GRS 80
- do obliczenia anomalii wysokości – gęstość mas ziemi, wysokość punktu
b) pływowej poprawki niwelacyjnej
Bezpośrednio – współczynnik sprężystości (elastyczności) skorupy ziemskiej (dla Polski 0,8) oraz
wartość poprawki lunosolarnej
Pośrednio – do obliczenia poprawki lunosolarnej:
- wyniki pomiarów niwelacji precyzyjnej,
- data i średni czas pomiaru (WTC),
- dane z rocznika astronomicznego dotyczące rektascensji i deklinacji słońca i księżyca oraz czasu
GMST0 na datę pomiaru,
- długość i szerokość geograficzna punktów sieci niwelacyjnej
Tok obliczeń:
- obliczenie czasu gwiazdowego grynickiego na średni moment pomiaru GMST
- obliczenie czasu gwiazdowego miejscowego ST = GMST + λ
- obliczenie momentu czasu TT = WTC + 64sek
- interpolacja rektascensji słońca i księżyca na średni moment pomiaru wzorem Stirlinga
- obliczenie kąta godzinnego na średni moment pomiaru
- obliczenie deklinacji Słońca i Księżyca na średni moment pomiaru (tak samo jak dla rektascensji)
- obliczenie kąta zenitalnego Słońca i Księżyca (z trójkąta paralaktycznego)
- obliczenie azymutu Słońca i Księżyca (wzorem sinusowym z trójkąta paralaktycznego)
- obliczenie poprawki lunosolarnej
- obliczenie niwelacyjnej poprawki pływowej
c) odstępu quasigeoidy od geoidy
Potrzebne dane: współrzędne geodezyjne (szerokość i długość geograficzna), wysokości normalne
punktów, wartości przyspieszenia siły ciężkości, gradient pionowy przyspieszenia siły ciężkości,
wartości poprawki topograficznej, wartości gęstości wierzchniej warstwy skorupy ziemskiej
Tok obliczeń:
- obliczenie anomalii Fay’a na geoidzie dla przyspieszenia siły ciężkości na elipsoidzie GRS 80
- obliczenie wartości anomalii Bouguera na elipsoidzie
- obliczenie wartości trzech składników wzoru na odstęp quasigeoidy od geoidy (najpierw składniki
1+2, potem obliczenie odstępu, obliczenie składowej 3, obliczenie ostatecznej wartości odstępu)
d) poprawki geopotencjalnej, ortometrycznej, normalnej
Poprawka geopotencjalna – potrzebna średnia wartość rzeczywistego przyspieszenia siły ciężkości na
odcinku niwelacji AB, pomierzone przewyższenie między A i B
Poprawka otrometryczna – potrzebna średnia wartość przyspieszenia na każdym odcinku
niwelacyjnym, wartość przyspieszenia normalnego dla równoleżnika 45°, przeciętna wartość
rzeczywistego przyspieszenia siły ciężkości dla punktu początkowego A oraz końcowego B, wysokości
punktów
Poprawka normalna – potrzebna przeciętna wartość przyspieszenia normalnego dla środka odcinka
niwelowanego AB, średnia wartość przyspieszenia na każdym odcinku niwelacyjnym, wartość
przyspieszenia normalnego dla równoleżnika 45°.
Zad. 27 Dane są wyniki pojedynczego pomiaru grawimetrycznego metodą profilową. Oblicz dryft i
różnice
Metoda profilowa: schemat opracowania pomiaru:
Pomiar : A; B; C; C; B; A; itd.
Obliczenie dryftu:
- najpierw należy pomnożyć odczyt grawimetru przez stałą instrumentu,
- następnie dodać poprawki uzyskując, referencyjna wartość poprawioną,
- następnie dla punktów dla których wystąpił dwukrotny pomiar obliczamy różnice dla referencyjnej
wartości poprawionej i także różnice czasu pomiaru w minutach dla tych punktów
Korzystamy ze wzoru:
[mGal/min]
d - dryft
n – ilość punktów na których był dwukrotny pomiar
- następnie obliczamy różnice czasu miedzy między pierwszym pomiarem na punkcie A, a kolejnymi
pomiarami, różnice podajemy w min.
-następnie obliczamy poprawkę na dryft mnożąc dryft i różnice w minutach
- następnie obliczamy różnice między wartością ostateczna a referencyjna wartością poprawioną,
- ostatecznie obliczamy średnią bezwzględna wartość różnic na poszczególnych punktach.
Wyszukiwarka
Podobne podstrony:
Elektrotechnika opracowanie wszystkie pytania
Opracowane wszystkie pytania
Wszystko pytania opracowane przez dziewczyny
ETYKA wszystkie pytania opracowane
MAS wszystkie pytania testowe 2007
licencjat - opracowania (wszystkie
wszystkie pytania
wszystkie pytania z platformy WORD
Biochemia wszystkie pytania
licencjat - opracowania (wszystkie
wszystkie pytania CIGA, Studia GWSH, Sem V
POLITYKA SPOŁECZNA WSZYSTKIE PYTANIA!
licencjat - opracowania (wszystkie
ZIK wszystkie pytania (1)
ZIK wszystkie pytania
BSI kolokwium wszystkie pytania
opracowania Wszystkie DU jamy ustnej
Biofizyka wszystkie pytania na kolo
więcej podobnych podstron