1

Artur Zieliński

Kwadraty magiczne i kwadraty greko-łacińskie w pracach Eulera

Kwadraty magiczne znano już w czasach prehistorycznych [6]. Najstarszym znanym
kwadratem magicznym jest kwadrat magiczny Loh-Shu, który powstał około 2800 r. p. n. e.
Jak głosi legenda, został on wyryty na skorupie żółwia, który wyszedł po powodzi z jednej z
rzek. Sam termin Loh-Shu oznacza „mapa rzeki”.

Prawdopodobnie problem konstrukcji kwadratów magicznych bierze swój początek w
Indiach [7]. Kwadrat magiczny

4

4

×

został odnaleziony w inskrypcjach Jaina pochodzących

z okresu XII-XIII w. n.e. i był on postaci:

7

12

1

14

2

13

8

11

16

3

10

5

9

6

15

4

W Europie kwadraty magiczne pojawiły się w XV wieku, a Grek Moscopulus wskazał
pierwsze prawidła ich konstruowania.
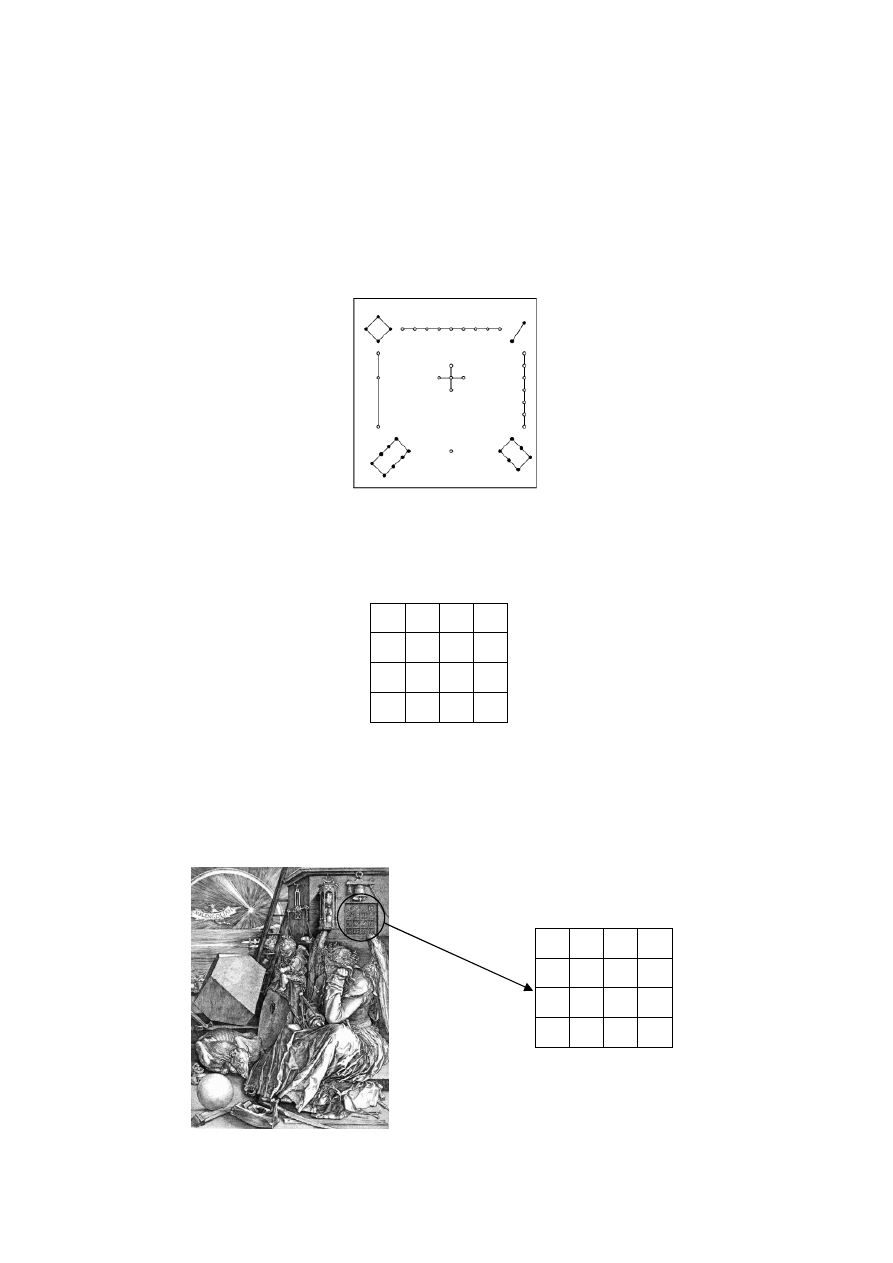
Jednym z najbardziej znanych kwadratów magicznych posiadających wiele ciekawych
własności jest kwadrat, który znalazł się na obrazie

Melancholia niemieckiego malarza

Albrechta Dürera.

16

3

2

13

5

10 11

8

9

6

7

12

4 15 14

1

2

W późniejszych wiekach matematycy nadal interesowali się tym tematem.
Leonard Euler napisał dwie prace poświęcone kwadratom magicznym i kwadratom greko-
łacińskim, a mianowicie prace [1] i [2]. Pierwszą z tych prac Euler przedstawił w
Petersburskiej Akademii Nauk 17 października 1776 roku. Zaraz w pierwszym paragrafie
wyjaśnia, że kwadrat magiczny jest to taka figura, w której rozmieszczamy liczby naturalne w
taki sposób, że suma liczb w każdej kolumnie, w każdym wierszu oraz obu przekątnych jest
równa. Euler używa do tworzenia kwadratów magicznych formuły mx + n, w której m
przyjmuje wartości 0, 1, 2, …,

1

−

x

, natomiast n wartości 1, 2, 3, …, x. Następnie formułę tą

dzieli na dwie części, tzn. mx oraz n. Każda wartość mx zastępowana jest literą łacińską,
natomiast wartość n literą grecką. W związku z tym każdą liczbę można przedstawić jako
kombinację litery łacińskiej i greckiej, np.

α

+

a

.

Konstrukcje kwadratów magicznych Euler zaczyna od przypadku

3

3

×

, ponieważ kwadrat

2

2

×

ma zbyt mało komórek, aby móc z niego zbudować kwadrat magiczny.

Omówię teraz sposób, w jaki Euler konstruuje kwadraty

3

3

×

oraz

4

4

×

.

Dla przypadku

3

3

×

mamy do dyspozycji trzy litery łacińskie a, b, c oraz trzy litery

greckie α, β, γ, gdzie litery łacińskie przyjmują wartości 0, 3, 6, natomiast litery greckie
1, 2, 3. Najpierw w kwadracie rozmieszczamy litery łacińskie, tj.

a b c
b c a
c a b

Widoczne jest, że w prawej przekątnej trzykrotnie pojawiła się litera c. Nie jest to jednak
żaden problem, wystarczy przyjąć, że

c

b

a

c

+

+

=

3

, czyli

c

b

a

2

=

+

. Stąd widać, że c może

przyjąć tylko wartość 3.
Następnie w kwadracie rozmieszczamy litery greckie w następujący sposób:

Podobnie, jak w przypadku rozmieszczenia liter łacińskich, należy założyć, że

γ

β

α

γ

+

+

=

3

, a stąd

γ

β

α

2

=

+

, co daje γ = 2.

Następnie oba kwadraty łączymy ze sobą, tzn. elementom pierwszego kwadratu
przypisujemy odpowiednie elementy kwadratu drugiego (patrz rysunek poniżej), w wyniku
czego otrzymujemy:






gdzie aγ nie oznacza iloczynu, lecz jest to raczej umowny i bardziej czytelny zapis sumy
wartości liter łacińskiej i greckiej (np.

2

2

0

=

+

=

+

=

γ

α

αγ

).

γ β α
α γ β
β α γ

aγ bβ cα
bα cγ aβ
cβ aα bγ

3

Podstawiając wartości liczbowe w miejsce liter otrzymamy kwadrat magiczny następującej
postaci:






przyjmujemy c i γ jw., natomiast a = 0, b = 6, α = 1, β = 3. Inne możliwe przypadki dla tego
typu kwadratu [4]:

3

,

1

0

,

6

=

=

=

=

β

α

b

a

1

,

3

6

,

0

=

=

=

=

β

α

b

a

1

,

3

0

,

6

=

=

=

=

β

α

b

a

Suma wszystkich linii w tych czterech kwadratach jest stała i wynosi 15.
Omówię teraz konstrukcję podaną przez Eulera dla kwadratu

4

4

×

.

W tym i kolejnych przypadkach, nie ma już konkretnego przepisu na rozmieszczanie liter
łacińskich i greckich. W pierwszym rzędzie rozmieszczamy litery łacińskie zgodnie z ich
porządkiem, a w drugiej komórce lewej przekątnej umieszczamy jedną z liter

c lub d. Jeśli

wpisaliśmy

c, pozostałe można już rozmieścić bez większych problemów.

Następnie rozmieszczamy litery greckie w taki sposób, że w lewej przekątnej do liter
łacińskich przypisujemy ich greckie odpowiedniki. Pozostałe litery greckie można rozmieścić
już bez żadnych problemów. Otrzymamy figurę:







W tym przypadku możemy utworzyć 576 figur (permutacji tych czterech liter mamy 4!, a
zatem kwadratów magicznych jest

576

24

24

!

4

!

4

=

⋅

=

⋅

). Jednak nie wszystkie możliwe

kwadraty otrzymamy dzięki tej metodzie, w której w każdym rzędzie i kolumnie są różne
litery greckie i łacińskie. Oto przykład kwadratu magicznego, w którym litery łacińskie
powtarzają się w rzędach, a litery greckie w kolumnach:

2 9 4
7 5 3
6 1 8

8 3 4
1 5 9
6 7 2

8 1 6
3 5 7
4 9 2

2 7 6
9 5 1
4 3 8

a b c d
d c b a
b a d c
c d a b

aα bδ cβ dγ
dβ cγ bα aδ
bγ aβ dδ cα
cδ dα aγ bβ

4

W

przypadku

kwadratów

5

5

×

mamy

już

14400

różnych

wariacji

)

14400

120

120

!

5

!

5

(

=

⋅

=

⋅

. Oto przykład kwadratu magicznego

5

5

×

(inne otrzymujemy

poprzez zamianę kolumn lub wierszy, ale należy pamiętać o warunku na przekątne):

Jeśli chodzi o kwadrat

6

6

×

, to Euler w swojej pracy [1] podaje tylko figurę składającą się

z połączonych liter greckich i łacińskich, nie podaje jednak żadnego konkretnego przykładu
kwadratu magicznego. Figura ta jest postaci:

Konstrukcja kwadratów łacińskich i greko-łacińskich jest bardzo dokładnie omówiona w
drugiej z prac Eulera [2]. Nazwy te wprowadził sam Euler, a wzięły się one stąd, że w
kwadraty były wpisywane zarówno litery łacińskie, jak i greckie.
Na początku swoje pracy, Euler przedstawia pewien problem, znany obecnie jako

Problem

36 oficerów [2]:
Kolumna żołnierzy składa się z 36 oficerów z 6 różnych regimentów i w 6 różnych rangach
(każdy regiment jest reprezentowany przez 6 oficerów w różnych rangach). Czy można ich
ustawić w kwadrat tak, aby żadna ranga i żaden regiment nie zostały powtórzone w tym
samym wierszu ani w tej samej kolumnie?
Podobnie jak w pracy [1], Euler wprowadza litery łacińskie (na oznaczenie 6 regimentów)
oraz litery greckie (na oznaczenie 6 rang). W ten sposób każdy oficer jest opisany przy
pomocy dwóch liter, z których pierwsza oznacza regiment z jakiego oficer pochodzi, a druga
jego rangę. Wszystkich kombinacji 6 liter greckich i 6 łacińskich jest 36 i wszystkie te
elementy musimy umieścić w kwadracie

6

6

×

.

Mamy zatem trzy warunki do spełnienia:
1) w każdym rzędzie musi znaleźć się 6 liter greckich i 6 łacińskich,
2) w każdej kolumnie musi znaleźć się również 6 liter greckich i 6 łacińskich,
3) wszystkie pary, których jest 36, muszą się znaleźć w kwadracie.
Euler stwierdził, że takie rozmieszczenie nie jest możliwe. W 1900 roku przypuszczenie to
potwierdził Gaston Tarry, który wypisał wszystkie możliwe kwadraty łacińskie (było ich
812851200) i nie znalazł żadnego kwadratu spełniającego wszystkie trzy warunki. Swoje
badania nad tym problemem przedstawił w pracach [8] i [9].

aα aδ dβ dγ
dα dδ aβ aγ
bδ bα cγ cβ
cδ cα bγ bβ

1

4

14 15

13 16

2

3

8

5

11 10

12

9

7

6

8

20

2

21 14

16

3

15

9

22

25

7

19 13

1

4

11 23 17 10

12 24

6

5

18

bδ cγ dβ eα aε
cα dδ aγ bε eβ
eγ bβ cε aδ dα
dε aα eδ cβ bγ
aβ eε bα dγ cδ

aα aζ aβ fε

fγ

fδ

fα fζ

fβ aε aγ aδ

bα bζ bβ eε eγ eδ
eζ eα eε bβ bδ bγ
cζ cα cε dβ dδ dγ
dζ dα dε cβ cδ cγ

5

Problem rozmieszczenia liter łacińskich i liter greckich został rozszerzony w [2] do
kwadratu

n

n

×

. Każdej literze łacińskiej, podobnie, jak to miało miejsce w [1], przypisujemy

wartości 0, n, 2n, ..., (n–1)n, natomiast literom greckim wartości 1, 2, 3, ..., n. Dla
przejrzystości zapisu litery łacińskie oraz greckie zastępujemy kolejnymi liczbami
naturalnymi 1, 2, 3, ..., n. Dla ułatwienia liczby reprezentujące litery greckie będziemy
zapisywać jako wykładnik. Obrazuje nam to poniższy przykład kwadratu

7

7

×

:

aα bζ cδ dγ eη fε

gβ

bβ cη aε eδ dα gζ fγ
cγ fα eζ gε aβ dη bδ
dδ eβ fη

aζ gγ bα cε

eε aγ gα bη fδ

cβ dζ

fζ

gδ dβ cα bε eγ aη

gη dε bγ fβ cζ aδ eα

Powyższy kwadrat spełnia trzy wymagane warunki. Przeanalizujmy teraz jego konstrukcję.
Opuszczamy wykładniki w wyniku czego otrzymujemy następujący kwadrat łaciński:











w którym to, w każdym rzędzie i w każdej kolumnie występują wszystkie liczby od 1 do 7.
Euler przyjął, że w pierwszej kolumnie wykładniki odpowiadają liczbie łacińskiej.
Zaczynamy od wykładnika równego jeden i rozmieszczamy go tak, aby pojawił się w każdej
kolumnie i przy różnych liczbach (od 1 do 7). Podobnie dla wykładników 2, 3, 4, 5, 6 i 7. W
wyniku czego otrzymamy następujące formuły dla:

wykładnika 1 mamy 1 6 7 3 4 2 5,
wykładnika 2 mamy 2 5 4 6 1 3 7,
wykładnika 3 mamy 3 1 2 4 7 5 6,
wykładnika 4 mamy 4 7 3 5 6 1 2,
wykładnika 5 mamy 5 4 1 7 2 6 3,
wykładnika 6 mamy 6 2 5 1 3 7 4,
wykładnika 7 mamy 7 3 6 2 5 4 1.

Formuły te będziemy nazywali formułami przewodnimi.
Dla przykładu wyznaczę formułę przewodnią dla wykładnika 6. Pierwsze cztery elementy
wybieramy przypadkowo i przyjmujemy je jako dane:

6 2 5 1

1

1

2

6

3

4

4

3

5

7

6

5

7

2

2

2

3

7

1

5

5

4

4

1

7

6

6

3

3

3

6

1

5

6

7

5

1

2

4

7

2

4

4

4

5

2

6

7

1

6

7

3

2

1

3

5

5

5

1

3

7

1

2

7

6

4

3

2

4

6

6

6

7

4

4

2

3

1

2

5

5

3

1

7

7

7

4

5

2

3

6

2

3

6

1

4

5

1

1

2

3

4

5

6

7

2

3

1

5

4

7

6

3

6

5

7

1

4

2

4

5

6

1

7

2

3

5

1

7

2

6

3

4

6

7

4

3

2

5

1

7

4

2

6

3

1

5

6

Wybrałem je z pierwszych czterech kolumn i z wierszy 6, 1, 3 i 4. Oczywiste jest, że
pozostałe trzy elementy należy wybrać z trzech ostatnich kolumn i wierszy 2, 5 i 7. Zatem
wykładnik 6 musimy umieścić w poniższym kwadracie:

4 7 6
6 3 4
3 1 5

Stąd widać, że w pierwszej kolumnie powyższego kwadratu wykładnik 6 powinien stać przy
3, w drugiej przy 7, a w trzeciej przy 4.
Przejdę teraz do klasyfikacji kwadratów, jakiej dokonał w swojej pracy Euler. Badał on
kwadraty stopnia pierwszego, drugiego, trzeciego i czwartego.
Ogólna postać kwadratu stopnia pierwszego wygląda następująco:

1

2

3

4

5

6

... n

2

3

4

5

6

... n

1

3

4

5

6

... n

1

2

4

5

6

... n

1

2

3

5

6

... n

1

2

3

4

6

... n

1

2

3

4

5

itd.

Widać, że komórki kolejnych wierszy różnią się mod n o 1 od tych znajdujących się powyżej.
W kwadracie stopnia drugiego pierwszy wiersz pozostaje bez zmian, w drugim z kolei
zamieniamy miejscami dwie kolejne liczby wiersza pierwszego, tzn. 1 z 2, 3 z 4, itd. Trzeci
wiersz otrzymamy dodając 2 do każdego elementu wiersza pierwszego, czwarty poprzez
dodanie 2 do każdego elementu wiersza drugiego. Czynność tą kontynuujemy dla pozostałych
wierszy kwadratu i otrzymujemy następującą ogólną postać kwadratu łacińskiego:

1

2

3

4

5

6

...

2

1

4

3

6

5

...

3

4

5

6

7

8

...

4

3

6

5

8

7

...

5

6

7

8

9

10 ...

6

5

8

7

10 9

...

itd.

Oczywiście kwadrat tej postaci może pojawić się tylko wówczas, gdy n będzie parzyste.
W kwadracie stopnia trzeciego bierzemy pod uwagę trzy liczby w pierwszym rzędzie i
zmieniamy je na trzy różne sposoby. Wiersz czwarty otrzymamy dodając 3 do każdego
elementu wiersza pierwszego, piąty dodając 3 do elementów wiersza 2, a szósty dodając 3 do
elementów wiersza trzeciego. Podobnie otrzymujemy kolejne wiersze naszego kwadratu, co
daje nam następującą postać kwadratu łacińskiego stopnia trzeciego:

7

1

2

3

4

5

6

7

8

9

...

2 3

1

5

6

4

8

9

7

...

3

1

2

6

4

5

9

7

8

...

4

5

6

7

8

9

10 11 12 ...

5

6

4

8

9

7

11 12 10 ...

6

4

5

9

7

8

12 10 11 ...

itd.

Oczywiste jest, że ten typ kwadratu jest tylko możliwy, gdy n jest podzielne przez 3.
Klasyfikację, o której przed chwilą wspomniałem, Euler szczegółowo omawia w [2].
Rozważania swoje prowadzi także nad kwadratem stopnia czwartego, dla którego nie można
już podać postaci ogólnej ponieważ pierwsze cztery wyrazy dają nam kilka różnych
transpozycji, a w związku z tym będziemy mieli kilka głównych postaci kwadratów stopnia
czwartego.
Omówię tylko pierwszą z tych klas, tzn. kwadraty łacińskie stopnia pierwszego.
Najprostszym przypadkiem jest kwadrat łaciński dla n = 2, jednak dla niego nie można
wybrać formuły przewodniej, ponieważ dwukrotnie pojawią się elementy 1

1

oraz 2

2

, a

zabraknie elementów 1

2

i 2

1

(rysunek poniżej):

Dla n = 3 mamy następujący kwadrat łaciński:

1 2 3
2 3 1
3 1 2

Przekątna tego kwadratu od razu daje nam formułę przewodnią dla elementu 1, dwie
pozostałe formuły jest już wówczas łatwo wyznaczyć. Otrzymujemy:

dla wykładnika 1 1 3 2
dla wykładnika 2 2 1 3
dla wykładnika 3 3 2 1

Jest to jedyne rozwiązanie dla tego przypadku.
Kolejnym przypadek, jaki odnajdujemy w pracy [2], dotyczy n = 4. Euler zauważa, że nie
jest możliwe wybranie żadnej formuły przewodniej dla następującego kwadratu łacińskiego:

1 2 3 4
2 3 4 1
3 4 1 2
4 1 2 3

W §20 [2] Euler stwierdza: Dla wszystkich przypadków, gdy n jest liczbą parzystą, kwadraty
łacińskie stopnia pierwszego nie posiadają rozwiązania, tzn. nie jest możliwe znalezienie dla
nich formuł przewodnich.

1 2
2 1

1

1

2

2

2

2

1

1

8

W tym samym paragrafie jest także podany dowód tego przypuszczenia.
Należy wykazać, że nie istnieje formuła przewodnia dla wykładnika 1 dla wszystkich
kwadratów łacińskich stopnia pojedynczego, gdzie n jest liczbą parzystą. Załóżmy, że taka
formuła istnieje i jest nią

1 a b c d e itd.

Litery a, b, c, d, itd., których mamy n-1, oznaczmy liczbami 2, 3, 4, …, n w jakimś porządku,
który odpowiada rzędom określonym przez litery α, β, γ, δ, ε, itd., którym także przypisujemy
liczby 2, 3, 4, …, n. W związku z tym suma liter greckich musi być równa sumie liter
łacińskich. Ponieważ druga litera a, naszej formuły jest wzięta z drugiej kolumny i z rzędu,
który odpowiada literze α, mamy:

)

(mod

1

n

a

+

≡

α

Podobnie czynimy dla pozostałych elementów i otrzymujemy:

.

)

(mod

5

,

4

,

3

,

2

itd

n

e

d

c

b

+

≡

+

≡

+

≡

+

≡

ε

δ

γ

β

Suma wszystkich liter greckich jest równa:

S

=

+

+

+

+

+

...

ε

δ

γ

β

α

,

natomiast liter łacińskich:

)

(mod

)

1

(

...

5

4

3

2

1

...

n

n

S

e

d

c

b

a

−

+

+

+

+

+

+

+

≡

+

+

+

+

+

,

lub

)

(mod

)

1

(

...

2

1

n

n

n

S

e

d

c

b

a

−

+

≡

+

+

+

+

+

.

n

S

e

d

c

b

a

λ

=

−

+

+

+

+

+

...

Stąd:

n

n

n

λ

=

−

)

1

(

2

1

,

co po podzielenie przez n daje:

λ

=

−

)

1

(

2

1

n

.

Ponieważ λ jest liczbą całkowitą, to n musi być liczbą nieparzystą. Na tym Euler kończy
dowód swojego przypuszczenia. Tym samym wykazał, że formułę przewodnią można znaleźć
tylko dla przypadków, gdy n jest liczbą nieparzystą.
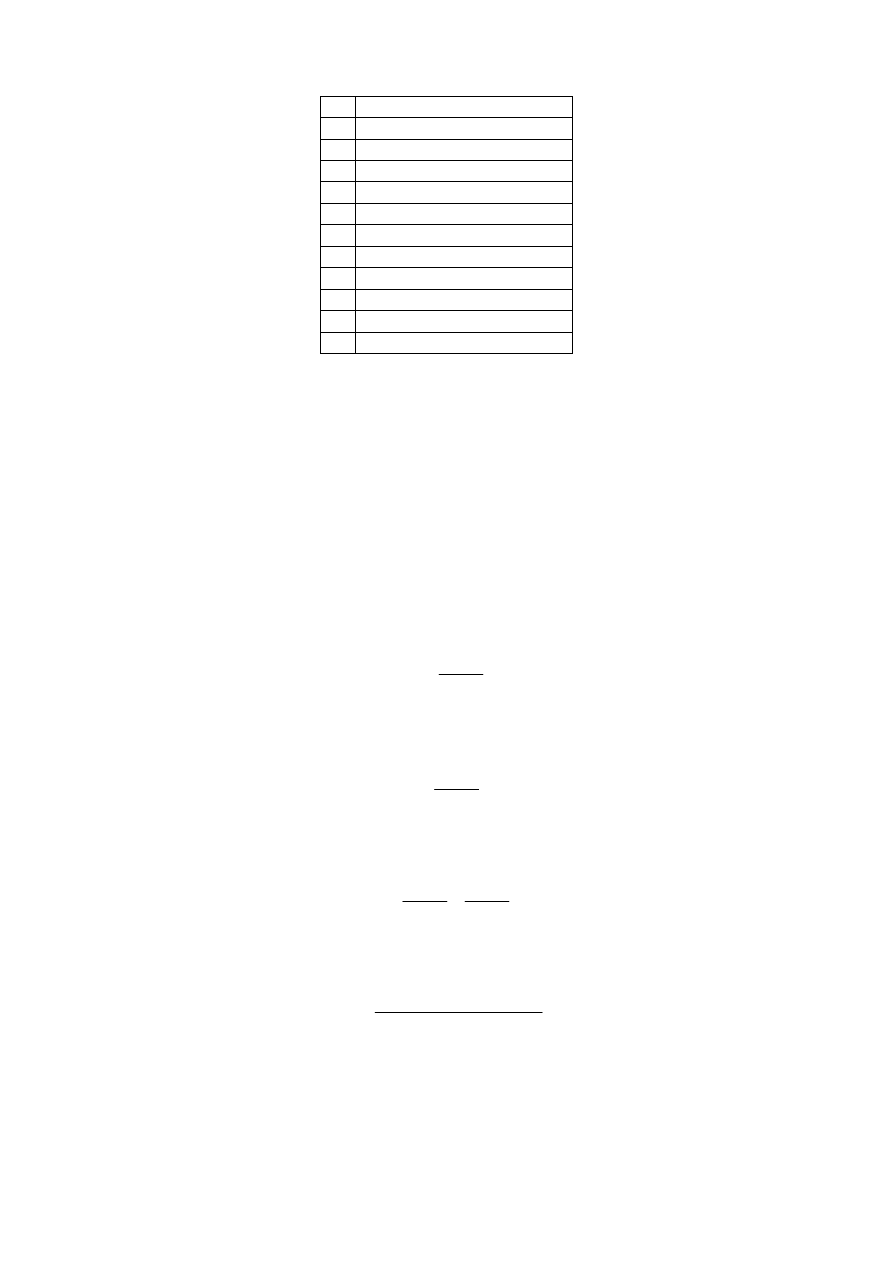
Na koniec chciałbym opowiedzieć o metodzie, jakiej Euler użył do obliczania wszystkich
możliwych odmian kwadratów łacińskich dla zadanego n. W poniższej tabeli są podane
wyniki dla początkowych liczb naturalnych.

9

n

Liczba odmian

1

0

2

1

3

1 = 1·1 + 0·0

4

3 = 2·1 + 1·1

5

11 = 3·3 + 2·1

6

53 = 4·11 + 3·3

7

309 = 5·53 + 4·11

8

2119 = 6·309 + 5·53

9

16687 = 7·2119 + 6·309

10 148329 = 8·16687 + 7·2119

itd

itd

Jeśli weźmiemy litery P, Q, R, S będące liczbą odmian kwadratów łacińskich, które
odpowiadają kolejno liczbom n, n+1, n+2, n+3 otrzymamy równania, które Euler podaje w
[2]:

P

n

nQ

R

)

1

(

−

+

=

oraz

nQ

R

n

S

+

+

=

)

1

(

.

Z tych dwóch równości możemy wyznaczyć formułę, która będzie określała S tylko prze P,
Q, R, a nie będzie zależała od n.
Z pierwszego równania mamy:

)

)(

1

(

P

Q

n

Q

R

+

−

=

−

skąd

(1)

Q

P

Q

R

n

+

−

=

−

1

.

Natomiast z drugiego równania:

)

(

R

Q

n

R

S

+

=

−

,

a stąd

(2)

R

Q

R

S

n

+

−

=

.

Wówczas odejmując (1) od (2), otrzymamy:

Q

P

Q

R

R

Q

R

S

+

−

−

+

−

=

1

.

Wyznaczamy stąd S, które będzie równe:

Q

P

PR

QR

PR

PQ

S

+

+

+

+

=

2

2

.

Zatem, biorąc np. wartości P = 53, Q = 309, R = 2119, otrzymamy, że S = 16687 (dla n = 9).

Podana przez Eulera liczba odmian kwadratów łacińskich jest błędna już dla kwadratu

łacińskiego rzędu 4. Rybnikow w swojej książce "Wwiedienie w kombinatornyj analiz"

10

(Moskwa 1972) podaje, że dla n=4 mamy 4 kwadraty łacińskie, dla n=5 56 (u Eulera jest ich
tylko 11), dla n=6 jest ich już 9408, a Euler w swojej pracy [2] podał, że jest ich tylko 53.

W ciągu ostatnich kilkudziesięciu lat praca [2] była bardzo często cytowana lub omawiana,

między innymi w:

-

Alter R., How many Latin squares are there, Amer. Math. Monthly, 82 (6) (1975),

632-634.

-

Bose R.C, Shrikhande SS., On the falsity of Euler's conjecture about the non-

existence of 2 orthogonal Latin squares of order 4T+2, Proc. Nat. Acad. Sci. USA, 45
(5) (1959), 734-737.

-

Finney D. J., Latin squares of the 6th order, Experientia, 2 (10) (1946), 404-405.

-

Hedayat A., On a statistical optimality of magic squares, Stat. Probabil. Lett., 5 (3)

(1987), 191-192.

-

Kirton H. C., Mutually orthogonal partitions of the

6

6

×

Latin squares, Utilitas

Mathematica, 27 (MAY) (1985), 265-274.

-

Parker E. T.,

Orthogonal Latin squares, Proc. Nat. Acad. Sci. USA, 45 (6) (1959),

859-862.

-

Uko L.U.,

The anatomy of magic squares, ARS Combinatoria, 67 (2003), 115-128.

-

Ullrich P.,

Officers, playing cards, and sheep - on the history of Eulerian squares and

of the design of experiments, Metrika, 56 (3) (2002), 189-204.

W szczególności, w drugiej z cytowanych prac obalone jest dla wszystkich

1

>

T

przypuszczenie Eulera, ż

e nie ma kwadratów greko-łacinskich rzędu

2

4

+

T

.

Tematyka kwadratów łacińskich jest nadal bardzo popularna. Autor [3] uważa, że

prekursorem tej popularnej obecnie gry był właśnie Leonard Euler, który badał kwadraty
łacińskie, w oparciu o które określa się sudoku .

Chciałbym podziękować Panu Profesorowi Witoldowi Więsławowi za udostępnione

materiały oraz wskazówki do mojej pracy, a także Panu Profesorowi Andrzejowi Schinzelowi
za cenne uwagi.

11

Literatura

[1] L

EONARD

E

ULER

, De quadratis magicis, Commentationes arithmeticae 2, 1849, s. 593-

602. [także : Opera posthuma 1 (1862), 140-151, oraz : Commentationes algebraicae, Opera
omnia, series prima, tom VII, Lipsiae 1923, 441-457].
[2] L

EONARD

E

ULER

, Recherches sur une nouvelle espece de quarres magiques,

Verhandelingen uitgegeven door het zeeuwsch Genootschap der Wetenschappen te Vlissingen
9 (Middelburg w 1782), 85-239. [przedruk w : Commentationes arithmeticae, 1849, 302-361;
także: Commentationes algebraicae, Opera omnia, series prima, tom VII, Lipsiae 1923, 292-
392].
[3] G

IL

G

ALANTI

, The History of Sudoku, 2006.

[4] C

HRISTOPHE

H

EBEISEN

, Euler et les carrés magiques, Lausanne, 2000.

[5] H

ERMANN

S

CHUBERT

, Mathematical Essays and Recreations, The Open Court Publishing

Company, 1899.
[6] H

AROLD

M

EAD

S

TARK

, An introduction to number theory, 1970.

[7] W

ILLIAM

S

YMES

A

NDREWS

, Magic Squares and Cubes, New York, 1960.

[8] G

ASTON

T

ARRY

, Le problème de 36 officiers, Compte Rendu de l'Assoc. Française Avanc.

Sci. Naturel 1 (1900), 122-123.*
[9]

G

ASTON

T

ARRY

, Le problème de 36 officiers, Compte Rendu de l'Assoc. Française Avanc.

Sci. Naturel 2 (1901), 170-203.*

* - prace te są dla mnie niedostępne.

Copyright © by Arczi 2009 All rights reserved