J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 9 • KMBiM WILiŚ PG
1
Ćwiczenie 9
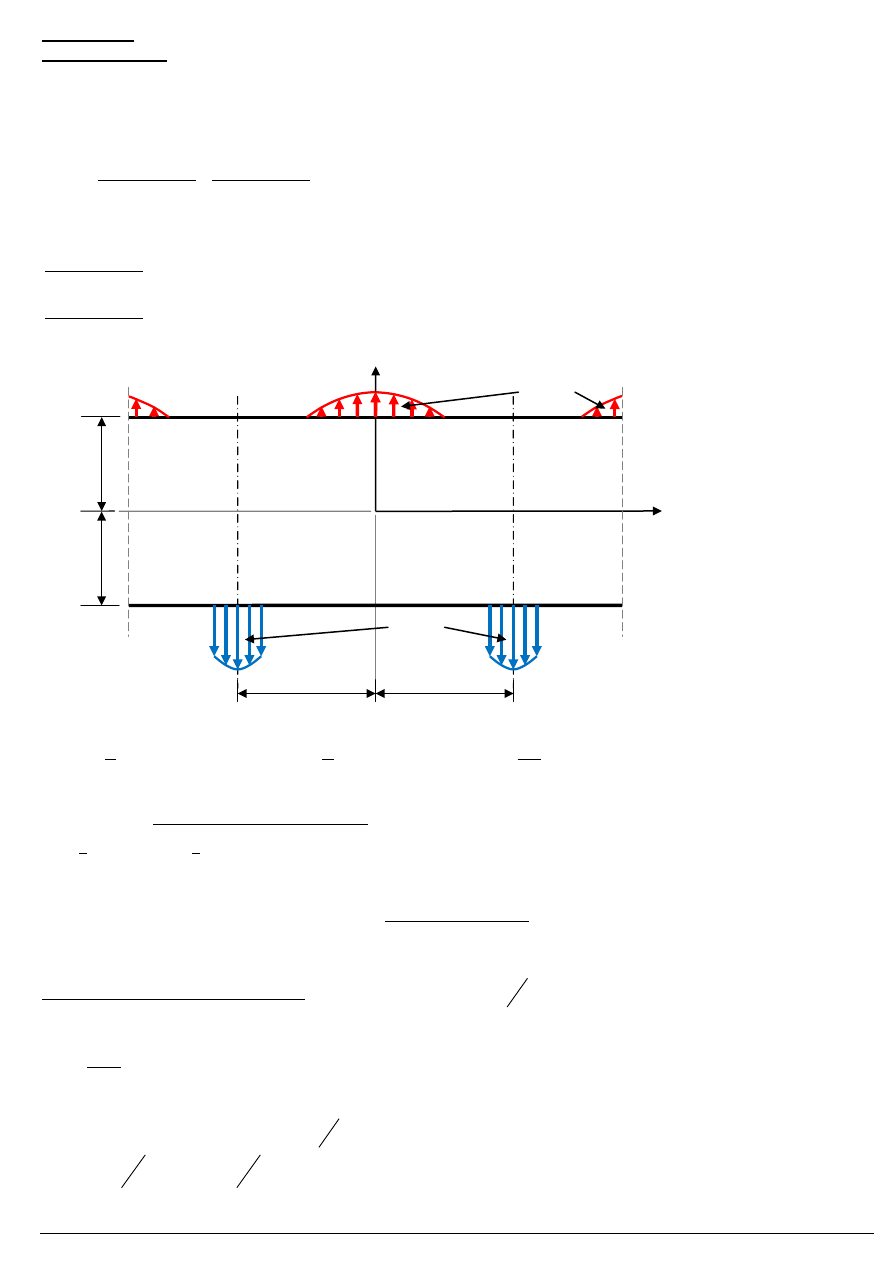
Rozważymy tarczę nieskończoną, o szerokości
Pasmo tarczowe
2b
i grubości g → model tarczy ciągłej
Zakładamy, że obciążenia na obu brzegach są okresowe i symetryczne względem osi
2
x .
Nie jest to ograniczenie metody –
istnieje bowiem rozkład:
( )
(
)
( )
(
)
( )
2
2
f x
f
x
f x
f
x
f x
+
−
−
−
=
+
,
gdzie:
( )
f x
→ dowolna funkcja
( )
(
)
2
f x
f
x
+
−
→ składnik symetryczny (funkcja parzysta)
( )
(
)
2
f x
f
x
−
−
→ składnik antysymetryczny (funkcja nieparzysta)
Dla obciążenia, które opisane jest funkcją parzystą, możemy zapisać szeregi cosinusowe:
( )
0
1
1
1
1
cos
2
n
n
n
p
a
x
x
a
α
∞
=
=
+
∑
,
( )
0
1
1
1
1
cos
2
n
n
n
p
a
a
x
x
α
∞
=
=
+
∑
;
n
n
l
π
α
=
Ze względu na globalny warunek równowagi
0
1
1
1
( )
l
l
a
p x dx
l
−
= ⋅
∫
(rzuty na oś pionową) otrzymamy:
1
1
0
1
( )
l
l
p x dx
a
l
−
= ⋅
=
∫
Do wyznaczenia funkcji naprężeń zastosujemy zasadę superpozycji
4
1
0
F
∇
=
:
oraz
4
2
0
F
∇
= zatem:
(
)
4
4
1
2
0
F
F
F
∇
+
= ∇
= (operator
( )
4
∇ jest liniowy!)
Pierwszą składową funkcji naprężeń
1
F
(przy obc. brzegowych
0
1
2
a
⋅ ) wyznaczymy, zakładając:
2
1
1
F
C x
= ⋅ , gdzie: C const
=
2
1
22
2
1
2
F
C
x
σ
∂
=
=
∂
Warunek brzegowy:
(
)
22
2
0
1
2
x
b
a
σ
= ± =
⋅
stąd:
0
4
a
C
=
oraz:
2
0
1
1
4
a
F
x
=
⋅
l
l
b
b
1
x
2
x
1
( )
p x
1
( )
p x
J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 9 • KMBiM WILiŚ PG
2
Przy wyznaczaniu funkcji
2
F
, ze względu na przyjętą metodę szeregów Fouriera, zakładamy rozdzielenie
zmiennych:
(
)
( )
2
1
2
2
1
1
,
cos
n
n
n
F x x
f
x
x
α
∞
=
=
⋅
∑
Podstawiając do równania biharmonicznego
4
2
0
F
∇
= , otrzymamy:
(
)
4
2
1
2
,
0
F x x
∇
=
( )
( )
( )
4
2
2
2
2
1
1
2
cos
0
n
n
n
n
n
n
n
f
x
f
x
f
x
x
α
α
α
∞
=
′′
′′′′
⋅
− ⋅
⋅
+
⋅
=
∑
Rozwinięcie w szereg funkcji zerowej daje wszystkie współczynniki równe zero!
Zatem,
porównując współczynniki szeregów po obu stronach:
( )
( )
( )
4
2
2
2
2
2
0
n
n
n
n
n
f
x
f
x
f
x
α
α
′′
′′′′
⋅
− ⋅
⋅
+
=
Jest to więc zwyczajne równanie różniczkowe o stałych współczynnikach!
Przewidujemy:
( )
2
2
r x
n
f
x
e
⋅
=
Zatem:
( )
( )
2
2
2
4
2
2
0
r x
r x
r x
n
n
e
e
e
α
α
⋅
⋅
⋅
′′
′′′′
⋅
− ⋅
⋅
+
=
2
2
2
4
2
2
4
2
0
r x
r x
r x
n
n
e
r
e
r
e
α
α
⋅
⋅
⋅
⋅
− ⋅ ⋅
⋅
+ ⋅
=
4
2
2
4
2
0
n
n
r
r
α
α
− ⋅ ⋅
+
=
(
)
2
2
2
0
n
r
α
−
= →
(
)(
)
2
0
n
n
r
r
α
α
−
+
=
(
) (
)
2
2
0
n
n
r
r
α
α
−
⋅
+
=
Stąd:
1,2
n
r
α
= + oraz
3,4
n
r
α
= − → pierwiastki podwójne
Z
warunku liniowej niezależności otrzymujemy:
( )
2
2
2
2
2
1
2
2
3
4
2
n
n
n
n
x
x
x
x
n
f
x
C e
C
x e
C e
C
x e
α
α
α
α
⋅
⋅
− ⋅
− ⋅
=
⋅
+
⋅ ⋅
+
⋅
+
⋅ ⋅
Podstawić można następujące zależności:
(
)
1
2
x
x
ch x
e
e
α
α
α
⋅
− ⋅
= ⋅
+
oraz
(
)
1
2
x
x
sh x
e
e
α
α
α
⋅
− ⋅
= ⋅
−
( )
2
n
f
x
Łącząc poprzednie wzory, otrzymamy:
[
]
2
2
2
2
2
2
2
1
n
n
n
n
n
n
n
n
n
n
n
A ch x
x B sh x
C
sh x
x D ch x
α
α
α
α
α
α
α
=
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
mnożnik wygodny do późniejszego różniczkowania
Otrzymujemy więc ostatecznie:
(
)
1
2
1
2
,
F x x
F
F
=
+
(
)
2
0
1
1
2
1
,
4
a
F x x
x
=
⋅
,
(
)
( )
2
1
2
2
1
1
,
cos
n
n
n
F x x
f
x
x
α
∞
=
=
⋅
∑
zatem:
(
)
2
0
1
2
1
,
4
a
F x x
x
=
⋅
[
]
2
2
2
2
2
2
1
2
1
1
cos
n
n
n
n
n
n
n
n
n
n
n
n
n
A ch x
x
B sh x
C
sh x
x
D ch x
x
α
α
α
α
α
α
α
α
∞
=
+
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
⋅
∑
Stałe , , ,
n
n
n
n
A B C D
wyznacza się z odpowiednich warunków brzegowych dla
22
σ
i
12
σ
, gdzie:
2
0
22
2
1
2
a
F
x
σ
∂
=
=
∂
[
]
2
2
2
2
2
2
1
1
cos
n
n
n
n
n
n
n
n
n
n
n
n
A ch x
x B sh x
C
sh x
x D ch x
x
α
α
α
α
α
α
α
∞
=
−
⋅
+
⋅
⋅
+
⋅
+
⋅
⋅
⋅
∑
oraz:
2
12
1
2
F
x x
σ
∂
= −
∂ ∂
(
)
(
)
2
2
2
2
2
2
1
1
sin
n
n
n
n
n
n
n
n
n
n
n
n
n
n
A
B
sh x
x
B ch x
C
D
ch x
x
D sh x
x
α
α
α
α
α
α
α
∞
=
=
+
⋅
+
⋅
⋅
+
+
⋅
+
⋅
⋅
⋅
∑

J. Górski, M. Skowronek,
M. Gołota, K. Winkelmann • Teoria sprężystości i plastyczności – Ćwicz. 9 • KMBiM WILiŚ PG
3
Warunki brzegowe:
dla:
( )
22
2
12
1
1)
2)
0
x
b
p x
σ
σ
+
=
=
=
oraz dla:
( )
22
2
12
1
3)
4)
0
x
b
p x
σ
σ
+
=
= −
=
gdzie:
( )
0
1
1
1
1
cos
2
n
n
n
p
a
x
x
a
α
∞
=
=
+
∑
,
( )
0
1
1
1
1
cos
2
n
n
n
p
a
a
x
x
α
∞
=
=
+
∑
;
n
n
l
π
α
=
Rozwiązując układ czterech równań algebraicznych liniowych, o czterech niewiadomych, otrzymujemy:
(
)
2
n
n
n
n
n
n
n
n
sh b
b ch b
A
a
a
sh 2
b
b
α
α
α
α
α
+
⋅
= −
+
⋅
+
(
)
2
n
n
n
n
n
n
sh b
B
a
a
sh 2
b
b
α
α
α
=
+
⋅
+
(
)
2
n
n
n
n
n
n
n
n
ch b
b sh b
C
a
a
sh 2
b
b
α
α
α
α
α
+
⋅
= −
−
⋅
−
(
)
2
n
n
n
n
n
n
ch b
D
a
a
sh 2
b
b
α
α
α
=
−
⋅
−
Zatem funkcja
(
)
1
2
,
F x x
jest
całkowicie określona!
Jej zróżniczkowanie prowadzi do uzyskania naprężeń
11
22
12
,
,
σ σ σ
w dowolnym punkcie danego pasma
tarczowego!
Najbardziej istotne, podobnie jak w belkach, są naprężenia
11
σ
:
2
11
2
2
F
x
σ
∂
=
∂
[
]
2
2
2
2
2
2
2
2
1
1
2
2
cos
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
A ch x
B ch x
x B sh x
C sh x
D sh x
x D ch x
x
α
α
α
α
α
α
α
α
α
∞
=
=
⋅
+
⋅
+
⋅ ⋅
+
⋅
+
⋅
+
⋅
⋅
⋅
∑
(
)
(
)
11
2
2
2
2
2
2
1
1
2
2
cos
n
n
n
n
n
n
n
n
n
n
n
n
n
n
A
B
ch x
x B sh x
C
D
sh x
x
D ch x
x
σ
α
α
α
α
α
α
α
∞
=
=
+
⋅
+
⋅
⋅
+
+
⋅
+
⋅
⋅
⋅
∑
Zatem:
Szeregi te są na ogół wolnozbieżne (szczególnie dla
2
x
b
= ± ).
Drogą przekształceń można z nich otrzymać szeregi o lepszej zbieżności:
(
)
11
2
x
b
σ
=
(
)
(
)
1
1
1
1
1
1
cos
cos
cos
n
n
n
n
n
n
n
n
n
n
n
n
n
a
x
a
a
c
x
a
a
d
x
α
α
α
∞
∞
∞
=
=
=
=
⋅
−
+
⋅ ⋅
+
−
⋅ ⋅
∑
∑
∑
oraz:
(
)
11
2
x
b
σ
= −
(
)
(
)
1
1
1
1
1
1
cos
cos
cos
n
n
n
n
n
n
n
n
n
n
n
n
n
a
x
a
a
c
x
a
a
d
x
α
α
α
∞
∞
∞
=
=
=
=
⋅
−
+
⋅ ⋅
−
−
⋅ ⋅
∑
∑
∑
gdzie:
2
2
n
n
n
n
b
c
sh 2
b
b
α
α
α
=
+
← nowe stałe!
oraz:
2
2
n
n
n
n
b
d
sh 2
b
b
α
α
α
=
−
← nowe stałe!
( )
1
1
0
1
1
cos
2
n
n
n
a
x
p x
a
α
∞
=
=
−
∑
Poza tym, z założenia:
,
( )
1
1
0
1
1
cos
2
n
n
n
a
x
p x
a
α
∞
=
=
−
∑
;
n
n
l
π
α
=
Document Outline
Wyszukiwarka
Podobne podstrony:
17) TSiP Cw 05 notatki
TSiP Cw 10-notatki
TSiP Cw 02-notatki
TSiP Cw 13-notatki
TSiP Cw 05-notatki
TSiP Cw 12-notatki
16) TSiP Cw 04 notatki
TSiP Cw 13 notatki
TSiP Cw 03 notatki
Cw 09 Indukcyjnosc id 97321
cw 09 (3)
ĆW 09
ĆW. VII, Notatki AWF
cw 09
CW 09 B LPT
Cw 09 Układy trójfazowe symetryczne [wersja 2]
więcej podobnych podstron