1

Jerzy Czesław Ossowski

Katedra Ekonomii i Zarz dzania Przedsi biorstwem

Wydział Zarz dzania i Ekonomii

Politechnika Gda ska

III Seminarium Naukowe Katedry Ekonomii i Zarz dzania Przedsi biorstwem Politechniki Gda skiej

nt.: „GOSPODARKA POLSKI W OKRESIE TRANSFORMACJI”,

26-27 wrzesie 1998 r. Jastrz bia Góra

WYDAJNO PRACY I WYNAGRODZENIA A STOPA BEZROBOCIA

W POLSCE W LATACH 1993-1997

1. SFORMUŁOWANIE PROBLEMU

Analiza informacji zawartych w tabeli 1 potwierdza powszechn opini , e lata 1992-1993
uzna nale y za przełomowe w zmianach gospodarczych kraju. W 1992 roku odnotowano, po
raz pierwszy po kilku latach załamania, wzrost Produktu Krajowego Brutto. W 1994 roku
stopa wzrostu PKB przekroczyła 5% stabilizuj c si w nast pnych latach na poziomie
przekraczaj cym 6%. Na tym tle interesuj co wygl daj zmiany nakładów inwestycyjnych.
Ich wzrost w latach 1992-1993 był bardzo skromny. Przełomowe okazały si lata 1994-1995.
Wówczas roczna stopa nakładów inwestycyjnych przybli yła si do 10%, a nast pnie
wielko t znacznie przekroczyła. W ci gu ostatnich dwóch lat roczna dynamika nakładów
inwestycyjnych ustabilizowała si na poziomie przekraczaj cym 22%. Wskazywałoby to, e
wzrost PKB w latach 1992-1993 miał charakter w wi kszej cz ci restytucyjny. Mo na
postawi hipotez , e wzrost produkcji nast pił w przedsi biorstwach, które potrafiły
dostosowa si do nowych warunków gospodarczych wynikaj cych z transformacji
systemowej oraz zaspakajaj cych potrzeby rynkowe nowego otoczenia. Zauwa my bowiem,

e cały czas w analizowanych latach nast pował kilkuprocentowy w skali rocznej przyrost

udziału zatrudnienia w sektorze prywatnym.

2

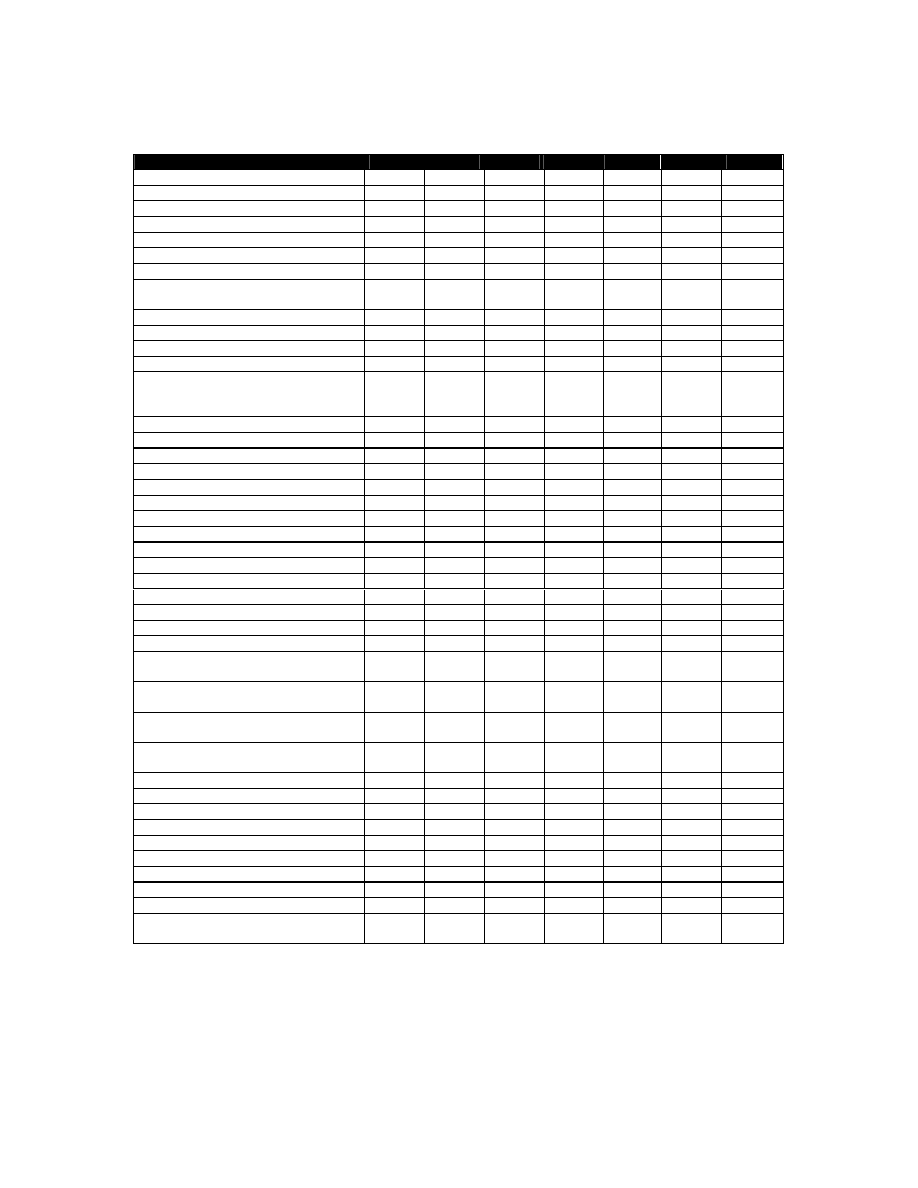
Tabela 1

Fakty gospodarcze dotycz ce Polski

1991

1992

1993

1994

1995

1996

1997

Ludno w mln. osób ( 31 XII )

38,309

38,418

38,505

38,581

38,609

38,639

38,660

Ludno w wieku produkcyjnym (30 VII)

22,006

22,118

22,257

22,417

22,573

22,733

22,901

Emeryci i renci ci w mln ( r. rocz.)

8,495

8,730

8,919

9,096

9,200

9,315

Aktywni zawodowo w mln. (31 XII)

18,271

18,449

17,622

17,737

17,644

17,848

17,390

Zatrudnieni w mln (cała gosp.)(31 XII)

16,115

15,940

14,732

14,899

15,015

15,492

15,564

Liczba bezrobotnych w mln (31 XII)

2,156

2,509

2,890

2,838

2,629

2,356

1,826

Stopa bezrobocia w % ( 30 XII)

11,80%

13,60%

16,40%

16,00%

14,90% 13,20%

10,50%

Procent. udział zatr. w sektorze pryw.

( r.rocz.)

50,2%

53,7%

56,8%

59,4%

61,9%

64,1%

66,5% *

Produkt Krajowy Brutto (91r.=1,00)

1,000

1,026

1,065

1,12

1,199

1,272

1,362 *

Stopa wzrostu PKB w %

-7,0%

2,6%

3,8%

5,2%

7,0%

6,1%

6,9%

PKB w mld zł (ceny bie ce)

82,4

114,9

155,8

210,4

288,7

362,8

445,1

PKB w mld USD (ceny bie ce)

77,7

84,5

86,1

92,7

119,3

134,4

135,7

PKB na 1 mieszka ca wg. parytetu siły

nabywczej w USD (GDP at PPP per

capita)

4466

4697

5114

5459

5900

6940

7390 *

Nakłady inwest. ceny stałe (91r.=1,00)

1,000

1,007

1,027

1,112

1,300

1,588

1,80 *

Stopa wzrostu nakładów inwest. w %

0,70%

1,99%

8,28%

16,91% 22,15%

22,3%*

Indeks cen dóbr konsump. (ICK) (91=1,00) 1,00

1,430

1,939

2,558

3,269

3,919

4,503

Stopa inflacji w %

70,3%

43,0%

35,3%

32,2%

27,8%

19,9%

14,9%

Stopa wzr. cen prod. sprz. Przemysłu

31,9%

25,3%

25,4%

12,4%

12,2%

Stopa wzr. cen. prod.bud.-monta .

24,6%

19,7%

21,9%

19,2%

14,2%

Wynagr. miesi czne nomin. netto w zł.

175,56

243,86

320,15

425,49

560,60

710,22

872,91

Wynagr. mies. realne w cenach 1991r.

175,56

170,55

165,47

166,35

171,49

181,20

193,85

Stopa wzrostu wynagr. realnych w %

-2,85%

-2,98%

+0,5%

+3,09% +5,66%

6,93%

Dochody bud etowe w mld zł.

45,9

63,1

83,7

99,7

119,8

Wydatki bud etowe w mld zł.

50,2

68,9

91,2

108,8

125,7

Nadwy ka bud etowa w mld zł.

-4,3

-5,7

-7,4

-9,2

-5,9

Proc. Udział deficytu bud etowego w PKB

2,8%

2,7%

2,6%

2,6%

1,33%

Poda pieni dza w mld zł.(stan w XII)

41,1

55,9

77,3

104,3

134,9

176,4

Gotówka w obiegu w mld zł.

7,8

10,0

12,3

19,5

23,6

27,3

Depozyty gospodarstw domowych w mld

zł.

22,0

31,7

43,0

59,4

77,8

80,9

Depozyty podmiotów gospodarczych. w

mld zł.

11,3

14,2

22,0

25,4

33,5

37,5

Nale . z tyt. kredytów dla gosp.dom. w

mld zł.

1,2

2,3

3,3

5,6

11,7

18,4

Nale . z tyt. kredytów dla pod.gosp. w mld

zł

23,7

30,9

38,2

50,6

68,4

89,8

Stopa oproc. kredytu redyskontowego w %

32%

29%

28%

25%

22%

24,5%

Stopa oproc. wkładów rocznych w PKO

38%

34%

29%

22%

18,5%

19,5%

Kurs USD w zł w NBP

1,36

1,81

2,27

2,42

2,70

3,28

Kurs DEM w zł. w NBP

0,88

1,1

1,41

1,69

1,79

1,89

Dług zagraniczny w mld USD (w XII)

47,2

42,2

44,0

44,1

44,2 *

Stan rezerwy dewizowych w mld USD

4,1

5,8

14,8

18,5

20,7

Import w mld USD

18,8

21,6

29,1

37,1

42,3

Export w mld zł

14,1

17,2

22,9

24,4

25,8

Bilans handlowy w mld USD **

-4,7

-4,3

-6,2

-12,7

-16,5

Relacja rezerw do jednomiesi cznego

importu

2,6

3,2

6,1

6,0

5,9

ródło: Opracowanie własne na podstawie [12],[13],[14]

*) prognozy własne na rok 1997

**) nie sklasyfikowane obroty bie ce (saldo) wynosiły: w 1996 roku 7,153 mld USD, w 1997roku 6,061 mld USD.

3

Z dalszej analizy danych statystycznych wynika, e udział zatrudnienia w sektorze

prywatnym w relacji do zatrudnienia ogółem wzrósł z poziomu 50% w 1992 roku do poziomu
przewy szaj cego 65% w 1997 roku. Z kolei wysoka dynamika nakładów inwestycyjnych w
ostatnich latach zwi zana była z modernizacj dotychczasowych stanowisk pracy oraz
powstawaniem nowych. Tym nale y tłumaczy obserwowany po 1994 roku spadek stopy
bezrobocia z poziomu przewy szaj cego 16% do poziomu 10,5% w ko cu 1997 roku.
Powstawanie nowych miejsc pracy i zwi zana z tym znacznie szybsza dynamika przyrostu
PKB ani eli zatrudnienia prowadziła do przyrostu wydajno ci pracy. To z kolei poci gało za
sob wzrost wynagrodze realnych. Wzrost ten jednak miał miejsce dopiero po roku 1994, a
wi c po okresie tzw. „wzrostu restytucyjnego”. Charakterystyczny jest jednak fakt, e
dynamika przyrostu wynagrodze realnych w 1997 roku zbli yła si do dynamiki wzrostu
PKB. Przyczyn tego zjawiska mo e by postawa zwi zków zawodowych zwi zanych z
sektorem pa stwowym w warunkach nierównomiernego rozwoju bran i sektorów
gospodarczych. W przedsi biorstwach prywatnych (sprywatyzowanych i nowo powstałych),
skoncentrowanych w cz ci bran , na skutek wysokich nakładów kapitałowych obserwuje si
wysoki poziom wydajno ci i zwi zany z nim poziom wynagrodze .

1

Zwi zkowcy z bran w

których nie obserwuje si wzrostu wydajno ci, zmierzaj do wzrostu wynagrodze celem
zachowania historycznie ukształtowanych, a nieodpowiadaj cych aktualnym realiom, struktur
płacowych. Taki sposób dostosowywania si wynagrodze w okre lonych warunkach
prowadzi mo e do niebezpiecznych konsekwencji gospodarczych. Zastanówmy si nad
mechanizmem wzajemnego dostosowywania si wynagrodze , wydajno ci pracy i bezrobocia
w warunkach wzrostu nakładów kapitałowych.

Punktem wyj cia jest długookresowa funkcja produkcji Y=Y(N,K), gdzie Y mierzy

wielko produktu krajowego brutto w cenach stałych, N nakłady pracy a K nakłady
kapitału

2

. W okresie wyj ciowym nakłady kapitału ustalmy na stałym poziomie K

1

. W

rezultacie wyrazi mo emy krótkookresow funkcj produkcji Y=Y(N,K

1

), której obraz

1

Z przeprowadzonych przez autora bada dla lat 1993-1997 wynika, e przeci tnemu rocznemu przyrostowi

wydajno ci pracy w przemy le przetwórczym o 12,41% towarzyszył przeci tny roczny przyrost wynagrodze

realnych o 5,29%. W górnictwie wydajno wzrastała o około 7,21% rocznie a wynagrodzenia o 5,75%. Z kolei

w sekcji zaopatrzenia w energi elektryczn , gaz i wod zerowemu przyrostowi wydajno ci towarzyszył

przeci tny roczny przyrost wynagrodze rz du 2,83% /por.:[9]s.47-48/. Jest to po redni objaw zró nicowanych

zwi zków pomi dzy wydajno ci i wynagrodzeniami w ró nych bran ach gospodarczych.

2

Przyj ty tutaj system oznacz w du ej cz ci odpowiada systemowi zaproponowanemu w pozycji [1].

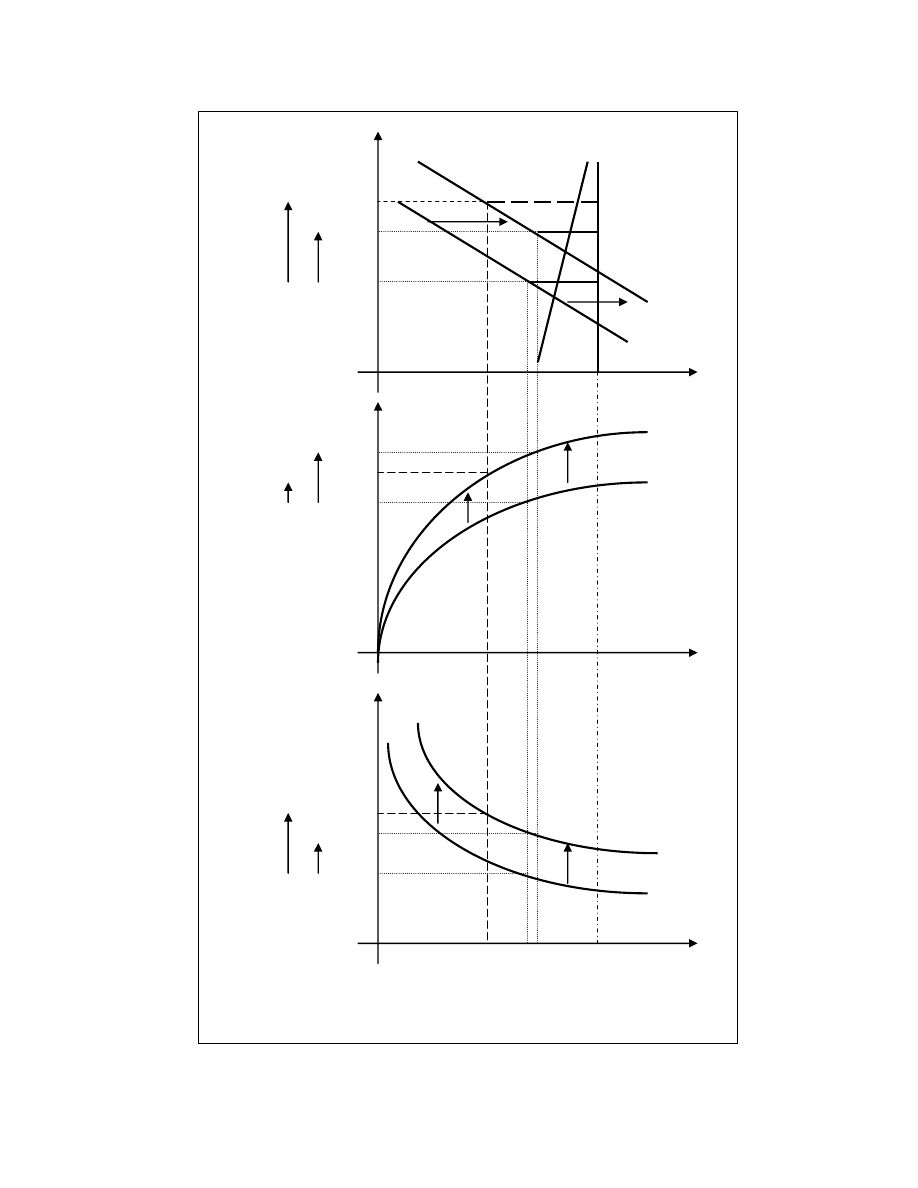
4

W

AJ LF

B

W

B

A

W

A

E

W

E

Wariant: B A LD

2

LD

1

N

Y

Y(N,K

2

)

Y

A

Y

B

Y(N,K

1

)

Y

E

Wariant: B A

Gdzie:

K

1

< K

2

K

1

, K

2

= const

N

AP

AP

B

AP

A

AP(N,K

2

)

AP

E

Wariant: B A AP(N,K

1

)

N

B

N

E

N

A

N

F

N

Rys.1 Wydajno pracy (AP), wynagrodzenia (W), produkt krajowy (Y) oraz bezrobocie

w warunkach zmian nakładów pracy (N) oraz kapitału (K) – dwuwariantowy zwi zek

wynagrodze , wydajno ci oraz bezrobocia .

ródło: opracowanie własne

5

graficzny przedstawiono na Rys.1. Funkcja ta wyznacza z jednej strony funkcj popytu na
prac LD

1

a z drugiej strony krótkookresow funkcj wydajno ci pracy AP

1

=AP(N,K

1

). Na

rynku pracy ukształtowana jest funkcja poda y siły roboczej (LF) oraz poda y pracowników
skłonnych i mog cych przyj ofert pracy w danych warunkach strukturalnych (AJ). Dla
ułatwienia analizy przyj to zało enie o zerowej elastyczno ci płacowej siły roboczej (LF).
Załó my, e w punkcie wyj cia wynagrodzenie ukształtowało si na poziomie W

E

. W tych

warunkach gospodarka zatrudni N

E

jednostek pracy. Tym samym produkt osi gnie poziom

Y

E

a wydajno pracy b dzie wynosi AP

E

jednostek. W takiej sytuacji stopa bezrobocia

wyniesie odpowiednio: SB

E

= [(LF-N

E

)/LF]*100%.

Załó my obecnie, e na skutek inwestycji głównie w bran ach rozwojowych, kapitał

(maj tek produkcyjny) w całej gospodarce wzrasta do poziomu K

2

. W rezultacie krzywa

produktu przesunie si w gór do pozycji Y(N,K

2

). W wyniku tego nast pi przesuni cie

krzywej wydajno ci pracy w gór do pozycji wyznaczonej przez funkcj AP(N,K

2

). Oznacza

to, e na skutek lepszego wyposa enia pracy w kapitał, wydajno pracy - przy tych samych
jej nakładach- wzro nie. Faktycznie wzrost ten wyst pi w „bran ach rozwojowych” rzutuj c
jednak na efektywno całej gospodarki

3

. Zmiana poło enia krótkookresowej funkcji

produkcji oraz wydajno ci powoduje jednoczesny wzrost popytu na prac , co wyra a si
przesuni ciem krzywej popytu do pozycji LD

2

. Oznacza to, e przy niezmiennym poziomie

płac gospodarka jest gotowa zatrudni wi ksz ilo jednostek pracy. O faktycznym
zatrudnieniu decydowa b d procesy dostosowawcze wydajno ci pracy i wynagrodze .
Celem sformułowania hipotez roboczych rozpatrzmy dwa warianty procesów
dostosowawczych .

W wariancie A zakładamy, e na skutek wzrostu wydajno ci w bran ach rozwojowych

nast pi w nich wzrost wynagrodze . W wyniku procesów dostosowawczych wynagrodzenia
w całej gospodarce zmierza b d do poziomu W

A

. Przy takim poziomie wynagrodze

gospodarka ostatecznie zatrudni N

A

jednostek pracy. To doprowadzi do wy szego poziomu

produktu Y

A

. W rezultacie wydajno pracy w całej gospodarce wzro nie do poziomu AP

A

.

W tych warunkach stopa bezrobocia wyniesie SB

A

=[(LF-N

A

)/LF]*100%. Z uwagi na fakt, e

LF nie zmieniło swojego poło enia, zachodzi nast puj ca nierówno : SB

E

>SB

A

. Tak wi c

rozpatrywany wariant wskazuje na mo liwo zachodzenia takich procesów

3

Przez bran e rozwojowe rozumie b dziemy te w których na skutek zmian systemowych nast puje ponad

przecietny przyrost efektywno ci.

6

dostosowawczych pomi dzy wydajno ci i wynagrodzeniami w wyniku których wyst puj
mo liwo ci spadku stopy bezrobocia.

W wariancie B zakładamy, e na skutek procesów dostosowawczych wynagrodzenia

zmierza b d do poziomu W

B

. W rezultacie tego zatrudnienie obni y si do poziomu N

B

. To

z kolei wyznaczy ni szy poziom produktu Y

B

. Zauwa my, e na skutek zmniejszonego

zatrudnienia w stosunku do wariantu A wydajno ta b dzie obecnie wy sza, gdy równa si
b dzie AP

B

jednostek. W analizowanych warunkach stopa bezrobocia SB

B

b dzie wy sza od

stopy bezrobocia SB

A

. Rozpatrywany tutaj wariant wskazuje na mo liwo zachodzenia

takich procesów dostosowawczych pomi dzy wydajno ci i wynagrodzeniami w wyniku
których nast puje wzrost stopy bezrobocia.

W kontek cie powy szych rozwa a interesuj ca mo e by próba odpowiedzi na

pytania:

1)

jakiego typu i jakie relacje dostosowawcze wyst puj pomi dzy wydajno ci i

wynagrodzeniami?,

2)

przy jakich relacjach wydajno ci i wynagrodze stopa bezrobocia b dzie rosła lub

malała?,

3)

który z wariantów teoretycznych (A lub B) dostosowa wynagrodze i wydajno ci

był realizowany?.

Prowadzona tutaj analiza jest prób wst pnego rozpoznania prawidłowo ci rz dz cych

wynagrodzeniami, wydajno ci i stop bezrobocia na obecnym etapie transformacji polskiej
gospodarki. Dlatego uproszczono j pomijaj c problem identyfikacji produktu potencjalnego i
naturalnej stopy bezrobocia. W rezultacie w procesie modelowania pomini to dyskusj
zwi zan ze zmiana poło enia krzywej AJ.

2. DYNAMIKA I SEZONOWO WYDAJNO CI PRACY I WYNAGRODZE W

GOSPODARCE POLSKIEJ

W badaniach wykorzystano dane statystyczne obejmuj ce okres od I kwartału 1993

roku do IV kwartału 1997 roku. Na podstawie materiałów ródłowych GUS zawartych w
pozycjach [12], [13] i [14] przygotowano informacje dla potrzeb prowadzonej tutaj analizy.
Podstawowe dane statystyczne wykorzystane w artykule zamieszczone zostały w tabeli 2.

7

Tabela 2

Podstawowe wska niki gospdarcze kraju w uj ciu kwartalnym

Okres

PKB

ICK

IZ

SB

BO

WNO

WRO

IEF

IWRO

Produkt

Krajowy

Brutto*

Indeks

Cen

Kons.*

Indeks

zatrud-

nienia*

Stopa

bezro-

bocia

Wielk.

bezro-

bocia

Wynagr.

nominal.

netto

Wynagr.

realne

Netto**

Indeks

wydajno

- ci*

Indeks

wynagr.

realnych

*

1993Q1

1,0000

1,0000 1,00000

14,4

2648,7

301,80

301,80

1,0000

1,0000

1993Q2

1,0673

1,0598 0,99902

14,8

2701,8

313,70

296,00

1,0683

0,9808

1993Q3

1,0908

1,1149 0,99120

15,4

2830,0

326,02

292,42

1,1005

0,9689

1993Q4

1,1009

1,2124 1,00780

16,4

2889,6

363,27

299,63

1,0924

0,9928

1994Q1

1,0527

1,3081 0,96872

16,7

2950,1

406,19

310,52

1,0867

1,0289

1994Q2

1,1132

1,3957 0,96872

16,6

2933,0

420,22

301,08

1,1492

0,9976

1994Q3

1,1536

1,4850 0,97263

16,5

2915,7

443,17

298,43

1,1861

0,9888

1994Q4

1,1614

1,6113 0,98045

16,0

2838,0

498,52

309,39

1,1846

1,0251

1995Q1

1,1300

1,7401 0,97165

15,5

2753,8

541,38

311,12

1,1630

1,0309

1995Q2

1,1917

1,8393 0,97752

15,2

2694,0

557,75

303,24

1,2191

1,0048

1995Q3

1,2388

1,8669 0,97458

15,0

2657,2

579,91

310,63

1,2711

1,0292

1995Q4

1,2354

1,9658 0,98925

14,9

2628,8

674,29

343,01

1,2489

1,1365

1996Q1

1,1715

2,0995 0,96872

15,4

2726,0

689,86

328,58

1,2094

1,0887

1996Q2

1,2567

2,2044 0,97165

14,3

2508,0

697,82

316,56

1,2934

1,0489

1996Q3

1,3296

2,2485 0,97263

13,5

2341,0

720,74

320,54

1,3670

1,0621

1996Q4

1,3296

2,3408 0,99022

13,2

2359,5

795,03

339,64

1,3427

1,1254

1997Q1

1,2534

2,4613 0,98827

12,6

2235,7

836,42

339,83

1,2682

1,1260

1997Q2

1,3520

2,5327 0,98729

11,6

2039,9

862,69

340,62

1,3694

1,1286

1997Q3

1,4213

2,5717 0,99022

10,6

1853,7

885,25

344,23

1,4353

1,1406

1997Q4

1,4182

2,6545 0,98729

10,5

1826,4

961,10

362,06

1,4364

1,1997

ródło: opracowanie własne na podstawie [12],[13],[14]

*) Indeksy jednopodstawowe: 1994 kwartał I =1,000.

**)Wynagrodzenie realne w cenach I kwartału 1993 roku.

Punktem wyj cia w prowadzonej analizie było oszacowanie dynamiki wydajno ci i

płac realnych. Z uwagi na charakter danych nale ało zało y mo liwo wyst pienia waha
sezonowych. W konsekwencji posłu ono si wykładniczym modelem tendencji rozwojowej o
nast puj cej postaci analitycznej:

y

t

= B

0

exp b t •••• exp( c

1

v

t1

+ c

2

v

t2

+ c

3

v

t3

) •••• exp u

t

(1)

gdzie: y

t

- zmienna obja niana

t = 1, 2, ..., 19, 20 - numer obserwacji dla okresu I kwartał 1993 IV kwartał 1997

j = 1, 2, 3, 4 - numer kwartału

v

tj

= ( x

tj

– x

t4

) - zmienna sztuczna dla

4

≠

j

,

x

tj

- zmienna zero-jedynkowa przyjmuj ca warto jeden w j-tym kwartale oraz zero w

pozostałych kwartałach.

Tr

t

= B

0

exp b t - trend obrazuj cy ogóln tendencj zmian zjawiska ekonomicznego,

8

yc

t j

= exp( c

1

v

t1

+ c

2

v

t2

+ c

3

v

t3

) - składnik cykliczny (sezonowy),

ys

t j

= Tr

t

• yc

t

- składnik systematyczny modelu

u

t

- składnik zakłócaj cy modelu (losowy)

Na podstawie trendu zawartego w modelu okre li mo emy kwartaln (KSW) i roczn

(RSW) stop wzrostu badanego zjawiska. Wielko ci te równaj si odpowiednio:

KSW =

%

100

)

(

1

1

⋅

−

−

−

t

t

t

Tr

Tr

Tr

= [(exp b

1

) -1] 100%

RSW = =

%

100

)

(

4

4

⋅

−

−

−

t

t

t

Tr

Tr

Tr

= [(exp 4 b

1

) -1] 100% = [ 1 + KSW/100]

4

100%

Kwartalna stopa wzrostu (KSW) wskazuje na przeci tny procentowy przyrost

badanego zjawiska w kolejnych okresach. Roczna stopa wzrostu pozwala okre li
procentowy przyrost badanego zjawiska w ci gu roku.

Ze zdefiniowania cz ci składowych składnika systematycznego modelu wynika

mo liwo okre lenia procentowego udziału kwartalnych odchyle tego składnika od trendu
w poziomie trendu ( KOT):

KOT

j

= [ (ys

t j

-Tr

t

)/Tr

t

]100% = [(exp c

j

) -1] 100%

Wła ciwo ci analizowanego modelu jest mo liwo okre lenia przeci tnej dynamiki

wzrostu zjawiska dla całego badanego okresu oraz przeci tnych relatywnych odchyle
kwartalnych badanego zjawiska od jego trendu.

Po uprzednim obustronnym zlogarytmowaniu rozpatrywanego modelu, wykorzystuj c

obliczone wcze niej indeksy wydajno ci pracy oraz wynagrodze realnych, dokonano
oszacowa parametrów strukturalnych rozpatrywanego modelu. W przypadku modelu
opisuj cego wydajno pracy przy szacowaniu korzystano z metody najmniejszych
kwadratów. Celem zlikwidowania skutków autokorelacji składników losowych model
opisuj cy wynagrodzenia oszacowano stosuj c iteracyjn metod Newtona-Raphsona.
Zbie no ocen osi gni to po czterech iteracjach. Odpowiednie wyliczenia proponowanych
wska ników oraz ogólne charakterystyki jako ci oszacowa zamieszczono w tabeli 3.

9

Tabela 3

Dynamika i sezonowo wydajno ci pracy oraz wynagrodze realnych

wyniki oszacowa dla lat 1993 kw.i - 1997 kw.iv

Stopa wzrostu

(SW)

Kwartalne odchylenia od trendu

w %

R2

DW

Odch

Stand

KSW.

RSW

Kw. I

Kw. II

Kw. III

Kw. IV

Wydajno

1,60% 6,56%

-4,14%

0,52%

3,09%

-0,58%

0,99

1,51

0,011

Wynagrodzenia

0,90% 3,81%

1,58%

-1,78%

-2,19%

2,48%

0,93

1,91

0,021

ródło: Opracowanie własne

Analizuj c tabel 3 zauwa amy, e warto ci teoretyczne analizowanych modeli

stosunkowo dobrze przylegaj do warto ci empirycznych. W przypadku modelu wydajno ci
udział zmienno ci teoretycznej zlinearyzowanej postaci modelu stanowił 99% jego
zmienno ci empirycznej. W przypadku modelu wynagrodze wska nik ten wynosił
odpowiednio 93%. Na podstawie odchylenia standardowego /por.:[6]/ powiemy, e warto ci
empiryczne odchylały si przeci tnie od warto ci teoretycznych o 1,1% w przypadku modelu
wydajno ci oraz o około 2,1% w przypadku modelu wynagrodze .

Oczyszczona z efektów sezonowych dynamika wzrostu wydajno ci była wy sza od

oczyszczonej dynamiki wzrostu wynagrodze realnych. W analizowanych latach przeci tny
kwartalny przyrost wydajno ci wynosił 1,6%, co wyznaczało przeci tny rednioroczny
przyrost rz du 6,56%. W przypadku wynagrodze realnych wska niki te wynosiły
odpowiednio 0,9% oraz 3,81%. Oznacza to, e w analizowanych latach jednoprocentowemu
przyrostowi wydajno ci towarzyszył przeci tny przyrost wynagrodze rz du 0,58%.

Analiza sezonowo ci wskazuje na rozbie ne odchylenia od trendów obu

analizowanych wska ników. W przypadku wydajno ci obserwujemy, i w ka dym
pierwszym kwartale wydajno ta była przeci tnie ni sza od poziomu trendu o około 4,14%.
W ka dym trzecim kwartale wydajno ta przewy szała poziom trendu o około 3,1%. W
kwartale drugim wydajno nieznacznie była wy sza od trendu a w kwartale czwartym w
zbli onym stopniu ni sza. W przypadku wynagrodze najwy sze odchylenie dodatnie od
trendu obserwujemy w kwartale czwartym. Wynosiło ono przeci tnie 2,48%, i to w sytuacji,
gdy jak pami tamy, wydajno nieznacznie obni a si . Nast puje to jednak po kwartale o
przeci tnie najwy szym poziomie wydajno ci. Z kolei w ka dym kwartale drugim
wynagrodzenia przeci tnie s ni sze od trendu o około 1,78%, a kwartale trzecim równie
ni sze - tym razem jednak o około 2,19%. Charakter odchyle wydajno ci i wynagrodze od

10

trendu wskazuje na mo liwo wyst pienia opó nie w dostosowywaniu si poziomu
wynagrodze do poziomu wydajno ci.

Tabela 4

Roczne indeksy wydajno ci pracy w gospodarce narodowej

(analogiczny okres ubiegłego roku = 1,000)

Okres

1994

1995

1996

1997

Kwartał I

1,0867 1,0702 1,0398 1,0487

Kwartał II

1,0757 1.0609 1.0609 1,0588

Kwartał III

1,0777 1.0717 1,0755 1,0500

Kwartał IV

1,0844 1,0542 1,0752 1,0698

redni indeks

1,0811 1,0642 1,0627 1,0568

rednia roczna stopa wzrostu

w %

8,11% 6,42% 6,27% 5,68%

ródło: obliczenia własne

Tabela 5

Roczne indeksy przeci tnych realnych wynagrodze netto w gospodarce narodowej

(analogiczny okres ubiegłego roku = 1,000)

Okres

1994

1995

1996

1997

Kwartał I

1,0289 1,0019 1,0561 1,0342

Kwartał II

1,0172 1,0072 1,0439 1,076

Kwartał III

1,0206 1,0409 1,0319 1,0739

Kwartał IV

1,0326 1,1087 0,9902 1,0660

redni indeks

1,0248 1,0388 1,0302 1.0624

rednia roczna stopa wzrostu

w %

2,48% 3,88% 3,02% 6,24%

ródło: obliczenia własne

Na tle wska ników przeci tnych dla lat 1993-1997 interesuj ce wydaj si roczne

indeksy wydajno ci pracy i wynagrodze realnych. Oszacowania tych wielko ci
zamieszczone zostały w Tabelach 4 i 5. Ten sposób prezentacji danych wzbogaca nasz
wiedz o ewentualnych zmianach tendencji w dynamice badanych wielko ci. Z analizy
informacji zawartych w obu tabelach wynika, e w analizowanych latach nast powało
przybli anie si do siebie dynamik rocznych wydajno ci i wynagrodze . Zauwa my, e w
1997 roku roczna dynamika wynagrodze przewy szyła roczna dynamik wydajno ci.

11

2. EKONOMETRYCZNA ANALIZA PROCESÓW DOSTOSOWAWCZYCH

WYNAGRODZE I WYDAJNO CI PRACY

Zastanawiaj c si nad zwi zkami pomi dzy agregatowymi wynagrodzeniami i

wydajno ci pracy trzeba rozstrzygn kwesti charakteru i sposobu dostosowywania si do
siebie obu tych zmiennych. Dlatego konstruuj c interesuj c nas zale no przyj to zało enie
w my l którego zasadnicza cz

wynagrodze zale y od oczekiwanego poziomu utrwalonej

wydajno ci. Mówi c oczekiwany poziom utrwalonej wydajno ci mamy na my li taki poziom,
który nie ma charakteru sezonowego i wynika ze stopnia wyposa enia pracy w kapitał. W
rezultacie funkcj wynagrodze zapisa mo emy nast puj co:

*

t

t

x

y

ββββ

++++

α

αα

α

====

(2)

gdzie:

t = 1,2,3...,n – numer obserwowanego okresu

t

y

- zasadnicza cz

wynagrodzenia (wielko oczyszczona z efektów

sezonowych),

*

t

x

- oczekiwany poziom utrwalonej wydajno ci (wielko nieobserwowana).

Załó my obecnie, e oczekiwana wielko utrwalonej wydajno ci podlega procesowi

adaptacji w zale no ci od stopnia realizacji przewidywa , co zgodnie z propozycj Nerlove
/por.: [2] s.353-354/ zapiszemy nast puj co:

)

x

x

)(

1

(

x

x

*

1

t

t

*

1

t

*

t

−−−−

−−−−

−−−−

γγγγ

−−−−

====

−−−−

, (3)

gdzie

t

x jest obserwowan rzeczywist wielko ci wydajno ci natomiast

)

1

(

γ

− jest

współczynnikiem adaptacji. Oznacza to, e wyst puj cy we współczynniku adaptacji
parametr spełnia musi warunek

1

0

γ

. Relacj (3) przekształci mo emy do nast puj cej

postaci:

t

*

1

t

*

t

x

)

1

(

x

x

γγγγ

−−−−

====

γγγγ

−−−−

−−−−

(4)

Aby przej do wielko ci obserwowanych relacj (2) zapiszmy dla okresu t-1. Mamy

wówczas:

*

1

t

1

t

x

y

−−−−

−−−−

ββββ

++++

α

αα

α

====

(5)

Po obustronnym przemno eniu modelu (5) przez parametr gamma otrzymujemy:

*

1

t

1

t

x

y

−−−−

−−−−

γβ

γβ

γβ

γβ

++++

γα

γα

γα

γα

====

γγγγ

(6)

Obecnie odejmuj c stronami od wyra enia (2) przekształcon posta (5) mamy:

)

x

x

(

)

1

(

y

y

*

1

t

*

t

1

t

t

−−−−

−−−−

γγγγ

−−−−

ββββ

++++

γγγγ

−−−−

α

αα

α

====

γγγγ

−−−−

(7)

12

Po uporz dkowaniu (7) dochodzimy do postaci:

t

1

t

t

x

)

1

(

y

)

1

(

y

γγγγ

−−−−

ββββ

++++

γγγγ

++++

γγγγ

−−−−

α

αα

α

====

−−−−

,

(8)

któr po przyj ci nast puj cych oznacze :

)

1

(

a

γγγγ

−−−−

α

αα

α

====

γγγγ

====

b

)

1

(

c

γγγγ

−−−−

ββββ

====

zapiszemy ostatecznie jako:

t

1

t

t

cx

by

a

y

++++

++++

====

−−−−

.

(9)

Na podstawie (9) okre li mo emy tzw. krótkookresowe i długookresowe efekty

oddziaływania zmiennej x na zmienn y. Zauwa my, e je li x w okresie t = 1 wzro nie o
jednostk i ustabilizuje si na nowym poziomie, wówczas przyrost y w kolejnych okresach
b dzie wynosił dla

t = 1:

c

y

1

====

∆∆∆∆

t = 2:

c

b

y

2

⋅⋅⋅⋅

====

∆∆∆∆

t = 3:

c

b

y

2

3

⋅⋅⋅⋅

====

∆∆∆∆

t = 4:

c

b

y

3

4

⋅⋅⋅⋅

====

∆∆∆∆

...

....................................

Ostateczny i całkowity przyrost zmiennej y wyniesie odpowiednio:

b

1

c

3

2

3

2

1

...

b

b

b

1

(

c

...

y

y

y

y

−−−−

====

++++

++++

++++

====

∆∆∆∆

++++

∆∆∆∆

++++

∆∆∆∆

====

∆∆∆∆

(10)

Parametr c okre la efekt krótkookresowy oddziaływania zmiennej x na y. Powiemy, e

je li w okresie t zmienna x wzro nie o jednostk to w tym samym okresie zmienna y wzro nie
o c jednostek. Wzrost ten spowoduje ostateczny przyrost zmiennej y o wielko opisan przez
(10). Jest to tzw efekt długookresowy. Zauwa my, e wielko ta faktycznie równa si
parametrowi

β

z równania drugiego.

Zauwa my, e je li zmienna x

t

ustabilizuje si na stałym poziomie x wówczas

zmienna y

t

zmierza b dzie do poziomu równowagi y

e

, który zdefiniujemy nast puj co

/por.:[10] s.78-79].:

b

1

x

c

a

y

e

−−−−

++++

====

(11)

Wnioski sformułowane dla liniowego modelu dynamicznego przenie mo na na

modele klasy logarytmiczno-liniowej. W tym przypadku przy okre laniu wpływu zmiennej

13

obja niaj cej na zmienn obja nian posługiwa b dziemy si elastyczno ciami. W
analizowanym przez nas przypadku dotycz cym wynagrodze i wydajno ci model ten b dzie
miał posta

4

:

t

3

t

3

2

t

2

1

t

1

c

t

b

1

t

0

t

u

exp

)

v

c

v

c

v

c

exp(

AP

w

a

w

⋅⋅⋅⋅

++++

++++

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

(12)

gdzie w

t

jest to wielko przeci tnego wynagrodzenia realnego netto w cenach z kwartału

pierwszego 1993r. Zmienn AP

t

definiujemy jako przeci tn wydajno pracy wyra ona

indeksem jednopodstawowym. Zmienne sezonowe v

i

opisane zostały wcze niej.

Model (12), po wcze niejszym obustronnym zlogarytmowaniu, oszacowano metod

najmniejszych kwadratów. Wyniki oszacowa przedstawiaj si nast puj co:

t

3

t

)

04

,

2

(

2

t

)

84

,

2

(

1

t

)

12

,

1

(

t

)

54

,

2

(

1

t

)

22

,

2

(

)

35

,

2

(

t

uˆ

v

0221

,

0

v

0243

,

0

v

0145

,

0

AP

ln

337

,

0

w

ln

485

,

0

901

,

2

w

ln

++++

−−−−

−−−−

++++

++++

++++

====

−−−−

(13)

922

,

0

R

2

====

DW = 1,844

0126

,

0

ˆ

±±±±

====

σσσσ

Na podstawie oszacowanej wersji modelu wynagrodze mo emy sformułowa

nast puj ce wnioski o charakterze przyczynowo-skutkowym.

Wzrost wydajno ci pracy w

kwartale

„t” o 1% prowadzi do wzrostu wynagrodze w tym samym kwartale o 0,337%.

Efekt ten implikuje w nast pnym kwartale dodatkowy przyrost wynagrodze o 0,173%, co po
dwóch kwartałach daje ł czny przyrost wynagrodze 0,51%. Graniczny ł czny przyrost
wynagrodze z tytułu wzrostu wydajno ci o 1% w kwartale t wynosi

0,665%. Wielko ta

nieznacznie przewy sza efekt roczny wynosz cy 0,645%. Wynik ten wyda mo e si jako
zaskakuj co niski. Pami tajmy jednak, e efekty zwi zane ze wzrostem wydajno ci pracy
nale y rozdysponowa nie tylko pomi dzy osoby zatrudnione w gospodarce. Cz

wypracowanych efektów przypa powinna wła cicielom kapitału a ponadto w skali
makroekonomicznej licznej i jednocze nie narastaj cej grupie emerytów i rencistów/patrz
tabela 1/. Je li zało ymy ponadto, e renty i emerytury podlegaj nie tylko prostej
waloryzacji, ale w jakim stopniu sprz one s z realnym wzrostem PKB, uzyskany wynik
uzna nale y za realny i uzasadniony. Jest to jednak wynik redni oszacowany dla okresu
1993 rok kwartał I – 1997 kwartał IV. Z analizy indeksów rocznych wynika, e w 1997 roku
roczne stopy wzrostu wynagrodze przewy szyły roczne stopy wzrostu wydajno ci /por.:
tabele 4 i 5/. Budzi mo e to niepokój wskazuj c na mo liwo realizacji niekorzystnego
wariantu B dostosowa wynagrodze do wydajno ci.

4

Rozpatrywany tutaj model słu y wst pnemu rozpoznaniu prawidłowo ci dotycz cych dostosowywania si

wynagrodze i wydajno ci. W procesie dalszej konkretyzacji nale y liczy si z innym sposobem adaptacji

wynagrodze wzgl dem inflacji a innym wzgl dem wydajno ci, co wymaga b dzie respecyfikacji

rozpatrywanegu tutaj modelu.

14

Obok opisanych powy ej efektów okre li mo emy efekty sezonowe zmian

wynagrodze . Na podstawie metody opracowanej dla modeli dynamicznych /por.: [8]/
stwierdzi mo emy, e przeci tne odchylenia wynagrodze od poziomu wynagrodze
wyznaczonych przez oczekiwan utrwalon wydajno pracy wynosz odpowiednio:

w kwartale pierwszym: 2.35%,
w kwartale drugim: –1,29%,
w kwartale trzecim: -2,80%,
w kwartale czwartym: 1,83%.

4. EKONOMETRYCZNA ANALIZA PROCESÓW DOSTOSOWAWCZYCH STOPY

BEZROBOCIA, WYDAJNO CI PRACY, WYNAGRODZE ORAZ CEN.

W literaturze ekonomicznej problematyka zwi zków stopy bezrobocia z wydajno ci i

wynagrodzeniami jest szeroko dyskutowana. Przegl d stosunkowo najnowszych metod
badawczych oraz wykaz bogatej literatury dotycz cej bezrobocia znajdzie czytelnik w pracy
monograficznej [5]. Z uwagi na fakt, i niniejszy artykuł słu y ma wst pnemu rozpoznaniu
mo liwo ci badania tego typu zwi zków na bazie materiału empirycznego dotycz cego
Polski, dokonano w nim wiadomych uproszcze . Chodziło o takie uproszczenia, dzi ki
którym mo liwa b dzie kontrola poprawno ci specyfikacji proponowanych rozwi za . W
rezultacie posłu ono si modelami o stałej elastyczno ci cz stkowej, eliminuj c z rozwa a
trudny problem szacowania produktu potencjalnego oraz naturalnej stopy bezrobocia.
Ostatecznie weryfikacji empirycznej poddano nast puj cy model dynamiczny:

t

a

t

a

t

a

t

b

1

t

t

u

exp

P

Wn

AP

SB

a

SB

3

2

1

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

(14)

gdzie SB jest stop bezrobocia, AP - wydajno ci pracy, Wn - przeci tnymi wynagrodzeniami
nominalnymi netto, P - jednopodstawowym indeksem cen dóbr i usług konsumpcyjnych
natomiast u

t

- składnikiem zakłócaj cym modelu. Model ma charakter dynamiczny. Wynika

to z zało enia, i stopa bezrobocia nie zmienia si gwałtownie na skutek zmian kształtuj cych
j przyczyn. Dostosowuje si ona do zmieniaj cych si warunków w sposób powolny. Z

uwagi na posta pot gow modelu, parametry strukturalne

i

a s stałymi krótkookresowymi

elastyczno ciami Długookresowe wzgl dne efekty oddziaływania czynnika i-tego na stop

bezrobocia okre limy, posługuj c si znan ju dla postaci liniowej formuł :

)

1

/(

b

a

i

− .

Analizuj c krótkookresow interpretacj oddziaływania czynników na stop bezrobocia

15

okre li mo emy warunki poprawnej specyfikacji

5

. Rozwa my wi c ka dy z mo liwych

przypadków cz stkowych.
1.

W warunkach stało ci pozostałych zmiennych (tzn. wynagrodze i cen) wzrost przeci tnej

wydajno ci pracy prowadzi do spadku stopy bezrobocia. Oznacza to, e parametr

1

a

winien by wi kszy od zera.

2.

W warunkach stało ci pozostałych zmiennych wzrost wynagrodze nominalnych

prowadzi do wzrostu bezrobocia. Zauwa my bowiem, e wzrost wynagrodze
nominalnych w warunkach stało ci cen oznacza wzrost wynagrodze realnych. W

konsekwencji parametr

2

a

winien by wi kszy od zera.

3.

W warunkach stało ci pozostałych zmiennych (tzn. wydajno ci i wynagrodze

nominalnych) wzrost przeci tnego poziomu cen prowadzi do spadku bezrobocia. Sytuacja
tutaj odwraca si w stosunku do rozpatrywanej poprzednio. Obecnie wzrost cen w
warunkach stało ci wynagrodze nominalnych oznacza spadek wynagrodze realnych w
warunkach stało ci wydajno ci pracy. To z kolei prowadzi do zwi kszonego popytu na
prac , co przy zało eniu niezmiennej poda y pracy oznacza spadek stopy bezrobocia.

Tym samym parametr

3

a winien by mniejszy od zera. Odpowiada to znanym

wła ciwo ciom krótkookresowej krzywej Philipsa.

Celem scharakteryzowania wewn trznej struktury parametrów dokonajmy przekształce

relacji (13), wykorzystuj c wła ciwo ci modelu pot gowego w sytuacji posługiwania si

zmiennymi maj cymi charakter wielko ci przeci tnych. Zauwa my bowiem, e wydajno

pracy definiujemy jako stosunek produktu krajowego brutto (Y) do nakładów pracy (N)

mierzonych wielko ci zatrudnionych w gospodarce. Przeci tne wynagrodzenie nominalne

faktycznie jest stosunkiem całego funduszu wynagrodze nominalnych (FWn) do

nakładów pracy (N). Oznacza to, e model (13) ma nast puj c równowa n posta :

t

a

t

a

t

a

t

a

t

b

1

t

t

u

exp

P

N

FWn

Y

SB

a

SB

3

12

2

1

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

⋅⋅⋅⋅

====

−−−−

(15)

gdzie parametr przy zmiennej N definiujemy jako

2

1

12

a

a

a

−

−

=

. Zastanówmy si nad

interpretacj tak zdefiniowanego parametru. Wskazuje on, o ile procent powinna zmieni si
stopa bezrobocia, je li zatrudnienie wzro nie o 1% a produkt krajowy brutto oraz fundusz

5

Mówi c o warunkach poprawnej specyfikacji zakładamy, e czynniki uwzgl dnone w modelu s czynnikami

głównymi. W stosunku do czynników pomini tych a mog cych mie wpływ na zmienn objasnian zakłada si ,

i w anlizowanym okresie badawczym s stałe wzgl dnie charakter ich zmian jest czysto losowy.

16

wynagrodze i poziom cen nie ulegn zmianie. Faktycznie oznacza to wzrost zatrudnienia
przy jednoczesnym spadku przeci tnego wynagrodzenia realnego ( dlatego ma prawo
nast pi ) mimo, e jednocze nie dochodzi do spadku wydajno ci. Spadek wydajno ci
spowodowany jest wzrostem zatrudnienia w warunkach stało ci produktu a tym samym

odbywa si w warunkach spadku stopy bezrobocia. Oznacza to, e parametr

12

a

powinien by

mniejszy od zera. Aby to nast piło musi by spełniona nast puj ca nierówno :

2

1

a

a

(16)

W kontek cie powy szych uwag zastanówmy si nad oszacowan wersj

zlinearyzowanej postaci modelu (15). Stosuj c metod najmniejszych kwadratów otrzymano
nast puj ce rezultaty:

t

t

)

28

,

1

(

t

)

22

,

1

(

t

)

13

,

1

(

1

t

)

15

,

9

(

)

99

,

0

(

t

uˆ

P

ln

439

,

0

Wn

ln

342

,

0

AP

ln

277

,

0

SB

ln

958

,

0

757

,

1

SB

ln

++++

−−−−

++++

−−−−

++++

−−−−

====

−−−−

(17)

972

,

0

R

2

====

DW = 2,032

0273

,

0

ˆ ±±±±

====

δδδδ

Bior c pod uwag ogólne miary dopasowania, rozpatrywany model uzna mo na za

zadawalaj cy. Z kolei warto ci statystyk t-Studenta umieszczone w nawiasach pod ocenami
oceni mo na za stosunkowo niskie. Zauwa my jednak, e przy testowaniu jednostronnym
prawdopodobie stwo przyj cia przez parametry znaku przeciwnego jest ni sze od 0,2. Wa ny
jest jednocze nie fakt, i oceny parametrów spełniaj nakre lone warunki poprawnej
specyfikacji ł cznie z zało on w (16) nierówno ci .

Przechodz c do analizy przyczynowo-skutkowej sformułowa mo na szereg

wniosków.
1.

W warunkach stało ci pozostałych zmiennych wzrost wydajno ci w okresie t o 1%

prowadzi do spadku stopy bezrobocia w tym samym okresie o około 0,277%, co zapewnia
graniczny spadek stopy bezrobocia o około 6,59%. Pami tajmy, e chodzi tutaj o
procentowy spadek stopy bezrobocia a nie punktowy. Czyli gdyby stopa bezrobocia
wynosiła 15% jej spadek o 6,59% oznacza w tym przypadku obni enie si jej do poziomu
14,01%., czyli punktowo obni yłaby si ona o około 0,99%.

2.

W warunkach stało ci pozostałych zmiennych wzrost wynagrodze w danym okresie o

1% powoduje wzrost stopy bezrobocia w tym samym okresie o 0,342%, co prowadzi do
granicznego wzrostu stopy bezrobocia o około 8,142%.

3.

W warunkach stało ci pozostałych zmiennych wzrostowi cen w danym kwartale o 1%

towarzyszy spadek stopy bezrobocia w tym samym kwartale o około 0,439%, co daje
graniczny spadek rz du 10,42%.

17

Powstaje pytanie, jakie powinny by procentowe zmiany wynagrodze umo liwiaj ce
utrzymanie stopy bezrobocia na niezmienionym poziomie w warunkach gdyby wydajno
pracy wzrosła o 1%?. Dokonuj c prostych przekształce oszacowanych parametrów
wyliczamy, e w tych warunkach wynagrodzenia nie powinny wzrasta w tempie
przekraczaj cym 0,81%. W ostatnim roku obserwujemy, e jednoprocentowemu
wzrostowi wydajno ci w skali rocznej towarzyszy nieco wy szy procentowo przyrost
wynagrodze . Oznacza to, e aby utrzyma dotychczasow tendencj spadku stopy
bezrobocia nale ałoby zahamowa wzrost wynagrodze w relacji do wzrostu wydajno ci.
W przeciwnym wypadku korzystne tendencje zmian przeci tnego poziomu cen ulec mog
odwróceniu. Do powy szych wyników, mimo stosunkowo rozs dnych oszacowa
parametrów, nale y podchodzi z du doz ostro no ci. Pami tajmy bowiem, e rynek
pracy cały czas ulega porz dkowaniu wynikaj cemu z jednej strony z procesów
transformacji systemowej a z drugiej strony ze zmieniaj cych si przepisów dotycz cych
mi dzy innymi bezrobotnych oraz warunków otrzymywania przez nich zasiłków. Cz

bezrobotnych na skutek tego, i nie spełniaj warunków umo liwiaj cych otrzymywanie
zasiłków przestało si rejestrowa w Urz dach Zatrudnienia. Z pewno ci przyczynia si
to do zniekształcenia wska nika stopy bezrobocia. Zmiany te maj , jak si wydaje,
charakter ewolucyjny i oszacowane parametry modelu ten fakt ujmuj . Na bazie
wykorzystywanych tutaj informacji nie potrafimy jednak efektów tych zmian oddzieli

5. WNIOSKI

Z przeprowadzonej w artykule analizy wynika, e gospodarka Polski w latach 1993-

1997 weszła na now cie k zmian. Cech charakterystyczn tych zmian był stosunkowo
szybki wzrost PKB w warunkach coraz wy szej dynamiki nakładów inwestycyjnych przy
jednoczesnym spadku stopy bezrobocia oraz zmniejszaj cej si inflacji. Procesy te mogły
zaj przy okre lonych relacjach dostosowawczych pomi dzy wydajno ci pracy i poziomem
wynagrodze . Z przeprowadzonej analizy wynika, e w latach 1993-1997 przeci tnemu
rocznemu wzrostowi wydajno ci wynosz cemu 6,56% towarzyszył przeci tny roczny
przyrost wynagrodze realnych rz du 3,81%. Ponadto wykazano, e jednoprocentowy wzrost
wydajno ci w danym kwartale prowadził do wzrostu wynagrodze w tym samym kwartale o
0,337%, co przy utrzymaniu si wydajno ci na tym samym poziomie dawało ostateczny
przyrost wynagrodze o około 0,665%. Z drugiej strony stwierdzono, e aby stopa bezrobocia
nie uległa wzrostowi, to w warunkach stało ci cen, dynamika wzrostu wynagrodze stanowi

18

powinna mniej ni 0,81% dynamiki wzrostu wydajno ci. Relacja ta w 1997 roku została
przekroczona na skutek lekkiego obni enia si dynamiki wzrostu wydajno ci przy
jednoczesnym wzro cie dynamiki wynagrodze . Sytuacja ta mo e by wyrazem pocz tku
zmian w charakterze procesów dostosowawczych pomi dzy wydajno ci pracy i
wynagrodzeniami. W kontek cie rozwa anego w artykule modelu teoretycznego, oznaczałoby
to odej cie od wariantu A do wariantu B procesów dostosowawczych. Rezultatem tego
byłoby odwrócenie dotychczasowych korzystnych tendencji spadku inflacji i stopy
bezrobocia.

BIBLIOGRAFIA

[1] Begg D., Fischer S., Dornbusch R.: Ekonomia t.2, PWE, Warszawa 1992
[2] Goldberger A.S.:Teoria Ekonometrii, PWN, Warszawa 1972
[3] Hall R. E., Taylor J.B.: Makroekonomia - teoria, funkcjonowanie i polityka, PWN,
Warszawa 1995
[4] Hardwick P., Khan B.: Langmead J. An Introduction to Modern Economics, Longman,
London and New York 1994
[5] Layard R., Nickell S., Jackman R.: Unemployment, Macroeconomic Performance and the
Labour Market, Oxford University Press, Oxford 1993
[6] Ossowski J. : Własno ci interpretacyjne składnika zakłócaj cego w modelu
multyplikatywnym, Przegl d Statystyczny, nr 2, 1989, s.131-142.
[7] Ossowski J. Cz.: Dynamika bezrobocia a dynamika produkcji sprzedanej polskiego
przemysłu, w „Dynamiczne Modele Ekonometryczne”, Instytut Wydawniczy Gravis,
Toru 1995, s. 31-42.
[8] Ossowski J.Cz.: Sezonowo w modelach dynamicznych - problemy interpretacyjne,
w „Dynamiczne modele ekonometryczne”, Katedra Ekonometrii i Statystyki,
Uniwersytet M.Kopernika, Toru 1997, s.51-56
[9] Ossowski J.Cz.: Produktywno pracy a wynagrodzenia w polskim przemy le w latach
1993-1997, Gospodarka w praktyce i teorii, Nr 1 1997, s. 45-51.
[10] Stewart M.B., Wallis K.F (1981), Introductory Econometrics,Basil Blackwel Oxford.
[11] Theil H.: Zasady ekonometrii, PWN, Warszawa 1984.

[12] Biuletyny statystyczne GUS z lat 1993-1998, GUS, Warszawa

[13] Poland Quarterly Statistics z lat 1995-1998, GUS, Warszawa.

[14] Rocznik statystyczny 1997, GUS, Warszawa 1998