Obciążenie śniegiem dachu wg PN-EN 1991-1-3

Dane:
Tarnów

miejscowość

3 strefa obciążenia śniegiem [rysunek

NB.1]

A

215m



wysokość nad poziomem morza

α

5deg



kąt nachylenia połaci dachowej

Dane geometryczne hali

b

90m



długość hali

a

30m



szerokość hali

h

10.3m



maksymalna wysokość hali

d

6m



rozstaw dźwigarów

hs

6m



wyskokość ściany

Podstawa obliczeniowa:

Obciążenie śniegiem dachu w trwałej i przejściowej sytuacji obliczeniowej:

s

μi Ce



Ct



sk



=

[5.2 wzór 5.1]

gdzie:

μi

współczynnik kształtu dachu

sk

wartość charakterystyczna obciążenia śniegiem gruntu

Ce

współczynnik ekspozycji

Ct

współczynnik termiczny

Współczynnik ekspozycji

Ce 1



teren normalny

[5.2 tablica 5.1]

Współczynnik termiczny

Ct 1



[5.2]

Wartość charakterystyczna obciążenia śniegiem gruntu

sk

1.2

kN

m

2





0,006A-0,6 lecz nie mniej niż 1,2

[tablica NB.1]

Współczynnik kształtu dachu

Brak zabezpieczeń przed zsunięciem sie śniegu z dachu

μ1

0.8



wartość współczynnika kształtu dachu dla połaci lewej i prawej [5.2 tablica 5.2]

Częściowy współczynnik bezpieczeństwa

γm

1.5



Obciążenie śniegiem dachu - wartość charakterystyczna

s

μ1 Ce



Ct



sk



0.96

kN

m

2







Obciążenie śniegiem dachu - wartość obliczeniowa

sd

s γm



1.44

kN

m

2







Ze względu na mały kąt nachylenia połąci dachu pomijamy działanie śniegu w kierunku poziomym

s

.k

s

.k

s

.k

0.5.s

.k

0.5s

.k

s

.k

1

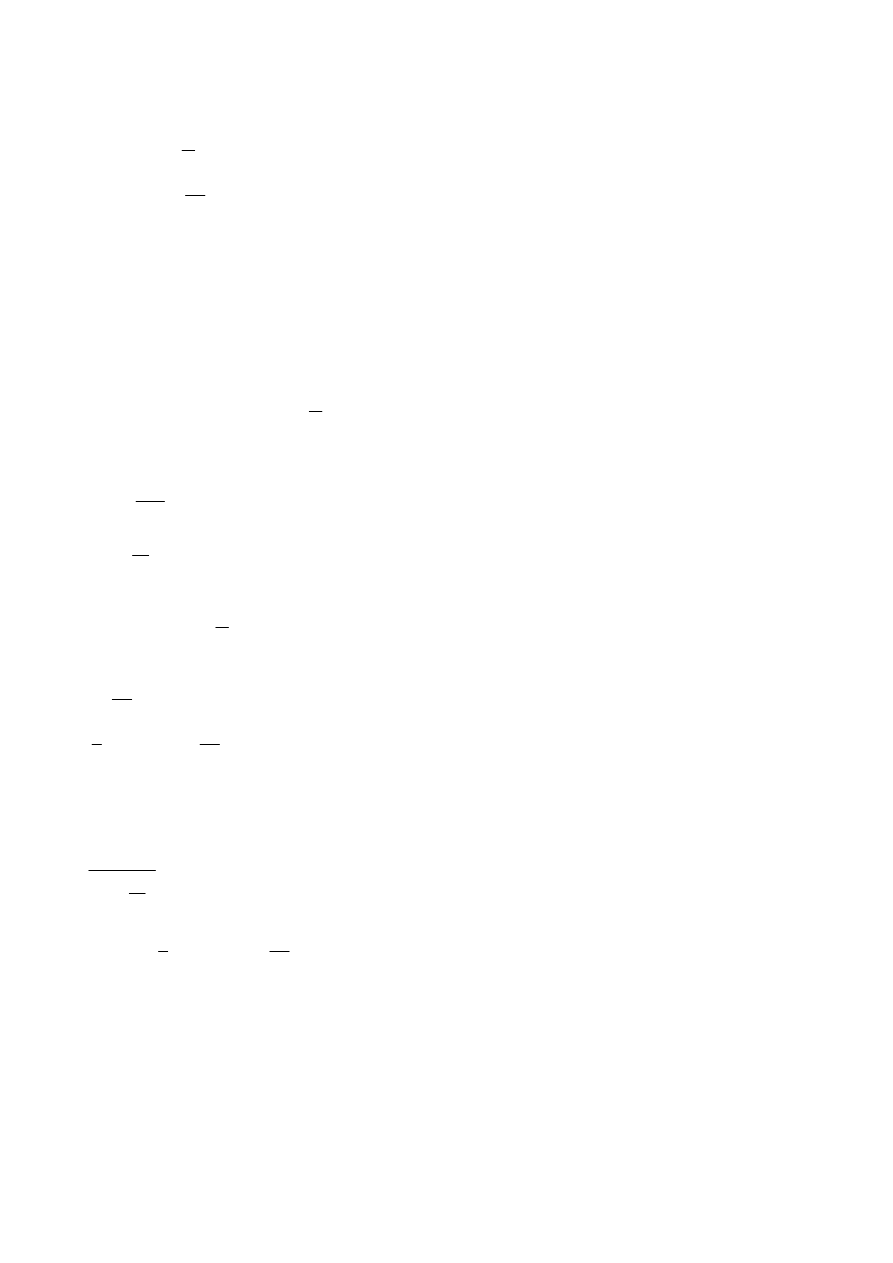
2. Obc. wiatrem

wg. PN-EN 1991-1-4

Przyjęto III kategorię terenu [tab.4.1 str.20]

1-strefa obciążenia wiatrem

vb.0 22

m

s



podstawowa bazowa prędkość wiatru

qb.0 0.3

kN

m

2



podstawowe bazowe cisnienie wiatru

z0

1m



z0.II 0.05m



z

7m

3.3m



10.3 m





kategoria terenu III

Cdir 1



współczynnik kierunkowy

Cseason 1



współczynnik sezonowy

vb

Cdir Cseason



vb.0



22

m

s





wzór 4.1

Średnia prędkość wiatru

kr 0.19

z0

z0.II













0.07



0.234





współczynnik terenu

cr kr ln

z

z0















0.546





chropowatość terenu

c0

1



współczynnik rzeźby terenu

vm cr c0



vb



12.023

m

s





średnia prędkość wiatru (4.3) str.19

Bazowe ciśnienie prędkośći wiatru

ρ

1.25

kg

m

3



gęstość powietrza

qb

1
2

ρ

 vb

2



0.303

kN

m

2







wartość bazowa ciśnienia prędkości

Szczytowe ciśnienie prędkośći wiatru

kl 1



współczynnik turbulencji

Iv

kl

c0 ln

z

z0















0.429





intensywność turbulencji

qp

1

7 Iv









1
2

 ρ

 vm

2



0.362

kN

m

2







wartość szczytowa ciśnienia prędkości (4.8) str.22

Określenie współczynników ciśnienia zewnętrznego

2

A) Ściany pionowe

ze z 10.3 m





wysokość odniesienia

Wiatr na ścianę dłuższą

h
a

0.343



stosunek wyskokości hali do szerokośći

b

90m



d

30m



e

min b 2 h





(

)

20.6 m





cpe.A

1.2





cpe.B

0.8





współczynniki
ciśnienia zewnętrzenego
tab.7.1 str 35

cpe.D 0.8



cpe.E

0.5





Wiatr na ścianę krótszą

h
a

0.343



stosunek wyskokości hali do szerokośći

b

30m



d

90m



e

min b 2 h





(

)

20.6 m





cpe.A

1.2





cpe.B

0.8





współczynniki
ciśnienia zewnętrzenego
tab.7.1 str 35

cpe.C

0.5





cpe.D 0.8



cpe.E

0.5





B) Dach

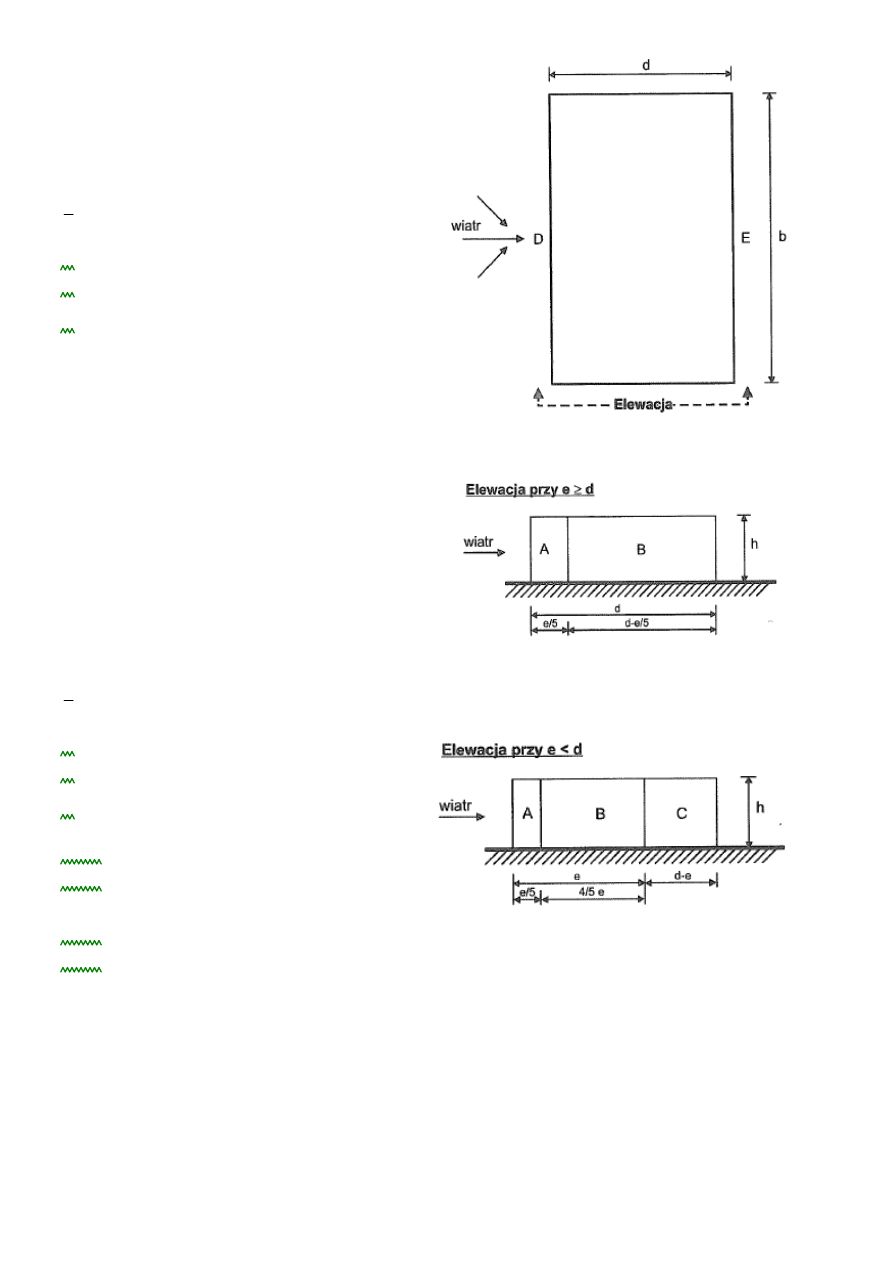
3

α

5deg



kąt pochyenia połaci dachu

Ze względu na kąt pochylenia połaci rozpatrujemy dach jako dach dwuspadowy

Wiatr na ścianę dłuższą (θ=0)

b

90m



d

30m



e

min b 2 h





(

)

20.6 m





Współczynniki:

cpe.F

1.7





/ +0.0

cpe.G

1.2





/ +0.0

cpe.H

0.6





/ +0.0

cpe.I

0.6





/ +0.0

cpe.I

0.6





/ +0.2

Wiatr na ścianę krótszą (θ=90)

b

30m



d

90m



e

min b 2 h





(

)

20.6 m





Współczynniki:

cpe.F

1.6





cpe.G

1.3





cpe.H

0.7





cpe.I

0.6





1.3.3 Określenie współczynników ciśnienia wewnętrznego

Ze względu na brak informaci o otworach w ścinach hali, przyjmujemy najniekorzystniejszy przypadek ssania bądź
parcia wiatru ( Cpi = 0.35 lub -0.4) rys7.13 str.47

cpi 0.35



/ -0.4

1.3.4 Rozpoznanie najnieorzystniejszych kombinacji oddziaływania wiatru

Wybrano dwie najbardziej niekorzystne sytuacje oddziaływania wiatru:

1.maksymalne parcie wiatru (pole I) oraz maksymalne ssanie wewnętrzne

we.1

qp 0.2



qp 0.4







0.217

kN

m

2







maksymalna wypadkowa siła parcia

2.maksymalne ssanie wiatru (pole F) oraz maksymalne parcie wewnętrzne

we.2

qp 1.7





qp 0.35





0.741

kN

m

2







maksymalna wypadkowa siła ssania

3. Obciążenie pokryciem dachowym

4

jako pokrycia bedzie zastosowana PŁYTA DACHOWA EPS d
(firmy BARDA) z rdzeniem z wełny mineralnej o gr. 15cm

gpk 9.81

m

s

2

13



kg

m

2

0.128

kN

m

2







ciężar charakterystyczny pokrycia
dachowego

gpd gpk 1.35



0.172

kN

m

2







ciężar obliczeniowy

PŁATEW Z KSZTAŁTOWNIKA GIĘTEGO

fy

235

N

mm

2





granica plastyczności

E

210GPa



modół plastyczności

ν

0.3



modół Poissona

γM0

1.00



współczynniki częściowe

γM1

1.00



γM2

1.25



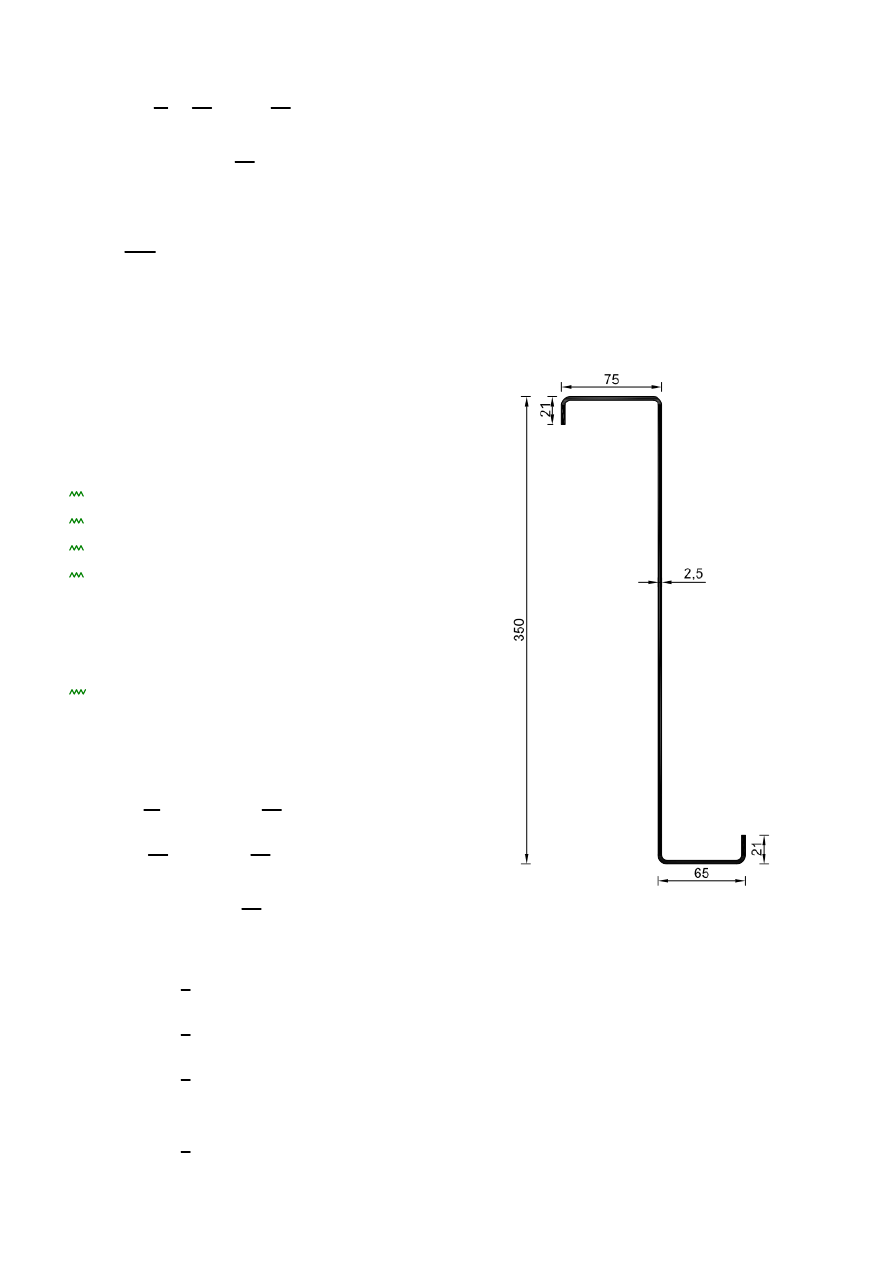
Charakterystyki przekroju:

h

350mm



wysokość środnika

b

75mm



szerokość stopki górnej

d

65mm



szerokość stopki dolnej

c

21mm



szerokość usztywnienia brzegowego

r

3.75mm



promień wewnętrzny zagięcia naroży

t

2.5mm



grubość ścianki

Iy

2062.37cm

4



moment bezwładności względem osi y-y

A

12.78cm

2



pole przekroju

zb

172.4mm



odległość półki górnej od środka ciężkości

zd

177.6mm



odległość półki dolnej od środka ciężkości

ϕ

90deg



kąt wygięcia

md.z

10.03

kg

m



g

 1.35



0.133

kN

m







ciężar własny zetownika 250

ciężar własny płyty warstwowej

md.pł 0.172

kN

m

2

3

 m 0.516

kN

m







Qd.g md.z md.pł



0.649

kN

m







ciężar stały

Sprawdzenie proporcji geometrycznych, wg. EC3 1-3 tab. 5.1

stopki

b

t

30



< 60

d

t

26



< 60

środnik

h

t

140



< 500 sin 90deg

(

)



500



usztywnienia brzegowe, wzór 5.2a

0.2 <

c
b

0.28



< 0.6

5

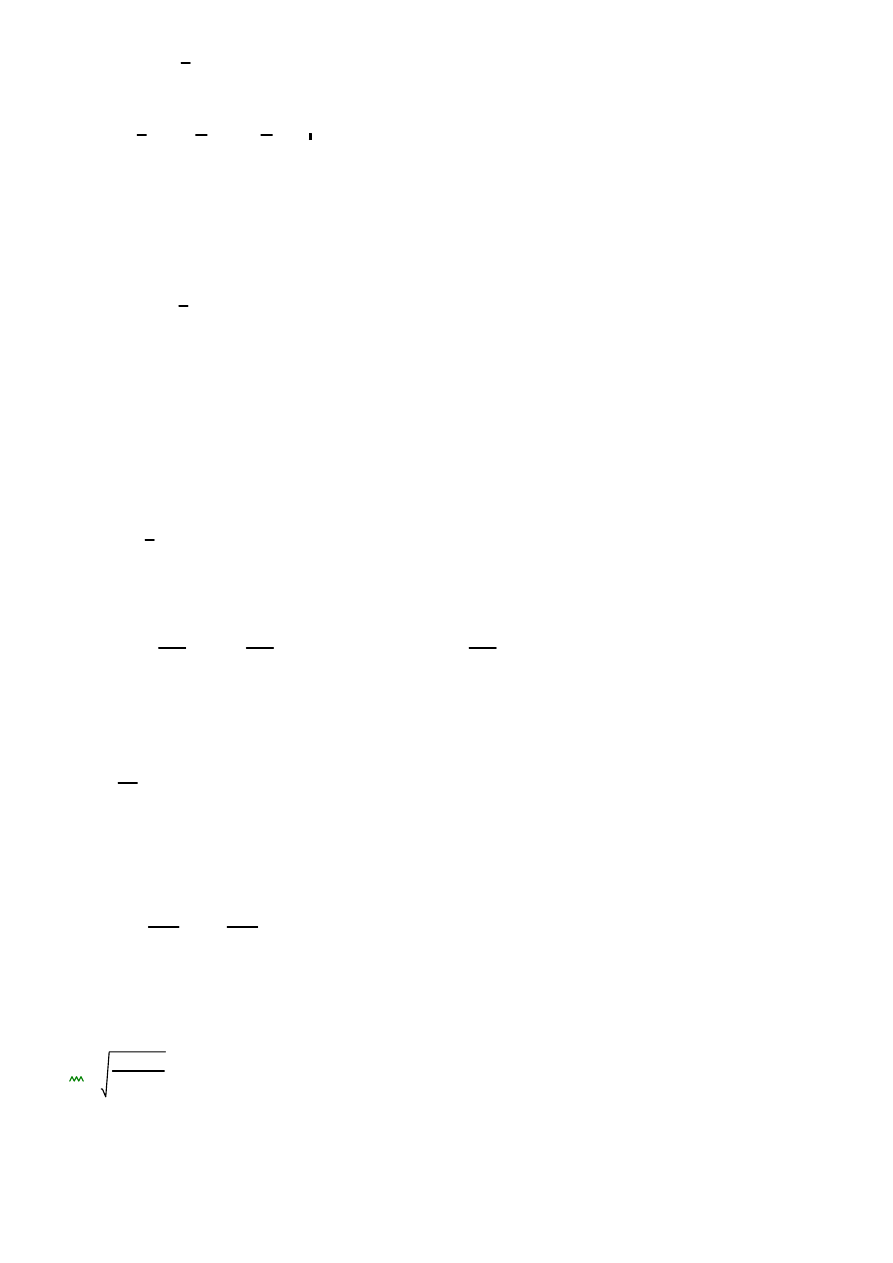
0.2 <

c
d

0.323



< 0.6

Wpływ zaokrąglenia naroży. EC3-1-3, 5.1

gr

r

t

2











tan

ϕ

2









sin

ϕ

2





















mm







Stąd wyliczam szerokości ścianek przekroju obliczeniowego:

bp.h.

h

2 gr





t



344.571 mm







środnik

bp.b.

b

2 gr





t



69.571 mm







stopka górna

bp.d.

d

2 gr





t



59.571 mm







stopka dolna

bp.c. c gr



t

2



18.286 mm







usztywnienia brzegowe

Jeśli promeń wewnętrzny r spełnia określone warunki, to przy określaniu nośności przekroju mośna pomijać
wpływ zaokrąglenia naroży, traktując przekrój jako zespół części płaskich o ostrych narożach.

Zatem szerokości ścianek przekroju obliczeniowego zmieniają się do wartości przy g

r

=0:

bp.h h t



347.5 mm







środnik

bp.b b t



72.5 mm







stopka górna

bp.d d t



62.5 mm







stopka dolna

bp.c

c

t

2



19.75 mm







usztywnienia brzegowe

Wyznaczam charakterystyki geometryczne przyjętego przekroju.

moment statyczny względem środka mniejszej półki

S1

bp.c t

bp.c

2



bp.h t

bp.h

2





bp.b t bp.h





bp.c t bp.h

bp.c

2



















231087 mm

3







Pole przekroju

A1

2 bp.c



bp.d



bp.h



bp.b







t



1.305

10

3



mm

2







Środek ciężkości

z1

S1

A1

177.079 mm







zb1 bp.h z1



170.421 mm







zasięg strefy ściskanej środnika

zd1 z1 177.079 mm







zasięg strefy rozciąganej środnika

Nośność przekroju przy zginaniu z wymuszonym kierunkiem deformacji:

σcom.Ed

fy

γM0

235

N

mm

2







Niestateczność miejscowa stopki górnej i jej usztywnienia brzegowego:

stosunek naprężeń jest równy:

ψ

1



ε

235MPa

fy

1





Zatem korzystając talbicy 4.1 EC3 1-5:

k

σ

4



6

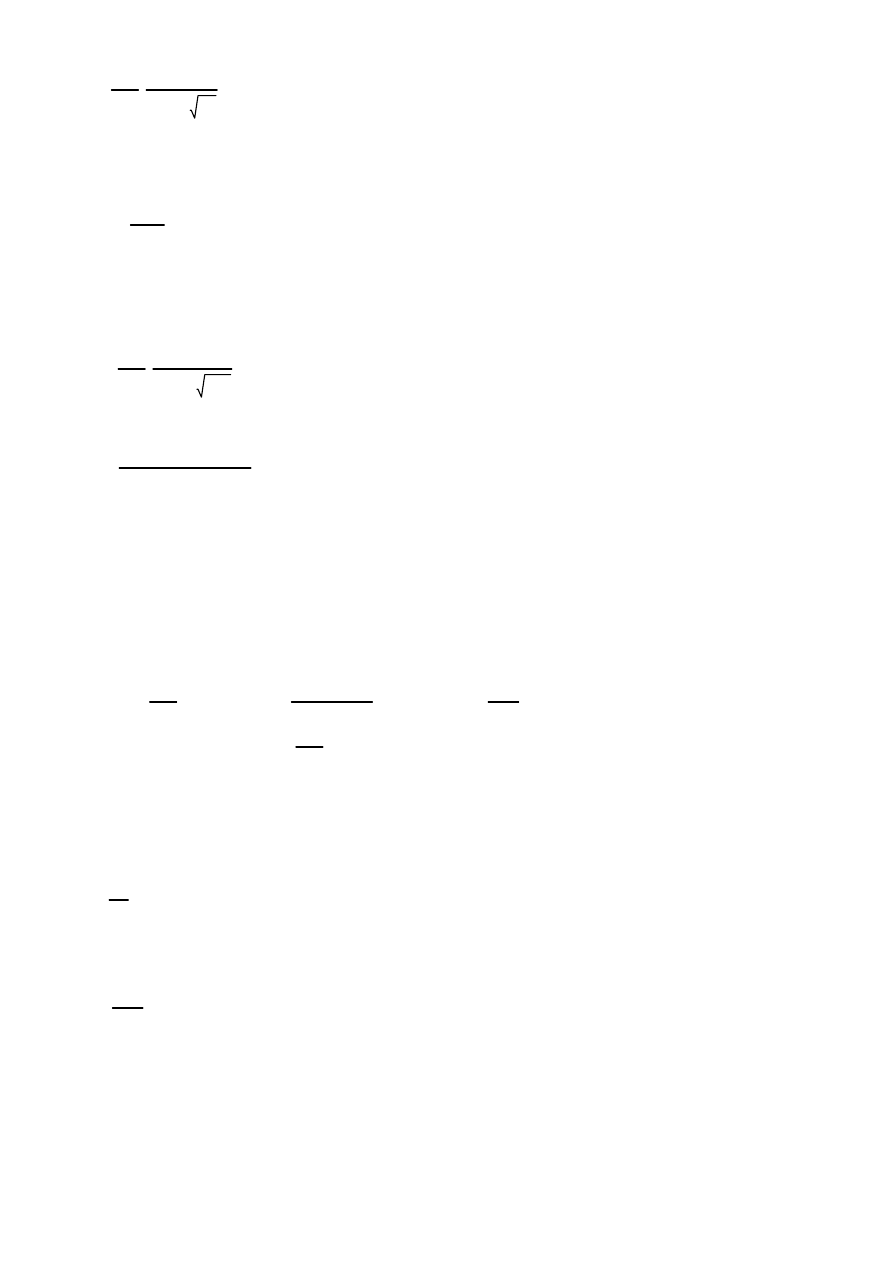
smukłość płytowa ścianki:

λp

bp.b

t

1

28.4 ε



k

σ





0.511





< 0.673

Ścianka nie jest wrażliwa na utratę stateczności miejscowej.

Niestateczność miejscowa środnika:

Stosunek naprężeń normalnych w środniku

ψ1

zd

 1

zb1

1.0421







Parametr niestateczności zginanej ścianki przęsłowej

k

σ

1

7.81

6.29 ψ1





9.78 ψ1

2





24.99





Smukłość płytowa ścianki:

λp1

bp.h

t

1

28.4 ε



k

σ

1





0.979





> 0.673

Ścianka jest wrażliwa na utratę stateczności miejscowej.

Współczynnik redukcyjny:

ρ1

λp1 0.055 3 ψ1









λp1

2

0.909





Szerokości współpracujące:

beff1 ρ1 zb1



154.9 mm







be11 0.4 beff1



62 mm







be21 0.6 beff1



92.9 mm







Druga iteracja:

Moment statyczny:

S2

bp.c t

bp.c

2



zd1 be21







t



zd1 be21







2





be11 t bp.h

be11

2



















bp.b t bp.h



bp.c t bp.h

bp.c

2























220.316

10

3



mm

3







Pole przekroju

A2

2 bp.c



bp.d



zd1



be21



be11



bp.b







t



1.266

10

3



mm

2







Środek ciężkości

z2

S2

A2

174 mm







zb2 bp.h z2



173.506 mm







zasięg strefy ściskanej środnika

zd2 z2 173.994 mm







zasięg strefy rozciąganej środnika

ψ2

zd2



zb2

1.003







Parametr niestateczności zginanej ścianki przęsłowej

k

σ

2

7.81

6.29 ψ2





9.78 ψ2

2





23.95





Smukłość płytowa ścianki:

7

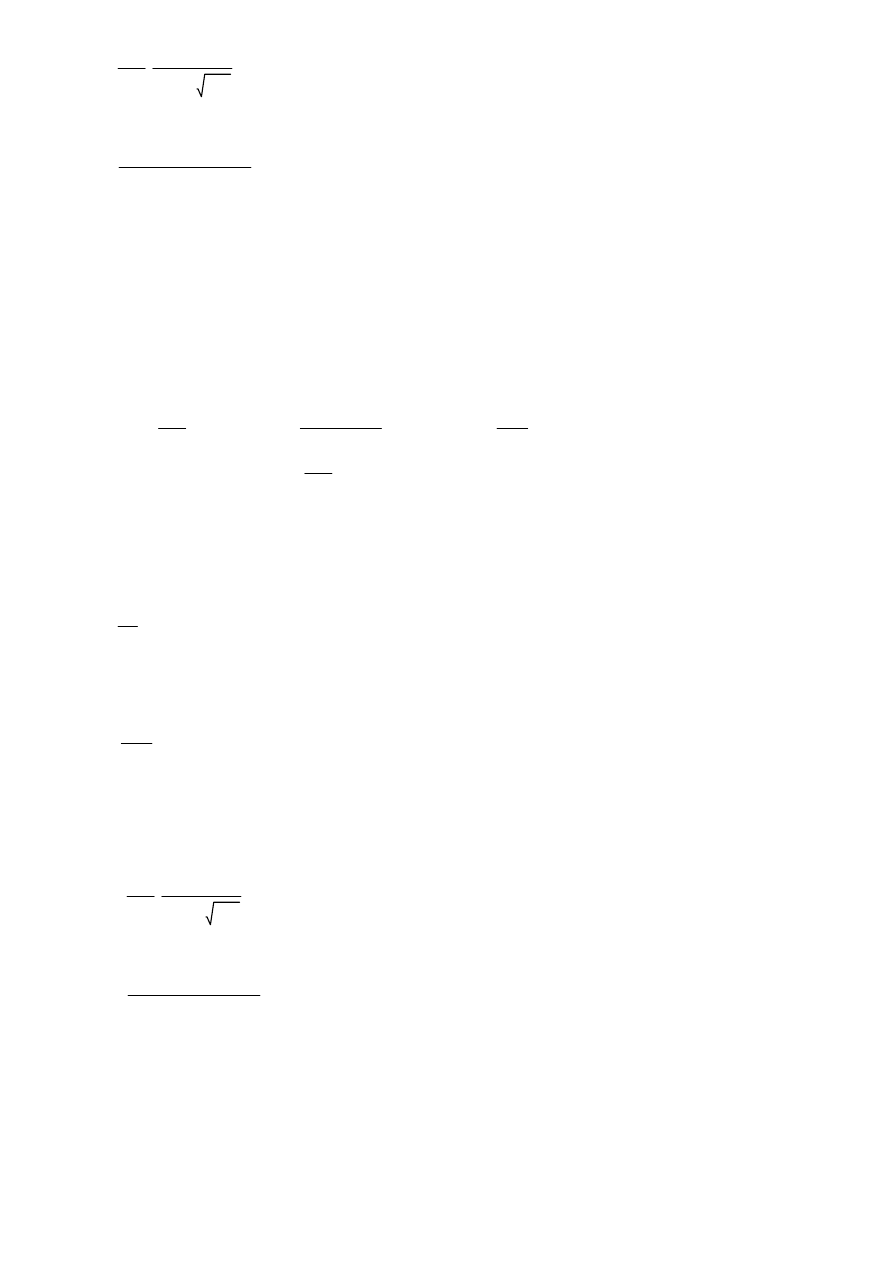
λp2

bp.h

t

1

28.4 ε



k

σ

2





1





> 0.673

Ścianka jest wrażliwa na utratę stateczności miejscowej.

Współczynnik redukcyjny:

ρ2

λp2 0.055 3 ψ2









λp2

2

0.89





Szerokości współpracujące:

beff2 ρ2 zb2



154.4 mm







be12 0.4 beff2



61.8 mm







be22 0.6 beff2



92.7 mm







Trzecia iteracja:

Moment statyczny:

S3

bp.c t

bp.c

2



zd2 be22







t



zd2 be22







2





be12 t bp.h

be12

2



















bp.b t bp.h



bp.c t bp.h

bp.c

2























217.924

10

3



mm

3







Pole przekroju

A3

2 bp.c



bp.d



zd2



be22



be12



bp.b







t



1.257

10

3



mm

2







Środek ciężkości

z3

S3

A3

173.3 mm







zb3 bp.h z3



174.178 mm







zasięg strefy ściskanej środnika

zd3 z3 173.322 mm







zasięg strefy rozciąganej środnika

ψ3

zd3



zb3

0.995







Parametr niestateczności zginanej ścianki przęsłowej

k

σ

3

7.81

6.29 ψ3





9.78 ψ3

2





23.75





Smukłość płytowa ścianki:

λp3

bp.h

t

1

28.4 ε



k

σ

3





1.004





> 0.673

Ścianka jest wrażliwa na utratę stateczności miejscowej.

Współczynnik redukcyjny:

ρ3

λp3 0.055 3 ψ3









λp3

2

0.886





Szerokości współpracujące:

beff3 ρ3 zb3



154.4 mm







be13 0.4 beff3



61.8 mm







be23 0.6 beff3



92.6 mm







8

Moment bezwładności przekroju współpracującego:

Ieff.y

t bp.c

3



12

t bp.c



zd3

bp.c

2















2





bp.d t

3



12



bp.d t zd3

2





t zd3

3



12



t zd3



zd3

2













2





t be23

3



12

t be23



be23

2













2





t be13

3



12



t be13



zb3

be13

2















2









bp.b t

3



12

bp.b t zb3

2





t bp.c

3



12



t bp.c



zb3

bp.c

2















2









2.11

10

3



cm

4







Wskaźniki przekroju współpracującego, gdy ściskana jest stopka b:

Weff.b

Ieff.y

zb3

120962 mm

3







Weff.d

Ieff.y

zd3

121560 mm

3







Weff.min min Weff.b Weff.d







120962 mm

3







Nośność przekroju przy zginaniu względem osi y-y

Mc.Rd

Weff.min fy



γM0

28.426 kN m









Mmax 24.4kN m





Sprawdzenie warunku nośności na zginanie:

Mmax

Mc.Rd

0.858



< 1.00 OK.

Dobór płatwi jednoprzęsłowej na podstawie tablic profili Pruszyński:

Dokonam sprawdzenia dla tej samej płatwi 1-przęsłowej, rozpiętości 6 m, przy rozstawie 3 m -
BP/Z350x75/65x2.50.

QRd 2.01

kN

m

2





Zebranie obciążeń:

sd

1.44

kN

m

2





śnieg

Qparcie 0.217

kN

m

2



parcie wiatru

QEd

sd Qparcie



1.657

kN

m

2







Sprawdzenie:

QEd
QRd

0.82



< 1.00 OK.

Porównując te dwa sposoby doboru płatwi 1-przęsłowej okazuje się, że większy zapas nośności o 3 % ma
płatew dobierana na podstawie tablic.

9

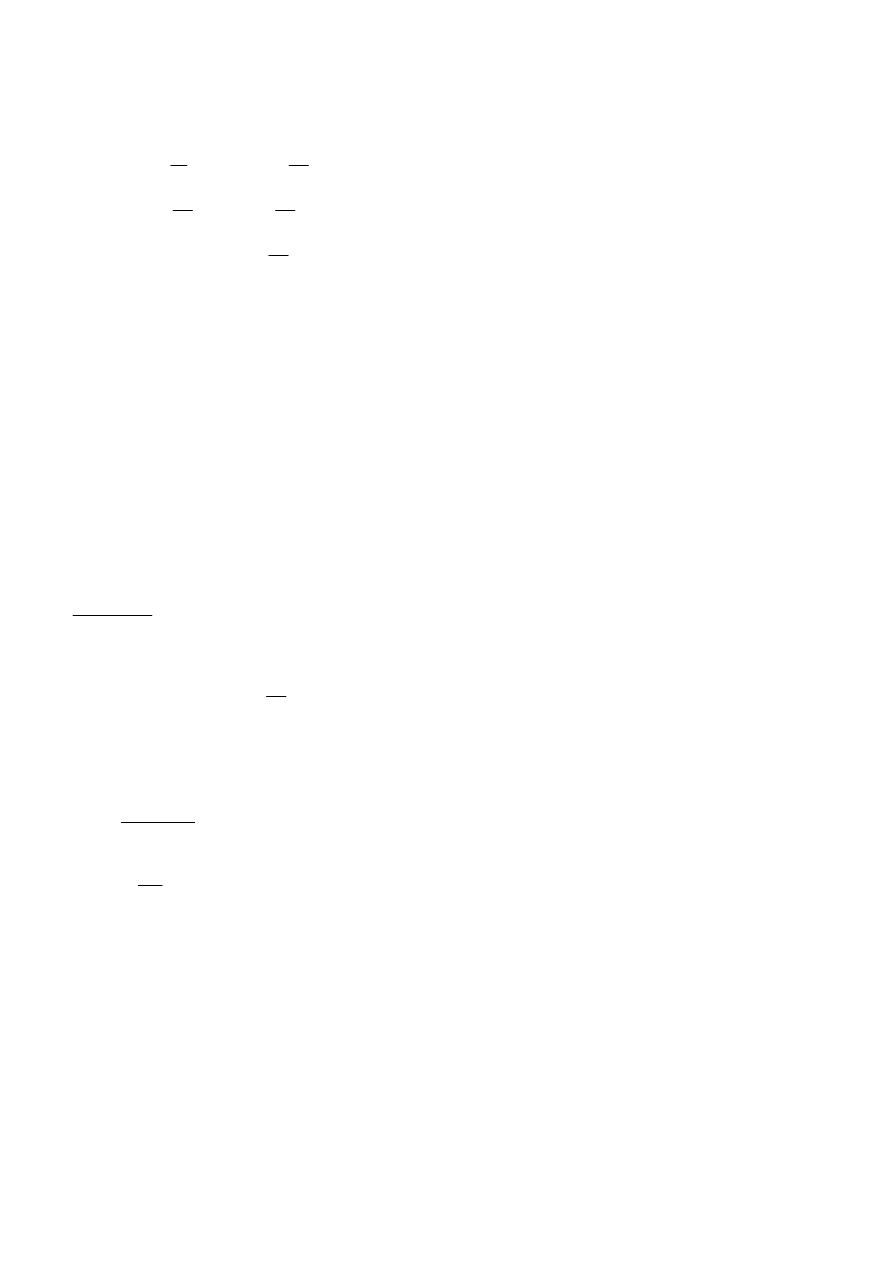
Sprawdzenie płatwi BP/Z350x75/65x2.50 w przypadku oddziaływania ssania wiatru:

Minimalny ciężar własny konstrukcji pokrycia dachu.

mk.z

10.03

kg

m



g

 1.00



0.098

kN

m







ciężar własny zetownika 350

ciężar własny płyty warstwowej

mk.pł 0.172

kN

m

2

3

 m 0.516

kN

m







Qk.g mk.z mk.pł



0.614

kN

m







ciężar stały

Rozpatruję różne kombinacje ze względu na rozmieszczenie płatwi w różnych strefach obciążenia śniegiem
(oddziaływanie ssania wiatru minus minimalny ciężar własny).

MFG

14.127 kN



m





MG 9.504kN m





MH 5.544kN m





MI 1.584kN m





MHI 5.121 kN



m





MFH

7.933kN m





MGH 6.575kN m





Mmax.ssanie max MFG MG



MH



MI



MHI



MFH



MGH







14.127 kN m









Mmax.ssanie

Mc.Rd

0.497



< 1.00 OK.

qEd

QEd rp



Qd.g



5.62

kN

m







wartość obciążenia na płatew

Sprawdzienie stanu granicznego użytkowalności:

w0

5 qEd



l

4



384 E

 Ieff.y



21.434 mm







wmax

l

200

30 mm







w0 wmax



1



OK.

10

3. Płatew (5-przęsłowa)

w

d

g

b.d

s

d

l

l

l

l

l

3.1.1 Obciążenia

l

6m



rozpietość płatwi

r

3m



rozstaw płatwi

Kombinacja 1 (max parcie)

gb.k.1 0.133

kN

m



ciężar własny belki

sk.1 sk r 3.6

kN

m







ciężar śniegu

wk.1 we.1 r 0.651

kN

m







parcie wiatru

MOMENTY ZGINAJĄCE

SIŁYT NĄCE

MEd.1 16.631kN m





VEd.1 15.921kN



Kombinacja 2 (max ssanie)

gb.k.2 0.133

kN

m



ciężar własny belki

wk.2

we.2



r



2.223



kN

m







ssanie wiatru

MOMENTY ZGINAJĄCE

SIŁY TNĄCE

MEd.2

5.861



kN m





VEd.2 7.59kN



MEd

max MEd.1 MEd.2







16.631 kN m









11

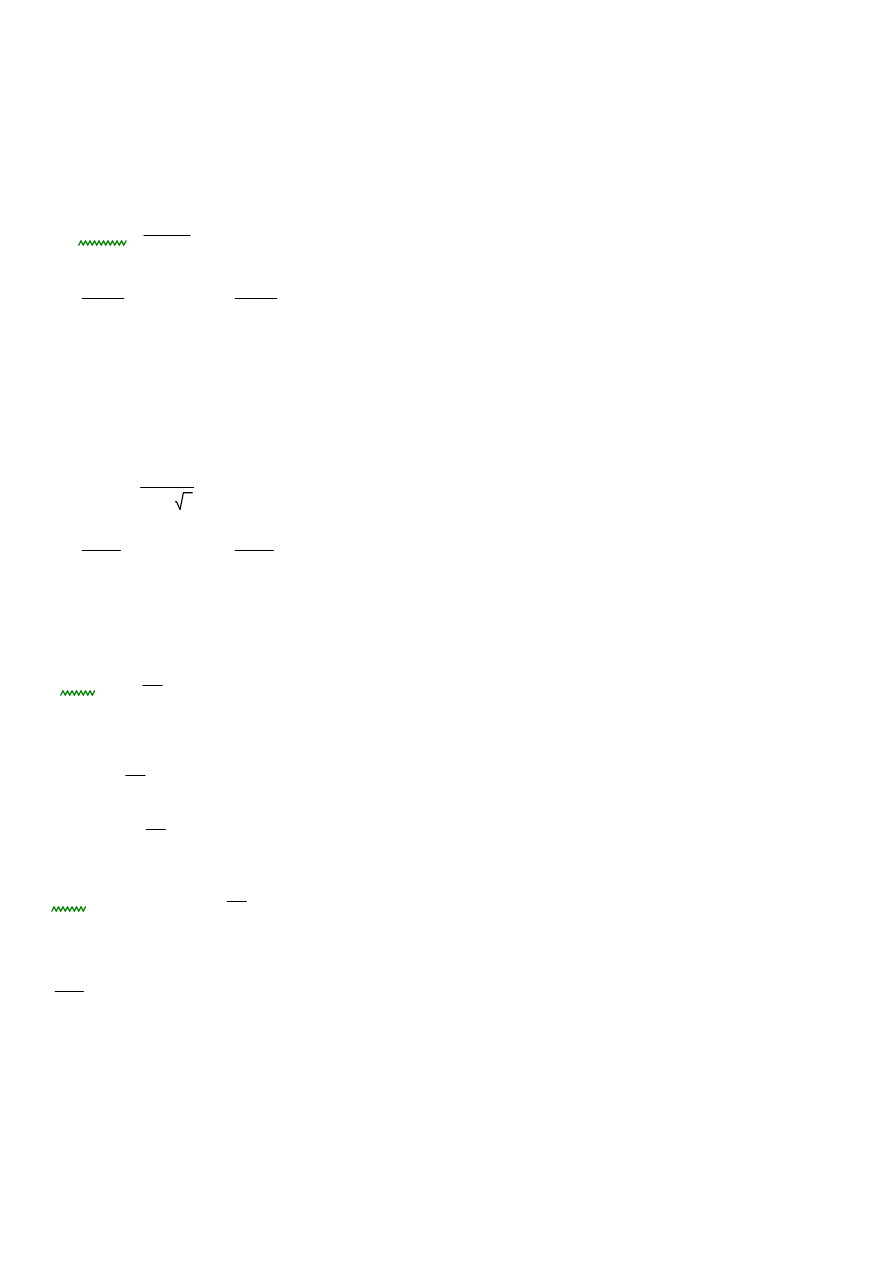
VEd

max VEd.1 VEd.2







15.921 kN







3.2 Stan graniczny nośności

3.2.1 Zginanie

(wg EC3 6.2.5)

Ze względu na mały kąt nachylenia dachu pomijamy siły poziome i rozpatrujemy siły w osi z płatwi

Mc.Rd

weff fy



γM0

28.426 kN m









obliczeniowa nośność przekroju

MEd

Mc.Rd

0.585



MEd

Mc.Rd

1



1



warunek został spełniony

2.2.2 Ścinanie

(wg EC3 6.2.6)

Av

A

12.78 cm

2







pole przekroju

Vc.Rd

Av fy



γM0 3



173.396 kN







obliczeniowa nośność przekroju

VEd

Vc.Rd

0.092



VEd

Vc.Rd

1



1



warunek został spełniony

Dobór płatwi pięcioprzęsłowej na podstawie tablic profili Pruszyński:

Sprawdzenie dla płatwi 5-przęsłowej, rozpiętości 6 m, przy rozstawie 2.5 m - BP/Z280x55/48x2.50.

QRd 2.59

kN

m

2





Zebranie obciążeń:

sd 1.44

kN

m

2





śnieg

wpd 0.217

kN

m

2



parcie wiatru

QEd

sd wpd







1.657

kN

m

2







Sprawdzenie:

QEd
QRd

0.64



< 1.00 OK.

12