ANALIZA KINEMATYCZNA

MANIPULATORÓW

ROBOTÓW METODĄ

MACIERZOWĄ

Jeśli dane są:

- współrzędne

w

xi

, w

yi

, w

zi

wektora w związane z ogniwem i

- współrzędne

p

x

, p

y

, p

z

początku układu i związane z ogniwem j

oraz

kosinusy kierunkowe osi układu i względem osi układu j





j

i

x

x

x

l

,

cos







j

i

y

y

x

l

,

cos







j

i

z

z

x

l

,

cos







j

i

x

x

y

m

,

cos







j

i

y

y

y

m

,

cos







j

i

z

z

y

m

,

cos







j

i

x

x

z

n

,

cos







j

i

y

y

z

n

,

cos







j

i

z

z

z

n

,

cos



to zależność pomiędzy współrzędnymi w układzie i
oraz j można zapisać jako

x

zi

x

yi

x

xi

x

xj

p

w

n

w

m

w

l

w









y

zi

y

yi

y

xi

y

yj

p

w

n

w

m

w

l

w









z

zi

z

yi

z

xi

z

zj

p

w

n

w

m

w

l

w









lub w formie symbolicznej

i

ij

j

w

w

T



gdzie:

T

T 

ij

w



- macierz przekształcenia współrzędnych

wektora z układu i do układu j

Wyznacznik macierzy

T

T 

ij



ij

T

{

1, gdy obydwa układy są prawoskrętne

-1, gdy jeden jest prawo- a drugi lewoskrętny

Macierz

T

ij

przekształcenia

złożonego

z

przesunięcia i obrotu można przedstawić w
postaci iloczynu macierzy:

0

T

ij

- obrotu
(rotacji)

p

ij

T

- przesunięcia (translacji)

czyli

p

ij

ij

ij

T

T

T

0





gdzie:



























1

0

0

0

0

0

0

T

0

z

z

z

y

y

y

x

x

x

ij

n

m

l

n

m

l

n

m

l



























1

0

0

0

1

0

0

0

1

0

0

0

1

z

y

x

p

ij

p

p

p

T

Zastosowanie do opisu przekształceń w kinematyce
i dynamice manipulatorów robotów macierzy
4x4 jest bardzo wygodne ponieważ umożliwia w
zwartej formie zapisać zarówno obrót jak i
przesunięcie oraz ułatwia mnożenie odpowiednich
macierzy przy użyciu komputerów osobistych bez
konieczności sprawdzania osobliwości.

0

T

ij

- obrotu (rotacji)

tylko trzy są niezależne, natomiast pozostałe
sześć muszą spełniać równania

Z dziewięciu zmiennych wyrazów macierzy

1

2

2

2







z

y

x

l

l

l

1

2

2

2







z

y

x

m

m

m

1

2

2

2







z

y

x

n

n

n

0







z

z

y

y

x

x

m

l

m

l

m

l

x

y

z

z

y

n

m

l

m

l





y

z

x

x

z

n

m

l

m

l





przy czy kwadraty kosinusów kierunkowych (trzy
pierwsze równania) są równe odpowiednim
kwadratom współrzędnych wersorów osi, których
długość jest równa 1; pozostałe trzy równania
wynikają z warunków prostopadłości wersorów osi
układu współrzędnych.

współrzędnych

przypadku

przekształceń

odwrotnych to znaczy przy przejściu z układu j do
układu i stosuje się macierze odwrotne, czyli

1

T

T





ij

ij

przy czym

E

T

T





ji

ij

gdzie: E jest macierzą jednostkową, czyli





























1

0

0

0

0

1

0

0

0

0

1

0

0

0

0

1

T

T

ji

ij

W celu uproszczenia analizy przestrzennego
łańcucha

kinematycznego

wprowadza

się

specjalne usytuowanie układów współrzędnych
poszczególnych

członów

tak,

aby

liczba

parametrów

wchodzących

do

macierzy

przekształceń była minimalna, a postać tej
macierzy była jednakowa tak w przypadku pary
obrotowej, jak i pary przesuwnej.
W dalszym ciągu przedstawiono najczęściej
stosowany sposób usytuowania wzajemnego
układów współrzędnych członów połączonych
parami obrotowymi i przesuwnymi, który jest
znany jako zapis

Hartenberga i Denavita

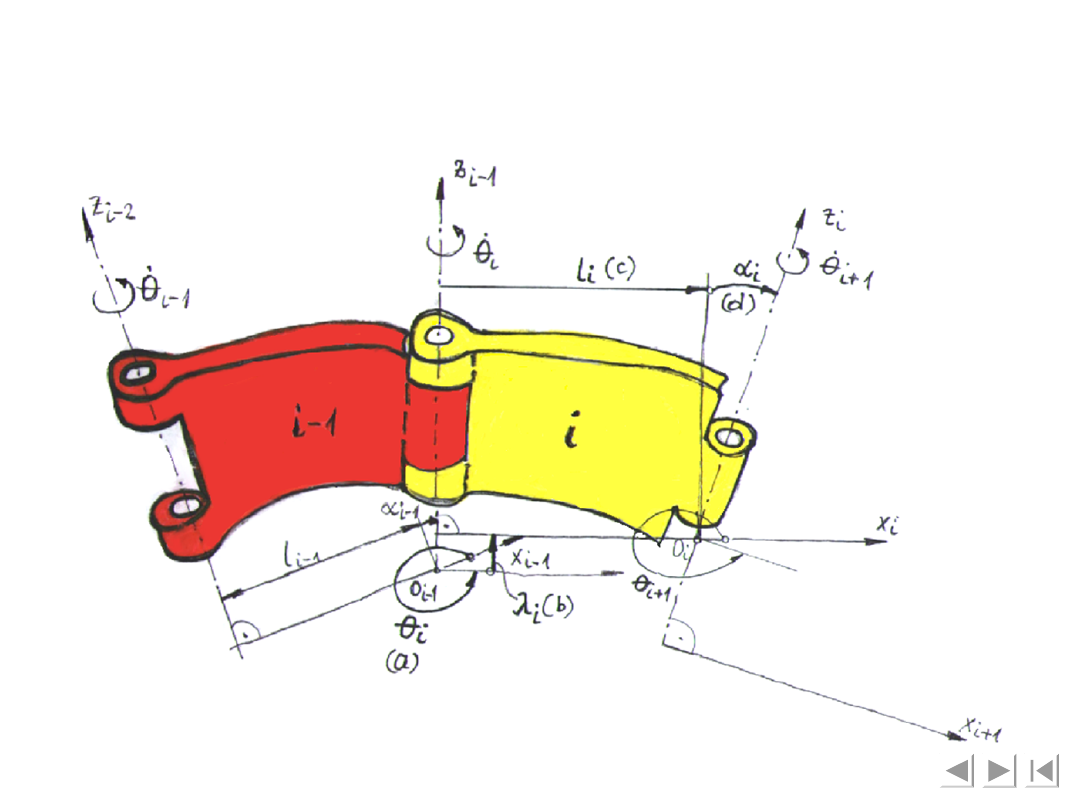
Na

rysunku

przedstawiono

dwa

układy

współrzędnych związanych z członami i – 1 oraz i,
(rys. ***)

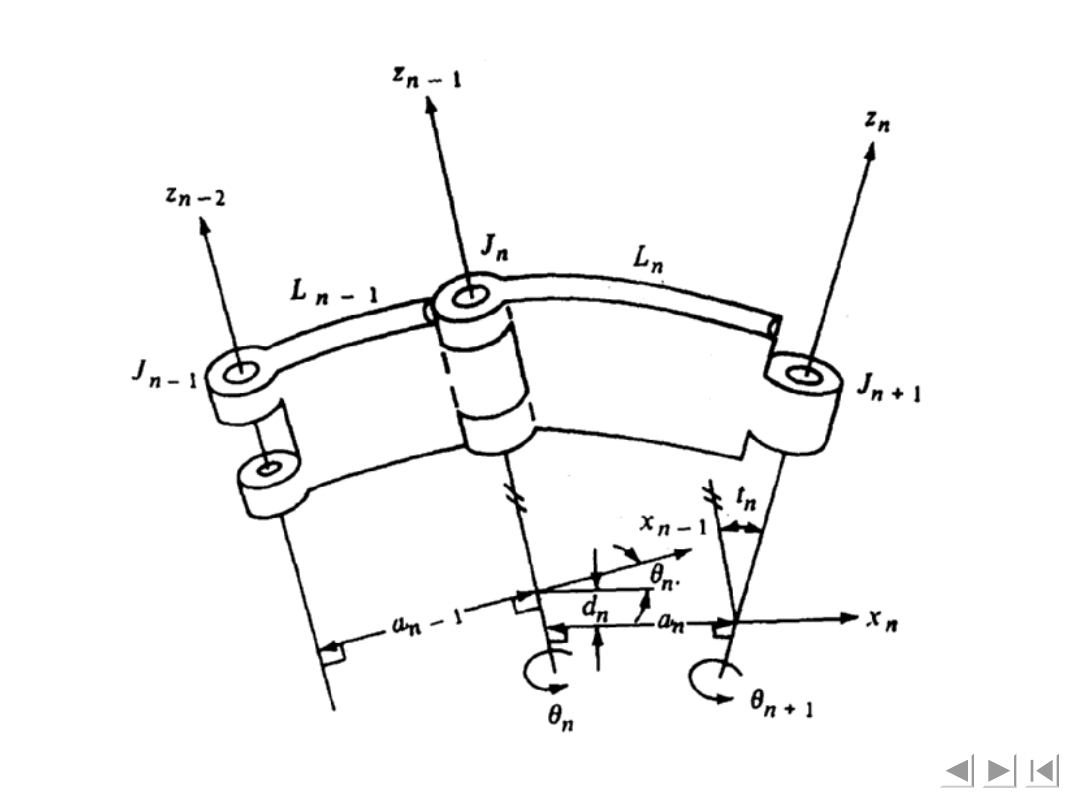
Figure 4-8 The variables in a link using the
notation of Paul [9]. The rules used to define the
notation are: (1) Axis z

n-1

defines the position of the

axis of rotation for joint J

n

, z

n

, for joint J

n+1

, and so

forth. (2) Axis x

n-1

is selected to be an extension for

the common perpendicular line of length a

n-1

between consecutive joints z

n-2

and z

n-1

. (3) The

axis y

n-1

– is selected to provide a right-hand

coordinate system with the other axes. (4) Axis x

n

is an extension of the common perpendicular line
of Iength a

n

.

Rys 4-8. Zapis zmiennych z użyciem notacji Paul’a
[7]. Według zasad: (1) Oś z

n-1

opisuje położenie osi

rotacji dla ogniwa J

n

, zaś oś z

n

dla ogniwa J

n+1

itd.

(2) Oś x

n-1

jest przedłużeniem linii znajdującej się

pomiędzy osią z

n-2

i z

n-1

i prostopadłą do nich o

długości a

n-1

. (3) Oś y

n-1

zapewnia prawoskrętny

układ współrzędnych. (4) Oś x

n

jest przedłużeniem

linii prostopadłej do osi z

n-1

o długości a

n

.

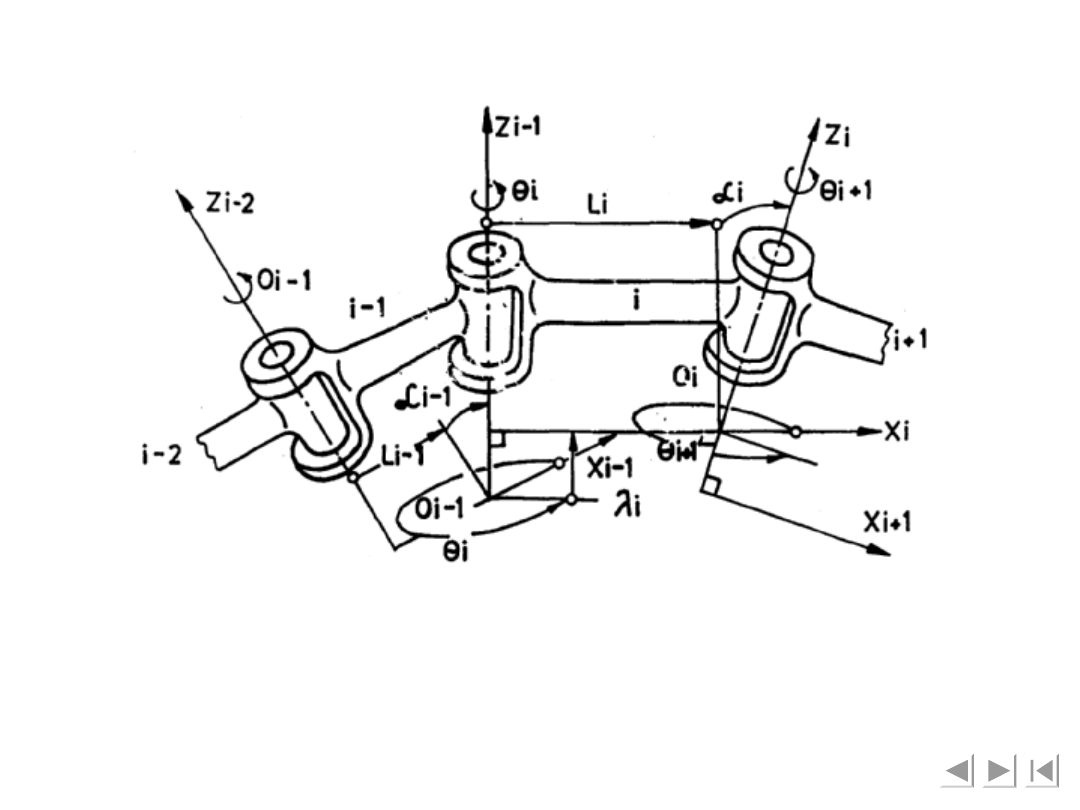
Usytuowanie układów współrzędnych

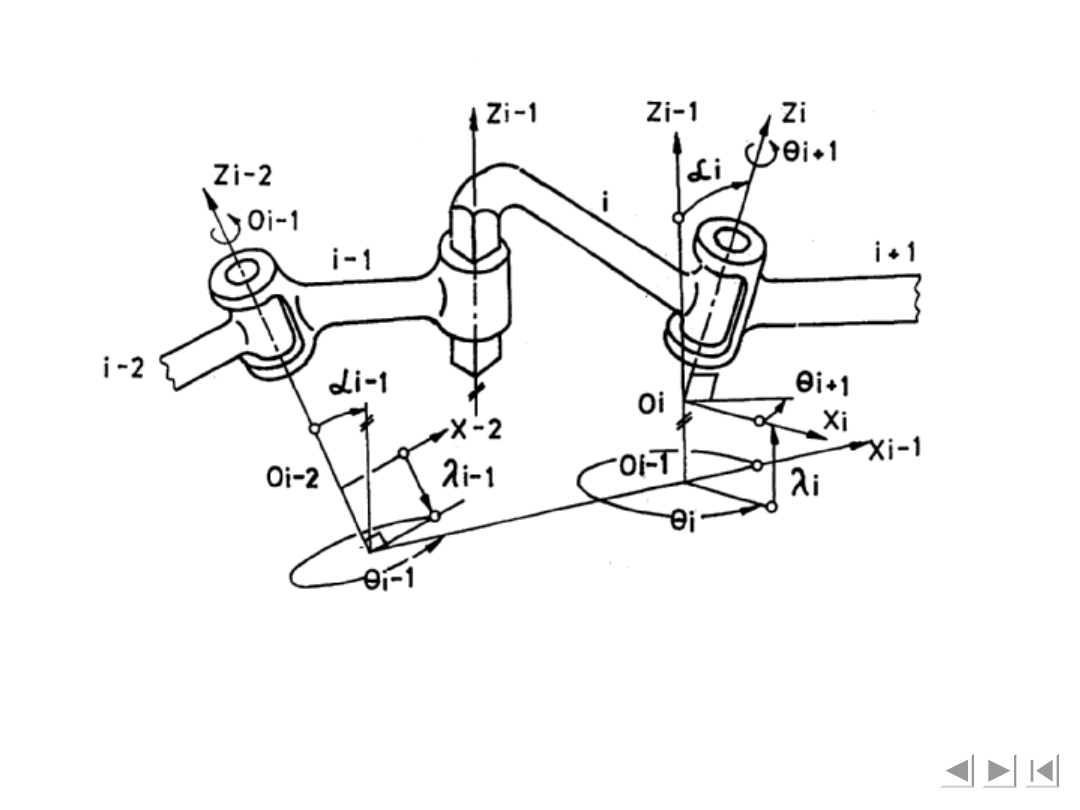
Usytuowanie układów współrzędnych

leży na wspólnej prostopadłej do osi par obrotowych
członu i-1, oś

przy czym oś

x

i-1

z

i-1

leży na osi pary obrotowej łączącej człony

i-1 z i

oś

y

i-

1

nie pokazana na rysunku stanowi uzupełnienie
prawoskrętnego układu współrzędnych

i-
1

Układ współrzędnych jest związany z członem

i

w podobny sposób, to znaczy oś

x

i

leży na wspólnej prostopadłej do osi par obrotowych członu

i

leży na osi pary obrotowej łączącej człon

z

i

oś

i z członem i + 1

Zaletą takiego usytuowania układów współrzędnych
jest to, że tylko cztery parametry określają
względne położenie dwóch sąsiednich układów,
przy czym dwa z nich to znaczy

l

i

oraz

α

i

są zawsze stałe, jeden z pozostałych jest zmienny
w zależności od typu pary kinematycznej

- w przypadku pary obrotowej zmienny jest kąt

θ

i

- w przypadku pary przesuwnej zmienne jest przesunięcie

λ

i

Dwa sąsiednie układy współrzędnych

i oraz i-1

mogą być przekształcone jeden w drugi za pomocą

obrotu

dwóch przesunięć

i jeszcze jednego obrotu

w następującej kolejności

a) obrót wokół osi

z

i-1

o kąt θ

i

tak, aż oś x

i-1

stanie się równoległa do osi x

i

b) przesunięcie wzdłuż osi

z

i-1

o wielkość λ

i

tak, aby oś x

i-1

pokryła się z osią x

i

c) przesunięcie wzdłuż osi

x

i

o wielkość l

i

tak, aby początki obu układów pokryły się

d) obrót wokół osi

x

i

o kąt

α

i

tak aż wszystkie osie będą pokrywać się

Każdemu z tych elementarnych ruchów odpowiada macierz

T

i,i-1

Przekształcenia, którą tutaj oznaczono przez

A

i

przy czym





























1

0

0

0

0

1

0

0

0

0

cos

sin

0

0

sin

cos

A

i

i

i

i

a

i



































1

0

0

0

1

0

0

0

0

1

0

0

0

0

1

A

i

b
i





























1

0

0

0

0

1

0

0

0

0

1

0

0

0

1

A

i

c
i

l





























1

0

0

0

0

cos

sin

0

0

sin

cos

0

0

0

0

1

A

i

i

i

i

d

i









Macierz A

i

opisująca przekształcenia z układu

i do układu i-1

będzie równa iloczynowi wyżej wymienionych
macierzy ruchów elementarnych, czyli

d

i

c

i

b
i

a

i

i

A

A

A

A

A









Zatem, po wykonaniu mnożeń macierzy zaczynając
od prawej strony otrzymuje się





























1

0

0

0

cos

sin

0

sin

sin

cos

cos

cos

sin

cos

sin

sin

cos

sin

cos

A

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

l

l































gdzie:

l

i

, α

i

- odległość i kąt pomiędzy osiami par

obrotowych ogniwa i,

λ

i

, θ

i

, - odległość i kąt obrotu pomiędzy

ogniwami i-1 oraz i

Przypadku pary obrotowej kąt θ

i

jest zmienny, a

odległość λ

i

jest stała; w przypadku pary przesuwnej

zmienna jest długość λ

i

a stały kąt θ

i

Macierz przekształcenia odwrotnego, to znaczy
układu współrzędnych członu i-1 do układu członu i
otrzymuje

się

jako

rozwiązanie

równania

macierzowego

E

A

A

1





i

i

gdzie: E – macierz jednostkowa

stąd







































1

0

0

0

cos

cos

sin

cos

sin

sin

sin

sin

cos

cos

cos

sin

0

sin

cos

A

1

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

i

l

































W przypadku otwartego łańcucha kinematycznego
wprowadza się macierz położenia i orientacji
układu związanego z członem n względem układu
związanego z członem i jako iloczyn macierzy
kolejnych przekształceń

n

i

i

i

n

A

...

A

A

T

2

1

,













przy czym

1

1

,

A

T







i

i

i

W

przypadku

zamkniętego

łańcucha

kinematycznego, zbudowanego z n członów
wprowadza się równanie zamknięcia w postaci

E

A

...

A

A

2

1









n

Mnożąc z lewej strony powyższe równanie przez
macierze odwrotne otrzymuje się równanie
zamknięcia łańcucha kinematycznego w bardziej
wygodnej postaci

1

1

3

2

A

A

...

A

A











n

1

1

1

2

4

3

A

A

A

...

A

A













n

1

1

1

2

1

3

5

4

A

A

A

A

...

A

A















n

………………….……………………

W przypadku, gdy dany jest wektor

 

i

pi

r

opisujący

położenie

dowolnego

punktu

P

i

należącego do członu i w układzie współrzędnych
związanym z tym członem oraz dane są macierze
kolejnych przekształceń, wtedy z równań











































































1

1

0

0

0

1

zi

yi

xi

z

z

z

z

y

y

y

y

x

x

x

x

zj

yj

xj

w

w

w

p

n

m

l

p

n

m

l

p

n

m

l

w

w

w

oraz

n

i

i

i

n

A

...

A

A

T

2

1

,













można wyznaczyć wektor

 

0

pi

r

opisujący położenie punktu P

i

w układzie podstawy

 

 

i

pi

i

pi

r

r















A

...

A

A

2

1

0

przy czym mnożenia macierzy trzeba zaczynać od
prawej strony (!!!)

Kolejność obliczeń jest zatem następująca

 

 

i

pi

i

i

pi

r

r











A

1

 

 

1

1

2

A











i

pi

i

i

pi

r

r





 

 

2

2

3

A











i

pi

i

i

pi

r

r





………….………………

 

 

1

1

0

A

pi

pi

r

r









(wzory na r)

Wektory prędkości i przyspieszenia punktu P

i

otrzymuje się jako pierwszą i drugą pochodną
względem czasu wektora

 

0

pi

r

A zatem

 

 

0

0

d

d

pi

pi

pi

r

t

r

v











 

 

0

2

2

0

d

d

pi

pi

pi

r

t

r

a











Różniczkując kolejno dwie ostatnie zależności przy
założeniu, że

 

idem

r

i

pi





otrzymuje się algorytm wyznaczania prędkości

pi

v

jako

 

 

i

pi

i

i

pi

r

v













A

1

 

 

 

1

1

1

1

2

A

A



















i

pi

i

i

pi

i

i

pi

v

r

v









……………………………………………

 

 

 

2

2

2

1

1

A

A

pi

pi

i

pi

v

r

v



















 

 

 

1

1

1

1

0

A

A

pi

pi

pi

v

r

v

















(wzory na v)

oraz algorytm wyznaczania przyśpieszenia

pi

a

jako

 

 

i

pi

i

i

pi

r

a













A

1

 

 

 

 

1

1

1

1

1

1

2

A

2

A

A

























i

pi

i

i

pi

i

i

pi

i

i

pi

v

a

r

a













………………………………………………….

 

 

 

 

2

2

2

2

2

2

1

A

2

A

A

pi

pi

pi

pi

v

a

r

a























 

 

 

 

1

1

1

1

1

1

0

A

2

A

A

pi

pi

pi

pi

v

a

r

a























(wzory na a)

Pochodne względem czasu macierzy

A

j

oblicza się według następujących wzorów

j

j

j

A

Q

A 







j

j

j

j

A

Q

Q

A

2



 



(wzory na A)

przy czym w przypadku pary obrotowej

































0

0

0

0

0

0

0

0

0

0

0

0

0

0

Q

j

j

j









































0

0

0

0

0

0

0

0

0

0

0

0

0

0

Q

j

j

j













































0

0

0

0

0

0

0

0

0

0

0

0

0

0

Q

2

2

2

j

j

j









natomiast w przypadku pary przesuwnej



























0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

Q

j

j































0

0

0

0

0

0

0

0

0

0

0

0

0

0

0

Q

j

j







0

Q

2



j

Podstawiając (wzory na A) do (wzorów na v) i
(wzorów na a) przy uwzględnieniu (wzorów na r)
otrzymuje się

 

 

1

1

Q









i

pi

i

i

pi

r

v





 

 

 

1

1

2

1

2

A

Q



















i

pi

i

i

pi

i

i

pi

v

r

v







…………………….……………………

 

 

 

2

2

1

2

1

A

Q

pi

pi

pi

v

r

v















 

 

 

1

1

0

1

0

A

Q

pi

pi

pi

v

r

v















(wzory na v)1

oraz

 





 

1

2

1

Q

Q











i

pi

i

i

i

pi

r

a







 





 

 

 

1

1

1

1

1

2

2

1

1

2

A

Q

2

A

Q

Q

































i

pi

i

i

i

pi

i

i

pi

i

i

i

pi

v

a

r

a











 





 

 

 

2

2

2

2

2

1

2
2

2

1

A

Q

2

A

Q

Q

pi

pi

pi

pi

v

a

r

a























 





 

 

 

1

1

1

1

1

0

2

1

1

0

A

Q

2

A

Q

Q

pi

pi

pi

pi

v

a

r

a























……………………………………..

(wzory na a)1

PRZYKŁAD

Gdy i = 2

wtedy (wzory na r) przyjmą postać

 

 

2

2

2

1

2

A

p

p

r

r









 

 

1

2

1

0

2

A

p

p

r

r









natomiast (wzory na v)1 są następujące

 

 

1

2

2

1

2

Q

p

p

r

v









 

 

 

1

2

1

0

2

1

0

2

A

Q

p

p

p

v

r

v















natomiast ( wzory na a)1 przyjmą formę

 





 

1

2

2
2

2

1

2

Q

Q

p

p

r

a













 





 

 

 

1

2

1

1

1

2

1

0

2

2

1

1

0

2

A

Q

2

A

Q

Q

p

p

p

p

v

a

r

a



























Wektory prędkości kątowej





i przyspieszenia kątowego





członów

można wyznaczyć z następujących równań:

1

,

1

2

1

32

2

1

21

1

1

A

...

A

A

...

...

A

A

A



















i

i

i

i





















(wzór na prędkość kątową członów)

21

1

21

1

1

1

2

A

A

Q































32

2

1

32

2

2

1

2

1

1

2

3

A

A

Q

A

A

A

Q





























A

………………………………………

1

,

1

2

1

1

,

1

1

2

1

1

3

2

2

1

1

i

2

1

1

1

A

...

A

A

A

Q

...

A

A

...

...

A

...

A

A

Q

A

...A

A

A

Q





























































i

i

i

i

i

i

i

i

i

i

















(wzór na przyśpieszenia kątowe członów)

gdzie:





T

i

i

i

i

0

0

0

0

0

0

1

,















































T

i

i

i

i

0

0

0

0

0

0

1

,









































