ANALIZA

KINEMATYCZNA

MANIPULATORÓW

ROBOTÓW METODĄ

WEKTOROWĄ

Względne usytuowanie osi par kinematycznych i
położenie

ogniw

przestrzennego

łańcucha

kinematycznego

można

opisać

za

pomocą

następujących iloczynów skalarowych i
wektorowych

i

i

i

e

e



cos

1











i

i

i

i

a

e

e



sin

1













1

1

cos









i

i

i

a

a







1

1

sin









i

i

i

i

e

a

a









z powyższych równań można wyprowadzić
następujące zależności





i

i

i

i

i

i

e

a

e

e





sin

cos

1





















i

i

i

i

i

i

a

e

a

a





sin

cos

1

















gdzie:

i

e

- wersor osi pary kinematycznej łączącej
ogniwo i z ogniwem i-1,

i

a

-

wersor

prostopadłej

do

osi

par

kinematycznych ogniwa i

α

i

- kąt zawarty między osiami par

kinematycznych ogniwa i, które mogą być
usytuowane skośnie,

θ

i

- kąt obrotu względnego członów i-1

oraz i

Kąty

α

i

i θ

i

przyjmuje się jako kąty zorientowane. Ich zwroty
określa się według śruby prawoskrętnej, czyli tak
aby trójka wersorów

i

e

1



i

e

i

a

tworzyła układ prawoskrętny

W podobny sposób definiuje się zwrot kąta θ

i

tak,

aby trójka wersorów

1



i

a

i

a

i

e

tworzyła układ prawoskrętny

Gdy znane są dwa wersory

i

e

j

e

oraz kąty jakie tworzą z trzecim nieznanym wersorem

k

e

wtedy stosując wzór Chace’a można otrzymać



 







2

1

ij

j

i

ij

j

ik

ij

jk

i

jk

ij

ik

k

c

e

e

D

e

c

c

c

e

c

c

c

e

























jk

ik

ij

jk

ik

ij

ij

c

c

c

c

c

c

D

2

1

2

2

2











j

i

ij

e

e

c









k

i

ik

e

e

c









k

j

jk

e

e

c









W wielu przypadkach analizy kinematycznej
wykorzystuje się równanie zamknięcia łańcucha
kinematycznego, które można zapisać w postaci
równania wektorowego













n

i

i

i

i

i

a

l

e

1

0







gdzie
:

λ

i

– odległość między ogniwem i-1 oraz

ogniwem i, mierzona wzdłuż osi pary łączącej
te człony w przypadku pary przesuwnej λ

i

jest

zmienna, a w przypadku pary obrotowej λ

i

=

idem;

Odległość

między

osiami

par

kinematycznych członu i oznaczono przez l

i

;

w przypadku, gdy jedna z par jest przesuwna
l

i

= 0

Z równania wektorowego













n

i

i

i

i

i

a

l

e

1

0







można wyznaczyć jeden niewiadomy wersom lub
trzy niewiadome wartości skalarów – długości i
kątów

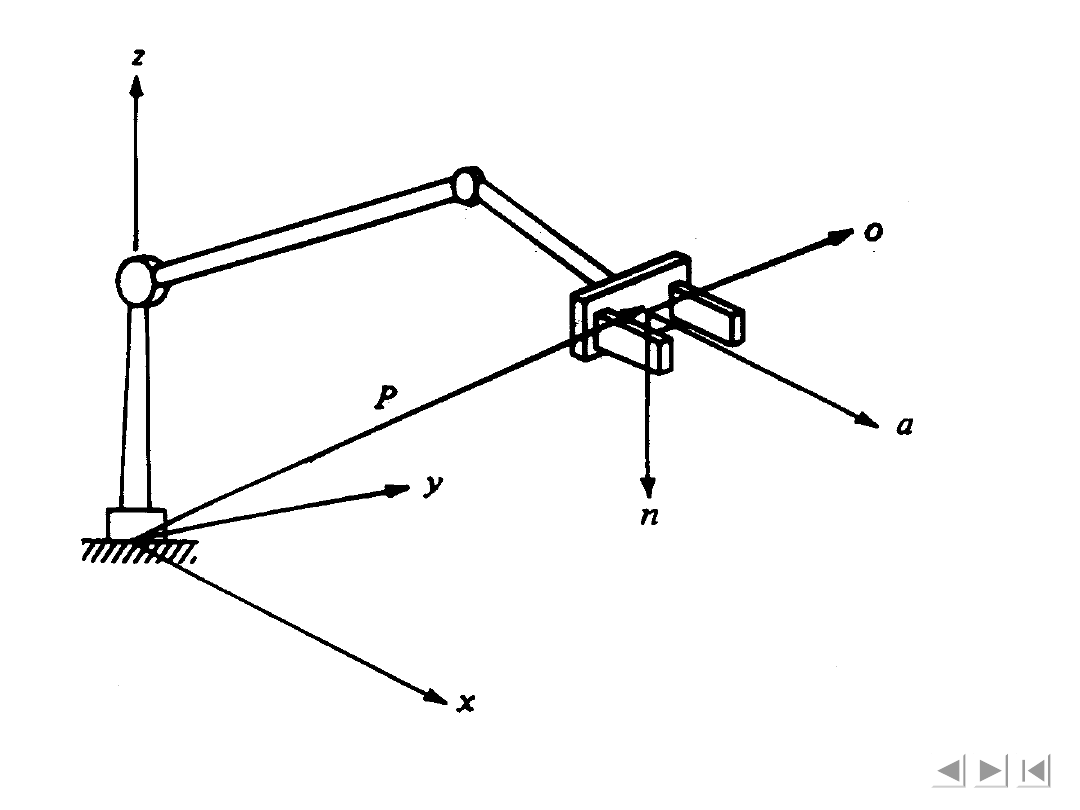
Figure 4-7 The vectors o, a,

n, and p for a robot

manipulator.

Rysunek 4-7 Wektory o, a, n oraz p dla

manipulatora robota.

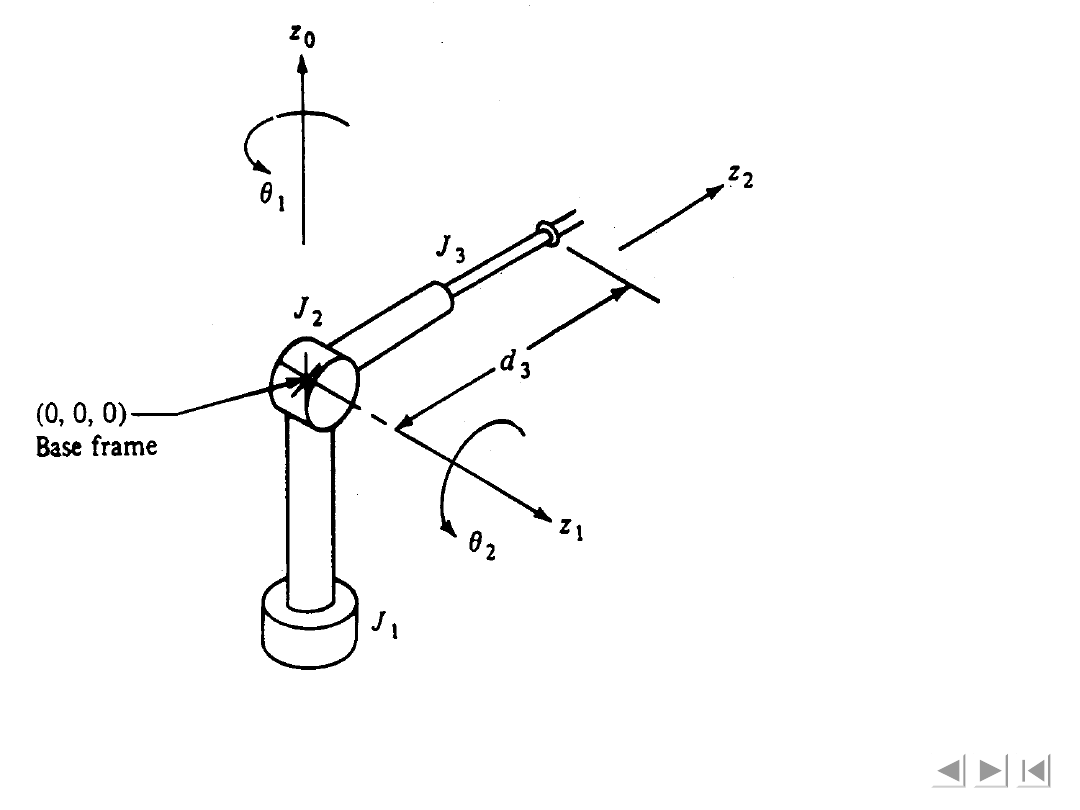
Figure 4-9 A three-dimensional 3 degree-of-freedom
manipulator (type TRL).

Rysunek

4-9

Trójwymiarowy,

trójczłonowy manipulator (typ: z
translacją, rotacją, wysuwem).