Krótkie podsumowanie
• Dotychczas przygotowania zbioru danych objęły:
• sprawdzenie poprawności wpisanych danych (częstości),
usunięcie ew. błędów (Edycja > znajdź)
• odwracanie skal odpowiedzi w kwestionariuszu (Rekodowanie
na te same zmienne)
• tworzenie wskaźników zmiennych (przekształcenia > oblicz
wartości)
• odsianie wyników skrajnych w Skali_K (Przekształcenia >
Ranguj obserwacje > Typy rang > N=10)
• zapoznanie się z rodzajami skal pomiarowych i liczonych miar
• Wnioski: wszystkie operacje na zbiorach danych dotyczą
ikony Przekształcenia lub Dane, wszystkie obliczenia w ikonie
analiza
• Skale pomiarowe wyznaczają ilość uzyskanych informacji ze
zmiennej.
• Zawsze można obniżyć poziom pomiaru kosztem utraty
informacji, nigdy nie można go sztucznie podwyższyć!!!
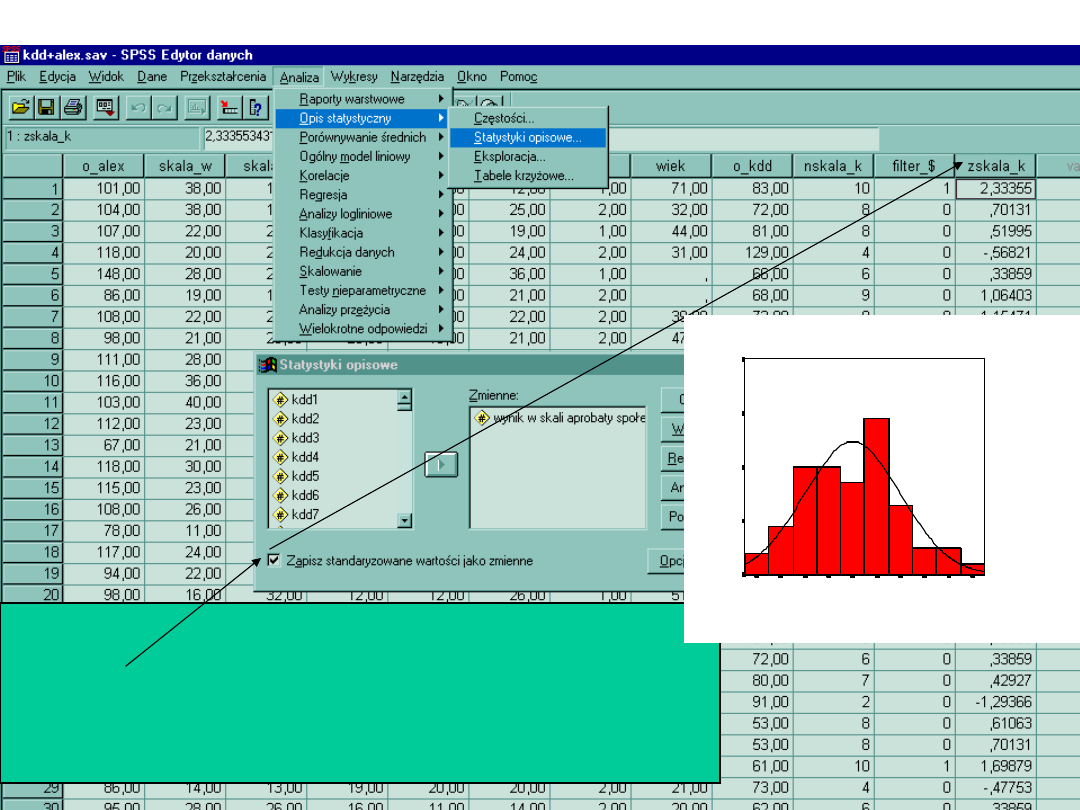
Standaryzacja wyników
Z = (X - M) / SD
Z = (X - M) / SD
Jeśli chcemy odsiać wyniki skali_K za pomocą zabiegu
standaryzacji wtedy
Używamy do tego Analiza > Opis statystyczny > Statystyki
opisowe> zaznaczamy, że chcemy aby operacja zapisana była
jako nowa zmienna
Zwróćmy uwagę, że wyniki lokujące się powyżej wartości Z=
1.28 odpowiadają 10 decylowi.
Jest tak ponieważ wartość 1.28 odcina właśnie górne 10 %
rozkładu normalnego
Stand : wynik w skali aprobaty społeczn
2,50
2,00
1,50
1,00
,50
0,00
-,50
-1,00
-1,50
-2,00
Stand : wynik w skali aprobaty społeczn
C
zę
st
oś
ć
40
30
20
10
0
Odch.Std = 1,00
Średnia = 0,00
N = 124,00
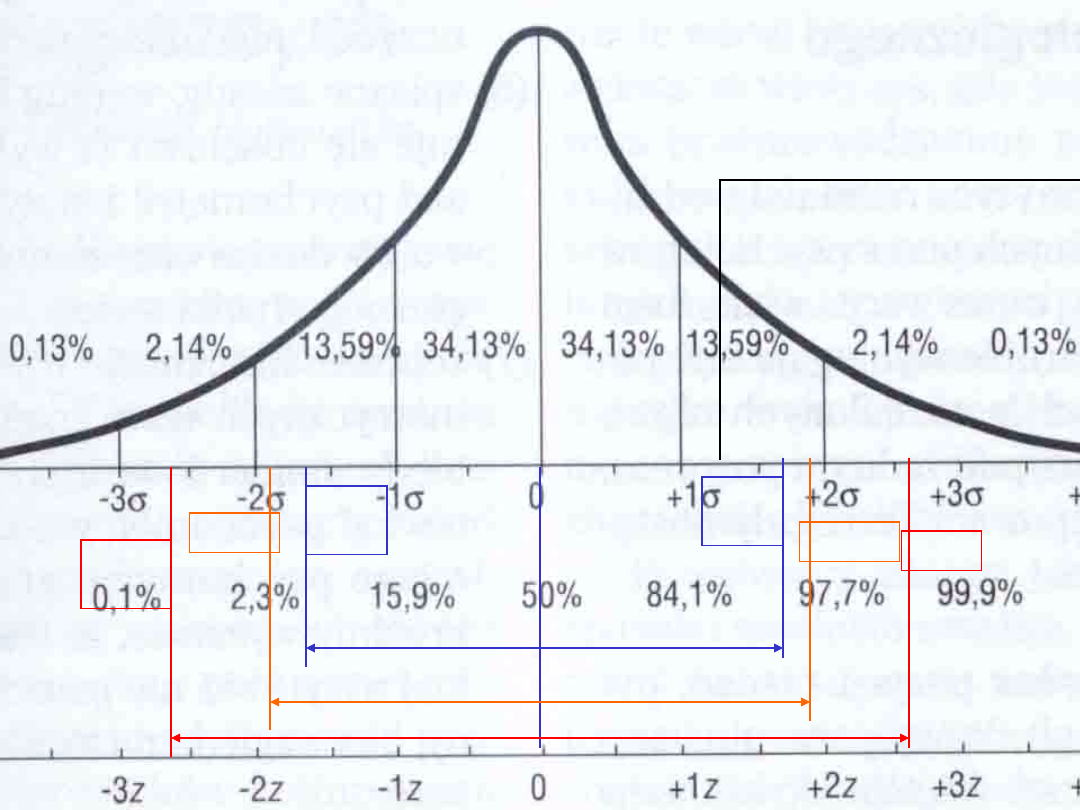
10%
1.28
45
%
45
%
47,5
%
47,5
%
49,5%
49,5
%
2,58
-
2,58
+1,96
-1,96
-
1,64
+1,6
4
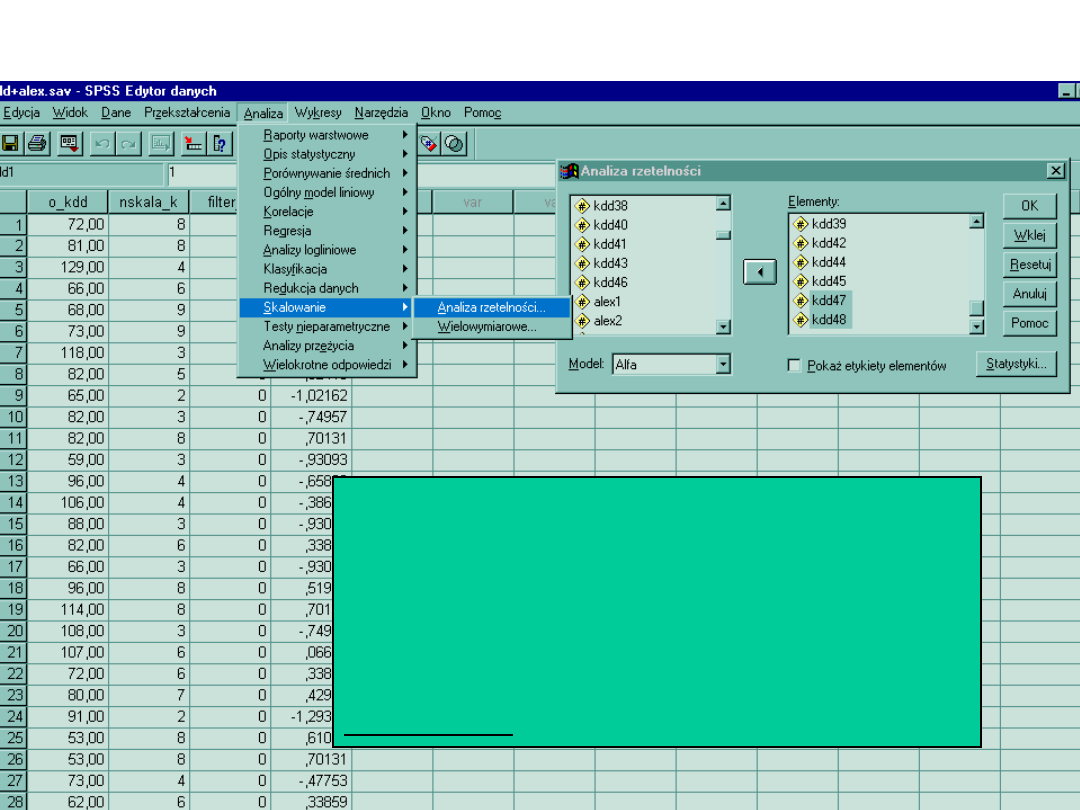
Analiza rzetelności (def.) precyzja z jaką test
mierzy to co mierzy
Rzetelność mierzona jest w przypadku gdy test ma
kafeterię odpowiedzi > 2 używana jest met. Alfa
Cronbacha liczona jako współczynnik korelacji.
Współczynnik Alfa jest Ok. dla kwestionariuszy gdy
osiąga 0,7 i więcej.
Dla testów psychologicznych od + 0,9
Teoretycznie precyzja (czyli rzetelność) może
wynosić 1
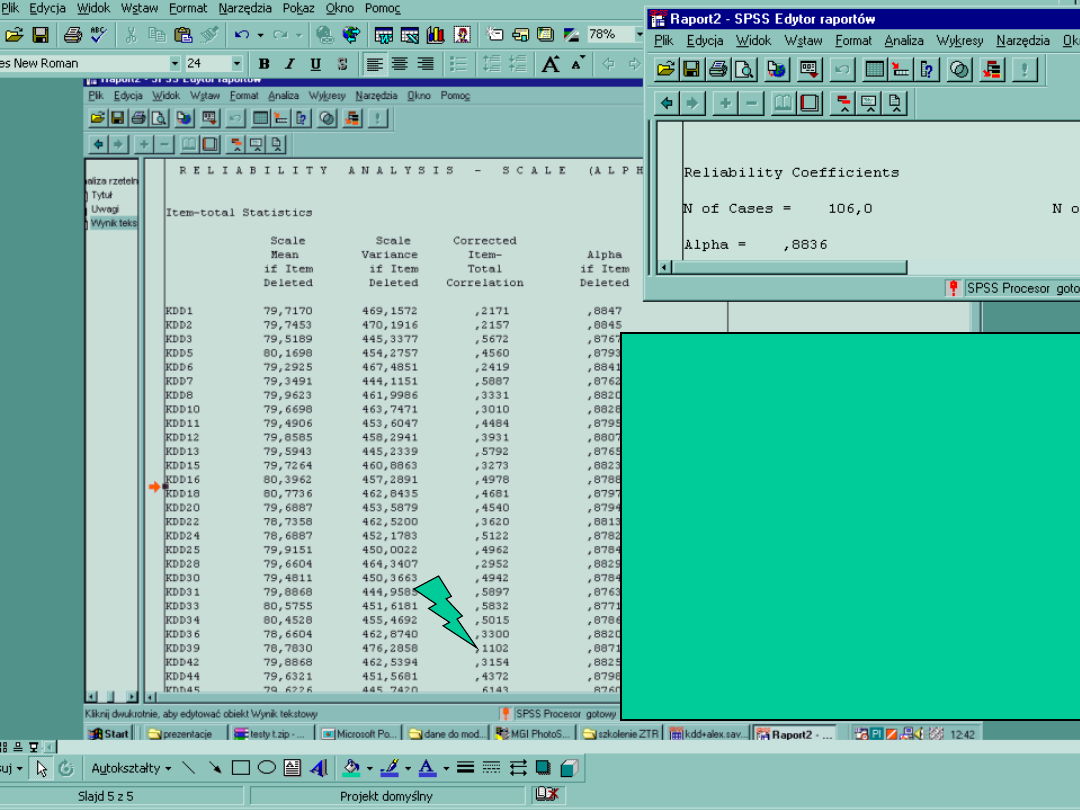
Tutaj kwestionariusz osiągnął wysoką
Alfę, więc nie ma potrzeby modyfikacji
pozycji
Regułą jest, że im dłuższy test tym
większa rzetelność.
Przy konstrukcji testu należy utworzyć
pulę matkę pozycji tak żeby zawierała
dwa razy większą ilość pozycji niż test
docelowy
Jeśli okaże się, że jakaś pozycja słabo
koreluje ze skalą, można ją zmienić
lub usunąć z analizy Wtedy rzetelność
wzrośnie. Modyfikacje można
prowadzić tak długo aż, wraz z
usuwaniem pozycji Alfa przestanie
rosnąć.
Testowanie hipotez
Testowanie hipotez
•
Wnioskowanie
Wnioskowanie
niewprost
niewprost
oznacza, że jeśli przypuszczamy, że
oznacza, że jeśli przypuszczamy, że
wraz ze zmianą poziomu aleksetymii związana będzie zmiana
wraz ze zmianą poziomu aleksetymii związana będzie zmiana
poziomu doświadczeń związanych z treningiem „nie czuj”,
poziomu doświadczeń związanych z treningiem „nie czuj”,
wtedy my używając metod statystycznych testujemy hipotezę
wtedy my używając metod statystycznych testujemy hipotezę
wprost przeciwną do nas interesującej.
wprost przeciwną do nas interesującej.
•
Hipoteza przeciwna do badawczej (HB) nazywana jest zerową
Hipoteza przeciwna do badawczej (HB) nazywana jest zerową
(H0). W statystyce zajmujemy się tylko i wyłącznie testowaniem
(H0). W statystyce zajmujemy się tylko i wyłącznie testowaniem
wiarygodności H0.
wiarygodności H0.
•
Jeśli okaże się, że z wybranym prawdopodobieństwem można
Jeśli okaże się, że z wybranym prawdopodobieństwem można
odrzucić HO, wtedy również z wybranym
odrzucić HO, wtedy również z wybranym
p
p
możemy powiedzieć,
możemy powiedzieć,
że nasze badawcze przewidywanie jest słuszne.
że nasze badawcze przewidywanie jest słuszne.
•
W badaniach psychologicznych zakłada się zwyczajowo:
W badaniach psychologicznych zakłada się zwyczajowo:
p<0.05
p<0.05
•
W badaniach
W badaniach
medycznych
medycznych
p< 0.001
p< 0.001
•
Oznacza to, że
Oznacza to, że
jeśli H0 zachodzi na poziomie p<0,05 to znaczy,
jeśli H0 zachodzi na poziomie p<0,05 to znaczy,
że H0 może zajść mniej niż w 5 przypadkach na 100 badanych.
że H0 może zajść mniej niż w 5 przypadkach na 100 badanych.
Czyli nasze przewidywania (Hb) znajdują odbicie w
Czyli nasze przewidywania (Hb) znajdują odbicie w
rzeczywistości w 95 %!!!
rzeczywistości w 95 %!!!
Błędy w testowaniu hipotez
Błędy w testowaniu hipotez
H0
prawdziwa
Decyzja co do HO
H0 fałszywa
Odrzucamy
przyjmujemy
Błąd I-ego rodzaju
Błąd II-ego rodzaju
Modele badawcze: korelacyjny i
Modele badawcze: korelacyjny i
eksperymentalny
eksperymentalny
W modelu korelacyjnym mowa jest tylko o
W modelu korelacyjnym mowa jest tylko o
współzmienności, czyli co z czym chodzi w
współzmienności, czyli co z czym chodzi w
parze.
parze.
Nie może być mowy o wnioskowaniu przyczyno-
Nie może być mowy o wnioskowaniu przyczyno-
skutkowym, ponieważ nie ma manipulacji
skutkowym, ponieważ nie ma manipulacji
zmiennymi
zmiennymi
Zależnie od skali pomiarowej na jakiej znajdują
Zależnie od skali pomiarowej na jakiej znajdują
się korelowane zmienne mamy do wyboru: wsp.
się korelowane zmienne mamy do wyboru: wsp.
Pearsona
Pearsona
(gdy obie zmienne są na skali przedziałowej)
(gdy obie zmienne są na skali przedziałowej)
wsp. Spearmana (obie zmienne na skali
wsp. Spearmana (obie zmienne na skali
porządkowej)
porządkowej)
Tau Kendalla (jedna na przedziałowej druga na
Tau Kendalla (jedna na przedziałowej druga na
porządkowej)
porządkowej)
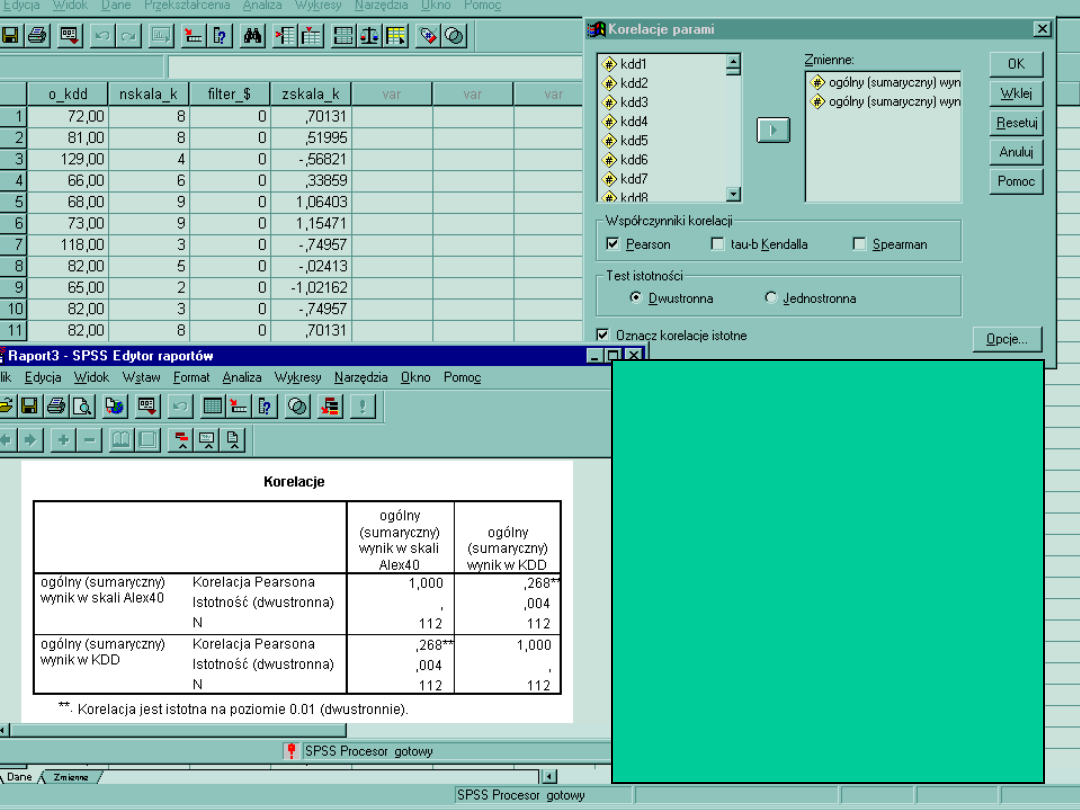
Obie zmienne idą ze sobą w
parze r=0,268
i jest to korelacja istotna na
poziomie p<0,01
a więc nie przypadkowa.
Te zmienne mają swoją
wariancję. Pytanie jest jak bardzo
mają je wspólne
wspólna wariancja obu
zmiennych to tzw. Siła związku,
jako
korelacja do kwadratu r kwadrat
= 0,071 * 100 % = 7.1%
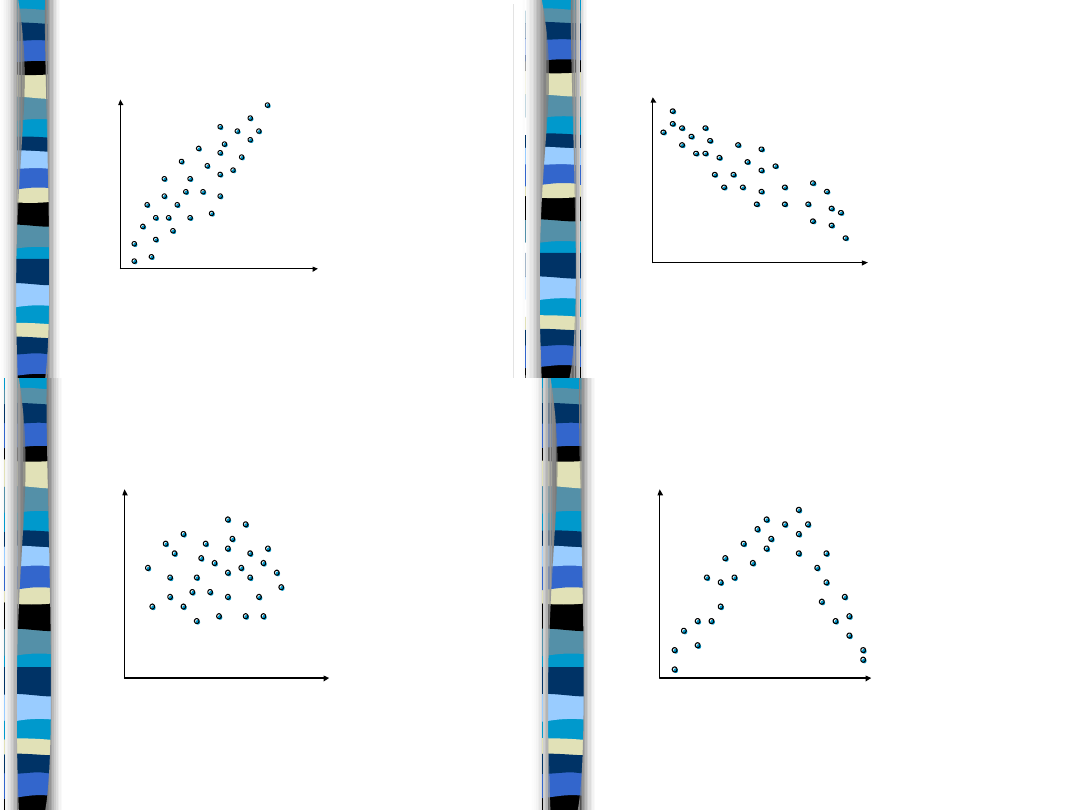
Korelacja dodatnia
Korelacja ujemna
Korelacja zerowa
Istnieje silny związek
(nieliniowy) korelacja zerowa
Korelacja jest miarą związku liniowego
•
Możliwe wartości współczynnika
Możliwe wartości współczynnika
korelacji <-1,+1>
korelacji <-1,+1>
•
proporcja wspólnej wariancji -
proporcja wspólnej wariancji -
współczynnik determinacji =
współczynnik determinacji =
•
kwadrat współczynnika korelacji
kwadrat współczynnika korelacji
Modele eksperymentalne i korelacyjne
Modele eksperymentalne i korelacyjne
•
W modelu
W modelu
eksperymentalnym
eksperymentalnym
można wyciągać wnioski
można wyciągać wnioski
najsilniejsze w sensie metodologicznym, czyli o zależności
najsilniejsze w sensie metodologicznym, czyli o zależności
przyczynowo- skutkowej, ponieważ:
przyczynowo- skutkowej, ponieważ:
•
zachodzi manipulacja zmiennymi niezależnymi (to te które w
zachodzi manipulacja zmiennymi niezależnymi (to te które w
naszej teorii wpływają na zmienną główną)
naszej teorii wpływają na zmienną główną)
•
wszystkie zmienne poboczne są pod kontrolą, lub są wyrównane
wszystkie zmienne poboczne są pod kontrolą, lub są wyrównane
•
istnieje losowy przydział do grup
istnieje losowy przydział do grup
•
W zależności od skali pomiarowej znajdują się zmienne, które
W zależności od skali pomiarowej znajdują się zmienne, które
mierzymy, takiej metody użyjemy:
mierzymy, takiej metody użyjemy:
•
jeżeli zmienna zależna jest na skali przedziałowej, rozkłada się
jeżeli zmienna zależna jest na skali przedziałowej, rozkłada się
normalnie wtedy (testy „t”, analiza wariancji ANOVA i UNIANOVA)
normalnie wtedy (testy „t”, analiza wariancji ANOVA i UNIANOVA)
•
jeżeli zmienne są na skali nominalnej Test Chi kwadrat
jeżeli zmienne są na skali nominalnej Test Chi kwadrat
•
Zmienna zależna jak każda zmienna posiada wariancję
Zmienna zależna jak każda zmienna posiada wariancję
(zmienność).
(zmienność).
•
Manipulując innymi czynnikami próbujemy wyjaśnić jak najwięcej
Manipulując innymi czynnikami próbujemy wyjaśnić jak najwięcej
tej wariancji.
tej wariancji.
Model eksperymentalny cd...
Model eksperymentalny cd...
•
W schemacie różnicowym, mimo braku manipulacji używa
W schemacie różnicowym, mimo braku manipulacji używa
się również metod zarezerwowanych dla eksperymentu
się również metod zarezerwowanych dla eksperymentu
•
Jeżeli chcemy dowiedzieć się czy alkoholicy i osoby nie
Jeżeli chcemy dowiedzieć się czy alkoholicy i osoby nie
mające problemu alkoholowego różnią się (istotnie!) pod
mające problemu alkoholowego różnią się (istotnie!) pod
względem aleksytymii to należy porównać obie grupy pod
względem aleksytymii to należy porównać obie grupy pod
względem średniego natężenia tej cechy.
względem średniego natężenia tej cechy.
•
Wtedy grupa to zmienna niezależna o dwóch poziomach:
Wtedy grupa to zmienna niezależna o dwóch poziomach:
1- kliniczna,
1- kliniczna,
2 - kontrolna
2 - kontrolna
•
O_Alex to zmienna zależna, która ma różnicować obie
O_Alex to zmienna zależna, która ma różnicować obie
grupy
grupy
•
Jeśli w obu grupach zachodziła by manipulacja jakimś
Jeśli w obu grupach zachodziła by manipulacja jakimś
kryterium wtedy wnioskowalibyśmy o wpływie tego
kryterium wtedy wnioskowalibyśmy o wpływie tego
kryterium na poziom aleksytymii
kryterium na poziom aleksytymii
•
Jeżeli zmienna niezależna ma nie więcej niż 2 poziomy,
Jeżeli zmienna niezależna ma nie więcej niż 2 poziomy,
•
jeżli rozkłady w obu grupach nie różnią się
jeżli rozkłady w obu grupach nie różnią się
•
Jeżeli zmienna zależna jest na sklali przedziałowej i rozkład
Jeżeli zmienna zależna jest na sklali przedziałowej i rozkład
normalny wtedy stosuje się Test
normalny wtedy stosuje się Test
„T- Studenta” dla prób
„T- Studenta” dla prób
niezależnych
niezależnych
•
Pomiary dokonywane są niezależnie w obu grupach
Pomiary dokonywane są niezależnie w obu grupach
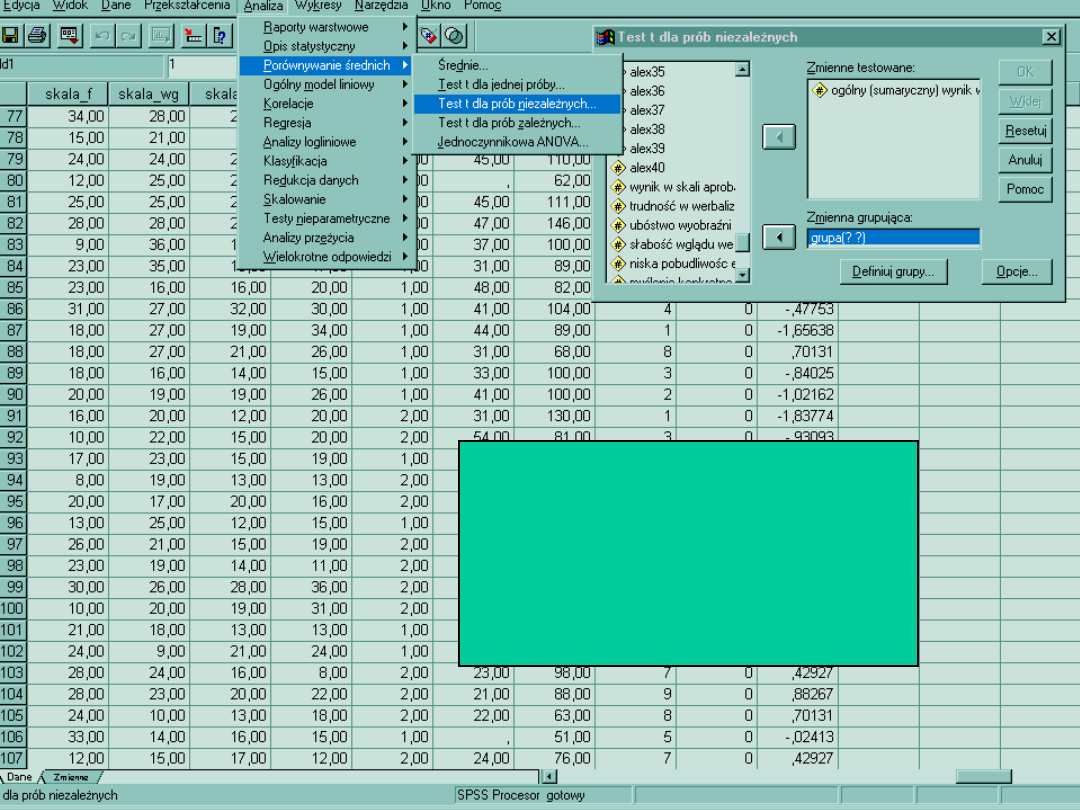
Jeśli zmienna jest na skali
przedziałowej to zrozumiałe jest, że
można obliczyć średnią, stąd
wymienione metody znajdują się w
tej ikonie. Zmienne testowane
dotyczą zmiennej zależnej. Zmienna
grupująca to zmienna niezależnej
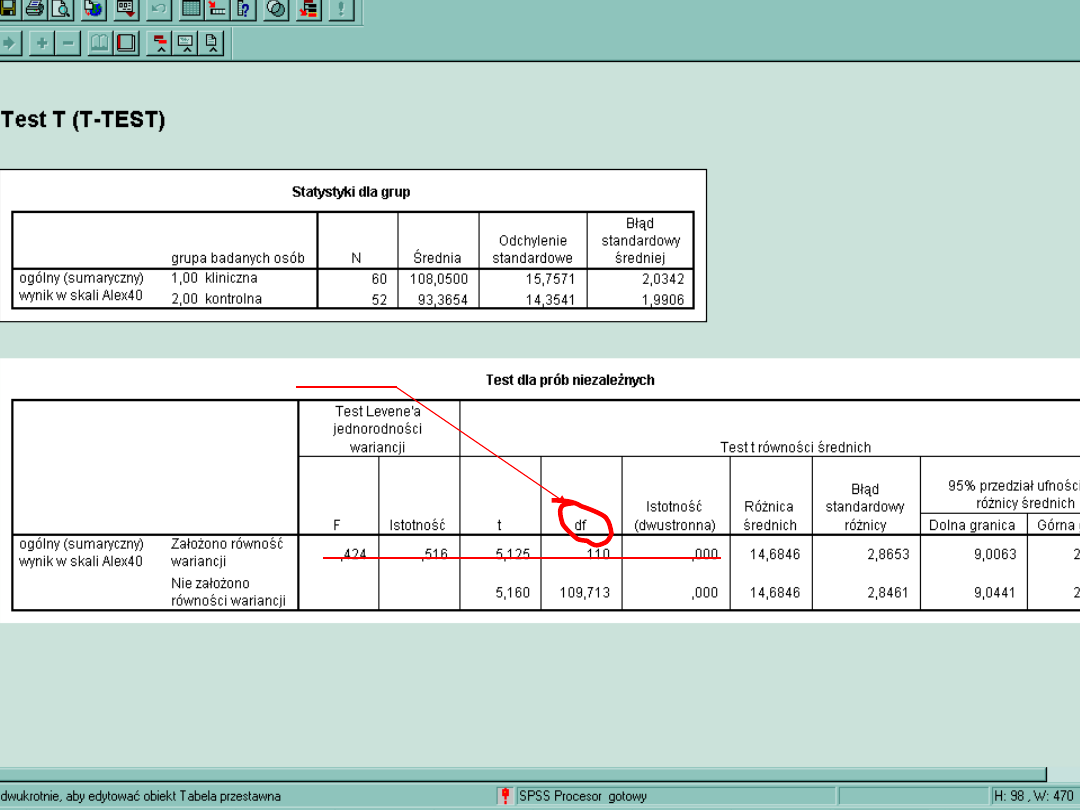
W Tab.1 zawarte są liczebności
i średnie
w obu grupach. Widać, że
istnieje między obiema
grupami różnica, ale pytanie
czy nieprzypadkowa?
Tabela odpowie nam na to pytanie, po sprawdzeniu jeszcze metodologicznych wymagań
stosowania testu T.
Wariancje w obu grupach muszą być równe. Sprawdza to test Levene’a. H0 mówi, że
wariancje są równe, jeśli test jest nieistotny, nie można jej odrzucić, a więc w naszym
przypadku wariancje są naprawdę równe.
Jęśli tak, to wtedy wartość testu T odczytujemy z górnej linijki i powinna być zapisana
t(110) = 5,125; p<0.001
Df to stopnie swobody, czyli liczba przypadków dla których liczona statystyka jest
wiarygodna.Testy T dla prób niezależnych df = N - 2
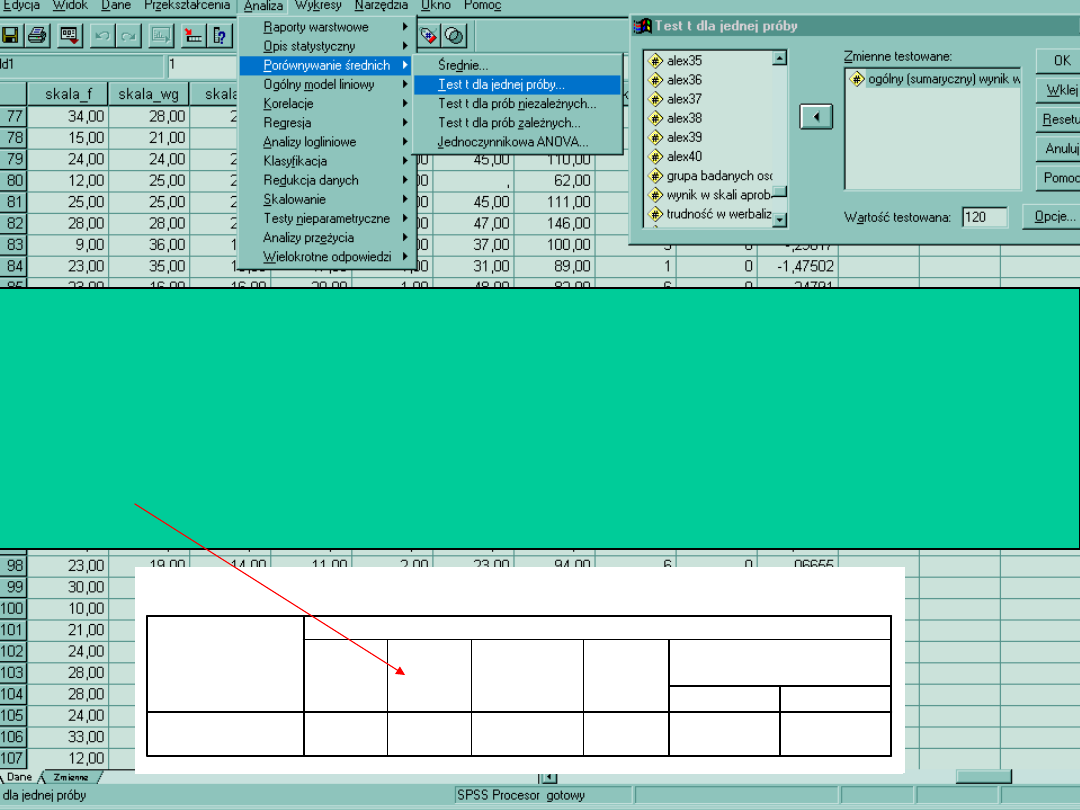
Załóżmy teraz, że pod kątem naszej aleksytymii, czytaliśmy raport z badań np. na
populacji niemieckiej
Z raportu dowiadujemy się, że tamtejsza porównywalna próba osiągnęła ŚREDNI
wynik w Alex40 = 120
Dzięki testowi dla jednej próby porównujemy czy nasza próba istotnie różni się od
próby z badań niemieckich. Ho = obie próby nie różnią się istotnie poziomem
aleksytymii. HO jest istotna, więc ją odrzucamy.
Nie mamy tutaj zmiennych niezależnych, ale warunkiem jest tutaj poziom pomiaru
zmiennej zależnej: przedziałowy
Df = N-1
Test dla jednej próby
-11,854
111
,000
-18,7679
-21,9052
-15,6305
ogólny (sumaryczny)
wynik w skali Alex40
t
df
Istotność
(dwustronna)
Różnica
średnich Dolna granica Górna granica
95% przedział ufności dla
różnicy średnich
Wartość testowana = 120
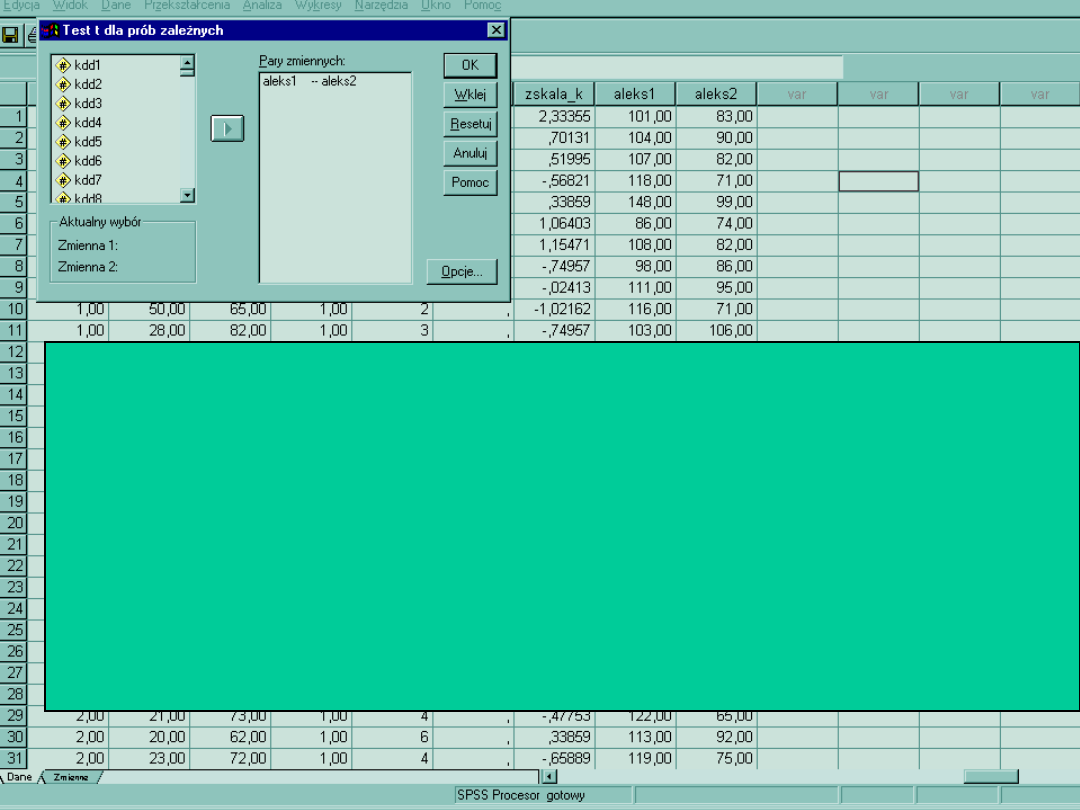
Wyobraźmy sobie, że chcemy przeprowadzić badania ewaluacyjne terapii osób z
problemem alkoholowym.
Wskaźnikiem zmiany będzie pomiar poziomu aleksytymii przed i po terapii na
próbie N = 60 osób.
Pomiar na tej samej grupie osób w czasie nazywa się pomiarem zależnym. Jak jest
przyjęte w testach T, porównujemy
średnie w grupie. H0 w tym wypadku mówi o tym, że w obu pomiarach średnie nie
będą się różnić.
Jak nie trudno się domyślić pomiar zależny obarczony jest błędami: jest bardzo
czuły na upływ czasu i wyuczenie, co może zaburzać
wyniki i wysuwane wnioski.
W długich odstępach czasu działać może wiele nie kontrolowanych czynników,
które same w sobie mogą powodować zmianę w wynikach. Zaś w krótkich
odstępach czasu zmiana może wynikać z efektu wyuczenia.
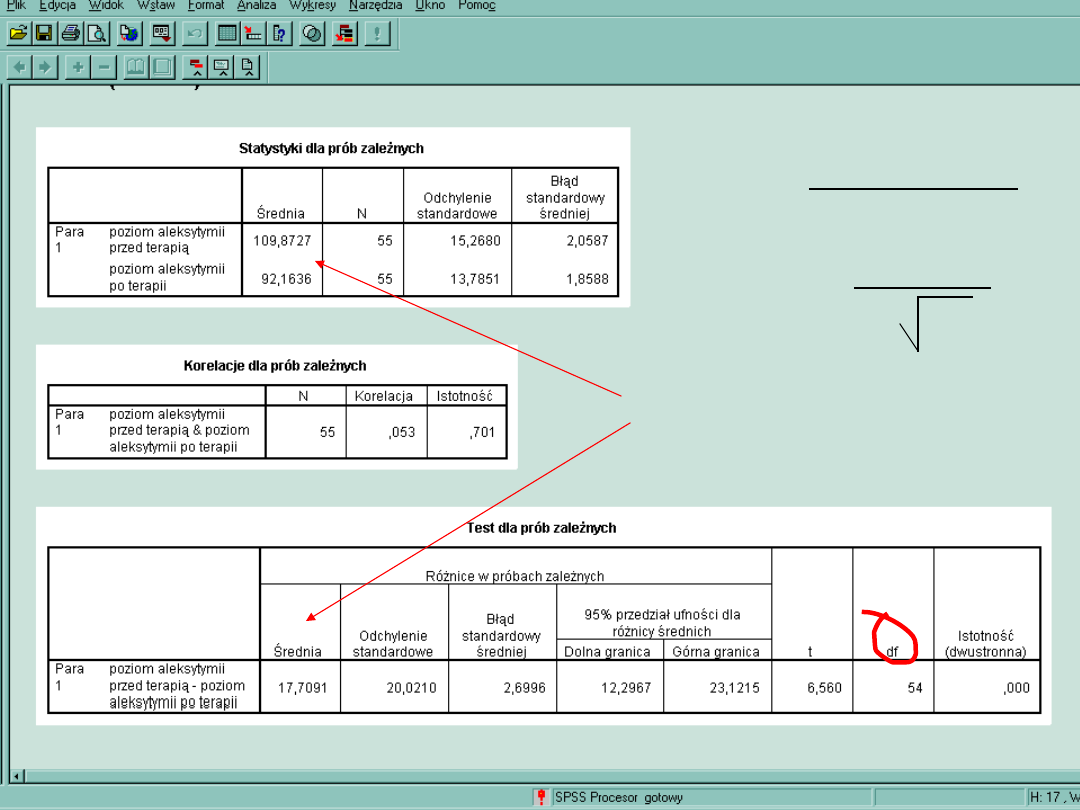
Wynika z Różnic średnich między
pomiarami. Test T sprawdza istotność
tych różnic.
Df = N-1
N- liczba par
SD
SEM
T =
M
1
- M
2
SEM
1
+ SEM
2
SEM =
N
S
D
Co zrobić jeśli jest więcej poziomów zmiennej
Co zrobić jeśli jest więcej poziomów zmiennej
niezależnej?
niezależnej?
•
Wyobraźmy sobie, że do porównania poziomu aleksytymii i
Wyobraźmy sobie, że do porównania poziomu aleksytymii i
doświadczeń typu „nie czuj” nie wystarczą tylko dwie grupy.
doświadczeń typu „nie czuj” nie wystarczą tylko dwie grupy.
•
Porównaliśmy dopiero dwie w zasadzie skrajne grupy i różnice
Porównaliśmy dopiero dwie w zasadzie skrajne grupy i różnice
rzeczywiście zachodzą. Ale być może to właśnie różnica w
rzeczywiście zachodzą. Ale być może to właśnie różnica w
wieku powoduje, że badani się różnią. Warto zbadać trzecią
wieku powoduje, że badani się różnią. Warto zbadać trzecią
grupę osób starszych i nie uzależnionych od alkoholu.
grupę osób starszych i nie uzależnionych od alkoholu.
•
Jest to schemat podobny do testu T dla prób niezależnych ale
Jest to schemat podobny do testu T dla prób niezależnych ale
porównać trzeba nie dwie a trzy średnie.
porównać trzeba nie dwie a trzy średnie.
•
ANOVA umożliwia taką analizę, nie tylko średnich ale i
ANOVA umożliwia taką analizę, nie tylko średnich ale i
wariancji!
wariancji!
•
Mówiliśmy, że chcemy poznać jak największą ilość wariancji
Mówiliśmy, że chcemy poznać jak największą ilość wariancji
zmiennej niezależnej. To tak jak sporządzanie mapy terenu za
zmiennej niezależnej. To tak jak sporządzanie mapy terenu za
pomocą narzędzia jakim jest zmienna niezależna.
pomocą narzędzia jakim jest zmienna niezależna.
•
Jeśli zmienna niezależna jest dobrze dobrana wtedy można
Jeśli zmienna niezależna jest dobrze dobrana wtedy można
wytłumaczyć 100 % wariancji
wytłumaczyć 100 % wariancji
•
Niestety zawsze występują pewne zakłócenia losowe i
Niestety zawsze występują pewne zakłócenia losowe i
wynikające z niedoskonałości narzędzia.
wynikające z niedoskonałości narzędzia.
Anova cd..
Anova cd..
•
W eksperymencie musimy kontrolować zmienne
zakłócające, grupy muszą być wyrównane pod wieloma
względami, aby po przeprowadzeniu manipulacji móc
powiedzieć, że różnice wynikają z zadziałania naszej
zmiennej niezależnej
•
Te błędy noszą nazwę właśnie wariancji błędu
(wewnątrzgrupową)
•
to co my kontrolujemy nazywane jest wariancją
kontrolowaną (międzygrupową). Zależy nam aby stanowiło
100 %
•
MS
T
= MS
M
+ MS
B
•
Analiza wariancji oparta jest na stosunku obu wariancji
•
F =
•
gdy F = 1 wtedy stosunek kontroli do błędu jest po 50%
•
gdy F > 1 kontrola > błędu i vice versa
MS
M
MS
B
Przykład
klasa otrzymuje z testu końcowego z matematyki oceny:
5,5, 4,4, 3,3, 2,2
Pytanie co wpływa na to, że jedni otrzymują oceny niskie a
inni wysokie?
Hipoteza: Na oceny wpływa inteligencja i to ona różnicuje te osoby
WI
Oceny
NI
5,5,4,4
3,3,2,2
M = 4,5
M = 2,5
WI
Oceny
NI
5,4,3,2
5,4,3,2
M = 3,5
M = 3,5
0!
Wariancja kontrolowana 100% F > 1 Wariancja błędu 100% F = 0
Document Outline