Instalacje pokładowe

Układy elektroenergetyczne –

obliczenia - 1

Potencjał elektryczny

Potencjał jest wielkością skalarną
charakteryzującą określony punkt pola
elektrycznego i wyraża liczbowo wartość
pracy wykonanej przeciwko siłom pola
(w przypadku potencjału dodatniego) lub
wykonanej przez te siły (w przypadku
potencjału ujemnego) przy przeniesieniu
dodatniego ładunku jednostkowego z
nieskończoności do tego punktu.

Potencjał elektryczny

Jednostka potencjału w układzie SI:

1 wolt

- taka różnica potencjałów dwóch punktów

pola elektrycznego, która wymaga wykonania pracy

1 J przy przeniesieniu ładunku 1C.

 

 

 

3

2

2

2

1

1

1

1

1

1

1

1

As

kgm

As

s

kgm

C

J

q

E

V

p









Potencjał elektryczny

Inaczej:

Przesuwanie ładunku Q wzdłuż linii sił pola
na dowolnie małą odległość dl wymaga
wykonania pracy:

Stosunek tej pracy do ładunku nazywamy

potencjałem:

Fdl

dA

Edl

Q

Fdl

dV





Potencjał elektryczny

Potencjał w punkcie B:







B

r

B

Edl

V

Napięcie

Różnica potencjałów w dwóch punktach pola A i
B, odległych od ładunku o r

A

i r

B

nazywana jest

napięciem U

AB

między tymi punktami:























B

A

B

A

r

r

r

r

B

A

AB

Edl

Edl

Edl

V

V

U

Napięcie

Jednostką napięcia (tak jak i potencjału)
jest

1 wolt

A

W

s

A

s

W

C

J

V

1

1

1

1

1

1

1











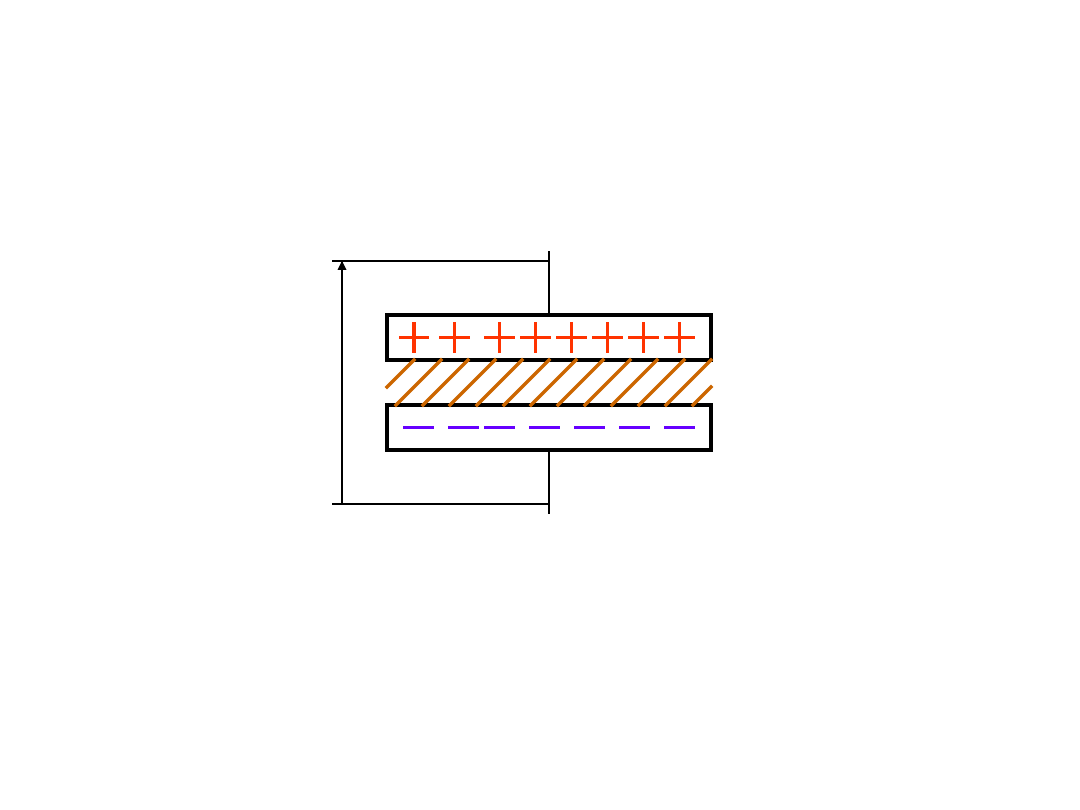
Kondensatory

Ładunek Q wprowadzony do kondensatora jest

proporcjonalny do napięcia ładowania U

U

+Q

-Q

Kondensatory

CU

Q 

gdzie C – pojemność elektryczna
kondensatora

Jednostką pojemności jest farad (1F).

Łączenie kondensatorów

Kondensatory mogą być
połączone:

- szeregowo
- równolegle
- szeregowo-równolegle

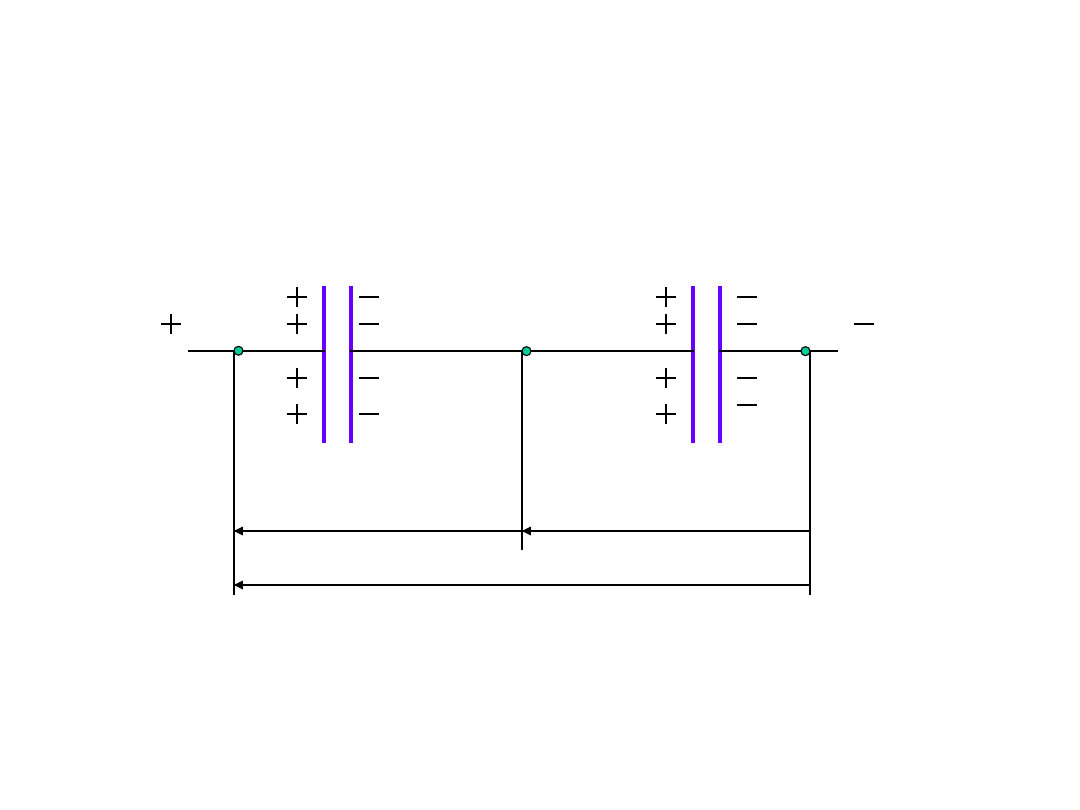
Połączenie szeregowe

kondensatorów

a

c

b

U

1

U

U

2

Q

2

Q

1

Połączenie szeregowe

kondensatorów

1

1

1

U

Q

C 

2

2

2

U

Q

C 

lub

1

1

1

C

Q

U 

2

2

2

C

Q

U 

Połączenie szeregowe

kondensatorów





















2

2

1

1

2

1

C

Q

C

Q

U

U

U

2

1

Q

Q

Q





















2

1

1

1

C

C

Q

U

Połączenie szeregowe

kondensatorów

2

1

1

1

1

C

C

C





U

Q

C 

Pojemność zastępcza układu dwóch
kondensatorów:

Połączenie szeregowe

kondensatorów







n

k

k

C

C

1

1

1

Pojemność zastępcza n kondensatorów
połączonych szeregowo:

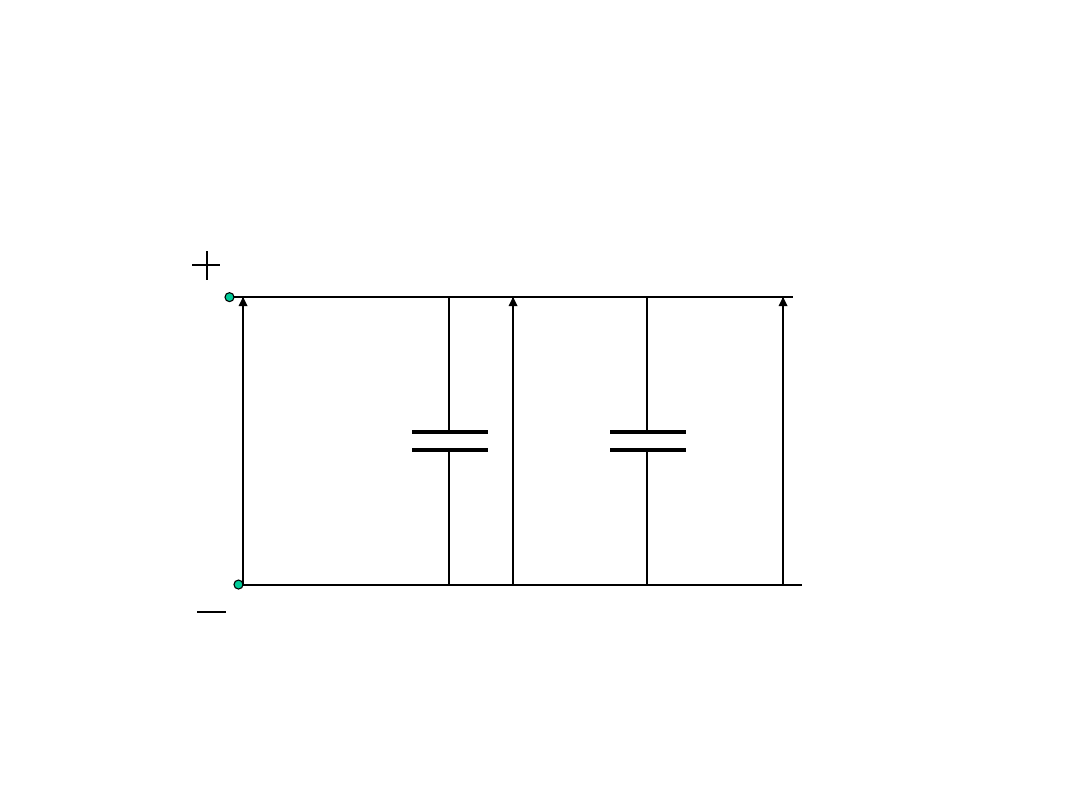
Połączenie równoległe

kondensatorów

U

U

2

U

1

Q

1

C

1

C

2

Q

2

Połączenie równoległe

kondensatorów

2

2

1

1

2

1

2

1

U

C

U

C

Q

Q

Q

U

U

U













Pojemność zastępcza dwóch kondensatorów
połączonych równolegle:

2

1

2

2

1

1

C

C

U

U

C

U

C

U

Q

C











Połączenie równoległe

kondensatorów

Pojemność zastępcza układu n
kondensatorów połączonych
równolegle:







n

k

k

C

C

1

Prąd elektryczny

Prąd elektryczny to ładunek elektryczny
poruszający się względem danego
układu odniesienia.

Ładunki mogą się poruszać wyłącznie
wtedy, gdy oddziaływuje na nie pole
elektryczne. Pole to można uzyskać
wytwarzając w różnych punktach
przewodnika różne potencjały.

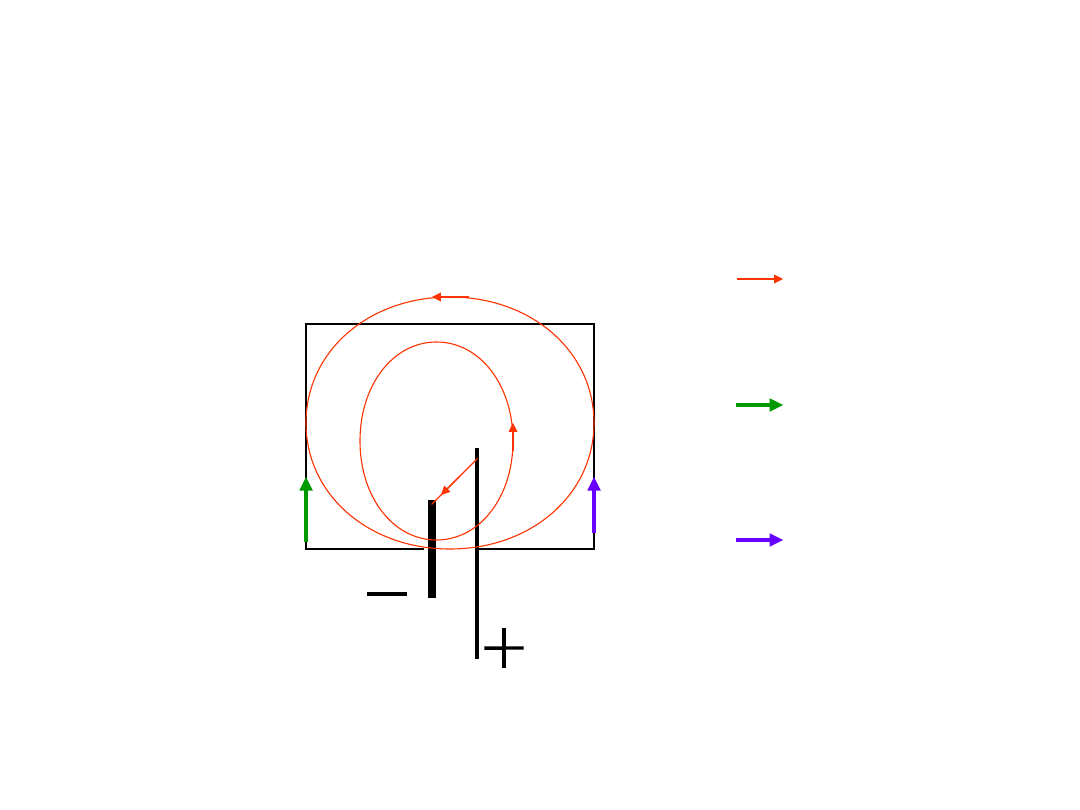
Źródło napięcia

Linie sił pola
elektrycznego

Kierunek ruchu
elektronów

Umowny kierunek
prądu

E

Natężenie prądu

Natężenie prądu I płynącego w
przewodniku to stosunek ładunku
elektrycznego Q przepływającego przez
poprzeczny przekrój przewodnika do czasu
jego przepływu:

t

Q

I 

 

t

Q

t

i

t











lim

0

Natężenie prądu

Jednostka natężenia prądu jest amper [A].

Jest to natężenie prądu polegającego na
przepływie ładunku 1 kulomba w czasie 1
sekundy.

s

C

A

1

1

1 

Prawo Ohma

Natężenie prądu płynącego w

przewodniku jest proporcjonalne do

napięcia, czyli różnicy potencjałów

między końcami tego przewodnika:

gdzie

R – opór przewodnika

U

R

I

1



Opór przewodnika

Jednostką oporu w układzie SI jest om []

Jest to opór takiego przewodnika, w
którym pod wpływem napięcia 1V płynie
prąd o natężeniu 1A.

A

V

1

1

1 



Opór przewodnika

Dla przewodnika

gdzie: l – długość przewodnika [m]

S – pole powierzchni przekroju

przewodnika

[mm

2

]



- opór właściwy (rezystywność)

S

l

R





Opór właściwy

W układzie SI jednostka rezystywności:

W elektrotechnice i energetyce używa się
powszechnie jednostki podwielokrotnej:

 

m



1

1



m

m

mm









 6

2

10

1

Opór właściwy

Opór właściwy:
miedzi -

aluminium -

m







 8

10

7

,

1



m







 8

10

8

,

2



Zależność oporu elektrycznego

od temperatury

0

R

R

R

t







0

t

t

t











0

0

0

t

t

R

R

R

t

R









Zależność oporu elektrycznego

od temperatury









0

0

1

t

t

R

R

R

t









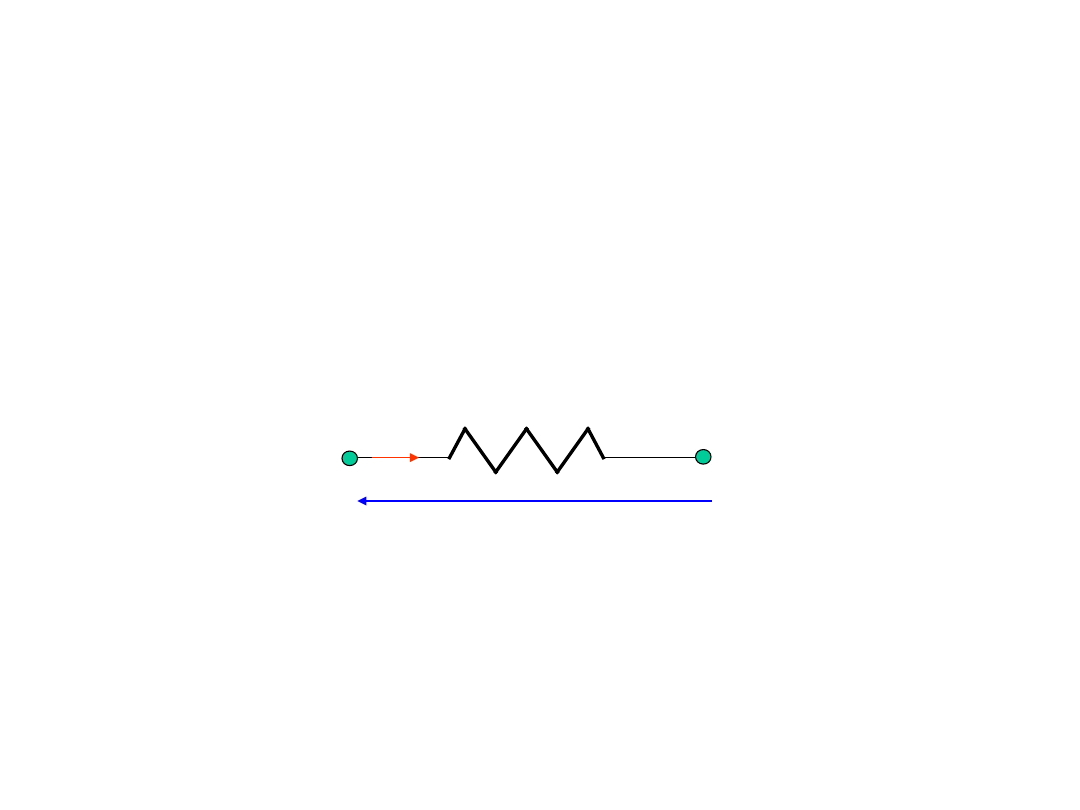
Proste obwody rezystancyjne

Opornik liniowy, czyli taki, w którym opór
(rezystancja) jest wartością niezależną od
prądu.

R

i

u

 

 

Ri

u

t

Ri

t

u





Proste obwody rezystancyjne

1







R

G

Gu

i

gdzie G –przewodność

Jednostka przewodności – simens:

V

A

S

1

1

1 

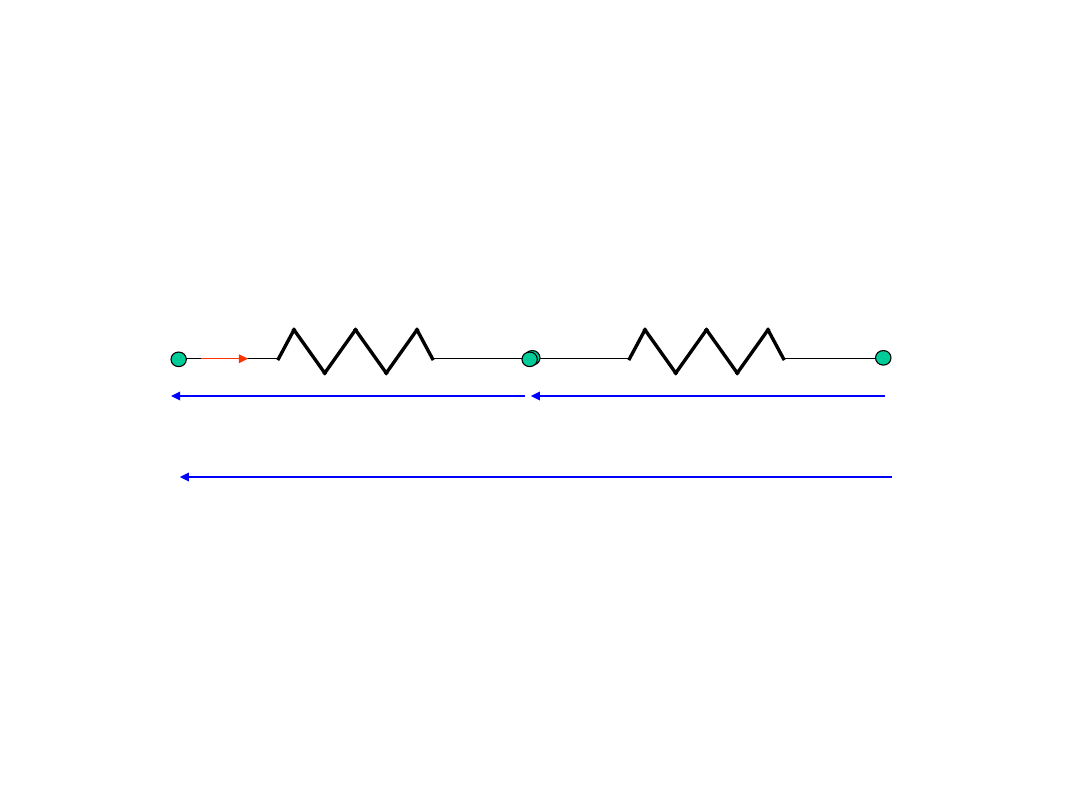
Szeregowe połączenie oporników

R

1

i

u

1

R

2

u

2

u





i

R

R

i

R

i

R

u

u

u

2

1

2

1

2

1













Szeregowe połączenie oporników

2

1

R

R

i

u





2

1

R

R

R





Opornik równoważny (zastępczy):

Szeregowe połączenie oporników

Napięcie na każdym z oporników:

u

R

R

R

i

R

u

u

R

R

R

R

R

u

R

i

R

u

2

1

2

2

2

2

1

1

2

1

1

1

1

















Szeregowe połączenie oporników

Dzielnik napięcia

2

1

2

2

1

2

1

1

2

1

R

R

u

R

R

R

R

R

u

R

u

u









Szeregowe połączenie oporników

Dla n szeregowo połączonych
oporników:







n

k

k

R

R

1

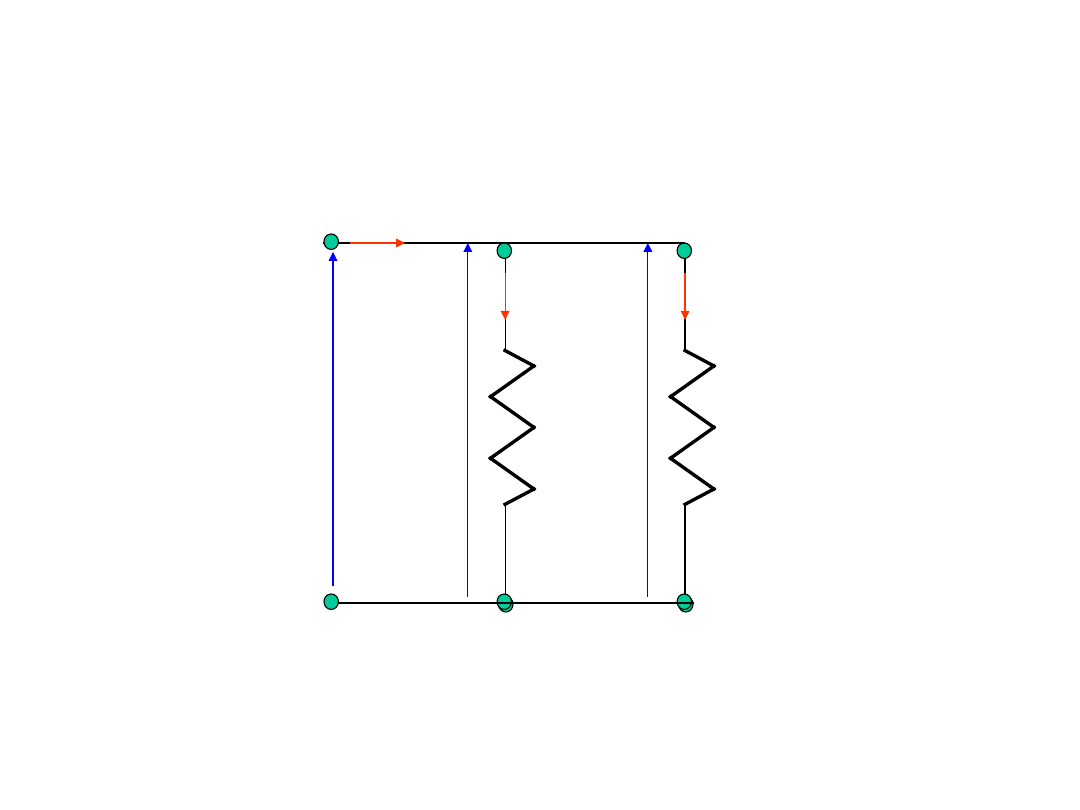
Równoległe połączenie

oporników

R

1

u

2

i

2

i

1

u

1

R

2

u

i

2

1

u

u

u





2

1

i

i

i





Równoległe połączenie

oporników

Zgodnie z prawem Ohma:

1

1

R

u

i 

2

2

R

u

i 

więc:

u

R

R

R

u

R

u

i

i

i

























2

1

2

1

2

1

1

1

zate
m:

2

1

1

1

R

R

u

i





Równoległe połączenie

oporników

więc:

















2

1

1

1

1

R

R

R

lub:

G

u

i



- przewodność opornika
zastępczego
(równoważnego)
połączenia równoległego

2

1

2

1

R

R

R

R

R





Równoległe połączenie

oporników

Obliczamy prądy i

1

oraz i

2

stosując

prawo Ohma:

Poniewa
ż:

i

R

R

R

R

Ri

u

2

1

2

1







i

R

R

R

R

u

i

2

1

2

1

1







i

R

R

R

R

u

i

2

1

1

2

2







Równoległe połączenie

oporników

Dla n oporników połączonych
równolegle:

Prąd podzielony jest w równoległym
połączeniu oporników w relacji:

1

2

1

2

1

2

1

2

2

1

R

R

i

R

R

R

R

R

i

R

i

i















n

k

k

R

R

1

1

1

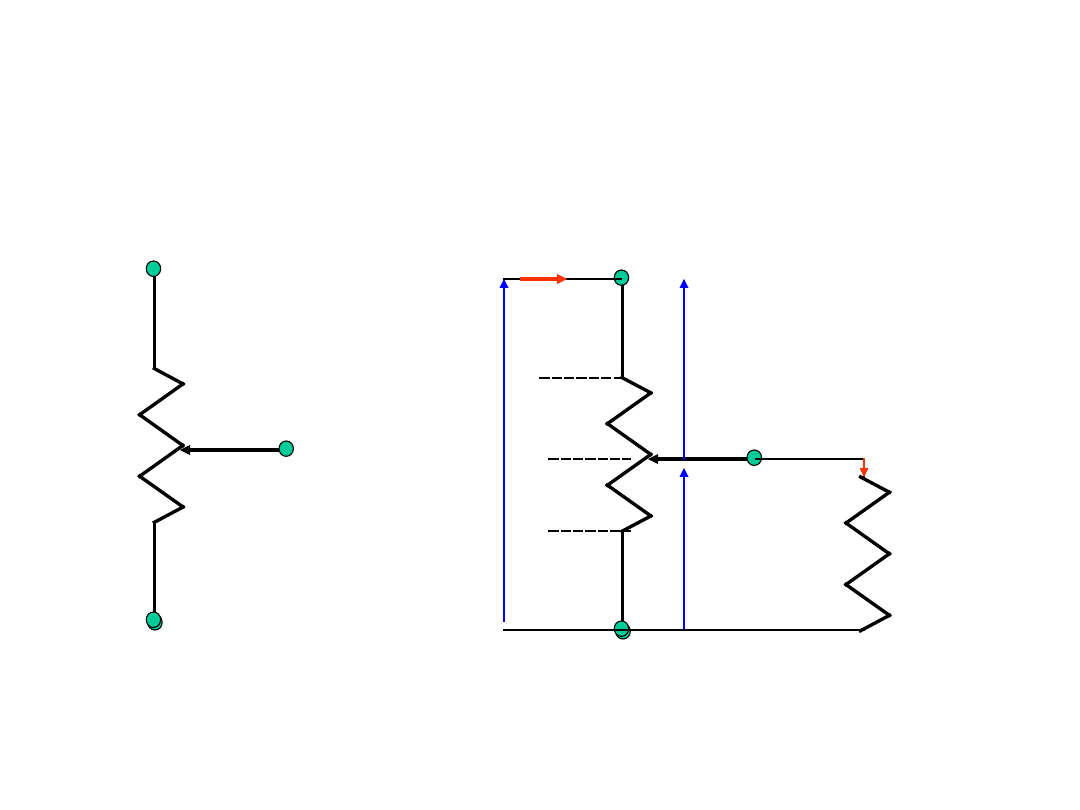
Potencjometr

3

1

2

R

p

3

1

2

R

u

i

R

x

R

y

u

y

u

x

i

2

y

x

p

R

R

R





Potencjometr

Opór widziany z zacisków 1 i 2:

R

R

R

R

R

R

y

y

x







Wobec tego prąd i:

R

R

R

R

R

u

R

u

i

y

y

x









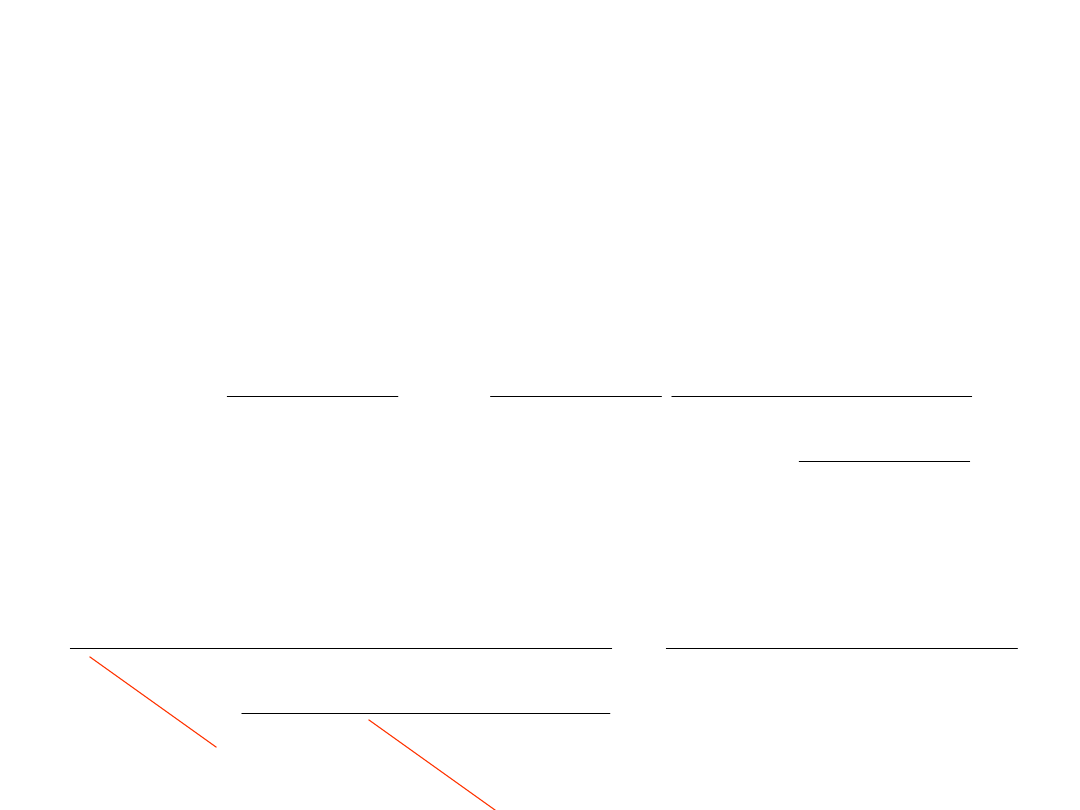
Potencjometr

Napięcie u

y :















R

R

R

R

R

u

R

R

R

R

i

R

R

R

R

u

y

y

x

y

y

y

y

y









u

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

Ru

R

y

y

x

y

y

y

x

y

x

y

y

















Potencjometr

Gdy suwak znajduje się w górnym krańcowym
położeniu, wówczas:

R

x

= 0 a u

y

= u

Gdy suwak znajduje się w dolnym krańcowym
położeniu, wówczas:

R

y

= 0 a u

y

= 0

Gdy suwak zajmie środkowe położenie, czyli
takie, że:

R

x

= R

y

to u

y



½ u

Potencjometr

Aby uzyskać

u

y

= ½ u

należy ustawić suwak w takim położeniu,
aby:

R

R

R

R

R

y

y

x





Poniewa
ż:

x

p

y

R

R

R





Obliczymy R

x

Potencjometr





R

R

R

R

R

R

R

x

p

x

p

x

















0

2

0

2

2

2

2



























R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

p

x

p

x

p

x

p

x

x

p

x

x

p

x

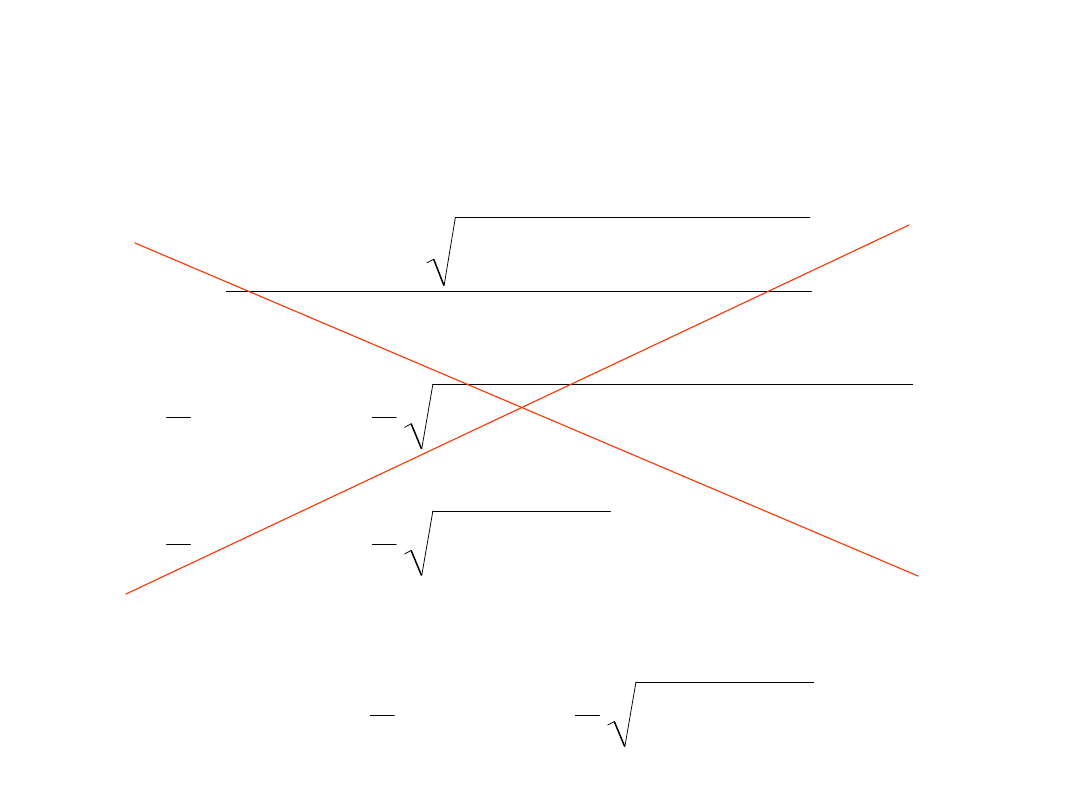
Potencjometr





p

p

p

p

p

p

p

p

p

p

x

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R

R





































2

2

2

2

2

4

2

1

2

1

4

4

4

2

1

2

1

2

4

2

2

2

2

4

2

1

2

1

R

R

R

R

R

p

p

x









Prawa Kirchhoffa

I prawo Kirchhoffa – prądowe prawo
Kirchhoffa

PPK

II prawo Kirchhoffa – napięciowe prawo
Kirchhoffa

NPK

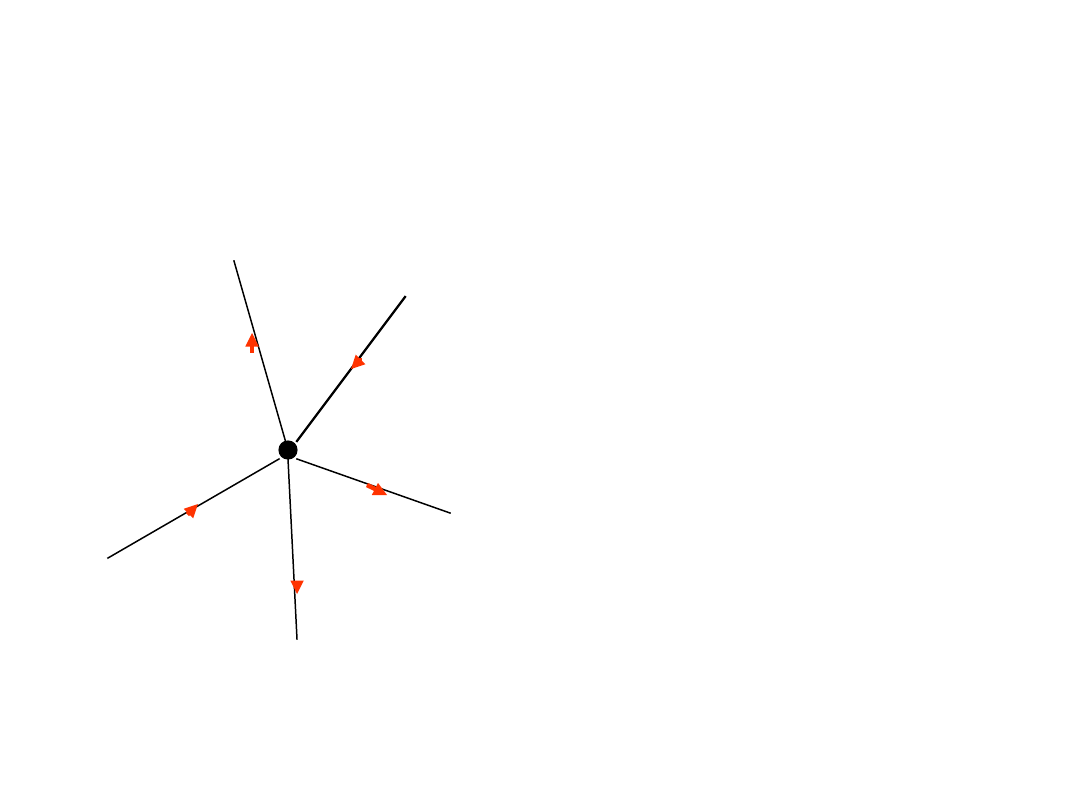
Prądowe prawo Kirchhoffa

W węźle obwodu
elektrycznego
ładunek ani nie może
być wytworzony, ani
nie może ulec
zniszczeniu, ani nie
może gromadzić się.

i

5

i

4

i

3

i

2

i

1

5

4

2

3

1

i

i

i

i

i









Prądowe prawo Kirchhoffa

Suma prądów dopływających do węzła równa się
sumie prądów od niego odpływających.

0

5

4

2

3

1











i

i

i

i

i

Suma algebraiczna prądów w węźle
równa się zeru.

0





k

k

i

Prądy dopływające do węzła - znak

„-”

Prądy odpływające od węzła – znak

„+”

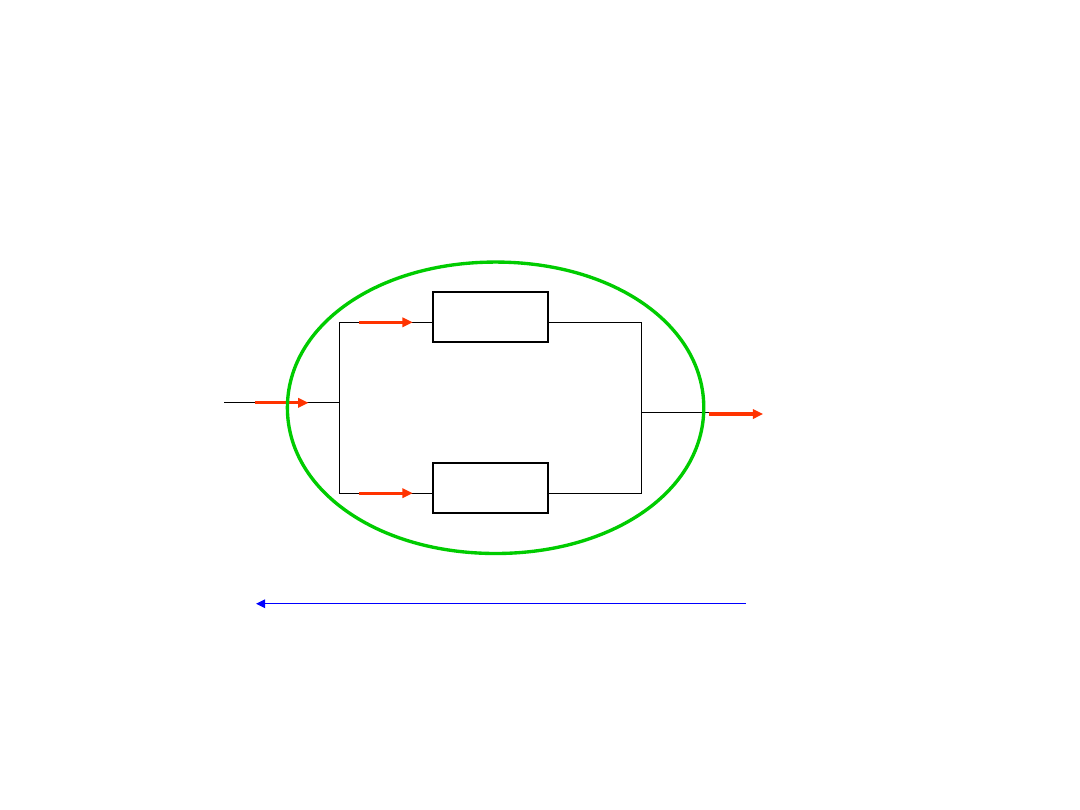
Uogólnione prądowe prawo

Kirchhoffa

i

i

2

i

1

u

i

S

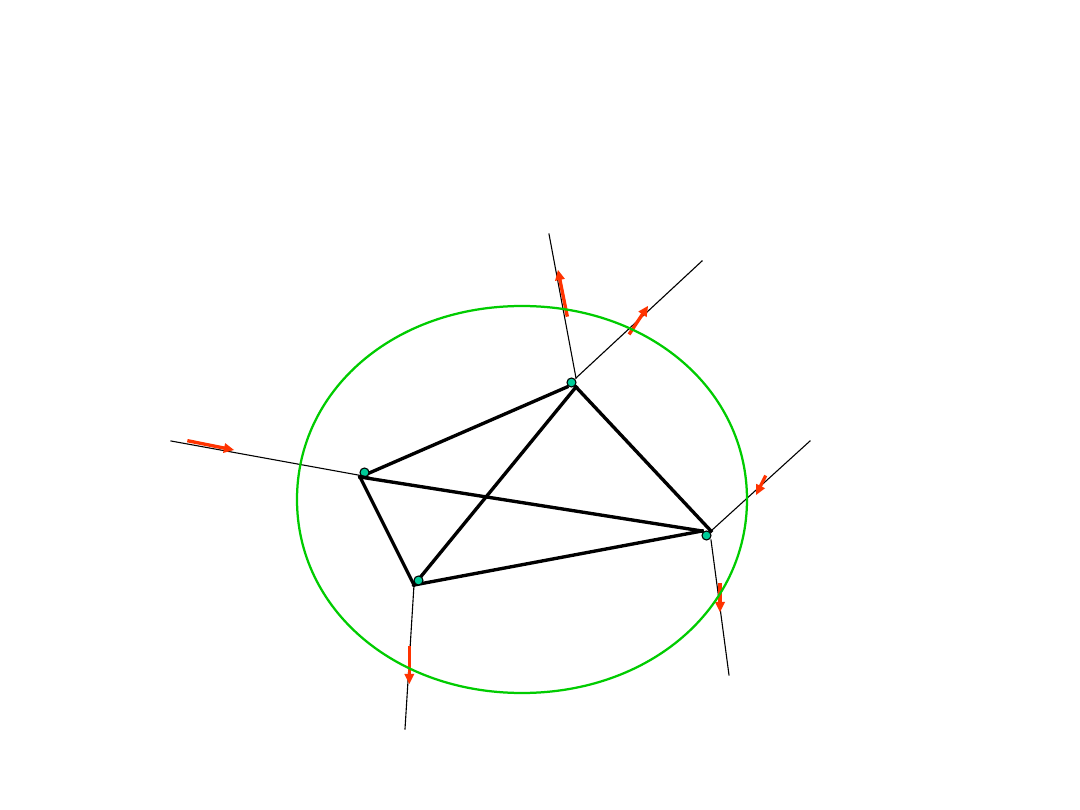
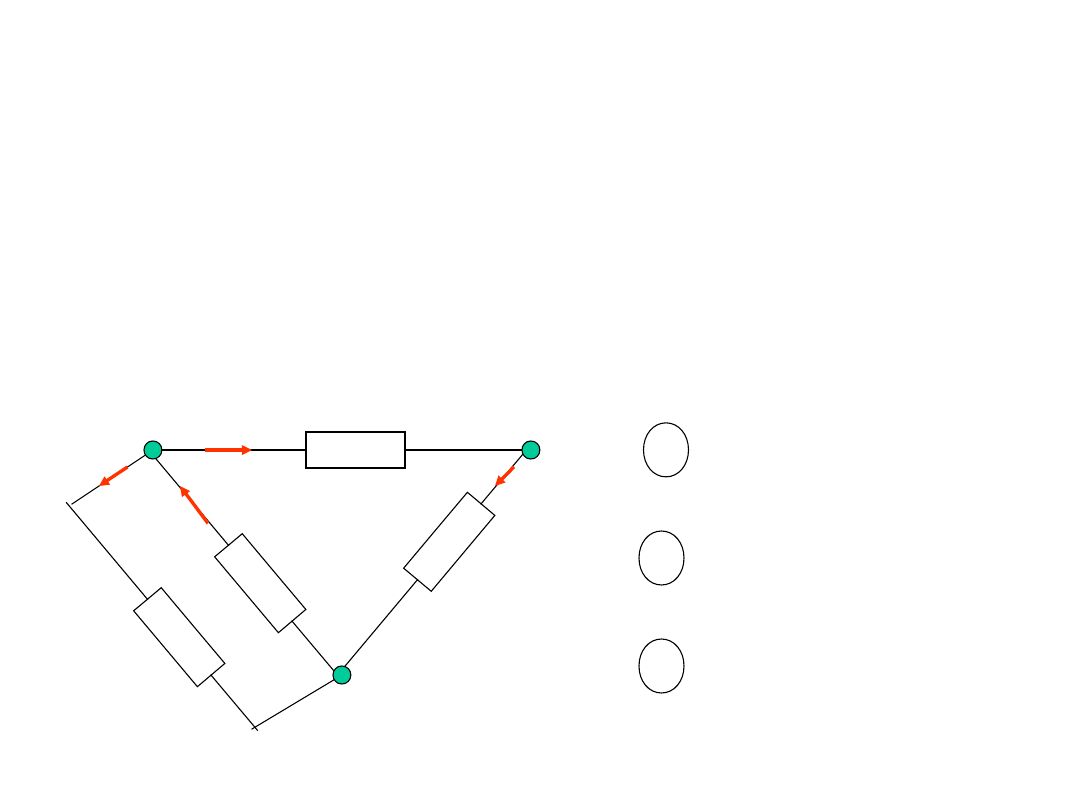
Uogólnione prądowe prawo

Kirchhoffa

i

1

i

2

i

3

i

4

i

5

i

6

S

Uogólnione prądowe prawo

Kirchhoffa

Suma algebraiczna prądów
dopływających do części obwodu
ograniczonej powierzchnią zamkniętą
równa się zeru.

Równania niezależne w PPK

Dla każdego węzła w obwodzie elektrycznym
można napisać równanie na podstawie PPK.

1

3

2

i

1

i

2

i

3

i

4

1

0

3

2

1







i

i

i

2

0

4

1







i

i

3

0

4

3

2







i

i

i

Równania niezależne w PPK

Jeżeli obwód ma



węzłów, to można dla

niego napisać



równań.

1

0

3

2

1







i

i

i

2

0

4

1







i

i

3

0

4

3

2







i

i

i

0

0

Równania niezależne w PPK

Równanie otrzymane na podstawie I
prawa Kirchhoffa dla wszystkich



węzłów tworzą układ równań liniowo
zależnych.
Każde równanie jest kombinacją liniową
pozostałych (



-1) równań.

Równania niezależne w PPK

1

2

+

0

0

0

4

3

2

4

3

2

4

1

3

2

1

























i

i

i

i

i

i

i

i

i

i

i

/

 

1



3

1

3

+

0

0

0

4

1

4

1

4

3

2

3

2

1























i

i

i

i

i

i

i

i

i

i

/

 

1



2

Równania niezależne w PPK

2

3

+

0

0

0

3

2

1

3

2

1

4

3

2

4

1

























i

i

i

i

i

i

i

i

i

i

i

/

 

1



1

Obwód zawierający



węzłów ma (



-1)

węzłów niezależnych.

Pozostały węzeł obwodu – węzeł zależny
(bilansujący).

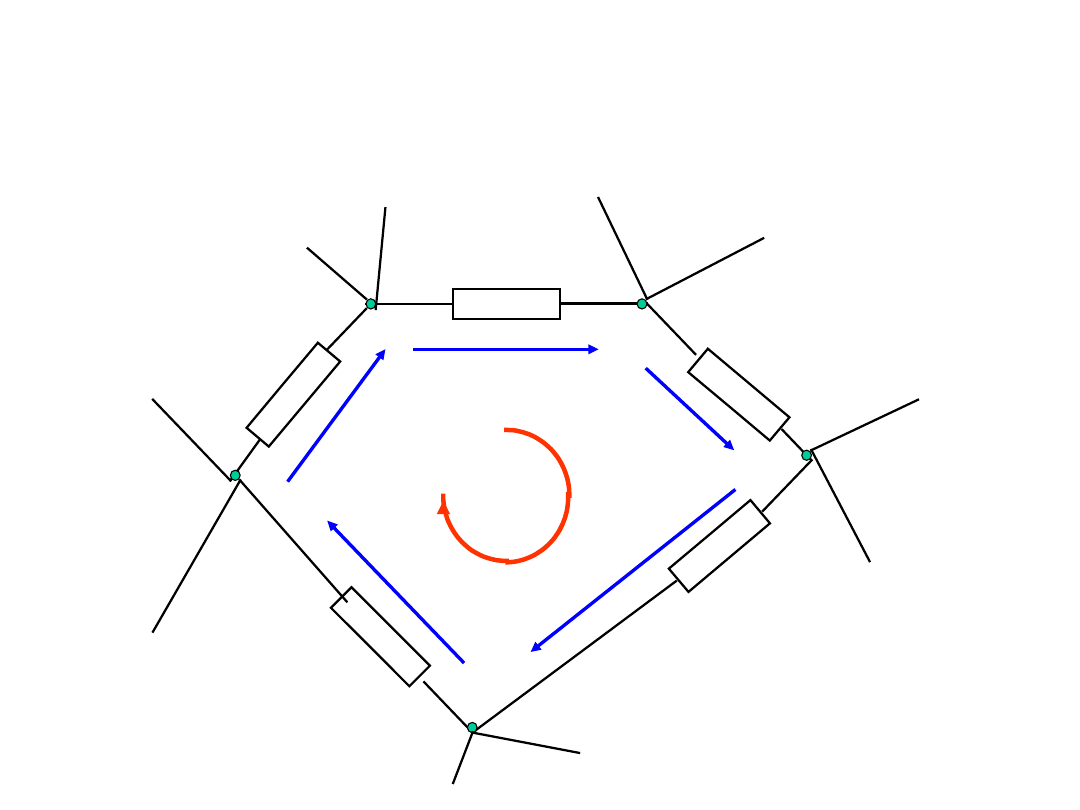
II prawo Kirchhoffa

A

B

C

D

E

u

BA

u

CB

u

DC

u

ED

u

AE

Napięciowe prawo Kirchhoffa

A

B

C

D

E

u

B

A

u

C

B

u

D

C

u

E

D

u

A

E

E

A

AE

D

E

ED

C

D

DC

B

C

CB

A

B

BA

V

V

u

V

V

u

V

V

u

V

V

u

V

V

u





















0











AE

ED

DC

CB

BA

u

u

u

u

u

Napięciowe prawo Kirchhoffa

0











AE

DE

DC

CB

BA

u

u

u

u

u

A

B

C

D

E

u

B

A

u

C

B

u

D

C

u

E

B

u

A

E

u

DE

ED

DE

u

u





Napięciowe prawo Kirchhoffa

(NPK)

Suma algebraiczna napięć wzdłuż
drogi zamkniętej w obwodzie
elektrycznym równa się zeru.





k

k

u

0

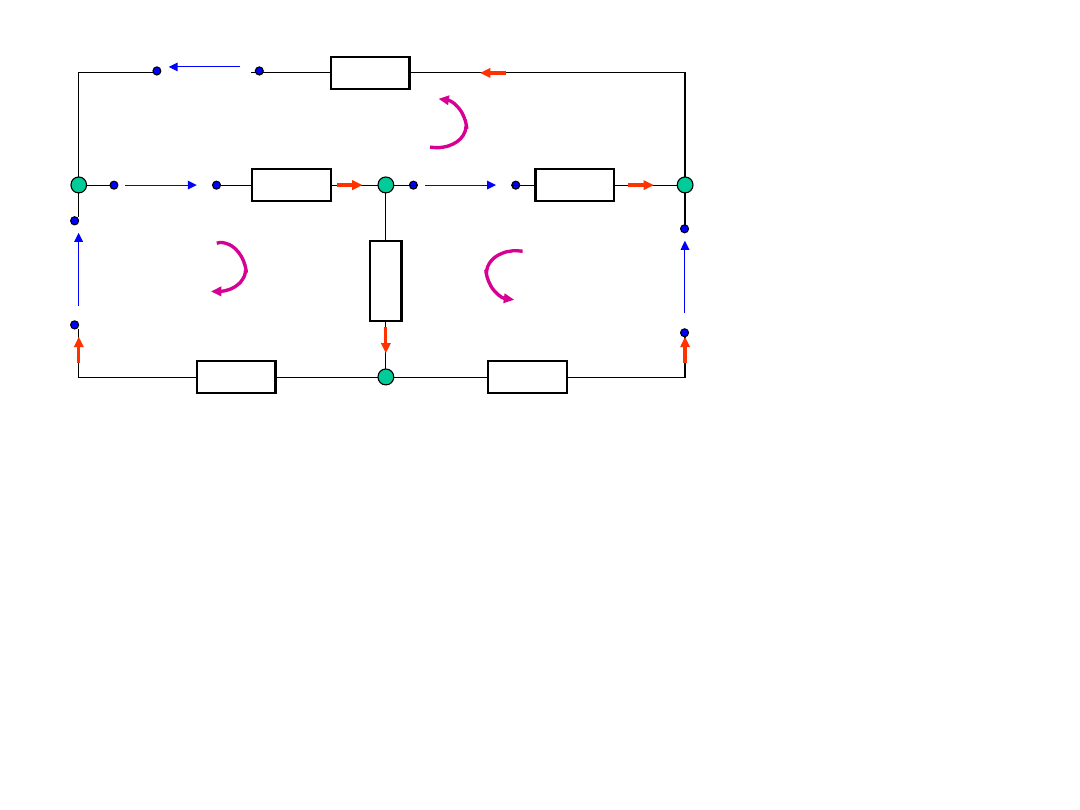
II prawo Kirchhoffa

Metoda postępowania przy układaniu
równań na podstawie II prawa Kirchhoffa:

1. Przyjmujemy (dowolnie) kierunek obiegu

obwodu zamkniętego zgodnie lub
przeciwnie do ruchu wskazówek zegara.

2. Oznaczamy napięcia za pomocą strzałek.
3. Układamy sumę algebraiczną





k

k

u

0

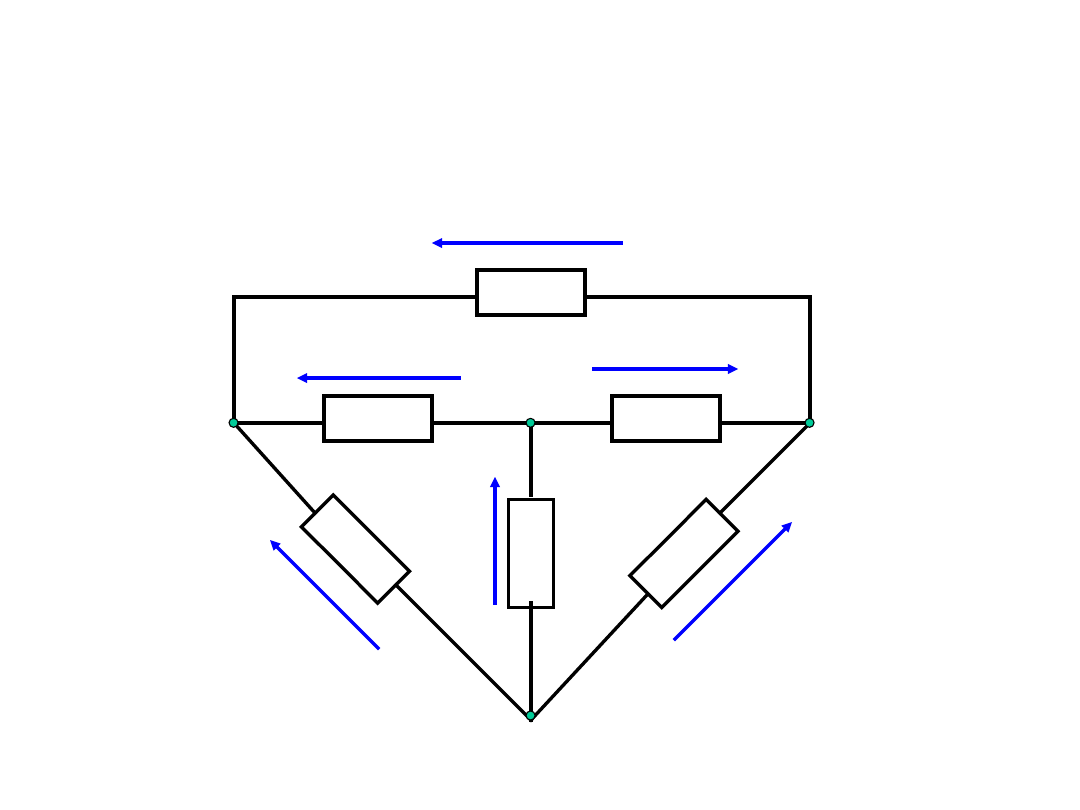
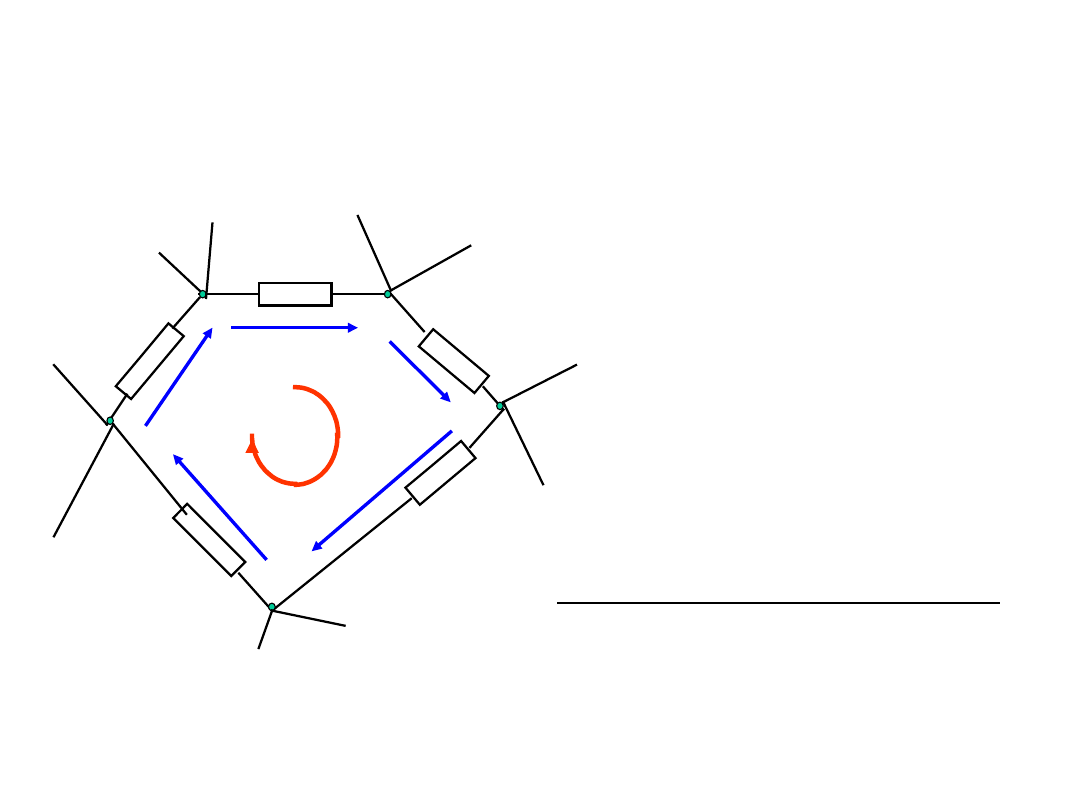
II prawo Kirchhoffa

u

1

u

2

u

3

u

4

u

5

u

6

1

2

3

4

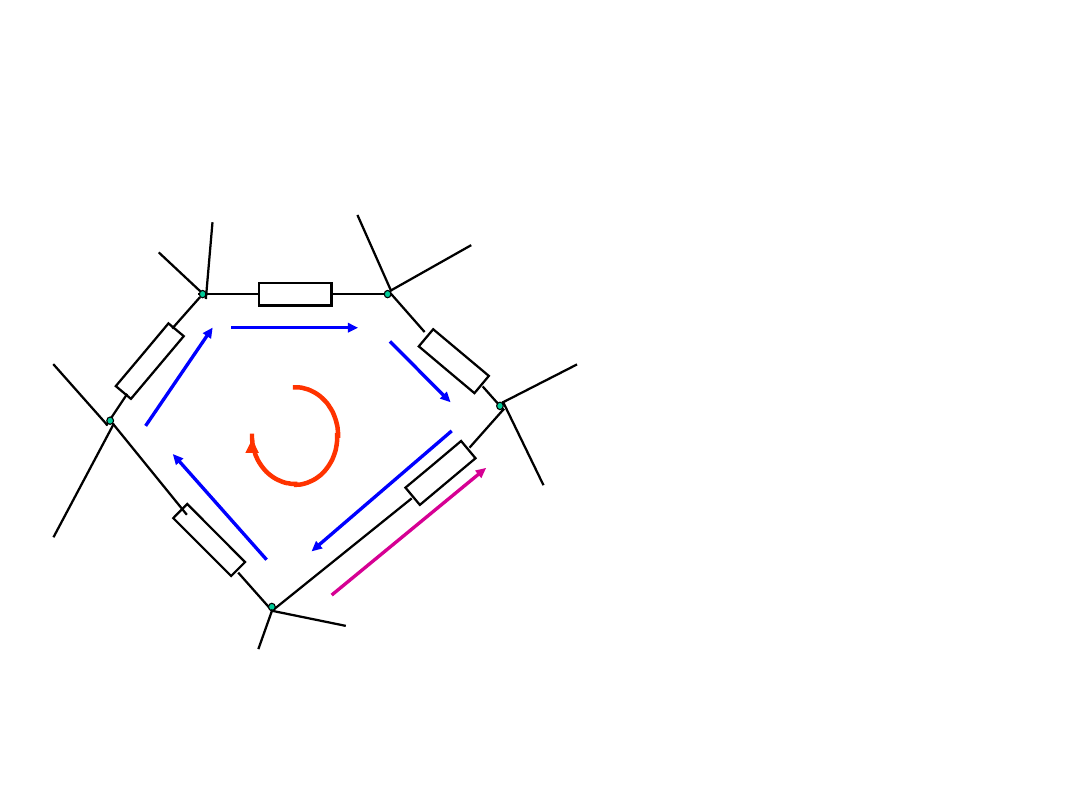
II prawo Kirchhoffa

W układzie złożonym z wielu obwodów

zamkniętych napięciowe prawo Kirchhoffa

formułujemy dla pętli (oczka).

Pętla – zbiór elementów zaczynających się

w jednym węźle, obejmujących kolejne

gałęzie i kończących się w tym samym

węźle, przy czym w każdym węźle pętli

łączą się

dwie i tylko dwie

gałęzie.

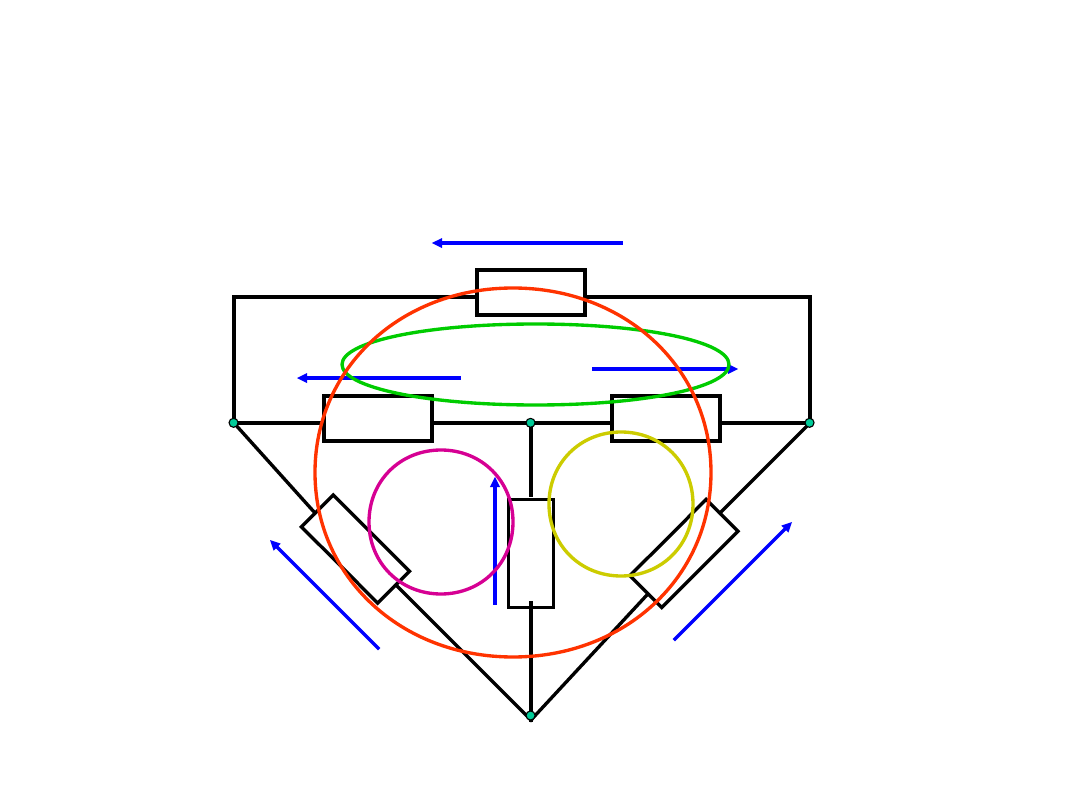
II prawo Kirchhoffa

u

1

u

2

u

3

u

4

u

5

u

6

1

2

3

4

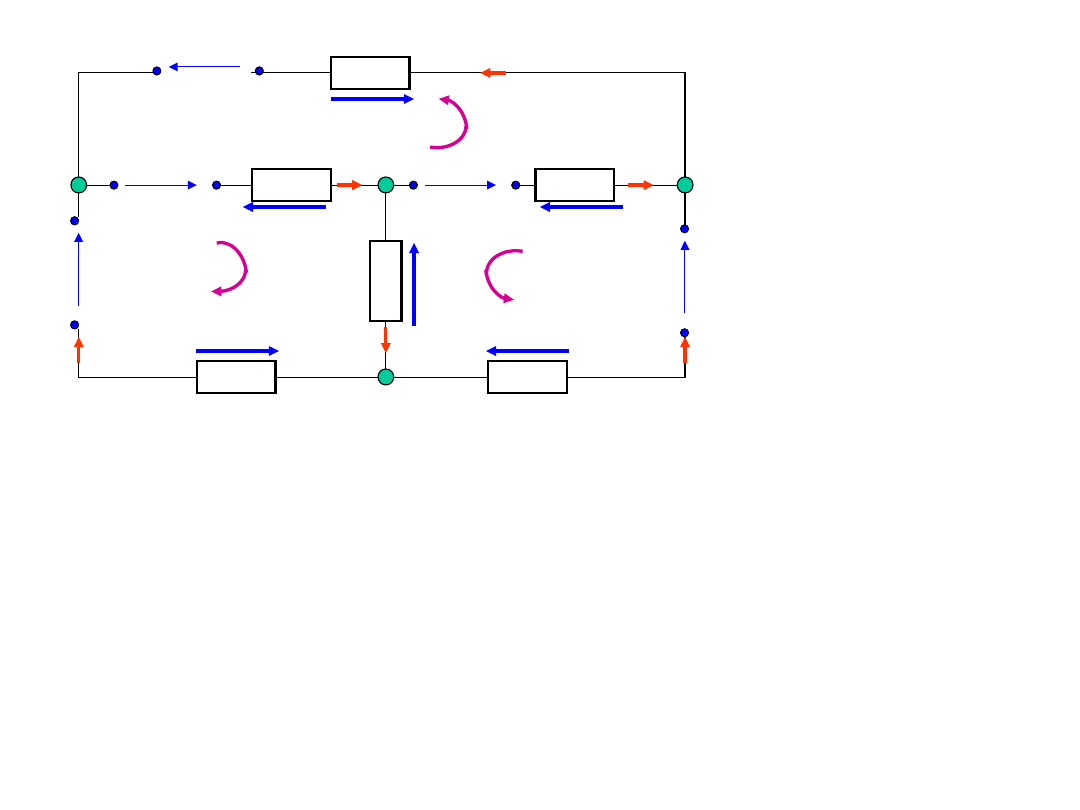
II prawo Kirchhoffa

Dla pętli 1 – 2 – 4 – 1 przy założeniu
obiegu zgodnego z ruchem
wskazówek zegara:

0

1

4

2









u

u

u

Dla pętli 1 – 3 – 4 – 2 - 1 przy
założeniu obiegu przeciwnego do
ruchu wskazówek zegara:

0

2

3

6











u

u

u

u

Obliczanie obwodów

elektrycznych

Wykorzystujemy I i II prawo Kirchhoffa.
Dla obwodu, który ma n gałęzi i



węzłów trzeba wyznaczyć n
niewiadomych prądów gałęziowych.
Układamy n równań:
-



- 1 niezależnych równań wg PPK

- n -



+ 1 równań wg NPK

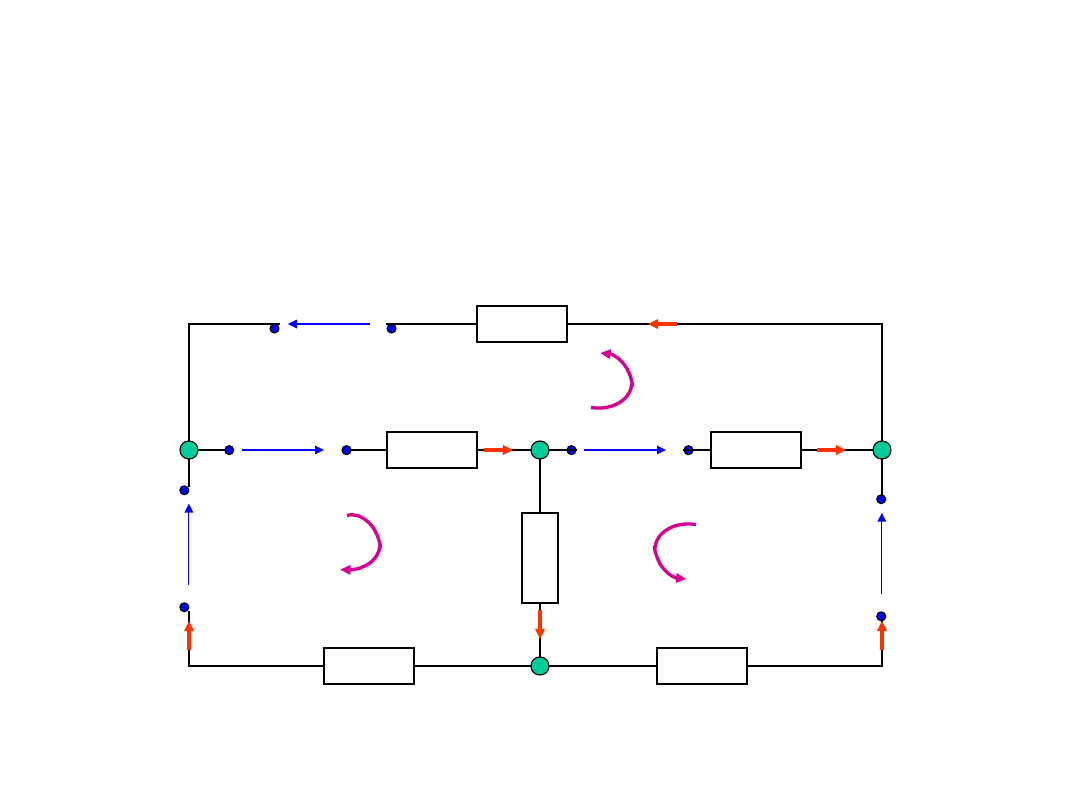
Obliczanie obwodów

elektrycznych - przykład

A

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

1

i

2

i

3

i

4

i

5

i

6

R

6

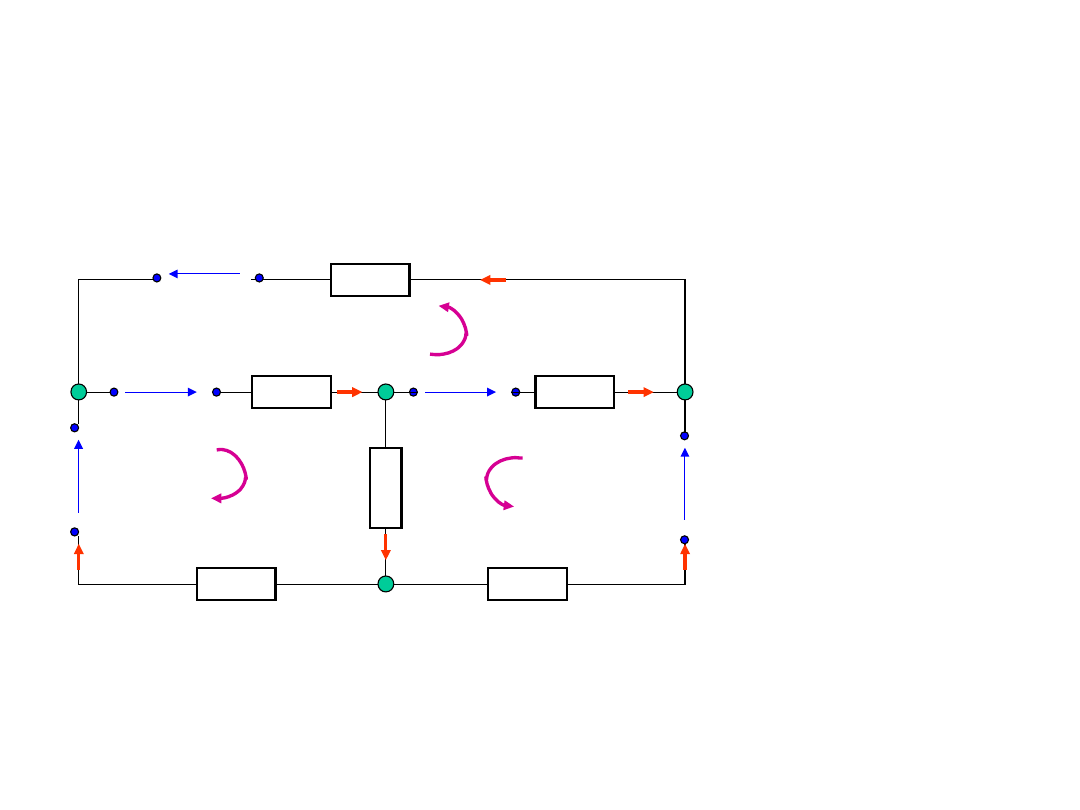
Obliczanie obwodów

elektrycznych - przykład

u

1

= 6V

u

2

= 30V

u

3

= u

4

=

10V

u

5

= 36V

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

R

1

= R

2

= R

3

= R

5

= 2 , R

4

= 4 , R

6

= 10



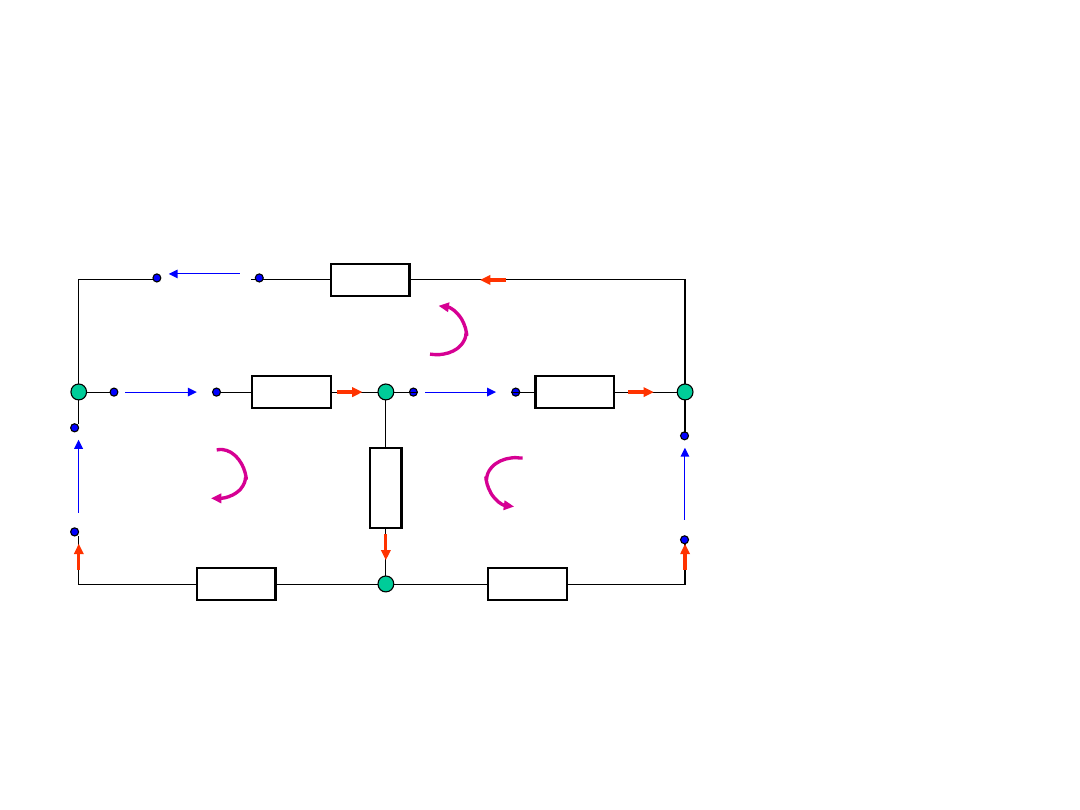
Obliczanie obwodów

elektrycznych - przykład

węzły:
 = 4

gałęzie

n = 6

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

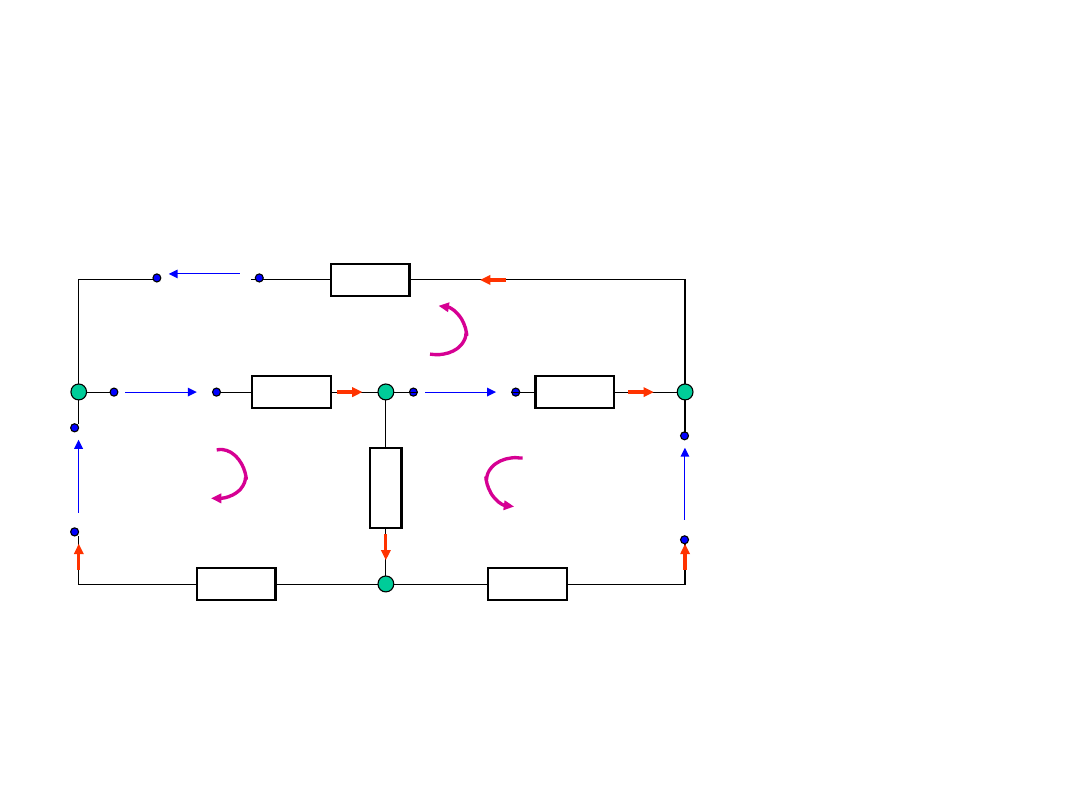
Obliczanie obwodów

elektrycznych - przykład

Liczba
równań wg
PPK:
 - 1 = 4 – 1
= 3

Liczba
równań wg
NPK:

n -  + 1 = 6

– 4 + 1 = 3

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Liczba niewiadomych – 6 (prądy od

i

1

do

i

6

).

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Dla węzła

A

0

3

1

5







i

i

i

Dla węzła

B

0

2

3

4







i

i

i

0

2

1

6







i

i

i

Dla węzła

C

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Dla pętli

ADCA

Dla pętli

BDCB

Dla pętli

ADBA

0

6

6

5

5

5

1

1

1













i

R

i

R

u

u

i

R

0

6

6

4

4

4

2

2

2













i

R

u

i

R

u

i

R

0

4

4

4

5

5

5

3

3

3















i

R

u

i

R

u

u

i

R

0

6

6

5

5

5

1

1

1













i

R

i

R

u

u

i

R

0

6

6

4

4

4

2

2

2













i

R

u

i

R

u

i

R

0

4

4

4

5

5

5

3

3

3















i

R

u

i

R

u

u

i

R

Po podstawieniu wartości:

0

10

2

36

6

2

6

5

1













i

i

i

0

10

10

4

30

2

6

4

2













i

i

i

0

4

10

2

36

10

2

4

5

3















i

i

i

czyli:

0

42

10

2

2

6

5

1











i

i

i

0

20

10

4

2

6

4

2











i

i

i

0

56

4

2

2

4

5

3











i

i

i

podstawiając:

2

1

6

3

1

5

2

3

4

i

i

i

i

i

i

i

i

i













otrzymujemy układ trzech równań z trzema
niewiadomymi:

42

2

10

14

3

2

1







i

i

i

20

4

16

10

3

2

1







i

i

i

56

8

4

2

3

2

1







i

i

i

a po jego rozwiązaniu:

A

i

A

i

A

i

10

5

2

3

2

1









pozostałe prądy:

A

i

i

i

A

i

i

i

A

i

i

i

3

5

2

8

10

2

5

5

10

2

1

6

3

1

5

2

3

4

































