Mechanika płynów

•

1. Hydrostatyka

1. Hydrostatyka

•

2. Hydrodynamika

2. Hydrodynamika

1. Hydrostatyka

•

1.1. Statyka cieczy i gazów

1.1. Statyka cieczy i gazów

•

1.2. Ciśnienie i gęstość

1.2. Ciśnienie i gęstość

•

1.3. Ciśnienie hydrostatyczne

1.3. Ciśnienie hydrostatyczne

•

1.4. Prawo Pascala

1.4. Prawo Pascala

•

1.5. Prawo Archimedesa

1.5. Prawo Archimedesa

1.1. Statyka cieczy i

gazów

•

płyny - ciecze i gazy

płyny - ciecze i gazy

•

gaz - ściśliwy, zajmuje całą objętość

gaz - ściśliwy, zajmuje całą objętość

•

ciecz - nieściśliwa, ma skończone

ciecz - nieściśliwa, ma skończone

wymiary

wymiary

•

naturalny kształt cieczy, bez oddziaływań

naturalny kształt cieczy, bez oddziaływań

zewnętrznych - kula

zewnętrznych - kula

ciecz

1.2. Ciśnienie i gęstość

•

siła przebija płyn, oddziaływanie tylko na

siła przebija płyn, oddziaływanie tylko na

powierzchnię płynu, prostopadle do niej

powierzchnię płynu, prostopadle do niej

•

ciśnienie: gęstość:

ciśnienie: gęstość:

p

F

S







 

m

V

T p

( , )

[p]= 1 Pa (paskal) 1 N/m

2

[



]= 1 kg/m

3

n.p. ciśnienie atmosferyczne - ~10

5

Pa

gęstość wody - 1000 kg/m

3

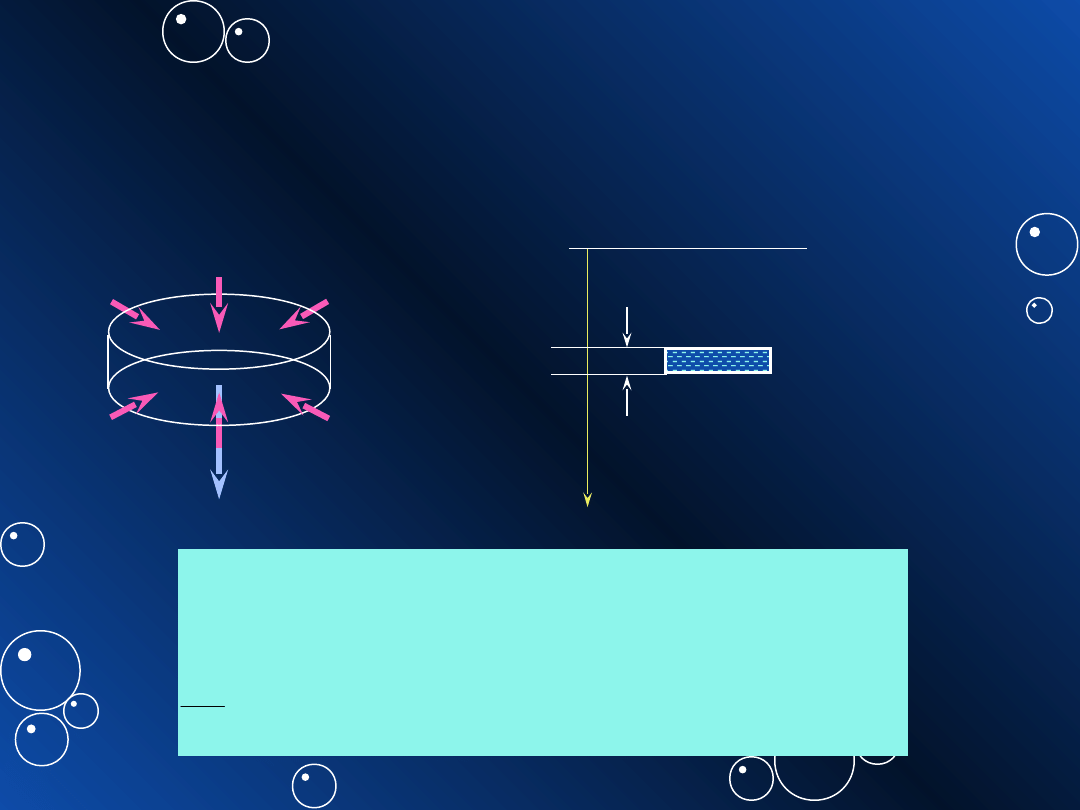
1.3. Ciśnienie

hydrostatyczne

•

element płynu w równowadze:

element płynu w równowadze:

p

p+dp

dG

S

dy

y

y=0

F

dG

p dp S pS

dG

gdV

gSdy Sdp

dp

dy

g

y

gy p

y

 



























0

0

0

(

)

p( )











dla

const.

1.4. Prawo

Pascala

„

„

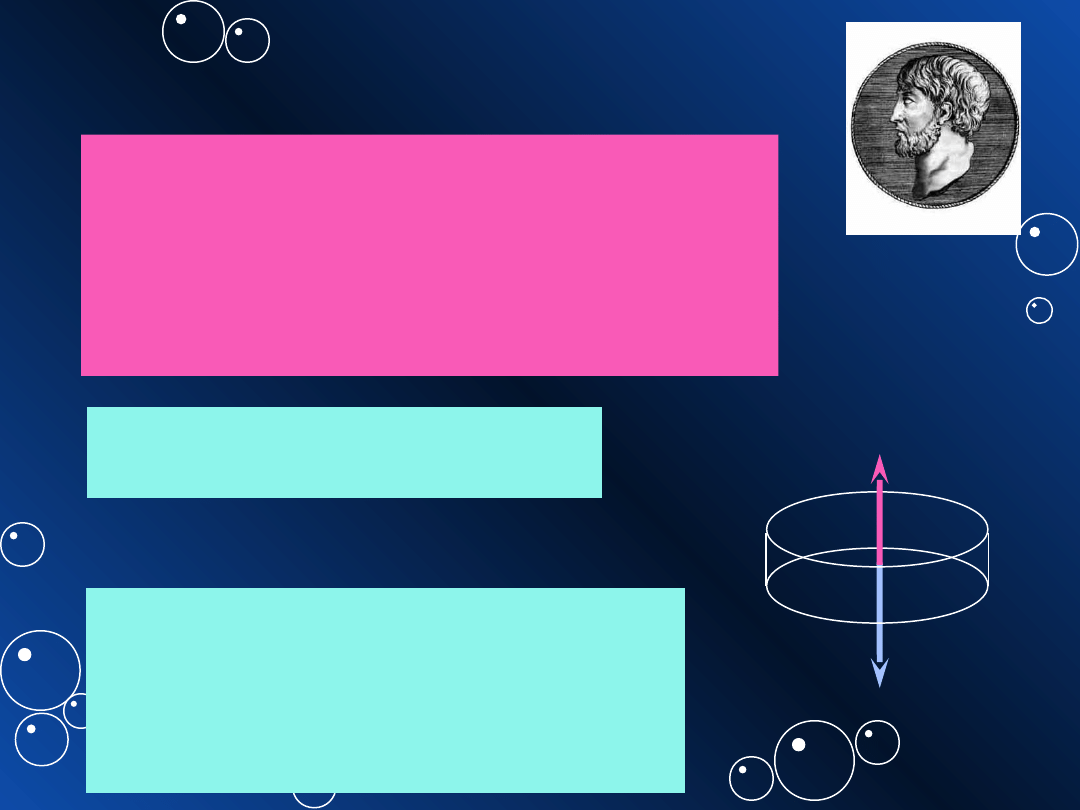
Ciśnienie wywierane na

Ciśnienie wywierane na

płyn w naczyniu jest

płyn w naczyniu jest

przenoszone na dowolny

przenoszone na dowolny

element tego płynu bez

element tego płynu bez

zmiany wartości oraz na

zmiany wartości oraz na

ścianki naczynia” (1653 r.)

ścianki naczynia” (1653 r.)



prasa hydrauliczna, podnośnik
samochodowy:

Blaise Pascal
(1623 - 1662)

1.5. Prawo

Archimedesa

Na ciało zanurzone w cieczy

Na ciało zanurzone w cieczy

działa siła wyporu, skierowana

działa siła wyporu, skierowana

do góry, równa ciężarowi

do góry, równa ciężarowi

cieczy wypartej przez to ciało

cieczy wypartej przez to ciało

F

gV

w

cieczy

cia a





ł

F

w

G

•warunek pływania ciał:

F

G

gV

gV

w

cieczy

cia a

cia a

cia a

cieczy

cia a















ł

ł

ł

ł

287-212
przed
Chrystusem

2. Hydrodynamika

•

2.1. Strumień płynu idealnego

2.1. Strumień płynu idealnego

•

2.2. Linie prądu płynu

2.2. Linie prądu płynu

•

2.3. Równanie ciągłości strumienia

2.3. Równanie ciągłości strumienia

•

2.4. Równanie Bernoullieg

2.4. Równanie Bernoullieg

•

2.6. Płyn rzeczywisty

2.6. Płyn rzeczywisty

2.1. Strumień płynu

idealnego

•

do opisu strumienia płynu są dwa

do opisu strumienia płynu są dwa

możliwe podejścia:

możliwe podejścia:

–

opisać każdy punkt (cząstkę) płynu

opisać każdy punkt (cząstkę) płynu

–

określić parametry “globalne”

określić parametry “globalne”

•

wybieramy drugą możliwość

wybieramy drugą możliwość

  

r

r r t t

 ( , , )

0 0

)

,

(

);

,

(

t

r

V

V

t

r

















•

cztery cechy strumienia płynu idealnego:

cztery cechy strumienia płynu idealnego:

a) stacjonarny

a) stacjonarny

b) bezwirowy (laminarny, brak ruchu

b) bezwirowy (laminarny, brak ruchu

obrotowego)

obrotowego)

c) nieściśliwy

c) nieściśliwy

d) nielepki (brak tarcia wewnętrznego)

d) nielepki (brak tarcia wewnętrznego)

2.1a. Strumień płynu

idealnego

)

(t

v

v







 

 ( , )



r t

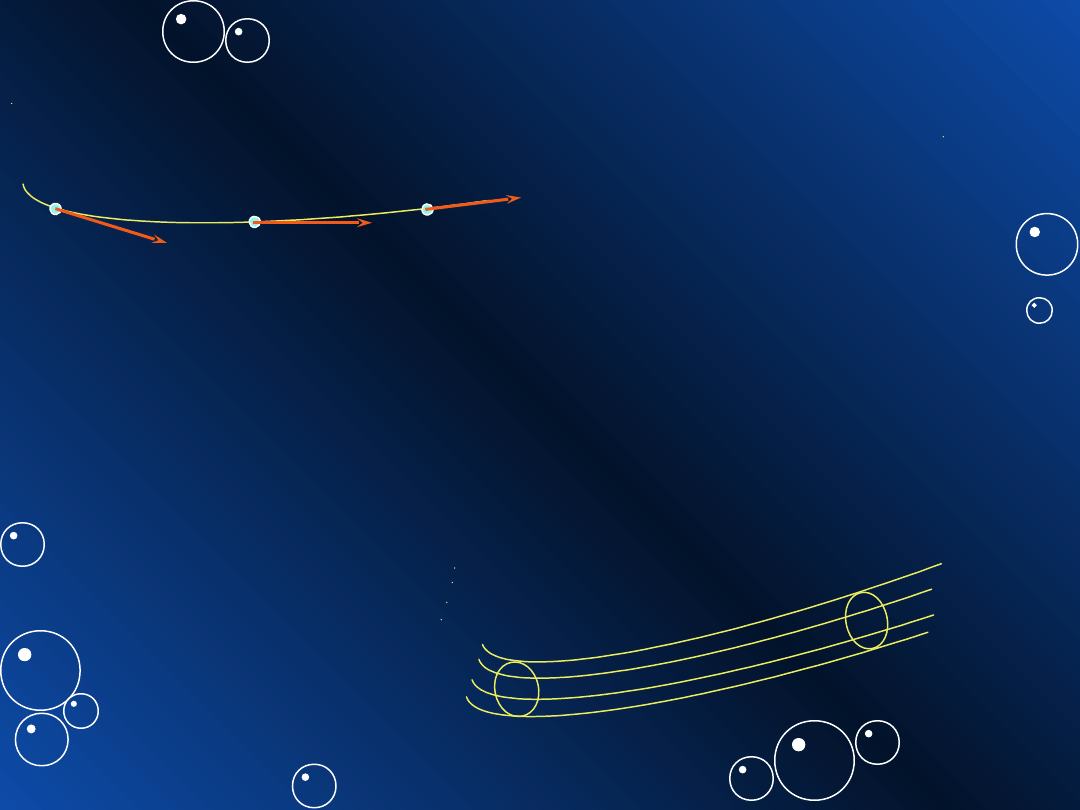
2.2. Linie prądu płynu

idealnego

–

wszystkie cząstki płynu przechodzą po

wszystkie cząstki płynu przechodzą po

jednym torze - linia prądu

jednym torze - linia prądu

–

linie prądu nie przecinają się

linie prądu nie przecinają się

–

przez każdy punkt płynu przechodzi linia

przez każdy punkt płynu przechodzi linia

prądu

prądu

–

rurka prądu (jak przewód):

rurka prądu (jak przewód):

P

Q

R



v



v



v

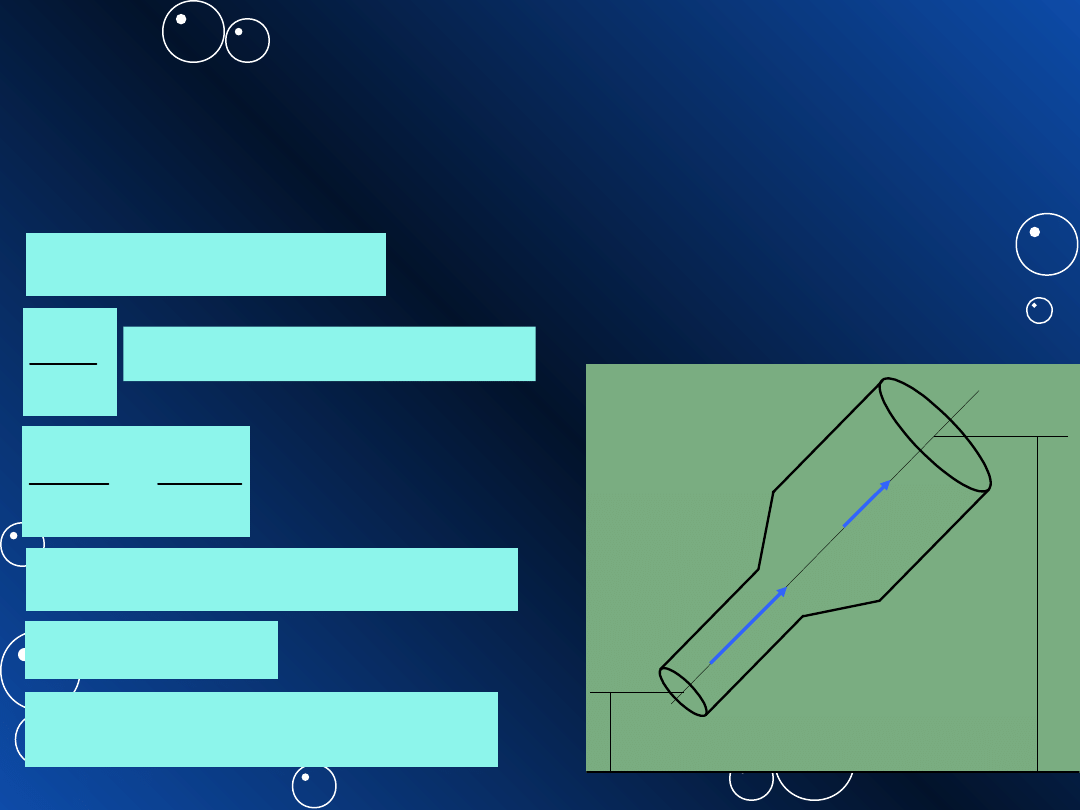
2.3. Równanie ciągłości

strumienia

y

1

y

2

A

1

A

2

v

1

v

2

t

v

A

m







1

1

1

1



t

m





t

m

t

m











2

1

2

2

2

1

1

1

v

A

v

A







const.



Av



2









1

dla

const.

Av

Strumień masy [kg/s]

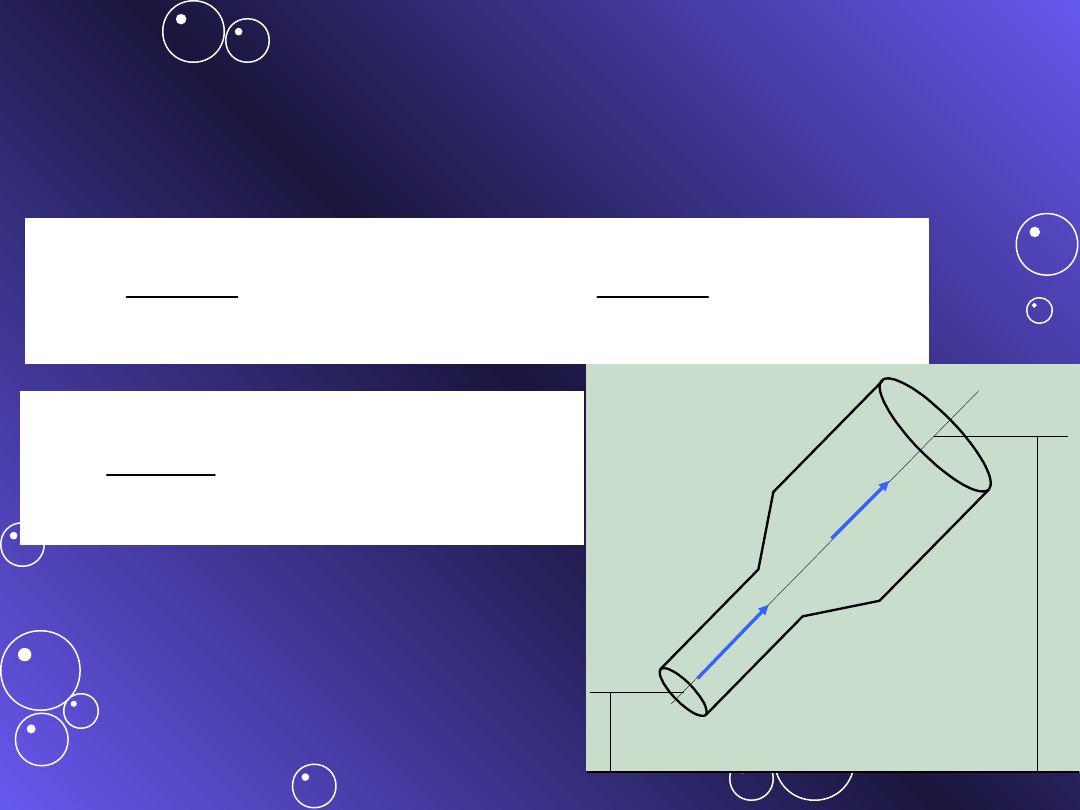
2.4. Równanie

Bernoulliego

v

1

v

2

A

1

A

2

y

1

y

2

2

2

2

2

1

2

1

1

2

2

y

g

v

p

y

g

v

p































.

2

2

const

y

g

v

p

















p

1

p

2

2.6. Płyn rzeczywisty

•

tarcie między warstwami płynu -

tarcie między warstwami płynu -

lepkość - profil prędkości:

lepkość - profil prędkości:

•

prawo Newtona:

prawo Newtona:





- dynamiczny współczynnik lepkości

- dynamiczny współczynnik lepkości





- kinematyczny współczynnik

- kinematyczny współczynnik

lepkości

lepkości

[

[





] = 1Ns/m

] = 1Ns/m

2

2

, [

, [





] =

] =

1

1

m

m

2

2

/

/

s

s

)

(r

v

r

dr

dv

A

F

T











