Praca i energia

Praca i energia



1. Praca stałej siły



2. Praca siły zmiennej



3. Przykład



4. Praca a energia kinetyczna



5. Moc



6. Energia układu



7. Układy zachowawcze i rozpraszające

1. Praca stałej siły

1. Praca stałej siły



wzdłuż ruchu:



pod stałym kątem - iloczyn
skalarny:



jednostka pracy:

[W] = 1J (dżul) = 1Nm

W F s

 

 

W F s



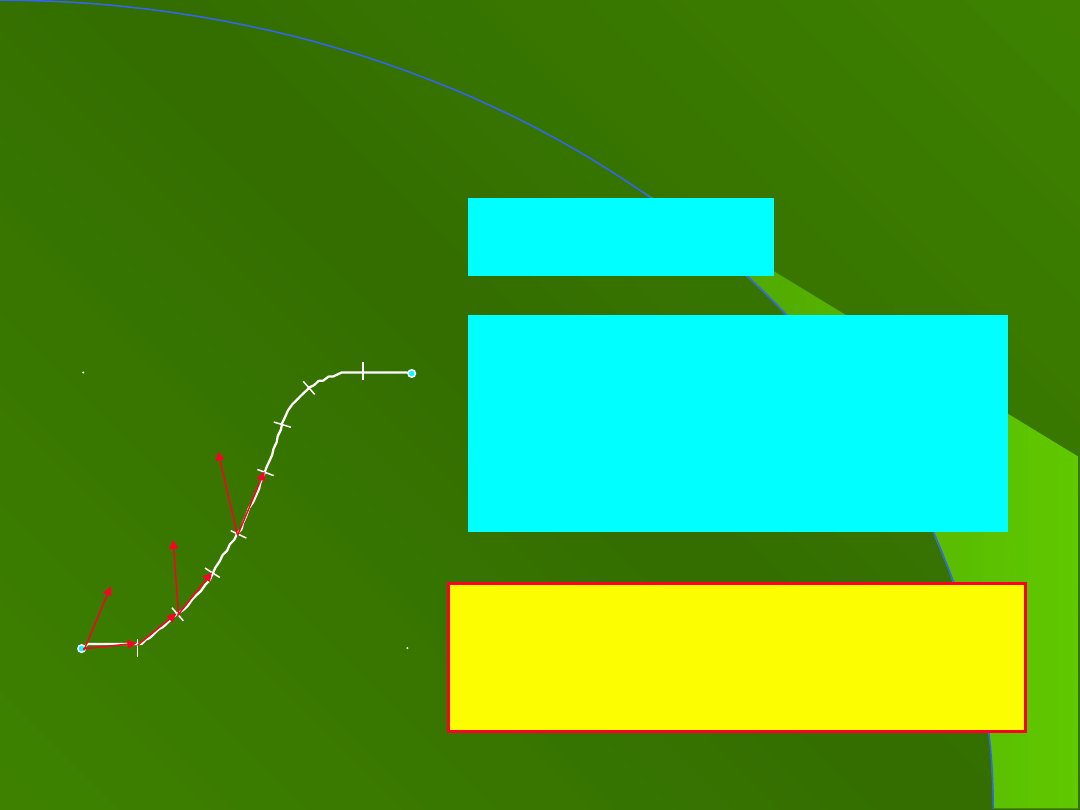
2. Praca siły zmiennej

2. Praca siły zmiennej

A

B



s

1



s

2



s

i

1

F







W

W

F

s

dla t

s

ds

i

i

n

i

i

i

n



















1

1

0















,



F const

W

F ds dW F ds

A

B









 

 

;

=

3

F



i

F



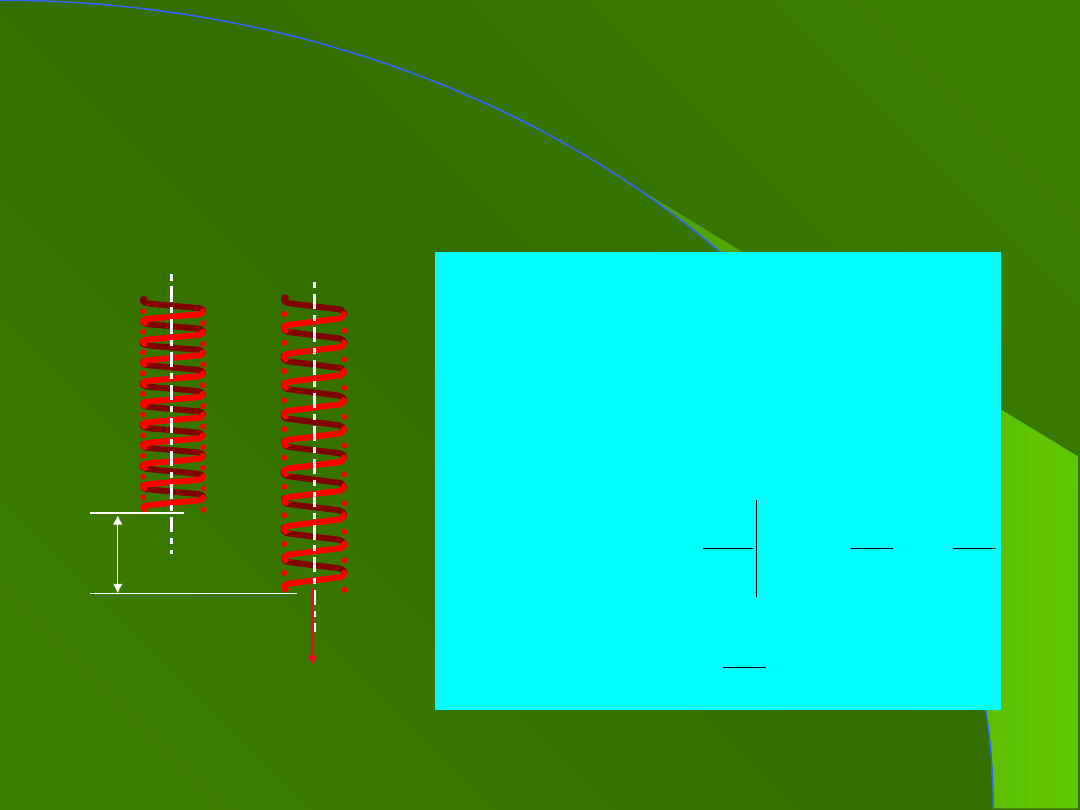
3. Przykład

3. Przykład



odkształcona sprężyna



F

x

2

0

2

2

2

'

'

'

'

'

0

cos

'

)

'

(

'

)

'

(

;

2

0

2

0

2

2

0

0

0

0

0

x

k

W

x

x

k

x

k

x

k

dx

x

k

W

dx

kx

dx

x

F

W

x

d

x

F

W

kx

F

x

x

x

x

x

x

x

x

x

x

































dla





4. Praca a energia

4. Praca a energia

kinetyczna

kinetyczna

v

2

W

F ds

ma ds m

dv

dt

ds m

ds

dt

dv

W m v dv m vdv m

v

m

v

m

v

w

v

v

v

v



 

 

 





 























 









 

1

2

1

2

1

2

1

2

1

2

2

2

2

1

2

1

2

1

2

2

2

2

E

m

v

k



2

2

Energia kinetyczna:



F

w

v

1

1

2

4a. Praca a energia

4a. Praca a energia

kinetyczna, c.d.

kinetyczna, c.d.



Praca siły wypadkowej

działającej na ciało jest równa

zmianie energii kinetycznej

tego ciała

W E

E

E

k

k

k







,

,

2

1



5. Moc

5. Moc



moc średnia i chwilowa:

P

W

t

W W

t t












2

1

2

1

P

dW

dt



[P] = 1W (wat) =

1J/s

P

dW

dt

F ds

dt

F

ds

dt

F v

w

w

w



     



    

6. Energia kinetyczna

6. Energia kinetyczna

układu

układu



układ - zbiór

i

ciał



siły względem układu -
wewnętrzne i zewnętrzne

E

E

E

W W

W

k uk

k i

i

k uk

i

i

wew

zew

,

,

,















F

z1

F

z2

F

w1

F

w2

7. Układy zachowawcze

7. Układy zachowawcze

i rozpraszające

i rozpraszające



siły zachowawcze (np. grawitacyjne,
elektrostatyczne) i rozpraszające
lub niezachowawcze (np. tarcie)



praca sił niezachowawczych =
strata energii mechanicznej

y

zachowawcz

jest

układ

to

albo

jeśli

:

0

:

:

2

,

1

,





ABA

AB

AB

W

W

W

1

2

A

B

Energia c.d.

Energia c.d.



8. Energia potencjalna



9. Przykłady



10. Zasada zachowania energii

mechanicznej



11. Zachowanie energii w
układach niezachowawczych

8. Energia potencjalna

8. Energia potencjalna



energia związana z zachowawczymi
siłami wewnętrznymi układu



E

W

F

ds E

E

p

wew zach

wew

p B

p A

A

B





 





,

,

,





jeśli:

:

,

,

E

to E

F

ds

p A

p B

wew

A

B









0





9. Przykład 1.

9. Przykład 1.



potencjalna energia grawitacyjna (blisko Ziemi)



G

dz

z

O

h

E h

F

z dz

F

z dz

F

dz

F

dz

E h

mgdz mg dz mgz

mgh

p

wew

h

wew

h

wew

wew

p

h

h

h

( )

( )

( )

cos(

, )

cos(

, )

( )



 



































0

0

0

0

0

1

10. Zasada Zachowania

10. Zasada Zachowania

Energii (mechanicznej)

Energii (mechanicznej)

W układzie zachowawczym, na który nie

działają siły zewnętrzne, lub działające

siły się równoważą, całkowita energia

mechaniczna pozostaje stała









E

W W

W

W

E

E

E

W

k

zew

wew

zew

p

k

p

zew

 











dla F

W

a E

E

E

E E E const

zew

zew

k

p

k

p













 



0

0

0

,







11. Zachowanie energii w

11. Zachowanie energii w

układach

układach

niezachowawczych

niezachowawczych



jeśli niektóre siły są niezachowawcze to
praca tych sił zmienia się w inną formę
energii (np. ciepło)

W W

W

E

W

E W

Q

E

E

Q

E

E

Q

zach

niezach

k

zach

p

niezach

k

p

k

p

















 













;

0