Metody opracowywania

i prezentacji danych

statystycznych

Podstawowe metody prezentacji

danych statystycznych:

- tablice,
- wykresy,
- forma opisowa.

szeregi statystyczne,
wskaźniki struktury,
prezentacja graficzna szeregów

statystycznych:

• histogram,
• diagram,
• krzywa liczebności.

Szeregi statystyczne

 Szereg statystyczny - jest to zbiór wyników

obserwacji uporządkowanych według określonych

cech (kryteriów), których miernikiem są zmienne.

 Szeregiem statystycznym

nazywamy ciąg

liczbowy monotoniczny, ograniczony z góry i z dołu

(tj. taki, którego wyrazy występują tylko w pewnym

przedziale wartości). Składa się zazwyczaj z dwóch

kolumn, z których jedna podaje wielkości cechy lub

czas, druga zaś informuje o liczbie jednostek

przypadających na dana kategorię przedmiotów lub

zjawisk lub mówi o ich natężeniu występującym w

danym czasie.

Najczęściej wyróżnia się dwa

kryteria podziału szeregów:

kryterium formalne - związane z

budową szeregu, na podstawie

którego możemy wyodrębnić:

szeregi

szczegółowe

,

szeregi rozdzielcze

i

szeregi skumulowane

, 

kryterium merytoryczne -

wynikające z typu badanej cechy

zbiorowości, według którego wyróżnia

się:

szeregi czasowe

i

szeregi

przestrzenne

.

Szeregi statystyczne

szczegółowe

rozdzielcze z cechą
mierzalną (

ilościową

)

:

- punktowe (proste,
skumulowane),
- przedziałowe
(proste,
skumulowane),

rozdzielcze z cechą
niemierzalną
(jakościową:

- geograficzne
- inne

czasowe

- momentów
- okresów

Szereg szczegółowy
– uporządkowany ciąg wartości badanej cechy

statystycznej, stosowany, gdy przedmiotem
badania jest niewielka liczba jednostek,

np.

zmienna

X

przyjmuje wartości:

x

1

, x

2

, ..., x

n

,

wartości cechy porządkujemy rosnąco:

x

1

 x

2

 ...  x

n

lub malejąco

x

1

 x

2

 ...  x

n

.

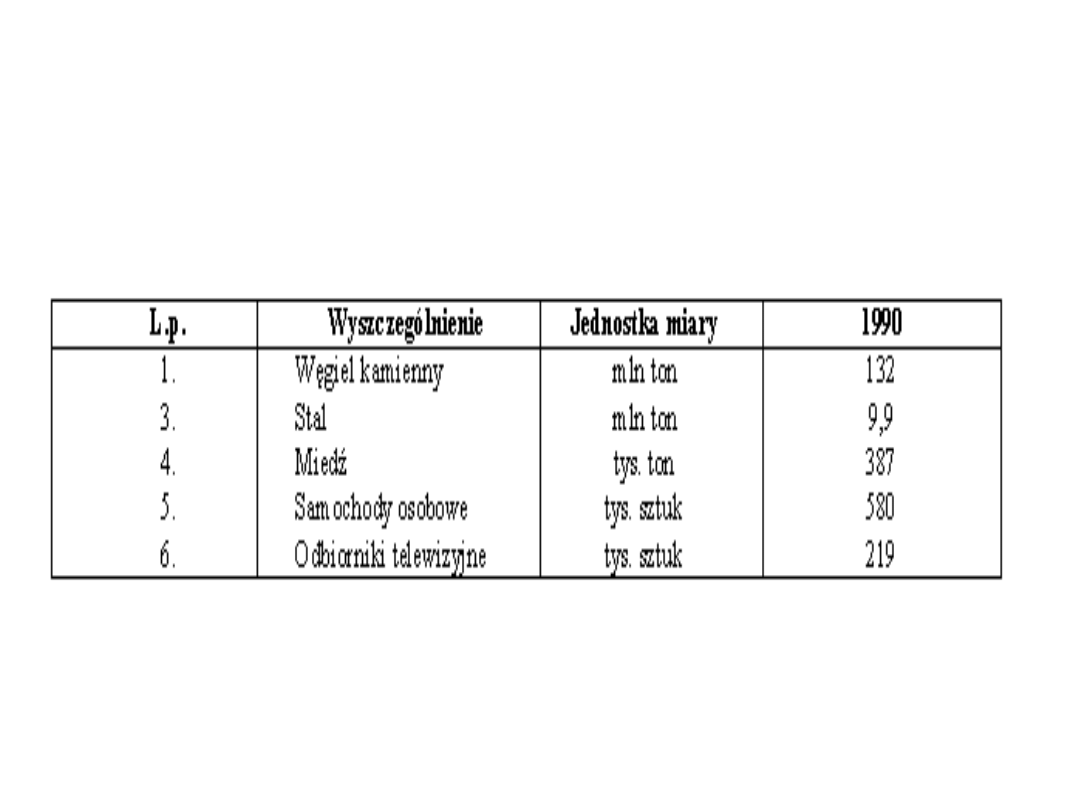
Przykład: „Ważniejsze dane o sytuacji społeczno-

gospodarczej kraju (produkcja wybranych wyrobów)”

 Szereg rozdzielczy - stanowi zbiorowość

statystyczną, podzieloną na części (klasy) według

określonej cechy jakościowej lub ilościowej z

podaniem liczebności lub częstości każdej z

wyodrębnionych klas.

 Szeregi rozdzielcze mogą dotyczyć zarówno

cechy jakościowej, jak i ilościowej. Charakteryzują

one strukturę danej zbiorowości stąd nazywane

są czasem

szeregami strukturalnymi

.

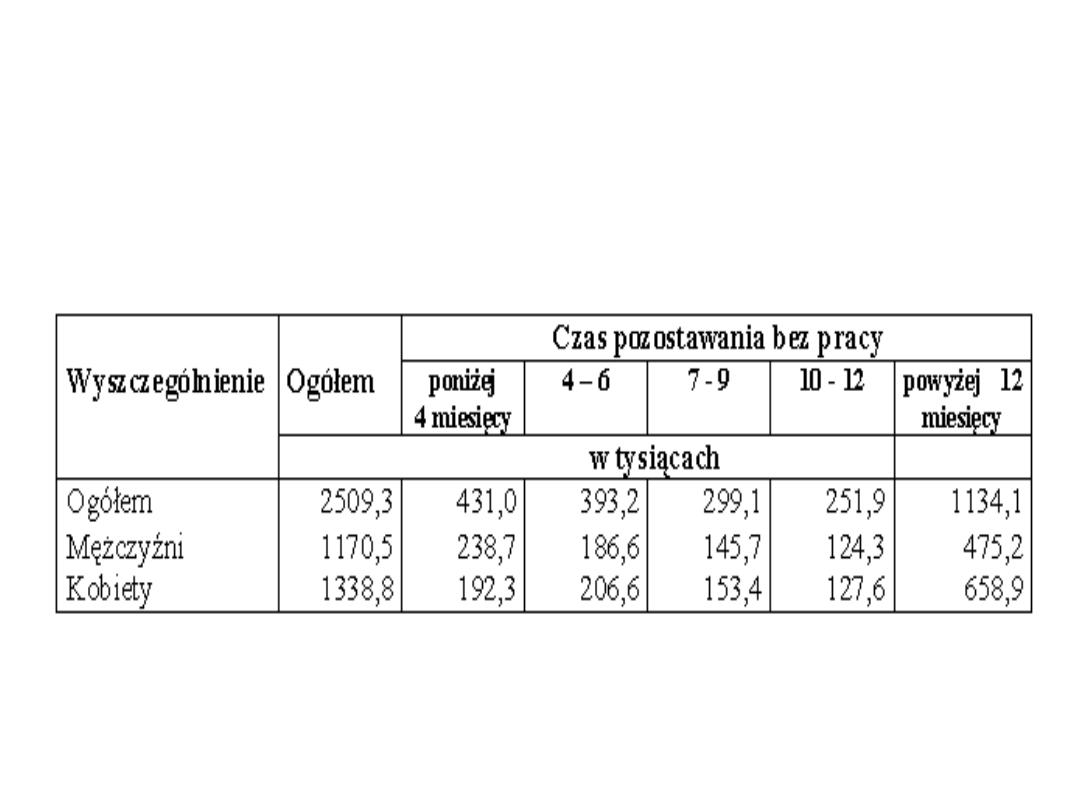
Przykład: Szereg rozdzielczy oparty o cechę mierzalną z

grupowaniem prostym.

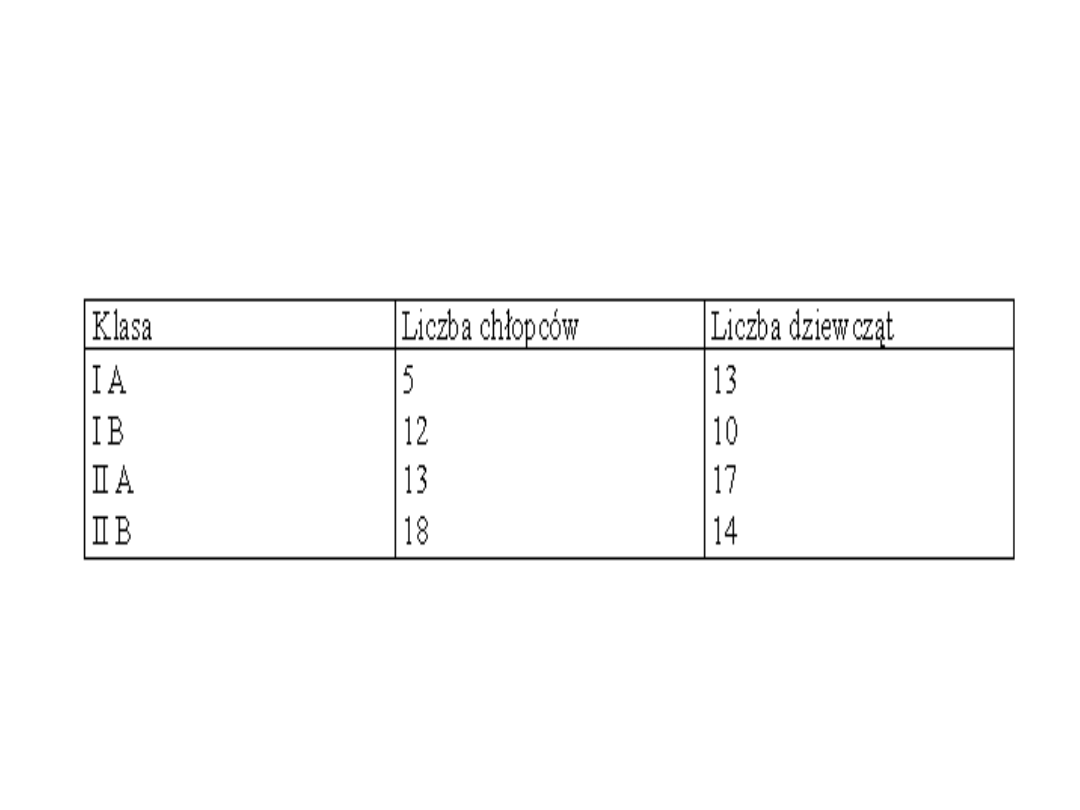
Przykład: Szereg rozdzielczy oparty o cechę mierzalną z

grupowaniem złożonym.

Przykład: Szereg rozdzielczy oparty o cechę niemierzalną z

grupowaniem prostym.

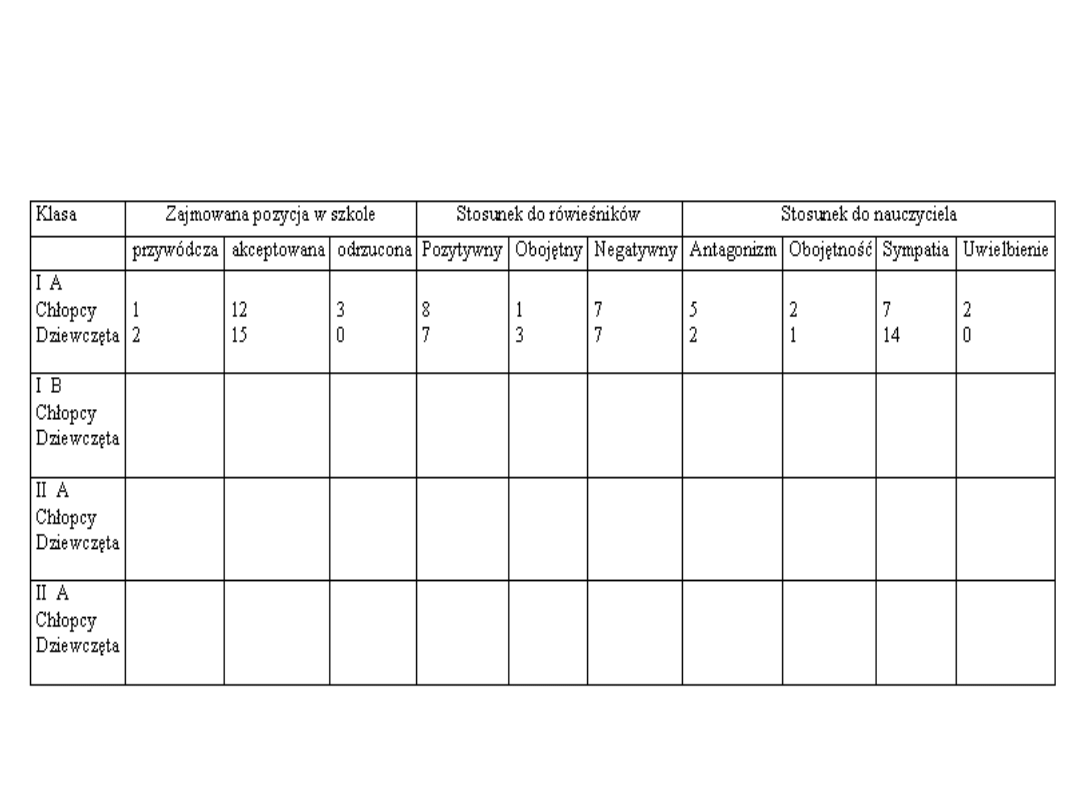
Przykład: Szereg rozdzielczy oparty o cechę niemierzalną z

grupowaniem złożonym

.

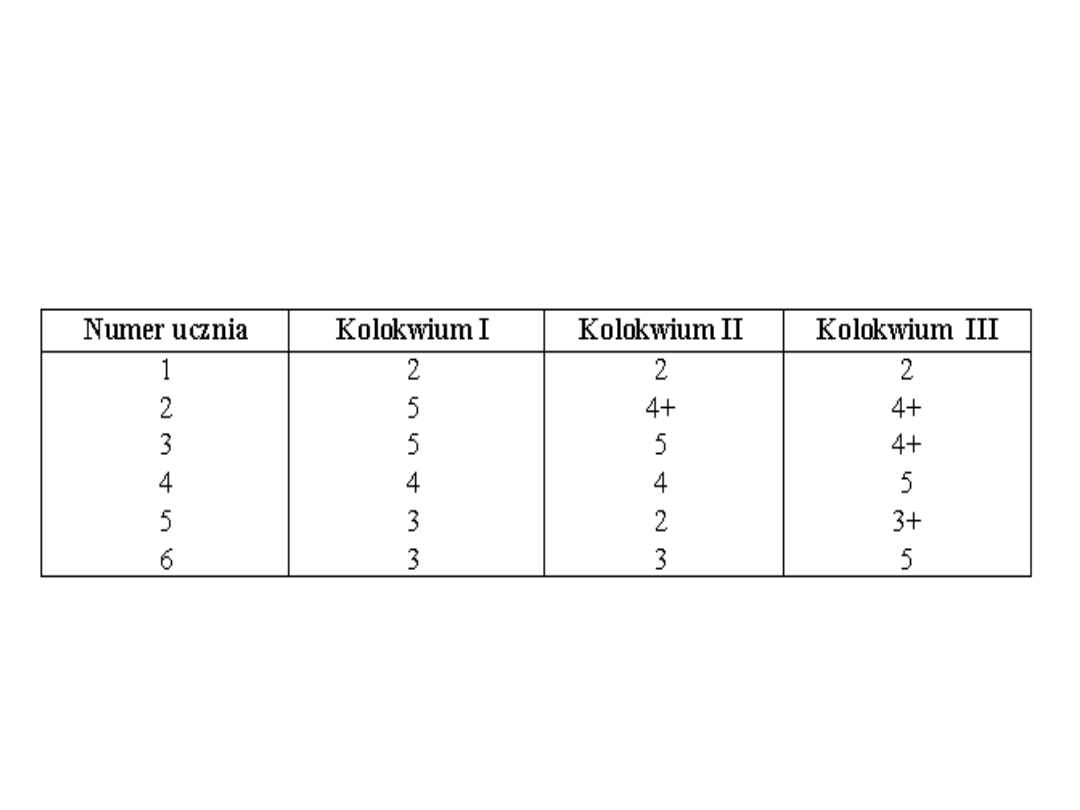
Przykład: Szereg rozdzielczy punktowy: „Wyniki uczniów

klasy III C uzyskane na trzech kolokwiach w semestrze
zimowym”.

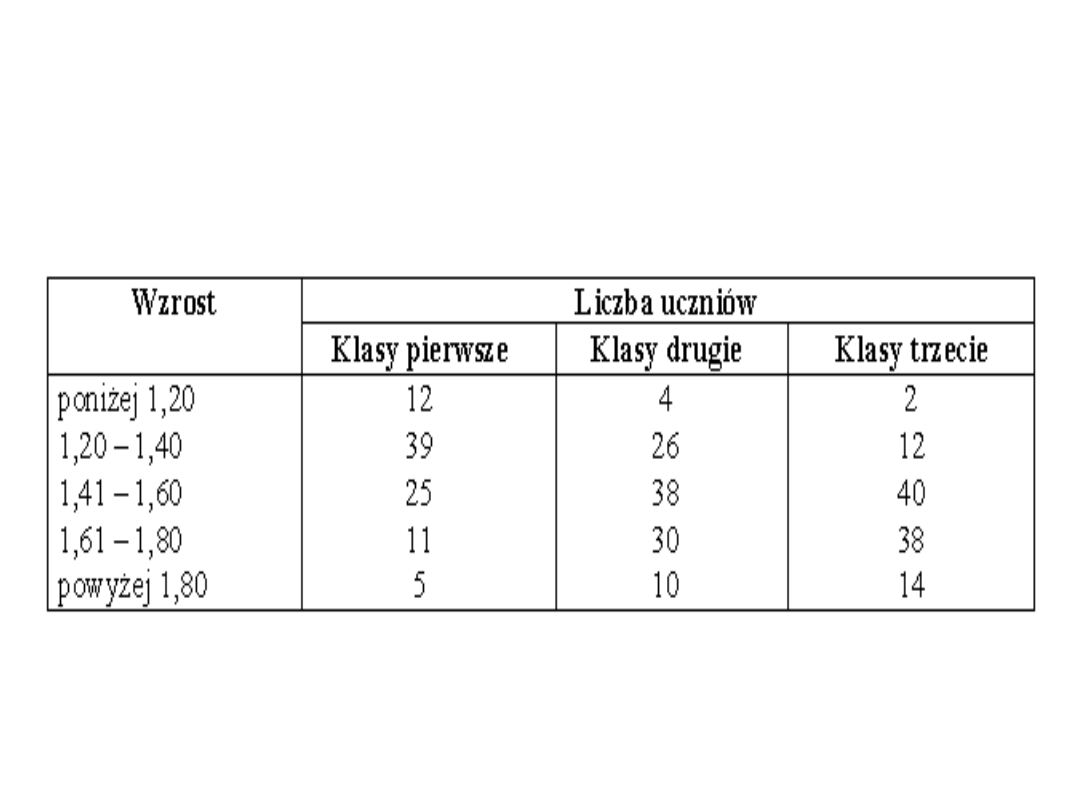
Przykład: Szereg rozdzielczy przedziałowy: „Uczniowie w

szkole według wzrostu”

Przykład: Szereg geograficzny: „Nauczyciele akademiccy

według wykształcenia pracujący w woj. Łódzkim”

Szeregi czasowe.

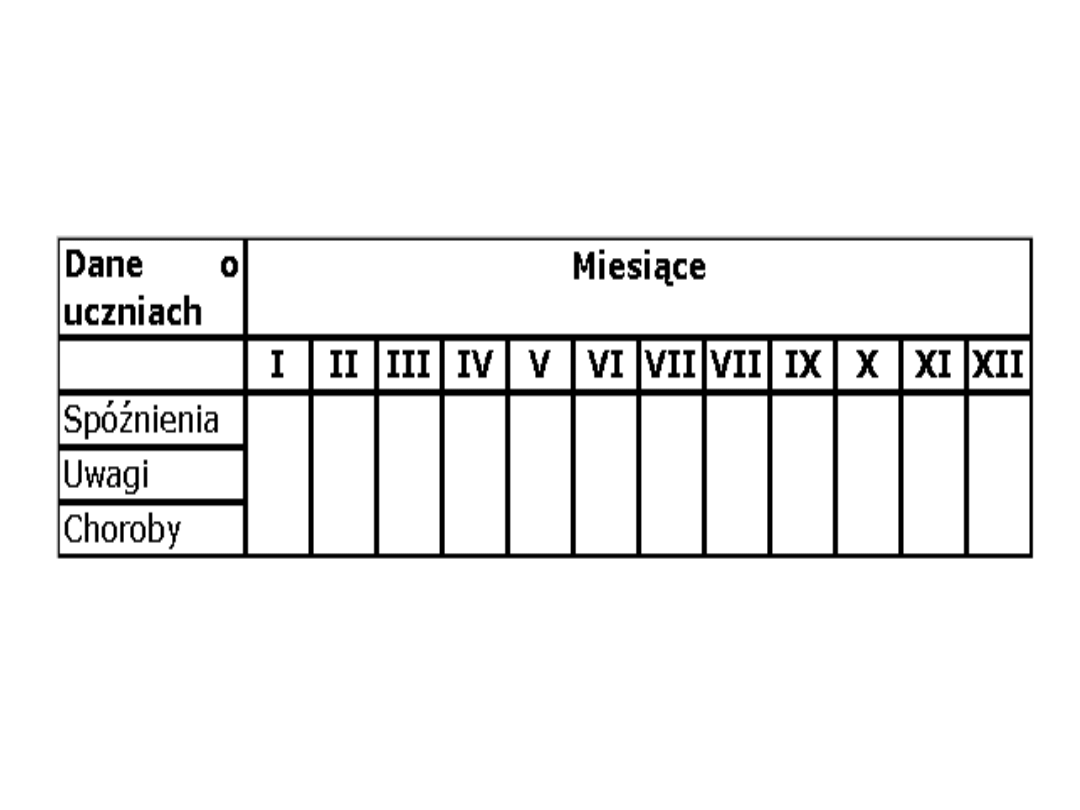
Przykład: Szereg dynamiczny okresów

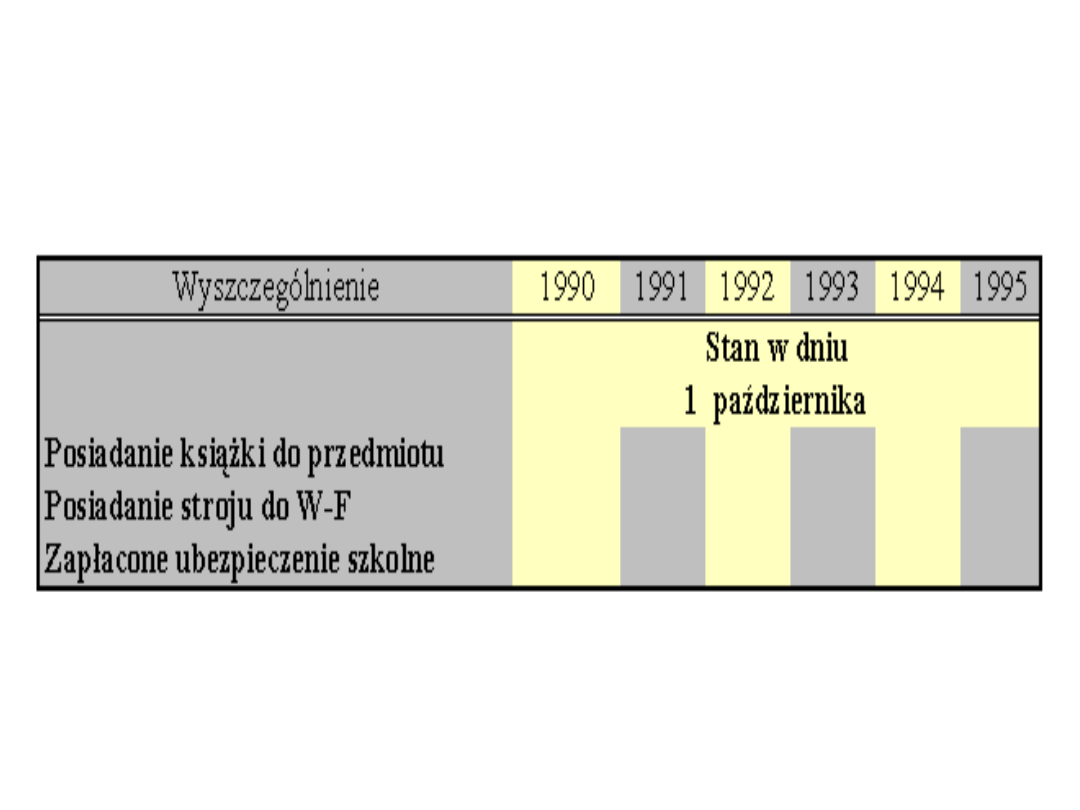
Przykład: Szereg dynamiczny momentów: „Dane o

uczniach w latach 1990 – 1995”

Rozkład empiryczny -

zestawienie

wyników w postaci szeregu
rozdzielczego z cechą mierzalną,
odzwierciedla strukturę badanej
zbiorowości z punku widzenia
określonej cechy statystycznej.

Stosowanie szeregów

statystycznych:

 szereg rozdzielczy z przedziałami klasowymi

- dla cech ciągłych

 szeregi rozdzielcze bez przedziałów klasowych

lub

z przedziałami

klasowymi

- dla cech mierzalnych skokowych - zależnie od

możliwości wartości (wariantów) cech: dla niewielkiej liczby

wariantów: szereg rozdzielczy punktowy, dla dużej szereg

rozdzielczy z przedziałami klasowymi. 

 szereg rozdzielczy z cechą niemierzalną

- szereg geograficzny

(terytorialny) - przedstawia rozmieszczenie pewnych zjawisk w

przestrzeni (np. zestawienie liczby gmin w Polsce).

 szereg czasowy

– (dynamiczny chronologiczny) powstaje w

wyniku grupowania typologicznego i wariacyjnego, gdy podstawą

grupowania jest zmiana badanego zjawiska w czasie:

- szereg czasowy okresów - zawiera informację o rozmiarach

zjawiska w krótszych lub dłuższych okresach.

- szereg czasowy momentów - ujmuje wielkość zjawiska w danym

momencie, najczęściej na początku lub końcu np. miesiąca.

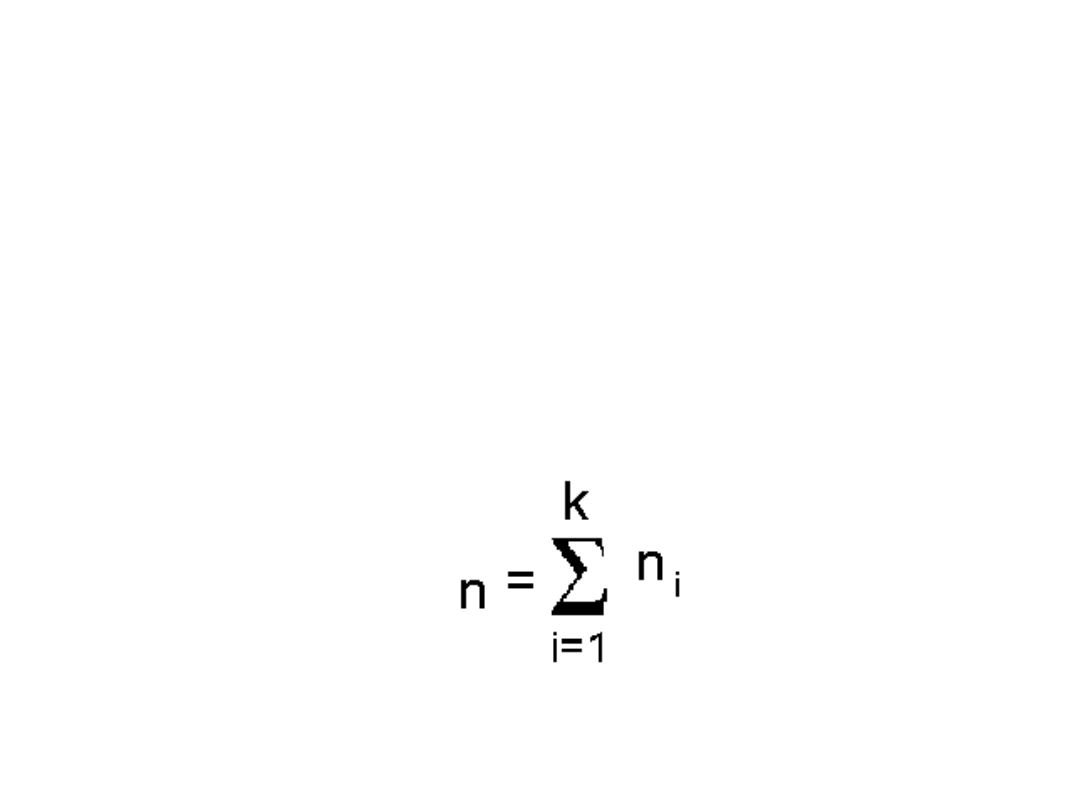
Podstawowe oznaczenia,

podstawowe wielkości

n - liczebność próby (zbiorowości próbnej),
x

i

- wariant cechy statystycznej (i = 1, 2 , ... , n),

n

i

- liczba jednostek o i-tym wariancie cechy,

k - liczba klas (wariantów cechy),

przy czym:

 

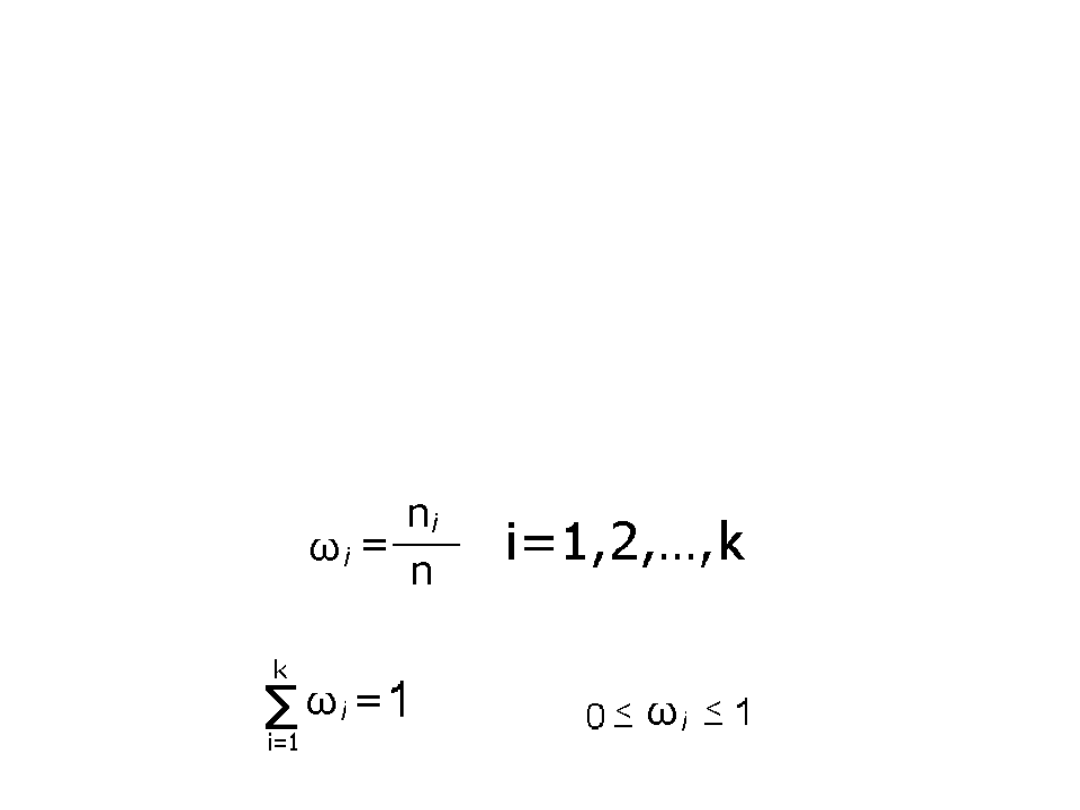
Szereg rozdzielczy

punktowy 

Wskaźnik struktury ω

i

lub częstość (liczebność

względna, frakcja, odsetek) - występowania
danego wariantu cechy nazywa się stosunek liczby
jednostek o danej wartości cechy do liczebności
próby.

przy czym:

Szereg rozdzielczy skumulowany

-

uzyskuje się poprzez

przyporządkowanie kolejnym wariantom
cechy odpowiadających im liczebności
(częstości) skumulowanych, informuje,
dla ilu jednostek badanej zbiorowości
cecha przyjmuje wartości nie większe od
górnej granicy poszczególnego
przedziału klasowego.

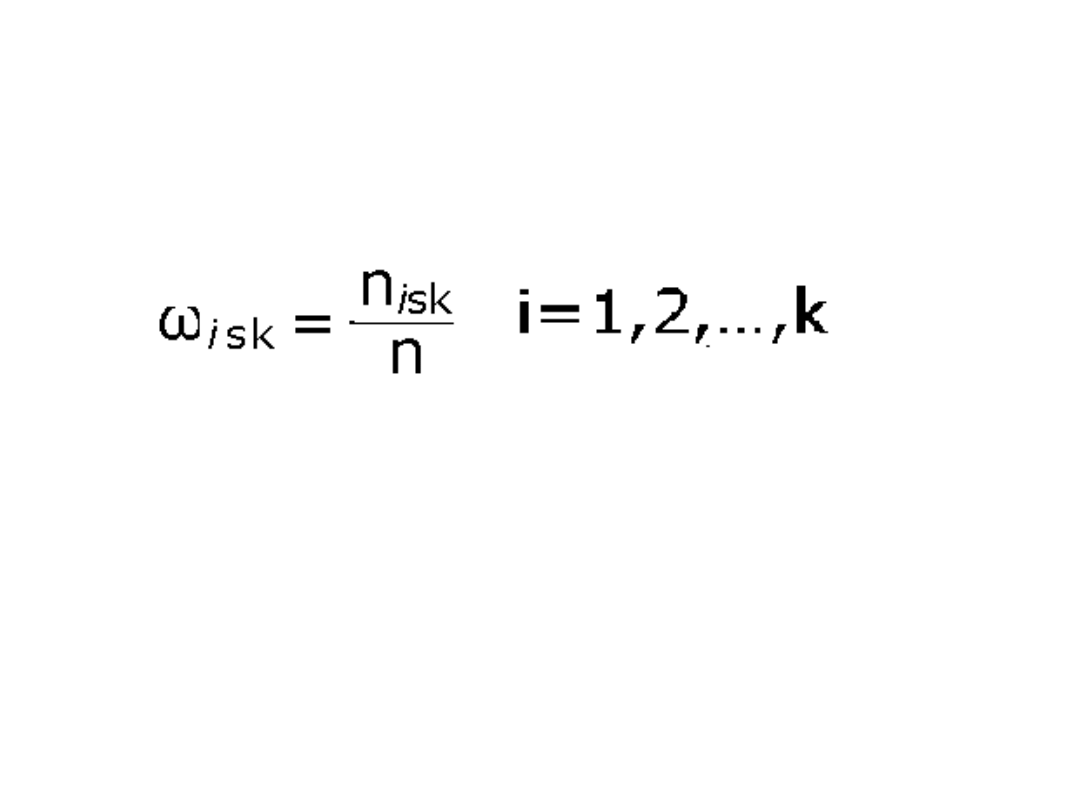
Skumulowany wskaźnik struktury

ω

isk

(częstość skumulowana)

:

gdzie n

isk

oznacza liczbę jednostek, których cechy

odpowiadają wartościom nie większym niż x

i

.

Dystrybuanta empiryczna

- przyporządkowanie kolejnym

wartościom cechy statystycznej
(zmiennej) odpowiadających im
częstości skumulowanych (względnie
liczebności skumulowanych).

Przykład 1

W wybranej grupie studentów

przeprowadzono kolokwium z
matematyki. Studenci otrzymali
następujące oceny:

2, 5, 3, 4, 3+, 4, 3, 4+, 3+ , 3+, 5,

4, 3+, 4+, 3+, 3+, 3, 2, 3, 3+, 3,
4, 5, 3+, 4, 3+, 4, 3, 4+, 4+, 3+.

Przykład 1 cd

Opracowanie materiału statystycznego
Zbiorowość (populacja) generalna: studenci
Zbiorowość próbna (próba): wybrana grupa

studentów

Cecha statystyczna: ocena z kolokwium z

matematyki

Studenci badani są pod względem ocen

otrzymanych z kolokwium z matematyki,

"ocena z matematyki" jest cechą mierzalną

skokową.

Liczebność próby n: 30
Liczba wariantów cechy k: 6
Warianty cechy x

i

: 2, 3, 3,5, 4, 4,5, 5

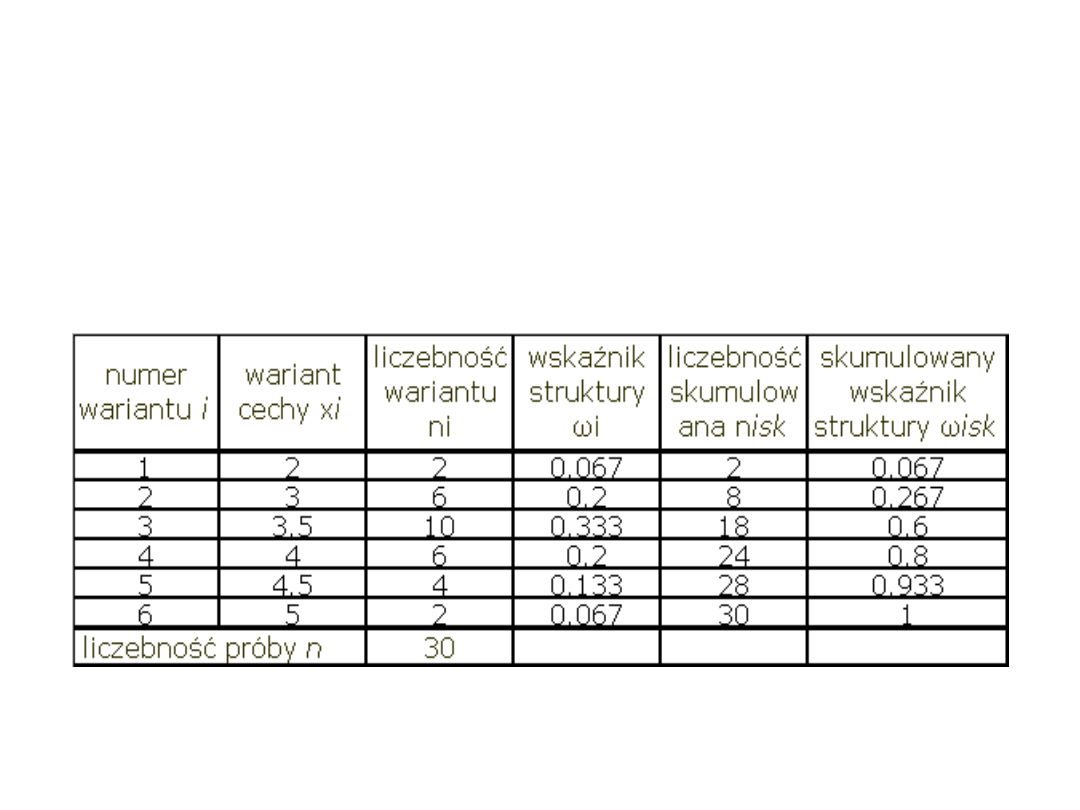
Przykład 1 cd

Szereg szczegółowy:
2; 2; 3; 3; 3; 3; 3; 3; 3,5; 3,5; 3,5; 3,5; 3,5; 3,5;

3,5;3,5; 3,5; 3,5; 4; 4; 4; 4; 4; 4; 4,5; 4,5; 4,5; 4,5;
5; 5;

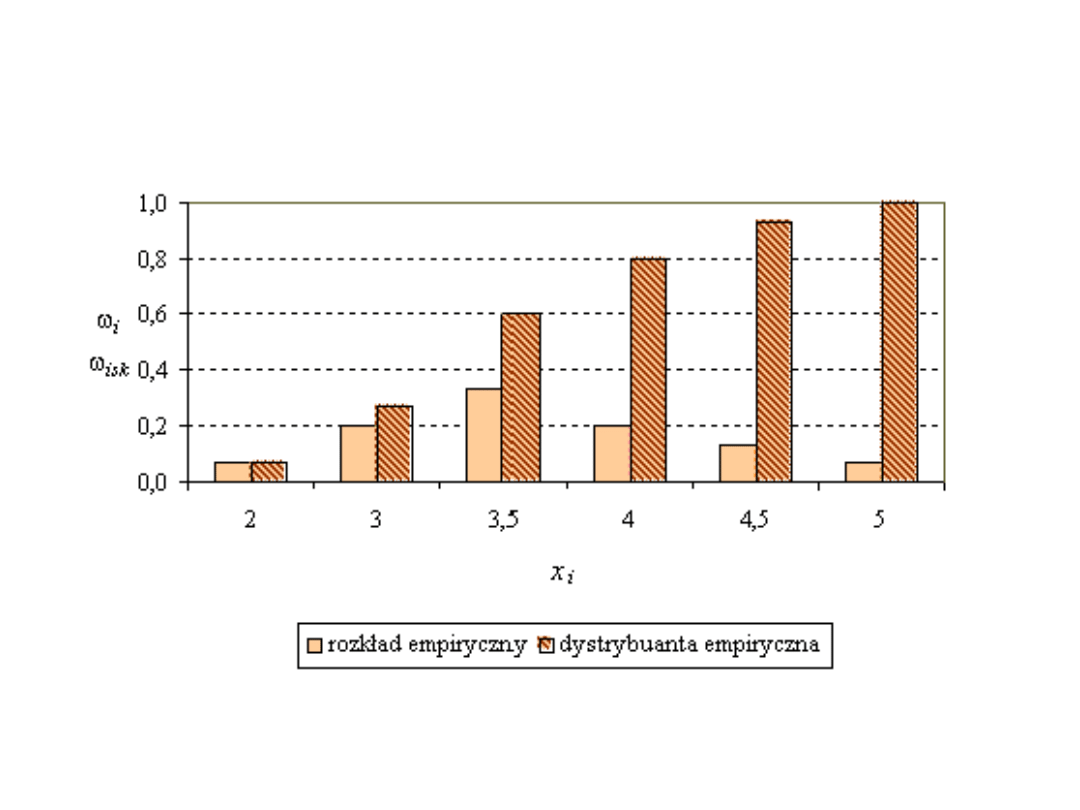
Przykład 1 cd

Szereg rozdzielczy z przedziałami

klasowymi

wzory:

Ustalanie liczby klas

 ustalenie rozpiętości przedziałów

klasowych

Rozpiętość (szerokość) przedziału klasowego h

i

- różnica pomiędzy górną x

1i

i dolną x

0i

granicą i-tego

przedziału klasowego.

Z reguły ustala się jednakowe rozpiętości przedziałów

klasowych. Przy równej rozpiętości przedziałów
klasowych liczebności (częstości) występujące w
poszczególnych klasach są porównywalne.

Przy różnych rozpiętościach (dla populacji niejednorodnej z

dużą koncentracją wartości w jednej grupie) zamiast

liczebności

(

częstości

) stosuje się wskaźnik:

gęstość

liczebności

(

gęstość częstości

).

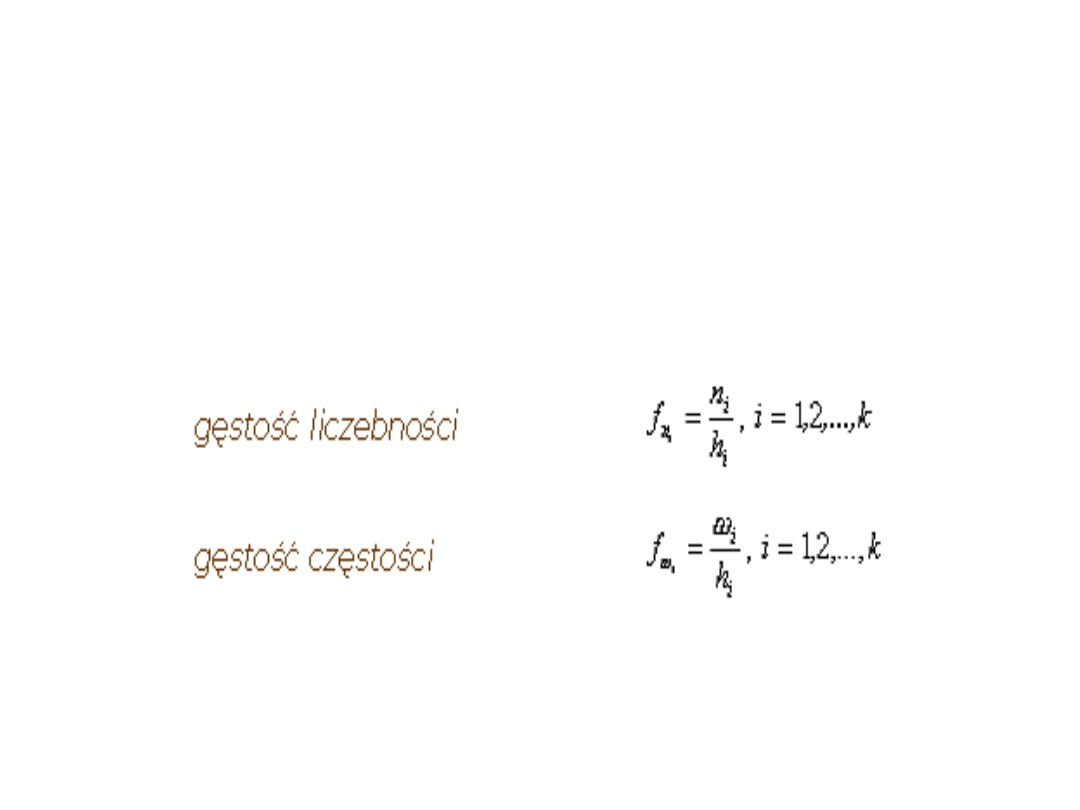
Gęstość liczebności (gęstość częstości)

-jest to stosunek liczebności (częstości) danej

klasy do rozpiętości przedziału klasowego:

Dla szeregu rozdzielczego o jednakowych

rozpiętościach przedziałów klasowych h

i

= h:

gdzie:

nazywa się

rozstępem

,

a k oznacza liczbę klas.

Uwaga: Jeżeli wybieramy przybliżoną wartość h, to
powinno to być zawsze przybliżenie z nadmiarem,
tzn. hk R.

 Ustalanie granic poszczególnych klas.

Jako dolną granicę najczęściej przyjmuje się najmniejszą

wartość cechy lub bliskiej tej wartości, czyli X

01

=X

min

.

Przy cechach ciągłych górne granice klas poprzednich
powinny być dolnymi granicami klas następnych, aby
nie było pomiędzy przedziałami luk Ponadto trzeba
ustalić, do które klasy zaliczyć wartości graniczne.

W szeregach o otwartych przedziałach klasowych,

konieczne jest czasami domknięcie tych przedziałów.
Stosuje się tutaj zasadę, że jeżeli liczebność w tych
przedziałach jest niewielka (nie większa niż 5% badanej
zbiorowości, można te przedziały domknąć taką
szerokością, jaka jest w sąsiednich przedziałach
klasowych.

Przykład 2:

 

Województwa Polski w układzie przestrzennym

sprzed 1999 r. charakteryzują dwie cechy:

- liczba gmin znajdująca się na terenie

województwa

(cecha skokowa X)

- powierzchnia ogólna w km

2

(cecha ciągła Y)

 

źródło: Roczniki statystyczny 1999,
tab. IV, s. XCV

Przykład 2a:

struktura województw wg liczby gmin – dla cechy

skokowej

 
Szereg szczegółowy:
17, 30, 32, 37, 37, 39, 40, 40, 40, 40, 41, 41, 42, 42, 43, 43, 43, 44, 45,

46, 46, 47, 47, 47, 48, 48, 49, 51, 54, 54, 55, 55, 55, 56, 57, 57, 58,

58, 58, 59, 59, 62, 63, 63, 65, 69, 74, 78, 91.

W przykładzie:
R = 91 – 17 = 74,
h = 74/7 » 10,57 » 11
początek pierwszego przedziału klasowego
x

01

= x

min

= 17

(przyjmujemy, że rozpiętość przedziałów klasowych jest taka sama dla

wszystkich klas)

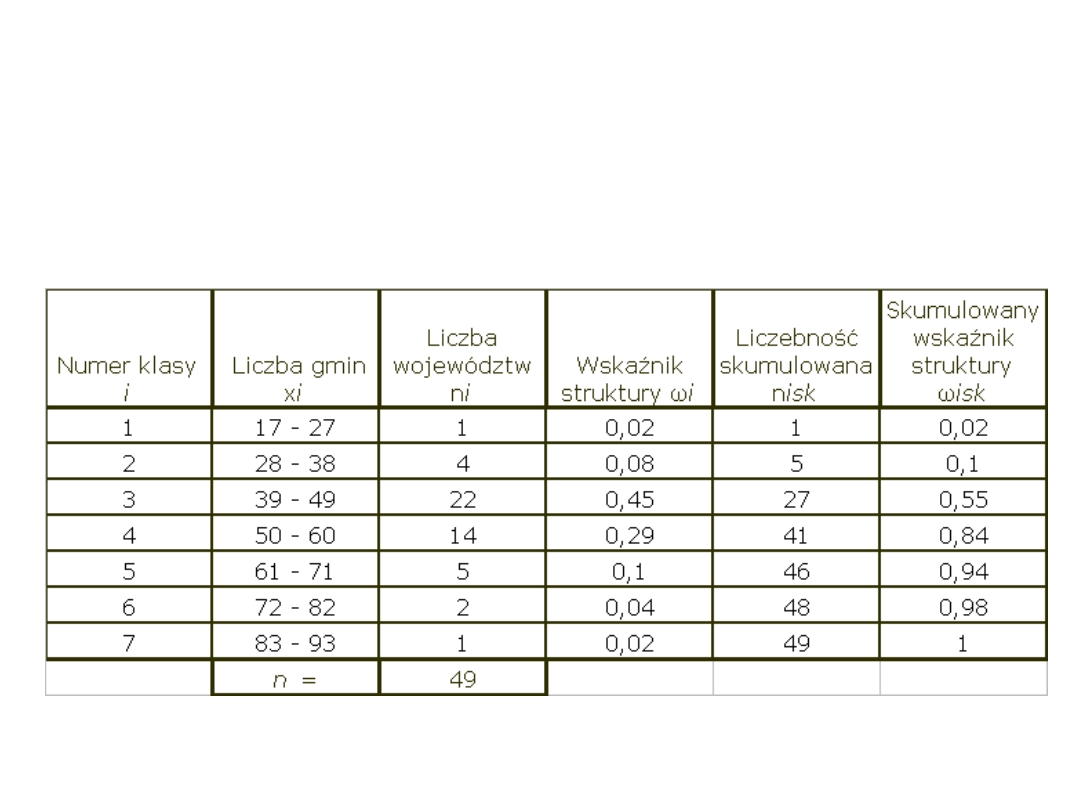
Przykład 2a cd:

Rozkład empiryczny i dystrybuanta empiryczna – Struktura

województw wg liczby gmin

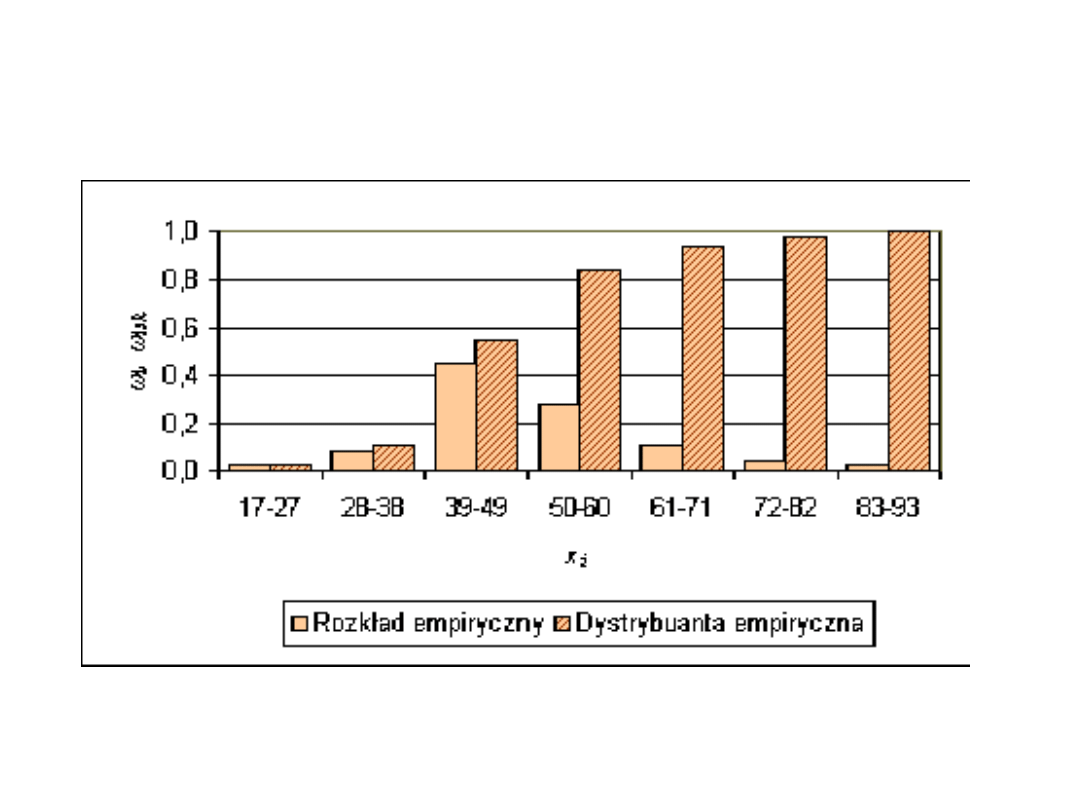
Przykład 2a cd:

Przykład 2b: struktura województw wg

powierzchni – dla cechy ciągłej

liczba klas: k = 7,
rozstęp:
R = x

max

– x

min

= 12327 – 1523 = 10804 km

2

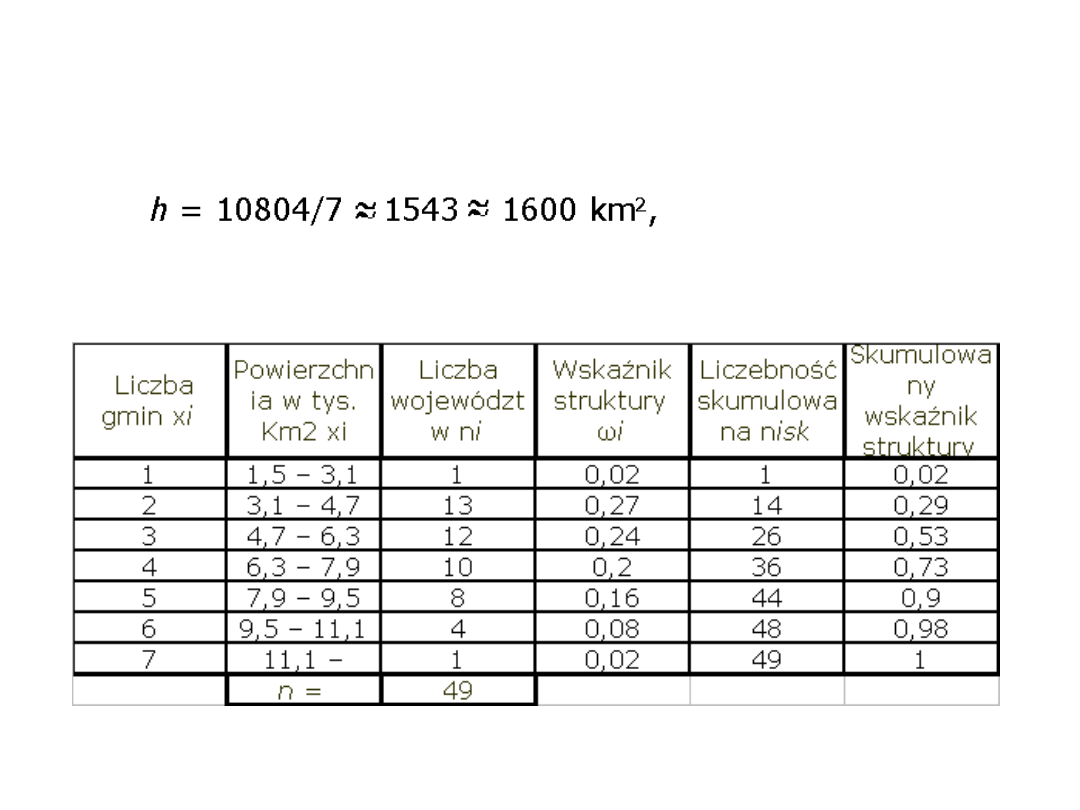
pierwszy wariant grupowania
h przyjmujemy z nadmiarem, tzn.

początek pierwszego przedziału klasowego

x

01

= 1,5 tys. km

2

Przykład 2b cd:

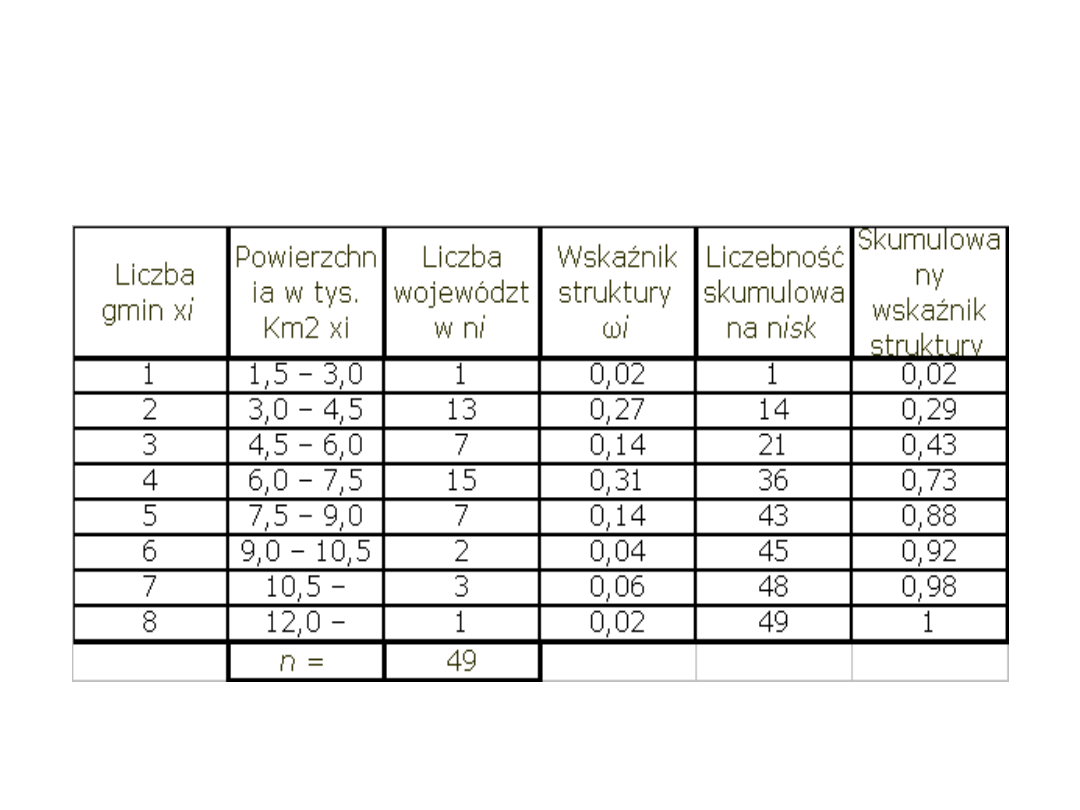
Przykład 2b cd:

drugi wariant grupowania
h bez nadmiaru np. h » 1500 km

2

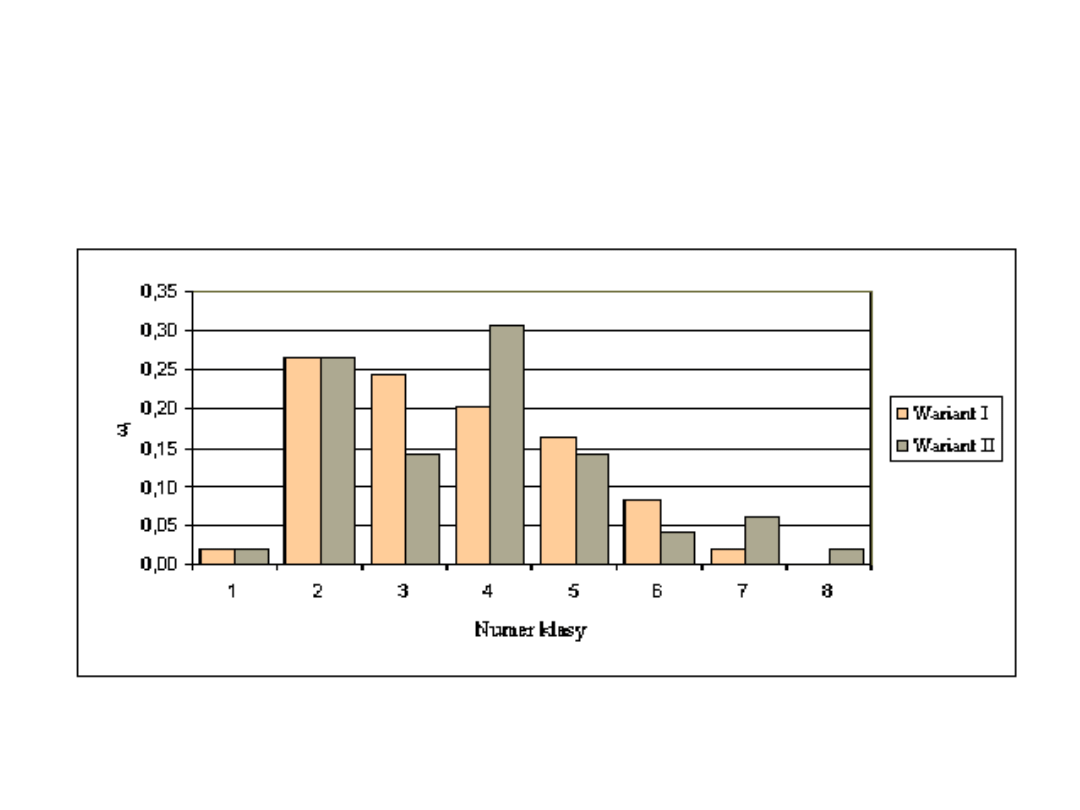
Przykład 2b cd:

Porównanie rozkładów empirycznych dla wariantów:

pierwszego i drugiego.

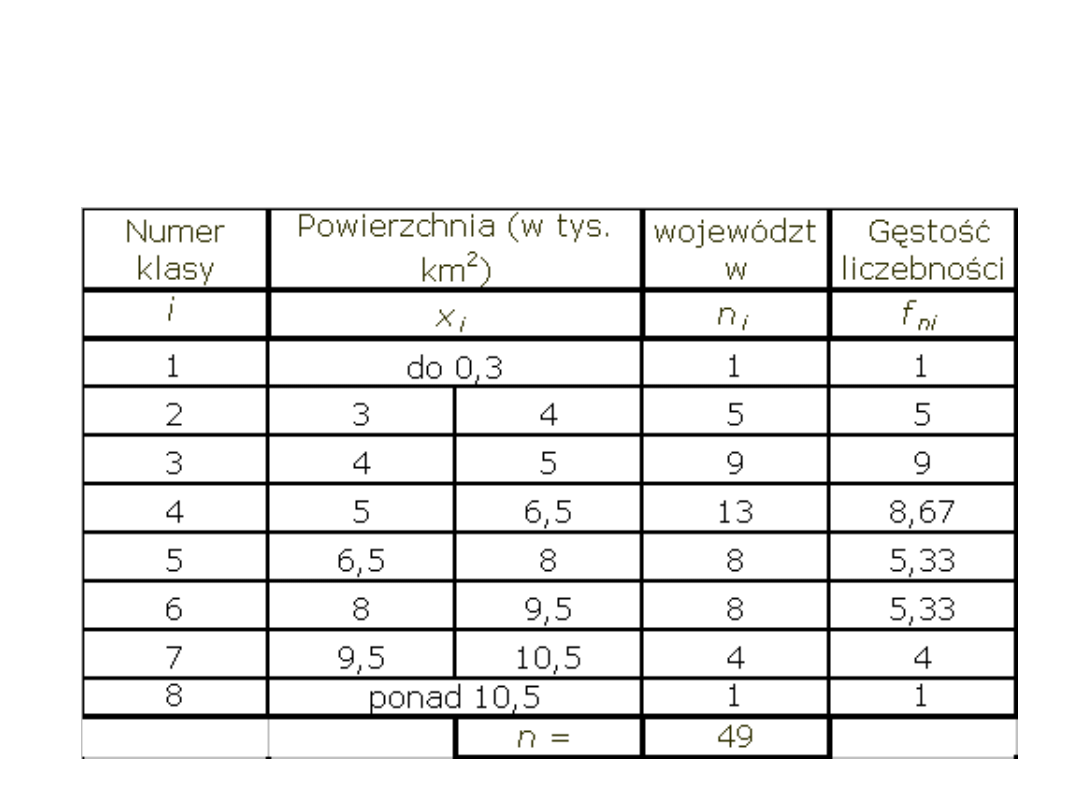
Przykład 2b cd:

trzeci wariant grupowania

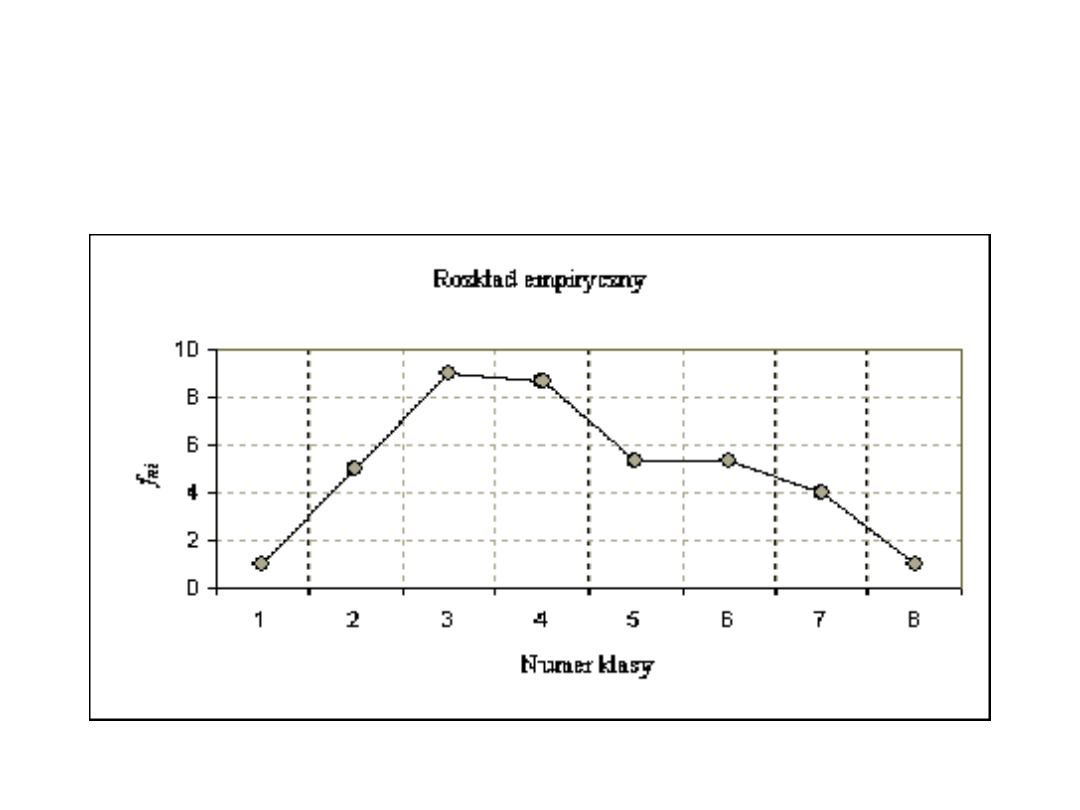
Przykład 2b cd:

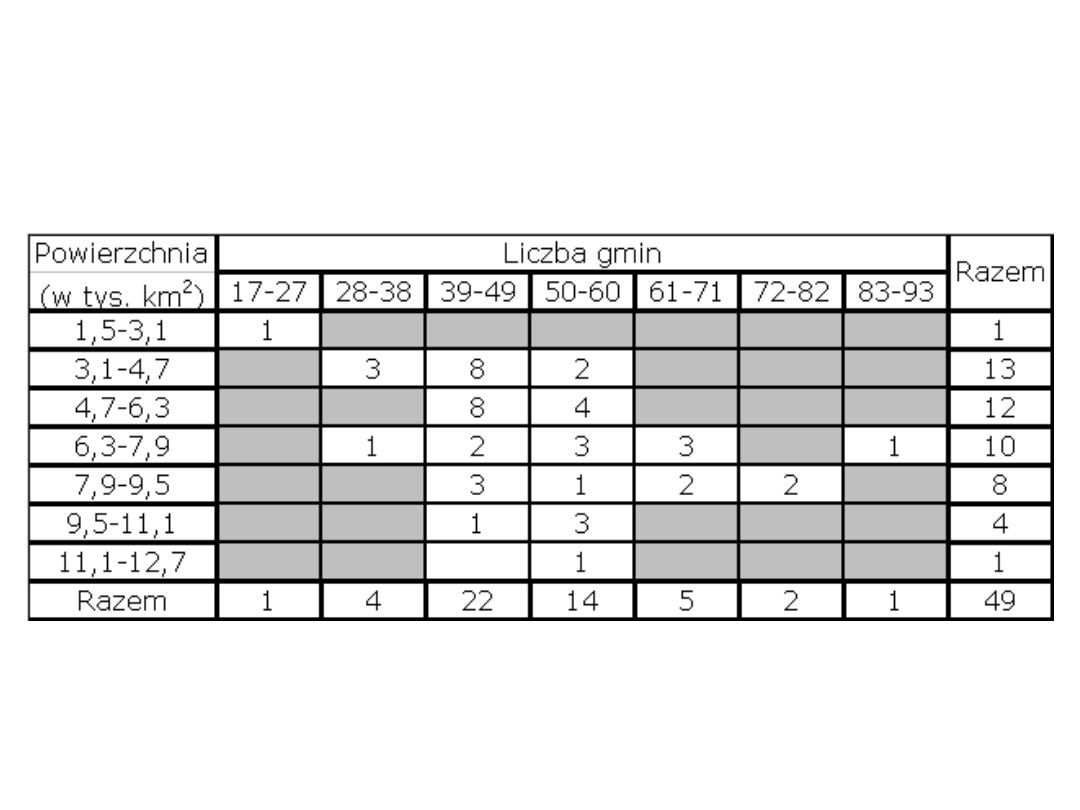
Przykład 3

:

Województwa Polski według liczby gmin i

powierzchni

Każda liczba w wewnętrznej części tabeli określa częstotliwość
występowania dwóch cech.

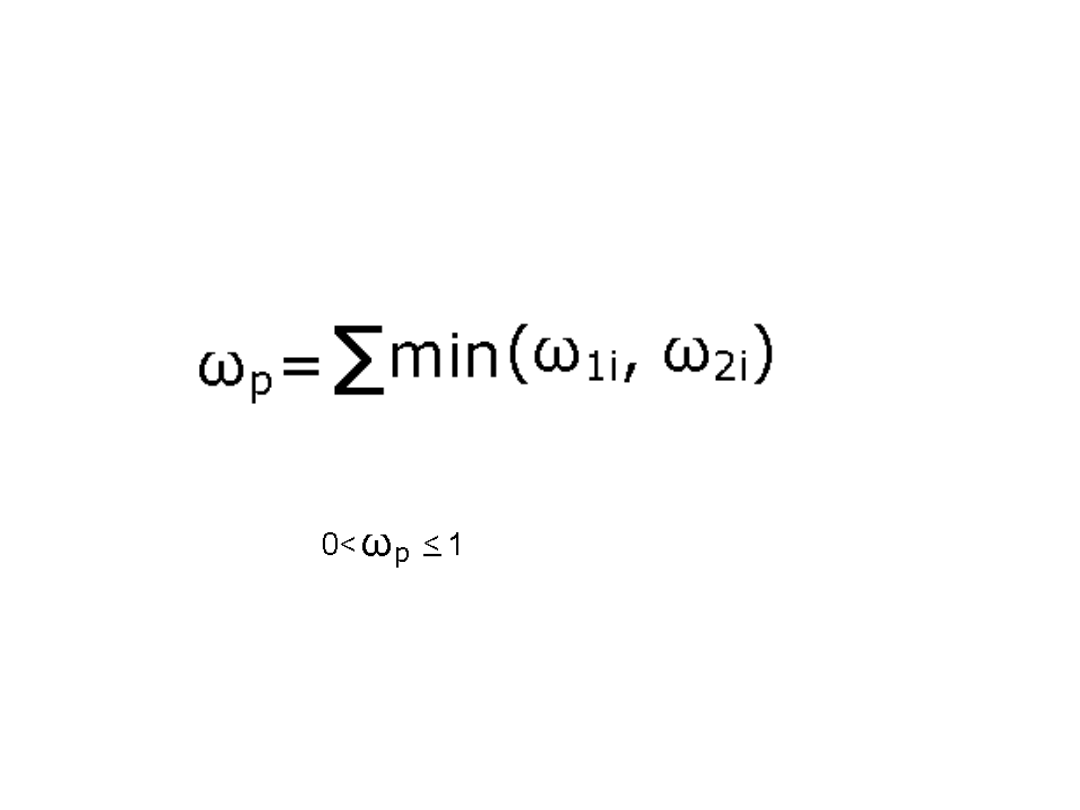
Wskaźnik podobieństwa struktury w

p

- służy do porównywania struktur
analizowanych zbiorowości.

przy czym:

(im wartość bliższa jedności, tym struktury
zbiorowości są bardziej podobne).

Wskaźniki natężenia

- są to wielkości stosunkowe,

wyrażające kształtowanie się
wielkości jednego zjawiska na tle
innego, logicznie z nim
związanego.

Przykładowe współczynniki natężenia:

 stopa bezrobocia

- stosunek liczby bezrobotnych do liczby

ludności czynnej zawodowo,

 gęstość zaludnienia

- liczba ludności przypadająca na 1 km

2

powierzchni,

 wskaźnik umieralności

- liczba zmarłych do średniej liczby

ludności, 

 wskaźnik rozwoju gospodarczego

- produkt krajowy brutto

(netto) do liczby ludności kraju,

 wskaźnik wydajności pracy

- wielkość produkcji do czasu

pracy,

 wskaźnik spożycia i usług

- wielkość spożycia i usług do liczby

ludności,

 wskaźnik rentowności

- zysk do wielkości sprzedaży,

 wskaźnik efektywności

- zysk do zaangażowanego kapitału,

 wskaźnik produktywności

- sprzedaż do do zaangażowanego

kapitału.

Sposoby prezentacji danych

Tablice statystyczne

- są

wykorzystywane do prezentacji danych

statystycznych według określonego
kryterium.

Podział tablic statystycznych:

 proste

- charakteryzują strukturę lub dynamikę

jednej zbiorowości pod względem jednej cechy

(ilościowej lub jakościowej),

 złożone

- opisują badaną zbiorowość według

kilku cech lub kilka zbiorowości według jednej

cechy (szczególna rola

tablic dwudzielnych

-

korelacyjnych

).

Wykres

- jest graficzną formą rejestracji danych oraz

narzędziem prezentacji i analizy uogólnionych informacji

statystycznych.

 

Najczęściej stosowane typy wykresów:

 histogramy (wykresy słupkowe)

- zbór przylegających

prostokątów, których podstawy, równe rozpiętości

przedziałów klasowych - znajdują się na osi odciętych, a

wysokości są liczebnościami (częstościami) przedziałów, w

przypadku nierównych szerokości przedziałów - gęstościami

liczebności (częstości).

 diagramy, wykresy liniowe (wielobok liczebności)

- jest

łamaną, powstałą przez połączenie punków, których

współrzędnymi są środki przedziałów klasowych i

odpowiadające im liczebności (częstości lub gęstości).

 krzywe liczebności (częstości) dla cechy ciągłej

- gęsta siatka

punktów wyznaczająca wielobok liczebności, w konsekwencji

wygładzona krzywa otrzymana przy zmniejszaniu rozpiętości

przedziałów klasowych.

W podobny sposób przedstawia się szeregi

kumulacyjne:

 histogramy liczebności (częstości)

skumulowanej

,

 diagramy liczebności (częstości) skumulowanej

- linia łącząca punkty, których współrzędne to:
górne granice przedziałów klasowych i
odpowiadające im liczebności (częstości)
skumulowane.

Graficzna prezentacja danych

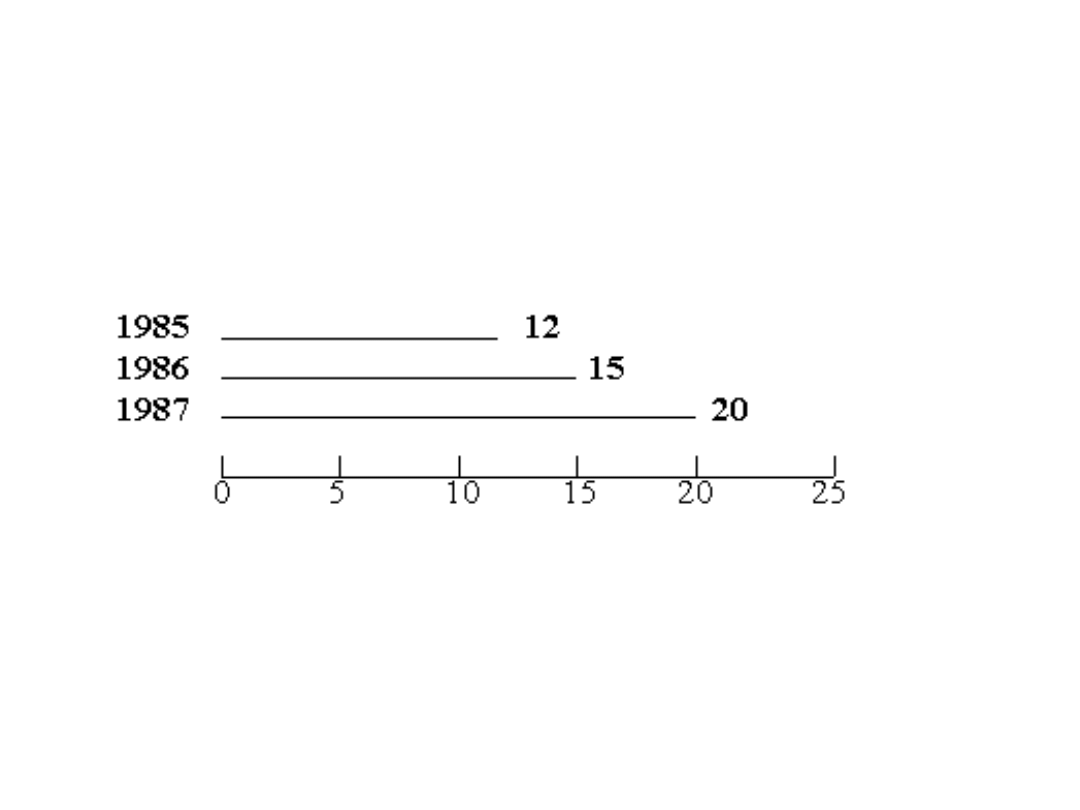
Metoda liniowa

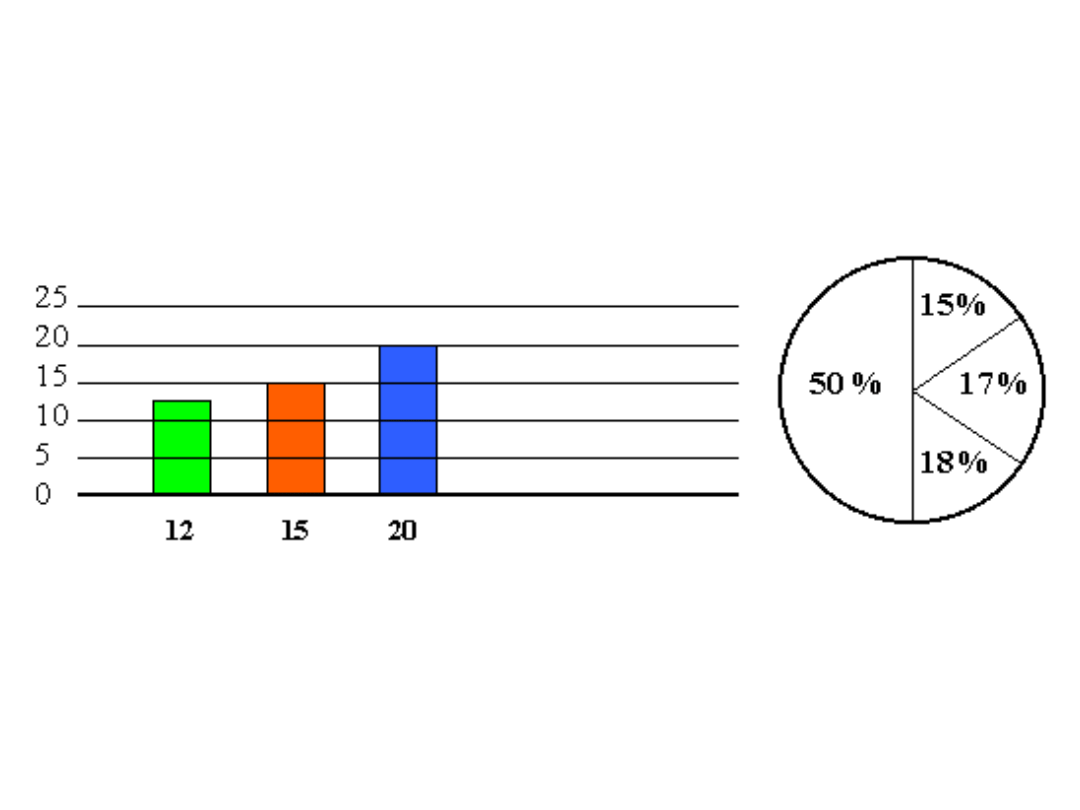
Metoda powierzchniowa

Metoda obrazkowa (symbolowa)

- w której dane zjawisko przedstawiane

jest za pomocą odpowiedniej wielkości
obrazka. Metoda ta jest jednak mało
dokładna.

Metoda ilościowo-symbolowa

– to przedstawienie wielkości zjawiska za

pomocą

wielokrotności

dowolnego

znaku

graficznego.

Pojedynczy

oznaczoną tym znakiem wyraża się
odpowiednią

ilością

dodatkowo

dorysowanych tych samych znaków i ich
części. Obok obrazka bądź wszystkich
obrazków

dodatkowo

podaje

się

wielkość liczbową.

Kartogram

Liczba

województw

Stopa

bezrobocia

%

31,5

25,5

22,5

19,5

16,5

13,5

10,5

7,5

6

5

7

10

14

3

4

Wykresy w układzie
współrzędnych

Histogram

Diagram

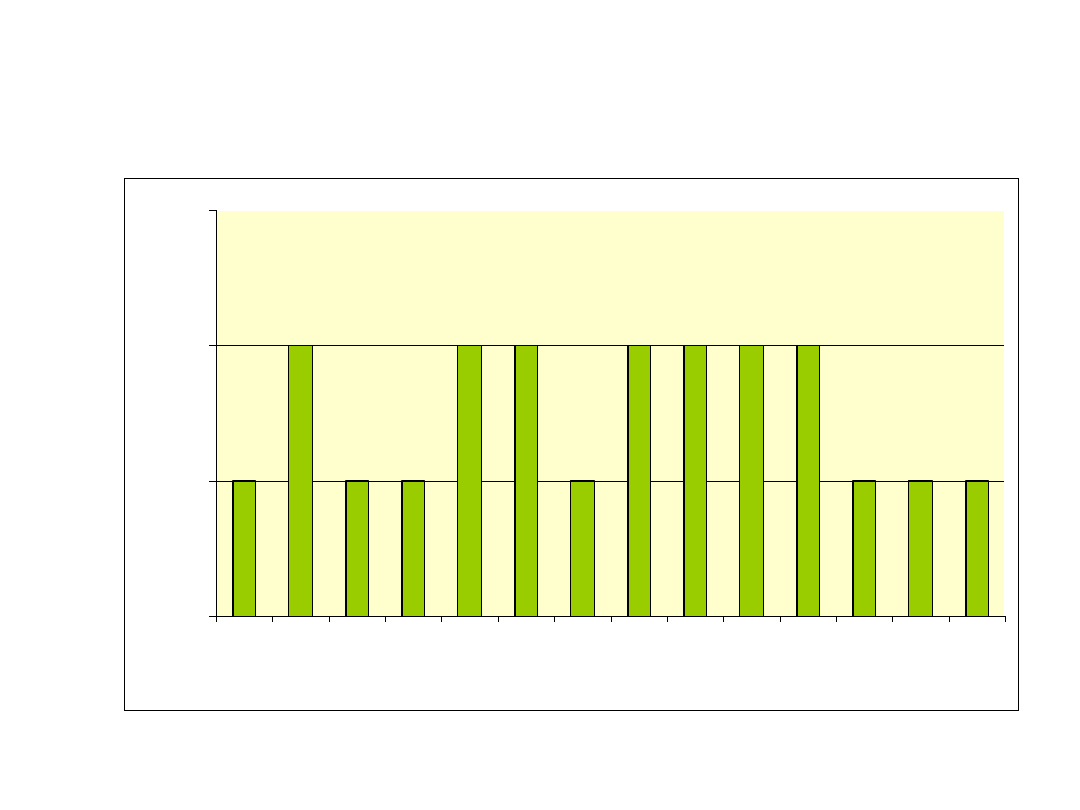
Histogram

0

1

2

3

2

3

4

5

6

9

10

11

12

14

16

18

20

23

Wartość cechy Xi

Li

cz

eb

no

ść

c

ec

hy

n

i

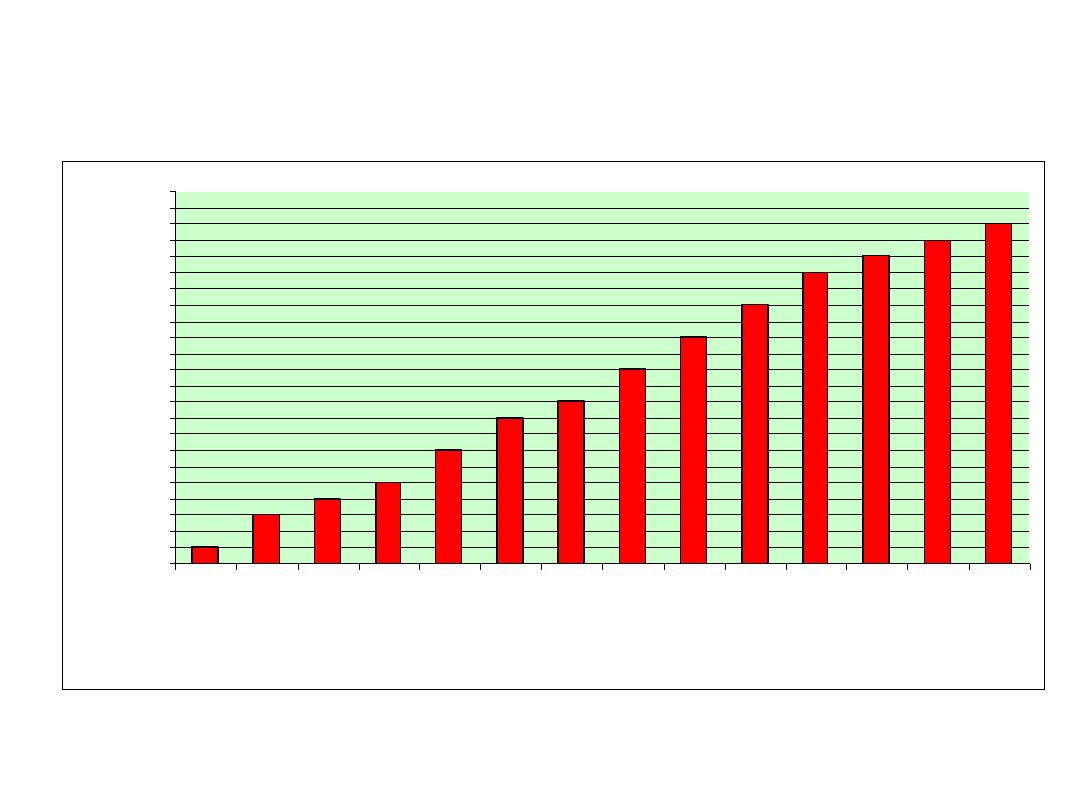
Histogram

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

21

22

23

2

3

4

5

6

9

10

11

12

14

16

18

20

23

Wartość cechy Xi

Li

cz

e

b

no

ść

sk

um

ul

o

w

an

a

n

i

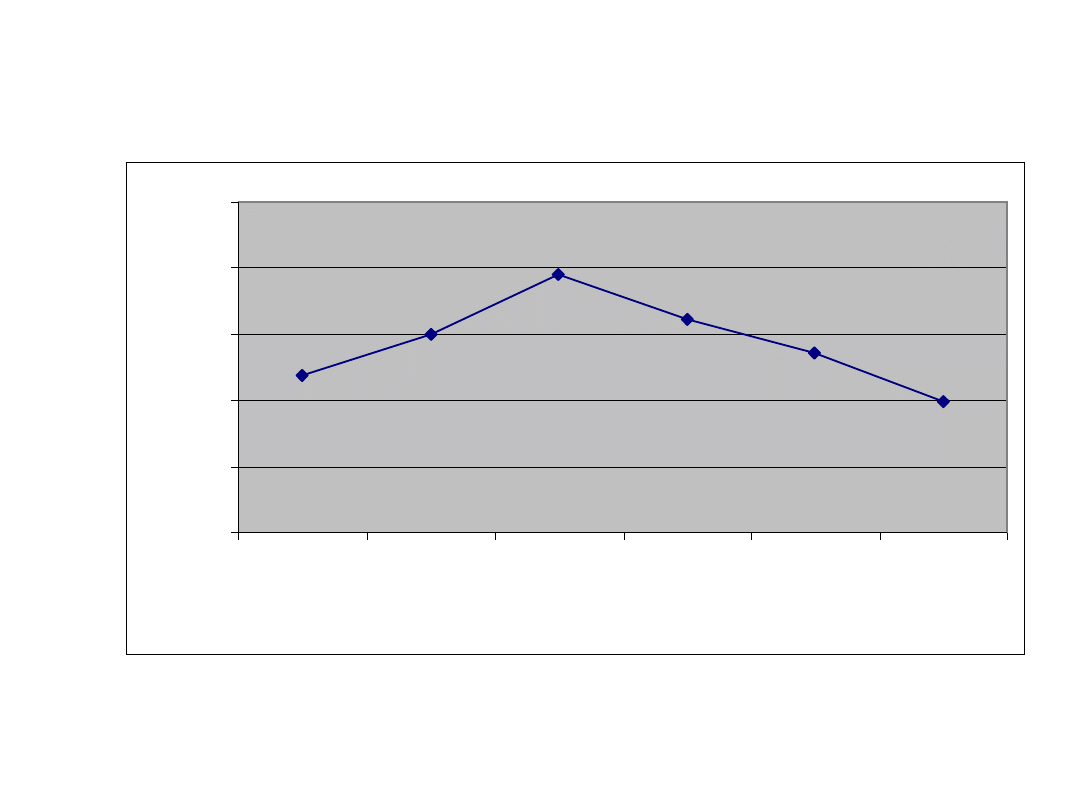
Diagram

0

5

10

15

20

25

1970

1975

1980

1985

1980

1992

Lata

P

ro

d

u

kc

ja

w

m

ln

t

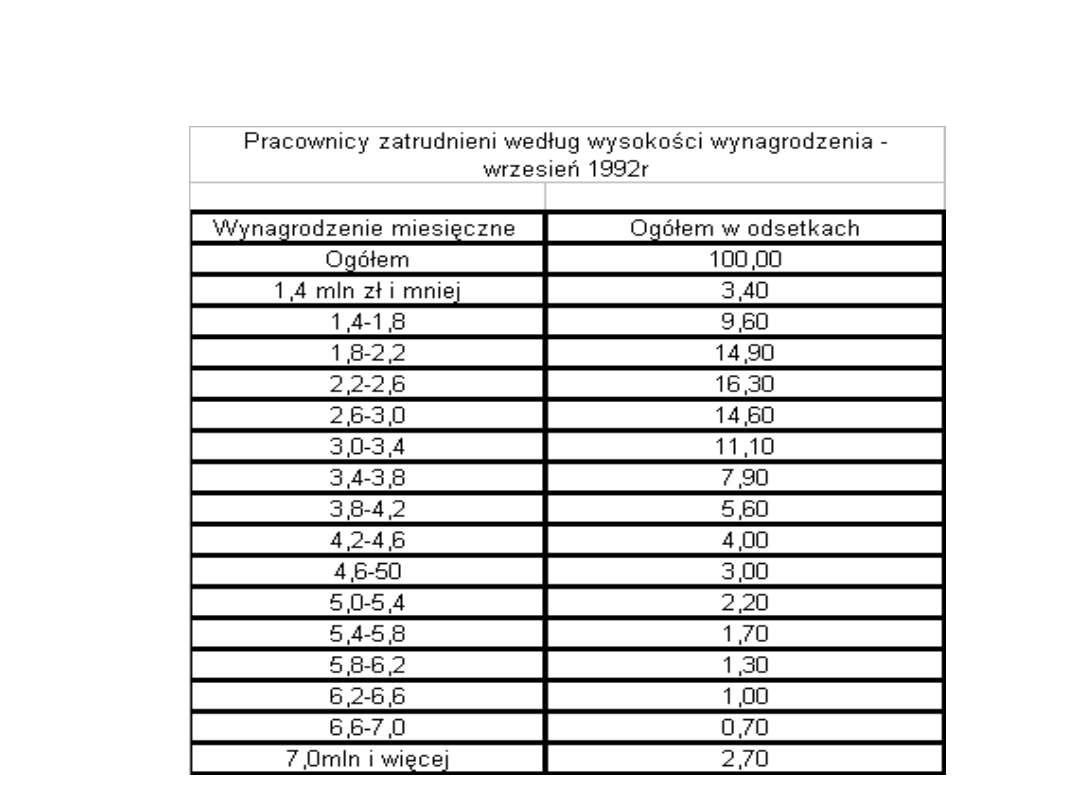
Krzywa liczebności

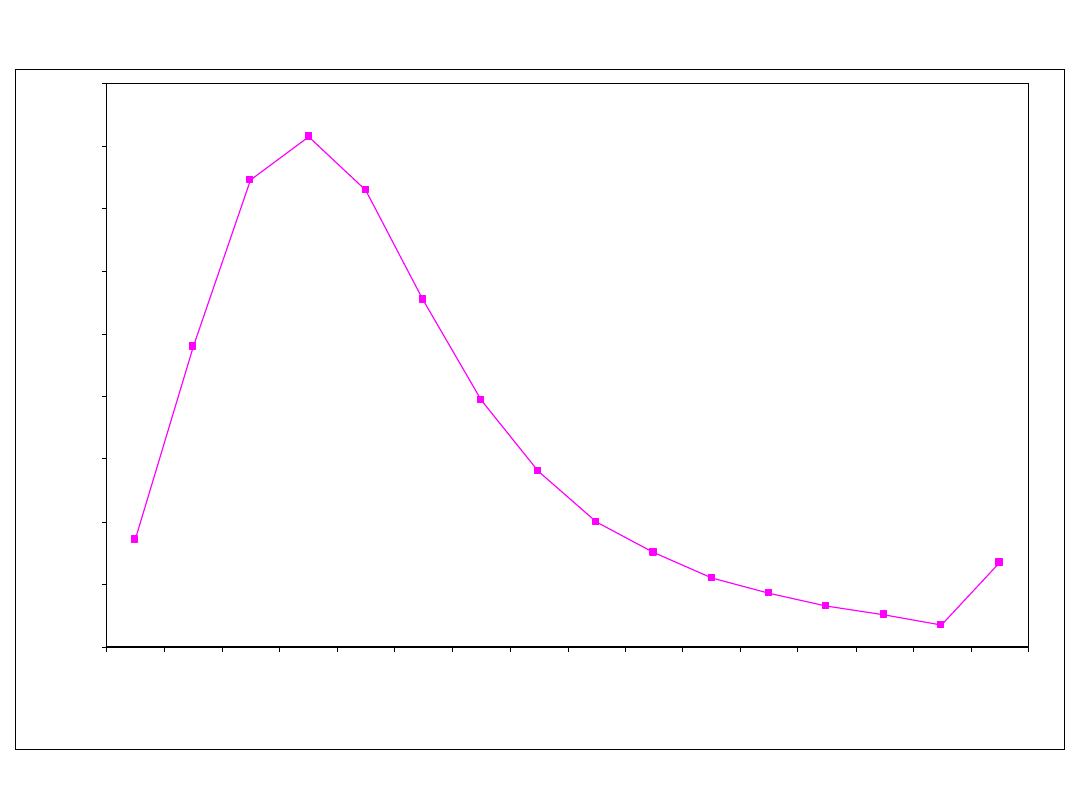
0,00

2,00

4,00

6,00

8,00

10,00

12,00

14,00

16,00

18,00

do 1,4 1,4-1,8 1,8-2,2 2,2-2,6 2,6-3,0 3,0-3,4 3,4-3,8 3,8-4,2 4,2-4,6 4,6-50 5,0-5,4 5,4-5,8 5,8-6,2 6,2-6,6 6,6-7,0 ponad

7,0

Wynagrodzenie w mln zł

Za

tr

u

d

n

ie

n

i

w

%

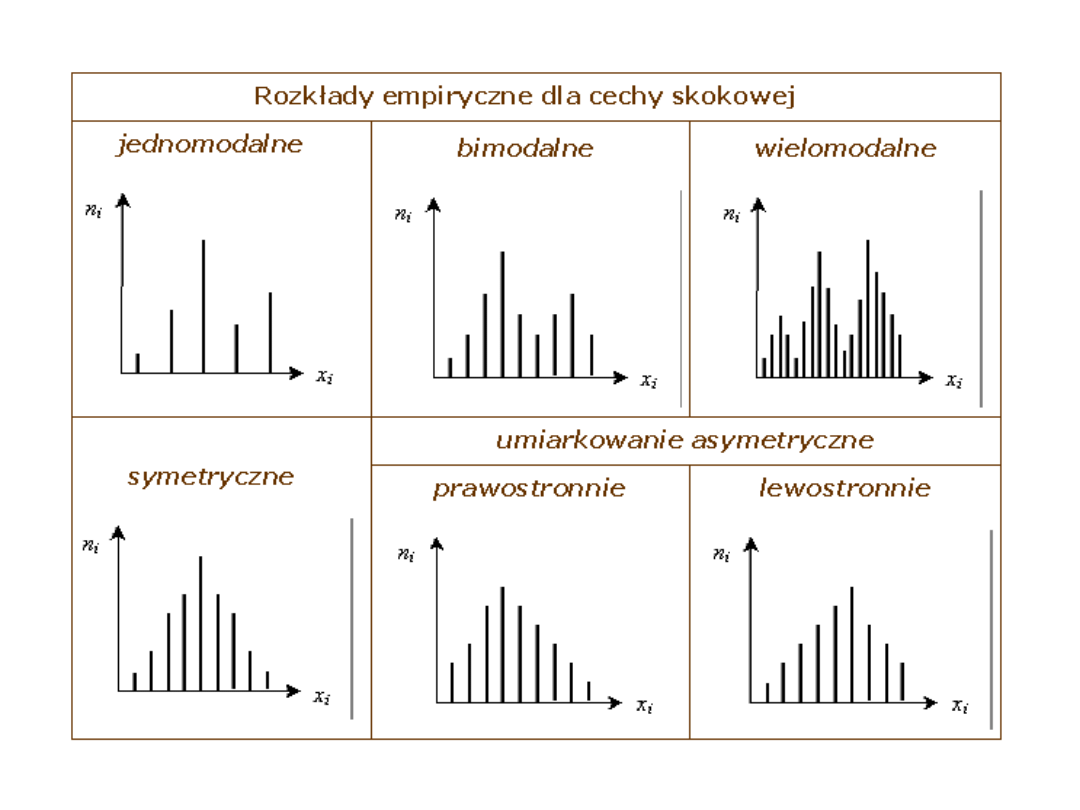
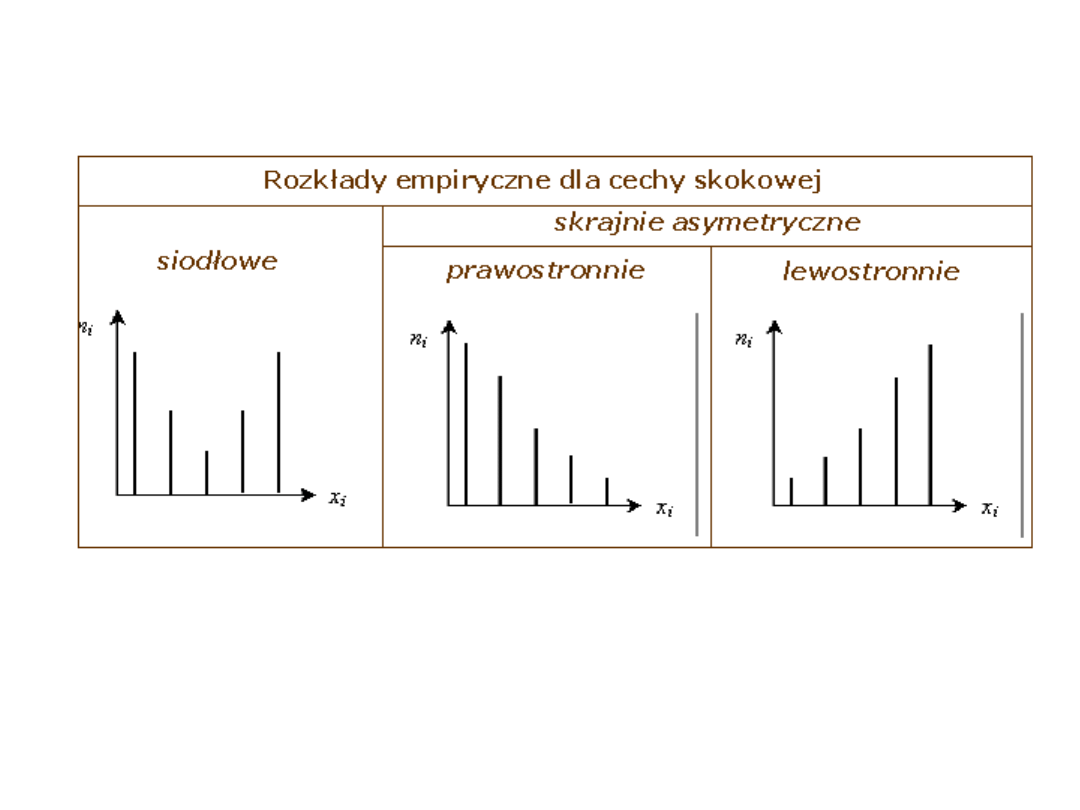
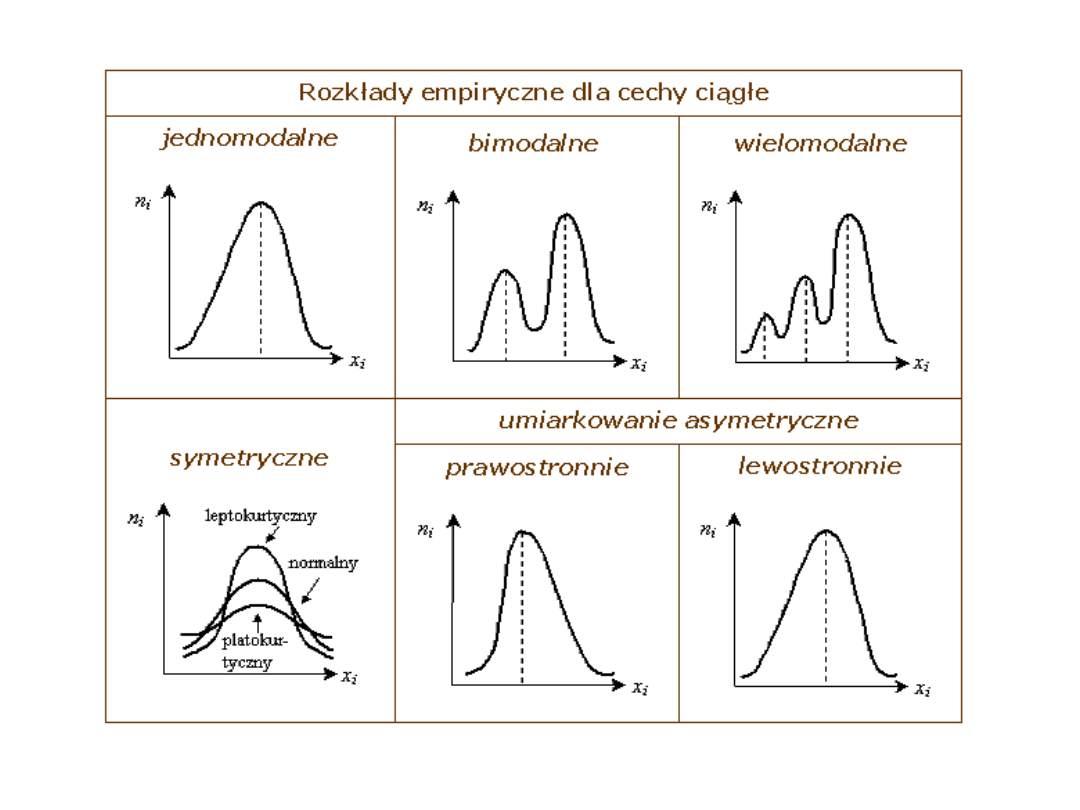
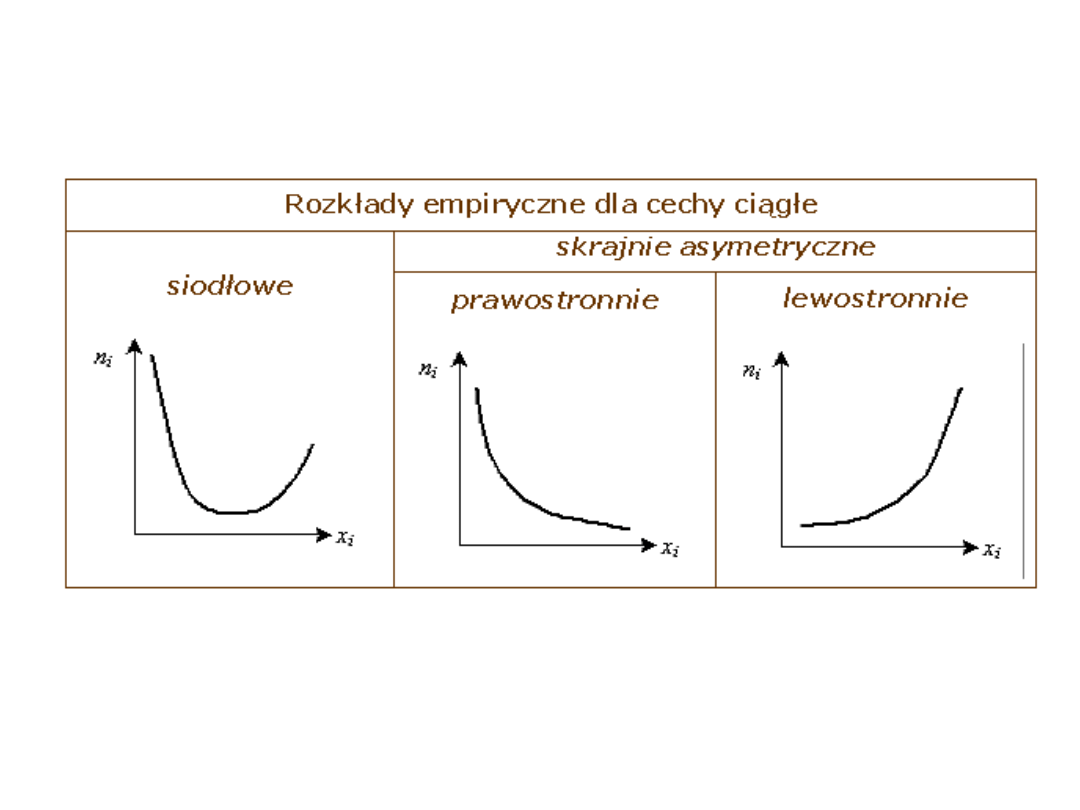
Typy rozkładów empirycznych