WYKRESY

SYSTEMATYCZNYCH BADAŃ

MODELOWYCH ŚRUB

SWOBODNYCH

Obliczenia śrub obecnie przeprowadza się numerycznie w oparciu o teorię

wirową śruby. Dla inżynierskich obliczeń wstępnych można z wystarczającą
dokładnością dobrać śruby na podstawie wykresów sporządzonych w oparciu o
wyniki systematycznych badań modelowych śrub swobodnych.

Przy modelowaniu pracy śruby w tunelu kawitacyjnym czy też w basenie

modelowym określa się jej charakterystyki hydrodynamiczne: napór T, moment
obrotowy Q, sprawność śruby przy różnych prędkościach postępowych i
obwodowych . Modele śrub mogę mieć różne absolutne wymiary
(np.średnicę D), ale powinny być geometrycznie podobne, tzn. musi być
zachowana skala.

Wyniki badań modelowych mogą być odnoszone do warunków rzeczywistych

tylko wtedy, gdy w trakcie badań zostały spełnione warunki podobieństwa
hydrodynamicznego. Śruby okrętowe można uznać za podobne, gdy liczba
skrzydeł dla modelu i śruby rzeczywistej jest jednakowa oraz gdy jednakowe są
współczynniki skoku H/D, powierzchni skrzydeł So/S, grubości skrzydła e/D itp.

P

v

M

D

k

D

=

2 n

w= p

Warunek podobieństwa kinematycznego spełnia równość

współczynników posuwu Jm= J. Przy zachowaniu podobieństwa
geometrycznego i kinematycznego jednakowe będą, dla modelu i
śruby naturalnej, współczynniki naporu momentu oraz
sprawność Zgodnie z teorią podobieństwa hydromechanicznego
badania modelowe śrub należy przeprowadzać przy zachowaniu
stałości liczb kryterialnych.

Stosuje się dwie metody badań modelowych śrub:

1. Przy zachowaniu stałej liczby Froude'a Fn = idem

Badania modelowe śrub przy zachowaniu podobieństwa

liczby Froude'a przeprowadza się wtedy, gdy zanurzenie osi śruby
pod powierzchnię wody jest niewielkie, a więc gdy występuje
wpływ swobodnej powierzchni wody na pracę śruby.

T

K

Q

K

p

h

n

D

v

Fn

n D

g l

g D

p�

=

�

�

�

�

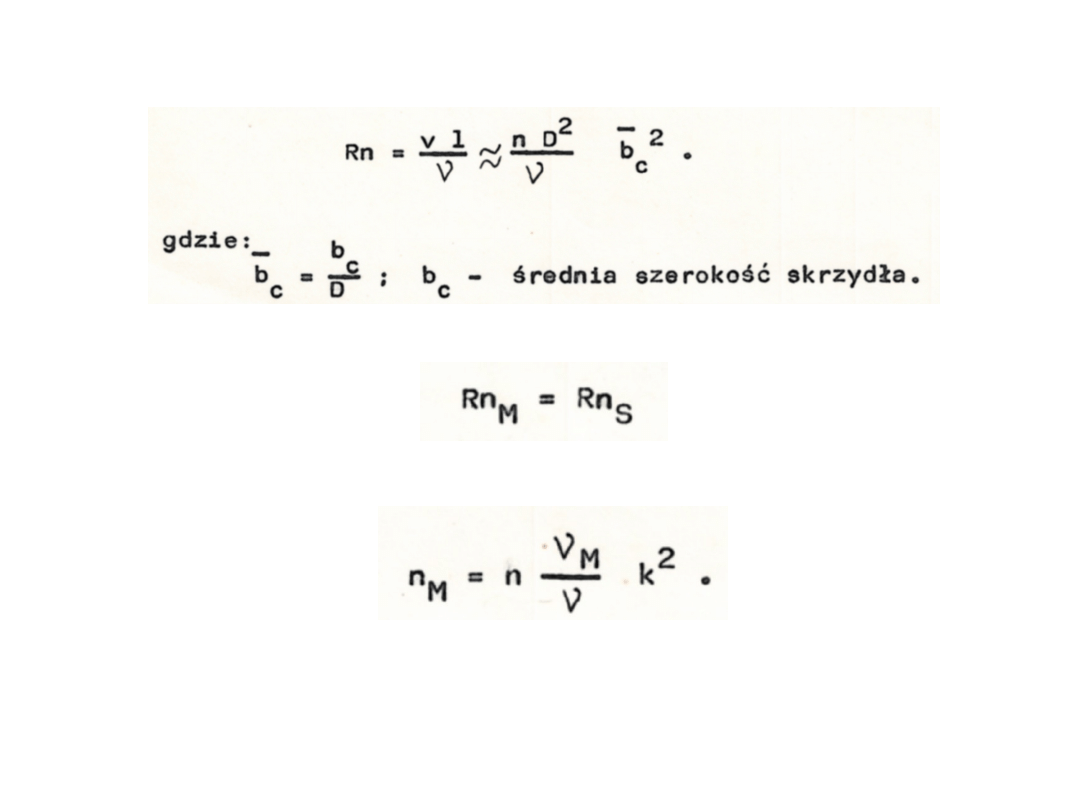
2. Przy zachowaniu stałej liczby Reynolds’a Rn=idem

Przy zachowaniu równości liczb Reynolds’a dla modelu i śruby

Prędkość obrotowa śruby wyniesie

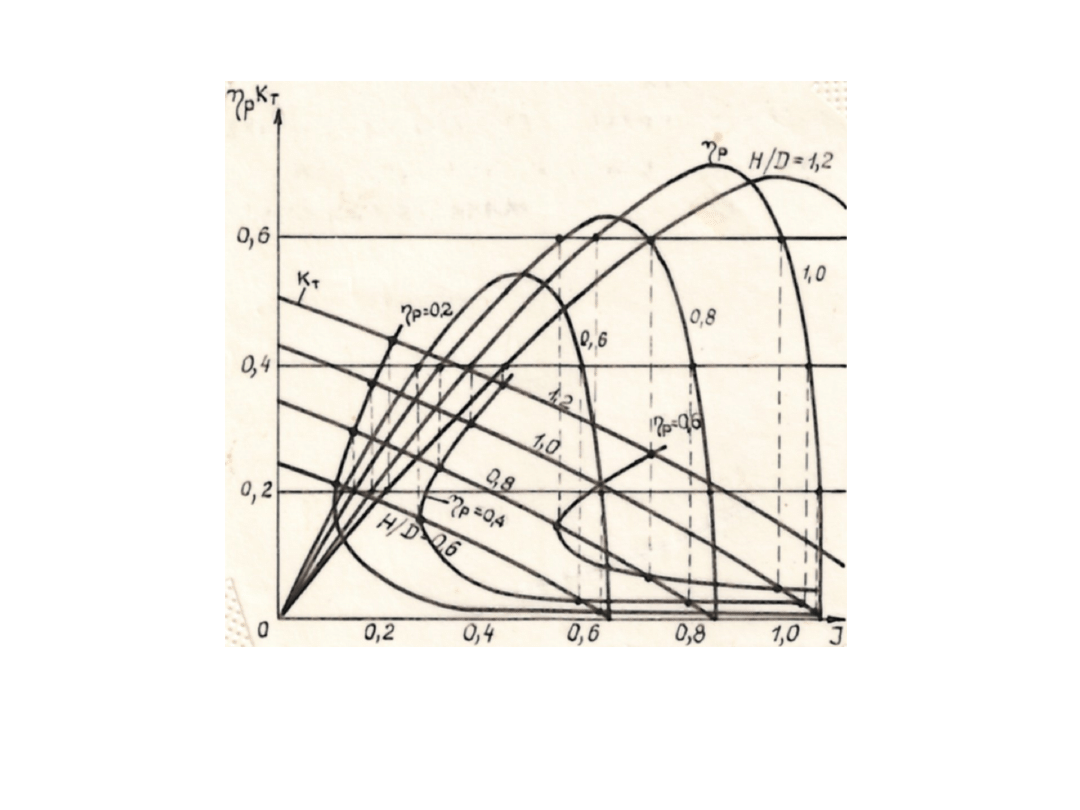
Rys.1. Konstruowanie linii stałej sprawności śruby

Badania modelowe śrub należy przeprowadzać w zakresie

prędkości obrotowych, którym odpowiada przekroczenie krytycznej
liczby Reynoldsa. Wyniki systematycznych badań mo delowych
przedstawione są w formie wykresów zbiorczych w postaci
umożliwiającej dobór śruby. W najprostszej formie przedstawione są
wyniki systematycznych badań modelowych prowadzonych przez
Papmiela, dla serii śrub nie kawitujących. Są one podane jako wykresy
i lub i dla różnych
współczynników skoku H/D. Każdy wykres jest odpowiedni dla śrub
podobnych, tzn. takich, dla których So/S= idem i z = idem.

Charakterystyka śrub wg Papmiela zbudowana jest w sposób

następujący. W układzie współrzędnych naniesiono linie
naporu dla różnych współczynników skoku H/D oraz linie stałej
sprawności śruby . Przykład konstruowania linii stałej sprawności
śruby pokazano na rys.1.

T

K

J

-

p

J

h -

Q

K

J

-

p

J

h -

T

K

J

-

T

K

p

h

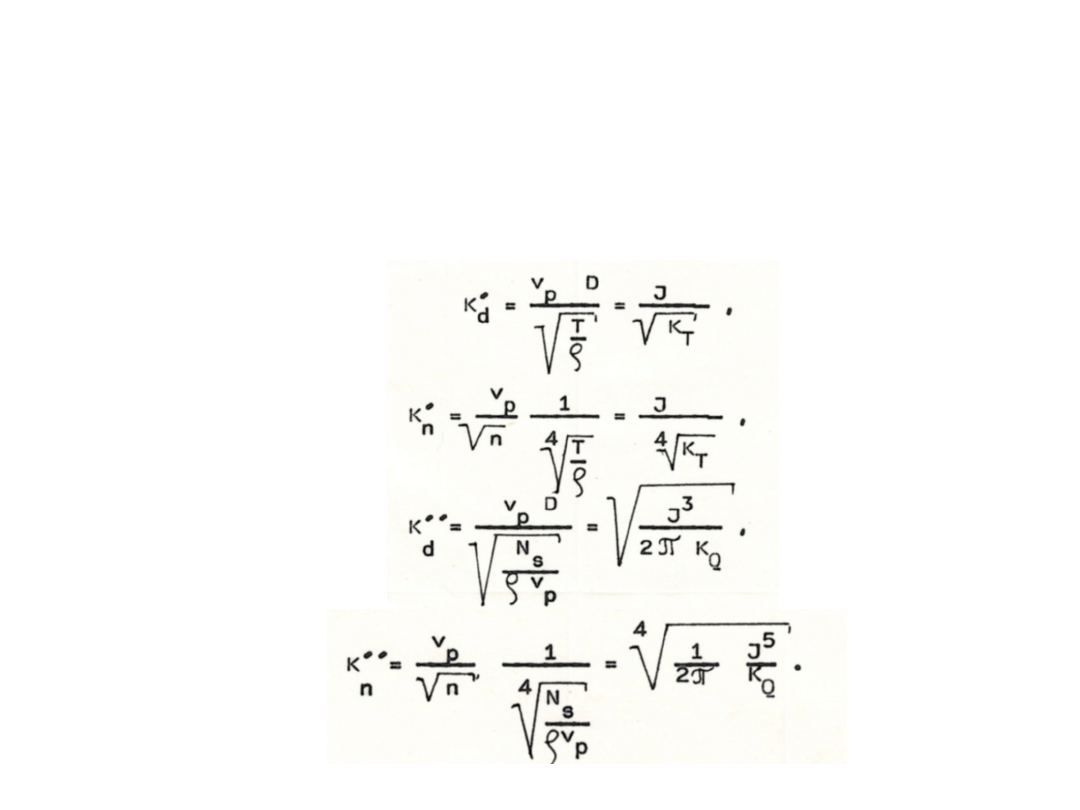
Ponadto na wykresach śrub Papmiela naniesiono dwie linie

pomocnicze: tzw. linię i (rys. 2-4), gdy wykres jest
podany w układzie współrzędnych oraz linie i
gdy wykres jest podany w układzie .

Linie te służą do optymalnego doboru średnicy śruby, gdy

dana jest prędkość obrotowa lub do optymalnego doboru
prędkości obrotowej śruby, gdy dana jest jej średnica.

'
d

K

'
n

K

T

K

J

-

"

d

K

"

n

K

Q

K

J

-

Współczynniki i wykorzystywane są wtedy, gdy dobiera

się śrubę dla danej charakterystyki oporowej okrętu.

Natomiast współczynniki i wykorzystywane są wtedy,

gdy dobiera się śrubę dla danej mocy doprowadzonej do stożka śruby.

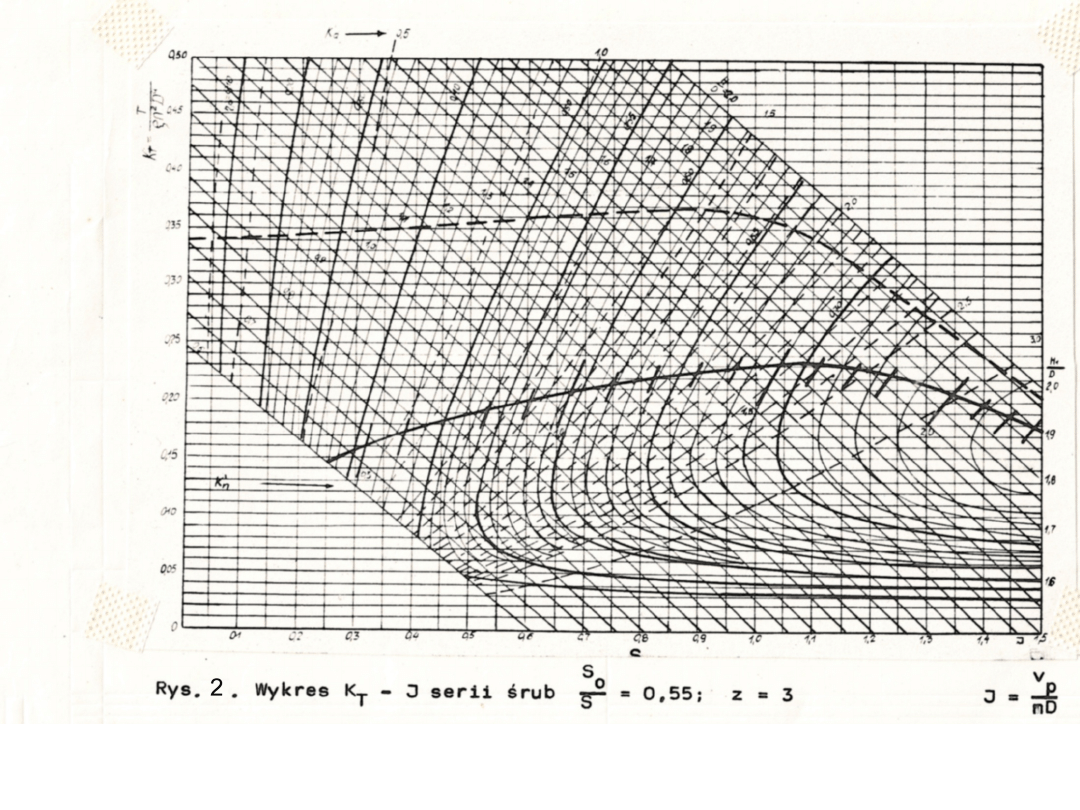
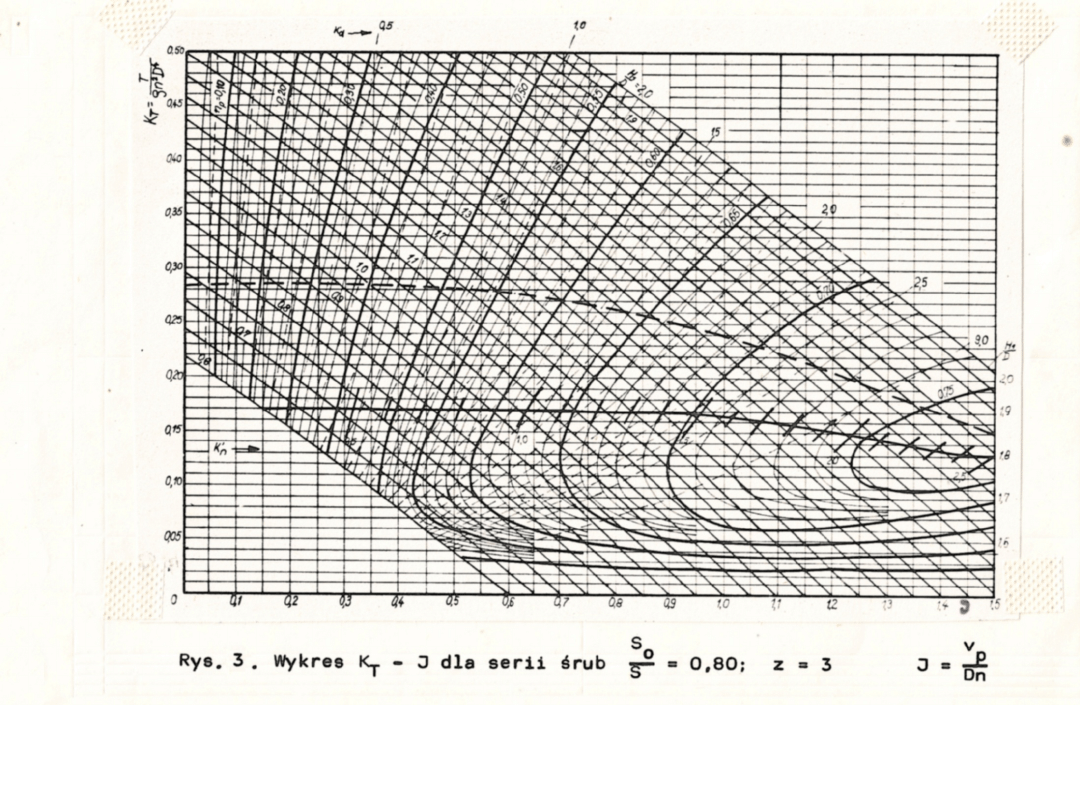
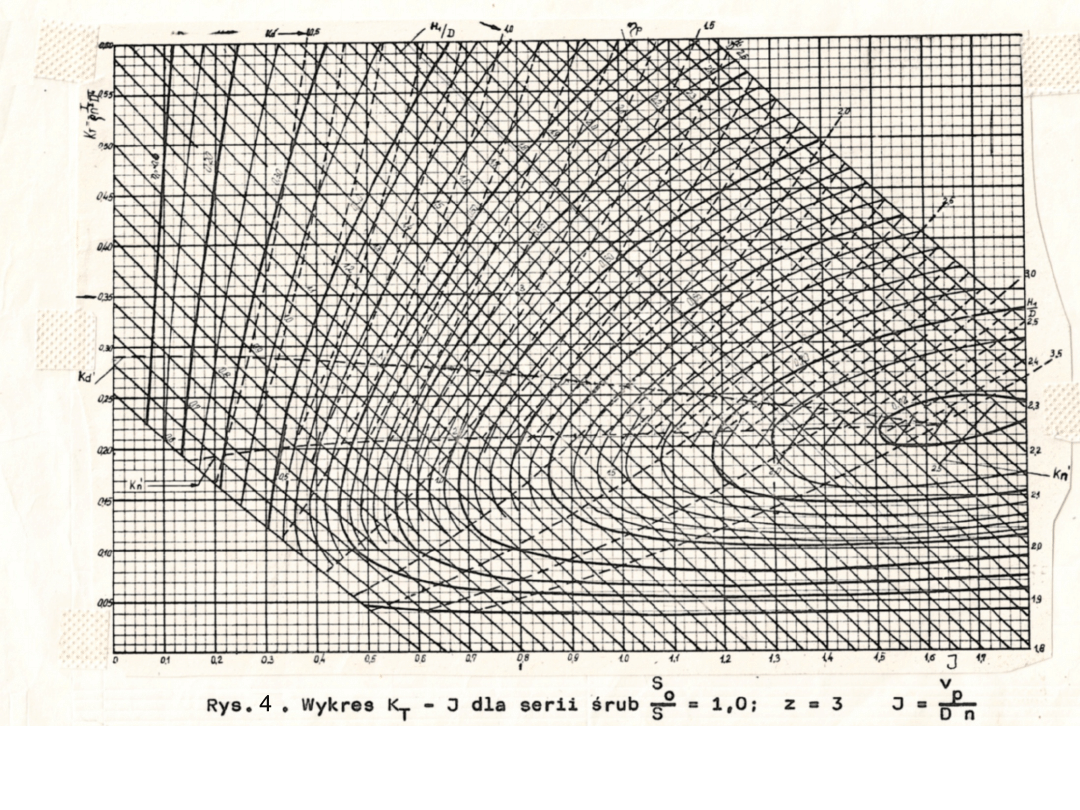
Przykładowe uniwersalne charakterystyki śrub swobodnych wg

Papmiela w układzie współrzędnych , czyli tzw.

"charakterystyki kadłubowe", dla So/S=0,55; 0,8 i 1 podano na

rys.2-4.

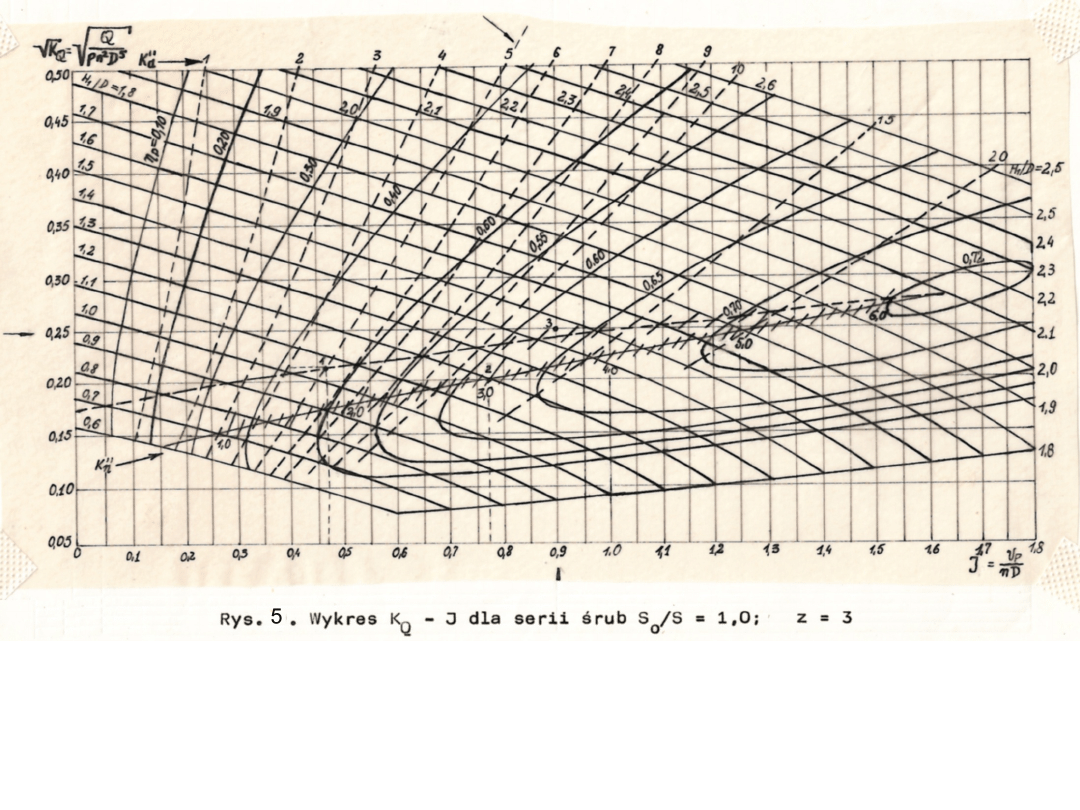
Na rys. 5 pokazano przykładową uniwersalną charakterystykę

śruby swobodnej wg Papmiela w układzie współrzędnych , czyli

tzw. "charakterystykę silnikową" dla So/S=1.

'
d

K

'
n

K

"

d

K

"

n

K

T

K

J

-

Q

K

J

-

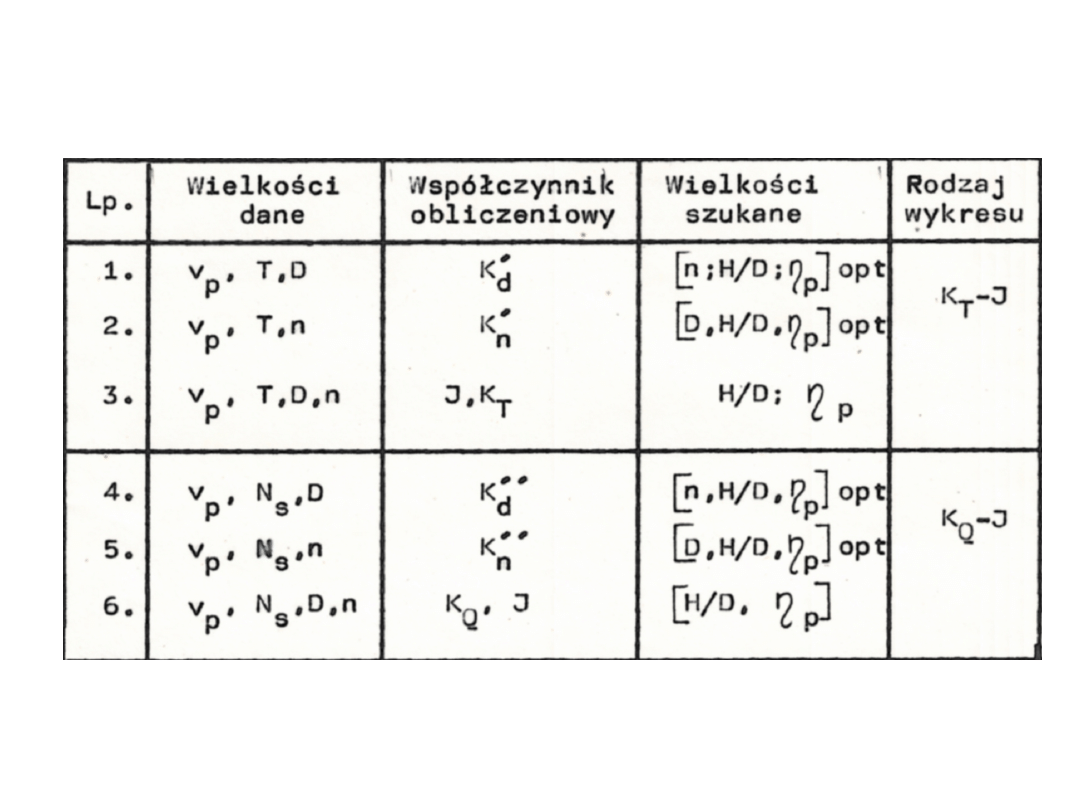
Charakterystyki te pozwalają zrealizować szereg zadań

związanych z doborem śruby okrętowej. Główne zadania i sposób
ich realizacji przedstawiono w tabeli:

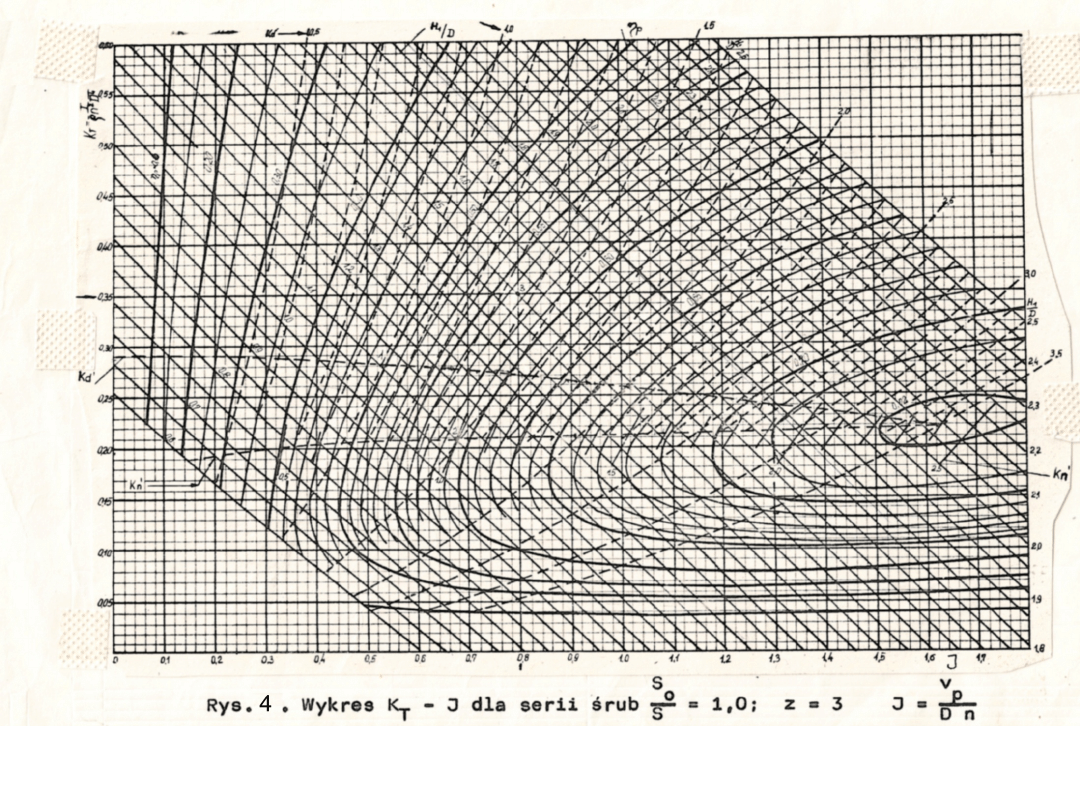
Sposób korzystania z wykresów Papmiela dla trzech przypadków
obliczeniowych, gdy podstawową daną wyjściową jest napór
zapotrzebowany przez śrubę T, przykładowo pokazano na rys.4. Gdy
np.:
a) dane są napór śruby T, prędkość postępowa śruby i średnica
śruby D o takich wartościach, że współczynnik =1,5, to wtedy idąc
po linii można znaleźć punkt pracy śruby 1, któremu odpowiada
współczynnik naporu =0,28, współczynnik posuwu J=0,53,
współczynnik skoku zerowego naporu H1/D=1,1 i sprawność śruby
swobodnej =0,498;
b) dane są napór śruby T, prędkość postępowa śruby i prędkość
obrotowa śruby n o takich wartościach, że =1, to na wykresie można
znaleźć punkt pracy śruby 2, któremu odpowiada współczynnik naporu
=0,208; współ czynnik posuwu J=0,675, współczynnik skoku
zerowego naporu H1/D=1,1 i sprawność śruby swobodnej =0,59
c) dane są napór śruby T, prędkość postępowa śruby średnica
śruby D i prędkość obrotowa śruby n, o takich wartościach, którym
odpowiada współczynnik naporu =0,35 i współczynnik posuwu
J=0.8, to na wykresie znajdujemy pkt.3, któremu odpowiada skok

zerowego naporu H1/D=1,5 i sprawność śruby swobodnej =0,58.

p

v

'
d

K

'
d

K

T

K

p

h

p

v

'
n

K

T

K

p

h

p

v

T

K

p

h

Często się zdarza, że dobierana śruba ma inne współczynniki

So/S lub inną liczbę skrzydeł śruby niż te, dla których sporządzone
są wykresy (z=3; So/S=0,55; 0,8; 1).

Wtedy stosuje się współczynniki korygujące:

naporu i sprawności

q

k

p

h

Oprócz wykresów podanych przez Papmiela, dla śrub

okrętów wojennych przydatne mogą być wykresy Instytutu

Wageningen (Holandia) oraz wykresy sporządzone przez Gawna.

Wykresy Instytutu Wageningen pozwalają na dobór śrub

dla jednostek o małych i średnich prędkościach ruchu. Obejmują

śruby 2,3,4 i 5-skrzydłowe o współczynnikach powierzchni skrzydeł

So/S=0,3-0,7 i współczynnikach skoku H/D=0,5-1,4. Śruby te

mają niesymetryczny obrys skrzydła o przekroju Göttingen lub

lotniczym.

Śruby Gawna mają symetryczny obrys skrzydła, a profil z

odcinka koła. Nadaję się one do napędu szybkich okrętów

wojennych lub motorówek. Wykresy podane przez Gawna

obejmują śruby trzyskrzydłowe o So/S=0,45-1,1 i H/D=0,8-l,4.

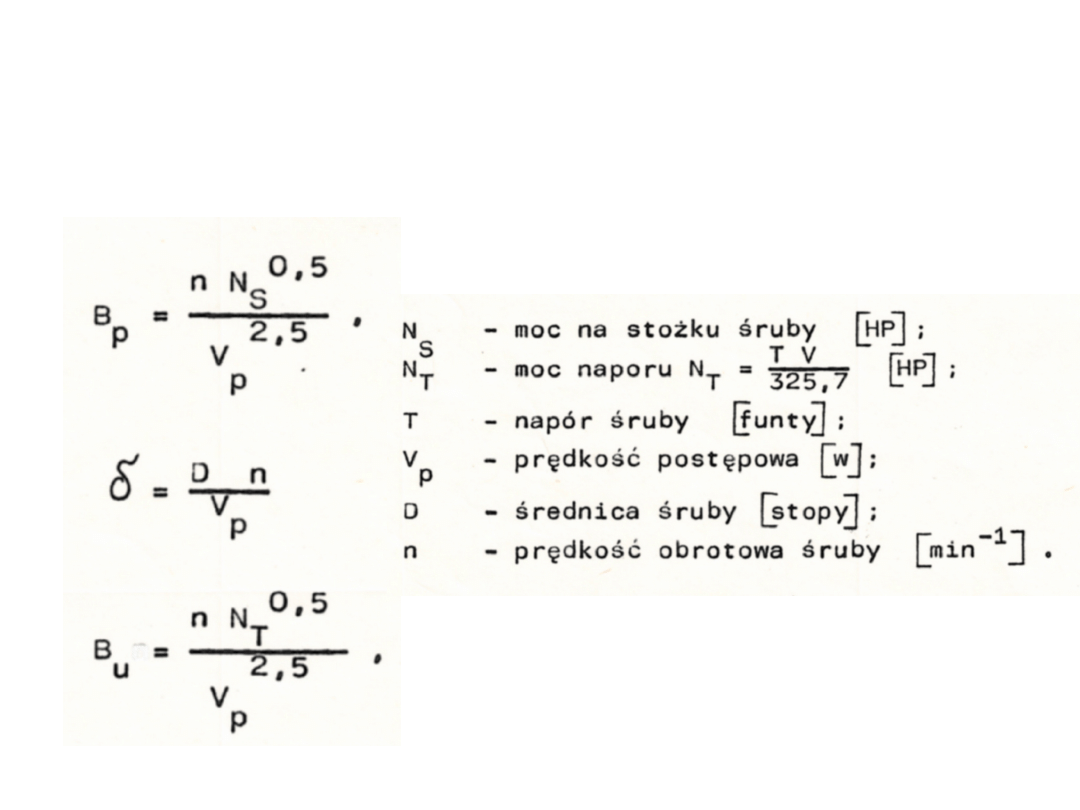
Wykresy z systematycznych badań modeli śrub swobodnych

opublikowane przez Instytut w Wageningen i Gawna podane są
w formie zbiorczej dla serii śrub w układzie współrzędnych
lub

gdzie:

p

B - d

U

B - d

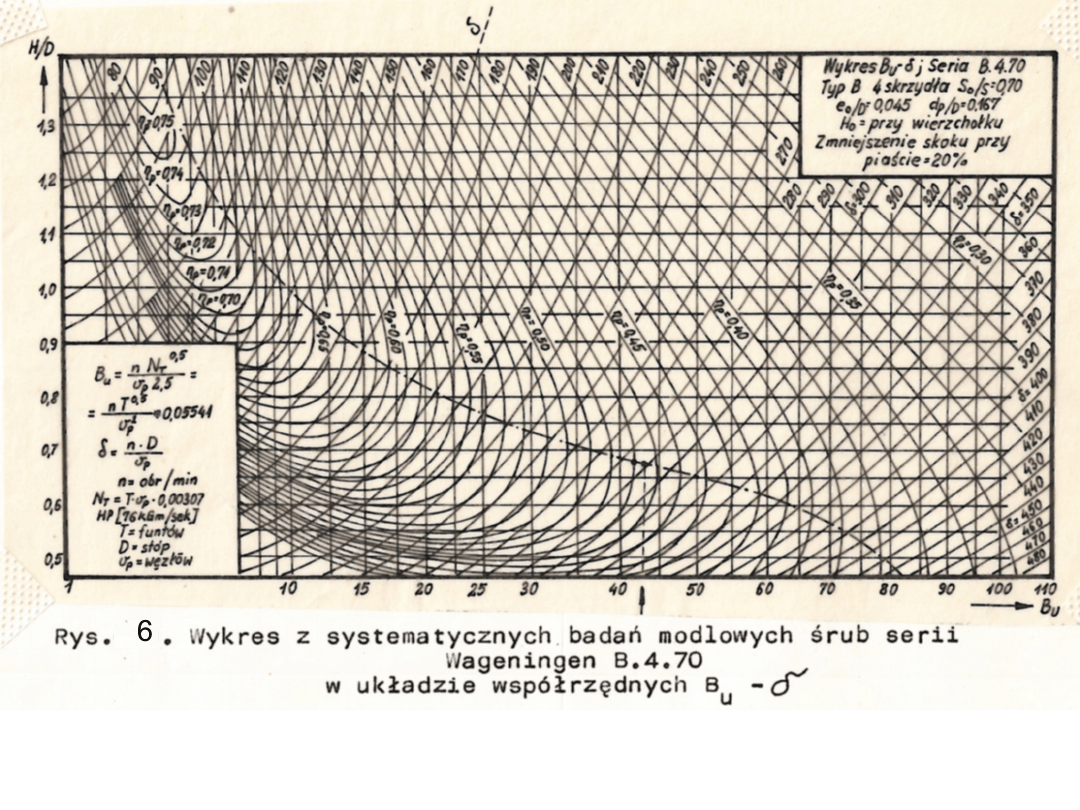
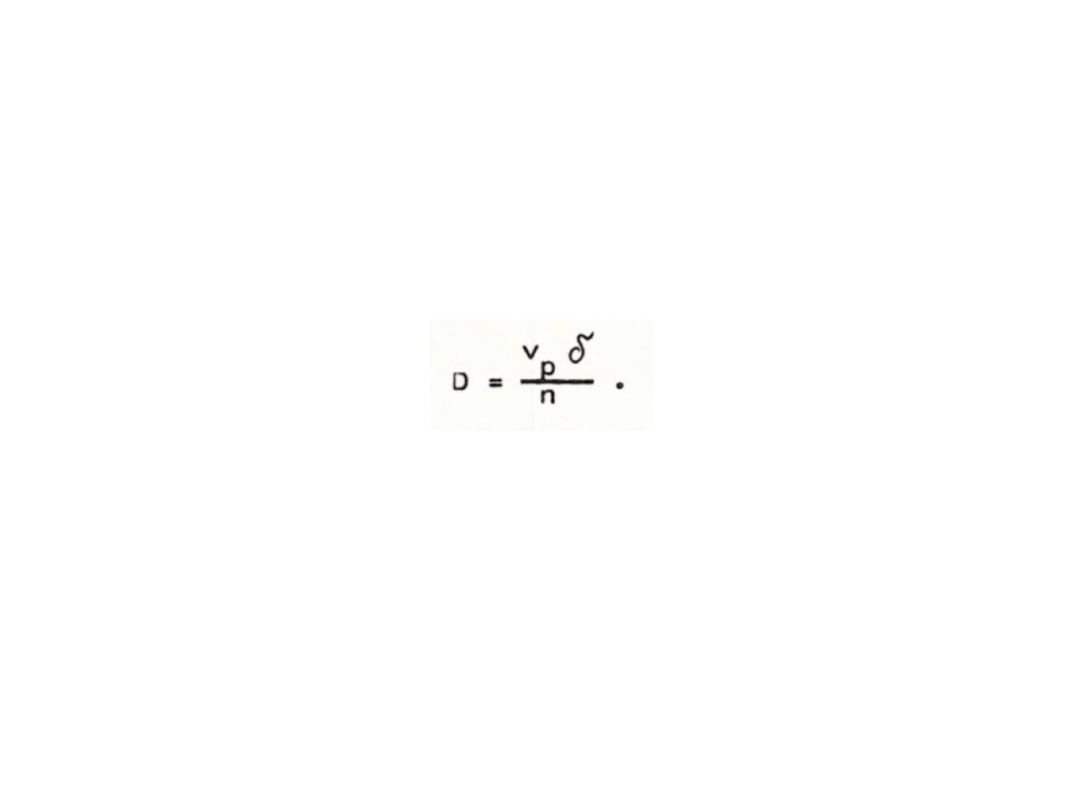
Na rys.6 przedstawiono wykresy śrub serii Wageningen B.4.70

(seria B,

` 4-skrzydłowa, So/S=0,7) w układzie współrzędnych . Na

wykresie naniesiona jest także linia optymalnej sprawności
(kreskowana). Z tego wykresu korzysta się, gdy znany jest napór
zapotrzebowany, pręd kość obrotowa śruby i jej prędkość postępowa.
Oblicza się wtedy współczynnik Bu i z nim wchodzi się na wykres do
przecięcia z linią optymalnej sprawności. Gdy np. Bu= 42, to na linii
optymalnych sprawności otrzymamy pkt 1, któremu odpowiada
δ=285; =0,47 i H/D=0,68. Następnie dla danej δ oblicza się
optymalną średnicę śruby:

Należy przy tym pamiętać, że przy doborze śruby dla okrętów

jednośrubowych zaleca się obniżyć wartość δ o około 5-8%, a przy
doborze śrub dla okrętów wielośrubowych o około 3-4%.

p

B - d

p

h

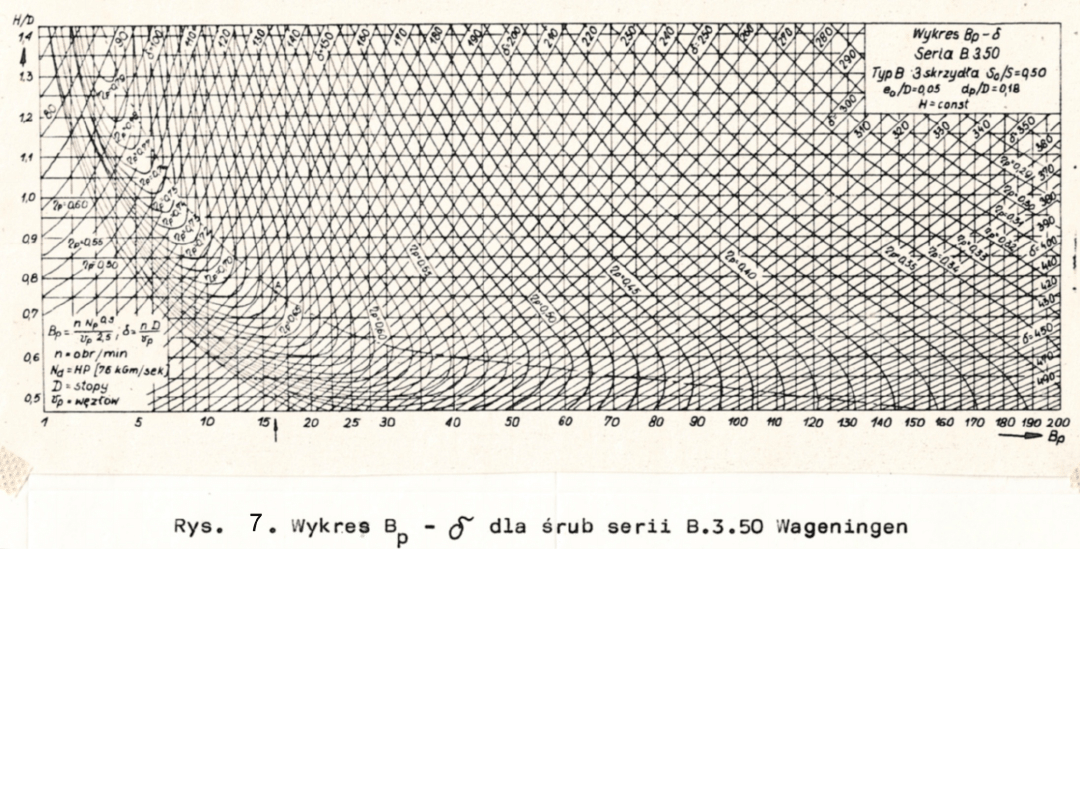
Na rys.7 przedstawiono wykresy śrub serii Wageningen

B.3.50. (seria B, 3-skrzydłowa, So/S=0,5) w układzie

współrzędnych . Z wykresów tych korzysta się, gdy dana

jest moc doprowadzona do śruby (dany jest silnik), prędkość

obrotowa śruby i jej prędkość postępowa. Oblicza się wtedy

bezśrednicowy współczynnik , z którym wchodzi się na

wykres aż do przecięcia linii optymalnej sprawności (linia

kreskowana).

Dla punktu przecięcia określa się wartości δ, i H/D. Np. gdy

=16, to na linii optymalnej sprawności znajduje się pkt A,

któremu odpowiada δ=178, =0,668 i H/D=0,76.

Przy korzystaniu z tych wykresów i poszukiwa niu optymalnej

wartości średnicy śruby należy δ zmniejszyć o 5-8% dla

jednośrubowców i 3-4% dla wielośrubowców.

p

B - d

p

B

p

B

p

h

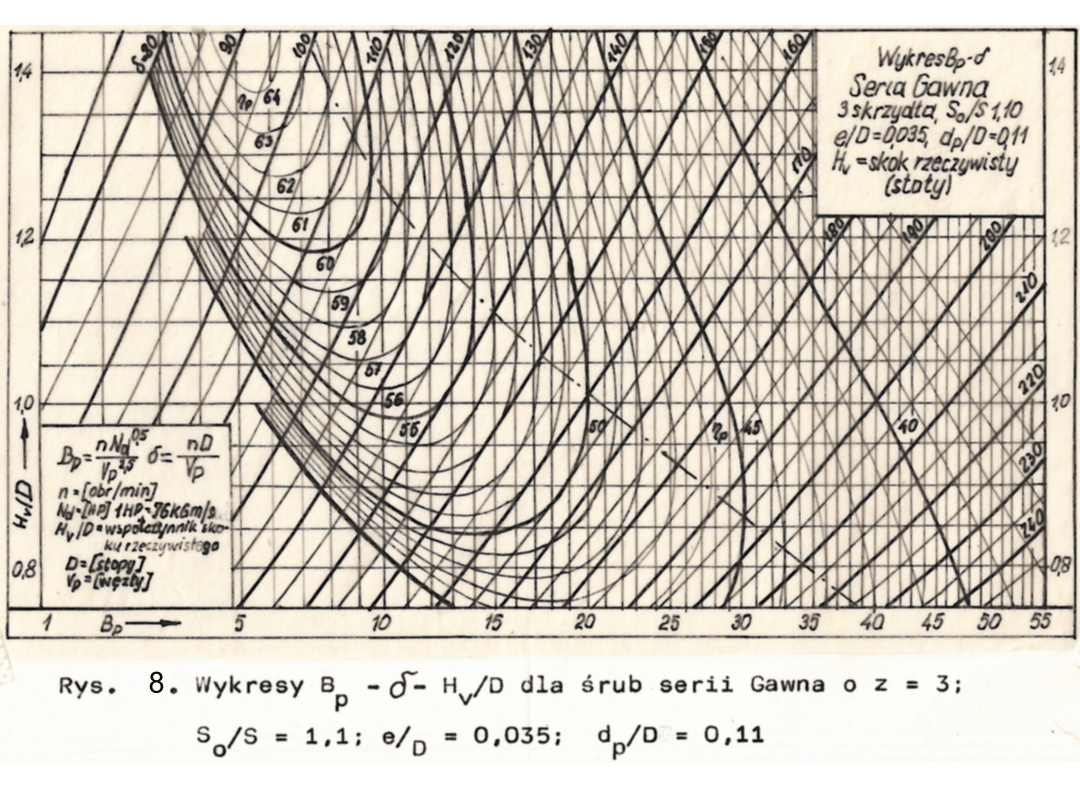
Śruby o profilach Gawna bardzo często stosowane są na

okrętach wojennych, zwłaszcza szybkich, np. typu niszczyciel czy
też kuter. Dobór śruby w oparciu o wyniki badań Gawna można
przeprowadzić wykorzystując wykresy sporządzone w układzie
współrzędnych ,

log lub , .

Na rys.8 przedstawiono wykres dla trzyskrzydłowej śruby

Gawna o So/S=1,1 w układzie współrzędnych . Sposób
korzystania z tego wykresu jest identyczny jak dla śrub serii
Wageningen. Należy tylko zwrócić uwagę, że na wykresie jest
naniesiony współczynnik skoku rzeczywistego

.

p

B - d

p

B - d

T

K

Q

K

J

-

p

B - d

V

H / D