1

Weryfikacja założeń modelu KMNK

Założenia klasycznej regresji liniowej:

1.

Prawdziwe powiązanie zmiennej objaśnianej Y ze zmiennymi objaśniającymi X reprezentuje stabilny hipotetyczny

model liniowy : y

t

=

β

1

x

t1

+

β

2

x

t2

+ … +

β

K

x

tK

,
w zapisie macierzowym Y = X

β.

β.

β.

β.

2.

Zaobserwowana wartość zmiennej objaśnianej Y w momencie t to wartość z modelu hipotetycznego zakłócona

działaniem składnika losowego, tzn.

Y

t

– zmienna losowa

Y

t

= (

β

1

x

t1

+

β

2

x

t2

+ … +

β

K

x

tK

) +

ε

t

,

w zapisie macierzowym

Y = Xβ

β

β

β + εεεε.

3.

Zmienne objaśniające X

1

,..., X

K

są nielosowe, znane.

4.

Oceny parametrów modelu (z punktu 1) wyznaczane są z klasycznej mnk: b = (X’X)

-1

X’y

5.

Przy założeniu, że zmienna objaśniana Y jest zmienną losową estymator wektora parametrów ββββ (z punktu 2) jest też

zmienną losową: b

b

b

b = (X’X)

-1

X’

Y .

6.

Pozostałe założenia dotyczą

składnika losowego

εεεε, tzn.

•

wartość oczekiwana składnika losowego jest równa zero, tj. E(εεεε) = 0 ,

•

wszystkie składniki losowe mają tę samą wariancję równą σ

2

i są wzajemnie nieskorelowane, tj. var(

εεεε) =

E(

εεεεεεεε′′′′)= σ

2

I , gdzie I – macierz jednostkowa oraz

σ

1

2

=

σ

2

2

= … =

σ

T

2

=

σ

2

,

(oznacza, że dyspersja łącznego wpływu zmiennych nie ujętych w modelu nie zmienia się w czasie),

•

składnik losowy ma rozkład normalny, tzn. εεεε ∼ N(0, σ).

Z powyższego wynika, że:

-) wartość oczekiwana losowej zmiennej objaśnianej E(

Y ) = Xβ

β

β

β ,

-) kowariancje składników losowych w różnych obserwacjach są zerowe, tzn. cov (

ε

s

,

ε

r

) = 0 dla s

≠ r,

-) E(X

′ε) = 0, co oznacza, że zmienne objaśniające są nie są skorelowane ze składnikiem losowym i nielosowe.

-) dodatnie i ujemne wahania losowe się znoszą,
-) liczba dodatnich odchyleń zbliżona jest do liczby odchyleń ujemnych,
-) w granicach

± trzech odchyleń standardowych powinno znaleźć się ponad 99,7% wszystkich odchyleń losowych.

Weryfikacja wybranych założeń KMNK:

1. Autokorelacja składnika losowego

Autokorelację składnika losowego rzędu I można zapisać

t

t

t

ξ

ρε

ε

+

=

−1

, gdzie

t

ξ

∼ N(0, σ).

Test Durbina - Watsona

0

:

0

=

ρ

H

wobec hipotezy alternatywnej

0

:

1

>

ρ

H

. Sprawdzianem jest statystyka:

∑

∑

=

=

−

−

=

n

t

t

n

t

t

t

e

e

e

DW

1

2

2

2

1

)

(

Z tablic rozkładu statystyki Durbina – Watsona odczytujemy wartości d (

α

, T, K)

oraz g

_

(

α, T, K), są to wartości:

odpowiednio dolna oraz górna wartość krytyczna:

1.

jeżeli

d

DW

<

, hipotezę

0

H

odrzucamy na rzecz hipotezy alternatywnej

1

H

, oznacza to autokorelację

składnika losowego,

2.

jeżeli

q

DW

>

, nie mamy podstaw do odrzucenia hipotezy

0

H

, oznacza to brak istotnej autokorelacji

składnika losowego,

3.

jeżeli

g

DW

d

≤

≤

, nie mamy podstaw do przyjęcia bądź odrzucenia żadnej z dwu hipotez, jest to tzw.

obszar nieokreśloności testu Durbina – Watsona.

Dla współczynnika korelacji z przedziału [-1,0) liczymy DW’ = 4 – DW i wykorzystujemy tablice jakby to była

korelacja dodatnia.

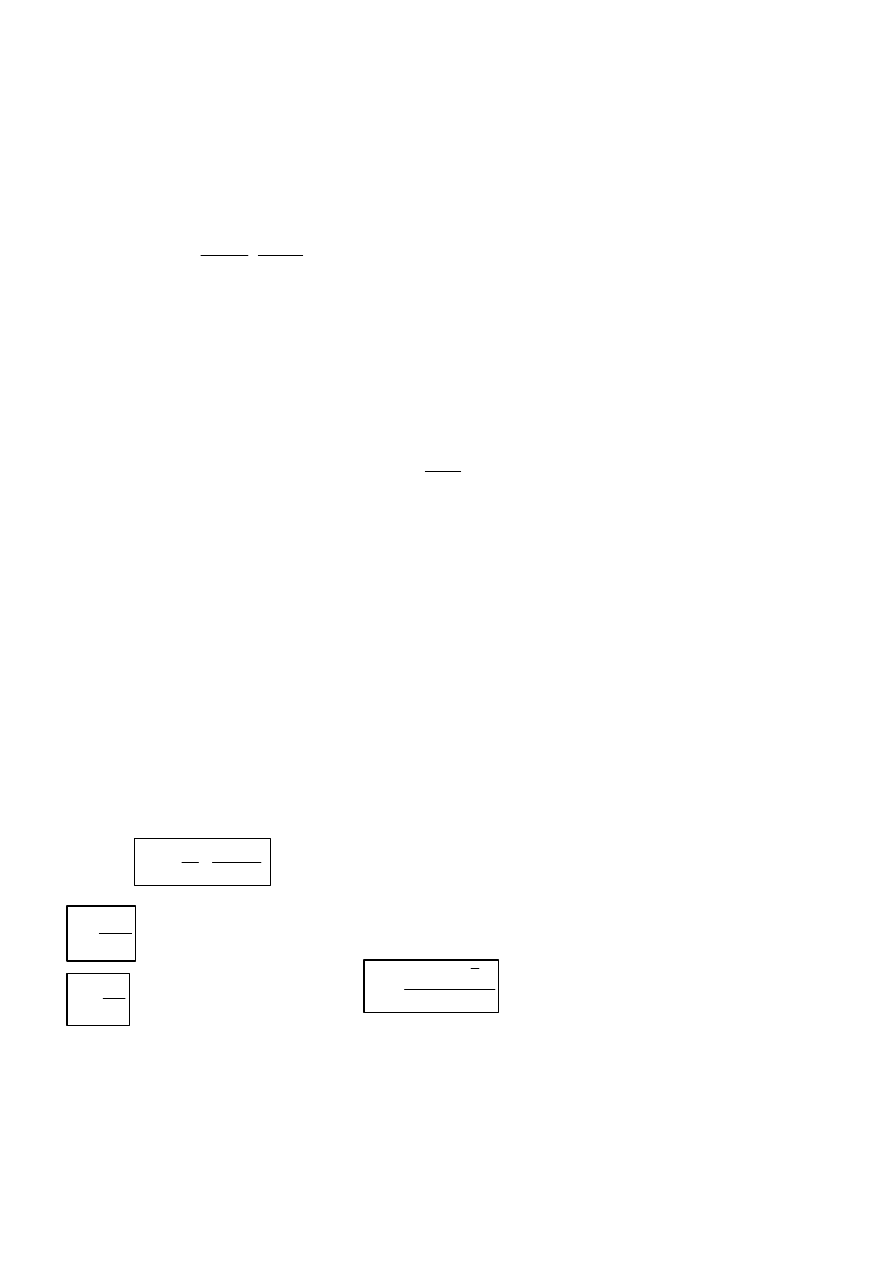
2

Test Breuscha-Godfrey’a do testowania autokorelacji wyższego rzędu.
Na podstawie reszt z modelu budujemy model testowy:

∑

∑

=

=

−

+

+

+

=

K

i

m

s

t

s

t

s

it

i

t

e

X

a

a

e

1

1

0

ε

ρ

H

0

: brak autokorelacji:

ρ

1

= … =

ρ

m

= 0

; H

1

: istotna autokorelacja rzędu m.

Statystyka testowa (mnożnika Lagrange’a) LM = TR

2

ma rozkład

χ

2

z m stopniami swobody lub lepsza

Statystyka

2

2

1

1 R

R

m

Q

T

LMF

−

⋅

−

=

(Q

1

= K+m+1) ma rozkład F dla m i T-Q

1

stopni swobody.

2.

Homoskedastyczność składnika losowego

Testowanie równości wariancji w podpróbach można poprowadzić w oparciu o test Goldfelda – Quanta:

H

0

:

σ

a

2

=

σ

b

2

=

σ

2

wobec H

1

:

σ

a

2

≠ σ

b

2

Wnioskowanie opiera się na porównaniu SKR dwóch funkcji regresji oszacowanych KMNK i przebiega następująco:

a)

Zbiór obserwacji dzielimy na 2 części o liczebności L (jeśli T jest nieparzyste usuwamy środkową

obserwację, uporządkowane względem czasu lub wybranej zmiennej).

b)

Szacujemy parametry funkcji regresji w podpróbach i wyznaczamy SKR

a

i SKR

b

,

c)

Wartość empiryczna statystyki F:

b

a

SKR

SKR

F

=

, jeśli SKR

a

> SKR

b

.

ma graniczny rozkład Fishera – Snedeckora. Wartość krytyczną odczytujemy dla określonego poziomu
istotności

α oraz Q stopni swobody licznika i Q stopni swobody mianownika (Q = ½*T-K-1) = L-K-1.

d)

Jeśli F ≥ F(

α

; Q; Q)

, to H

0

odrzucamy na korzyść hipotezy alternatywnej (składniki losowe mają różne

wariancje).

Test White’a zakłada sprawdzenie istotności regresji wyznaczonej dla kwadratów reszt z zestawem zmiennych modelu i ich
kwadratami. Jeżeli:
Y

t

=

β

0

+

β

1

X

t1

+ …

β

2

X

2

+

ε

t

,

a

σ

t

2

=

α

0

+

α

1

X

t1

+

α

2

X

t2

+

α

3

X

t1

2

+

α

4

X

t2

2

+

α

5

X

1t

X

2t

,

to dla hipotezy H

0

:

α

1

=

α

2

=

α

3

=

α

4

=

α

5

= 0 , wartość statystyki TR

2

ma rozkład

χ

2

dla k stopni swobody. TR

2

>

χ

2

(k)

nakazuje odrzucić hipotezę H

0

i przyjąć, że składnik losowy jest heteroskedastyczny.

3.

Normalność rozkładu składnika losowego

Test Jarque-Bera wykorzystuje własności rozkładu normalnego: symetryczność, skośność (w = 0 – trzeci moment
centralny) i kurtozę, będącą miarą koncentracji wokół średniej(k = 3 - czwarty moment centralny).
H

0

:

ε~N(0,σ); rozkład składnika losowego modelu jest rozkładem normalnym,

H

1

:

¬ε~N(0,σ); składnik losowy modelu ma rozkład różny od normalnego.

Sprawdzianem testu jest statystyka



gdzie:

to współczynnik skośności,

to współczynnik kurtozy.

Przy założeniu prawdziwości H

0

statystyka JB ma rozkład

χ

2

z dwoma stopniami swobody. Obszar odrzucenia hipotezy

zerowej jest prawostronny.













−

+

=

24

)

3

(

6

2

2

K

S

n

JB

2

/

3

2

3

µ

µ

=

S

2

2

4

µ

µ

=

K

n

e

e

k

t

k

)

(

−

=

∑

µ