
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
1
1
Preliminaria
Stosujemy nast puj ce oznaczenia zbiorów liczbowych:
N − zbiór
liczb naturalnych
,
Z − zbiór
liczb całkowitych
,
Q
}
,
:
{
N
Z
∈
∈
=
q
p
q
p
− zbiór
liczb wymiernych
,
R zbiór
liczb rzeczywistych
,
R \Q zbiór
liczb niewymiernych
.
Liczby rzeczywiste mo na te zapisywa w systemie dziesi tnym. Liczby wymierne maj rozwini cia sko -
czone albo niesko czone i okresowe. Natomiast liczby niewymierne (elementy zbioru
R \Q) maj rozwini cia niesko -
czone i nieokresowe.
1. Przykład
...
14159265
,
3
=
=
π
rednica
okr gu
dlugo
π∈ R \Q - Lambert (1766)
Archimedes -
∈
=
≈
π
)
142857
(
,
3
7
22
Q
Mówi c o zdaniach mamy zawsze na uwadze zdania oznajmiaj ce prawdziwe lub fałszywe. Aby upro ci wy-
ra ane własno ci u ywa b dziemy nast puj cych spójników zdaniowych: implikacji ( ), koniunkcji (
∧), alternatywy
(
∨), równowa no ci (⇔) i negacji (~). Dla dowolnych zda α i β napisy
β
α
,
β
∧
α
,
β
∨
α
,
β
⇔
α
, ~
α odpowied-
nio czytamy: „je li
α, to β”, „α i β”, „α lub β”, „α wtedy i tylko wtedy, gdy β”, „nie α”.
Wyra enia maj ce formaln posta zda i staj ce si zdaniami, gdy za wyst puj ce w nich zmienne wstawimy
nazwy konkretnych przedmiotów, nazywa si
funkcjami zdaniowymi
. Niech
α b dzie funkcj zdaniow . Zamiast
• Dla ka dego x zachodzi α piszemy
α
∀
x
,
• Dla pewnego x (istnieje x) zachodzi α piszemy
α
∃
x
.
Znaki
∀ i ∃ nazywa si
kwantyfikatorami
: ogólnym (du ym) i szczegółowym (małym, egzystencjalnym).
Zapis x
∈X oznacza, ze x jest elementem zbioru X.
Zbiór
A nazywa si
podzbiorem zbioru
X, A⊂X, gdy ∀
x
(x
∈A x∈X).
Zbiór nie posiadaj cy adnego elementu oznaczamy symbolem
∅ i nazywamy
zbiorem pustym
.
Niech
A i B b d dowolnymi niepustymi zbiorami. Zbiór
A×B = {(a, b): x∈A ∧ x∈B}
nazywamy produktem kartezja skim zbiorów
A i B.
Dowolny podzbiór
ℜ
ℜ
ℜ
ℜ produktu kartezja skiego A×B nazywamy 2-członow relacj zachodz c mi dzy ele-
mentami zbioru
A i elementami zbioru B.
Iloczyn kartezja ski
[−2,3]×[−1, 2]

Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
2
Niech
2
A
⊂
ℜ
, tzn.
ℜ jest relacj w zbiorze A. ℜ nazywamy
porz dkiem
w
A, je li:
ℜ jest zwrotna:
a
a
a
ℜ
∀
∈A
;
ℜ jest przechodnia:
)
(
,
,
c
a
c
b
b
a
c
b
a
ℜ
ℜ
∧
ℜ
∀
∈A
;
ℜ jest antysymetryczna:
)
(
,
b
a
a
b
b
a
b
a
=
ℜ
∧
ℜ
∀
∈A
.
Relacja
≤ jest porz dkiem w zbiorze liczb.
Relacja
⊂ jest porz dkiem w rodzinie wszystkich podzbiorów dowolnego zbioru.
Zbiór
X⊂R jest ograniczony z dołu, je li ∃
m
∈R
∀
x
∈X
m
≤ x. Liczb m nazywamy
minorant
zbioru
X.
Zbiór
X⊂R jest ograniczony z góry, je li ∃
M
∈R
∀
x
∈X
x
≤ M. Liczb M nazywamy
majorant
zbioru
X.
Zbiór
X⊂R jest ograniczony, je li jest ograniczony z góry i z dołu: ∃
m
∈R
∃
M
∈R
∀
x
∈X
m
≤ x ≤ M
Liczba a jest elementem najmniejszym zbioru
X⊂R, co zapisujemy a = min X, wtedy i tylko wtedy, gdy
a
∈X oraz ∀
∀
∀
∀
x
∈X
a
≤ x
Liczba a jest elementem najwi kszym zbioru
X⊂R, co zapisujemy a = max X, wtedy i tylko wtedy, gdy
a
∈X oraz ∀
∀
∀
∀
x
∈X
x
≤ a
Niech zbiór
X⊂R b dzie ograniczony z dołu. Liczba a jest kresem dolnym tego zbioru, co zapisujemy a = infX, wtedy i
tylko wtedy, gdy a jest elementem najwi kszym w zbiorze minorant zbioru
X.
Niech zbiór
X⊂R b dzie ograniczony z góry. Liczba a jest kresem górnym tego zbioru, co zapisujemy a = supX, wtedy i
tylko wtedy, gdy a jest elementem najmniejszym w zbiorze majorant zbioru
X.
•
}
:
{
1
N
A
∈
=
n
n
, tzn.
A jest zbiorem wyrazów ci gu
)
(
n
a ,
n
a
n
1
= .
1
max
=
A
,
A
min nie istnieje;
1
=
A
sup
,
0
=
A
inf
.
•
}
3
:
{
>
∈
=
x
x
R
A
, tzn.
)
,
3
(
)
3
,
(
∞
∪
−
−∞
=
A
.
A
max nie istnieje,
A
min nie istnieje;
A
sup nie istnieje,
A
inf
nie istnieje.
2
Grupa
Definicja.
Grup
nazywa si struktur (
G, •) zło on z niepustego zbioru G i działania • w tym zbiorze spełniaj cego warunki:
1
° działanie • jest ł czne:
z
y
x
z
y
x
z
y
x
•
•
=
•
•
∀
∈
)
(
)
(
,
,
G
,
2
° istnieje w zbiorze G element neutralny tego działania:
x
x
e
e
x
x
x
=
•
=
•
∀
∃
∈
∈
G
G
,
3
° dla ka dego elementu ze zbioru G istnieje jego element odwrotny wzgl dem działania •:
e
a
a
a
a
a
a
=
•
′
=
′
•
∃
∀
∈
′
∈
G
G
.
Je li ponadto
4
° działanie • jest przemienne:
a
b
b
a
b
a
•
=
•
∀
∈G
,
,
to struktur (
G, •) nazywa si
grup przemienn
(
abelow
).
2. Przykład
Grupami s (i tak si nazywaj ):
(
Z, +) − addytywna grupa liczb całkowitych,
(
Q, +) − addytywna grupa liczb wymiernych,
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
3
(
R, +) − addytywna grupa liczb rzeczywistych,
(
Q
,
⋅) − multiplikatywna grupa liczb wymiernych,
(
R
,
⋅) − multiplikatywna grupa liczb rzeczywistych,
)
},
0
({
+ ,
)
},
1
({
⋅ − grupy jednoelementowe.
)
},
1
,
1
({
⋅
−
− grupa dwuelementowa.
3. Zadanie
Czy
)
,
(
∗
R
, gdzie
1
+
+
=
∗
y
x
y
x
, jest grup przemienn ?
Rozwi zanie.
Poniewa
2
1
)
1
(
1
)
(
)
(
+
+
+
=
+
+
+
+
=
+
∗
+
=
∗
∗
z
y
x
z
y
x
z
y
x
z
y
x
,
2
1
)
1
(
1
)
(
)
(
+
+
+
=
+
+
+
+
=
+
+
∗
=
∗
∗
z
y
x
z
y
x
z
y
x
z
y
x
,
wi c
z
y
x
z
y
x
∗
∗
=
∗
∗
)
(
)
(
, co oznacza, e działanie jest ł czne.
Poniewa
x
y
y
x
y
x
∗
=
+
+
=
∗
1
, wi c działanie jest przemienne.
Element neutralny e działania (przemiennego) jest rozwi zaniem równania
x
e
x
=
∗
:
x
e
x
=
∗
⇔
x
e
x
=
+
+
1
⇔
1
−
=
e
.
Element odwrotny x′ elementu x wzgl dem działania (przemiennego) jest rozwi zaniem równania
e
x
x
=
∗
′
, gdzie e jest elementem neutralnym tego działania.
e
x
x
=
∗
′
⇔
1
1
−
=
+
+
′ x
x
⇔
x
x
−
−
=
′
2
.
Odpowied .
)
,
(
∗
R
, gdzie
1
+
+
=
∗
y
x
y
x
, jest grup przemienn . Elementem neutralnym działania jest
liczba
−1, elementem odwrotnym elementu x jest −2−x.
4. Zadanie
Czy
)
,
(
R
, gdzie
y
x
y
x
y
x
⋅
+
+
=
, jest grup przemienn ?
Rozwi zanie.
Poniewa
xyz
yz
xz
xy
z
y
x
yz
z
y
x
yz
z
y
x
z
y
x
z
y
x
z
y
x
+
+
+
+
+
+
=
+
+
+
+
+
+
=
+
+
=
)
(
)
(
)
(
)
(
)
(
,
xyz
yz
xz
xy
z
y
x
z
xy
y
x
z
xy
y
x
z
y
x
z
y
x
z
y
x
+
+
+
+
+
+
=
+
+
+
+
+
+
=
+
+
=
)
(
)
(
)
(
)
(
)
(
,
wi c
z
y
x
z
y
x
)
(
)
(
=
, co oznacza, e działanie jest ł czne.
Poniewa
x
y
y
x
y
x
=
+
+
=
1
, wi c działanie jest przemienne.
Element neutralny e działania (przemiennego) jest rozwi zaniem równania
x
e
x
= , dla ka dego x∈R:
x
e
x
= , dla ka dego x∈R ⇔
x
xe
e
x
=
+
+
, dla ka dego x
∈R ⇔
0
=
e
.
Element odwrotny x′ elementu x wzgl dem działania (przemiennego) jest rozwi zaniem równania
e
x
x
=
′
, gdzie e jest elementem neutralnym tego działania.
e
x
x
=
′
⇔
0
=
′
+
+
′
x
x
x
x
⇔
x
x
x
+
−
=
′
1
, o ile
1
−
≠
x
.
Odpowied
. Nie. Grup przemienn jest
)
},
1
{
\
(
−
R
. Elementem neutralnym działania jest 0, elementem
odwrotnym elementu x jest
1
+
−
x
x
.

Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
4
3
Pier cie
Definicja.
Pier cieniem
nazywamy trójk
)
,
,
(
2
1
P
, gdzie P jest niepustym zbiorem a
1
,
2
dwoma działaniami w zbiorze P
takimi, e para
)
,
(
1
P
jest grup abelow , działanie
2
jest ł czne oraz obustronnie rozdzielne wzgl dem działania
1
,
tzn.
dla ka dych
P
z
y
x
∈
,
,
:
)
(
)
(
)
(
2
1
2
1
2
z
x
y
x
z
y
x
=
,
dla ka dych
P
z
y
x
∈
,
,
:
)
(
)
(
)
(
2
1
2
2
1
z
y
z
x
z
y
x
=
.
W tej definicji nie damy przemienno ci działania
2
, ani istnienie dla niego elementu neutralnego.
Działanie
1
nazywa si
dodawaniem
, działanie
2
nazywa si
mno eniem
.
Pier cie , w którym mno enie jest przemienne, nazywa si
pier cieniem przemiennym
.
Je eli w pier cieniu istnieje element neutralny mno enia (działania
2
), to element taki nazywa si
jedno ci
pier cienia
, za pier cie zawieraj cy jedno nazywa si
pier cieniem z jedno ci
.
5. Przykład
Pier cieniami s trójki (
Z, +, ⋅), (Q, +, ⋅), (R, +, ⋅).
Zbiory liczbowe, tzn. podzbiory zbioru
R, w których działaniami s dodawanie i mno enie liczb i które s pier-
cieniami, nazywa si
pier cieniami liczbowymi
.
Wy ej wymienione pier cienie s pier cieniami liczbowymi.
Trójka
)
,
},
0
({
⋅
+
te jest pier cieniem liczbowym.
Innymi przykładami pier cieni liczbowych s : pier cie liczb całkowitych parzystych (jest to pier cie bez jed-
no ci), pier cie całkowitych wielokrotno ci liczby naturalnej n.
Pier cienie liczbowe s przemienne.
Pier cieniami s (nie s to pier cienie liczbowe) trójki
)
,
,
(
2
1
Z
,
)
,
,
(
2
1
Q
,
)
,
,
(
2
1
R
, gdzie
1
1
+
+
=
y
x
y
x
,
xy
y
x
y
x
+
+
=
2
.
Trójka
)
,
],
[
(
⋅
+
x
P
, gdzie
]
[x
P
jest zbiorem wielomianów o współczynnikach z pier cienia P, jest pier cieniem.
W szczególno ci pier cieniami s :
)
,
],
[
(
⋅
+
x
Z
,
)
,
],
[
(
⋅
+
x
Q
,
)
,
],
[
(
⋅
+
x
R
.
6. Zadanie
Czy (
Z, +, ), gdzie a b = 1, jest pier cieniem?
Rozwi zanie.
Struktura (
Z, +) jest grup abelow .
Działanie jest ł czne, gdy a (b c) = 1 = (a b c.
Poniewa a (b c) = 1, a b+ a c) = 1 + 1 = 2, wi c działanie nie jest rozdzielne wzgl dem dodawania.
Dlatego (
Z, +, ), gdzie a b = 1, nie jest pier cieniem.
Je li pier cie
)
,
,
(
2
1
P
jest taki, e para
)
},
0
{
\
(
2
P
, gdzie 0 jest elementem neutralnym działania
1
, jest
grup , to nazywamy go
ciałem
. Bardziej precyzyjnie wyra a to kolejna definicja.
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
5
4
Ciało
Definicja.
Rozwa my struktur z dwiema operacjami i dwoma wyró nionymi elementami.
Operacje nazwijmy dodawaniem i mno eniem, a elementy wyró nione oznaczmy symbolami 0 i 1.
Struktura
)
,
,
(
⋅
+
= F
F
jest
ciałem
wtedy i tylko wtedy, gdy
1)
)
,
(
+
F
jest grup przemienn ,
2)
)
,
(
⋅
{0}
\
F
jest grup ,
3) mno enie jest obustronnie rozdzielne wzgl dem dodawania.
Je li w punkcie (2) u yjemy zwrotu „jest grup przemienn ”, to ciało nazywamy
ciałem przemiennym
. W tym
przypadku punkt (3) ma posta „mno enie jest rozdzielne wzgl dem dodawania”.
Ciało, którego elementy s liczbami, a działania s działaniami arytmetycznymi, nazywa si
ciałem liczbowym
.
7. Przykład
Ciałami przemiennymi s :
(
Q, +, ⋅) - ciało liczb wymiernych. Jest to najmniejsze ciało liczbowe.
(
R, +, ⋅) - ciało liczb rzeczywistych.
Fakt.
Zbiór liczb jest ciałem liczbowym wtedy i tylko wtedy, gdy wykonalne s w nim dodawanie, odejmowanie, mno enie i
dzielenie przez element ró ny od zera.
8. Zadanie
Wykaza , e
}
,
:
2
{
)
2
(
Q
Q
∈
+
=
b
a
b
a
jest ciałem liczbowym.
Rozwi zanie
.
Wynika to z nast puj cych równo ci:
2
)
(
)
(
)
2
(
)
2
(
d
b
c
a
d
c
b
a
+
+
+
=
+
+
+
,
2
)
(
)
(
)
2
(
)
2
(
d
b
c
a
d
c
b
a
−
+
−
=
+
−
+
,
2
)
(
)
2
(
)
2
)(
2
(
bc
ad
bd
ac
d
c
b
a
+
+
+
=
+
+
,
2
2
2
2
)
2
)(
2
(
)
2
)(
2
(
2
2
2
2
2
2
d
c
ad
bc
d
c
bd
ac
d
c
d
c
d
c
b
a
d
c
b
a
−
−
+
−
−
=
−
+
−
+
=
+
+
.
5
Ciało liczb zespolonych
Definicja.
Zbiór
}
,
:
)
,
{(
2
R
R
R
∈
∈
=
y
x
y
x
nazywa si
płaszczyzn
, za jego elementy – punktami.
Struktura
)
,
,
(
2
⋅
+
= R
C
, gdzie + i
⋅ s działaniami okre lonymi nast puj co:
)
,
(
)
,
(
)
,
(
2
2
1
1
2
1
2
1
b
a
b
a
b
b
a
a
+
+
=
+
,
)
,
(
)
,
(
)
,
(
1
2
2
1
2
2
1
1
2
1
2
1
b
a
b
a
b
a
b
a
b
b
a
a
+
−
=
⋅
jest ciałem. Nazywa si je
ciałem liczb zespolonych
(interpretacja Hamiltona).
Zatem liczba zespolona to para liczb rzeczywistych. Liczba a nosi nazw cz ci rzeczywistej, za b cz ci uro-
jonej liczby zespolonej
)
,
( b
a
z
=
.

Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
6
Liczb zespolon
)
0
,
(a
mo na uto samia z liczb rzeczywist a. W zwi zku z tym mo emy powiedzie , e
C
R ⊂ .
Liczb zespolon
)
1
,
0
(
oznaczamy symbolem i i nazywamy
jedno ci urojon
. (Symbol „i ” pochodzi od
imaginarius (łac. urojony); wprowadzili go Tartaglia i Cardano).
Zauwa my, e
bi
a
b
a
b
a
b
a
+
≡
⋅
+
=
+
=
)
1
,
0
(
)
0
,
(
)
0
,
(
)
,
0
(
)
0
,
(
)
,
(
.
Zatem
)
(
}
1
,
,
:
{
2
i
i
b
a
bi
a
R
R
C
=
−
=
∈
+
=
Liczb
bi
a
z
−
=
nazywamy sprz on z liczb
bi
a
z
+
=
.
Oczywi cie
2
2
)
)(
(
b
a
bi
a
bi
a
z
z
+
=
−
+
=
⋅
.
Działania na liczbach zespolonych w postaci algebraicznej wykonujemy tak, jak na wielomianach, pami taj c o
warunku
1
2
−
=
i
.
9. Przykład
i
i
i
i
i
i
i
10
5
8
10
3
8
6
4
3
)
4
3
)(
2
1
(
2
+
=
+
+
−
=
−
+
+
−
=
+
−
−
,
i
i
i
i
i
i
i
i
i
i
i
i
5
6
5
13
2
2
5
6
13
4
5
10
4
8
)
2
)(
2
(
)
2
)(
5
4
(
2
5
4
+
=
+
=
−
−
+
−
=
+
−
−
+
=
+
+
.
10. Zadanie
W zbiorze liczb zespolonych rozwi emy równanie
0
3
4
2
=
+
− x
x
.
0
5
4
2
=
+
− x
x
⇔
0
1
)
2
(
2
=
+
−
x
⇔
0
)
2
(
2
2
=
−
−
i
x
⇔
0
)
2
)(
2
(
=
+
−
−
−
i
x
i
x
⇔
}
2
,
2
{
i
i
x
−
+
∈
6
Macierze
Definicja macierzy.
Niech b dzie dany zbiór
{
} {
}
m
n
,...,
2
,
1
,...,
2
,
1
×
par liczb naturalnych. Je li ka dej spo ród tych par przyporz dkujemy
element z ciała F, to takie przyporz dkowanie nazywa si
macierz o elementach z ciała F
. Liczb przyporz dkowan
parze
)
,
( j
i
oznaczamy symbolem
ij
a .
Macierze zapisujemy zwykle w postaci tabel
=
nm
n
n
m
m
a
a
a
a
a
a
a
a
a
2
1
2
22
21
1
12
11
A
.
Liczby
ij
a
nazywamy
wyrazami
lub
elementami macierzy
, poziome rz dy
−
wierszami macierzy
, a pionowe
− jej
kolum-
nami
. O elemencie
ij
a
mówimy, e nale y do i
−−−−tego wiersza oraz j−−−−tej kolumny. Macierze oznacza si du ymi literami.
Macierz kwadratowa
− ka da macierz, której liczba wierszy jest równa liczbie kolumn. Liczb wierszy (kolumn) nazy-
wa si
stopniem macierzy
kwadratowej. Elementy macierzy, które maj ten sam numer wiersza i kolumny, tworz
głów-
n przek tn macierzy
.
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
7
Definicja dodawania macierzy.
Dwie macierze mo na doda wtedy i tylko wtedy, gdy maj te same wymiary;
dodajemy elementy na tych samych
pozycjach
.
11. Przykład
Je li
−
−
=
0
7
5
32
12
11
A
,
=
16
7
12
3
4
1
B
, to
=
+
+
−
+
−
+
+
+
=
+
−
−
=
+
16
0
7
35
16
12
16
0
7
7
12
5
3
32
4
12
1
11
16
7
12
3
4
1
0
7
5
32
12
11
B
A
.
Fakt
.
Zbiór
m
n
M
×
(wszystkich macierzy o n wierszach, m kolumnach) z dodawaniem macierzy jako działaniem jest grup
przemienn
.
Twierdzenie to wypowiadamy te nast puj co:
Struktura (
m
n
M
×
, +) jest addytywn grup macierzy.
Definicja mno enia macierzy przez liczb (skalar)
.
Ka d macierz mo na pomno y przez ka dy element ciała (skalar)
−
mno ymy wszystkie elementy macierzy przez
ten skalar
.
12. Przykład
Je li
=
3
7
8
4
5
6
3
2
1
A
, to
=
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
=
⋅
=
9
21
24
12
15
18
9
6
3
3
3
7
3
8
3
4
3
5
3
6
3
3
3
2
3
1
3
3
7
8
4
5
6
3
2
1
3
3
A
.
Definicja iloczynu Cauchy’ego macierzy.
Mno enie macierzy
jest uzale nione od spełnienia wymagania dotycz cego wymiaru czynników, a mianowicie
liczba
kolumn czynnika pierwszego jest równa liczbie wierszy czynnika drugiego
.
Iloczynem macierzy
A i B nazywamy macierz C, której element
is
c
powstaje przez pomno enie skalarne i
−tego wiersza
macierzy
A przez s−t kolumn macierzy B.
Tak okre lone mno enie macierzy nie jest działaniem w zbiorze wszystkich macierzy nad danym ciałem, gdy
nie jest wykonalne dla ka dej pary macierzy.
13. Przykład
=
⋅
−
+
⋅
+
⋅
⋅
−
+
⋅
+
⋅
−
⋅
−
+
⋅
+
⋅
⋅
+
⋅
−
+
⋅
⋅
+
⋅
−
+
⋅
−
⋅
+
⋅
−
+
⋅
=
−
⋅
−
−
7
)
7
(
5
4
4
3
2
)
7
(
4
4
3
3
)
1
(
)
7
(
7
4
2
3
7
5
5
)
3
(
4
2
2
5
4
)
3
(
3
2
)
1
(
5
7
)
3
(
2
2
7
2
1
5
4
7
4
3
2
7
4
3
5
3
2
−
−
17
11
41
28
4
22
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
⋅
=
⋅
4
1
4
4
4
1
1
4
4
0
0
4
1
0
0
2
0
2
0
2
2
0
4
0
0
0
1
0
1
0
2
2
0
4
0
0
0
1
2
1
2
0
2
0
1
1
0
2
0
2
1
2
1
0
B
A
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
⋅
=
⋅
4
4
1
1
4
4
4
1
4
0
0
4
0
2
2
0
1
0
1
0
0
0
4
0
2
2
0
2
0
2
0
0
1
4
0
0
1
0
2
0
2
1
2
1
0
0
1
2
1
2
0
2
0
1
A
B
=
⋅
f
e
d
c
b
a
f
e
d
c
b
a
1
0
0
1
,
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
8
=
⋅
f
e
d
c
b
a
f
e
d
c
b
a
1
0
0
0
1
0
0
0
1
.
Macierz jednostkowa
- macierz diagonalna, w której elementy poło one na głównej przek tnej s jedynkami. Symbo-
lem
n
E oznacza si macierz jednostkow stopnia n, gdzie
2
≥
n
.
Fakt.
Trójka
)
,
),
(
(
⋅
+
×
F
M
n
n
jest pier cieniem nieprzemiennym z jedno ci .
14. Zadanie
Wykonaj wskazane działania
−
−
−
−
−
1
5
1
2
2
4
3
2
1
3
1
1
6
2
.
Rozwi zanie.
Korzystaj c z definicji mno enia macierzy przez liczb (mno ymy wszystkie wyrazy macierzy przez t liczb ) i definicji
dodawania macierzy (dodajemy wyrazy na tych samych pozycjach) otrzymamy
−
−
−
−
−
1
5
1
2
2
4
3
2
1
3
1
1
6
2
−
−
−
−
+
−
−
=
3
15
3
6
6
12
4
2
6
2
2
12
−
−
−
=
7
13
9
4
4
0
.
15. Zadanie
Wykonaj wskazane działania
−
−
−
1
2
1
3
0
2
5
5
2
4
2
1
3
.
Rozwi zanie.
−
−
−
1
2
1
3
0
2
5
5
2
4
2
1
3
−
−
−
−
+
−
=
5
10
5
15
0
10
5
2
4
2
1
3
−
−
−
−
=
10
12
1
13
1
7
.
16. Zadanie
Rozwi za równanie macierzowe
)
1
0
0
2
1
0
3
2
1
(
2
2
1
3
1
3
2
3
2
1
+
−
=
+
X
X
.
Rozwi zanie
Korzystaj c z definicji dodawania macierzy i mno enia macierzy przez liczb kolejno otrzymamy
)
1
0
0
2
1
0
3
2
1
(
2
2
1
3
1
3
2
3
2
1
+
−
=
+
X
X
⇔
−
−
=
+
1
0
0
2
1
0
3
2
1
2
2
1
3
1
3
2
3
2
1
2
X
X
⇔
−
−
−
−
−
−
+
−
−
−
−
−
−
−
−
−
=
2
0
0
4
2
0
6
4
2
2
1
3
1
3
2
3
2
1
3
X
⇔
−
−
−
−
−
−
−
−
−
=
−
−
−
−
−
−
−
−
−
=
3
4
3
1
3
5
3
5
3
2
3
1
1
3
2
1
4
1
3
5
5
2
9
6
3
X
.
Rozwi zaniem równania jest macierz
−
−
−
−
−
−
−
−
−
=
3
4
3
1
3
5
3
5
3
2
1
3
2
1
X
.
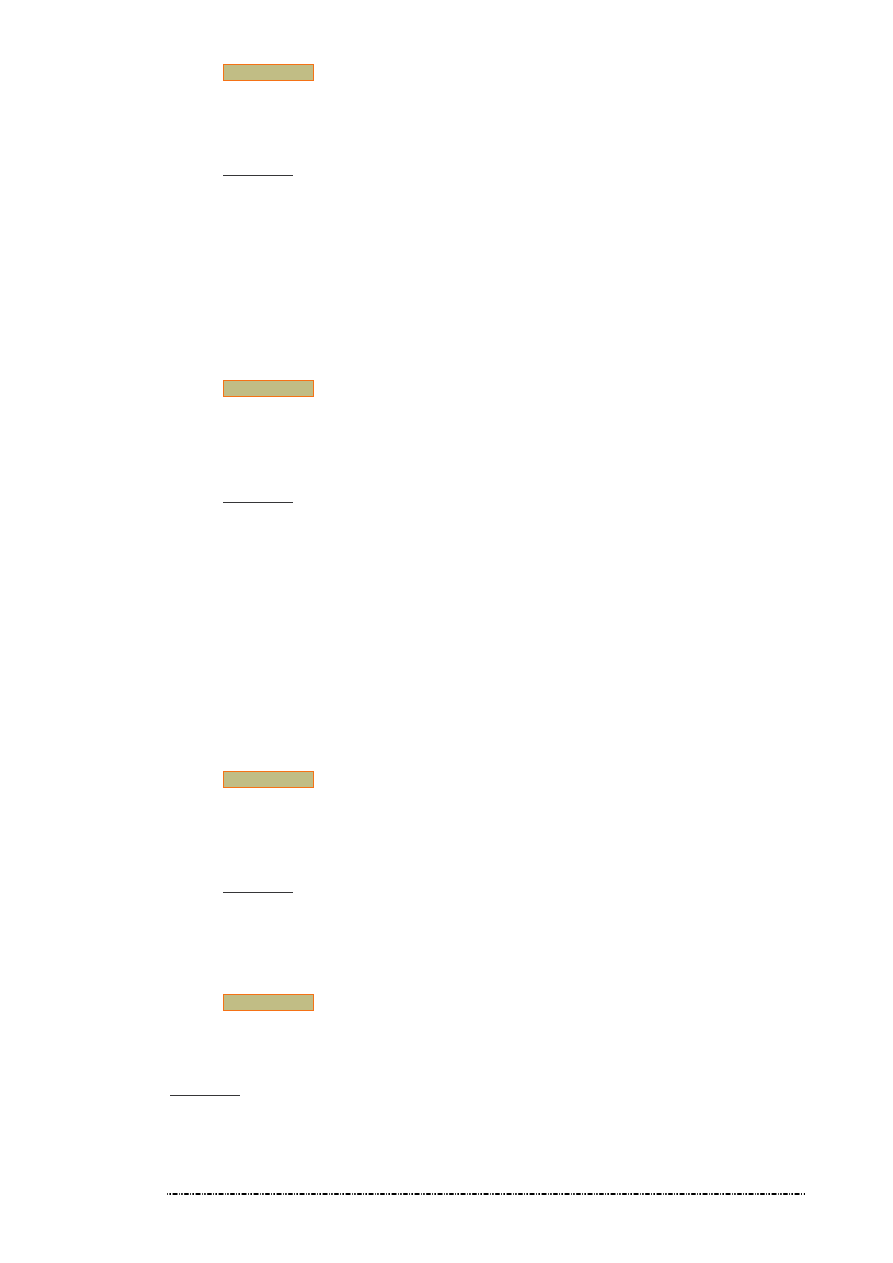
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
9
17. Zadanie
Obliczy iloczyn macierzy
−
−
=
7
4
3
5
3
2
A
,
−
=
7
2
1
5
4
7
4
3
2
B
.
Rozwi zanie
Pierwsza macierz jest wymiaru 2
×3, a druga wymiaru 3×3, wi c mno enie
B
A ⋅
jest wykonalne. Natomiast iloczyn
A
B ⋅ nie istnieje, gdy pierwszy czynnik ma 3 kolumny, a drugi czynnik ma 2 wiersze.
=
−
⋅
−
−
=
⋅
7
2
1
5
4
7
4
3
2
7
4
3
5
3
2
B
A
⋅
−
+
⋅
+
⋅
⋅
−
+
⋅
+
⋅
−
⋅
−
+
⋅
+
⋅
⋅
+
⋅
−
+
⋅
⋅
+
⋅
−
+
⋅
−
⋅
+
⋅
−
+
⋅
7
)
7
(
5
4
4
3
2
)
7
(
4
4
3
3
)
1
(
)
7
(
7
4
2
3
7
5
5
)
3
(
4
2
2
5
4
)
3
(
3
2
)
1
(
5
7
)
3
(
2
2
a wi c
−
−
=
⋅
17
11
41
28
4
22
B
A
.
18. Zadanie
Obliczy macierz
A
B
B
A
⋅
−
⋅
, je li:
=
1
0
2
0
2
1
2
1
0
A
,
=
0
1
2
1
2
0
2
0
1
B
.
Rozwi zanie
Poniewa
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
⋅
=
⋅
4
1
4
4
4
1
1
4
4
0
0
4
1
0
0
2
0
2
0
2
2
0
4
0
0
0
1
0
1
0
2
2
0
4
0
0
0
1
2
1
2
0
2
0
1
1
0
2
0
2
1
2
1
0
B
A
,
=
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
+
=
⋅
=
⋅
4
4
1
1
4
4
4
1
4
0
0
4
0
2
2
0
1
0
1
0
0
0
4
0
2
2
0
2
0
2
0
0
1
4
0
0
1
0
2
0
2
1
2
1
0
0
1
2
1
2
0
2
0
1
A
B
,
wi c
−
−
−
=
−
=
⋅
−
⋅
0
3
3
3
0
3
3
3
0
4
4
1
1
4
4
4
1
4
4
1
4
4
4
1
1
4
4
A
B
B
A
.
19. Zadanie
Dla macierzy
=
0
0
0
1
0
0
1
1
0
A
obliczy
2
A ,
3
A ,
4
A .
Rozwi zanie
=
⋅
=
⋅
=
0
0
0
0
0
0
1
0
0
0
0
0
1
0
0
1
1
0
0
0
0
1
0
0
1
1
0
2
A
A
A
,
=
⋅
=
=
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
1
1
0
0
0
0
0
0
0
1
0
0
2
3
A
A
A
,
=
0
0
0
0
0
0
0
0
0
4
A
.
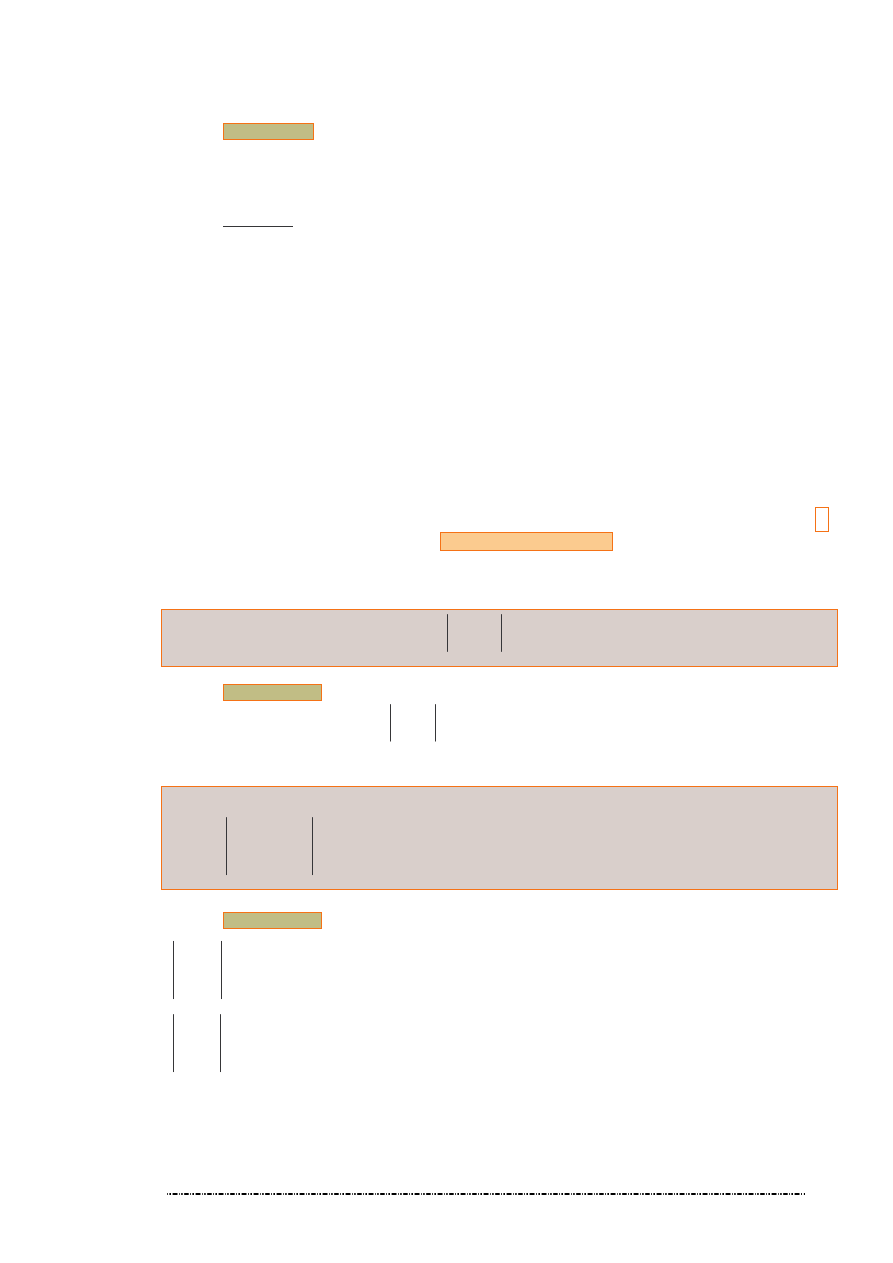
20. Zadanie
Obliczy
9
16
B
B −
dla
−
=
1
1
1
1
B
.
Rozwi zanie
−
=
−
⋅
−
=
0
2
2
0
1
1
1
1
1
1
1
1
2
B
,
−
−
=
−
⋅
−
=
=
4
0
0
4
0
2
2
0
0
2
2
0
2
2
4
B
B
B
,
=
−
−
⋅
−
−
=
=
16
0
0
16
4
0
0
4
4
0
0
4
4
4
8
B
B
B
,
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
10
=
−
−
−
=
−
⋅
−
−
=
−
0
0
0
0
16
16
16
16
16
16
16
16
1
1
1
1
16
0
0
16
16
16
16
16
16
9
B
B
.
21. Zadanie
Obliczy warto wielomianu
5
13
7
)
(
2
3
−
+
−
=
x
x
x
x
P
dla macierzy
−
−
−
=
1
2
2
1
3
1
3
2
5
A
.
Rozwi zanie
Znajdujemy macierze
−
−
−
=
⋅
=
7
8
10
5
9
6
14
10
21
2
A
A
A
,
−
−
−
=
=
31
30
44
22
29
29
59
44
87
2
3
A
A
A
.
Dlatego
=
−
+
−
=
E
A
A
A
A
5
13
7
)
(
2
3
P
−
−
−
=
31
30
44
22
29
29
59
44
87
−
−
−
−
7
8
10
5
9
6
14
10
21
7
−
−
−
+
1
2
2
1
3
1
3
2
5
13
=
−
1
0
0
0
1
0
0
0
1
5
0
0
0
0
0
0
0
0
0
7
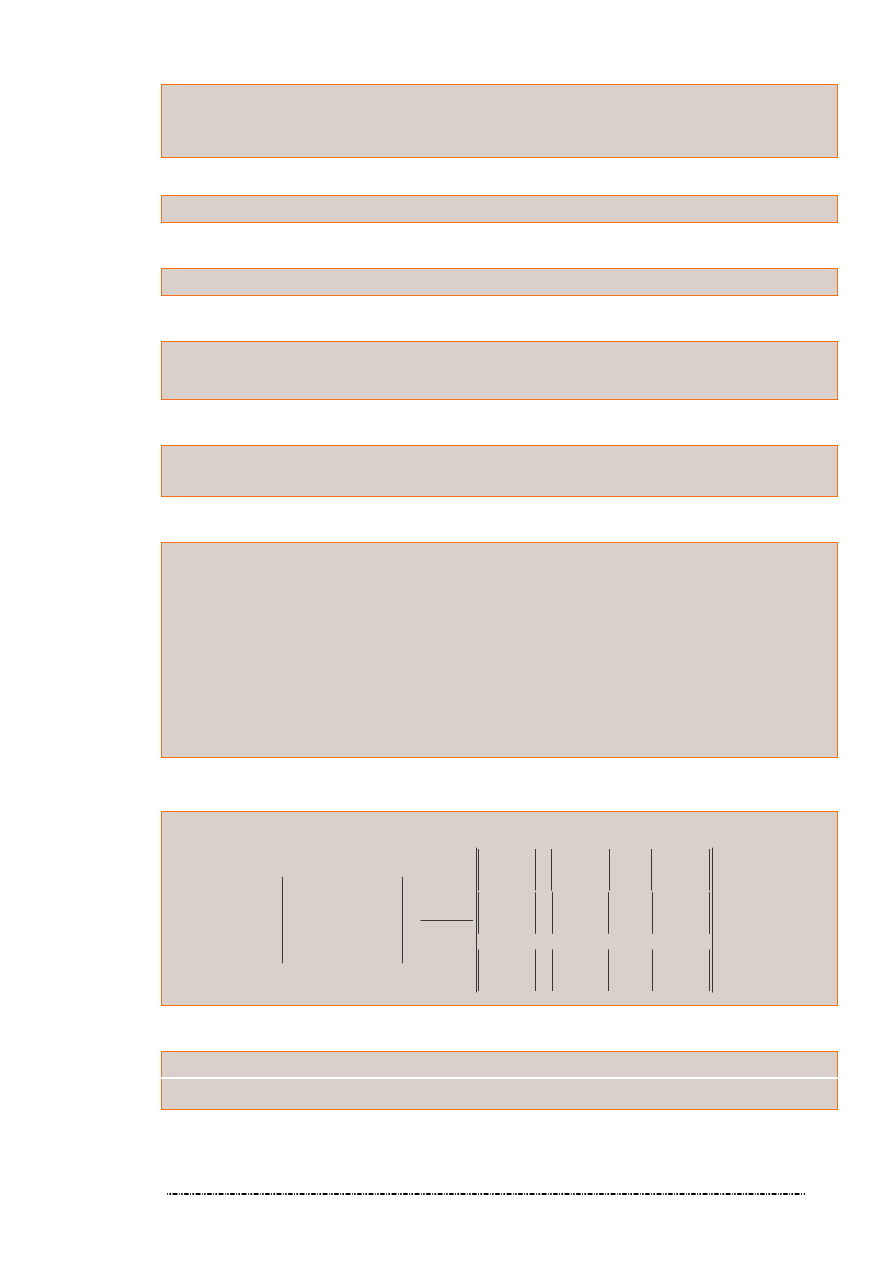
Wyznacznik macierzy
Obliczanie wyznacznika macierzy 2-go stopnia.
21
12
22
11
22
21
12
11
a
a
a
a
a
a
a
a
−
=
.
22. Przykład
1
15
16
5
3
)
8
(
)
2
(
8
5
3
2
=
−
=
⋅
−
−
⋅
−
=
−
−
Obliczanie wyznacznika macierzy 3-go stopnia.
Schemat Sarrusa
.
=
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
(
)
32
21
13
31
23
12
33
22
11
a
a
a
a
a
a
a
a
a
+
+
−
(
)
32
23
11
33
21
12
31
22
13
a
a
a
a
a
a
a
a
a
+
+
.
23. Przykład
202
3
2
5
2
7
5
7
8
8
7
7
2
8
5
5
3
8
2
3
7
8
5
8
2
7
5
2
30
70
448
98
200
48
−
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
−
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
0
1
2
3
4
5
6
7
8
0
)
3
1
8
0
7
5
6
4
2
(
)
3
7
2
6
1
5
0
4
8
(
24
0
48
42
30
0
=
⋅
⋅
+
⋅
⋅
+
⋅
⋅
−
⋅
⋅
+
⋅
⋅
+
⋅
⋅
=
Podstawowe informacje o wyznacznikach
Omówimy kilka podstawowych własno ci wyznaczników, które s wspólne dla wyznaczników macierzy kwa-
dratowych wszystkich stopni.
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
11
Informacja 1
Transponowanie macierzy kwadratowej nie zmienia wyznacznika tej macierzy (wyznacznik macierzy transponowanej
jest równy wyznacznikowi wyj ciowej macierzy):
A
A
det
det
=
T
.
Informacja 2
Zamiana dwu wierszy (kolumn) macierzy kwadratowej zmienia warto wyznacznika tej macierzy na przeciwn .
Informacja 3
Je li w macierzy dwa wiersze (dwie kolumny) s identyczne, to wyznacznik tej macierzy jest zerem.
Informacja 4
Je li macierz
B powstaje z macierzy A przez pomno enie wszystkich elementów pewnego wiersza (kolumny) przez
liczb
α
, to
A
B
det
det
⋅
α
=
.
Informacja 5
Dodanie do wiersza (kolumny) macierzy kwadratowej wielokrotno ci innego wiersza (kolumny) nie zmienia wyznaczni-
ka tej macierzy.
Informacja 6 - rozwini cia Laplace'a
ks
M
det
−−−− minor elementu
ks
a
macierzy
A −−−−
ks
M
powstaje przez wykre lenie k−−−−tego wiersza oraz s−−−−tej ko-
lumny z macierzy
A,
ks
s
k
ks
A
M
det
)
1
(
+
−
=
−−−− dopełnienie algebraiczne elementu
a
ks
macierzy
A,
in
in
i
i
i
i
n
j
ij
ij
A
a
A
a
A
a
A
a
+
+
+
=
=
=
...
det
2
2
1
1
1
A
[rozwini cie według i
−−−−tego wiersza],
nj
nj
j
j
j
j
n
i
ij
ij
A
a
A
a
A
a
A
a
+
+
+
=
=
=
...
det
2
2
1
1
1
A
[rozwini cie według j
−−−−tej kolumny].
Informacja 7 - algorytm Chio
Wyznacznik macierzy n
−−−−tego stopnia mo na obliczy według wzoru (o ile
0
11
≠
a
):
nn
n
n
n
n
n
n
n
n
n
n
n
nn
n
n
n
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
1
1
11
3
1
13
11
2
1
12
11
3
31
1
11
33
31
13
11
32
31
12
11
2
21
1
11
23
21
13
11
22
21
12
11
2
11
2
1
2
22
21
1
12
11
)
(
1
−
=
.
Informacja 8 - twierdzenie Cauchy'ego
Wyznacznik iloczynu dwu macierzy kwadratowych jest równy iloczynowi wyznaczników tych macierzy:
A
B
B
A
B
A
det
det
det
det
)
det(
⋅
=
⋅
=
⋅
.
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
12
Informacja 9
nn
nn
n
n
nn
n
n
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
⋅
⋅
⋅
=
=
22
11
2
1
22
21
11
2
22
1
12
11
0
0
0
det
0
0
0
det
.
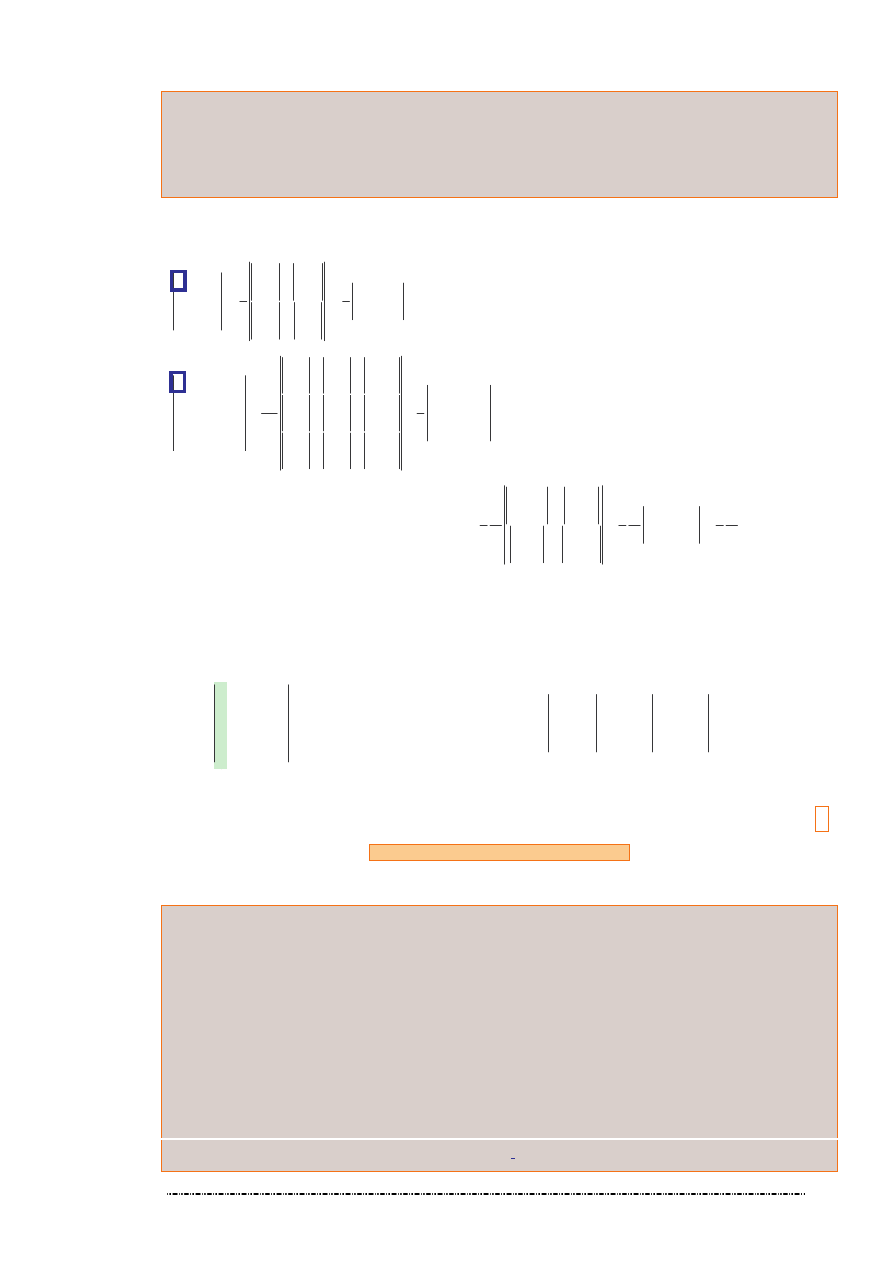
Poka emy stosowanie
algorytmu Chió
:
3
7
8
5
8
2
7
5
8
=
=
3
8
7
8
7
8
5
8
5
2
7
8
8
2
5
8
8
1
202
32
16
26
54
8
1
−
=
−
=
−
=
−
−
−
=
−
12
6
3
7
1
4
9
6
15
4
0
1
3
2
0
1
3
1
0
2
3
2
1
1
3
0
1
1
3
2
1
2
3
3
0
1
3
2
0
1
3
5
0
2
3
3
1
4
2
1
0
2
0
2
1
3
2
5
0
1
1
2
3
9
1
2
=
−
=
−
=
−
=
−
−
)
10935
(
153
72
69
39
12
3
9
15
6
3
6
15
7
4
9
15
1
4
6
15
15
1
9
1
4968
5967
15
1
9
1
15
1
9
1
−81
Zastosujemy
rozwini cie Laplace’a
wzgl dem pierwszej kolumny (
ij
A oznacza
dopełnienie algebraiczne
elementu
ij
a , tj. liczb
j
i
+
− )
1
(
pomno on przez wyznacznik macierzy powstałej przez skre lenie i
−tego wiersza i j−tej
kolumny tej macierzy – minor); dwa składniki rozwini cia s równe zeru, wobec czego
=
⋅
+
⋅
+
⋅
+
⋅
=
−
41
31
21
11
0
1
0
3
4
2
1
0
2
0
2
1
3
2
5
0
1
1
2
3
A
A
A
A
81
4
2
1
3
2
5
1
1
2
)
1
(
4
2
1
2
0
2
3
2
5
)
1
(
3
21
1
3
20
1
1
−
=
−
−
+
−
⋅
−
+
−
+
8
Przestrzenie wektorowe (liniowe)
Definicja.
Przestrzeni wektorow
nad ciałem
R liczb rzeczywistych nazywa si dowolny niepusty zbiór V wraz z dwoma działa-
niami:
V
V
V
→
×
+ :
i
V
V
R
→
×
⋅:
(elementy zbioru
V nazywa si
wektorami
, elementy zbioru
R nazywa si
skala-
rami
, działanie + nazywa si
dodawaniem wektorów
, za działanie
⋅ nazywa si
mno eniem wektorów przez skalary
)
takimi, e:
1. (
V, +) jest grup przemienn ,
2.
x
x
⋅
β
⋅
α
=
⋅
β
⋅
α
)
(
)
(
,
3.
y
x
y
x
⋅
α
+
⋅
α
=
+
⋅
α
)
(
,
4.
x
x
x
⋅
β
+
⋅
α
=
⋅
β
+
α
)
(
,
5.
x
x =
⋅
1
.
Element neutralny dodawania nazywa si
wektorem zerowym
(oznacza si 0 ).
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
13
Aby poda przykład przestrzeni wektorowej nale y:
1.
okre li zbiór
V,
2.
okre li działania
V
V
V
→
×
+ :
i
V
V
R
→
×
⋅:
,
3.
sprawdzi , czy te działania spełniaj aksjomaty przestrzeni wektorowej.
Przykład 1.
Dwuwymiarowa przestrze kartezja ska
.
}
,
:
]
,
[
{
2
1
2
1
2
R
x
R
V
∈
=
=
=
x
x
x
x
;
]
,
[
]
,
[
]
,
[
2
2
1
1
2
1
2
1
y
x
y
x
y
y
x
x
+
+
=
+
=
+ y
x
,
]
,
[
]
,
[
2
1
2
1
x
x
x
x
⋅
α
⋅
α
=
α
=
⋅
α x
.
Przykład 2.
Trójwymiarowa przestrze kartezja ska
.
}
,
,
:
]
,
,
[
{
3
2
1
3
2
1
3
R
x
R
V
∈
=
=
=
x
x
x
x
x
x
;
]
,
,
[
]
,
,
[
]
,
,
[
3
3
2
2
1
1
3
2
1
3
2
1
y
x
y
x
y
x
y
y
y
x
x
x
+
+
+
=
+
=
+ y
x
,
]
,
,
[
]
,
,
[
3
2
1
3
2
1
x
x
x
x
x
x
⋅
α
⋅
α
⋅
α
=
α
=
⋅
α x
.
Przykład 3.
n – wymiarowa przestrze kartezja ska
.
}
,
,
,
:
]
,
,
,
[
{
2
1
2
1
R
x
R
V
∈
=
=
=
n
n
n
x
x
x
x
x
x
;
1
≥
n
;
]
,
,
,
[
]
,
,
,
[
]
,
,
,
[
2
2
1
1
2
1
2
1
n
n
n
n
y
x
y
x
y
x
y
y
y
x
x
x
+
+
+
=
+
=
+ y
x
,
]
,
,
,
[
]
,
,
,
[
2
1
2
1
n
n
x
x
x
x
x
x
⋅
α
⋅
α
⋅
α
=
α
=
⋅
α x
.
Przykład 4.
Przestrze macierzy wymiaru m
×n
.
}
:
]
[
{
R
A
M
V
∈
=
=
=
×
ij
ij
n
m
a
a
;
]
[
]
[
]
[
ij
ij
ij
ij
b
a
b
a
+
=
+
=
+ B
A
,
]
[
]
[
ij
ij
a
a
⋅
α
=
⋅
α
=
⋅
α A
.
Przykład 5.
Przestrze wielomianów stopnia co najwy ej n
.
}
,
,
,
,
:
{
]
[
2
1
0
2
2
1
0
R
R
V
∈
+
+
+
+
=
=
n
n
n
n
a
a
a
a
x
a
x
a
x
a
a
x
.
Wektor
k
k
a
a
a
c
⋅
α
+
+
⋅
α
+
⋅
α
=
...
2
2
1
1
nazywa si
kombinacj liniow wektorów
k
a
a
a
,...,
,
2
1
o współczynnikach
k
α
α
α
,...,
,
2
1
.
Zbiór wszystkich kombinacji liniowych wektorów
k
a
a
a
,...,
,
2
1
oznacza si
)
,...,
,
2
1
k
a
a
a
(
Lin
.
24. Zadanie
Przedstawimy wektor
]
6
,
13
[
−
=
x
w postaci kombinacji liniowej wektorów
]
4
,
3
[
],
3
,
2
[
−
=
=
b
a
.
Rozwi zanie
Nale y w równo ci
b
a
x
⋅
β
+
⋅
α
=
wyznaczy współczynniki
β
α, .
⇔
−
=
β
+
α
=
β
−
α
⇔
β
+
α
β
−
α
=
β
β
−
+
α
α
=
−
⇔
−
⋅
β
+
⋅
α
=
−
6
4
3
13
3
2
]
4
3
,
3
2
[
]
4
,
3
[
]
3
,
2
[
]
6
,
13
[
]
4
,
3
[
]
3
,
2
[
]
6
,
13
[
−
=
β
=
α
3
2
Zatem
b
a
x
3
2
−
=
.
Stanisław Kowalski,
Wykłady z matematyki –
Struktury algebraiczne
–
Wykład 1.
14
25. Zadanie
Przedstawimy wektor
]
7
,
2
,
6
[
−
=
x
w postaci kombinacji liniowej wektorów
]
3
,
1
,
2
[
1
−
=
b
,
]
5
,
2
,
3
[
2
−
=
b
,
]
1
,
1
,
1
[
3
−
=
b
.
Rozwi zanie
Wystarczy rozwi za równanie
x
b
b
b
=
β
+
β
+
β
3
3
2
2
1
1
, czyli równanie
]
7
,
2
,
6
[
]
1
,
1
,
1
[
]
5
,
2
,
3
[
]
3
,
1
,
2
[
3
2
1
−
=
−
⋅
β
+
−
⋅
β
+
−
⋅
β
,
]
7
,
2
,
6
[
]
,
,
[
]
5
,
2
,
3
[
]
3
,
,
2
[
3
3
3
2
2
2
1
1
1
−
=
β
β
−
β
+
β
−
β
β
+
β
−
β
β
,
]
7
,
2
,
6
[
]
5
3
,
2
,
3
2
[
3
2
1
3
2
1
3
2
1
−
=
β
+
β
−
β
−
β
−
β
+
β
β
+
β
+
β
.
Wektory s równe wtedy i tylko wtedy, gdy maj równe współrz dne. Dostajemy układ równa :
−
=
β
+
β
−
β
−
=
β
−
β
+
β
=
β
+
β
+
β
.
7
5
3
,
2
2
,
6
3
2
3
2
1
3
2
1
3
2
1
Jego rozwi zaniem jest
1
3
2
1
=
β
=
β
=
β
, wi c
x
b
b
b
=
+
+
3
2
1
.
26. Zadanie
Przedstawimy wektor
]
7
,
2
,
6
[
−
=
x
w postaci kombinacji liniowej wektorów
]
1
,
1
,
1
[
1
=
b
,
]
0
,
1
,
1
[
2
=
b
,
]
0
,
0
,
1
[
3
=
b
.
Rozwi zanie
Wystarczy rozwi za równanie
x
b
b
b
=
β
+
β
+
β
3
3
2
2
1
1
, czyli równanie
]
7
,
2
,
6
[
]
0
,
0
,
1
[
]
0
,
1
,
1
[
]
1
,
1
,
1
[
3
2
1
−
=
⋅
β
+
⋅
β
+
⋅
β
,
]
7
,
2
,
6
[
]
0
,
0
,
[
]
0
,
,
[
]
,
,
[
3
2
2
1
1
1
−
=
β
+
β
β
+
β
β
β
,
]
7
,
2
,
6
[
]
,
,
[
1
2
1
3
2
1
−
=
β
β
+
β
β
+
β
+
β
.
Wektory s równe wtedy i tylko wtedy, gdy maj równe współrz dne. Dostajemy układ równa :
−
=
β
=
β
+
β
=
β
+
β
+
β
.
7
,
2
,
6
1
2
1
3
2
1
Jego rozwi zaniem jest
4
,
9
,
7
3
2
1
=
β
=
β
−
=
β
, wi c
x
b
b
b
=
+
+
−
3
2
1
4
9
7
.
Wyszukiwarka
Podobne podstrony:
algebra 2006 wyklad id 57189 Nieznany (2)
algebra 2006 wyklad id 57189 Nieznany (2)
wykład 7 struktura kryształów
Podstawy Informatyki Wykład V Struktury systemów komputerowych
LOGIKA wyklad 5 id 272234 Nieznany
ciagi liczbowe, wyklad id 11661 Nieznany
0 konspekt wykladu PETid 1826 Nieznany
AF wyklad1 id 52504 Nieznany (2)
Neurologia wyklady id 317505 Nieznany
MATERIALY DO WYKLADU CZ VIII i Nieznany
MATERIALY DO WYKLADU CZ V id 2 Nieznany
ZP wyklad1 id 592604 Nieznany
GOGN Wyklad 6 scalenie i podzia Nieznany
CHEMIA SA,,DOWA WYKLAD 7 id 11 Nieznany
Pionowa struktura dystrybucji i Nieznany
C Wyklady, Struktury
więcej podobnych podstron