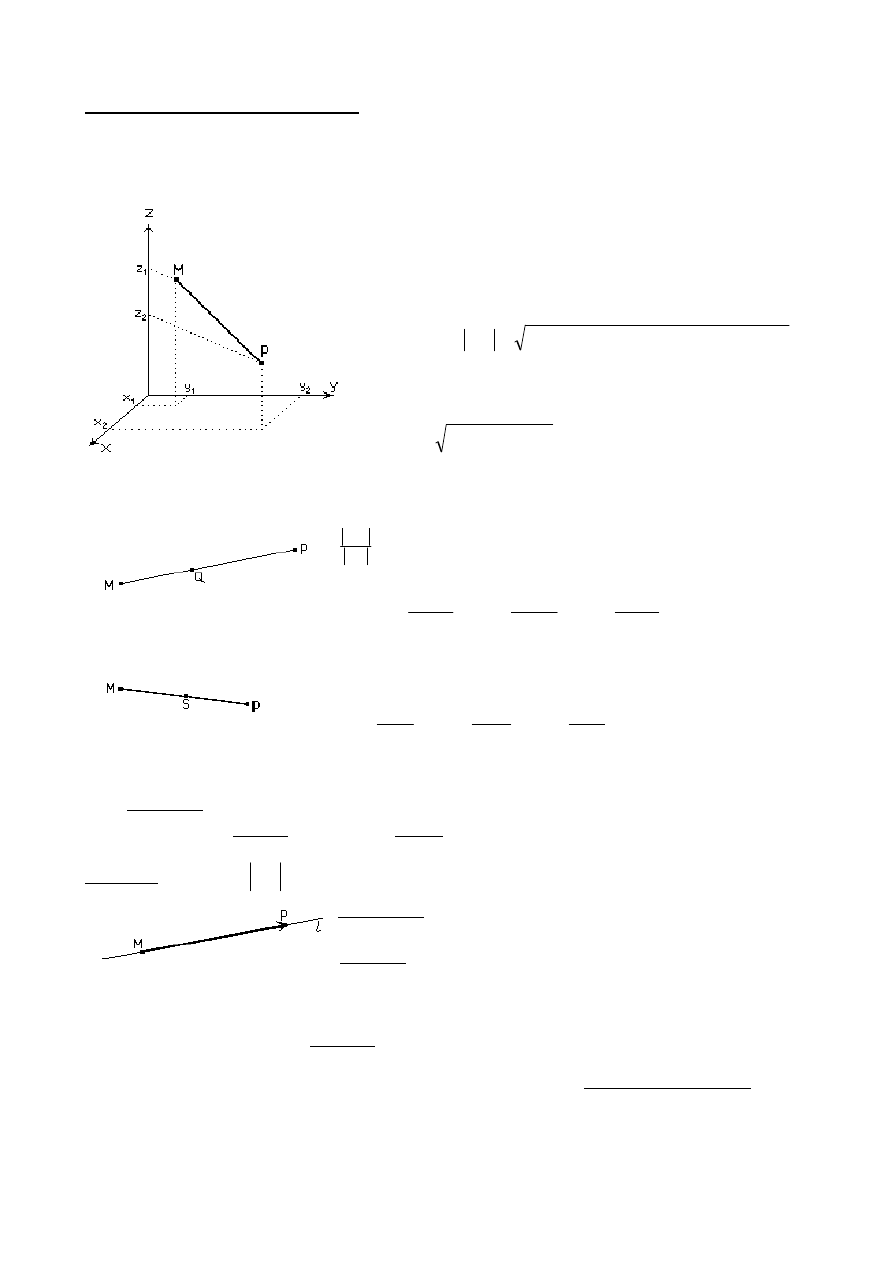
Algebra wektorów w przestrzeni R
3
.
Niech w przestrzeni R
3
b
ędzie zadany prostokątny prawoskrętny układ współrzędnych Oxyz.
Mówimy,
że punkt M ma współrzędne
1
1
1
,
,
z
y
x
pisz
ąc
)
,
,
(
1
1
1
z
y
x
M
=
.
Niech
)
,
,
(
2
2
2
z
y
x
P
=
.
Odległo
ść między dwoma punktami
)
,
,
(
1
1
1
z
y
x
M
=
i
)
,
,
(
2
2
2
z
y
x
P
=
okre
ślamy wzorem:
2
1
2
2
1
2
2
1
2
)
(
)
(
)
(
)
,
(
z
z
y
y
x
x
MP
P
M
d
−
+
−
+
−
=
=
(jest to długo
ść odcinka MP
).
W szczególno
ści odległość punktu M od początku układu
współrz
ędnych
)
0
,
0
,
0
(
=
O
wynosi
2
1
2
1
2
1
z
y
x
d
+
+
=
.
Podział odcinka.
Je
żeli punkt Q dzieli odcinek MP w stosunku
λ
(tzn.
)
λ
=
QP
MQ
, to współrz
ędne punktu
)
,
,
(
3
3
3
z
y
x
Q
=
okre
ślamy
wzorami
λ
λ
λ
λ
λ
λ
+
=
+
=
+
=
+
+
+
1
,
1
,
1
2
1
3
2
1
3
2
1
3
z
z
y
y
x
x
z
x
y
.
W szczególno
ści współrzędne środka
)
,
,
(
0
0
0
z
y
x
S
=
odcinka MP
okre
ślamy wzorami
2
,
2
,
2
2
1
0
2
1
0
2
1
0
z
z
y
y
x
x
z
x
y
+
+
+
=
=
=
.
Wektorem
P
M
r
(dokładnie: wektorem zwi
ązanym) nazywamy parę uporządkowaną punktów
M i P. Punkt M to pocz
ątek, punkt P to koniec wektora P
M
r
. Je
żeli
P
M
=
, to wektor
0
r
r
=
M
M
nazywamy wektorem zerowym.
Długo
ścią (modułem) P
M
r
wektora
P
M
r
nazywamy długo
ść odcinka MP
.
Kierunkiem wektora
P
M
r
nazywamy kierunek prostej, do której
odcinek MP jest równoległy.
Zwrotem wektora
P
M
r
nazywamy jedno z dwu mo
żliwych
uporz
ądkowań punktów na prostej l wyznaczonej przez punkty
M i P.
Dwa wektory nazywamy równymi, je
żeli mają tę samą długość, ten sam kierunek i ten sam
zwrot.
Zbiór wszystkich wektorów równych mi
ędzy sobą nazywamy wektorem swobodnym (krótko:
wektorem) i oznaczamy symbolem
...
,
,
...,
,
,
r
u
b
a
r
r
r
r
Ka
żdy wektor związany wyznacza jednocześnie pewien wektor swobodny.
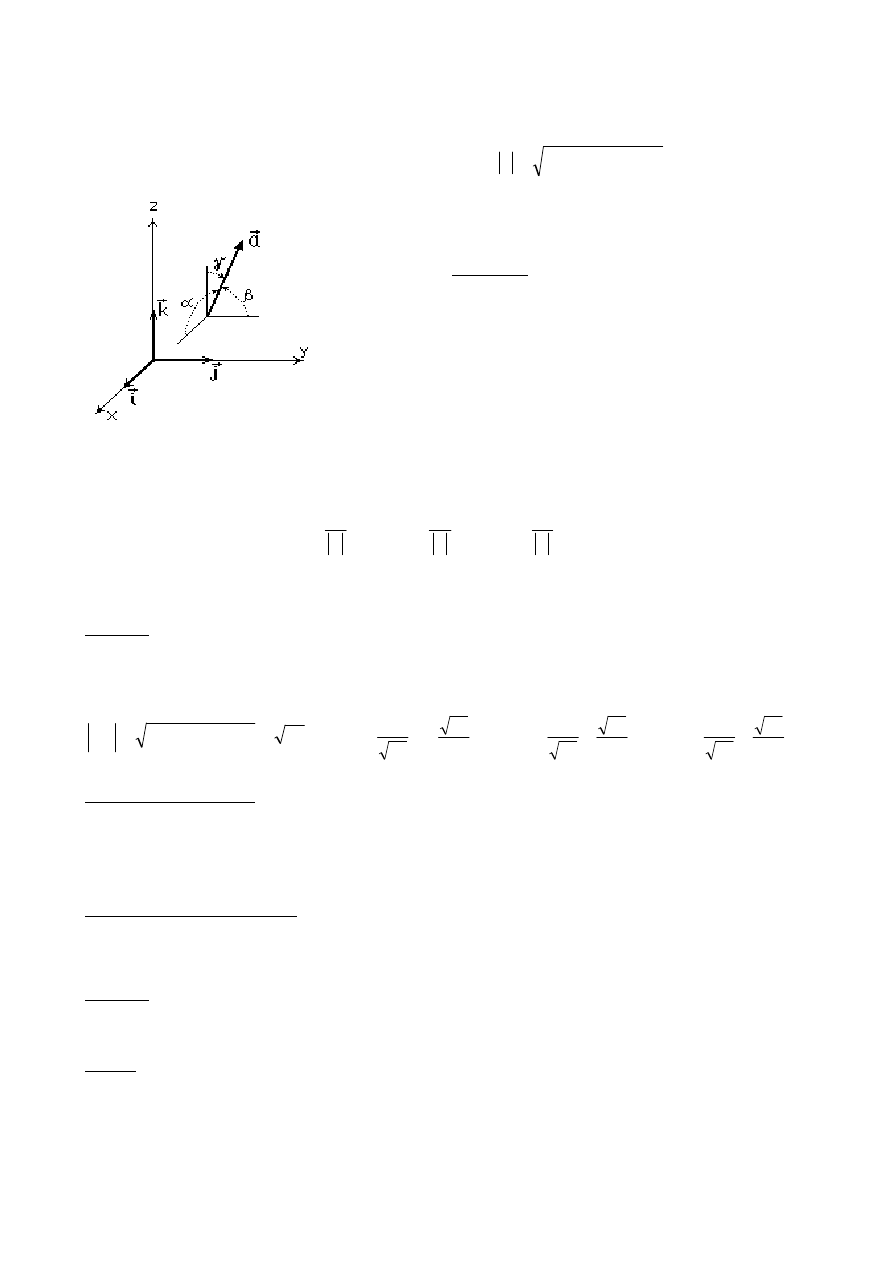
Współrz
ędne wektora
]
,
,
[
z
y
x
a
a
a
a
=
r
, gdy dany jest pocz
ątek
)
,
,
(
1
1
1
z
y
x
M
=
i koniec
)
,
,
(
2
2
2
z
y
x
P
=
obliczamy nast
ępująco:
1
2
1
2
1
2
,
,
z
z
a
y
y
a
x
x
a
z
y
x
−
=
−
=
−
=
.
St
ąd długość wektora
]
,
,
[
z
y
x
a
a
a
a
=
r
okre
śla wzór
2
2
2
z
y
x
a
a
a
a
+
+
=
r
.
W układzie kartezja
ńskim Oxyz określamy wektory
jednostkowe, równoległe do poszczególnych osi układu
współrz
ędnych i mające zwrot zgodny ze zwrotem tych osi.
Nazywamy je wersorami:
]
0
,
0
,
1
[
=
i
r
,
]
0
,
1
,
0
[
=
j
r
,
]
1
,
0
,
0
[
=
k
r
Ka
żdy wektor
]
,
,
[
z
y
x
a
a
a
a
=
r
mo
żemy zapisać jako
kombinacj
ę liniową wersorów
k
j
i
r
r
r
,
,
:
k
a
j
a
i
a
a
z
y
x
r
r
r
r
+
+
=
Oznaczmy przez
γ
β
α
,
,
k
ąty, jakie tworzy wektor a
r
z odpowiednimi osiami układu
współrz
ędnych.
γ
β
α
cos
,
cos
,
cos
to cosinusy kierunkowe wektora
]
,
,
[
z
y
x
a
a
a
a
=
r
:
a
a
a
a
a
a
z
y
x
r
r
r
=
=
=
γ
β
α
cos
,
cos
,
cos
.
Zachodzi zwi
ązek:
1
cos
cos
cos
2
2
2
=
+
+
γ
β
α
.
Przykład. Niech
k
j
i
B
A
r
r
r
r
5
2
+
+
−
=
oraz
)
2
,
1
-
,
1
(
=
B
. Znale
źć współrzędne początku A tego
wektora, jego długo
ść i cosinusy kierunkowe.
Je
śli oznaczymy
)
,
,
(
1
1
1
z
y
x
A
=
, to
5
-
2
,
1
-
1
-
,
2
-
-
1
1
1
1
=
=
=
z
y
x
St
ąd
3
-
,
2
-
,
3
1
1
1
=
=
=
z
y
x
, czyli
)
3
-
,
2
-
,
3
(
=
A
;
30
5
1
)
2
(
2
2
2
=
+
+
−
=
B
A
r
;
6
30
30
5
30
30
30
1
15
30
30
2
cos
,
cos
,
cos
=
=
−
=
−
=
=
=
γ
β
α
.
Suma dwóch wektorów:
Je
żeli
]
,
,
[
z
y
x
a
a
a
a
=
r
,
]
,
,
[
z
y
x
b
b
b
b
=
r
,
to
]
,
,
[
z
z
y
y
x
x
b
a
b
a
b
a
b
a
+
+
+
=
+
r
r
Iloczyn wektora przez liczb
ę
λ
:
Je
żeli
]
,
,
[
z
y
x
a
a
a
a
=
r
, to
]
,
,
[
z
y
x
a
a
a
a
λ
λ
λ
λ
=
r
.
Przykład. Wyznaczy
ć
b
a
r
r
3
5
−
je
żeli
]
1
,
2
-
,
3
[
=
a
r
i
]
2
-
,
3
,
2
[
=
b
r
.
k
j
i
b
a
r
r
r
r
r
11
19
9
]
1
1
,
19
-
,
9
[
]
6
,
9
-
,
6
-
[
]
5
,
10
-
,
15
[
3
5
+
−
=
=
+
=
−
.
Uwaga. Wektory
i
a
a
r
r
λ
s
ą równoległe i mają ten sam zwrot gdy
0
>
λ
, a przeciwne zwroty, gdy
0
<
λ
.
Uwaga. Mno
żąc wektor a
r
przez liczb
ę
a
r
1 otrzymamy wektor jednostkowy (wersor) o zwrocie
wektora a
r
:
1
=
a
a
r
r
. Współrz
ędnymi wektora
a
a
r
r
s
ą cosinusy kierunkowe wektora a
r
.
Przykład. Je
żeli
]
6
,
1
-
,
3
[
=
a
r
, to
4
16
6
1
9
=
=
+
+
=
a
r
i wtedy wektor
]
[
4
6
,
4
1
-
,
4
3
=
a
a
r
r
jest wektorem jednostkowym (o długo
ści 1).
Iloczyn skalarny dwóch wektorów.
Iloczynem skalarnym dwóch wektorów
a
r
i
b
r
nazywamy liczb
ę równą iloczynowi długości tych
wektorów przez cosinus k
ąta zawartego między nimi:
)
,
(
cos
b
a
b
a
b
a
r
r
r
r
r
o
r
∠
⋅
⋅
=
Zauwa
żmy, że dla wersorów
k
j
i
r
r
r
,
,
mamy:
0
90
cos
1
1
o
=
⋅
⋅
=
j
i
r
o
r
,
0
=
k
i
r
o
r
,
0
=
k
j
r
o
r
,
1
0
cos
1
1
o
=
⋅
⋅
=
i
i
r
o
r
,
1
=
j
j
r
o
r
,
1
=
k
k
r
o
r
.
Je
żeli więc
k
a
j
a
i
a
a
a
a
a
z
y
x
z
y
x
r
r
r
r
+
+
=
=
]
,
,
[
,
k
b
j
b
i
b
b
b
b
b
z
y
x
z
y
x
r
r
r
r
+
+
=
=
]
,
,
[
, wtedy
.
)
(
)
(
z
z
y
y
x
x
z
z
z
x
z
z
y
y
y
x
y
z
x
y
x
x
x
z
y
x
z
y
x
b
a
b
a
b
a
k
k
b
a
j
k
b
a
i
k
b
a
k
j
b
a
j
j
b
a
i
j
b
a
k
i
b
a
j
i
b
a
i
i
b
a
k
b
j
b
i
b
k
a
j
a
i
a
b
a
y
+
+
=
+
+
+
+
+
+
+
+
+
=
+
+
+
+
=
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
r
r
r
o
r
r
r
r
o
r
Iloczyn skalarny dwóch wektorów obliczamy wi
ęc też wg wzoru:
z
z
y
y
x
x
b
a
b
a
b
a
b
a
+
+
=
r
o
r
Nieznany cosinus k
ąta między wektorami a
r
i
b
r
mo
żemy wyznaczyć ze wzoru
b
a
b
a
b
a
r
r
r
o
r
r
r
⋅
=
∠
)
,
(
cos
Własno
ści iloczynu skalarnego wektorów:
1.
2
a
a
a
r
r
o
r
=
(czyli
a
a
a
r
o
r
r
=
),
2.
b
a
b
a
b
a
r
r
r
r
r
r
r
o
r
⊥
∨
=
∨
=
⇔
=
0
0
0
,
3.
a
b
b
a
r
o
r
r
o
r
=
(iloczyn skalarny jest przemienny)
,
4.
c
a
b
a
c
b
a
r
o
r
r
o
r
r
r
o
r
+
=
+
)
(
(rozdzielno
ść mnożenia skalarnego względem dodawania wektorów),
5.
)
(
)
(
)
(
b
a
m
b
m
a
b
a
m
r
o
r
r
o
r
r
o
r
=
=
.
Przykład. Niech
w
u
a
v
r
r
3
+
=
,
w
u
b
v
r
r
−
=
2
,
2
=
u
r
,
1
=
w
r
,
3
)
,
(
π
=
∠
w
u
r
r
.
Obliczy
ć
b
a
r
o
r
,
a
r
,
b
r
,
)
,
(
cos
b
a
r
r
∠
.
Rozwi
ązanie:
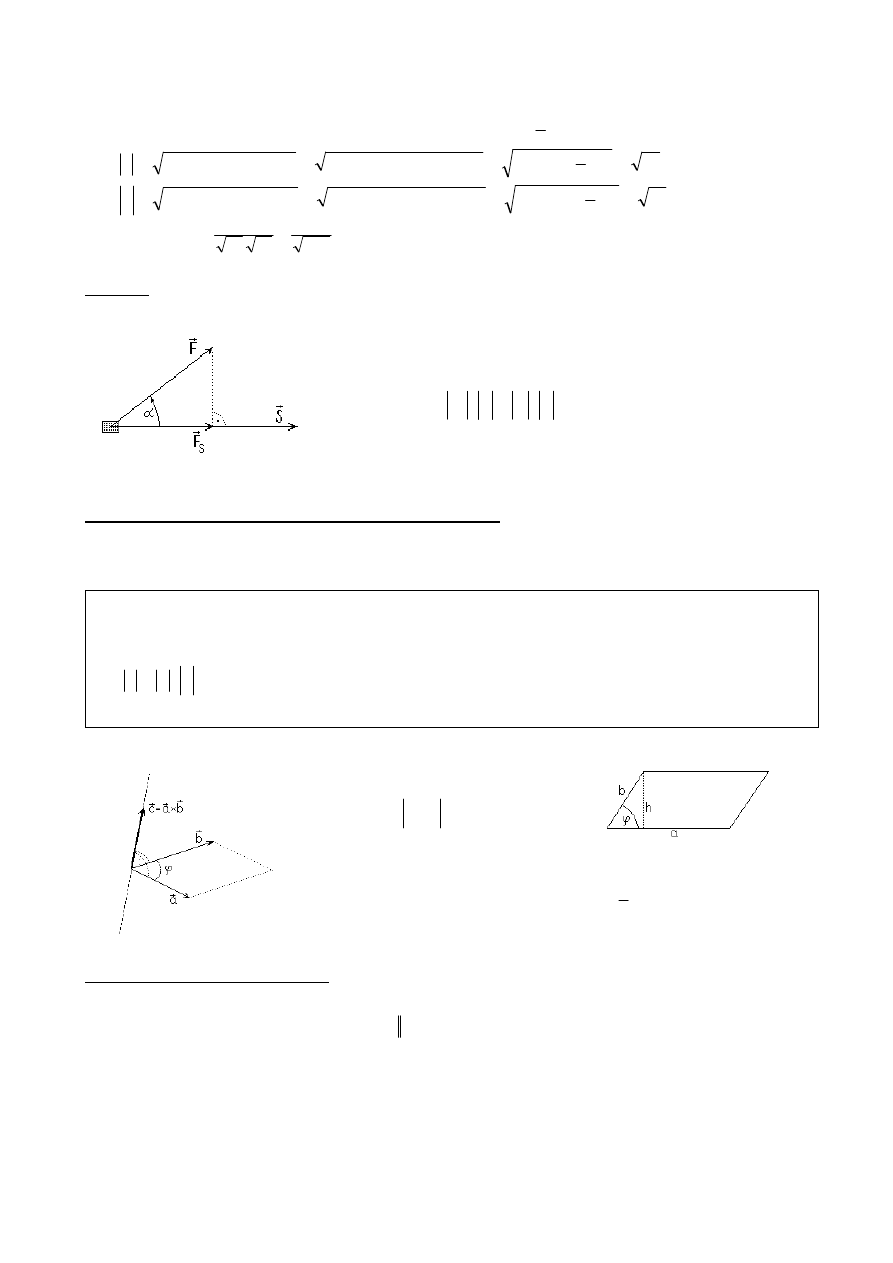
.
10
10
5
)
,
(
cos
1
2
5
5
1
3
5
4
2
3
6
2
)
2
(
)
3
(
2
1
=
⋅
+
=
⋅
⋅
⋅
+
=
⋅
−
+
⋅
=
=
−
+
−
=
−
+
=
∠
w
u
w
u
w
w
u
w
w
u
u
u
w
u
w
u
b
a
v
r
r
o
r
r
o
r
r
o
r
r
o
r
r
o
r
v
r
o
v
r
r
o
r
19
9
2
6
4
9
6
)
3
(
)
3
(
2
1
=
+
⋅
⋅
+
=
+
+
=
+
+
=
w
w
w
u
u
u
w
u
w
u
a
v
o
v
v
o
r
r
o
r
v
r
o
v
r
r
.
13
1
2
4
16
4
4
)
2
(
)
2
(
2
1
=
+
⋅
⋅
−
=
+
−
=
−
−
=
w
w
w
u
u
u
w
u
w
u
b
v
o
v
v
o
r
r
o
r
v
r
o
v
r
r
.
6363
,
0
247
10
13
19
10
)
,
(
cos
≈
=
⋅
=
∠
b
a
r
r
.
Przykład. Iloczyn skalarny wykorzystywany jest w fizyce, np. przy obliczaniu pracy:
Ciało przesuwa si
ę pod działaniem siły F
r
o wektor
S
r
.
Interesuje
nas praca L tej siły wzdłu
ż przesunięcia
S
r
. Prac
ę wykonuje
składowa
s
F
r
.
S
F
S
F
S
F
L
s
r
o
r
r
r
r
r
=
⋅
⋅
=
⋅
=
α
cos
Praca jest równa iloczynowi skalarnemu wektora siły przez wektor
przesuni
ęcia.
Iloczyn wektorowy dwóch wektorów w przestrzeni R
3
.
Iloczyn wektorowy wektorów a
r
i
b
r
oznaczamy symbolem:
b
a
r
r
×
Definicja.
Je
żeli
0
r
r
≠
a
i
0
r
r
≠
b
i a
r
nie jest równoległy do
b
r
, to
c
b
a
r
r
r
=
×
, przy czym
1
o
.
a
c
r
r
⊥
i
b
c
r
r
⊥
,
2
o
.
)
,
(
sin
b
a
b
a
c
r
r
r
r
r
∠
⋅
⋅
=
,
3
o
. układ wektorów
c
b
a
r
r
r
,
,
jest prawoskr
ętny
(zorientowany zgodnie z układem kartezja
ńskim Oxyz).
Geometrycznie długo
ść iloczynu
wektorowego
b
a
r
r
×
jest równa ilo
ści
jednostek
pola
równoległoboku
zbudowanego na wektorach a
r
i
b
r
.
Przypomnijmy,
że pole
równoległoboku
h
a
S
⋅
=
ale
ϕ
sin
=
b
h
, wi
ęc
ϕ
sin
⋅
=
b
h
,
sk
ąd
ϕ
sin
⋅
⋅
=
b
a
S
.
Własno
ści iloczynu wektorowego:
1.
b
a
a
b
r
r
r
r
×
−
=
×
(antyprzemienno
ść)
,
2.
0
r
r
r
=
×
b
a
je
śli
0
r
r
=
a
lub
0
r
r
=
b
lub
b
a
r
r
,
3.
)
(
)
(
)
(
b
a
m
b
m
a
b
a
m
r
r
r
r
r
r
×
=
×
=
×
,
4.
c
a
b
a
c
b
a
r
r
r
r
r
r
r
×
+
×
=
+
×
)
(
(rozdzielno
ść mnożenia wektorowego względem dodawania wektorów),
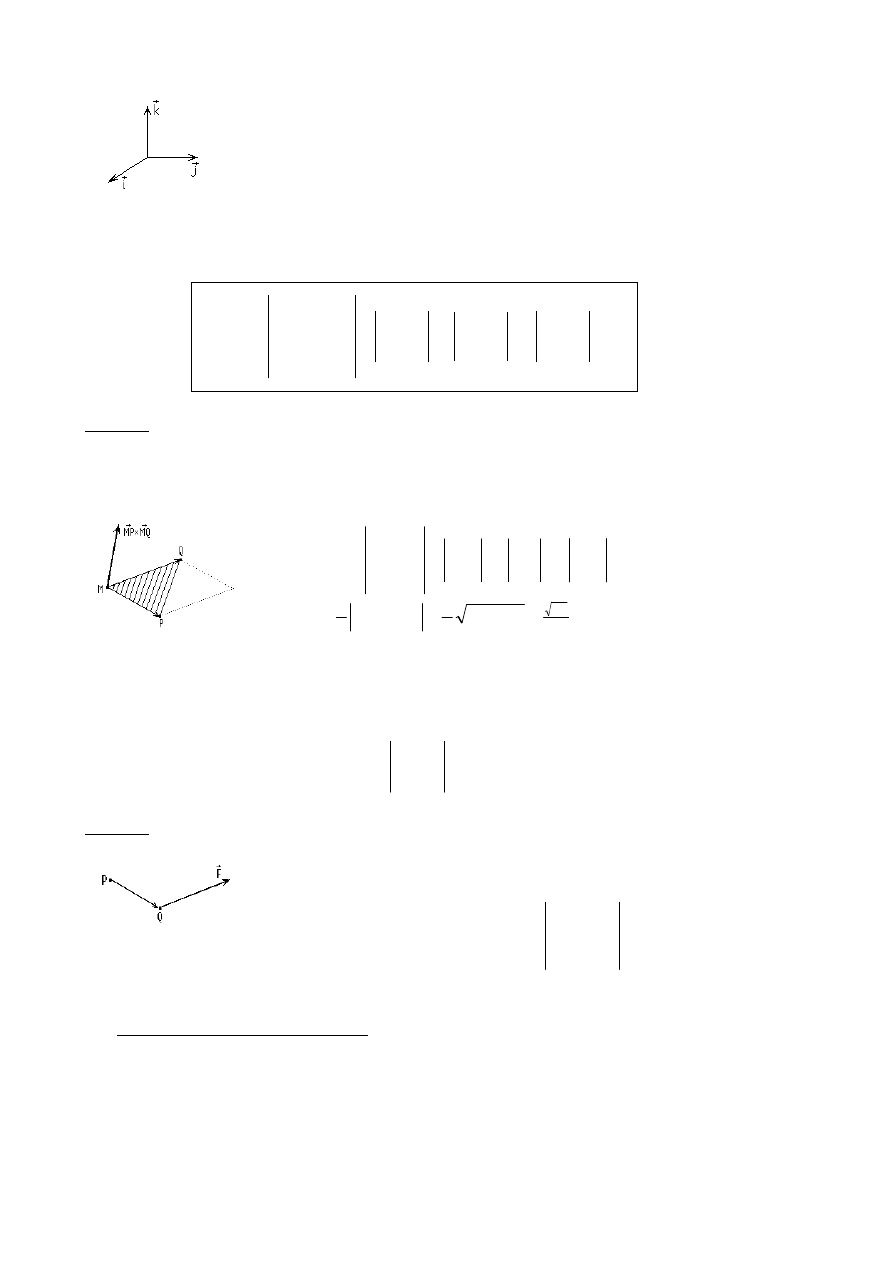
Zauwa
żmy, że dla wersorów
k
j
i
r
r
r
,
,
mamy:
0
r
r
r
r
r
r
r
=
×
=
×
=
×
k
k
j
j
i
i
;
k
j
i
r
r
r
=
×
,
i
k
j
r
r
r
=
×
,
j
i
k
r
r
r
=
×
,
k
i
j
r
r
r
−
=
×
,
i
j
k
r
r
r
−
=
×
,
j
k
i
r
r
r
−
=
×
.
Współrz
ędne iloczynu wektorowego wektorów
]
,
,
[
z
y
x
a
a
a
a
=
r
i
]
,
,
[
z
y
x
b
b
b
b
=
r
najwygodniej
jest oblicza
ć wg następującego wzoru, w którym wykorzystujemy symboliczny wyznacznik:
k
b
b
a
a
j
b
b
a
a
i
b
b
a
a
b
b
b
a
a
a
k
j
i
b
a
y
x
y
x
z
x
z
x
z
y
z
y
z
y
x
z
y
x
r
r
r
r
r
r
r
r
+
−
=
=
×
Przykład. Dane s
ą trzy punkty w przestrzeni R
3
:
)
1
-
2,
,
1
(
=
M
,
2)
2,
,
3
(
=
P
,
1)
1,
,
2
(
=
Q
.
Obliczy
ć iloczyn wektorowy wektorów P
M
r
i
Q
M
r
. Wyznaczy
ć pole trójkąta o wierzchołkach
M, P, Q.
Mamy tu
3]
0,
,
2
[
=
P
M
r
,
2]
1,
-
,
1
[
=
Q
M
r
.
]
2
-
,
1
-
,
3
[
2
3
1
-
1
0
2
2
1
3
2
2
1
-
3
0
2
1
-
1
3
0
2
=
−
−
=
+
−
=
=
×
k
j
i
k
j
i
Q
M
P
M
k
j
i
r
r
r
r
r
r
r
r
r
r
r
.
2
14
2
1
2
1
4
1
9
=
+
+
=
×
=
∆
Q
M
P
M
S
MPQ
r
r
.
Uwaga.
Dla wektorów na płaszczy
źnie R
2
:
]
,
[
y
x
a
a
a
=
r
,
]
,
[
y
x
b
b
b
=
r
, pole równoległoboku zbudowanego
na tych wektorach obliczamy wg wzoru:
S =
│
y
x
y
x
b
b
a
a
│.
Przykład. Iloczyn wektorowy ma zastosowanie w fizyce do obliczania np. momentu siły.
(wektor
Q
P
r
to
rami
ę siły)
Obliczy
ć moment siły
1]
2,
,
3
[
=
F
r
wzgl
ędem punktu
3)
2,
,
2
(
=
P
. Siła F
r
zaczepiona jest w punkcie
0)
2,
,
1
(
=
Q
.
].
2
-
,
8
-
,
6
[
2
8
6
]
1
,
2
,
3
[
]
3
-
,
0
,
1
-
[
)
(
M
1
2
3
3
-
0
1
-
=
−
−
=
=
×
=
×
=
k
j
i
F
Q
P
F
k
j
i
P
r
r
r
r
r
r
r
r
r
Iloczyn mieszany trzech wektorów.
Niech
]
,
,
[
z
y
x
a
a
a
a
=
r
,
]
,
,
[
z
y
x
b
b
b
b
=
r
,
]
,
,
[
z
y
x
c
c
c
c
=
r
. Iloczyn mieszany tych trzech wektorów
zapisujemy symbolicznie
c
b
a
r
r
r
. Zachodz
ą równości:
)
(
)
(
c
b
a
c
b
a
c
b
a
r
r
o
r
r
o
r
r
r
r
r
×
=
×
=
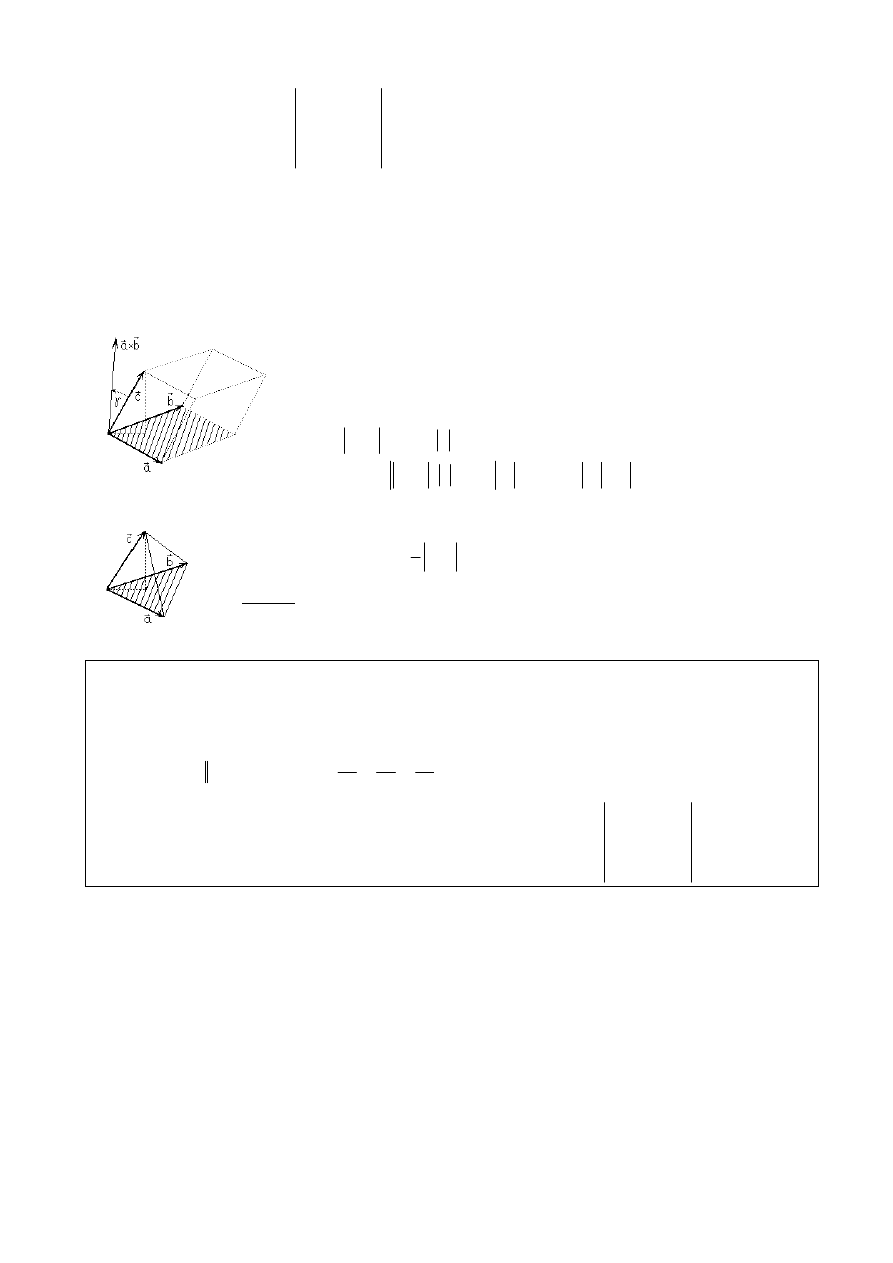
z
y
x
z
y
x
z
y
x
c
c
c
b
b
b
a
a
a
c
b
a
=
r
r
r
Iloczyn mieszany trzech wektorów jest równy zero je
żeli:
a) co najmniej jeden z tych wektorów jest zerowy,
b) dwa z tych wektorów s
ą równoległe (są kolinearne),
c) wszystkie trzy wektory s
ą równoległe do jednej płaszczyzny (są komplanarne).
Interpretacja geometryczna iloczynu mieszanego wektorów:
Warto
ść bezwzględna iloczynu mieszanego trzech wektorów
c
b
a
r
r
r
,
,
jest równa ilo
ści jednostek objętości równoległościanu zbudowanego
na tych wektorach.
(
h
S
V
p
⋅
=
(
p
S
oznacza pole podstawy),
b
a
S
p
r
r
×
=
,
γ
cos
⋅
=
c
h
r
,
c
b
a
c
b
a
c
b
a
h
S
V
p
r
r
r
r
o
r
r
r
r
r
=
×
=
⋅
⋅
×
=
⋅
=
)
(
cos
γ
).
Obj
ętość czworościanu zbudowanego na wektorach
c
b
a
r
r
r
,
,
:
c
b
a
V
czw
r
r
r
6
1
=
.
Zadanie. Dane s
ą punkty
)
0
1,
,
0
(
=
M
,
1)
1,
,
2
(
=
P
,
2)
2,
,
3
(
=
Q
,
1)
3,
,
0
(
=
S
.
Wyznaczy
ć objętość czworościanu o wierzchołkach MPQS
.
Do zapami
ętania.
Niech
0
]
,
,
[
r
r
≠
=
z
y
x
a
a
a
a
,
0
]
,
,
[
r
r
≠
=
z
y
x
b
b
b
b
,
0
]
,
,
[
r
r
≠
=
z
y
x
c
c
c
c
.
0
0
=
+
+
⇔
=
⇔
⊥
z
z
y
y
x
x
b
a
b
a
b
a
b
a
b
a
r
o
r
r
r
;
b
m
a
b
a
b
a
b
a
b
a
b
a
z
z
y
y
x
x
r
r
r
r
r
r
r
=
⇔
=
=
⇔
=
×
⇔
0
dla pewnego
0
≠
m
;
c
b
a
r
r
r
,
,
s
ą współpłaszczyznowe (komplanarne)
0
=
=
⇔
z
y
x
z
y
x
z
y
x
c
c
c
b
b
b
a
a
a
c
b
a
r
r
r
.
Wyszukiwarka
Podobne podstrony:
5 Algebra wektorów
algebra 2006 wyklad id 57189 Nieznany (2)
C 03 Algebra wektorow
120 Algebra wektorów
Wyklad7ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Relacje i funkcje ćw 2(2), stud, I semsetr, ALGEBRA, Ćwicenia i wyklady
Wyklad8ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Wyklad2ALG2001a, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych
Wyklad5ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Algebra wektory
algebra 200x wyklad 43 strony
algebra wektorów i tensorów
Wyklad6ALG2001, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszych r
Egzamin z algebry, Informatyka i Ekonometria SGGW, Semestr 1, Algebra Liniowa, materialy od starszyc
Algebra wektorów
Bud algebra i wektory lista4
5 Algebra wektorów
więcej podobnych podstron