
Z
ALICZENIE
z
MECHANIKI PŁYNÓW
1.
Przedmiot mechaniki płynów. Pojęcia podstawowe
2.
Klasyfikacja płynów
3.
Pojęcie lepkości. Miary lepkości. Jednostki
4.
Metody pomiaru ciśnienia. Wakuometry, barometry, manometry. Jednostki ciśnienia
5.
Warunek równowagi. Powierzchnie stałego potencjału. Paradoks hydrostatyczny
6.
Równowaga względna. Powierzchnie stałego potencjału. Przykłady równowagi względnej
7.
Napór na ściany płaskie. Współrzędne środka naporu
8.
Napór na ściany zakrzywione. Współrzędne środka naporu
9.
Zjawisko wyporu. Odkrycie Archimedesa (czas, epoka i miejsce)
10.
Stany stateczności pływania. Metacentrum i odległość metacentryczna
11.
Kinematyka płynów. Cele, zadania, parametry kinematyczne
12.
Metoda Eulera i Lagrange'a w kinematyce płynów
13.
Pochodna wędrowna. Operator Stokesa, przyśpieszenie elementu płynu
14.
Pojęcie cyrkulacji. Interpretacja fizyczna i analogia
15.
Równania toru i linii prądu, rurka i powierzchnia prądu, struga
16.
Przepływy potencjalne. Funkcja prądu i potencjału, jej interpretacja. Potencjał zespolony
17.
Przepływy elementarne. Superpozycja przepływów
18.
Zasada zachowanie masy. Równanie ciągłości
19.
Zasada zachowania pędu. Równanie Eulera i Naviera – Stokesa
20.
Równanie Daniela Bemoulliego dla płynu doskonałego, rzeczywistego i gazów
21.
Formalizm matematyczny, zastosowania
22.
Przygotować wykaz zagadnień opracowanych samodzielnie (poza wykładem i ćwiczeniami)

1. Przedmiot mechaniki płynów. Poj
ę
cia podstawowe
Zagadnienia mechaniki płynów wyst
ę
puj
ą
niemal we wszystkich dziedzinach techniki,
mi
ę
dzy innymi:
- lotnictwie;
- maszynach przepływowych (turbiny, spr
ęż
arki, pompy); - przepływowych układach regulacji
automatycznej;
- układach hydrauliki siłowej, - itd..
Mianem płynów okre
ś
lamy te ciała wyst
ę
puj
ą
ce w przyrodzie, które w odró
ż
nieniu od
ciał stałych zmniejszaj
ą
swe kształty w sposób trwały pod działaniem dowolnie małych sił
mechanicznych, je
ś
li działanie tych sił trwa dostatecznie długo.
Płyny dzielimy na ciecze i gazy.
Cieczami nazywamy te spo
ś
ród płynów, które zmieniaj
ą
bardzo nieznacznie sw
ą
obj
ę
to
ść
pod działaniem nawet bardzo wielkich sił mechanicznych. Inaczej mówimy,
ż
e ciecze
s
ą
nie
ś
ci
ś
liwe.
Gazami nazywamy te płyny, które pod działaniem sił mechanicznych zmieniaj
ą
swe
obj
ę
to
ś
ci bardzo znacznie. Mówimy równie
ż
,
ż
e gazy s
ą
to płyny
ś
ci
ś
liwe.
Przedmiotem mechaniki płynów jest badanie zjawisk wyst
ę
puj
ą
cych podczas ruchu,
spoczynku płynów, ze zwróceniem uwagi na oddziaływanie płynów na
ś
cianki ciał stałych
ograniczaj
ą
cych płyn i
ś
cianki ciał zanurzonych całkowiciew płynie.
Zadaniem mechaniki płynów jako dyscypliny podstawowej jest poznanie praw
rz
ą
dz
ą
cych spoczynkiem i ruchem płynów oraz stworzenie podstaw teoretycznych
i do
ś
wiadczalnych dla całego szeregu dziedzin specjalistycznych.
W zale
ż
no
ś
ci od rodzaju u
ż
ytych kryteriów mechanik
ę
płynów mo
ż
na podzieli
ć
na:
1. hydromechanik
ę
, to znaczy mechanik
ę
cieczy;
- mechanik
ę
cieczy idealnej;
- mechanik
ę
cieczy rzeczywistej;
2. aeromechanik
ę
, to znaczy mechanik
ę
gazu. Ponadto mechanik
ę
płynów dzieli si
ę
na:
- statyk
ę
;
- kinematyk
ę
;
- dynamik
ę
.
Statyka płynów jest nauk
ą
o zjawiskach zachodz
ą
cych podczas spoczynku cieczy
i gazów.

Kinematyka płynów zajmuje si
ę
analiz
ą
ruchu w oderwaniu od wyst
ę
puj
ą
cych sił.
Dynamika płynów, czyli dynamika cieczy (hydrodynamika) i dynamika gazów (aerodynamika),
jest nauk
ą
o ruchu cieczy i gazów w powi
ą
zaniu z wyst
ę
puj
ą
cymi siłami.
Istnieje równie
ż
inny podział mechaniki płynów, a mianowicie w oparciu o własno
ś
ci
dyssypatywne płynów. Bior
ą
c za podstaw
ę
wła
ś
ciwo
ś
ci takie jak lepko
ść
i przewodno
ść
ciepln
ą
mo
ż
na podzieli
ć
mechanik
ę
płynów na tak zwan
ą
mechanik
ę
płynów doskonałych
opart
ą
o model płynu nielekkiego i nie przewodz
ą
cego ciepła i na mechanik
ę
płynów
rzeczywistych.
Z podziałem mechaniki płynów wi
ąż
e si
ę
poj
ę
cie hydrauliki. Jest ona najstarszym
historycznie działem mechaniki cieczy i opiera si
ę
na modelu jednowymiarowego przepływu
cieczy lepkiej i nie
ś
ci
ś
liwej. Model ten polega na stosowaniu empirycznych współczynników
ujmuj
ą
cych straty tarcia w przepływie cieczy. Przez mechanik
ę
płynów rozumiemy nauk
ę
,
zajmuj
ą
c
ą
si
ę
badaniem ruchów płynów ( cieczy i gazów b
ę
d
ą
cych pod działaniem sił ).
W obliczeniach stosuje si
ę
przybli
ż
one modele dotycz
ą
ce idealnych, cieczy
rzeczywistych, gazów pół-doskonałych i rzeczywistych.
Prekursorami w dziedzinie mechaniki płynów byli Newton, który sformułował pojecie
lepko
ś
ci, Euler jako pierwszy napisał ró
ż
niczkowe równania cieczy i Archimedes staro
ż
ytny
konstruktor, który zbudował maszyn
ę
, na jego cz
ęść
nazwan
ą
" Spiral
ą
Archimedesa " ,
słu
żą
c
ą
do wymuszania przepływu cieczy.

2. Klasyfikacja płynów
Płyn nielepki i nie
ś
ci
ś
liwy - zwany idealnym.
Jego definicja wynika wprost z definicji cieczy idealnej
Mówimy,
ż
e płyn jest nie
ś
ci
ś
liwy, je
ś
li jego współczynnik
ś
ci
ś
liwo
ś
ci k równa si
ę
zero.
Współczynnik
ś
ci
ś
liwo
ś
ci oznacza si
ę
wzorem.
dp
d
k
σ
=
Wyra
ż
a on zmian
ę
g
ę
sto
ś
ci
σσσσ
pod wpływem zmiany ci
ś
nienia p
Jak wiemy ciecze s
ą
nieznacznie
ś
ci
ś
liwe, to znaczy, ich współczynnik
ś
ci
ś
liwo
ś
ci jest
bardzo mały, podobnie zachowuj
ą
si
ę
równie
ż
gazy przy małych pr
ę
dko
ś
ciach. Opisuj
ą
c
przepływ cieczy, oraz przepływ gazu przy małych pr
ę
dko
ś
ciach, mo
ż
emy przyj
ąć
stał
ą
warto
ść
g
ę
sto
ś
ci.
Ten typ płynu opisuje równanie Eulera
gradp
p
F
dt
dv
1
−
−
=
Definicja lepko
ś
ci znajduje si
ę
w dalszej cz
ęś
ci rozprawki.
Płyn lepki i nie
ś
ci
ś
liwy
Modelem płynu lepkiego i nie
ś
ci
ś
liwego badamy przepływy w warstwie przy
ś
ciennej.
dn
dv
Warstwa przy
ś
cienna charakteryzuje si
ę
tym,
ż
e gradienty pr
ę
dko
ś
ci przepływu, s
ą
w niej bardzo du
ż
e, oddalaj
ą
c si
ę
od
ś
cianek w gł
ą
b strumienia pr
ę
dko
ś
ci te gwałtownie
rosn
ą
. Poza warstw
ą
przy
ś
cienn
ą
gradienty pr
ę
dko
ś
ci s
ą
bardzo małe.
υ
υ
2
∇
+
−
=
gradp
F
dt
dv
2
2
2
2
2
2
2
dz
v
d
dy
v
d
dx
v
d
+
+
=
∇
υ
W obszarze warstwy przy
ś
ciennej napr
ęż
enia styczne, uzyskuj
ą
znaczne warto
ś
ci,
niezale
ż
nie od lepko
ś
ci płynu jest niewielka, ze wzgl
ę
dem na gradienty pr
ę
dko
ś
ci napr
ęż
enia
styczne s
ą
pomijalnie małe. Ten typ płynu opisuje równanie:

Płyn nielepki i
ś
ci
ś
liwy
Modelem tego płynu posługujemy si
ę
w dynamice gazów. Jest to nauka zajmuj
ą
ca si
ę
przepływami z du
ż
ymi pr
ę
dko
ś
ciami.
Poniewa
ż
zachodz
ą
wyra
ź
ne zmiany g
ę
sto
ś
ci s nale
ż
y uwzgl
ę
dni
ć
zale
ż
no
ść
p od ci
ś
nienia
i temperatury. Tymi zale
ż
no
ś
ciami zajmuje si
ę
termodynamika. Powi
ą
zania z termodynamik
ą
mog
ą
by
ć
daleko bardziej id
ą
ce np.: w przepływach w których doprowadzamy lub
odprowadzamy ciepło lub prac
ę
. Gazy s
ą
płynami ekspansywnymi, to znaczy zajmuj
ą
cał
ą
woln
ą
przestrze
ń
, w której s
ą
zamkni
ę
te.
Płyn lepki i
ś
ci
ś
liwy
Charakteryzuje si
ę
lepko
ś
ci
ą
i niewielk
ą
ś
ci
ś
liwo
ś
ci
ą
, jest modelem płynów rzeczywistych
wyst
ę
puj
ą
cych w przyrodzie. Na tym modelu bazuj
ą
najbardziej ogólne i
ś
cisłe rozwi
ą
zania.
Jednak
ż
e przy rozwi
ą
zywaniu równa
ń
opisuj
ą
cych ten typ płynu napotykamy na ogromne
trudno
ś
ci, głównie natury matematycznej, ze wzgl
ę
du na du
ż
y stopie
ń
skomplikowania tych
równa
ń
.
Obserwuj
ą
c zjawisko przepływu płynów zauwa
ż
amy,
ż
e jest ono ogromnie
skomplikowane. Opisanie tak zło
ż
onych zjawisk nie jest łatwe. Dlatego te
ż
ze wzgl
ę
du na
trudno
ś
ci w ich rozwi
ą
zywaniu staramy si
ę
je nieco upro
ś
ci
ć
, pomijaj
ą
c te wielko
ś
ci które
w stosunku do pozostałych s
ą
bardzo małe.
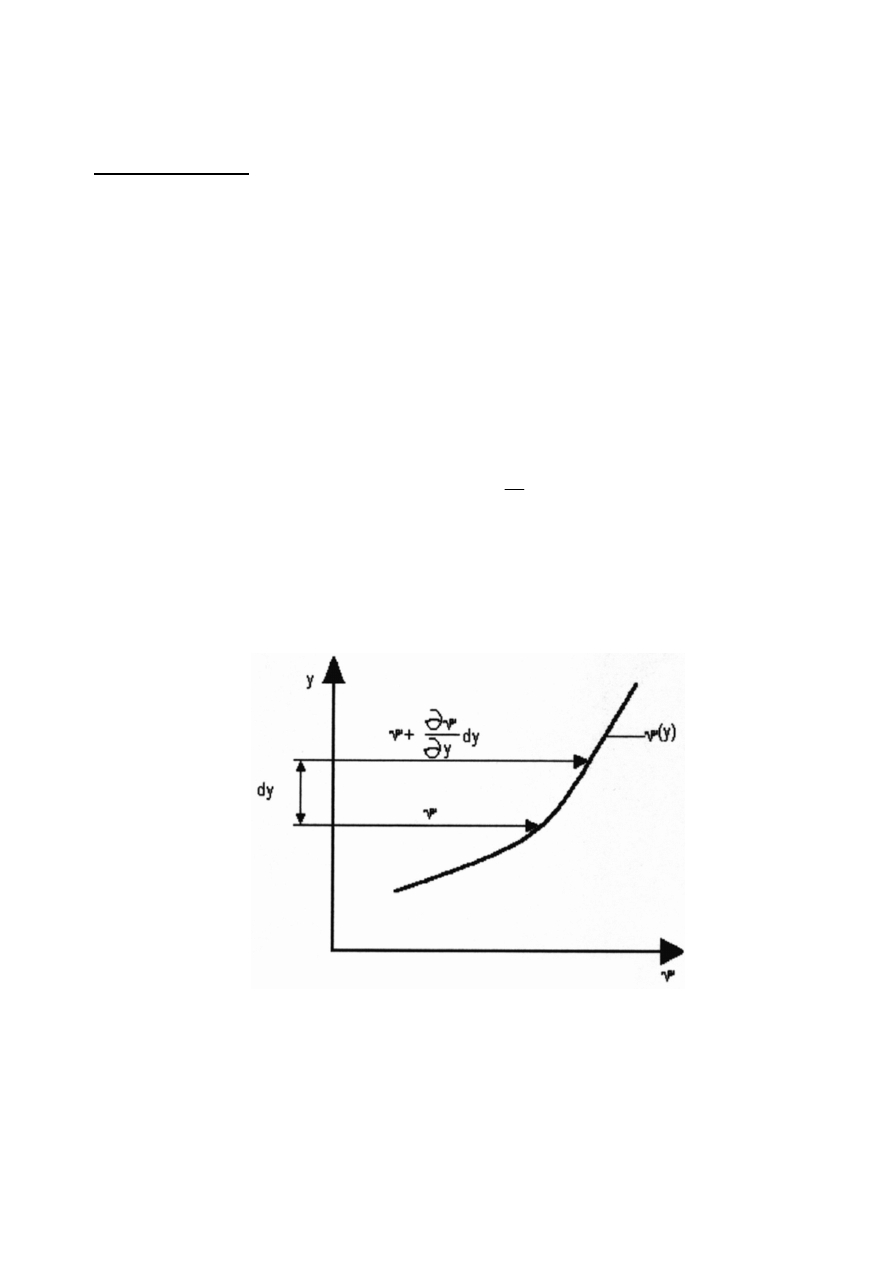
3. Poj
ę
cie lepko
ś
ci. Miary lepko
ś
ci. Jednostki
Hipoteza Newtona
Płyny rzeczywiste wykazuj
ą
zdolno
ść
przenoszenia napr
ęż
e
ń
stycznych, przy czym
napr
ęż
enia
powstaj
ą
mi
ę
dzy
s
ą
siednimi
warstwami
płynu
poruszaj
ą
cymi
si
ę
z ró
ż
nymi pr
ę
dko
ś
ciami. Napr
ęż
enia styczne powstaj
ą
równie
ż
pomi
ę
dzy poruszaj
ą
cym si
ę
płynem i ciałem stałym, nie wyst
ę
puj
ą
natomiast w czasie spoczynku, lub w płynie
poruszaj
ą
cym si
ę
z wyrównan
ą
pr
ę
dko
ś
ci
ą
przepływu w całym przekroju. Zgodnie
z hipotez
ą
Newtona, napr
ęż
enia styczne i wyst
ę
puj
ą
ce mi
ę
dzy s
ą
siednimi warstwami, lub
elementami płynu s
ą
proporcjonalne do przyrostu pr
ę
dko
ś
ci w kierunku normalnym do
kierunku przepływu. Sytuacje t
ą
przedstawia rysunek numer 1, oraz opisuje poni
ż
szy wzór.
y
v
∂
∂
=
η
τ
gdzie:
τ
- napr
ęż
enia styczne;
η
- współczynnik lepko
ś
ci dynamicznej, zwany lepko
ś
ci
ą
dynamiczn
ą
.
Rys.1. Ilustracja do równania opisuj
ą
cego hipotez
ę
Newtona
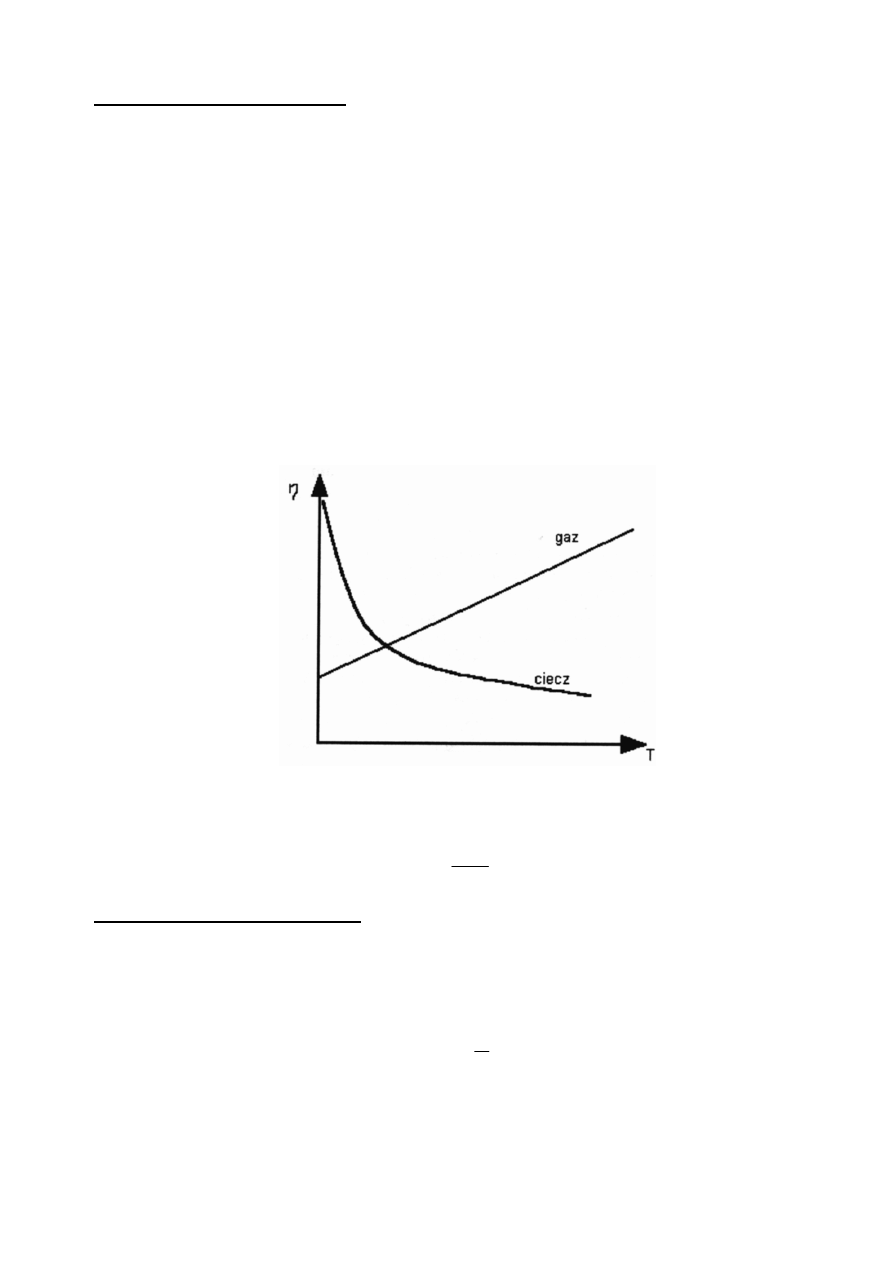
Pojecie lepko
ś
ci dynamicznej
Lepko
ść
dynamiczna
η
jest funkcj
ą
temperatury, ci
ś
nienia i rodzaju płynu. Zale
ż
no
ść
lepko
ś
ci płynu od ci
ś
nienia jest nieznaczna, i ro
ś
nie bardzo wolno wraz z jego wzrostem,
a jedynym wyj
ą
tkiem jest woda, która w zakresie poni
ż
ej 32°C maleje ze wzrostem ci
ś
nienia.
Zale
ż
no
ść
lepko
ś
ci
η
od temperatury jest natomiast bardzo znaczna i zupełnie odmienna dla
cieczy i gazów. Zale
ż
no
ść
t
ą
ilustruje rysunek 2 . lepko
ść
dynamiczna
η
cieczy maleje ze
wzrostem temperatury. Wynika z tego,
ż
e w cieczach ruch molekuł jest stosunkowo mało
intensywny, wobec czego napr
ęż
enia styczne powstaj
ą
głównie w skutek molekularnych sil
spójno
ś
ci; przy wzro
ś
cie temperatury rosn
ą
odległo
ś
ci pomi
ę
dzy molekułami, a zatem malej
ą
siły spójno
ś
ci. W gazach, jak mo
ż
emy wnioskowa
ć
z rysunku jest na odwrót.
Rys.2. Zale
ż
no
ść
lepko
ś
ci od temperatury
Jednostka lepko
ś
ci dynamicznej
η
w układzie SI wynika z równania Newtona:
s
m
kg
*
1
Pojecie lepko
ś
ci kinematycznej
Współczynnik lepko
ś
ci kinematycznej, zwany lepko
ś
ci
ą
kinematyczn
ą
, okre
ś
lony jest
wzorem:
ρ
η
υ
=
Jednostk
ą
lepko
ś
ci kinematycznej jest:

1stokes [1St]=
s
m
2
4
10
−
W u
ż
yciu s
ą
stosowane jednostki mniejsze, takie jak:
1centistokes [1cSt]
Poza układem SI dla okre
ś
lenia lepko
ś
ci u
ż
ywa si
ę
szeregu innych jednostek, takich
- stopie
ń
Eulera [E];
- sekunda Redwood'a [R sek];
- i inne.
Jednostki te wynikaj
ą
ze sposobu pomiaru i rodzaju u
ż
ytej aparatury.
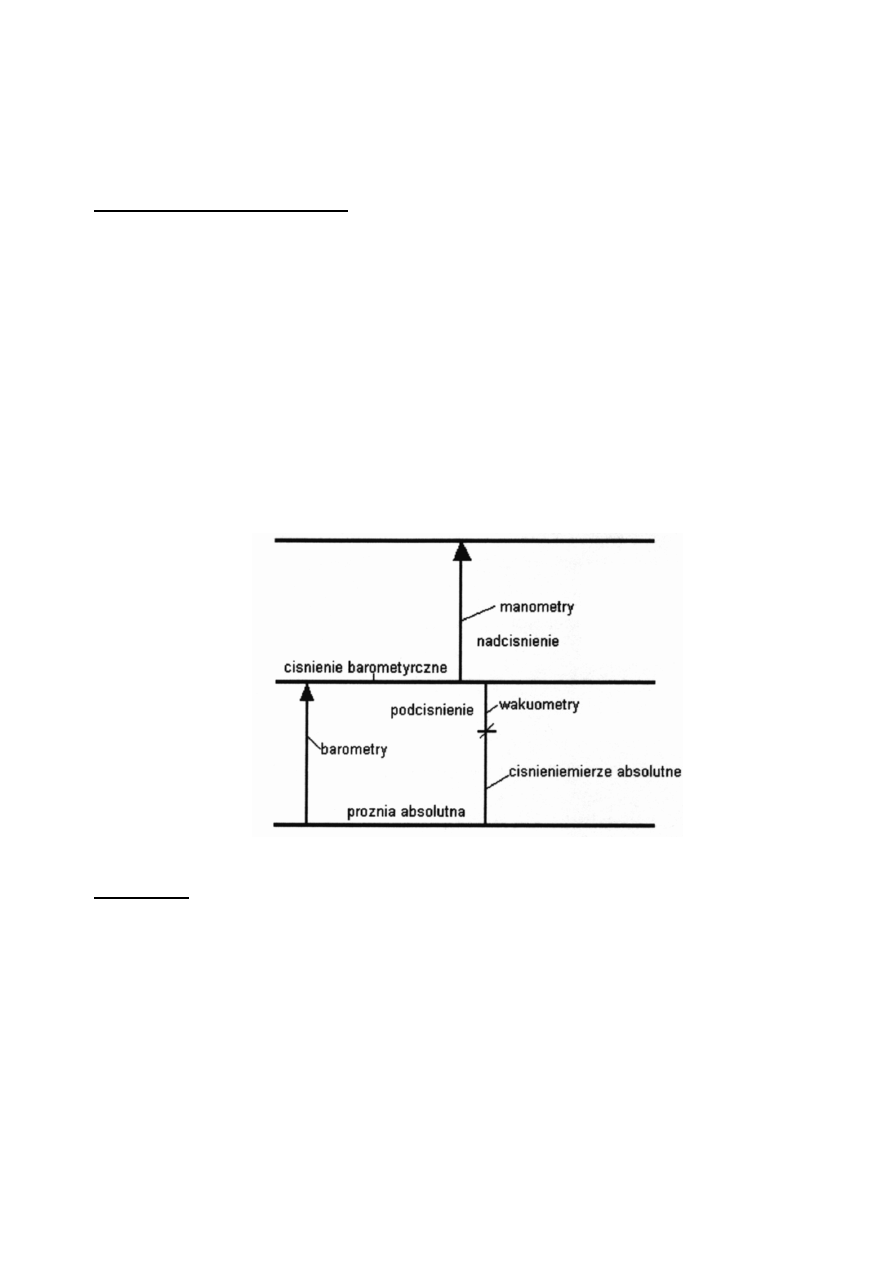
4. Metody pomiaru ci
ś
nienia.
Manometry, barometry, wakuometry. Jednostki ci
ś
nienia
Przyrz
ą
dy do pomiaru ci
ś
nie
ń
Przyrz
ą
dy do pomiaru ci
ś
nienia mierz
ą
nie jego warto
ść
lecz ró
ż
nice tej warto
ś
ci
i warto
ś
ci ci
ś
nienia odniesienia. Ci
ś
nieniem odniesienia najcz
ęś
ciej jest:
- pró
ż
nia absolutna (bezwzgl
ę
dna);
- ci
ś
nienie panuj
ą
ce aktualnie w miejscu i czasie pomiaru.
Ogólnie przyrz
ą
dy do pomiaru ci
ś
nie
ń
nazywaj
ą
si
ę
ci
ś
nieniomierzami. Przyrz
ą
dy do
pomiaru ci
ś
nie
ń
absolutnych nazywaj
ą
si
ę
barometrami i ci
ś
nieniomierzami ci
ś
nienia
absolutnego, nad ci
ś
nie
ń
- manometrami, a podci
ś
nie
ń
wakuometrami. Poza tym wyró
ż
nia si
ę
jeszcze ci
ś
nieniomierze (manometry) ró
ż
nicowe - do pomiaru ró
ż
nicy ci
ś
nie
ń
. Poni
ż
szy
rysunek przedstawia wy
ż
ej wymienione zale
ż
no
ś
ci w sposób graficzny.
Rys.3. Rodzaje ci
ś
nie
ń
Manometry
Dzielimy je na:
- hydrostatyczne ( cieczowe )
- pr
ęż
ne ( rurkowe lub przeponowe )
- przeponowe
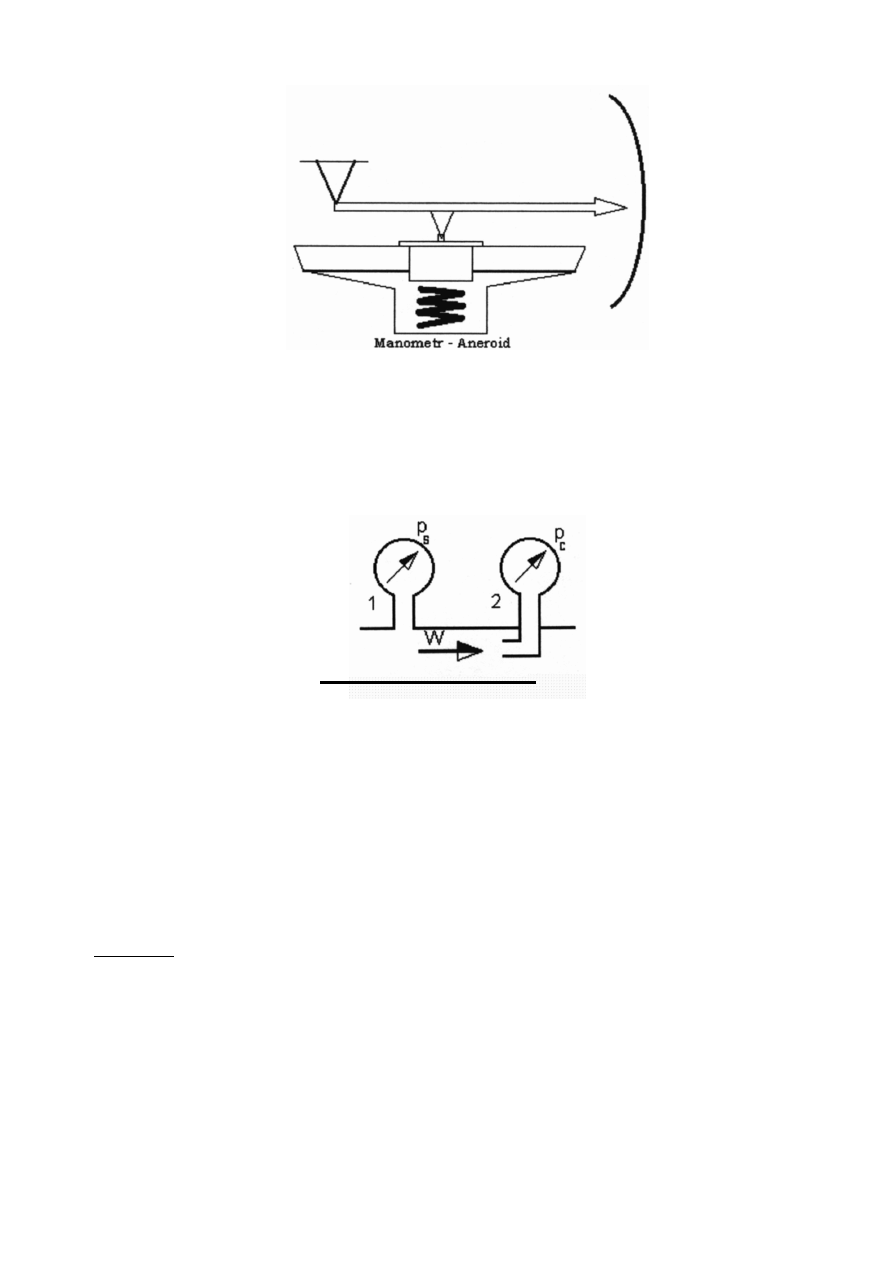
Elementem pr
ęż
nym tego manometru jest przepona (0) płaska lub falista. Pod wpływem
ci
ś
nienia p przepona ulega odkształceniu. Odkształcenie to przenosi si
ę
przez przekładni
ę
(S)
na wskazówk
ę
(W)
Poni
ż
szy rysunek przedstawia zasad
ę
działania manometru.
Metoda pomiaru manometrem
Manometr (1) mierzy ci
ś
nienie statyczne ps płynu (wektor pr
ę
dko
ś
ci w płynie jest styczny do
otworu wlotowego manometru). Je
ż
eli otwór wlotowy manometru jest prostopadły do wektora
pr
ę
dko
ś
ci w, to manometr (2) wska
ż
e wzrost ci
ś
nienia. Wzrost ten jest wywołany zmian
ą
energii kinetycznej płynu o pr
ę
dko
ś
ci w i g
ę
sto
ś
ci p na energi
ę
potencjaln
ą
, jest ci
ś
nieniem
kinematycznym i zwyczajowo nazywamy je ci
ś
nieniem dynamicznym
Barometr
Barometr - przyrz
ą
d do pomiaru ci
ś
nienia atmosferycznego. Pierwszy tak zwany barometr
rt
ę
ciowy został wynaleziony w roku 1643 przez E. Torricellego w zwi
ą
zku z jego badaniami
nad ci
ś
nieniem sferycznym. Barometr rt
ę
ciowy został ulepszony w 1665 przez R. Hook'ea
który wprowadził podziałk
ę
umo
ż
liwiaj
ą
c
ą
bezpo
ś
rednie odczytywanie wielko
ś
ci.
Poni
ż
szy rysunek przedstawia zasad
ę
działania barometru.
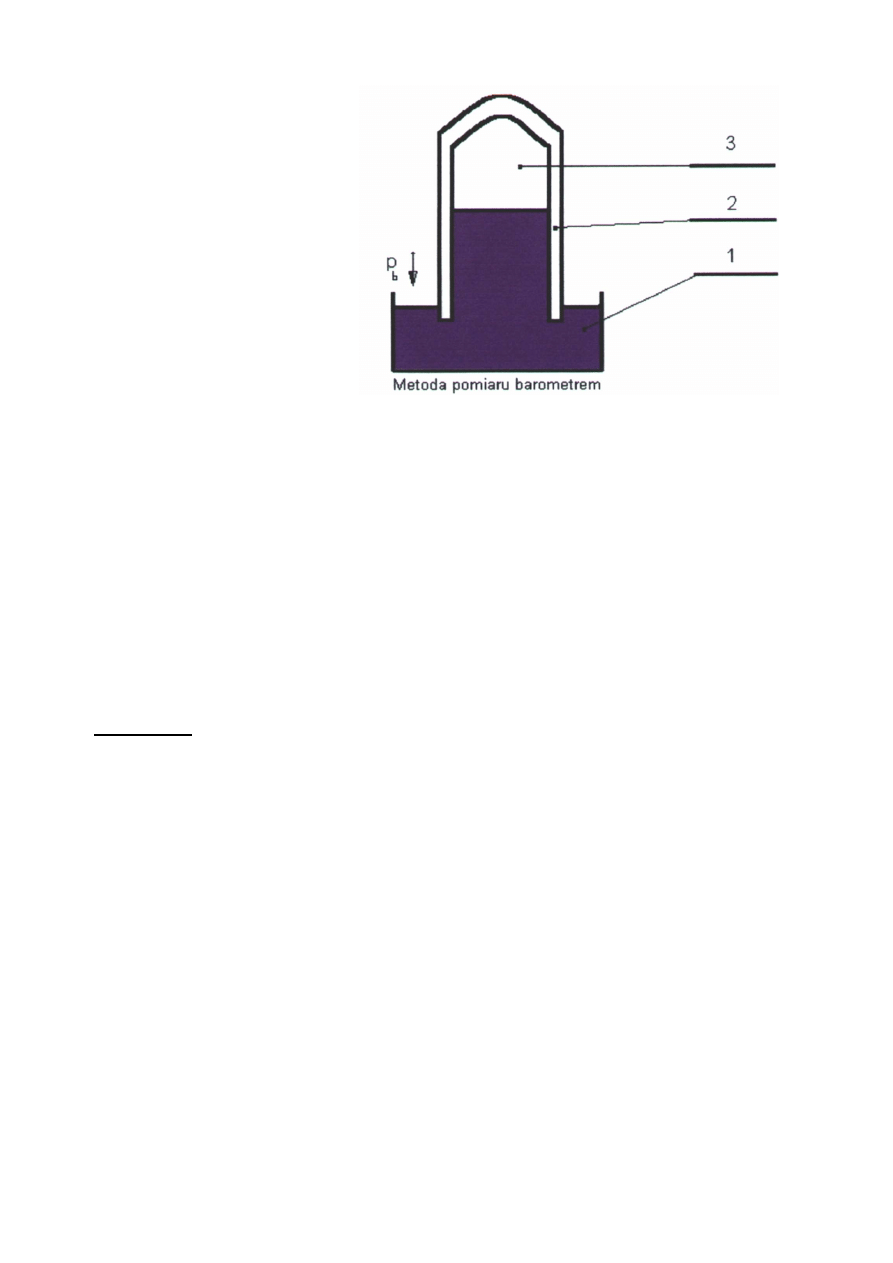
Barometr
wykorzystuje
si
ę
do
pomiaru
ci
ś
nie
ń
barometrycznych.
Do zbiorniku (1) wstawiona jest szklana rurka manometryczna (2), z której uprzednio
wypompowano cale powietrze, do stanu pró
ż
ni absolutnej. W przestrzeni pomi
ę
dzy jej
górnym zamkni
ę
tym ko
ń
cem, a meniskiem rt
ę
ci panuje pró
ż
nia Torrcelleogo (3) pró
ż
nia
bezwzgl
ę
dna Poło
ż
enie słupka rt
ę
ci okre
ś
la ci
ś
nienie barometryczne (otoczenia) pb.
Wynaleziony
barometr
odegrał
podstawowe
znaczenie
dla
rozwoju
metrologii.
B. Pascal powtarzaj
ą
c i kontynuuj
ą
c badania Torricellego, zauwa
ż
ył,
ż
e ci
ś
nienie
atmosferyczne zale
ż
y nie tylko od wysoko
ś
ci miejsca, w którym przyrz
ą
d si
ę
znajduje, ale
tak
ż
e od stanu pogody.
Wakuometr
Wakuometr jest ci
ś
nieniomierzem słu
żą
cym do pomiaru podci
ś
nie
ń
. Zasada działania i
budowa nie ró
ż
ni
ą
si
ę
od manometrów pr
ęż
nych i hydrostatycznych. Cz
ę
sto wykonuje si
ę
manometry pr
ęż
ne, które mog
ą
słu
ż
y
ć
do pomiaru nadci
ś
nie
ń
i podci
ś
nie
ń
. Nazywamy je
mano-wakuometrami.

Jednostki ci
ś
nienia.
W układzie jednostek miar SI główn
ą
jednostk
ą
ci
ś
nienia jest Pascal ( Pa ) czyli niuton na
metr kwadratowy
2
2
*
1
1
1
s
m
kg
m
N
Pa
=
=
Pascal jest jednostk
ą
mał
ą
, dlatego w praktyce stosuje si
ę
megapascal
1MPa =10
6
Pa
oraz bar
1bar =10
5
Pa
Dawniej manometry skalowano w atmosferach technicznych, czyli kilogramach siły na
centymetr kwadratowy.
Pa
cm
kG
at
4
2
10
*
80665
,
9
1
1
=
=
Cz
ę
sto mierzy si
ę
ci
ś
nienie za pomoc
ą
wysoko
ś
ci słupa cieczy
Przy małych ci
ś
nieniach wzgl
ę
dnych cz
ę
sto mierzy si
ę
ci
ś
nienie za pomoc
ą
wysoko
ś
ci słupa
wody:
Pa
m
kG
O
mmH
80665
,
9
1
1
2
2
=
=
Przy wi
ę
kszych ci
ś
nieniach wzgl
ę
dnych cz
ę
sto mierzy si
ę
ci
ś
nienie za pomoc
ą
wysoko
ś
ci
słupa rt
ę
ci ( Hg )
Tor ( Tr ) jest jednostk
ą
ci
ś
nienia równ
ą
ci
ś
nieniu wywieranemu w pró
ż
ni przez słup rt
ę
ci
o wysoko
ś
ci 1 mm i temperaturze 0°C przy normalnym przyspies zeniu ziemskim.
g
n
= 9,8066
2
s
m
1 Tr = 1 mm Hg = 133,3224 Pa
Jako normalne ci
ś
nienie fizyczne przyj
ę
to ci
ś
nienie jednej atmosfery fizycznej
Pn = 1 atm = 760 Tr = 101325 Pa
Wnioski
Nauka mechaniki płynów skłania nas do rozwa
ż
a
ń
nad procesami zachodz
ą
cymi obok nas,
a nawet w nas. Układ krwiono
ś
ny jest takim specyficznym układem hydrodynamicznym.
Układ krwiono
ś
ny jest takim specyficznym układem hydrodynamicznymi, w którym zachodzi
wiele przemian. Wiemy ze ci
ś
nienie jaki temperatura krwi nie jest stała a co si
ę
z tym wi
ąż
e

jej g
ę
sto
ść
jest zmienna. St
ą
d te
ż
wyznaczenie relacji krew - zastawki jest ogromnie
skomplikowane, ale ciekawe.
Wchodz
ą
c w XXI wiek coraz bardziej modne staje si
ę
pozyskiwanie energii
w sposób ekologiczny. Jednym ze sposobów pozyskiwania energii ekologicznej jest
budowanie elektrowni wodnych, zarówno szczytowo - pompowych jak i zaporowych.
Dziedzina hydroenergetyki wi
ąż
e si
ę
ś
ci
ś
le z mechanik
ą
płynów. Projektowanie tych
elektrowni wymaga bowiem znajomo
ś
ci praw rz
ą
dz
ą
cych cieczami, jak na przykład: prawa
naporu hydrostatycznego, i innych, bez których wykorzystanie energii tkwi
ą
cej
w cieczach byłoby niemo
ż
liwe.
5 i 6. Warunek równowagi , równowaga wzgl
ę
dna, powierzchnie stałego
potencjału
W hydrostatyce modele cieczy lepkiej i idealnej s
ą
równowa
ż
ne sobie. Rozpatruj
ą
c
równowag
ę
ciała płynnego poddanego działaniu sił powierzchniowych mo
ż
emy okre
ś
li
ć
jego
stan napi
ę
cia przy pomocy tensora napr
ęż
enia, podstawiaj
ą
c w nim zerowe warto
ś
ci
napr
ęż
e
ń
stycznych.
zx
yz
xy
τ
τ
τ
=
=
=
z
y
x
ij
δ
δ
δ
δ
0
0
0
0
0
0
i,j=x,y,z
δ
=
δ
ij
e
i
e
j
W przypadku cieczy w której nie uwzgl
ę
dniamy sił masowych , tensor napr
ęż
e
ń
tworzy
przynale
ż
n
ą
mu struktur
ę
, poniewa
ż
wszystkie składowe tensora s
ą
sobie równe.
δ
xx
=
δ
yy
=
δ
zz
=p
Otrzymali
ś
my w ten sposób twierdzenie które w hydrostatyce nosi nazw
ę
prawa
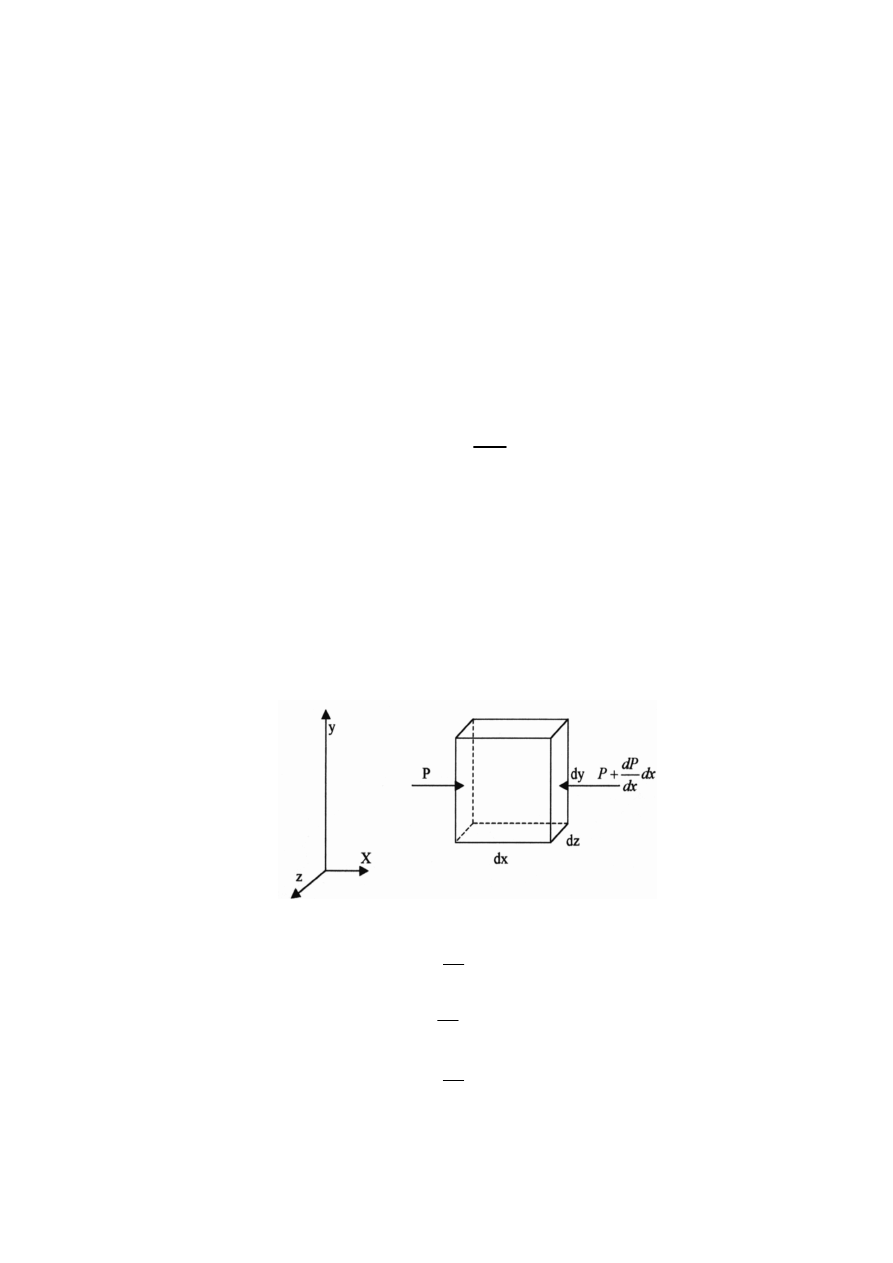
Pascala. Ustalmy element płynu P(x,y,z) za pomoc
ą
prostopadło
ś
cianu o wymiarach dx,dy,dz
i
ś
cianach zorientowanych równolegle do osi układu współrz
ę
dnych, a ponadto funkcja
ci
ś
nienia p(x,y,z) jest niewiadom
ą
.
Układamy warunki równowagi na kolejne osie układu współrz
ę
dnych
0
)
(
:
=
−
+
dydz
dx
dx
dp
p
pdydz
XdV
X
ρ
0
)
(
:
=
−
+
dxdz
dy
dy
dp
p
pdxdz
YdV
Y
ρ
0
)
(
:
=
−
+
dxdy
dz
dz
dp
p
pdxdy
ZdV
X
ρ
Po podstawieniu otrzymujemy
0
=
−
dx
dp
X
ρ
0
=
−
dy
dp
Y
ρ
0
=
−
dZ
dp
Z
ρ
Otrzymali
ś
my w ten sposób równanie równowagi płynu pozostaj
ą
cego w spoczynku lub
ogólnie warunki równowagi płynów
Powy
ż
sze równania mo
ż
na zast
ą
pi
ć
równaniem wektorowym
−
+
+
)
(
k
j
i
Z
Y
X
ρ
i
dx
dp
−
j
dy
dp
−
k
dz
dp
−
= 0
(1)
0
=
−
gradp
F
ρ
Skalarne pole ci
ś
nie
ń
mo
ż
na wyznaczy
ć
całkuj
ą
c te równania, otrzymamy wtedy
szukan
ą
funkcj
ę
p(x,y,z). Je
ś
li funkcja ta jest stała to otrzymujemy powierzchni
ę
stałego
ci
ś
nienia nazywane powierzchniami izobarycznymi. Stwierdzamy ,
ż
e wektor siły obj
ę
to
ś
ciowej
jest prostopadły w ka
ż
dym punkcie powierzchni izobarycznej prostopadły do niej.
Na podstawie (1) mo
ż
na wyprowadzi
ć
prawo Pascala :
dx
dp
dy
dp
=
0
=
=
dz
dp
Je
ś
li (1) pomno
ż
y
ć
przez przyrost wektora promienia , to otrzymamy
r
gradpd
r
Fd
=
ρ
(2)
dp
r
Fd
=
ρ
Niech F b
ę
dzie sił
ą
potencjaln
ą
. Wtedy musi istnie
ć
takie U(x,y,z) ,
ż
e F=-gradU (3).
Uwzgl
ę
dniaj
ą
c ( 1 ) i (2) otrzymujemy
dp
gradUdr
=
−
ρ
0
=
+
dp
dU
ρ
Je
ś
li p=const , to mo
ż
emy to scałkowa
ć
i otrzymamy
const
p
U
=
+
ρ

Jedynie siły masowe s
ą
w stanie wywoła
ć
równowag
ę
cieczy nie
ś
ci
ś
liwej.
W szczególnym przypadku gdy p=const ( dp=0 ) , to pdU=0 ~ U=const. Czyli powierzchnie
stałego ci
ś
nienia s
ą
równie
ż
powierzchniami ekwipotencjalnymi.
Wyra
ż
enie w nawiasie jest równe zupełnej dU, st
ą
d
dp=
ξ
*dU
Z równania tego wynika,
ż
e dla dp=0 jest dU=0. Oznacza to,
ż
e powierzchnie jednakowego
ci
ś
nienia (dp=0, p=const), czyli powierzchnie izobaryczne, s
ą
w polu sił masowych
jednocze
ś
nie powierzchniami stałego potencjału (dU=0, U=const), czyli powierzchniami
ekwipotencjalnymi.
Powierzchnie ekwipotencjalne z natury rzeczy nie mog
ą
si
ę
wzajemnie przecina
ć
i ka
ż
da z nich jest albo powierzchni
ą
zamkni
ę
t
ą
, albo ko
ń
czy si
ę
na
ś
cianie zbiornika
(naczynia). Swobodne powierzchnie cieczy, czyli powierzchnie oddzielaj
ą
ce cieczy od gazu,
s
ą
oczywi
ś
cie powierzchniami ekwipotencjalnymi.
Dla powierzchni ekwipotencjalnych (dU=0) z równania wy
ż
ej wynika,
ż
e siły masowe przy
przesuni
ę
ciu wzdłu
ż
tych powierzchni nie wykonuj
ą
ż
adnej pracy (X*dx=Y*dy=Z*dz=0).
Parcie cieczy na powierzchnie
ś
cian
Parcie jest to siła, jak
ą
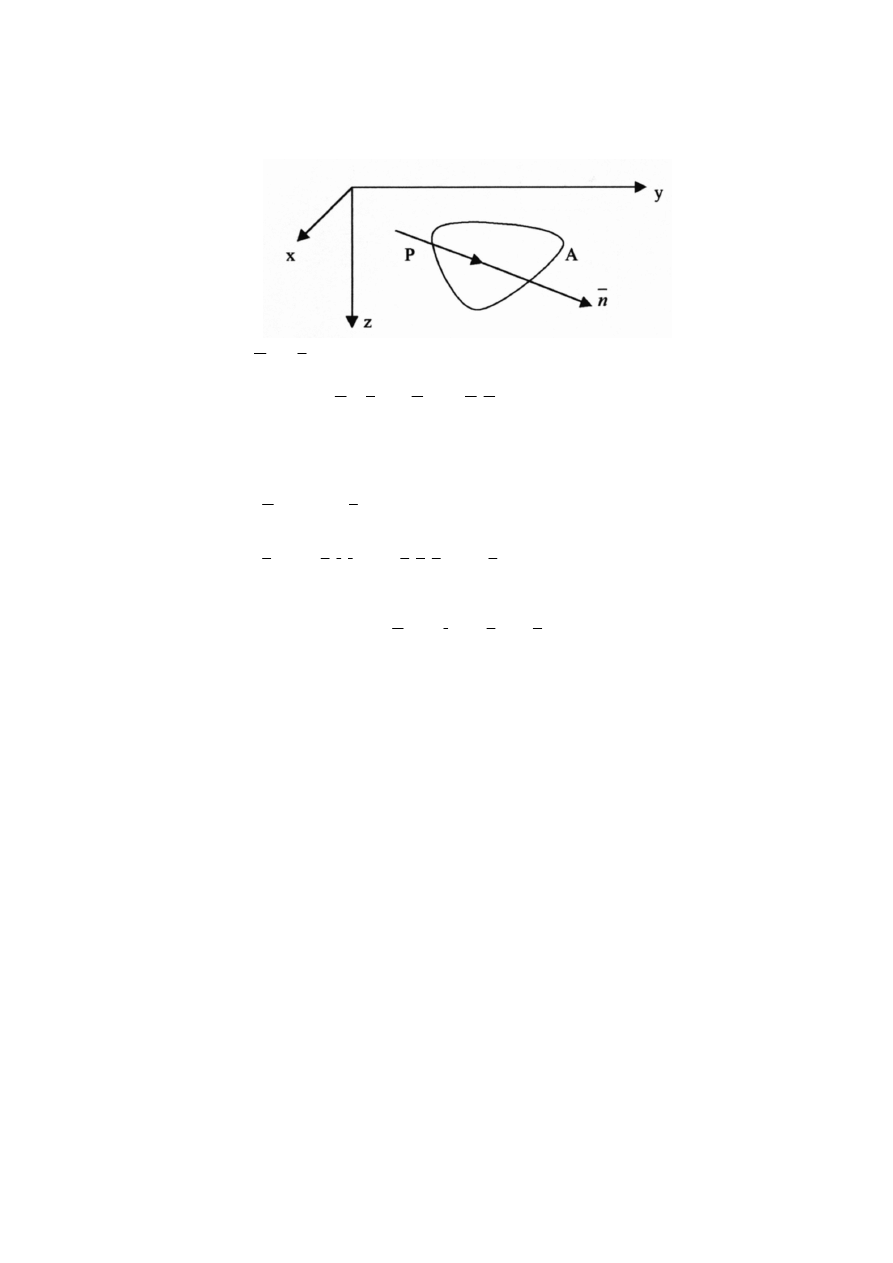
wywiera ciecz w spoczynku na dowolnie zorientowan
ą
powierzchni
ę
. Rozwa
ż
ania obejm
ą
parcie na powierzchnie płask
ą
i zakrzywion
ą
.
Powierzchnia płaska lub
ś
ciana płaska jest w ogólnym przypadku nazywana
płaszczyzn
ą
pochylon
ą
pod k
ą
tem
α
wzgl
ę
dem poziomu (rys. 4) za
ś
w szczególnych
przypadkach – płaszczyzn
ą
pionow
ą
lub poziom
ą
.
)
(
dz
z
U
dy
y
U
dx
x
U
dp
∂
∂
+
∂
∂
+
∂
∂
=
ς
)
(
dz
z
U
dy
y
U
dx
x
U
dp
∂
∂
+
∂
∂
+
∂
∂
=
ς
dz
Z
dy
Y
dx
X
dU
*
*
*
+
+
=

Rys 4. Parcie cieczy na
ś
cian
ę
płask
ą
W przypadku zbiornika (naczynia) otwartego, ci
ś
nienie atmosferyczne P
a
nie jest
uwzgl
ę
dniane, gdy
ż
działa ono jednocze
ś
nie tak
ż
e na zewn
ę
trzn
ą
stron
ę
ś
ciany.
W przypadku zbiornika (naczynia) zamkni
ę
tego nale
ż
y uwzgl
ę
dni
ć
ewentualn
ą
ró
ż
nic
ę
ci
ś
nie
ń
, jaka istnieje pomi
ę
dzy czynnikami gazowymi wewn
ą
trz i na zewn
ą
trz.
Parcie F na płaszczyzn
ę
pochyła A, o
ś
rodku ci
ęż
ko
ś
ci S i współrz
ę
dnych
ś
rodka
ci
ęż
ko
ś
ci Xs, Ys, Zs, wynosi
gdzie
∫∫
z*dA=z
S
*A – moment statyczny powierzchni A wzgl
ę
dem powierzchni cieczy
p
S
– ci
ś
nienie hydrostatyczne na gł
ę
boko
ś
ci z
S
ś
rodka ci
ęż
ko
ś
ci S.
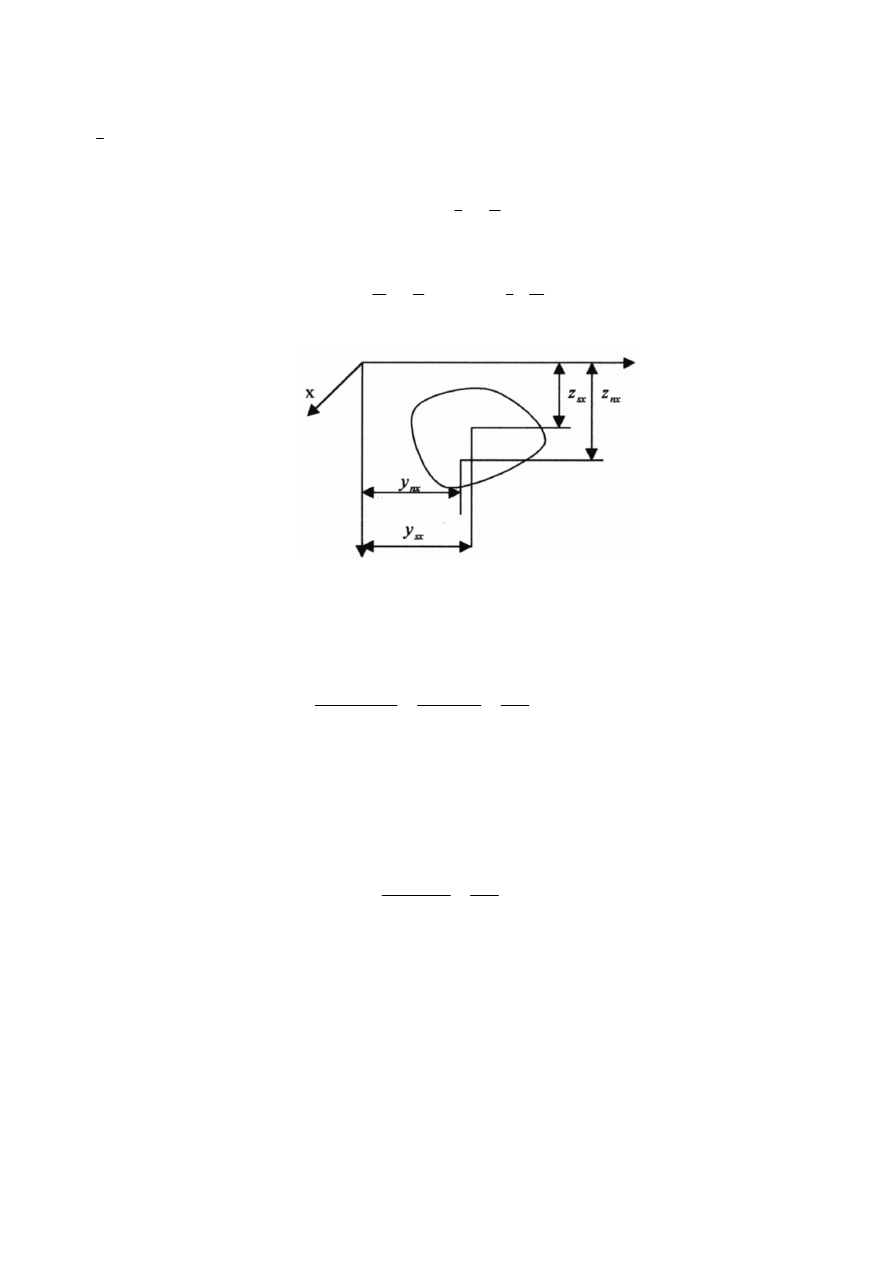
Powierzchnie zakrzywione
Parcie na powierzchnie zakrzywione sprowadza si
ę
w ogólnym przypadku do skr
ę
tnika,
tzn. parcia wypadkowego i pary sił, wzgl
ę
dnie do dwóch sił sko
ś
nych. Tak wi
ę
c utrzymanie
zakrzywionej powierzchni w równowadze wymaga przyło
ż
enia nie tylko siły przeciwnej parciu,
ale i pary sił o odpowiednim momencie.
Znalezienie parcia polega praktycznie na znalezieniu jego rzutów na kierunki osi
współrz
ę
dnych. W tym celu zostanie przyj
ę
ty układ współrz
ę
dnych prostok
ą
tnych,
w którym osie X, Y le
żą
na swobodnej powierzchni cieczy, a o
ś
z skierowania jest na dół (rys.
5). Element dA stanowi cz
ęść
powierzchni cylindrycznej o tworz
ą
cych prostopadłych do
płaszczyzny yz.
∫∫
∫∫
=
=
=
=
A
A
S
S
A
p
A
z
g
dA
z
g
dA
p
F
*
*
*
*
*
*
*
ξ
ξ
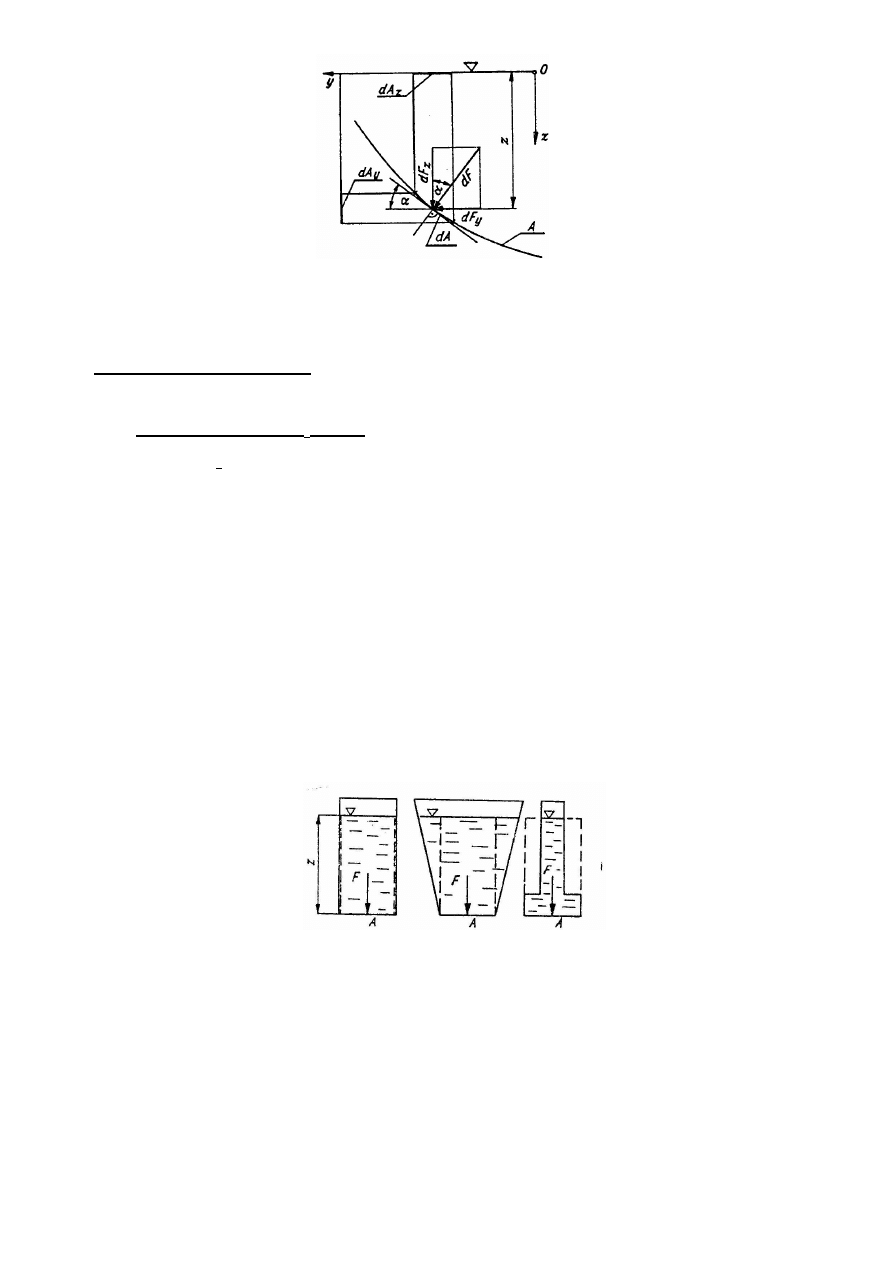
Rys 5. Parcie cieczy na element powierzchni zakrzywionej
dF=
ξ
*g*z*dA
Paradoks hydrostatyczny
Składowa pozioma F
y
parcia na powierzchni
ę
zakrzywion
ą
A równa si
ę
zatem parciu na
powierzchni
ę
A
y
, która jest rzutem powierzchni A na płaszczyzn
ę
pionow
ą
. Tak samo oblicza
si
ę
poziom
ą
składow
ą
parcia na płaszczyzn
ę
pochyl
ą
. Sposób obliczania poziomej skł
ą
dowej
parcia nie ró
ż
ni si
ę
jak wida
ć
, od sposobu obliczania parcia na płaszczyzn
ę
pionow
ą
.
gdzie V, m, G – obj
ę
to
ść
, masa i ci
ęż
ar słupa cieczy nad powierzchni
ą
zakrzywion
ą
gdzie
M
X
=Z
S
*A
W przypadku płaszczyzn poziomych (
α
=0), zale
ż
no
ś
ci upraszczaj
ą
si
ę
.
Ś
rodek parcia
le
ż
y w
ś
rodku ci
ęż
ko
ś
ci płaszczyzny dna naczynia lub zbiornika.
Rys.6. Paradoks hydrostatyczny
∫∫
∫∫∫
∫∫
=
=
=
=
=
=
Z
Z
A
V
A
Z
Z
Z
G
g
m
V
g
dV
g
dA
z
g
dF
F
*
*
*
*
*
*
ξ
ξ
ξ

a
a
z
z
y
x
z
y
x
p
gz
p
p
c
z
c
gz
p
c
gz
p
gdz
p
d
dz
f
p
d
g
f
f
f
dz
f
dy
f
dx
f
dp
+
=
=
⇒
=
+
⇒
+
=
=
=
=
=
=
+
+
=
ρ
ρ
ρ
ρ
ρ
ρ
'
0
'
/*
0
1
Jak wida
ć
z powy
ż
szego równania ci
ś
nienie na dnie zbiornika , a wi
ę
c i napór na jego dno
nie zale
ż
y od kształtu zbiornika , ale od wysoko
ś
ci słupa cieczy. To zjawisko okre
ś
la si
ę
mianem paradoksu hydrostatycznego.
Moment siły naporu
Moment siły naporu wzgl
ę
dem dowolnego punktu definiujemy nast
ę
puj
ą
co:
(
)
*
S
L
r pn dS
= −
∫
(4)
Gdzie r jest promieniem ł
ą
cz
ą
cym punkt, wzgl
ę
dem którego liczymy moment,
z elementem powierzchni dS.
Tak wi
ę
c siły hydrostatyczne sprowadzaj
ą
si
ę
do naporu hydrostatycznego
i momentu hydrostatycznego. Jak wiadomo ze statyki, taki układ przestrzennych sił daje si
ę
sprowadzi
ć
do wypadkowej siły wtedy i tylko,wtedy, kiedy
N
⊥
⊥⊥
⊥
L. (5)
Prostopadło
ść
momentu i naporu jest oczywista dla płaskich
ś
cian. Wówczas
wektorem r
n
mo
ż
na okre
ś
li
ć
poło
ż
enie linii działania siły naporu
r
n
*N = L. (6)
Punkt przebicia
ś
ciany lini
ą
działania siły naporu nazywamy
ś
rodkiem naporu.
Je
ż
eli obliczone s
ą
ju
ż
N i L to równanie (6) staje si
ę
równaniem dla trzech składowych
r
x
, r
y
, r
z
wektora r
n
0
0
0
x
z y
y z
x
z x
y
x z
y
y x
x y
z
z
r
N r
N r
L
N r
r
N r
L
N r
N r
r
L
+
−
=
−
+
+
=
−
+
=
(7)
7 i 8. Napór hydrostatyczny na
ś
ciany płaskie i zakrzywione Współrz
ę
dne
ś
rodka naporu
Pole sił masowych
k
g
f
=
∫ ∫
=
=
=
→
A
pdA
p
A
pd
p
d
dA
n
A
d
dA
,
,
,
0
∫
∫ ∫
∫
−
=
+
=
+
=
pomijamy
p
gzdA
p
dA
p
gz
p
p
gz
p
a
A
a
A
a
,
,
)
(
,
ρ
ρ
ρ
∫ ∫
=
dA
n
gz
p
A
ρ
k
k
n
j
j
n
i
i
n
n
)
,
cos(
)
,
cos(
)
,
cos(
+
+
=
Po podstawieniu i uporz
ą
dkowaniu otrzymujemy
k
p
j
p
i
p
p
z
y
x
+
+
=
∫ ∫
=
Ax
x
gzdA
p
,
ρ
∫ ∫
=
Ay
y
gzdA
p
,
ρ
∫ ∫
=
Az
z
gzdA
p
,
ρ
Dla p
X
, p
y
obliczamy sił
ę
naporu
∫ ∫
=
=
Ax
x
gzdA
p
ρ
x
sx
Ax
A
gz
zdA
g
ρ
ρ
∫ ∫
=
Analogicznie
y
sy
y
A
gz
p
ρ
=
z
sx
, z
sy
, -współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci rzutu powierzchni w kierunku osi x i y.
A
x
, A
y
-pola powierzchni rzutów w kierunku osi x i y.
Warto
ść
p
Z
wyliczamy w sposób odmienny.
∫ ∫
=
=
z
Az
z
gV
zdA
g
p
ρ
ρ
V
z
-obj
ę
to
ść
słupa cieczy nad poziomym rzutem powierzchni.
Ś
rodek naporu
]
,
,
[
n
n
n
n
z
y
x
r
=
Sumaryczny moment od naporów elementarnych wynosi
∫ ∫
×
p
d
r
A
Moment od wypadkowej
dA
n
r
gz
p
d
r
A
n
)
(
×
=
×
∫ ∫
ρ
x
x
x
AX
x
AX
nx
AX
x
nx
x
x
x
x
sx
x
x
AX
x
nx
M
J
M
dA
z
gM
dA
gz
z
dA
gz
gM
z
gzdA
dp
gM
A
gz
p
zdp
p
z
=
=
=
=
=
=
=
∫ ∫
∫ ∫
∫ ∫
∫ ∫
2
2
2
*
,
*
ρ
ρ
ρ
ρ
ρ
ρ
ρ
J
x
- moment bezwładno
ś
ci
M
x
- moment statyczny
x
xy
x
Ax
nx
Ax
x
nx
x
Ax
x
nx
M
J
M
yzdA
y
gyzdA
gM
y
ydp
p
y
=
=
=
=
∫ ∫
∫ ∫
∫ ∫
ρ
ρ
;
*
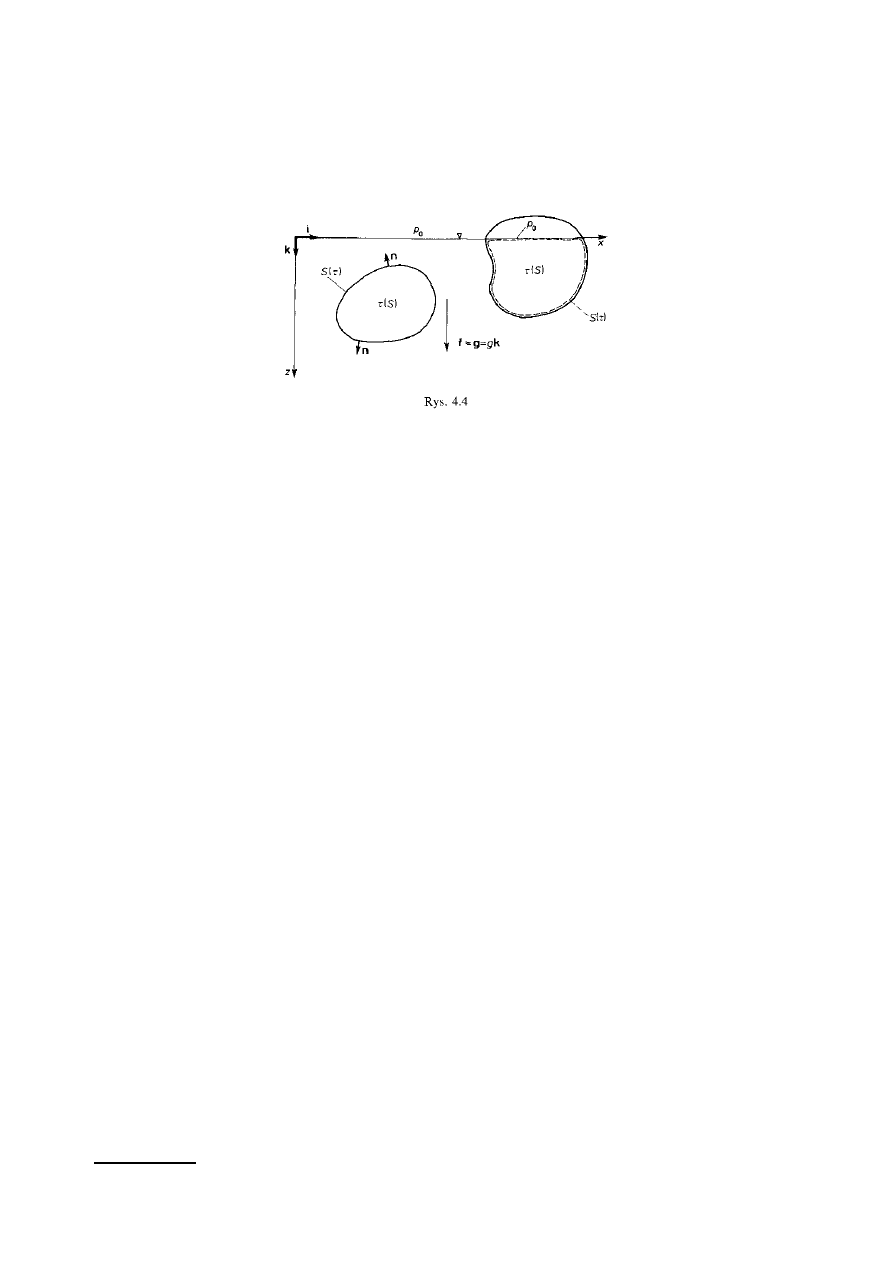
9. Zjawisko wyporu. Odkrycie Archimedesa (czas, epoka, miejsce)
Je
ż
eli ciało jest zanurzone w płynie (rys.4.4),wypór hydrostatyczny jest okre
ś
lony wzorem:
∫
−
=
S
pndS
N
(9.1)
W takim przypadku całk
ę
zawart
ą
w powy
ż
szym wzorze mo
ż
na przekształci
ć
na całk
ę
obj
ę
to
ś
ciow
ą
:
∫
−
=
S
gradpd
N
τ
(9.2)
a po uwzgl
ę
dnieniu równania równowagi powy
ż
sze wyra
ż
enie przyjmuje posta
ć
:
∫
∫
−
=
−
=
S
S
d
gk
fd
N
τ
τ
τ
ρ
τ
ρ
(9.3)
Ale
∫
=
)
(
)
(
s
S
d
τ
τ
τ
Jest obj
ę
to
ś
ci
ą
ciała zanurzonego w płynie. St
ą
d siła wyporu
N= -
ρρρρ
gk=-G
(9.4)
jest równa ci
ęż
arowi cieczy wypartej przez zanurzone ciało i skierowana jest przeciwnie do
zwrotu siły ci
ęż
ko
ś
ci. Tak wi
ę
c otrzymali
ś
my znane prawo Archimedesa.
Siła wyporu N przechodzi przez
ś
rodek ci
ęż
ko
ś
ci obj
ę
to
ś
ci płynu zajmowanej przez
zanurzone ciało, i wyra
ż
a si
ę
wzorem:
N
r
G
r
L
n
n
××××
====
−−−−
××××
====
)
(
(9.5)
Archimedes

Jeden z najwybitniejszych greckich matematyków i fizyków staro
ż
ytno
ś
ci, odkrył wiele praw
matematycznych i fizycznych, sformułował wa
ż
ne zasady mechaniczne. Archimedes urodził
si
ę
w 287 roku przed Chrystusem w Syrakuzach; a o jego
ż
yciu opowiadaj
ą
Livius, Polibius.
Nie sprawował
ż
adnego urz
ę
du, oddaj
ą
c si
ę
wył
ą
cznie nauce. Przebywał przez pewien czas
w sławnej akademii Aleksandryjskiej, jako ucze
ń
matematyka Konona, z którym utrzymywał
pó
ź
niej tak
ż
e korespondencj
ę
. Zgin
ą
ł tragicznie w roku 212 przy zdobywaniu Syrakuz przez
Rzymian pod wodz
ą
Marcellusa ( podczas drugiej wojny Punickiej )
Prawo Archimedesa
Ka
ż
de ciało zanurzone w cieczy traci pozornie na ci
ęż
arze tyle, ile wynosi ci
ęż
ar cieczy
wypartej przez to ciało tzn. ciało zanurzone w cieczy doznaje ze strony tej cieczy parcia do
góry, równego co do warto
ś
ci ci
ęż
arowi cieczy wypartej przez to ciało.
Z czasem prawo to uogólniono na gazy ( i ciała sypkie spełniaj
ą
ce okre
ś
lone warunki)
Jak głosi legenda, Hieron II zamówił dla siebie koron
ę
z czystego złota. Władca nie dowierzał
jednak złotnikowi. Pos
ą
dzał go to,
ż
e koron
ę
wykonał ze srebra i z zewn
ą
trz tylko pozłocił.
Zwrócił si
ę
wtedy do przebywaj
ą
cego na jego dworze Archimedesa, aby ten sprawdził jego
przypuszczenie, nie niszcz
ą
c pi
ę
knej korony.
Archimedes długo my
ś
lał nad tym zadaniem, niestety bez skutku. Zastanawiał si
ę
nad
tym nawet w k
ą
pieli. Siedz
ą
c kiedy
ś
w wannie zauwa
ż
ył,
ż
e ciała zanurzone
w cieczy wydaj
ą
si
ę
l
ż
ejsze. W tym momencie przyszło na
ń
ol
ś
nienie. Z okrzykiem eureka!
(ła
ć
. znalazłem) Archimedes pono
ć
wyskoczył z wanny i w stroju mocno niekompletnym
pobiegł przez miasto do swego króla, aby mu zakomunikowa
ć
o rozwi
ą
zaniu problemu. Je
ś
li
wi
ę
c wierzy
ć
legendzie, to dzi
ę
ki zadaniu króla Hierona Archimedes odkrył wa
ż
ne prawo,
zwane dzi
ś
prawem Archimedesa, które stanowi podstaw
ę
teorii pływania ciał.
Je
ż
eli rzeczywi
ś
cie Archimedes odkrył to prawo w wannie, to trudno si
ę
dziwi
ć
,
ż
e był
zaskoczony prostot
ą
metody, jak
ą
nale
ż
ało zastosowa
ć
, aby rozwi
ą
za
ć
postawione mu
zadanie. Srebro ma bowiem g
ę
sto
ść
prawie dwa razy mniejsz
ą
ni
ż
złoto. Fałszywa korona
musiałaby wi
ę
c mie
ć
znacznie wi
ę
ksz
ą
obj
ę
to
ść
ni
ż
korona z czystego złota o tej samej
masie i - co za tym idzie - wypierałaby wi
ę
cej wody, a zatem wi
ę
cej " traciłaby pozornie na
ci
ęż
arze ". Inaczej fałszywa korona byłaby w wodzie znacznie l
ż
ejsza ni
ż
próbka czystego
złota o tej samej masie.

Prawo Archimedesa jest najwa
ż
niejszym, lecz bynajmniej nie jedynym osi
ą
gni
ę
ciem
Archimedesa w zakresie hydrostatyki. Jego badania i spostrze
ż
enia dotycz
ą
ce warunków
równowagi cieczy i warunków pływania ciał legły u podstaw rozwoju tej dziedziny. Oprócz
praw fizyki i matematyki Archimedes odkrył równie
ż
podstawow
ą
zasad
ę
mechaniki ciał
płynnych, zwi
ęź
le sformułowana brzmi: ciało zanurzone w cieczy ulega parciu do góry i traci
pozornie na ci
ęż
arze tyle, ile wa
ż
y wyparta prze ze
ń
ciecz. Z tej zasady korzysta si
ę
przy
wyznaczaniu ci
ęż
aru wła
ś
ciwego, mianowicie dzieli si
ę
ci
ęż
ar bezwzgl
ę
dny przez obj
ę
to
ść
,
równ
ą
liczbowo ci
ęż
arowi wypartej wody. Wszystkie przyrz
ą
dy, słu
żą
ce do pomiaru ci
ęż
aru
wła
ś
ciwego, jak piknometr, waga hydrostatyczna, wolumometr, a dla cieczy areometr,
opieraj
ą
si
ę
na zasadzie Archimedesa.
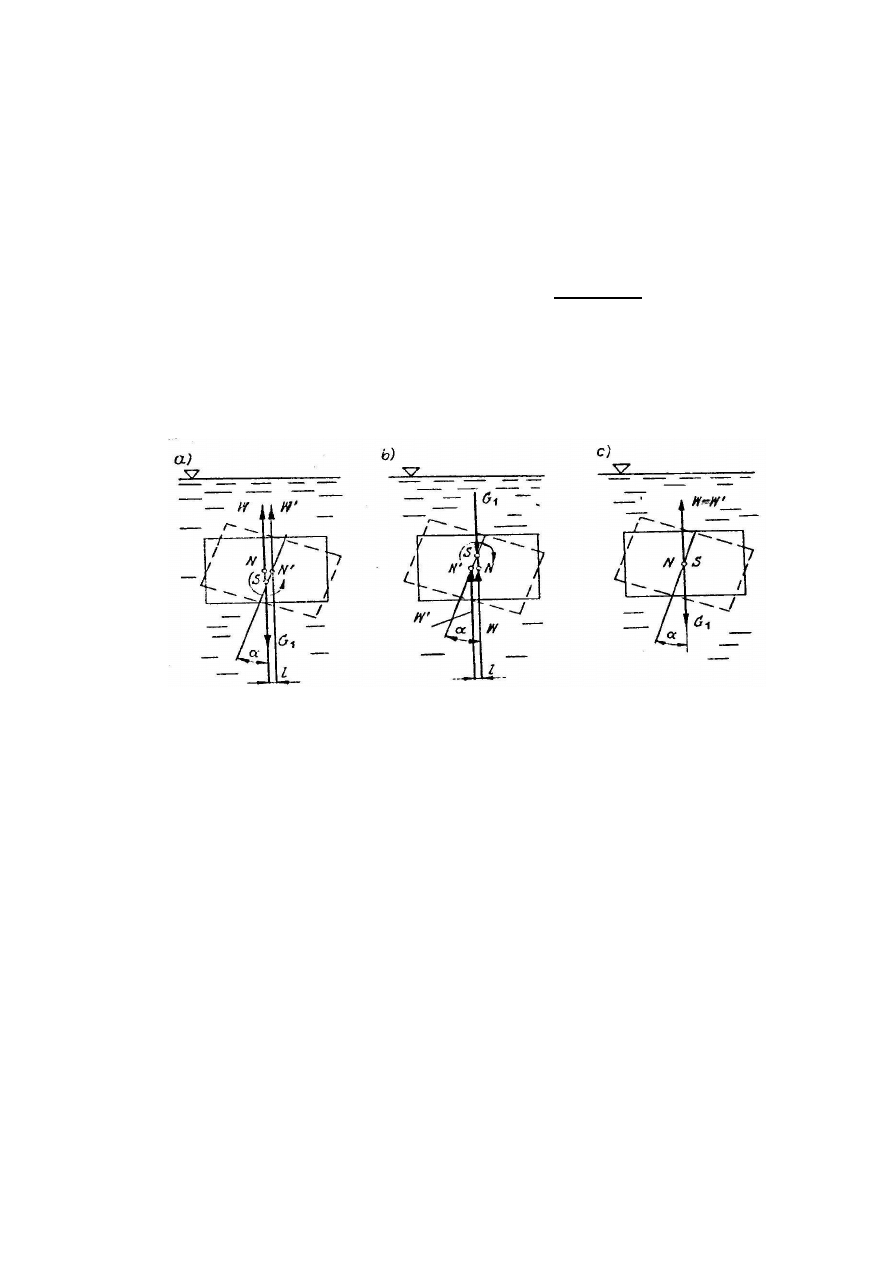
10. Stan stateczno
ś
ci pływania. Metacentrum i odległo
ść
metacentryczna
Na ciało zanurzone w cieczy działa ci
ęż
ar ciała G
1
i wypór W. Je
ż
eli potraktuje si
ę
wypór
W jako wypór ciała całkowicie zanurzonego, to mo
ż
liwe s
ą
trzy przypadki:
•
G
1
<W, siła (w-G
1
) wypiera ciało do góry powoduj
ą
c jego cz
ęś
ciowe wynurzenie; stan
równowagi zostaje osi
ą
gni
ę
ty wtedy, gdy ci
ęż
ar ciała b
ę
dzie równy wyporowi
zanurzonej cz
ęś
ci ciała; w tym stanie równowagi ciało pływa
•
G
1
=W, ciało jest całkowicie zanurzone na dowolnej gł
ę
boko
ś
ci
•
G
1
>W, ciało tonie.
Stateczno
ść
pływania jest to zdolno
ść
powrotu ciała pływaj
ą
cego wychylonego ze stanu
równowagi do pierwotnego poło
ż
enia.
rys.7. Stateczno
ść
ciała całkowicie zanurzonego: a) równowaga stała, b) chwiejna,
c) oboj
ę
tna
Pływanie ciała całkowicie zanurzonych. Na ciało całkowicie zanurzone działaj
ą
dwie siły;
wypór W i ci
ęż
ar G
1
(rys. wy
ż
ej). Punkt S oznacza
ś
rodek ci
ęż
ko
ś
ci ciała zanurzonego
i w ogólnym przypadku nie musi pokrywa
ć
si
ę
ze
ś
rodkiem wyporu N, który le
ż
y w
ś
rodku
geometrycznym ciała. Równowaga pływania, jak wiadomo, zachodzi wówczas gdy W= G
1
i gdy W i G
1
le
żą
wzdłu
ż
tej samej osi pionowej, czyli wzdłu
ż
osi pływania. Mo
ż
liwe s
ą
trzy
przypadki:
•
Punkt S le
ż
y poni
ż
ej punktu N,
•
Punkt S le
ż
y powy
ż
ej punktu N
•
Punkt S i N pokrywaj
ą
si
ę
Mo
ż
na zatem stwierdzi
ć
,
ż
e:
1) równowaga stała –
ś
rodek ci
ęż
ko
ś
ci S le
ż
y poni
ż
ej
ś
rodka wyporu N,
2) równowaga chwiejna – S le
ż
y powy
ż
ej N,
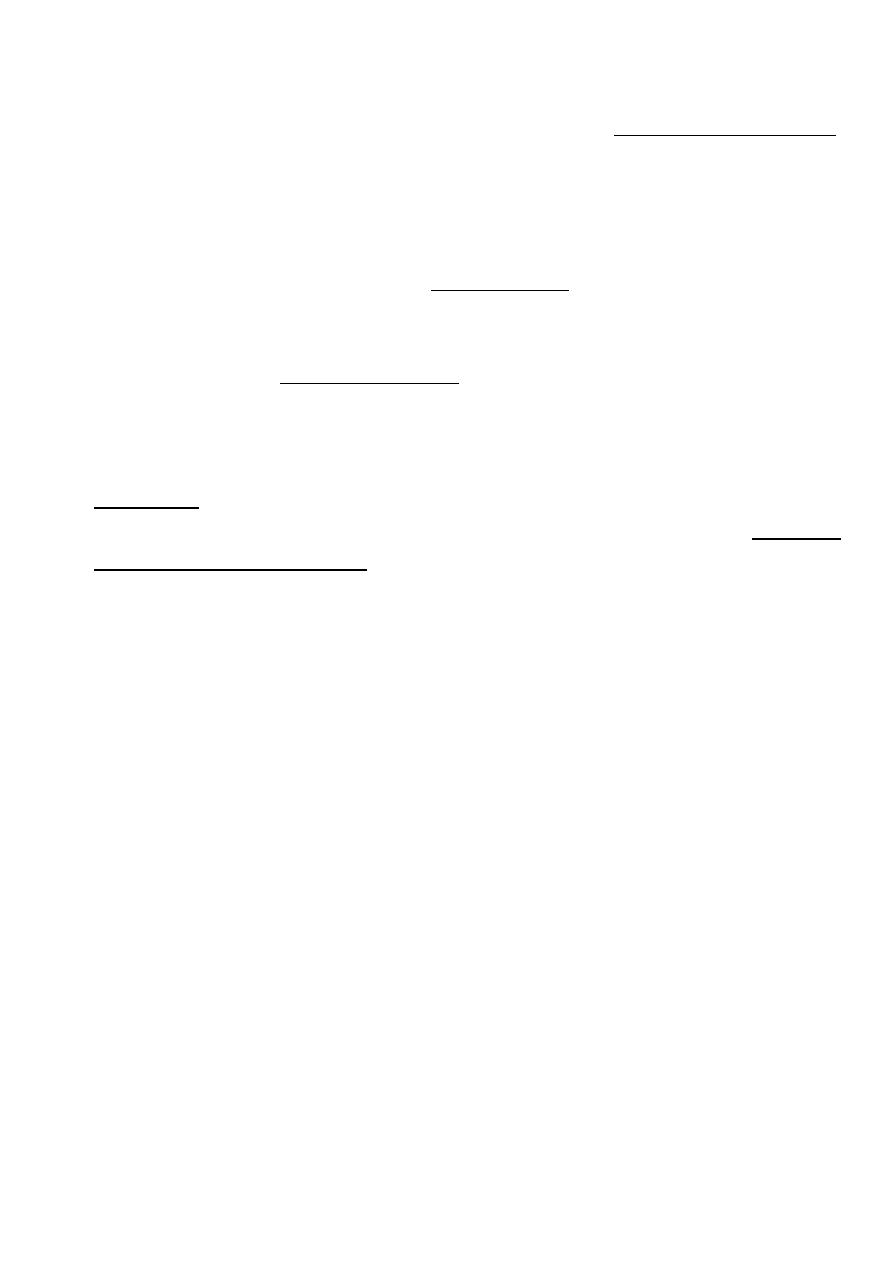
3) równowaga oboj
ę
tna – punkt S i N pokrywaj
ą
si
ę
.
Bardziej zło
ż
onym zagadnieniem jest stateczno
ść
pływania ciał cz
ęś
ciowo zanurzonych.
Dowolne wychylenie ciała jest, ogólnie bior
ą
c, wypadkow
ą
trzech przesuni
ęć
i trzech obrotów
wzgl
ę
dem osi X, Y, Z., przy czym o
ś
x jest prostopadła do płaszczyzny. Przy takim poło
ż
eniu
ś
rodka ci
ęż
ko
ś
ci mo
ż
liwe jest zachowanie stateczno
ś
ci pływania, co było wykluczone
w przypadku ciała pływaj
ą
cego całkowicie zanurzonego.
Ciało jest stateczne, czyli posiada równowag
ę
stał
ą
, przy przesuni
ę
ciu wzdłu
ż
osi z.
Przy takiej wymuszonej zmianie gł
ę
boko
ś
ci zanurzenia zostaje naruszona równowaga
pomi
ę
dzy ci
ęż
arem ciała G
1
i wyporem W, co prowadzi do zmiany zanurzenia i powrotu do
stanu pocz
ą
tkowego. Równowaga oboj
ę
tna ma miejsce, natomiast, podczas przesuni
ęć
równoległych do zwierciadła cieczy, czyli podczas przesuni
ęć
wzdłu
ż
osi x i y oraz podczas
obrotu wokół osi z..
Te rozwa
ż
ania mo
ż
na uzupełni
ć
, wprowadzaj
ą
c poj
ę
cia punktu M., zwanego
metacentrum, czyli punkt przeci
ę
cia linii działania wyporu chwilowego W i pionowej osi ciała
pływaj
ą
cego. Odległo
ść
punktu M od
ś
rodka ci
ęż
ko
ś
ci ciała S nosi nazw
ę
odległo
ś
ci
ą
(wysoko
ś
ci
ą
) metacentrycznej m. Dla informacji mo
ż
na poda
ć
,
ż
e minimalna odległo
ść
metacentryczna statków wynosi m = 0,5
÷
4,5 m.
Odległo
ść
metacentryczna m. mo
ż
na wyrazi
ć
przez parametry geometryczne ciała
pływaj
ą
cego. Przy wychyleniu o mały k
ą
t
ϕ
, wypór chwilowy W jest równy sumie algebraicznej
wyporu pocz
ą
tkowego W i wyporów W
k
obj
ę
to
ś
ci klinowych.

11. Kinematyka płynów. Cele, zadania, parametry kinematyczne.
DWIE METODY OPISU STANU PŁYNU
Wprowadzaj
ą
c omówion
ą
we Wst
ę
pie cech
ę
ci
ą
gło
ś
ci, mo
ż
emy traktowa
ć
płyn wypełniaj
ą
cy
rozwa
ż
any przez nas obszar jako kontinuum materialne. Ka
ż
demu punktowi tego obszaru
przyporz
ą
dkowujemy pewne jego otoczenie, o wymiarach małych w porównaniu z wymiarami
ciał opływanych lub wymiarami obszaru, a du
ż
ych w porównaniu z odległo
ś
ciami mi
ę
dzy
molekułami. Otoczenie takie nazywamy elementem płynu, a przestrze
ń
traktujemy jako
wypełnion
ą
tymi elementami w sposób ci
ą
gły. Posługiwanie si
ę
poj
ę
ciem elementu płynu jest
bardzo dogodne — mo
ż
emy uto
ż
sami
ć
go z punktem któremu przypisane s
ą
wszystkie
parametry charakteryzuj
ą
ce płyn lub te
ż
traktowa
ć
go jako sko
ń
czon
ą
obj
ę
to
ść
o cechach
kontinuum materialnego.
Stan płynu zajmuj
ą
cego okre
ś
lony obszar przestrzeni mo
ż
emy opisa
ć
w dwojaki sposób.
Pierwszy z nich polega na okre
ś
leniu parametrów w ka
ż
dym punkcie przestrzeni zajmowanej
przez płyn. Parametry te mog
ą
si
ę
zmienia
ć
zarówno w przestrzeni (mog
ą
by
ć
funkcj
ą
współrz
ę
dnych przestrzeni), jak i w czasie. Metoda ta nosi nazw
ę
metody Eulera albo metody
lokalnej.
Omawiaj
ą
c drugi sposób, wyobra
ź
my sobie,
ż
e wyodr
ę
bnili
ś
my element płynu
i
ś
ledzimy jego zachowanie si
ę
w czasie. Znaj
ą
c wszystkie interesuj
ą
ce nas parametry
dowolnych elementów płynu, mamy opisany stan płynu w całym zajmowanym przez niego
obszarze.
Ta metoda nosi nazw
ę
metody Lagrange^a lub metody w
ę
drownej.
KINEMATYCZNY PODZIAŁ PRZEPŁYWÓW
Je
ż
eli parametry opisuj
ą
ce stan płynu s
ą
niezale
ż
ne od czasu f, to d/dt = O i stan taki
nazywamy stanem stacjonarnym (ustalanym). Je
ż
eli za
ś
parametry te zale
żą
jawnie od
czasu,
to przepływ nazywamy przepływem niestacjonarnym (nieustalonym}.
Z punktu widzenia kinematycznego b
ę
dziemy rozró
ż
niali przepływy jednowymiarowe,
w których mamy tylko jedn
ą
składow
ą
wektora pr
ę
dko
ś
ci
przepływy dwuwymiarowe

oraz przepływy trójwymiarowe
W ka
ż
dym z tych przypadków składowe wektora pr
ę
dko
ś
ci mog
ą
by
ć
funkcj
ą
dowolnej
kombinacji zmiennych niezale
ż
nych x, y, z, t. Tak na przykład, mo
ż
emy mie
ć
przepływ
jednowymiarowy niestacjonarny, w którym
u
x
= u
x
(x,f),
lub przepływ dwuwymiarowy stacjonarny
u
x
= u
x
(x,y), u
y
= u
y
(x,y)

12. Metoda Eulera i Lagrange’a w kinematyce płynów
METODA EULERA
Je
ż
eli wybrany zostanie układ współrz
ę
dnych odniesienia, to obszar zajmowany przez
płyn b
ę
dzie opisany promieniem wodz
ą
cym r. W najprostszym przypadku, je
ż
eli układ
współrz
ę
dnych b
ę
dzie układem kartezja
ń
sktm, to
Wówczas parametry opisuj
ą
ce stan płynu b
ę
d
ą
funkcjami promienia wodz
ą
cego r
i czasu t. Ka
ż
demu poło
ż
eniu elementu płynu w chwili r, które jest okre
ś
lone współrz
ę
dnymi
x, y, z, odpowiada
ć
b
ę
dzie poło
ż
enie *„, y
(i
, z<> w chwili poprzedzaj
ą
cej t
t
,. Zapisujemy t
ę
odpowiednio
ść
w nast
ę
puj
ą
cej postaci:
(12.1)
W metodzie Eulera mamy nast
ę
puj
ą
cy zapis dla wektora pr
ę
dko
ś
ci:
co oznacz,a,
ż
e wektor pr
ę
dko
ś
ci mo
ż
e by
ć
przedstawiony nast
ę
puj
ą
co:
(12.2)
lub w skrócie
:
Nie tylko składowe wektora pr
ę
dko
ś
ci s
ą
funkcjami współrz
ę
dnych przestrzennych i czasu,
ale i inne parametry, takie jak: ci
ś
nienie, g
ę
sto
ść
, temperatura
(12.3)
Je
ś
li posługujemy si
ę
t
ą
metod
ą
opisu parametrów płynu, to w dowolnym miejscu układu
współrz
ę
dnych i w dowolnym czasie powinny by
ć
okre
ś
lone powy
ż
sze funkcje czterech
zmiennych x, y, z, t.
Istotnym poj
ę
ciem dla metody Eulera jest poj
ę
cie pochodnej substancjalnej, oznaczonej dla
dowolnej funkcji f (x, y, z, t) symbolem d//dr.
Pochodn
ą
substancjaln
ą
buduje si
ę
bior
ą
c za punkt wyj
ś
cia poj
ę
cie ró
ż
niczki zupełnej funkcji
wielu zmiennych. W tym przypadku

k
z
j
y
i
x
∂
∂
+
∂
∂
+
∂
∂
=
∇
(12.4)
W wyra
ż
eniu tym przyrosty dx, dy i dz s
ą
przyrostami dowolnymi w przestrzeni ryz. Je
ż
eli na
przyrosty te nało
ż
ymy ograniczenia
(12.5)
co oznacza,
ż
e s
ą
one wybierane wzdłu
ż
kierunku ruchu cz
ą
stki, to wyra
ż
enie (12.4) mo
ż
na
zapisa
ć
nast
ę
puj
ą
co:
(12.6)
Odnosz
ą
c przyrost d/ do przyrostu czasu dt, z (12.6) otrzymujemy
(12.7)
Zapis ten mo
ż
e by
ć
zastosowany do dowolnej funkcji/. Istotny jest jedynie operator typu:
(12.8)
Ze sposobu budowania operatora pochodnej substancjalnej wynika nast
ę
puj
ą
ca interpretacja
fizyczna poszczególnych wyra
ż
e
ń
:
d/df oznacza zmian
ę
danej wielko
ś
ci w czasie z punktu widzenia obserwatora poruszaj
ą
cego
si
ę
wraz z elementem płynu,
d/dt oznacza zmian
ę
w czasie danej wielko
ś
ci w danym punkcie przestrzeni (przy ustalonym
x, y, z) — jest to pochodna lokalna,
oznacza zmian
ę
danej wielko
ś
ci w przestrzeni w danym
ustalonym czasie t — jest to pochodna konwekcyjna (cz
ę
sto tak
ż
e zwana adwekcyjn
ą
).
Tak wi
ę
c pochodna substancjalna jest sum
ą
pochodnej lokalnej i pochodnej
konwekcyjnej (adwekcyjnej).
Mo
ż
na łatwo zauwa
ż
y
ć
,
ż
e pochodna konwekcyjna jest iloczynem skalarnym
wektora pr
ę
dko
ś
ci u i operatora gradient (nabla) grad =
(12.9)
Stosuj
ą
c operator ró
ż
niczkowania substancjalnego do składowych wektora pr
ę
dko
ś
ci,
otrzymujemy przyspieszenie substancjalne

(12.10; 12.11; 12.12)
Po pomno
ż
eniu powy
ż
szych równa
ń
przez wektory i, j, k oraz ich zsumowaniu mo
ż
emy
relacje (1.10)—(1.12) zapisa
ć
w sposób zwarty
(12.13)
Podobnie, stosuj
ą
c operator (1.8) do innych parametrów, otrzymujemy
(12.14; 12.15; 12.16)
Z powy
ż
szych wzorów wida
ć
, i
ż
zmiana parametru w elemencie płynu okre
ś
lona jest
zmienno
ś
ci
ą
w czasie i zmienno
ś
ci
ą
w przestrzeni, co wymaga znajomo
ś
ci pola pr
ę
dko
ś
ci.
Ponadto człony okre
ś
laj
ą
ce pochodn
ą
konwekcyjn
ą
s
ą
członami nieliniowymi typu iloczynu
pr
ę
dko
ś
ci i pochodnej danego parametru.
Nieliniowo
ść
ta, pojawiaj
ą
ca si
ę
w podstawowych relacjach mechaniki płynów, jest przyczyn
ą
znacznych trudno
ś
ci w rozwi
ą
zywaniu problemów przepływowych.
METODA LAGRANGE'A
W metodzie tej opisujemy histori
ę
zmiany danego parametru, zwi
ą
zanego z wybranym
elementem płynu. Oznaczamy wybrany element płynu w chwili f
(l
współrz
ę
dnymi x
0
, Y
0
, Z
0
.
Z czasem b
ę
dzie si
ę
zmieniało jego poło
ż
enie i inne parametry. Zapisujemy ten fakt
nast
ę
puj
ą
co:
(12.17)
lub w zapisie wektorowym
Dla ci
ś
nienia, g
ę
sto
ś
ci i temperatury mamy
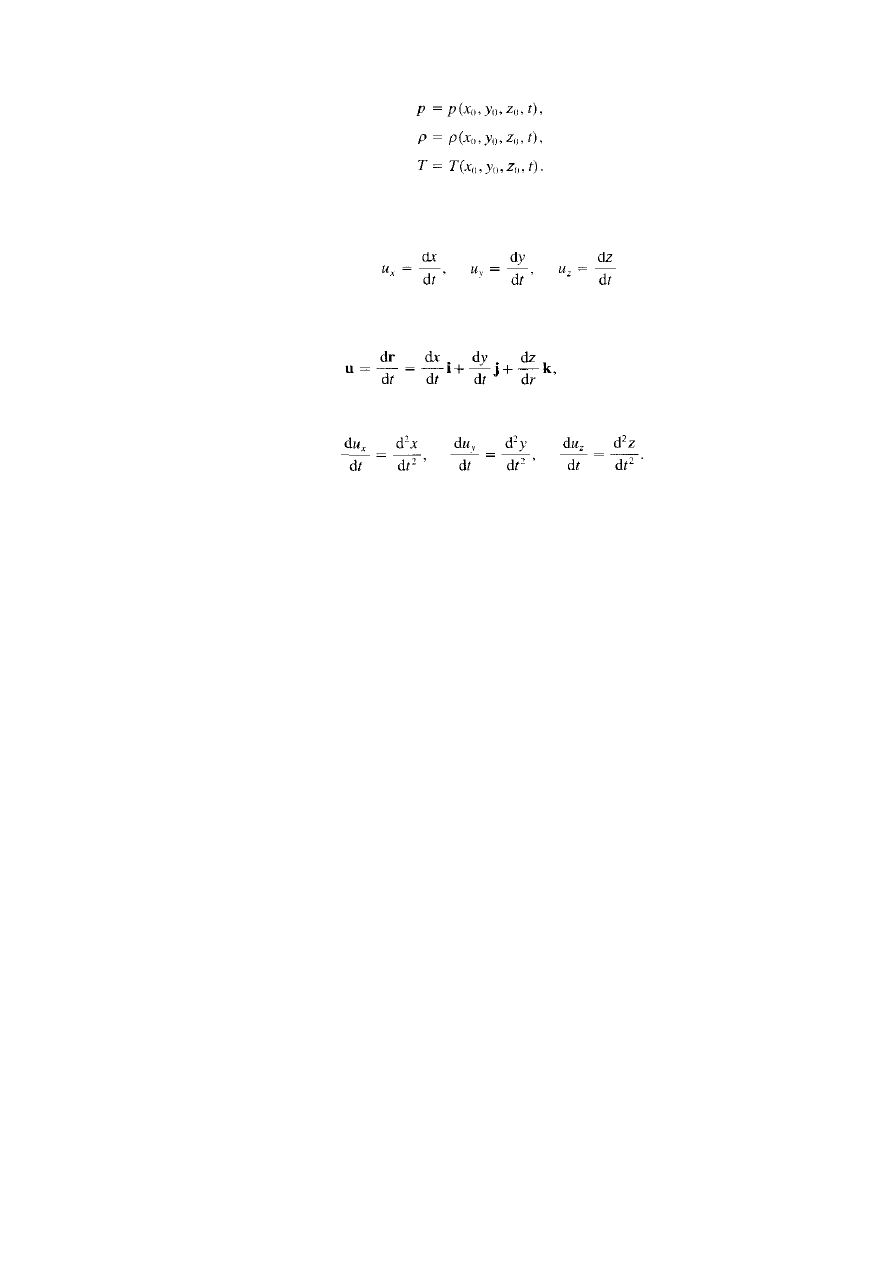
(12.18)
Pr
ę
dko
ś
ci i przyspieszenia w metodzie Lagrange'a otrzymujemy przez ró
ż
niczkowanie
współrz
ę
dnych poło
ż
enia elementu płynu wzgl
ę
dem czasu. Tak wi
ę
c dla pr
ę
dko
ś
ci
(12.19)
lub w zapisie wektorowym
a dla przyspiesze
ń
(12.20)
W dalszym ci
ą
gu posługiwa
ć
si
ę
b
ę
dziemy przewa
ż
nie metod
ą
Eulera.
13.Pochodna w
ę
drowna. Operator Stokesa, przy
ś
pieszenie elementu
płynu.

Je
ś
li wezmiemy pod uwag
ę
dowoln
ą
wielko
ść
fizyczn
ą
f, skalarn
ą
lub wektorow
ą
,
zwi
ą
zan
ą
z poruszaj
ą
cym si
ę
elementem płynu, to wyra
ż
enie zmian tej wielko
ś
ci w czasie
przy u
ż
yciu zmiennych Eulera napotka na pewne trudno
ś
ci. Mamy wyrazi
ć
zmiany f,
zwi
ą
zane z poruszaj
ą
cym si
ę
po swym torze elementem płynu, przy pomocy wielko
ś
ci
zwi
ą
zanych z wybranym punktem przestrzeni x,y,z i wybran
ą
chwil
ę
czasu t. Mamy zatem
obliczy
ć
dla elementu płynu
Chc
ą
c to wyrazi
ć
za pomoc
ą
operacji ró
ż
niczkowania wzgl
ę
dem x,y,z,t musimy x,y,z w
powy
ż
szym wzorzepotraktowa
ć
jako równanie parametryczne toru elementu płynu
przechodz
ą
cego przez wybranu punkt przestrzeni, a wi
ę
c jako:
Uwzgl
ę
dniaj
ą
c to piszemy
Korzystaj
ą
c ze zwi
ą
zków dla toru elementu płynu otrzymujemy
Przy u
ż
yciu operatora mo
ż
emy ten wzór zapisa
ć
nast
ę
puj
ą
co
Wyra
ż
enie
uwa
ż
amy formalnie za iloczyn skalarny
i wektora pr
ę
dko
ś
ci
Wynik tej operacji traktujemy jako operator, którym działamy na dowoln
ą
wielko
ś
c skalarn
ą
np.
lub wektorow
ą
np.
Gdy podstawimy
to równanie oznacza przy
ś
pieszenie elementu płynu
Składowe przy
ś
pieszenia w układzie współrz
ę
dnych kartezja
ń
skich s
ą
okre
ś
lone wzorami
Pochodn
ą
df/dt dowolnej wielko
ś
ci f nazywamy pochodn
ą
substancjaln
ą
. Ma to okre
ś
lony
sens fizyczny, gdy
ż
d/dt oznacza zmiany dla tego samego poruszaj
ą
cego si
ę
elementu płynu,
czyli zmiany zwi
ą
zane z jego „substancj
ą
’’.
We współrz
ę
dnych Eulera zmiany dotycz
ą
ce poruszaj
ą
cego so
ę
elementu trzeba
wyrazi
ć
przy pomocy pochodnych cz
ą
stkowych wzgl
ę
dem czasu i pkt. Przestrzeni. Pochodna
substancjalna jest sum
ą
pochodnej lokalnej
∂
f /
∂
t wyra
ż
aj
ą
cej zmiany wielko
ś
ci f w czasie
lecz w tym samym punkcie przestrzeni i pochodnej konwekcyjnej.
wyra
ż
aj
ą
cej
zmiany wielko
ś
ci f przy przej
ś
ciu z pkt. X,y,z do jego najbli
ż
szego otoczenia, co zwi
ą
zane jest
z polem pr
ę
dko
ś
ci.
14.Poj
ę
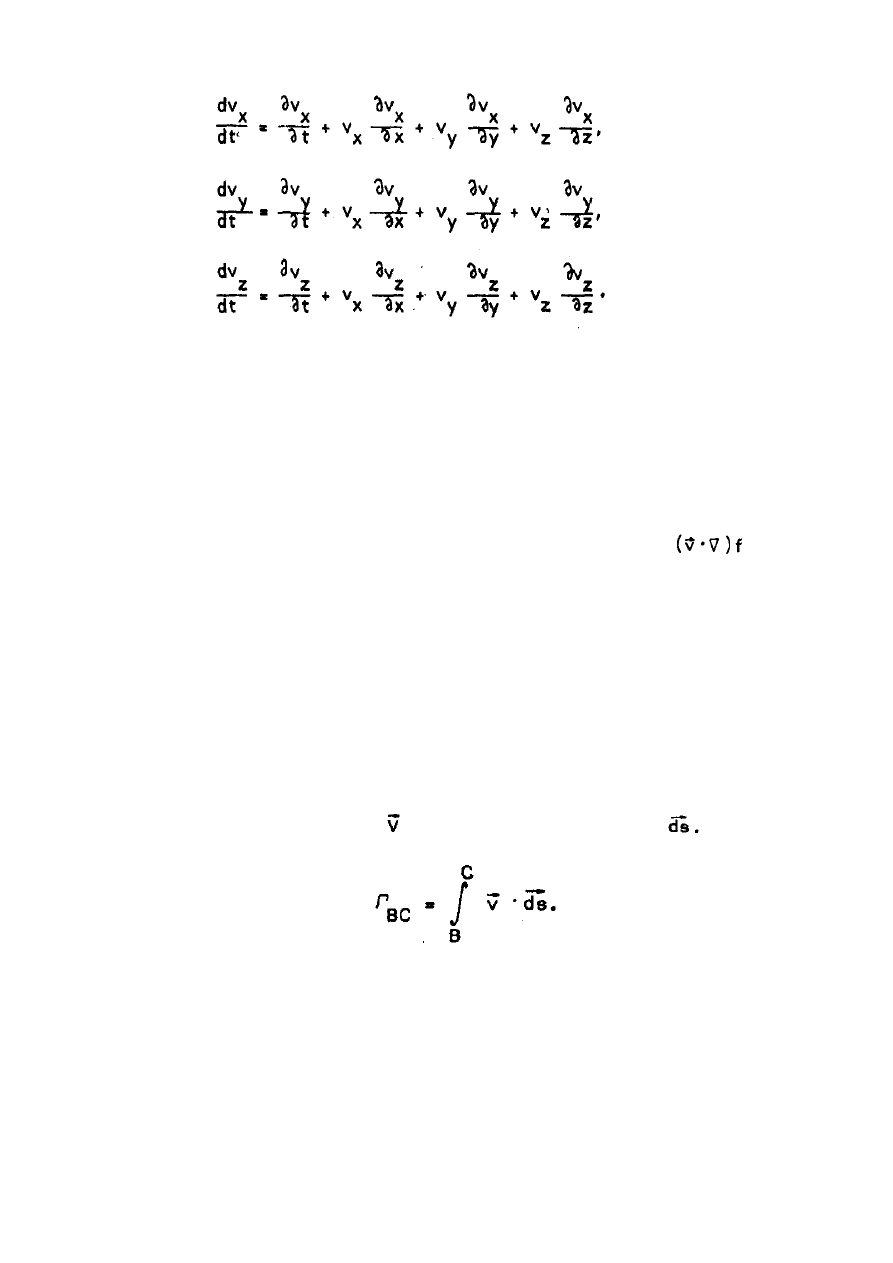
cie cyrkulacji. Interpretacja fizyczna i analogia.
Cyrkulacja pr
ę
dko
ś
ci wzdłu
ż
odcinka BC krzywej s w ogólnej krzywej przestrzennej, jest to
całka liniowa z iloczynu skalarnego
i skierowanego elementu tej lini
czyli
Cyrkulacja pr
ę
dko
ś
ci wyra
ż
ona równaniem wcze
ś
niejszym mo
ż
e by
ć
równie
ż
przedstawiona
w nast
ę
puj
ą
cy sposób:

gdzie
- rzut wektora
na kierunek
W przypadku całki liniowej po krzywej zamkni
ę
tej s , czyli całki
cyrkulacja pr
ę
dko
ś
ci
wynosi:
Jako dodatni kierunek obchodu zamkni
ę
tej linii konturowej przy obliczaniu całki przyjmiejmy
kierunek przeciwny do ruch wskazówek zegara.
Poj
ę
cie cyrkulacji pr
ę
dko
ś
ci wyst
ę
puje w zagadnieniach opływu ciał, profili, łopatek itd.
Poj
ę
cie to jest podobne do poj
ę
cia pracy z tym,
ż
e zamiast wektora siły wyst
ę
puje wektor
pr
ę
dko
ś
ci.
Cyrkulacja pr
ę
dko
ś
ci wzdłu
ż
zewn
ę
trznej lini konturowej równa si
ę
sumie cyrkulacji wzdłu
ż
konturów składowych. Zilustrowano to na rys. gdzie lini
ę
konturow
ą
s podzielono odcinkiem
BD na dwie linie konturowe. Zatem mo
ż
na napisa
ć
ż
e:

gdy
ż
cyrkulacja wzdłu
ż
BD znosz
ą
si
ę
z uwagi na przeciwne znaki.
W teorii pola dowodzi si
ę
tw. Stokesa, Które dotyczy zwi
ą
zku mi
ę
dzy całk
ą
liniow
ą
i
powierzchniow
ą
. Dla ró
ż
niczkowalnych pól wektorowych
ma ono posta
ć
:
gdzie
oznacza elementarny skierowany odcinek zamkni
ę
tej lini s stanowi
ą
cej lini
ę
konturow
ą
powierzchni A.
Inaczej tw. Stokesa mo
ż
na napisa
ć
:
Twierdzenie formułowane w kategoriach kinematycznych mówi
ż
e cyrkulacja pr
ę
dko
ś
ci
wzdłu
ż
zamkni
ę
tej krzywej s równa si
ę
strumieniowi wirowa
ń
(rotacji) przechodz
ą
cemu przez
powierzchni
ę
A, której brzegiem jest krzywa s.
15.Równania toru i lini pr
ą
du, rurka i powierzchnia pr
ą
du, struga.
Linia pr
ą
du jest to linia pola wektorowego pr
ę
dko
ś
ci. Je
ś
li mamy pole pr
ę
dko
ś
ci
o składowych w układzie Kartezja
ń
skim
oraz element linii pr
ą
du
o skł. Dx, dy, dz to warunek równoległo
ś
ci
w ka
ż
dym
punkcie pola dla dowolnej chwili czasu mo
ż
emy napisa
ć
w postaci
czyli
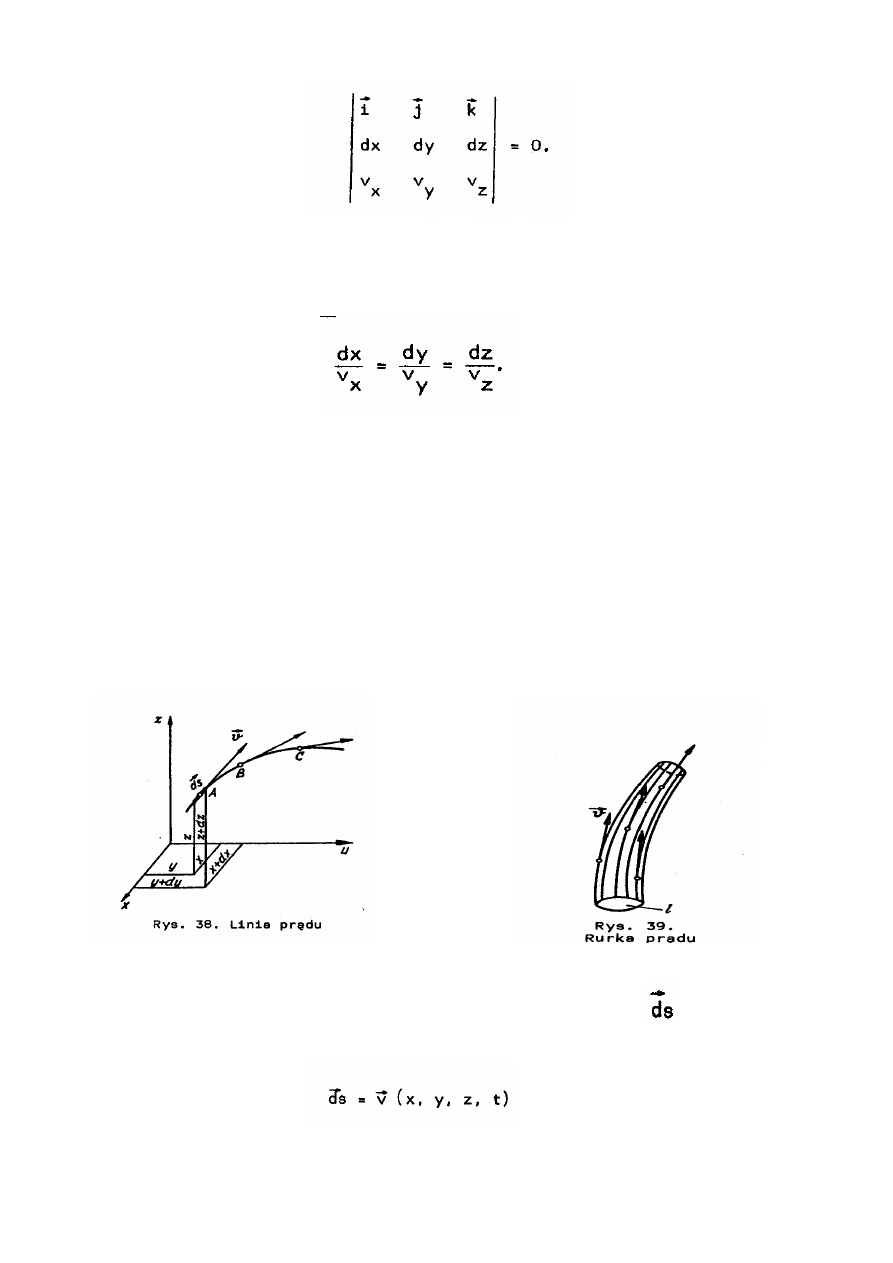
ka
ż
da składowa tego iloczynu musi by
ć
równa zeru i st
ą
d otrzymujemy równanie lini pr
ą
du
W równaniu tym czas wyst
ę
puje jako parametr, od którego zale
żą
warto
ś
ci Vx, Vy, Vz ale nie
jest on zmienn
ą
niezale
ż
n
ą
. W ruchu nieustalonym obraz linii pr
ą
du ma charakter chwilowy,
zale
ż
ny od warto
ś
ci t. W ruchu ustalonym obraz linii pr
ą
du dla danego przepływu jest
niezmienny w czasie, tzn. kształt ka
ż
dej linii pr
ą
du dla przepływu ustalonego nie zmienia si
ę
w czasie.
Powierzchnia pr
ą
du jest to powierzchnia utworzona z linii pr
ą
du przecinaj
ą
cych
dowoln
ą
lini
ę
l nie b
ę
d
ą
c
ą
lini
ą
pr
ą
du. Je
ś
li linia jest zamkni
ę
ta, powierzchnia pr
ą
du
nazywana jest rurk
ą
pr
ą
du.
Zbiór linii pr
ą
du wypełniaj
ą
cych w sposób ci
ą
gły rurk
ę
pr
ą
du nazywamy włoknem pr
ą
du lub
strug
ą
pr
ą
du.
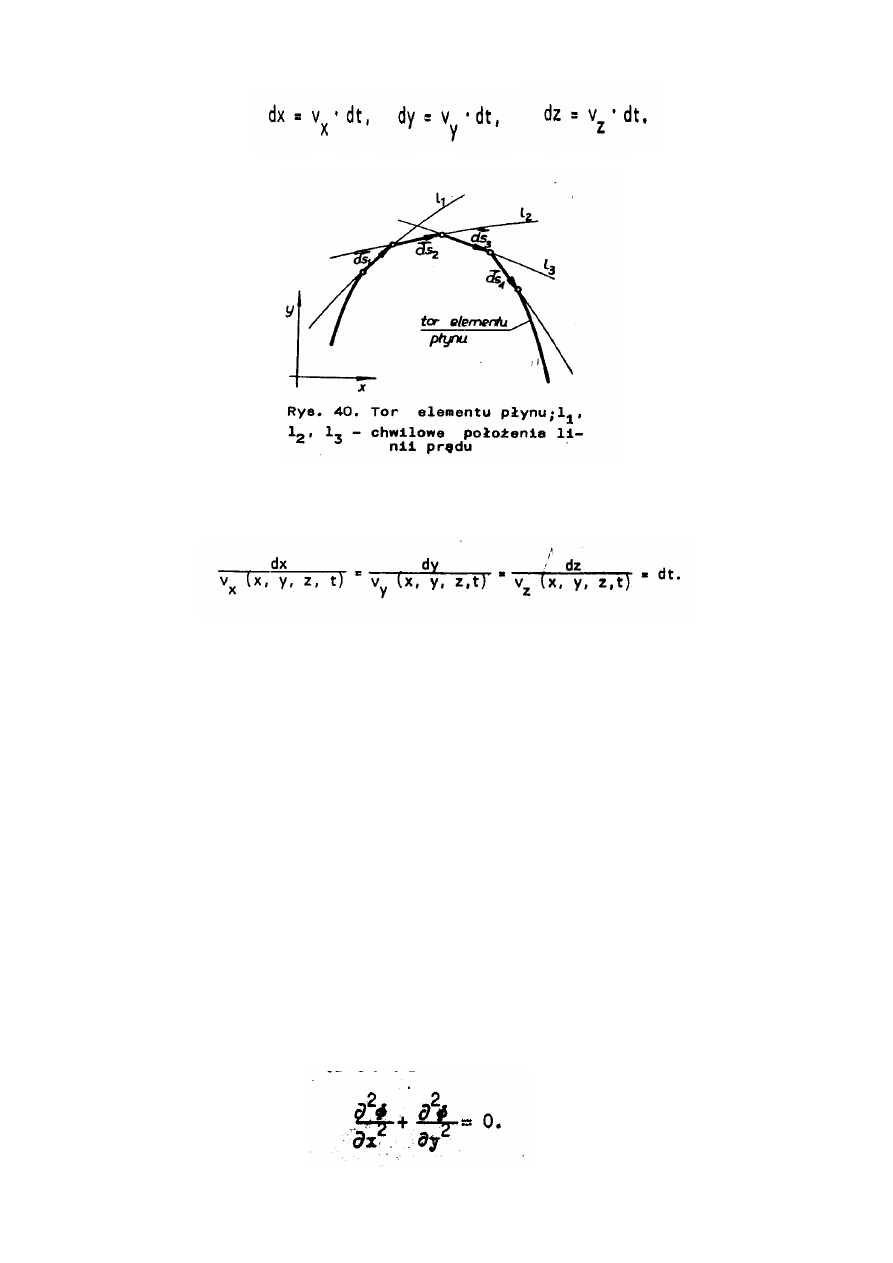
Torem elementu płynu nazywamy lini
ę
, po której porusza si
ę
Element płynu dV traktowany
jako pkt materialny. Gdy elementarny odcinek toru oznaczymy przez
o składowych dx,
dy, dz a elementarny odcinek czasu przez dt, to równanie ró
ż
niczkowe toru jest nast
ę
puj
ą
ce:
Równania skalarne toru elementu wynikaj
ą
ce ze wzoru to:
Czas odgrywa tu rol
ę
zmiennej niezale
ż
nej. Ostatnie równanie ró
ż
niczkowe toru wyra
ż
ona za
pomoc
ą
składowych mal
ą
posta
ć
:
16.Przepływy potencjalne.
Prawie zawsze mo
ż
na potraktowa
ć
w przybli
ż
eniu ka
ż
dy przepływ przestrzenny jako
przepływ dwuwymiarowy (płaski lub osiowo – symetrycznu). Takie uproszczenie jest
niezmiernie korzystne ze wzgl
ę
dów matematycznych, gdy
ż
pozwala stosowa
ć
bardzo
dogodn
ą
i dobrze opracowan
ą
teori
ę
funkcji zmiennej zespolonej. W niniejszych
rozwa
ż
aniach b
ę
d
ą
omawiane tylko płaski przepływy potencjalne.\
Mimo,
ż
e poj
ę
cie potencjału ma charakter abstrakcyjny, to przy jego pomocy
rozwi
ą
zuje si
ę
szereg wa
ż
nych zagadnie
ń
praktycznych. W dalszej tre
ś
ci b
ę
d
ą
podane
przykłady takich rozwi
ą
za
ń
.
Zale
ż
no
ś
ci podstawowe.
Niektóre podst. poj
ę
cia przepływów potencjalnych, jak potencjał pr
ę
dko
ś
ci
Φ
i
równanie Laplace’a, zostały podane przy opisie pola bezwirowego.
Równania Laplace’a, tj. równanie dla układu płaskiego ma nast
ę
puj
ą
c
ą
posta
ć
:

Jak wiadomo, wa
ż
n
ą
cech
ą
równania Laplace’a jest jego liniowo
ść
, co jest wykorzystywane
przy superpozycji, czyli nakładaniu przepływów. Zagadnienie superpozycji b
ę
dzie omawiane
w dalszej cz
ęś
ci tre
ś
ci.
Przyrost potencjału pr
ę
dko
ś
ci mo
ż
e by
ć
wyra
ż
ony jako ró
ż
niczka zupełna:
17.Przepływy elementarne. Superpozycja przepływów
1. Przepływy elementarne.
a. Przepływ jednostajny.
W
ogólnym
przypadku,
jednostajny
przepływ
potencjalny
odbywa
si
ę
z
pr
ę
dko
ś
ci
ą
v
skierowan
ą
pod
k
ą
tem
a
wzgl
ę
dem
jednej
z
osi
układu,
np. wzgl
ę
dem osi x. Składowe pr
ę
dko
ś
ci v
x
i v
y
wynikaj
ą
z zale
ż
no
ś
ci trygonometrycznych.
Potencjał pr
ę
dko
ś
ci
Φ
obliczymy z równania
Otrzymuj
ą
c
dy
y
dx
x
d
∂
Φ
∂
+
∂
Φ
∂
=
Φ
∫
∂
Φ
∂
+
∂
Φ
∂
=
Φ
dy
y
dx
x

Z równa
ń
ν
X
=
x
∂Φ
∂
ν
y
=
y
∂Φ
∂
jak i rysunku wynika:
* cos
x
x
ν
α
∂Φ =
∂
* sin
y
y
ν
α
∂Φ =
∂
st
ą
d
Funkcj
ę
pr
ą
du obliczymy z równania
d
dx
dy
x
y
∂Ψ
∂Ψ
Ψ =
+
∂
∂
w
i
edz
ą
c,
ż
e
,
y
x
x
y
∂Ψ ∂Φ
∂Ψ ∂Φ
=
−
=
∂
∂
∂
∂
, otrzymamy
(
)
* sin
* cos
x
y
ν
α
α
Ψ = −
+
Podstawiaj
ą
c do równania
( )
f x
i
= Φ + Ψ
otrzymuje si
ę
warto
ść
potencjału zespolonego
( ) (
)
(
)
(
)(
)
* cos
*
sin
*
cos
sin
* *
i
f z
x i y
i x y
x i y
i
z e
α
ν
α
α ν
α
α ν
−
=
+
+ − +
=
+
−
=
(17.1)
Potencjał zespolony wyra
ż
ony równaniem ( ) ma zatem posta
ć
f(z)=a*z
(17.2)
gdzie a jest liczb
ą
zespolon
ą
.
Jest to potencjał zespolony przepływu jednostajnego.
b.
Ż
ródlo płaskie.
Ź
ródło płaskie mo
ż
e by
ć
dodatnie, lub ujemne.
Ź
ródło dodatnie nazywane jest po
prostu
ź
ródłem, za
ś
ź
ródło ujemne nosi nazw
ę
upustu. Potencjał zespolony wyra
ż
a si
ę
równaniem
f(z)=a*lnz
(a)
V gdzie: a
=
2
V
Π
- liczba rzeczywista
,
V-wydajno
ść
ź
ródła, lub upustu płaskiego.
(
) (
)
α
α
ν
α
ν
α
ν
sin
*
cos
*
sin
*
*
cos
*
y
x
dy
dx
+
=
+
=
Φ
∫

W układzie współrz
ę
dnych biegunowych potencjał zespolony, przy wykorzystaniu
równania z = r * e
i
ϕ
przyjmie posta
ć
:
( )
* ln
ln( *
)
(ln *
)
2
2
i
V
V
f z
i
a
z
r e
r i
ϕ
ϕ
= Φ + Ψ =
=
=
Π
Π
(17.3)
Potencjał pr
ę
dko
ś
ci jako cz
ęść
rzeczywista wynosi
ln
2
V
r
Φ =
Π
Linie
stałego
potencjału
pr
ę
dko
ś
ci
s
ą
okr
ę
gami
współ
ś
rodkowymi,
gdy
ż
dla
Φ
= const jest r = const.
Funkcja pr
ą
du jako cz
ęść
urojona wynosi
ln( *
)
2
i
V
r e
ϕ
Π
gdzie
ϕ
-k
ą
t(współrz
ę
dna biegunowa).
Linie pr
ą
du (
Ψ
= const) s
ą
ortogonalne do linii
Φ
= const, a wi
ę
c s
ą
prostymi
wychodz
ą
cymi z pocz
ą
tku układu współrz
ę
dnych (
ϕ
= const).
W
ź
ródle i upu
ś
cie istnieje tylko pr
ę
dko
ść
promieniowa
ν
r
gdy
ż
pr
ę
dko
ść
obwodowa V
u
jest równa zero. Zwrot pr
ę
dko
ś
ci
ν
r
w
ź
ródle i upu
ś
cie jest odwrotny, przy czym przyjmuje si
ę
,
ż
e w niesko
ń
czenie bliskim otoczeniu punktu
ś
rodkowego płynu pojawia si
ę
lub przestaje
istnie
ć
.
Warto
ść
pr
ę
dko
ś
ci
ν
r
mo
ż
na znale
źć
w nast
ę
puj
ą
cy sposób. Ró
ż
niczkuj
ą
c równanie (a)
i wykorzystuj
ą
c równania z=r*e
i
ϕ
i
( )
1
*
2
i
df z
V
e
dz
r
ϕ
=
Π
otrzymujemy kolejno
( )
1
1
*
*
2
2
i
i
df z
V
V
e
e
dz
r
r
ϕ
ϕ
−
=
=
Π
Π
( )
1
*
2
i
df z
V
e
dz
r
ϕ
=
Π
Pr
ę
dko
ść
ν
r
jako rzeczywista równania wynosi
1
*
2
V
Vr
r
=
Π
,
Pr
ę
dko
ść
ν
u
jest równa zero gdy
ż
cz
ęść
urojona pr
ę
dko
ś
ci zespolonej nie istnieje.

c. Wir płaski potencjalny.
W ruchu cieczy nazywamy kołowym, płaskim wirem potencjalnym(swobodnym) cyrkulacja
pr
ę
dko
ś
ci po dowolnej krzywej nie obejmuj
ą
cej
ś
rodka wiru jest równa zero-st
ą
d wir
potencjalny. Cyrkulacja po krzywej jeden raz obejmuj
ą
cej
ś
rodek wiru jest równa F.
Dla kołowego wiru płaskiego warto
ść
potencjału zespolonego wynosi
f(z)=-i*a*lnz, (17.4)
gdzie: a=
2
V
Π
-liczba rzeczywista,
Γ
- cyrkulacja pr
ę
dko
ś
ci.
W układzie współrz
ę
dnych biegunowych potencjał zespolony, uwzgl
ę
dniaj
ą
c powy
ż
sze
warunki przyjmie posta
ć
ƒ
( )
+
Φ
=
z
i
Ψ
(
)
(
)
r
i
i
r
i
e
r
i
z
a
i
i
ln
*
2
2
ln
2
*
ln
2
ln
*
*
π
ϕ
π
ϕ
π
π
ϕ
Γ
−
Γ
=
+
Γ
−
=
Γ
−
=
−
=
(17.5)
Potencjał pr
ę
dko
ś
ci jako cz
ęść
rzeczywista wynosi
ϕ
π
2
Γ
=
Φ
Linie stałego potencjału pr
ę
dko
ś
ci s
ą
prostymi wychodz
ą
cymi z pocz
ą
tku układu
współrz
ę
dnych, gdy
ż
dla
Φ
= const jest
φ
= const
Funkcja pr
ą
du jako cz
ęść
urojona wynosi :
r
1
*
2
π
Γ
=
Φ
Linie pr
ą
du s
ą
okr
ę
gami współ
ś
rodkowymi, gdy
ż
dla Y = const jest r = const.
Role
φ
i
Ψ
s
ą
dla
ź
ródła i wiru zamienne. W zwi
ą
zku z tym, pr
ę
dko
ść
promieniowa jest równa
zett| a pr
ę
dko
ść
obwodowa wynosi :
r
u
1
*
2
π
ν
Γ
=
(17.6)
Ogólnie mo
ż
na powiedzie
ć
,
ż
e zamiana ról
Φ
i
Ψ
zachodzi w tzw. Przepływach
sprz
ęż
onych, którymi s
ą
w danym przypadku
ź
ródło i wir płaski.
d. Dipol.
Dipol, lub
ź
ródło podwójne płaskie ma miejsce wówczas, gdy odległo
ść
/ pomi
ę
dzy
ź
ródłem i upustem wynosi l
→
∞
.Obowi
ą
zuje przy tym taka zale
ż
no
ść
,
ż
e

odległo
ść
l maleje w takim stopniu, w jaki wzrasta strumie
ń
obj
ę
to
ś
ci V
ź
ródła
i upustu, czyli l
→
O, V
→
∞
, przy czym l*V=M = const. Moment dipola M. zostaje stały
i ró
ż
ny od zera.
Potencjał zespolony dipola wynosi
z
a
z
f
=
)
(
(17.7)
gdzie
π
2
M
a
=
Po uwzgl
ę
dnieniu równania z=x+z * y i pomno
ż
eniu licznika i mianownika przez
(x-i * y) otrzymuje si
ę
:
)
(
2
)
*
(
)
*
(
2
)
*
(
)
(
2
2
2
2
2
y
x
y
i
x
M
y
i
x
y
i
x
M
z
f
+
−
=
−
−
=
π
π
(17.8)
Potencjał pr
ę
dko
ś
ci jako cz
ęść
rzeczywista potencjału zespolonego wynosi :
)
(
2
*
2
2
y
x
x
M
+
=
Φ
π
(17.9)
Funkcja pr
ą
du jako cz
ęść
urojona wynosi
)
(
2
*
2
2
y
x
x
M
+
=
Ψ
π
(17.10)
Z tych zale
ż
no
ś
c
i
wynika,
ż
e linie pr
ą
du (
Ψ
= const ) stanowi
ą
rodzin
ę
okr
ę
gów stycznych do
osi x w pocz
ą
tku układu, za
ś
linie
Φ
=
const s
ą
tak
ż
e okr
ę
gami, lecz stycznymi w pocz
ą
tku
układu do osi y.
Okr
ę
gi
Φ
= const i
Ψ
= const s
ą
wzajemnie ortogonalne. Osi
ą
dipola jest wspólna
styczna okr
ę
gów
Ψ
= const
.
Jej zwrot jest zgodny z kierunkiem przepływu.
2. Superpozycja przepływów.
Wa
ż
n
ą
cech
ą
równania Laplace'a jest jego liniowo
ść
wykorzystywana przy
superpozycji,
czyli
nakładaniu
dwóch,
lub
wi
ę
cej
przepływów
potencjalnych.
W przypadku dwóch przepływów mo
ż
na zapisa
ć
1
1
1
*
)
(
Ψ
+
Φ
=
i
z
f
2
2
2
*
)
(
Ψ
+
Φ
=
i
z
f
(17.11)
sk
ą
d
)
(
*
)
(
*
)
(
2
2
1
1
z
f
k
z
f
k
z
f
+
=
(17.12)
gdzie k
1
, k
2
- dowolne współczynniki.
W wyniku superpozycji został otrzymany nowy przepływ o potencjale zespolonym
f(z), którego cz
ęś
ci
ą
rzeczywist
ą
i urojon
ą
s
ą
odpowiednio
Φ
i
Ψ
2
2
1
1
*
*
Φ
+
Φ
=
Φ
k
k
2
2
1
1
*
*
Ψ
+
Ψ
=
Ψ
k
k
(17.13)
Superpozycja
mo
ż
e
by
ć
wykonywana
metod
ą
analityczn
ą
,
lub
wykre
ś
ln
ą
.
W metodzie analitycznej zadanie sprowadza si
ę
do znalezienia wypadkowego
(sumarycznego) potencjału zespolonego, a zwłaszcza cz
ęś
ci urojonej tego potencjału.
W metodzie wykre
ś
lnej natomiast nale
ż
y nanie
ść
linie
Ψ
1
,
Ψ
2
=const, zachowuj
ą
c mi
ę
dzy nimi
takie odleg
ł
o
ś
ci, jakie wynikaj
ą
z równo
ś
ci strumieni obj
ę
to
ś
ci obu przepływów,
a wi
ę
c :
2
1
V
V
∆
=
∆
(17.14)
Utworzona w ten sposób siatka linii pr
ą
du mo
ż
e by
ć
oznakowana w sposób umowny.
Zagadnienie superpozycji sprowadza si
ę
wła
ś
ciwie do sumowania wektorów
pr
ę
dko
ś
ci.
Szczególne znaczenie w aerodynamice posiadaj
ą
przypadki superpozycji przepływu
jednostajnego i
ź
ródła, lub układu
ź
ródeł.

∫∫
∫∫∫
=
A
V
dV
v
p
div
dA
n
v
p
)
*
(
*
*
*
r
r
r
n
r
∫∫∫
∂
∂
V
dV
dt
t
p
*
18.Zasada zachowania masy. Równanie ci
ą
gło
ś
ci
Równanie ci
ą
gło
ś
ci przepływu w wynika z zasady zachowania masy (niezniszczalno
ś
ci
materii). Równanie ci
ą
gło
ś
ci odnosi si
ę
tylko do pól bez
ź
ródłowych tzn.
ż
e w
ż
adnym
punkcie pola masy nie mo
ż
e si
ę
tworzy
ć
ani znika
ć
.
Równanie ci
ą
gło
ś
ci przepływu ma charakter kinematyczny i z tej racji jest identyczny dla
płynów nielepkich i lepkich. Warunek ci
ą
gło
ś
ci ma jednak inny sens dla płynów
nie
ś
ci
ś
liwych i
ś
ci
ś
liwych.
Dla płynów nie
ś
ci
ś
liwych (p=const), w obj
ę
to
ś
ci kontrolnej musi by
ć
zawarta
w ka
ż
dej chwili tak sama masa płynu, czyli przez powierzchni
ę
kontroln
ą
musi dopływa
ć
i wypływa
ć
taka sama masa płynu. Warunek ten jest taki sam dla przepływów ustalonych
i nieustalonych.
W przepływie ustalonym musi by
ć
zachowany powy
ż
szy warunek, bo masa zawarta
wewn
ą
trz powirzchni kontrolnej jest niezmienna w czasie. W przepływie nieustalonym
natomiast, mog
ą
mie
ć
miejsca lokalne zmiany g
ę
sto
ś
ci płynu, które wywołuj
ą
ró
ż
nic
ę
w bilansie dopływaj
ą
cym przez powierzchni
ę
kontroln
ą
strumieni masy.
1. Sformułowanie ogólne
Równanie ci
ą
gło
ś
ci zostanie wyprowadzone dla trójwymiarowego nieustalonego
przepływu
ś
ci
ś
liwego, w którym został wyodr
ę
bniony obszar o obj
ę
to
ś
ci V otoczony
zamkni
ę
t
ą
powierzchni
ą
kontroln
ą
A.
Przyrost masy na obszarze V w czasie dt mo
ż
e nast
ą
pi
ć
na skutek dopływu
z zewn
ą
trz
znak minus wynika st
ą
d,
ż
e przyrost masy ma miejsce wtedy, gdy przepływ odbywa si
ę
do
ś
rodka, czyli przeciwnie do jednostkowego normalnego zewn
ę
trznie skierowanego
wektora n.
Wyra
ż
enie całkowe jest strumieniem masy.
Przyrost masy mo
ż
e, w przypadku nieustalonego ruchu
ś
ci
ś
liwego, nast
ą
pi
ć
tylko na
skutek lokalnego przyrostu g
ę
sto
ś
ci
Z równo
ś
ci obydwu wyra
ż
e
ń
otrzymuje
si
ę
równanie ci
ą
gło
ś
ci w formie całkowej
∫∫
−
A
n
dA
v
p
dt
*
*
;
0
)
*
(
)
*
(
)
*
(
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
v
p
y
v
p
x
v
p
t
p
z
y
x
∫∫∫
∫∫
=
+
∂
∂
V
A
n
dA
v
p
dV
t
p
0
*
*
∫∫∫
∫∫
=
V
A
n
dA
v
p
dV
v
p
div
)
*
(
)
*
(
r
∫∫∫
=
+
∂
∂
V
dV
v
p
div
t
p
0
)]
*
(
[
r
0
*
=
+
∂
∂
v
div
p
t
p
r
0
)
*
(
=
v
p
div
r
0
=
v
div
r
;
0
=
∂
∂
+
∂
∂
+
∂
∂
z
v
y
v
x
v
z
y
x
(a)
Drugi wyraz równania mo
ż
na przekształci
ć
zgodnie z twierdzeniem Gaussa-Ostrogradskiego. Zgodnie
z tym twierdzeniem
Po podstawieniu otrzymuje si
ę
(18.1)
Przy zało
ż
eniu ci
ą
gło
ś
ci v i p (brak fal uderzeniowych) i z uwagi na dowolno
ść
obszaru całkowania
mo
ż
na zapisa
ć
to równanie w formie ró
ż
niczkowej, czyli dla elementu dV
(b)
Równania (a) i (b) s
ą
równaniami ci
ą
gło
ś
ci przepływu w postaci całkowej i ró
ż
niczkowej w zapisie
wektorowym. W zapisie skalarowym równanie (b) przyjmuje posta
ć
(c)
Która obowi
ą
zuje w kartezja
ń
skim układzie współrz
ę
dnych.
Równanie (c) mo
ż
na zapisa
ć
w nast
ę
puj
ą
cy sposób:
Pierwsze
cztery
wyrazy
stanowi
ą
pochodn
ą
substancjaln
ą
g
ę
sto
ś
ci,
a
wyra
ż
enie
w nawiasie jest diwergencj
ą
wektora pr
ę
dko
ś
ci. Zatem równanie (b) przyjmie posta
ć
:
(18.2)
Dla przepływu ustalonego z równania (b) wynika
(f)
czyli
(18.3)
Dla cieczy (p = const) z równania (f) otrzymuje si
ę
(18.4)
czyli w układzie kartezja
ń
skim
(18.5)
;
0
)
*
(
)
*
(
)
*
(
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
v
p
y
v
p
x
v
p
t
p
z
y
x
;
0
*
*
*
*
=
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
z
v
y
v
x
v
p
z
p
v
y
p
v
x
p
v
t
p
z
y
x
z
y
x
0
)
*
(
)
*
(
)
*
(
=
∂
∂
+
∂
∂
+
∂
∂
z
v
p
y
v
p
x
v
p
z
y
x

0
)
*
(
*
=
∇
+
∇
+
∂
∂
v
p
p
v
t
p
r
r
Inn
ą
form
ą
zapisu wektorowego równania (b) jest
(18.6)
19.Zasada zachowania p
ę
du. Równanie Eulera i Naviera-Stokesa
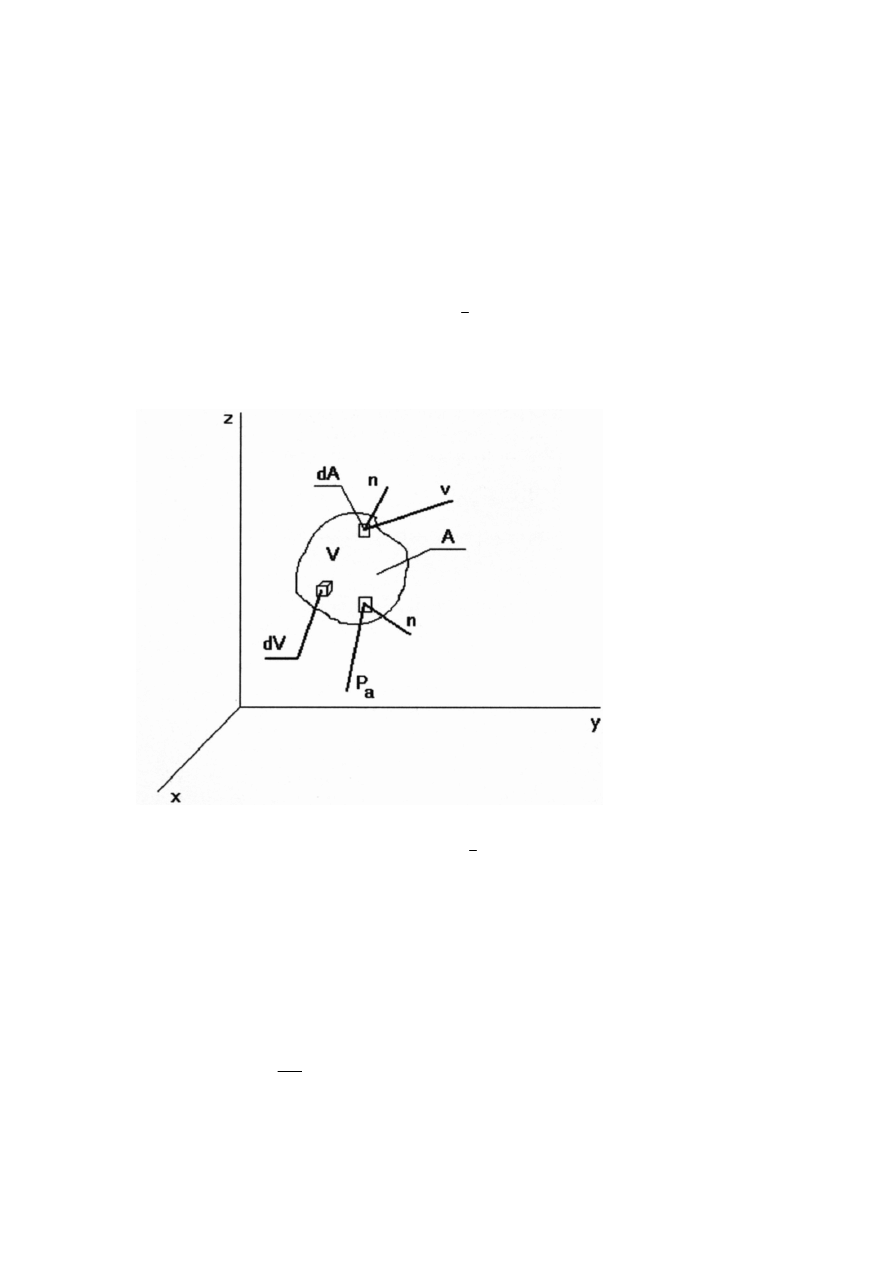
Równanie zachowania p
ę
du.
Zasad
ę
zachowania p
ę
du zastosujemy do obszaru płynnego V, ograniczonego
powierzchni
ą
płynn
ą
A
Zasad
ę
t
ę
sformułujemy nast
ę
puj
ą
co: pochodna p
ę
du płynu zwartego wewn
ą
trz V wzgl
ę
dem
czasu jest równa sumie sil zewn
ę
trznych działaj
ą
cych na ten obszar.
Elementarny p
ę
d płynu zwartego w niesko
ń
czenie małej obj
ę
to
ś
ci dV jest równy
dV
v
*
*
ς
P
ę
d płynu zwartego w całym obszarze płynnym jest równy sumie tych wszystkich
p
ę
dów elementarnych, któr
ą
wyra
ż
amy za pomoc
ą
całki
(ilustracja do równania zachowania p
ę
du )
∫ ∫ ∫
v
dV
v
*
*
ς
Siły zewn
ę
trzne działaj
ą
ce na obszar V podzielimy na siły powierzchniowe i siły masowe
(obj
ę
to
ś
ciowe).
Siłami powierzchniowymi b
ę
dziemy nazywa
ć
siły oddziaływania płynu znajduj
ą
cego si
ę
na
zewn
ą
trz obszaru V na płyn znajduj
ą
cy si
ę
wewn
ą
trz V, przyło
ż
one na powierzchni płynnej A.
Na ka
ż
dym niesko
ń
czenie małym elemencie dA działa jednostkowa siła powierzchniowa
wymiarze napr
ęż
enia [
3
m
N
] zwrócona w kierunku obszaru płynnego. Oznaczamy j
ą
przez pA.
Linia jej działania tworzy w przypadku poruszaj
ą
cego si
ę
płynu lepkiego pewien kat ró
ż
ny od
zera z kierunkiem jednostkowego wektora normalnego n. Polem sił pA, które jest polem

tensorowym, zajmiemy si
ę
szczegółowo przy wyprowadzaniu równa
ń
ruchu płynów lepkich.
W przypadku płynu nieruchomego lub nielepkiego jednostkow
ą
sił
ę
powierzchniow
ą
wyra
ż
amy za pomoc
ą
ci
ś
nienia i zgodnie z tym ci poprzednio powiedzieli
ś
my o kierunku siły
powierzchniowej, oznaczamy - n p.
Suma sił powierzchniowych działaj
ą
cych na cał
ą
powierzchni
ę
A b
ę
dzie okre
ś
lona
całk
ą
∫ ∫
A
A
dA
p *
Dla płynu nieruchomego lub płyn
ą
cego, ale nielepkiego, siła powierzchniowa jest równa
∫ ∫
A
dA
p
n
*
*
Siły masowe ( obj
ę
to
ś
ciowe ) s
ą
to siły wywierane na ka
ż
dy element masy
q dV zawarty wewn
ą
trz V przez zewn
ę
trzne pola sił ,np. pole grawitacyjne,
elektromagnetyczne
gdy
płyn
jest
przewodnikiem
elektryczno
ś
ci,
od
ś
rodkowe
i Coriolisa - gdy płyn porusza si
ę
w wiruj
ą
cym układzie współrz
ę
dnych. Załó
ż
my,
ż
e układ
współrz
ę
dnych, w który rozpatrujemy ruch jest nieruchomy lub porusza si
ę
ruchem
jednostajnym po linii prostej i uwzgl
ę
dniamy tylko siły masowe niezale
ż
nie od ruchu płynu
w tym układzie. Reprezentantem pola sił masowych jest siła masowa przypadaj
ą
ca na
jednostk
ę
masy czynnika, czyli mierzymy je w [N/kg] i oznaczamy przez Fm. W przypadku sił
grawitacyjnych b
ę
dzie to po prostu g, czyli przyspieszenie ziemskie. Suma sił masowych
działaj
ą
cych na obszar płynny wynosi zatem
∫ ∫ ∫
V
m
dV
F
q
*
*
Ostatecznie zapisujemy powy
ż
sz
ą
zasad
ę
zachowania p
ę
du dla całego obszaru
płynnego V, a wi
ę
c w formie całkowej
∫ ∫
A
A
dA
p *
=
∫ ∫
A
dA
p
n
*
*
=
∫ ∫ ∫
V
m
dV
F
q
*
*
Zasad
ę
t
ę
wyrazi
ć
mo
ż
na równie
ż
według sformułowania d'Alamberta, które mówi,
ż
e
suma sił zewn
ę
trznych i siły bezwładno
ś
ci musi by
ć
w ka
ż
dej chwili równa zeru.
Poniewa
ż
siła bezwładno
ś
ci b
ę
dzie tutaj równa
∫ ∫ ∫
−
V
dV
q
dt
dv
*
*
To zamiast powy
ż
szego wzoru mo
ż
na zapisa
ć
Z powy
ż
szych dwóch równa
ń
wynika,
ż
e istnieje to
ż
samo
ść

∫∫∫
V
dV
p
v
*
*
r
n
r
n
r
dA
p
A
A
*
∫∫
r
dA
p
n
A
*
*
∫∫
−
r
∫ ∫ ∫
=
V
dV
v
q
dt
d
*
*
∫ ∫ ∫
V
dV
dt
dv
q
*
*
Której udowodnienie jest mo
ż
liwe na innej drodze rozumowania. Nale
ż
y podkre
ś
li
ć
ż
e wy
ż
ej
napisana równo
ść
(to
ż
samo
ść
) obowi
ą
zuje równie
ż
w przypadku, gdy zamiast v podstawimy
w niej dowolny inny skalar lub wektor.
Analogicznie do zasady zachowania p
ę
du mo
ż
emy napisa
ć
zasad
ę
zachowania kr
ę
tu.
∫ ∫ ∫
∫ ∫
∫ ∫ ∫
×
+
×
=
×
V
A
V
m
A
dV
F
r
q
dA
p
r
dV
q
v
r
dt
d
)
(
)
(
*
)
(
Zasada zachowania p
ę
du.
Zasad
ę
zachowania p
ę
du zastosujemy do obszaru płynnego V, ograniczonego powierzchni
ą
płynn
ą
A. Zasad
ę
t
ę
sformułujemy nast
ę
puj
ą
co: pochodna p
ę
du płynu zawartego wewn
ą
trz F
wzgl
ę
dem czasu jest równa sumie sił zewn
ę
trznych działaj
ą
cych na ten obszar.
Elementarny p
ę
d płynu zawartego w niesko
ń
czenie małej obj
ę
to
ś
ci dVjest równy
v * p * dV . P
ę
d płynu zawartego w całym obszarze płynnym jest równy sumie tych
wszystkich p
ę
dów elementarnych, któr
ą
wyra
ż
amy za pomoc
ą
całki
(19.1)
Siły zewn
ę
trzne działaj
ą
ce na obszar V podzielimy na siły powierzchniowe i siły
masowe(obj
ę
to
ś
ciowe).
Siłami powierzchniowymi b
ę
dziemy nazywa
ć
siły oddziaływania płynu znajduj
ą
cego si
ę
wewn
ą
trz V, przyło
ż
one na powierzchni płynnej A. Na ka
ż
dym niesko
ń
czenie małym
elemencie dA działa jednostkowa siła powierzchniowa zwrócona w kierunku obszaru
płynnego. Oznaczymy j
ą
przez p
A
. Linia jej działania tworzy w przypadku poruszaj
ą
cego si
ę
płynu
lepkiego
pewien
k
ą
t
ró
ż
ny
od
zera
z kierunkiem jednostkowego wektora normalnego
W
przypadku płynu nieruchomego, lub nielepkiego jednostkow
ą
sił
ę
powierzchniow
ą
wyra
ż
amy za pomoc
ą
ci
ś
nienia i zgodnie z tym
oznaczamy - .p.
Suma sił powierzchniowych działaj
ą
cych na cał
ą
powierzchni
ę
A b
ę
dzie okre
ś
lana całk
ą
.
Dla płynu nieruchomego, lub
płyn
ą
cego, ale nie lepkiego, siła
powierzchniowa jest równa

∫∫∫
V
dV
m
F
p
*
*
r
dV
p
m
F
dA
p
dV
p
v
dt
d
V
A
V
A
*
*
*
*
*
∫∫∫
∫∫
∫∫∫
+
=
r
r
r
∫∫∫
−
V
dV
p
dt
v
d
;
*
*
r
dV
p
m
F
dA
p
dV
p
dt
v
d
V
A
V
A
*
*
*
*
*
∫∫∫
∫∫
∫∫∫
+
=
r
r
r
∫∫∫
∫∫∫
=
V
V
dv
dt
v
d
p
dV
v
p
dt
d
*
*
*
*
r
r
(19.3)
Siły masowe(obj
ę
to
ś
ciowe) s
ą
to siły wywierane na ka
ż
dy element masy p *dV zawarty
wewn
ą
trz V przez zewn
ę
trzne pola sił, np. pole grawitacyjne, elektromagnetyczne-gdy płyn
jest przewodnikiem elektryczno
ś
ci, od
ś
rodkowe i Coriolisa-gdy płyn porusza si
ę
w wiruj
ą
cym
układzie współrz
ę
dnych. Załó
ż
my,
ż
e układ współrz
ę
dnych, w którym rozpatrujemy ruch jest
nieruchomy, lub porusza si
ę
ruchem jednostajnym po linii prostej i uwzgl
ę
dniamy tylko siły
masowe
niezale
ż
ne
od
ruchu
płynu
w tym układzie. Reprezentantem pola sił masowych jest siła masowa przypadaj
ą
ca na
jednostk
ę
masy czynnika, czyli mierzymy jaw [N/kg] i oznaczamy przez F
m
. W przypadku sił
grawitacyjnych b
ę
dzie to po prostu g, czyli przy
ś
pieszenie ziemskie. Suma sił masowych
działaj
ą
cych na obszar płynny wynosi zatem
(19.4)
Ostatecznie zapisujemy zasad
ę
zachowania p
ę
du dla całego obszaru płynnego V w formie
całkowej
(19.5)
Zasad
ę
t
ę
mo
ż
na wyrazi
ć
równie
ż
według sformułowania d'Alemberta, które mówi,
ż
e suma
sił zewn
ę
trznych i sił bezwładno
ś
ci musi by
ć
w ka
ż
dej chwili równa zero.
Poniewa
ż
siła bezwładno
ś
ci b
ę
dzie tutaj równa
(19.6)
to zamiast (19.5) mo
ż
na zapisa
ć
(19.7)
Z równa
ń
(19.5) i (19.6) wynika,
ż
e istnieje to
ż
samo
ść
(19.8)
To
ż
samo
ść
(19.8) obowi
ą
zuje równie
ż
w przypadku, gdy zamiast v podstawimy w niej
dowolny inny skalar, lub wektor.
2.Równanie Eulera.

0
*
*
*
*
*
*
=
−
+
∫∫∫
∫∫∫
∫∫
dV
p
m
F
dA
p
n
dV
p
dt
v
d
V
V
A
r
r
r
∫∫
∫∫∫
=
A
V
dV
gradp
dA
p
n
*
*
*
r
0
*
*
*
=
−
+
∫∫∫
V
dV
m
F
p
gradp
dt
v
d
p
r
r
0
)
*
(
=
+
v
p
div
dt
v
d
r
r
0
)
*
(
=
+
v
p
div
dt
dp
r
m
F
gradp
dt
v
d
r
r
=
+
ρ
1
Zasad
ę
zachowania p
ę
du w postaci całkowej podaje równanie (19.7). Dla płynu nielepkiego,
gdy podstawimy p
A
=-n* p, otrzymamy
(19.9)
Stosuj
ą
c twierdzenie Gaussa-Ostrogradzkiego do przekształcenia całki wyra
ż
aj
ą
cej
siły powierzchniowe na całk
ę
obj
ę
to
ś
ciow
ą
, czyli
(19.10)
otrzymujemy
(19.11)
Ze wzgl
ę
du na dowolno
ść
w wyborze obszaru całkowania V, dla ka
ż
dego elementu
dV funkcja podcałkowa musi si
ę
zerowa
ć
, czyli dla przepływu o ci
ą
głych zmianach v, p, p
b
ę
dzie
(19.12)
Równanie (19.12) nazwane równaniem Eulerajest bilansem sił bezwładno
ś
ci, ci
ś
nienia
i sił masowych dla niesko
ń
czenie małego elementu płynu o obj
ę
to
ś
ci dV podczas ruchu tego
płynu.
Równanie to ł
ą
cznie z równaniem ci
ą
gło
ś
ci w formie ró
ż
niczkowej stanowi zamkni
ę
ty
układ równa
ń
wystarczaj
ą
cy do rozwi
ą
zywania zada
ń
dotycz
ą
cych przepływów cieczy
nielepkiej. Mamy wtedy cztery niewiadome
ν
x
,
ν
y
,
ν
z
, p i cztery równania skalarne.
Przepływy gazu doskonałego opisujemy za pomoc
ą
układu
(19.13)
(19.14)
3.Równania Naviera-Stokesa.

∫∫
A
A
dA
p *
r
z
z
y
y
x
x
A
n
p
n
p
n
p
p
*
*
*
r
r
r
v
+
+
=
z
p
y
p
x
p
F
p
dt
v
d
p
z
y
x
m
∂
∂
+
∂
∂
+
∂
∂
+
=
r
r
r
r
r
*
*
xz
xy
xx
x
k
j
p
i
p
τ
τ
*
*
*
r
r
r
r
+
+
=
yz
yy
yx
y
k
p
j
i
p
τ
τ
*
*
*
r
r
r
r
+
+
=
zz
zy
zx
z
p
k
j
i
p
*
*
*
r
r
r
r
+
+
=
τ
τ
z
y
x
p
X
p
dt
dv
p
xz
xy
xx
x
∂
∂
+
∂
∂
+
∂
∂
+
=
τ
τ
*
*
z
p
y
x
Z
p
dt
dv
p
zz
zy
zx
z
∂
∂
+
∂
∂
+
∂
∂
+
=
τ
τ
*
*
z
y
p
x
Y
p
dt
dv
p
yz
yy
yx
y
∂
∂
+
∂
∂
+
∂
∂
+
=
τ
τ
*
*
Równanie zachowania p
ę
du płynu lepkiego w postaci całkowej dla sko
ń
czonego obszaru
płynnego V podałem jako równanie (19.7). W przypadku obszaru V, w którym wyst
ę
puj
ą
ci
ą
głe zmiany parametrów , p,pitd., równanie zachowania p
ę
du mo
ż
na wyrazi
ć
dla
elementów obj
ę
to
ś
ci dV, czyli w formie ró
ż
niczkowej. Przej
ś
cie z formy (19.7) do
ró
ż
niczkowej wymaga przedstawienia wszystkich wyst
ę
puj
ą
cych w (19.7) sił jako sił
obj
ę
to
ś
ciowych. W równaniu (19.7) sił
ą
powierzchniow
ą
jest
Korzystaj
ą
c z zale
ż
no
ś
ci znanych
i analizy wektorowej wzorów na przekształcenie całek powierzchniowych na obj
ę
to
ś
ciowe,
mianowicie
mo
ż
emy (19.7) zapisa
ć
w nast
ę
puj
ą
cej formie
Z powy
ż
szego równania wida
ć
,
ż
e wyra
ż
enie typu jest
charakterystyczne dla siły powierzchniowej, przypadaj
ą
cej na jednostk
ę
obj
ę
to
ś
ci.
Ze wzgl
ę
du na dowolno
ść
obszaru V musi by
ć
spełniony warunek zerowania si
ę
funkcji
podcałkowej, czyli
Jest to najogólniejsze równanie zachowania p
ę
du w formie ró
ż
niczkowej. Zwane ono jest
równie
ż
równaniem p
ę
du w napr
ęż
eniach. Mo
ż
na je przepisa
ć
jako trzy równania skalarne
wykorzystuj
ą
c zwi
ą
zki
otrzymujemy
(19.15)
(19.16)
(
)
dV
z
p
y
p
x
p
dA
n
p
n
p
n
p
V
z
y
x
A
z
z
y
y
X
X
∫∫∫
∫∫
∂
∂
+
∂
∂
+
∂
∂
=
+
+
r
r
r
r
r
r
*
*
*
0
*
*
*
=
∂
∂
+
∂
∂
+
∂
∂
−
−
∫∫∫
dV
z
p
y
p
x
p
m
F
p
dt
v
d
p
V
z
y
x
r
r
r
r
r
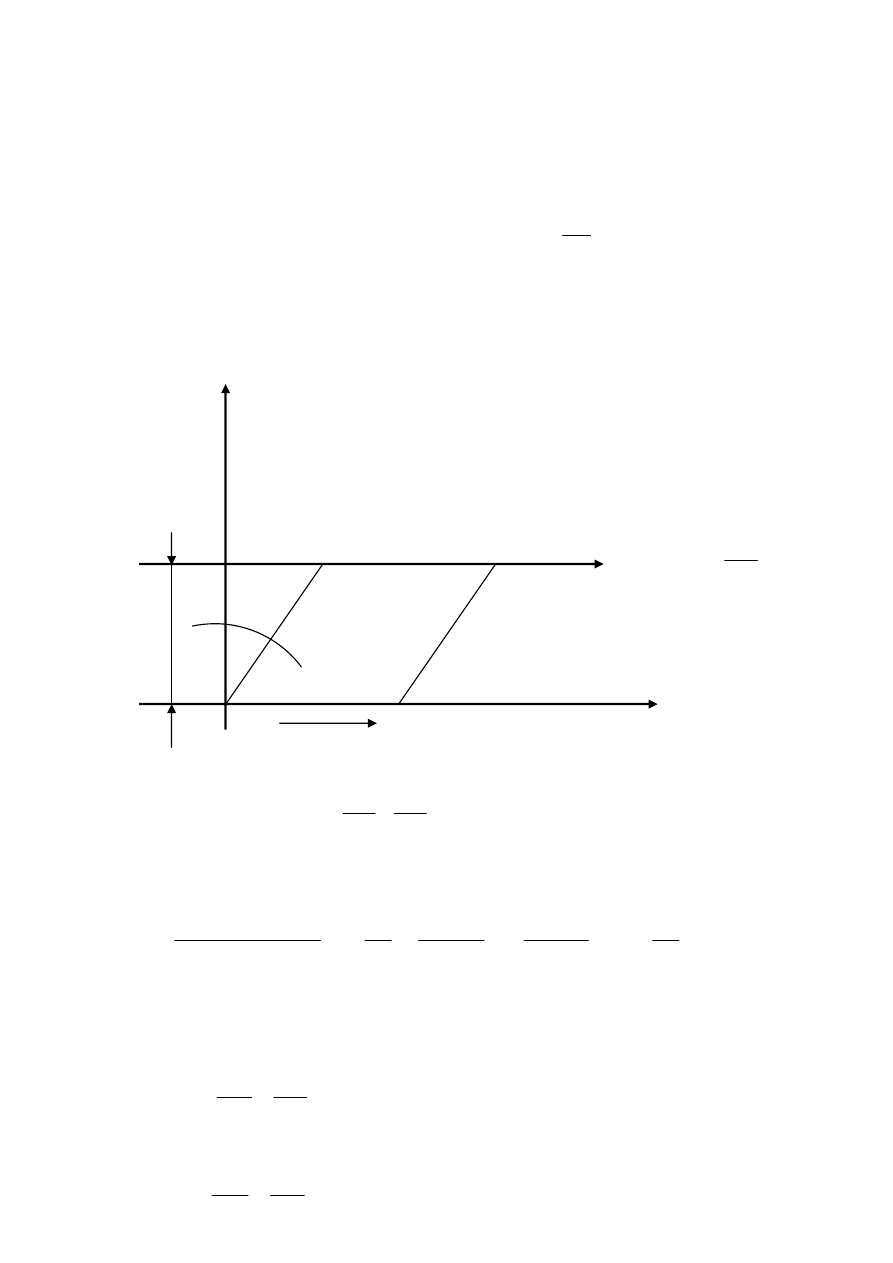
dz
z
V
y
∂
∂
z
x
y
y
v
dx
dv
Θ
=
∂
∂
+
x
p
x
∂
∂
r
0
=
∂
∂
=
∂
∂
=
=
y
x
Y
Y
X
Z
ν
ν
ν
ν
Aby uzale
ż
ni
ć
wyst
ę
puj
ą
ce w tym równaniu składowe napr
ęż
e
ń
od parametrów przepływu musimy
skorzysta
ć
z hipotez dotycz
ą
cych zwi
ą
zku mi
ę
dzy napr
ęż
eniami i odkształceniami elementu płynu,
które s
ą
wyra
ż
one poprzez pola pr
ę
dko
ś
ci. Hipotezy te pochodz
ą
z obserwacji empirycznych.
Skorzystamy z hipotezy Newtona mówi
ą
cej,
ż
e napr
ęż
enia w poruszaj
ą
cym si
ę
płynie s
ą
proporcjonalne do pr
ę
dko
ś
ci deformacji elementu płynu. Gdy
zastosujemy prosty newtonowski
model przepływu mi
ę
dzy dwoma warstwami cieczy
T
=
η
* i porównamy go z ogólniejszym
odkształceniem postaciowym elementu płynu, to zauwa
ż
ymy, model Newtona opisuje szczególny
przypadek odkształcenia.
Z
Vy +
dz V
z
=0
d
ββββ
d
αααα
=0
V
y
Y
W modelu Newtona
i wszystkie wyrazy tensora pr
ę
dko
ś
ci
deformacji elementu
płynu sprowadzaj
ą
si
ę
zgodnie ze wzorami
do członów
X
Y
Z
z
v
y
v
dt
d
d
Θ
=
∂
∂
+
∂
∂
=
+
2
1
2
1
2
β
α
Y
Z
X
x
v
z
v
Θ
=
∂
∂
+
∂
∂
z
v
y
∂
∂
+
2
1
z
v
y
yz
∂
∂
=
*
η
τ
,
*
2
1
*
1
z
v
k
z
yz
∂
∂
=
τ
[ ]
,
2
1
2
1
2
1
2
1
2
1
2
1
z
x
y
x
y
z
y
z
z
d
T
ε
ε
ε
Θ
Θ
Θ
Θ
Θ
Θ
=
[ ]
,
zz
yz
xz
zy
yy
xy
zx
yx
xx
p
p
p
τ
τ
τ
τ
τ
τ
=
Π
[ ]
Π
=
*
n
p
A
r
r
(19.17)
Hipoteza Newtona mówi w tym przypadku,
ż
e napr
ęż
enie
τ
yz
wynosi
(19.18)
Je
ś
li przyjmiemy,
ż
e napr
ęż
enia zawsze proporcjonalne do pr
ę
dko
ś
ci deformacji, czyli w tym
przypadku na podstawie (19.17)
(19.19)
gdzie k
1
-współczynnik proporcjonalno
ś
ci mi
ę
dzy tensorem deformacji i napr
ęż
e
ń
.
Porównuj
ą
c (18) i (19) widzimy,
ż
e:
k
1 =
2
η
(19.20)
Je
ś
li przeniesiemy ten rezultat na ogólne przypadki płynu, opisanych członami
Θ
tensora
deformacji
to porównuj
ą
c tensory
[ ]
,
2
1
2
1
2
1
2
1
2
1
2
1
z
x
y
x
y
x
y
z
x
x
y
x
d
y
v
y
v
x
v
x
v
z
v
y
v
x
v
x
v
T
ε
Θ
Θ
Θ
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
Θ
i

,
*
∂
∂
+
∂
∂
=
y
v
x
v
z
y
yz
η
τ
,
*
∂
∂
+
∂
∂
=
x
v
z
v
z
x
zx
η
τ
,
*
∂
∂
+
∂
∂
=
y
v
x
v
x
y
xy
η
τ
0
=
v
r
p
n
p
A
r
r
*
−
=
0
≠
v
r
otrzymamy:
Wyja
ś
nimy teraz struktur
ę
napr
ęż
e
ń
normalnych p
xx
, p
yy
, p
zz
, wyst
ę
puj
ą
cych
przek
ą
tnej tensora napr
ęż
e
ń
.
Przyjmiemy,
ż
e ci
ś
nienie musi by
ć
zwarte we wzorach okre
ś
laj
ą
cych p
xx
, p
yy
, p
zz
.
Gdy
p
ę
dko
ść
czynnika , to napr
ęż
enia normalne s
ą
sobie równe i
równe ci
ś
nieniu, a wi
ę
c
p
xx
+p
yy
+p
zz
=
-3p
(19.25)
Znak minus przy ci
ś
nieniu wi
ąż
e si
ę
z wyja
ś
nionym ju
ż
zwi
ą
zkiem: dla v=0 jest
Jednoczenie suma napr
ęż
e
ń
normalnych na podstawie ogólnych
twierdze
ń
rachunku tensorowego jest stała i wynosi -3p równie
ż
, gdy
Pr
ę
dko
ś
ci wydłu
ż
e
ń
elementu płynu E
x
, E
y
, E
z
musz
ą
si
ę
wi
ą
za
ć
z napr
ęż
eniami normalnymi. Dla cieczy, gdzie divv =0, napr
ęż
enia normalne
mo
ż
emy nast
ę
puj
ą
co uzale
ż
ni
ć
od pr
ę
dko
ś
ci wydłu
ż
e
ń
:
(19.26)
Miar
ą
dodatkowego odkształcenia obj
ę
to
ś
ci gazów jest ró
ż
na od zera warto
ść
divv. Przyjmujemy zatem,
ż
e dla gazów napr
ęż
enia normalne dodatkowo zale
żą
od
(19.24)
x
v
p
k
p
p
X
X
XX
∂
∂
+
−
=
−
=
*
2
*
*
1
η
ε
y
v
p
k
p
p
Y
Y
YY
∂
∂
+
−
=
−
=
*
2
*
*
1
η
ε
z
v
p
k
p
p
Z
Z
ZZ
∂
∂
+
−
=
−
=
*
2
*
*
1
η
ε

divv,
a wi
ę
c:
(19.27)
Sumuj
ą
c stronami równanie (19.27) z uwzgl
ę
dnieniem (19.25) otrzymamy
- 3 p = -3 p + k
1
* divv + 3k
2
* divv,
st
ą
d
(19.28)
Ostatecznie piszemy zwi
ą
zki napr
ęż
e
ń
normalnych z polem pr
ę
dko
ś
ci dla gazów:
(19.29)
Dla cieczy zale
ż
no
ś
ci te sprowadzaj
ą
si
ę
do (19.26). Do równania (19.16)
podstawimy zwi
ą
zki napr
ęż
e
ń
z polem pr
ę
dko
ś
ci i ci
ś
nie
ń
. Dla pierwszego z równa
ń
(19.16) otrzymujemy w wyniku drobnych przekształce
ń
przy zało
ż
eniu,
ż
e
η
= const,
(19.30)
st
ą
d:
v
div
k
k
p
p
X
XX
r
*
*
2
1
+
+
−
=
ε
v
div
k
k
p
p
Y
YY
r
*
*
2
1
+
+
−
=
ε
v
div
k
k
p
p
Z
ZZ
r
*
*
2
1
+
+
−
=
ε
η
3
2
3
1
2
−
=
−
=
k
k
v
div
x
v
p
p
X
XX
r
*
3
2
*
2
η
η
−
∂
∂
+
−
=
v
div
y
v
p
p
Y
YY
r
*
3
2
*
2
η
η
−
∂
∂
+
−
=
v
div
z
v
p
p
Z
ZZ
r
*
3
2
*
2
η
η
−
∂
∂
+
−
=
v
div
x
z
x
v
y
x
v
x
v
z
v
y
v
x
v
x
p
X
p
t
v
p
X
X
X
X
X
X
X
r
*
*
3
2
*
*
*
*
2
2
2
2
2
2
2
2
2
2
∂
∂
−
∂
∂
∂
+
∂
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
+
∂
∂
−
=
∂
∂
η
η
η
p
v
η
=
(19.31)
gdzie lepko
ść
kinematyczna
Analogicznie mo
ż
na zapisa
ć
równanie dla kierunku y i z.
(19.32)
Układ (19.31) i (19.32) mo
ż
emy zapisa
ć
w postaci wektorowej
(19.33)
Jest to równanie zachowania p
ę
du płynu lepkiego,
ś
ci
ś
liwego w formie
ró
ż
niczkowej, tzw. Równanie Naviera-Stokesa. Dla cieczy odpada ostatni człon
równania ze wzgl
ę
du na to,ze divv = O. Dla płynu nielepkiego v = O i równanie
(19.33) przechodzi w równanie Eulera (19.12).
Równanie (19.33) jest najogólniejszym równaniem p
ę
du jakie znamy dla
nieustalonych trójwymiarowych przepływów lepkiego płynu newtonowskiego.
Fizycznie uzasadnionym warunkiem brzegowym, który stosuje si
ę
przy
rozwi
ą
zywaniu równa
ń
N - S jest znikanie pr
ę
dko
ś
ci na nieruchomych
ś
ciankach
kanałów lub ciał opływanych. Gdy
ś
cianka porusza si
ę
, pr
ę
dko
ść
płynu na niej
równa si
ę
pr
ę
dko
ś
ci
ś
cianki.
Rozwi
ą
zanie analityczne równania (19.33) jest mo
ż
liwe tylko dla bardzo
uproszczonych jego postaci. Metody numeryczne i wykorzystanie maszyn
v
div
x
v
v
v
x
p
p
X
dt
dv
X
X
r
*
*
3
1
*
*
1
2
∂
∂
+
∇
+
+
∂
∂
−
=
v
div
y
v
v
v
y
p
p
Y
dt
dv
Y
Y
r
*
*
3
1
*
*
*
1
2
∂
∂
+
∇
+
∂
∂
−
=
v
div
z
v
v
v
z
p
p
Z
dt
dv
Z
Z
r
*
*
3
1
*
*
*
1
2
∂
∂
+
∇
+
∂
∂
−
=
v
graddiv
v
v
v
gradp
p
m
F
dt
v
d
r
r
r
r
*
3
1
*
*
1
2
+
∇
+
−
=

cyfrowych umo
ż
liwiaj
ą
rozwi
ą
zanie tego równania w szerszym zakresie. Jednak
ż
e
nawet metody numeryczne nie zezwalaj
ą
obecnie na teoretyczne rozwi
ą
zywanie
dowolnych przepływów lepkich w oparciu o równanie N - S. Problemy te zostan
ą
szczegółowiej omówione w dalszym ci
ą
gu tego rozdziału. Równanie N- S jest
podstaw
ą
w badaniu zjawisk podobie
ń
stwa przepływu płynów bez potrzeby ich
rozwi
ą
zywania.
20. Równanie Daniela Bernoulliego
Przy nast
ę
puj
ą
cych zało
ż
eniach :
1. Płyn jest nielepki (
, = 0 )
2. Przepływ jest stacjonarny
3. Pole sił masowych ma potencjał II ( f = -grad II )
4. Płyn jest barotropowy (
=
(p) )
Równanie za chowania ilo
ś
ci ruchu mo
ż
na zapisa
ć
nast
ę
puj
ą
co:
rotu
u
p
P
u
grad
dt
du
×
=
Π
+
+
+
)
(
2
2
Trójmian
Π
+
+
=
)
(
2
2
p
P
u
E
nazywamy trójmianem Bernoulliego.
Jest pi
ęć
przypadków stało
ś
ci tego trójmianu:
1.
rotu
u
gradE
×
=
0
*
=
=
ds
dE
I
gradE
I - wektor jednostkowy
0
=
ds
dE
2.
0
*
=
=
dw
dE
I
gradE
w
Iw,- wektor styczny do linii wirowej
0
=
dw
dE

3.
u
rotu
λ
=
u
u
rotu
u
λ
×
=
×
st
ą
d
grad E = 0
4.
rotu=0
grad E = 0
5. Dla u=0
const
p
P
E
=
Π
+
=
)
(
Stało
ść
trójmianu Bernoulliego wykazana dla pi
ę
ciu przypadków, stanowi podstaw
ę
do sformułowania równania Bernoulliego. Ma ono posta
ć
:
E
const
P
u
=
=
Π
+
+
2
2


ERROR: syntaxerror
OFFENDING COMMAND: --nostringval--
STACK:
(ZALICZENIE Z MECHANIKI P£YNW _Czarno-Bia‡e_Wojnar Brak
)
/Title
()
/Subject
(D:20041124224136)
/ModDate
()
/Keywords
(pdfcreator Version 0.8.0)
/Creator
(D:20041124224136)
/CreationDate
(root)
/Author
-mark-
Wyszukiwarka
Podobne podstrony:
mechanika plynow opracowane zagadnienia (2), Sprawka
mechana plynow opracowane zagadnienia kolo1, PG inżynierka, Semestr 3, Mechanika płynów, wykład
Mechanika płynów opracowane zagadnienia, Inżynieria Środowiska-Szczecin, Mechanika płynów, Wykłady+k
mechana plynow opracowane zagadnienia, OiO sem. III, mechanika płynów
mechanika płynów opracowanie
mechanika płynów 46-49, Mechanika płynów 1, Opracowania
Mechanika płynów opracowanie
mechanika plynow opracowanie
Mechanika plynow opracowanie
Mechanika plynow opracowanie wersja zmniejszona
mechanika plynow opracowanie
OPRACOWANE ZAGADNIENIE NR 3, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Se
OPRACOWANE ZAGADNIENIA z Mechaniki Płynów, Hydrologia i Hydraulika
Opracowane pytania na mechanikę płynów
więcej podobnych podstron