WYBRANE ZAGADNIENIA Z MECHANIKI PŁYNÓW DLA ENERGETYKI-2 (Mgr)
ROZWIĄZANIE PYTAŃ DO ZALICZENIA
1. Jaką zasadę fizyczną przedstawia równanie Naviera-Stokesa? Podaj słownie
interpretację fizyczną poszczególnych członów tego równania.
Równanie Naviera-Stokesa przedstawia równanie zachowania pędu:
[ ]
(
)
D
div
u
div
grad
gradp
f
Dt
u
D
µ
µ
ρ
ρ
2
3
2
+
−
−
=
Gdzie po podstawieniu:
λ
- objętościowy współczynnika lepkości, który zgodnie z hipotezą Stokesa:
µ
λ
3
2
−
=
.
Ostatecznie równanie Naviera-Stokesa w formie wektorowej ma postać:
(
)
[ ]
(
)
D
div
u
div
grad
gradp
f
Dt
u
D
µ
λ
ρ
ρ
2
+
−
−
=
E
D
C
B
A
+
+
+
=
gdzie:
A
- prędkość zmiany pędu elementu płynu
B
- siła masowa
C
- siła powierzchniowa ciśnienia
D
- siła powierzchniowa związana z lepkością płynu, wynikająca ze zmiany objętości
elementu płynu ściśliwego (kompresji lub ekspansji)
E
- siła powierzchniowa związana z lepkością płynu, wynikająca z deformacji liniowej i
postaciowej elementu płynu
2. Napisz równanie Bernoulliego i podaj jego interpretację fizyczną.
Równanie Bernoulliego wyraża zasady zachowania pędu i zachowania energii płynu przy
spełnieniu odpowiednich założeń.
Założenia:
• przepływ jest stacjonarny:
0
=
∂
∂
t
• płyn jest nielepki:
0
=
µ
• płyn jest barotropowy:
( )
p
ρ
ρ
=
• pole sił masowych jest potencjalne:
Π
−
=
grad
f
Równanie Bernoulliego można zapisać dwoma sposobami:
1) Suma energii potencjalnej pola sił masowych, energii ciśnienia oraz energii kinetycznej
płynu jest stała.
const
u
p
gz
=
+
+
2
2
ρ
2) Suma wysokości geometrycznej, wysokości ciśnienia (czyli wysokości, na jaką wzniesie
się słup cieczy pod ciśnieniem p) oraz wysokości prędkości (czyli wysokości, z której
spadający element płynu uzyska prędkość u) jest stała.
const
g
u
g
p
z
=
+
+
2
2
ρ
3. Co to jest masa towarzysząca płynu? Jak wpływa masa towarzysząca płynu na
drgania obiektu zanurzonego w płynie?
W niestacjonarnym ruchu obiektu (ciała stałego) zanurzonego w płynie masa towarzysząca
jest to umowna masa płynu, wykonująca ruch z tą samą prędkością z jaką porusza się obiekt.
Masa towarzysząca zwiększa bezwładność obiektu i przez to wpływa na charakterystyki jego
ruchu.
W rzeczywistości ruch obiektu zanurzonego w płynie wywołuje ruch innej masy płynu ze
zróżnicowanymi prędkościami – większymi blisko obiektu i mniejszymi w większej
odległości od niego. Ta rzeczywista masa płynu w taki sam sposób zwiększa bezwładność
obiektu jak umowna masa towarzysząca.
Przy ruchu ciał stałych w gazach z reguły nie uwzględnia się masy towarzyszącej ze względu
ma niewielką gęstość gazów.
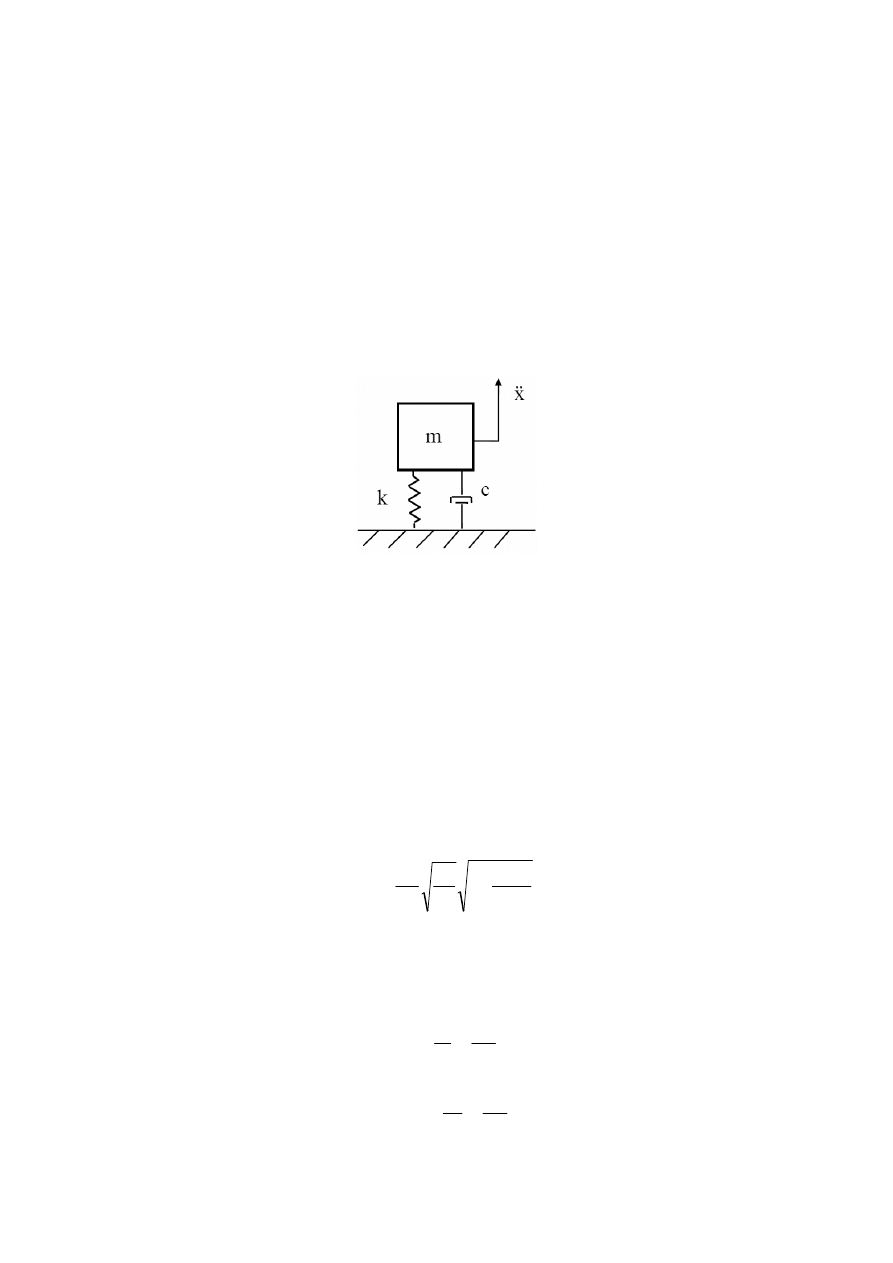
Wpływ masy towarzyszącej na oscylacje ciała sztywnego zanurzonego w płynie – prosty
przykład jednowymiarowy.
m
- masa ciała
c
- współczynnik tłumienia (efekt lepkości płynu)
k
- współczynnik sztywności
x
- przemieszczenie ciała
Masa towarzysząca zwiększa bezwładność ciała, czyli przeciwdziała oscylacjom. Wobec tego
równanie drgań swobodnych ma postać:
x
m
kx
x
c
x
m
a
−
=
+
+
&
&
&
(
)
0
=
+
+
+
kx
x
c
x
m
m
a
&
&
&
0
=
+
+
kx
x
c
x
m
e
&
&
&
gdzie:
a
m - masa towarzysząca
e
m - masa „efektywna”
Częstość własną drgań układu w płynie można wyznaczyć jako:
k
m
c
m
k
f
e
e
n
4
1
2
1
2
−
=
π
Jak widać, zanurzenie obiektu drgającego w płynie powoduje zmniejszenie częstości własnej
drgań.
4. Przedstaw interpretację fizyczną liczb Reynoldsa, Froude’a, Strouhala i Eulera.
Liczba Strouhala:
u
t
l
tu
l
Sh
′
′
′
=
=
Liczba Froude’a wyraża stosunek sił bezwładności do sił masowych:
( )
l
f
u
fl
u
Fr
′′
′
=
=
2
2
2
Liczba Eulera wyraża stosunek sił ciśnienia do sił bezwładności:
2
2
u
p
u
p
Eu
′
′
=
=
ρ
ρ
Liczba Reynoldsa wyraża stosunek sił bezwładności do sił lepkości:
µ
ρ
µ
ρ
′
′
′
′
=
=
l
u
ul
Re
5. Scharakteryzuj przepływy laminarne i turbulentne.
Przepływ laminarny – uporządkowany ruch płynu po torach równoległych, elementy płynu
nie mieszają się ze sobą, działa czysto lepkościowy mechanizm wymiany pędu i energii.
Przepływ ten występuje do wartości Re=2300.
Przepływ turbulentny – chaotyczny ruch płynu o stochastycznym charakterze,
niestacjonarny nawet przy ustalonych warunkach brzegowych, elementy płynu mieszają się ze
sobą, co prowadzi do intensyfikacji wymiany masy, pędu i energii. Przepływ ten występuje
powyżej wartości Re=2300.
6. W jaki sposób uwzględnia się turbulentny charakter przepływu w obliczeniach
numerycznych?
W przepływie turbulentnym wszystkie charakteryzujące go parametry, w tym prędkość i
ciśnienie płynu mogą być przedstawione w postaci sum ich wartości średnich
(wolnozmiennych) oraz fluktuacji turbulentnych.
7. Na czym polega oderwanie warstwy przyściennej i w jakich warunkach może ono
wystąpić?
Oderwanie warstwy przyściennej jest spowodowane przez wystąpienie dodatniego gradientu
ciśnienia wzdłuż warstwy przyściennej (czyli wzrost ciśnienia w kierunku przepływu).
Element płynu przy samej ściance jest hamowany siłami lepkości i siłami ciśnienia, co
powoduje jego zatrzymanie, a następnie ruch w kierunku przeciwnym do przepływu.
Oderwanie może wystąpić zarówno w laminarnej jak i w turbulentnej warstwie przyściennej
(w turbulentnej występuje później, czyli przy wyższym gradiencie ciśnienia). Oderwanie
warstwy przyściennej jest zjawiskiem niekorzystnym, zakłóca pracę maszyn i urządzeń
przepływowych oraz obniża ich sprawność.
8. Kiedy i w jaki sposób chropowatość powierzchni wpływa na opór tarcia obiektu
umieszczonego w przepływie?
Miarą chropowatości powierzchni jest średnia wysokość chropowatości
s
k . Z punktu
widzenia oporu tarcia istotna jest relacja średniej wysokości chropowatości do grubości
podwarstwy lepkiej w turbulentnej warstwie przyściennej. Jeżeli chropowatość mieści się w
tej podwarstwie, to chropowatość nie wywołuje zmiany profilu prędkości w warstwie i nie
wpływa na opór tarcia - powierzchnię nazywamy hydrodynamicznie gładką. Natomiast jeżeli
wysokość chropowatości wykracza poza tę podwarstwę, to jej obecność zmienia profil
prędkości w warstwie i wpływa na wzrost oporu tarcia.
9. Od jakich wielkości zależy prędkość dźwięku w gazie?
Z liniowego równania falowego wynika, że małe zaburzenia propagują się w gazie ze stałą
prędkością. Ponieważ fale dźwiękowe są również małymi zaburzeniami, to prędkość ich
propagacji można interpretować jako prędkość dźwięku:
0
0
ρ
κ
p
a
=
Lokalna prędkość dźwięku określa zależność:
T
R
p
p
a
⋅
⋅
=
=
∂
∂
=
κ
ρ
κ
ρ
gdzie:
v
p
c
c
=
κ
- wykładnik adiabaty Poissona
R
- indywidualna stała gazowa
T
- temperatura
Z powyższej zależności wynika, że prędkość dźwięku jest tym większa im mniej ściśliwy jest
ośrodek. W powietrzu na poziomie morza prędkość dźwięku jest rzędu 340 [m/s], a w wodzie
rzędu 1500 [m/s].
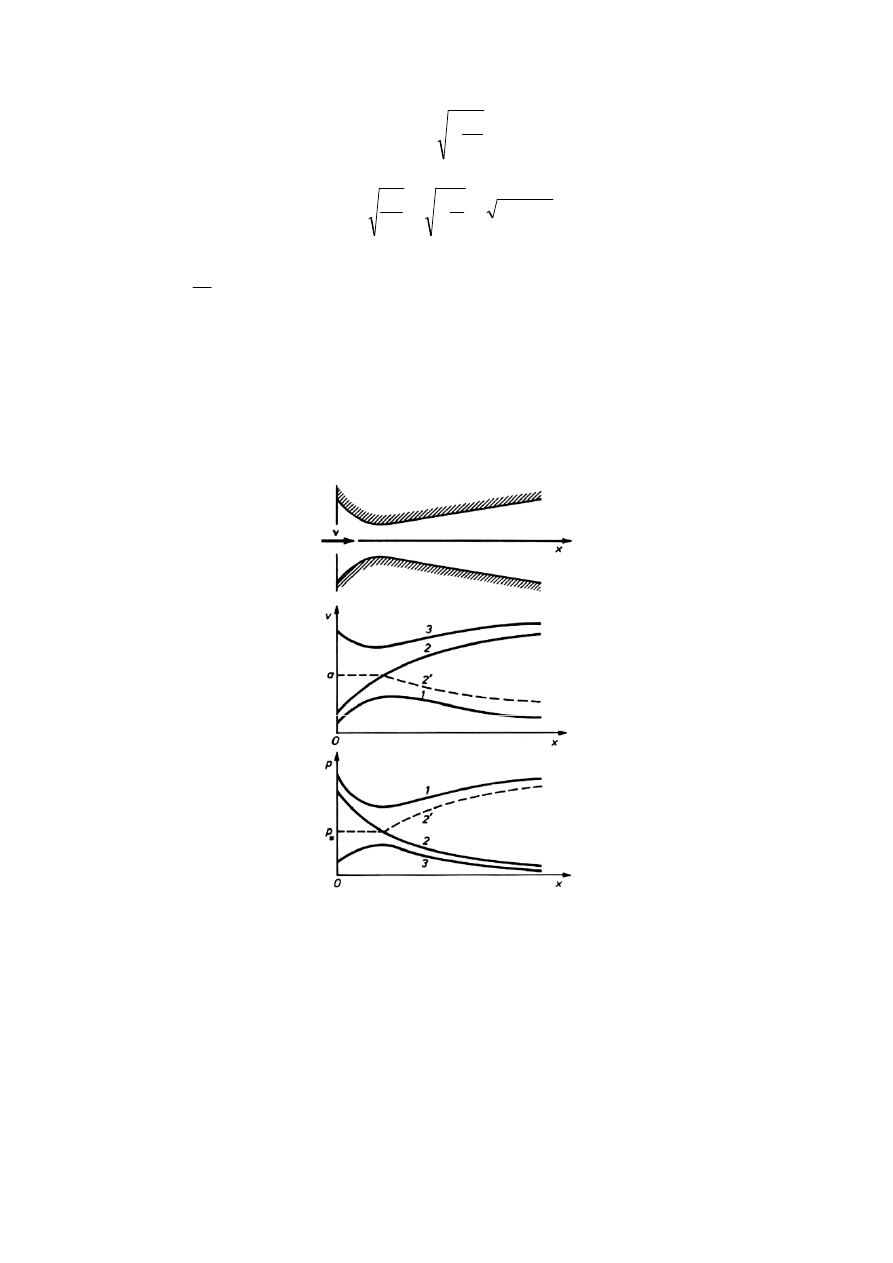
10. Jakie są możliwe rodzaje przepływu przez dyszę de Lavala?
Możliwe przypadki przepływu przez dyszę de Lavala:
1 – przepływ poddźwiękowy – można ich zrealizować nieskończenie wiele w zależności od
wartości ciśnienia na wylocie (czyli tzw. przeciwciśnienia).
2 – w konfuzorze przepływ poddźwiękowy, w gardzieli prędkość dźwięku, w dyfuzorze
przepływ nad- lub poddźwiękowy zależnie od wartości przeciwciśnienia.
3 – gaz wpływa do dyszy już z prędkością naddźwiękową, w konfuzorze jest lekko
przyhamowany, ale w gardzieli jest nadal prędkość naddźwiękowa. W dyfuzorze przepływ
nadal przyspiesza, czyli w całej dyszy mamy przepływ naddźwiękowy.
11. Co to jest fala uderzeniowa? Jak zmieniają się parametry przepływu przy przejściu
przez prostopadła falę uderzeniową?
Fala uderzeniowa jest to występująca w naddźwiękowych przepływach gazu bardzo cienka
(o grubości rzędu kilkunastu mikronów) strefa (powierzchnia) nagłej zmiany parametrów
przepływu.
Fala uderzeniowa:
• powstaje, gdy Ma>1,0
• przy przejściu prostopadłej fali uderzeniowej mamy spadek prędkości, wzrost ciśnienia,
gęstości, temperatury i energii gazu
• prostopadła fala uderzeniowa jest wtedy gdy Ma<1,0.
12. Na czym polega zjawisko kawitacji i w jakich warunkach może wystąpić?
Kawitacja jest to zjawisko powstawania, dynamicznego rozwoju i zaniku pęcherzy parowo-
gazowych w cieczach, wywołane lokalnymi zmianami ciśnienia przy stałej temperaturze.
O przebiegu zjawiska decydują:
• dyfuzja/odgazowanie,
• parowanie/kondensacja,
• bezwładność cieczy,
• napięcie powierzchniowe,
• adhezja,
• lepkość cieczy.
Występowanie kawitacji:
• ciekłe gazy – paliwa silników rakietowych,
• ciekłe metale – chłodziwo reaktorów jądrowych,
• ciecze naturalne – czynniki robocze w maszynach hydraulicznych (na przykład paliwo w
silniku wysokoprężnym),
• krew – w przepływie przez sztuczną zastawkę serca.
13. W jaki sposób można modelować obliczeniowo przepływy potencjalne?
Jeżeli przepływ płynu jest bezwirowy, czyli wszędzie lub prawie wszędzie w polu przepływu
jest
0
=
u
rot
to oznacza, że istnieje funkcja skalarna
(
)
t
z
y
x
,
,
,
ϕ
, taka że
ϕ
grad
u
=
.
Przepływ taki nazywamy przepływem potencjalnym, a funkcję
ϕ
nazywamy potencjałem
prędkości.
Mamy:
x
u
x
∂
∂
=
ϕ
y
u
y
∂
∂
=
ϕ
z
u
z
∂
∂
=
ϕ
W przypadku przepływu potencjalnego płynu nieściśliwego równanie zachowania masy
przekształca się w równanie Laplace’a:
( )
0
0
2
2
2
2
2
2
=
∂
∂
+
∂
∂
+
∂
∂
=
∆
=
→
=
+
∂
∂
z
y
x
divgrad
u
div
t
ϕ
ϕ
ϕ
ϕ
ϕ
ρ
ρ
Równanie Laplace’a jest liniowe, co oznacza, że suma jego rozwiązań jest również
rozwiązaniem. W praktyce więc można składać bardzo skomplikowane funkcje potencjału,
opisujące złożone przepływy, z funkcji opisujących tzw. przepływy elementarne.
14. Na czym polegają metody różnic skończonych i elementów skończonych w
zastosowaniu do obliczania przepływów?
Metoda różnic skończonych polega na przekształceniu równań różniczkowych w ich
równoważniki różnicowe. Autorstwo metody jest przypisywane B. Taylorowi. W praktyce
spotyka się trzy schematy różnicowe. Jeżeli pochodna funkcji jest określona jako:
(
) ( )
h
x
f
h
x
f
dx
df
dh
df
h
−
+
=
=
→
0
lim
To można ją aproksymować jako:
• Różnicę „w przód”:
(
) ( )
h
x
f
h
x
f
h
f
−
+
=
∆
• Różnicę „wstecz”:
( ) (
)
h
h
x
f
x
f
h
f
−
−
=
∆
• Różnicę centralną:
h
h
x
f
h
x
f
h
f
−
−
+
=
∆
2
1
2
1
O błędach względnych aproksymacji równych odpowiednio:
( )
h
O
dx
df
h
f
=
−
∆
( )
2
h
O
dx
df
h
f
=
−
∆
Metoda elementów skończonych: Analizowany obszar przepływu jest dzielony na części,
tzw. elementy skończone. W wybranych punktach każdego elementu chcemy określić
wartości poszukiwanej funkcji, np. prędkości, ciśnienia itp. Rozkład tej funkcji postulujemy w
postaci funkcji bazowej aproksymującej rozwiązanie. Parametry funkcji aproksymującej
ustalamy przy pomocy metody wariacyjnej.
15. Na czym polega metoda objętości skończonych w zastosowaniu do obliczania
przepływów?
Metoda objętości skończonych polega na przekształceniu równań różniczkowych w
równania algebraiczne poprzez całkowanie tych równań w granicach każdej objętości
skończonej w oparciu o założoną aproksymację zmienności parametrów opisujących
przepływ w granicach objętości (np. liniową, kwadratową itp.).
16. W jaki sposób uwzględnia się straty przepływu w równaniu Bernoulliego
zastosowanym do rurociągu?
Równanie Bernoulliego dla rzeczywistego przepływu ze stratami ma postać:
∫
=
+
+
−
+
+
2
1
2
2
2
2
1
1
2
1
2
~
2
~
dl
S
C
p
gz
p
u
gz
p
u
ρ
ρ
ρ
τ
albo:
const
H
h
z
g
p
g
u
z
g
p
g
u
s
=
=
+
+
+
=
+
+
2
2
2
2
1
1
2
1
2
~
2
~
ρ
ρ
gdzie:
s
h - wysokość strat
Wysokość strat możemy podzielić na dwa składniki:
• wysokość strat liniowych związanych z tarciem płynu o ścianki przewodu prostoliniowego o
stałym przekroju, wyrażona wzorem:
d
l
g
u
h
s
λ
2
~
2
=
• wysokość strat lokalnych związanych z obecnością zaworów, kolan, zwężeń, rozgałęzień i
innych elementów, wyraża się wzorem:
g
u
g
u
h
s
2
~
2
~
2
2
2
1
ς
ς
′
=
=
Gdzie
ς
jest współczynnikiem strat lokalnych, który może być określony w odniesieniu do
prędkości przed elementem lub prędkości za elementem. Współczynniki
ς
są określane
eksperymentalnie i można je znaleźć w odpowiednich tablicach.
W przypadku gdy przepływ odbywa się w przewodach o znacznej średnicy, równanie
Bernoulliego powinno być jeszcze uzupełnione o współczynnik Coriolisa (lub de Saint-
Venanta)
α
const
H
h
z
g
p
g
u
z
g
p
g
u
s
=
=
+
+
+
⋅
=
+
+
⋅
2
2
2
2
2
1
1
2
1
1
2
~
2
~
ρ
α
ρ
α
Wynika to z faktu, że rzeczywista energia strumienia niejednorodnego różni się od energii
obliczonej według średniej prędkości wydatkowej dla tego strumienia. Wobec tego mamy:
A
u
dA
u
A
⋅
=
∫
3
3
~
α
Współczynnik
α
jest tym większy im bardziej niejednorodne jest pole prędkości przepływu.
17. W jaki sposób średnia prędkość przepływu w kanale otwartym zależy od napełnienia
kanału?
Prędkość przepływu jest proporcjonalna do kwadratu grubości warstwy cieczy, czyli:
prędkość przepływu w kanale otwartym rośnie ze wzrostem stopnia napełnienia kanału.
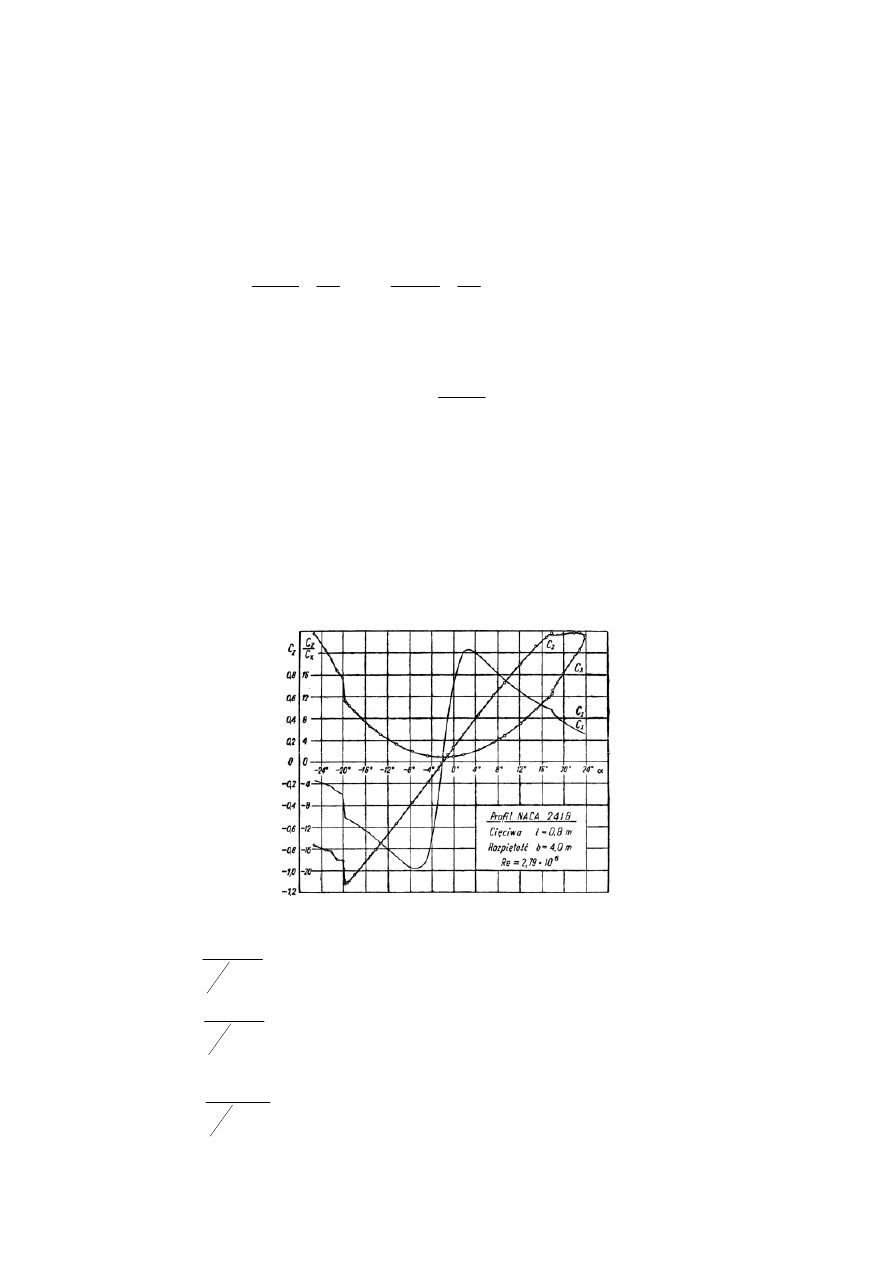
18. Narysuj i zinterpretuj charakterystyki aerodynamiczne profilu.
Charakterystyki aerodynamiczne profilu to zależność współczynników siły nośnej i siły oporu
(ewentualnie także momentu) od kąta natarcia.
Gdzie:
S
V
P
C
Z
Z
2
2
∞
=
ρ
– współczynnik siły nośnej
S
V
P
C
X
X
2
2
∞
=
ρ
– współczynnik siły oporu
Sl
V
M
C
M
2
2
∞
=
ρ
– współczynnik siły aerodynamicznej
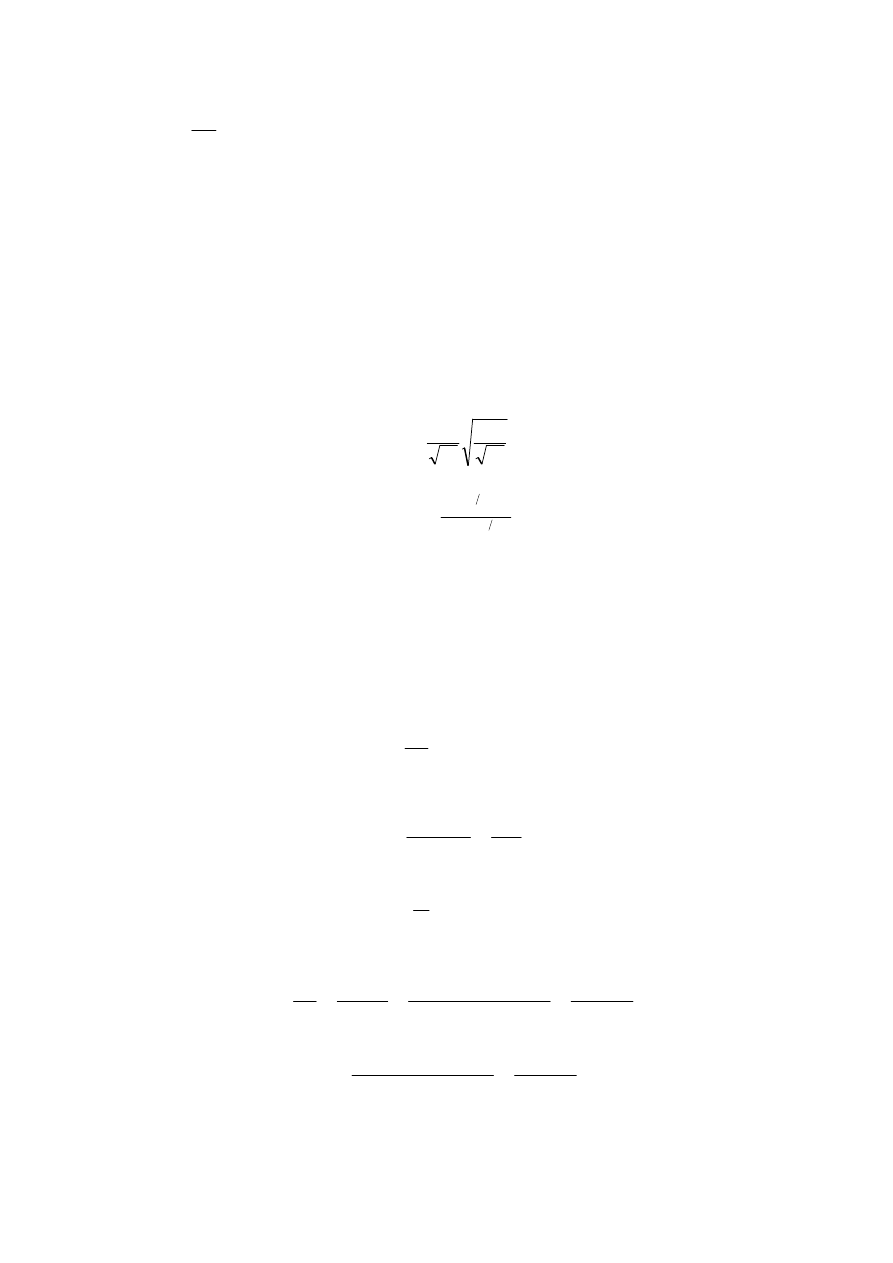
X
Z
C
C
=
ε
– współczynnik doskonałości profilu
S – powierzchnia płata (w przypadku profilu – powierzchnia odcinka o jednostkowej
rozpiętości)
P – wypadkowa siła aerodynamiczna
Z
P
– siła nośna
X
P
– siła oporu
M – moment siły aerodynamicznej
∞
V
– prędkość przepływu
α
– kąt natarcia
19. Co to jest wyróżnik szybkobieżności wirnikowych maszyn przepływowych?
Kinematyczny wyróżnik szybkobieżności maszyny wirnikowej to prędkość obrotowa pompy
geometrycznie podobnej o jednostkowej wysokości hydraulicznej i jednostkowej wydajności:
H
Q
H
n
n
sQ
=
Bezwymiarowy wyróżnik szybkobieżności:
(
)
4
3
2
1
H
g
Q
n
n
sf
⋅
⋅
=
Wyróżnik szybkobieżności jednoznacznie charakteryzuje typ wirnika maszyny. Wartość
wyróżnika wzrasta ze wzrostem wydajności i prędkości obrotowej a maleje ze wzrostem
wysokości hydraulicznej.
20. Jakie czynniki wchodzą w skład zależności opisującej sprawność pompy wirnikowej?
Moc dostarczona do pompy
N jest większa od mocy użytecznej z powodu strat, które dzielimy
na straty hydrauliczne, objętościowe i mechaniczne. Łączny wpływ strat ujmuje sprawność
pompy, którą można przedstawić jako iloczyn sprawności hydraulicznej, sprawności
objętościowej i sprawności mechanicznej:
m
v
h
u
N
N
η
η
η
η
⋅
⋅
=
=
Straty hydrauliczne wywołane są tarciem cieczy o ścianki wirnika i kadłuba pompy oraz tarciem
wewnętrznym.
t
p
p
p
p
h
H
h
h
h
h
∆
=
+
∆
∆
=
η
Gdzie teoretyczna wysokość podnoszenia dla pompy o skończonej liczbie łopatek wynosi:
(
)
u
u
t
v
r
v
r
g
H
1
1
2
2
−
Ω
=
Straty objętościowe są spowodowane przepływem wstecznym pomiędzy wirnikiem a kadłubem
pompy, który sprawia, że rzeczywistyprzepływ przez wirnik jest większy od wydajności pompy.
(
)
w
v
w
t
w
v
w
t
v
w
v
N
N
N
H
Q
g
Q
Q
H
g
Q
Q
Q
Q
Q
−
=
⋅
⋅
⋅
−
⋅
⋅
⋅
=
+
=
=
ρ
ρ
η
Teraz wzór na sprawność hydrauliczną można zapisać:
(
)
v
w
u
t
v
w
p
h
N
N
N
H
Q
Q
g
h
Q
g
−
=
⋅
−
⋅
⋅
∆
⋅
⋅
⋅
=
ρ
ρ
η
Straty mechaniczne są spowodowane tarciem w łożyskach i uszczelnieniach, a także tarciem
zewnętrznej części wirnika o ciecz.
N
N
N
N
N
w
m
w
w
m
=
−
=
η
Ostatecznie:
m
v
h
w
w
v
w
v
w
u
u
N
N
N
N
N
N
N
N
N
N
η
η
η
η
⋅
⋅
=
⋅
−
⋅
−
=
=
21. Jakie zagrożenia dla pracy maszyn i urządzeń przepływowych niesie kawitacja?
Kawitacja ma na ogół negatywny wpływ na pracę maszyn i urządzeń przepływowych, powodując
następujące niekorzystne zjawiska:
• spadek sprawności maszyn przepływowych,
• erozję elementów maszyn i urządzeń przepływowych,
• generację drgań i emisji akustycznej.