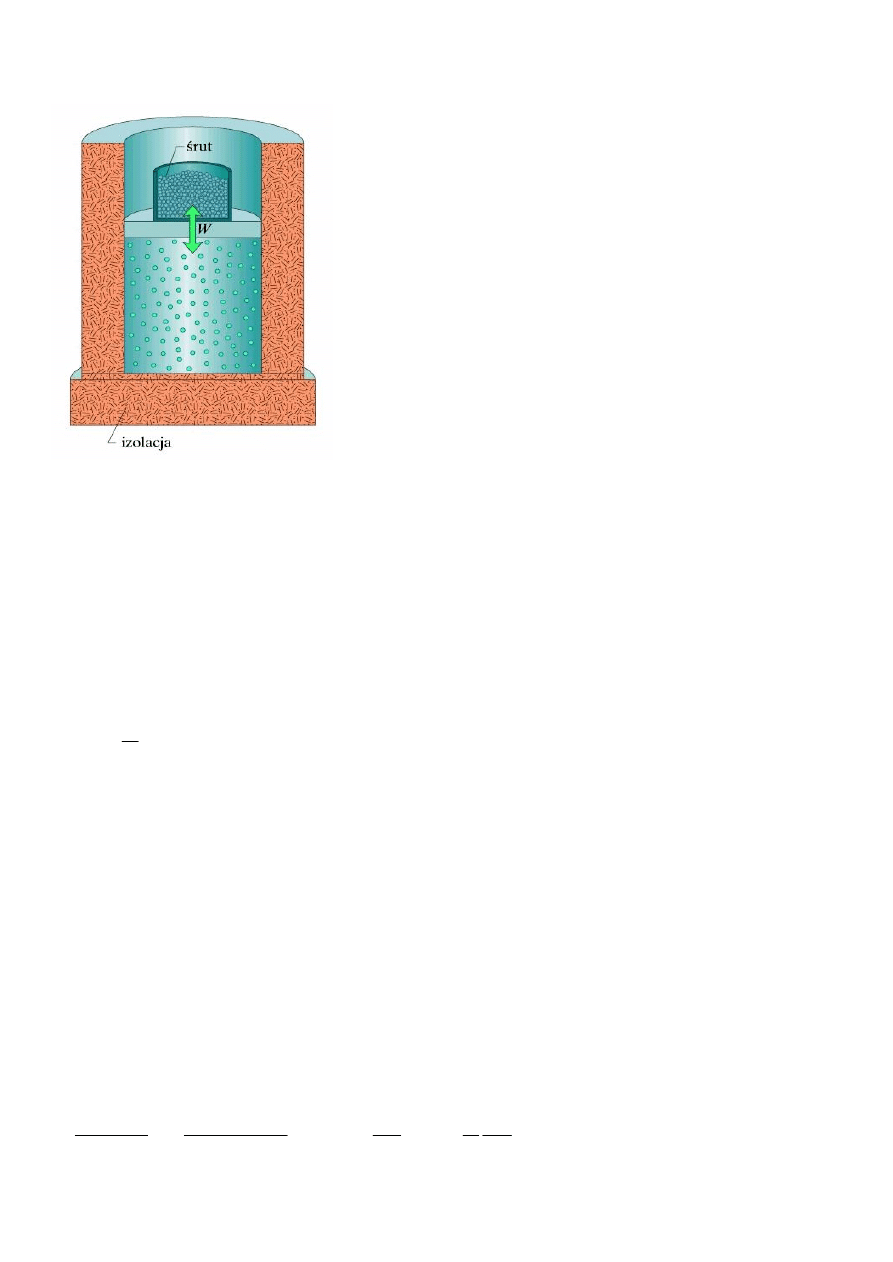
Przemiana adiabatyczna gazu doskonałego

Wyprowadzenie równania Poissona

I zasada termodynamiki w postaci różniczkowej

{

W

d

Q

d

d

w

+

=

=

0

ε

(1)

gdzie różniczkowa praca wykonana nad gazem

V

d

p

W

d

−

=

(2)

energia wewnętrzna gazu doskonałego

T

C

n

T

R

n

f

V

w

=

=

2

ε

stąd:

T

d

C

n

d

V

w

=

ε

(3)

podstawiamy (2) i (3) do (1):

V

d

p

T

d

C

n

V

−

=

(4)

obliczamy różniczkę równania stanu gazu doskonałego

T

R

n

V

p

=

(zmienne: p, V, T)

T

d

R

n

dp

V

V

d

p

=

+

podstawiamy

V

p

C

C

R

−

=

T

d

C

C

n

dp

V

V

d

p

V

p

)

(

−

=

+

(5)

dzielimy stronami (5) przez (4), a następnie zamieniamy stronę lewą z prawą:

V

d

p

dp

V

V

d

p

C

C

C

V

V

p

+

−

=

−

→

1

1

−

−

=

−

V

d

dp

p

V

C

C

V

p

przemiana

adiabatyczna

– bez

wymiany ciepła z otoczeniem

V

d

dp

p

V

C

C

V

p

−

=

/

⋅ dV, : V

p

dp

V

V

d

C

C

V

p

−

=

całkujemy obustronnie (czynniki stałe wyłączamy przed znak całki)

∫

∫

−

=

dp

p

V

d

V

C

C

V

p

1

1

α

+

−

=

p

V

C

C

V

p

ln

ln

korzystamy z własności logarytmu naturalnego (obowiązuje dla logarytmu o dowolnej
podstawie): a ln x = ln x

a

:

α

=

+

p

V

V

p

C

C

ln

ln

suma logarytmów jest równa logarytmowi iloczynu

α

=

















V

p

C

C

V

p

ln

stosujemy obustronnie funkcję odwrotną do logarytmu naturalnego – funkcję wykładniczą e

x

const

e

=

=

=

β

α

V

p

C

C

V

p

stosujemy oznaczenie

κ

≡

V

p

C

C

κ –

współczynnik Poissona

ostatecznie równanie przyjmuje postać:

const

=

κ

V

p

(6)

jest to najczęściej używana forma równania Poissona

korzystając z równania stanu gazu doskonałego można zapisać równanie Poissona
korzystając z innej pary parametrów termodynamicznych (np. T i V lub T i p)

T

R

n

V

p

1

=

→

1

1

−

=

=

κ

κ

κ

V

T

R

n

V

T

R

n

V

V

p

const

=

=

β

κ

V

p

→

const

1

1

=

=

−

β

κ

R

n

V

T

stała całkowania

druga forma równania Poissona:

const

1

=

−

κ

V

T

(7)

T

R

n

p

V

1

=

→

)

1

(

)

(

1

−

−

=













=

κ

κ

κ

κ

p

T

R

n

T

R

n

p

p

V

p

const

=

=

β

κ

V

p

→

const

)

(

1

1

=

=

−

β

κ

κ

κ

R

n

p

T

→

const

)

(

1

1

1

1

=









=

−

−

κ

κ

β

κ

κ

R

n

pT

trzecia forma równania Poissona:

const

1

=

−

κ

κ

pT

(8)

Obliczenie całkowitej pracy wykonanej nad gazem

przy przejściu gazu doskonałego od stanu początkowego (objętość V

P

) do stanu końcowego

(objętość V

K

) nad gazem wykonywana jest praca

∫

−

=

K

P

V

V

V

d

p

W

(9)

z równania Poissona (6):

κ

κ

P

P

V

p

V

p

=

=

const

→

κ

κ

V

V

p

p

P

P

1

=

podstawiamy do (9):















−









−

=

=

















−

−

=

















−

−

=

=













+

−

−

=

−

=

−

=

−

−

−

−

−

−

+

−

∫

∫

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

κ

K

P

P

P

K

P

P

P

P

P

K

P

P

V

V

P

P

V

V

P

P

V

V

P

P

V

V

V

p

V

V

V

V

p

V

V

V

p

V

V

p

V

d

V

V

p

V

d

V

V

p

W

K

P

K

P

K

P

z równania stanu gazu doskonałego podstawiamy

P

P

P

T

R

n

V

p

=

i otrzymujemy















−













−

=

−

1

1

1

1

κ

κ

K

P

P

V

V

T

R

n

W

(10)