Zespół Szkół Nr 1 im. Jana Kilińskiego w Pabianicach

Przedmiot: Proces projektowania cz

ęś

ci maszyn

1

Orientacyjne warto

ś

ci współczynnika z wytrzymało

ś

ci spoin

k

z

k

⋅

=

′

(1.1)

gdzie:
k – napr

ęż

enia dopuszczalne dla materiału ł

ą

czonych cz

ęś

ci

k

’

– napr

ęż

enia dopuszczalne dla spoiny

z – współczynnik wytrzymało

ś

ci spoiny.

Warto

ś

ci współczynnika z oraz zale

ż

no

ść

1.1 stosuje si

ę

do oblicze

ń

przy-

bli

ż

onych. Przy bardzo dokładnych obliczeniach spoin warto

ść

przyjmowanego

współczynnika z uzale

ż

nia si

ę

od wielu innych czynników, w tym od:

— rodzaju spoiny (I, V, U itd.),
— wytrzymało

ś

ci materiału (im wy

ż

sza warto

ść

R

m

, tym mniejsza warto

ść

współczynnika

z),
— rodzaju obci

ąż

enia (statyczne, dynamiczne) i warunków pracy poł

ą

czenia,

— sposobu kontrolowania jako

ś

ci spoiny.

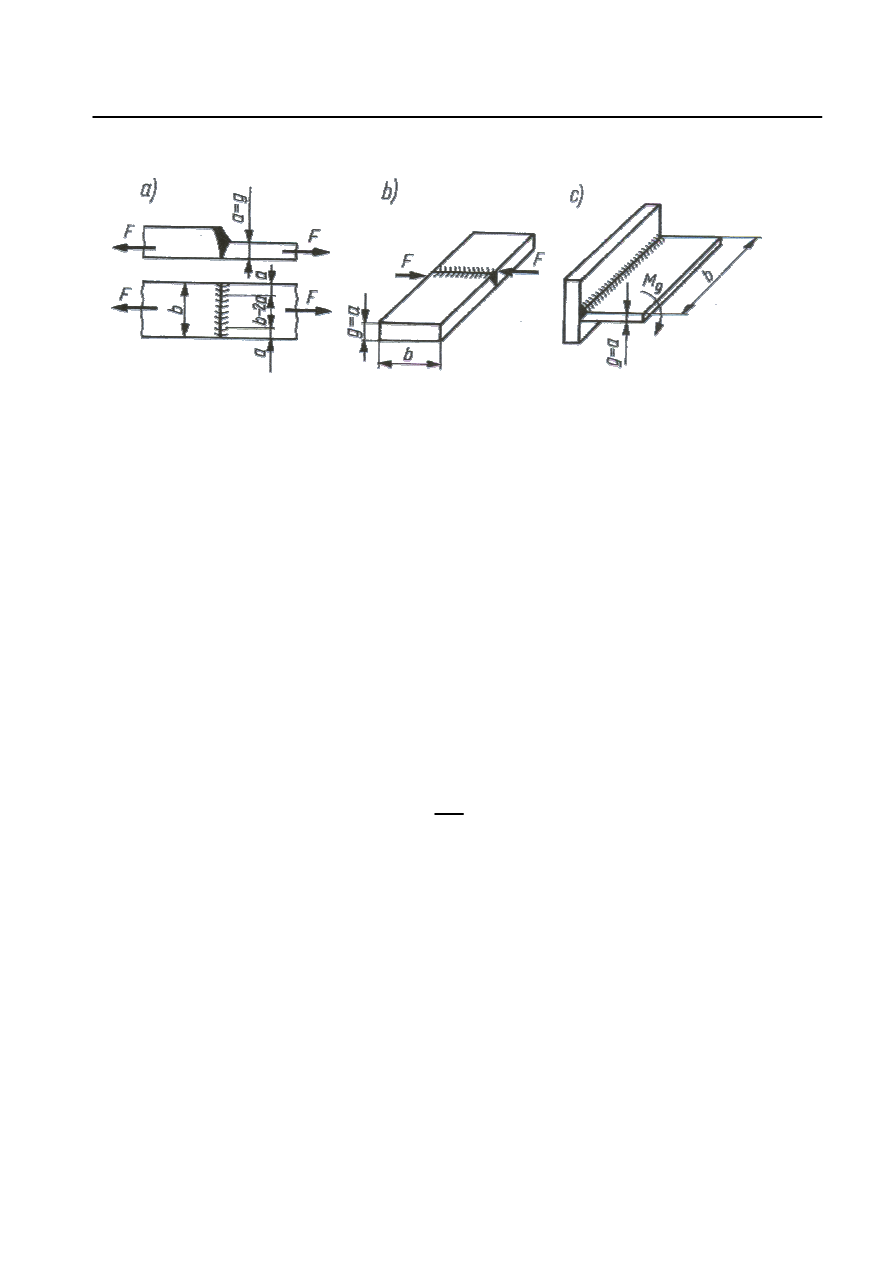
Spoiny czołowe.

W zale

ż

no

ś

ci od rodzaju obci

ąż

enia spoiny czołowe oblicza si

ę

:

— na rozci

ą

ganie lub

ś

ciskanie (rys. 1a)

'

r

r

k

S

F

≤

=

σ

lub

'

c

c

k

S

F

≤

=

σ

— na

ś

cinanie (rys. 1b)

'

t

S

F

t

k

≤

=

τ

— na zginanie (rys. 1c)

'

g

x

g

g

k

W

M

≤

=

σ

Spoiny

Rodzaj obci

ąż

enia

z

Czołowa

rozci

ą

ganie

0,8

ś

ciskanie

1,0

zginanie

0,9

ś

cinanie

0,65

Pachwinowa

wszystkie rodzaje
obci

ąż

e

ń

0,65

Zespół Szkół Nr 1 im. Jana Kilińskiego w Pabianicach

Przedmiot: Proces projektowania cz

ęś

ci maszyn

2

Wymiary spoin czołowych

Rys. 1.

Wymiary spoin czołowych przyjmuje si

ę

równe przekrojowi geometrycznemu

cz

ęś

ci spawanej o mniejszym przekroju, czyli wg rys. 1: a = g, b = l.

Pocz

ą

tek i koniec długo

ś

ci spoiny, czyli tzw. kratery, s

ą

najsłabszymi miej-

scami w spoinie, zatem uwzgl

ę

dniaj

ą

c długo

ść

dwóch kraterów, przyjmuje si

ę

rzeczywist

ą

długo

ść

spoiny l

rz

= b = l + 2a lub l = b — 2a (np. wg rys. 1a). Gdy

konieczne jest pełne wykorzystanie wytrzymało

ś

ci spoiny czołowej, stosuje si

ę

wyprowadzenie spoiny na podkładki (przyspawane płytki, na których zaczyna si

ę

i

ko

ń

czy spoin

ę

); płytki te odcina si

ę

po wykonaniu spoiny. W tym przypadku przyjmuje

si

ę

l = b.

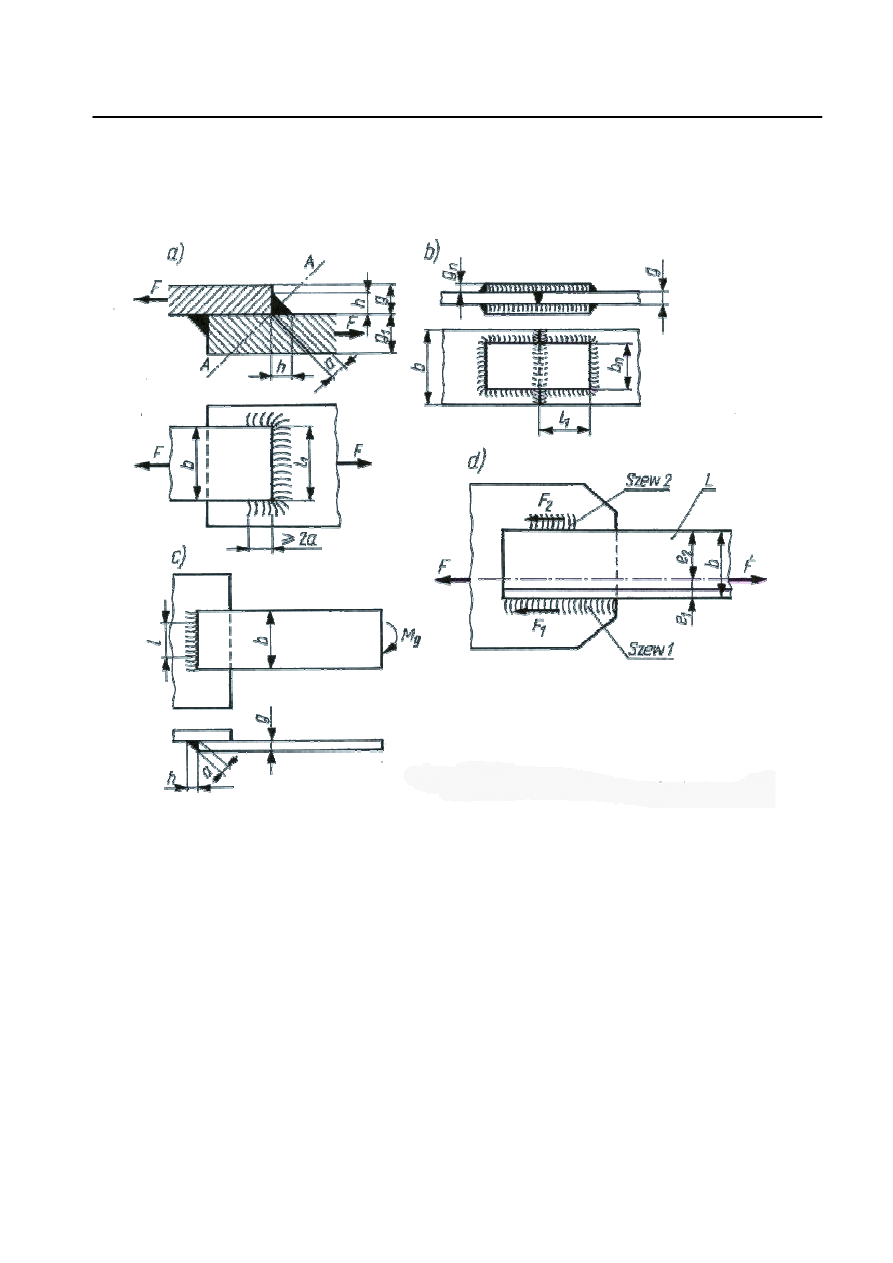
Spoiny pachwinowe.

W spoinach pachwinowych wyst

ę

puje w rzeczywisto

ś

ci zło

ż

ony stan

napr

ęż

e

ń

, pomijany w obliczeniach uproszczonych. Zwykle spoiny pachwinowe

oblicza si

ę

umownie na

ś

cinanie w najmniejszym przekroju spoiny A — A (rys. 2a). W

przypadku obci

ąż

e

ń

rozci

ą

gaj

ą

cych,

ś

ciskaj

ą

cych i

ś

cinaj

ą

cych stosuje si

ę

wzór

'

t

S

F

k

≤

=

τ

Obliczeniow

ą

grubo

ść

spoiny a (rys. 2a) przyjmuje si

ę

w zale

ż

no

ś

ci od wysoko

ś

ci spoiny

h

h

h

a

o

7

,

0

45

cos

≈

⋅

=

(1.2)

W poł

ą

czeniach, w których h = g, przyjmuje si

ę

a

≈

0,7g, przy czym grubo

ść

spoiny

a zaokr

ą

gla si

ę

do całych milimetrów (z niedomiarem). Nale

ż

y równie

ż

zachowa

ć

warunek: 3 mm

≤

a

≤

15 mm.

Jako długo

ść

obliczeniow

ą

spoiny przyjmuje si

ę

całkowit

ą

długo

ść

spoin,

przenosz

ą

c

ą

obci

ąż

enie, np. wg rys. 2a: l=2l

1

, wg rys. 2b: l = 2(2l

1

+ b

n

). W spoinach

pachwinowych na jeden krater przyjmuje si

ę

1,5a, st

ą

d długo

ść

rzeczywista spoiny wynosi

l

rz

= l + 3a.

Zespół Szkół Nr 1 im. Jana Kilińskiego w Pabianicach

Przedmiot: Proces projektowania cz

ęś

ci maszyn

3

W poł

ą

czeniach, w których wyst

ę

puj

ą

tylko szwy wzdłu

ż

ne lub tylko poprzeczne,

mo

ż

na przeci

ą

gn

ąć

szwy poza naro

ż

a (gdy jest to mo

ż

liwe konstrukcyjnie) na długo

ść

≥

2a, pomijaj

ą

c t

ę

długo

ść

przy obliczeniach (np. rys. 2a).

Wymiary spoin pachwinowych.

Rys. 2.

Zaleca si

ę

, aby długo

ść

spoin no

ś

nych w szwach wzdłu

ż

nych wynosiła 10a < l < 60a przy

l

min

= 40 mm.

Według PN-EN 22553:1997 i PN-EN ISO 4063:2002 na rysunkach podaje si

ę

długo

ść

spoin bez kraterów ko

ń

cowych, w zwi

ą

zku z tym ustalanie długo

ś

ci rzeczywistej

l

rz

jest konieczne tylko w przypadku, gdy długo

ść

spoiny wraz z kraterami wpływa

decyduj

ą

co na wymiary spawanych elementów.

W poł

ą

czeniach nakładkowych (rys. 2b) przekrój nakładek ustala si

ę

przy

zało

ż

eniu równej wytrzymało

ś

ci wszystkich elementów poł

ą

czenia. Gdy w poł

ą

czeniu

stosuje si

ę

tylko spoin

ę

pachwinow

ą

, nale

ż

y przyjmowa

ć

g

n

≥

0,60 przy nakładkach

dwustronnych oraz g

n

≥

1,1g — przy jednostronnych. Je

ż

eli pasy s

ą

poł

ą

czone spoin

ą

czołow

ą

i jednocze

ś

nie stosuje si

ę

nakładki poł

ą

czone spoin

ą

pachwinow

ą

, to wówczas

g

n

= (0,3÷0, 5)g przy nakładkach dwustronnych i g

n

= (0,7÷1)g — przy jednostronnych.

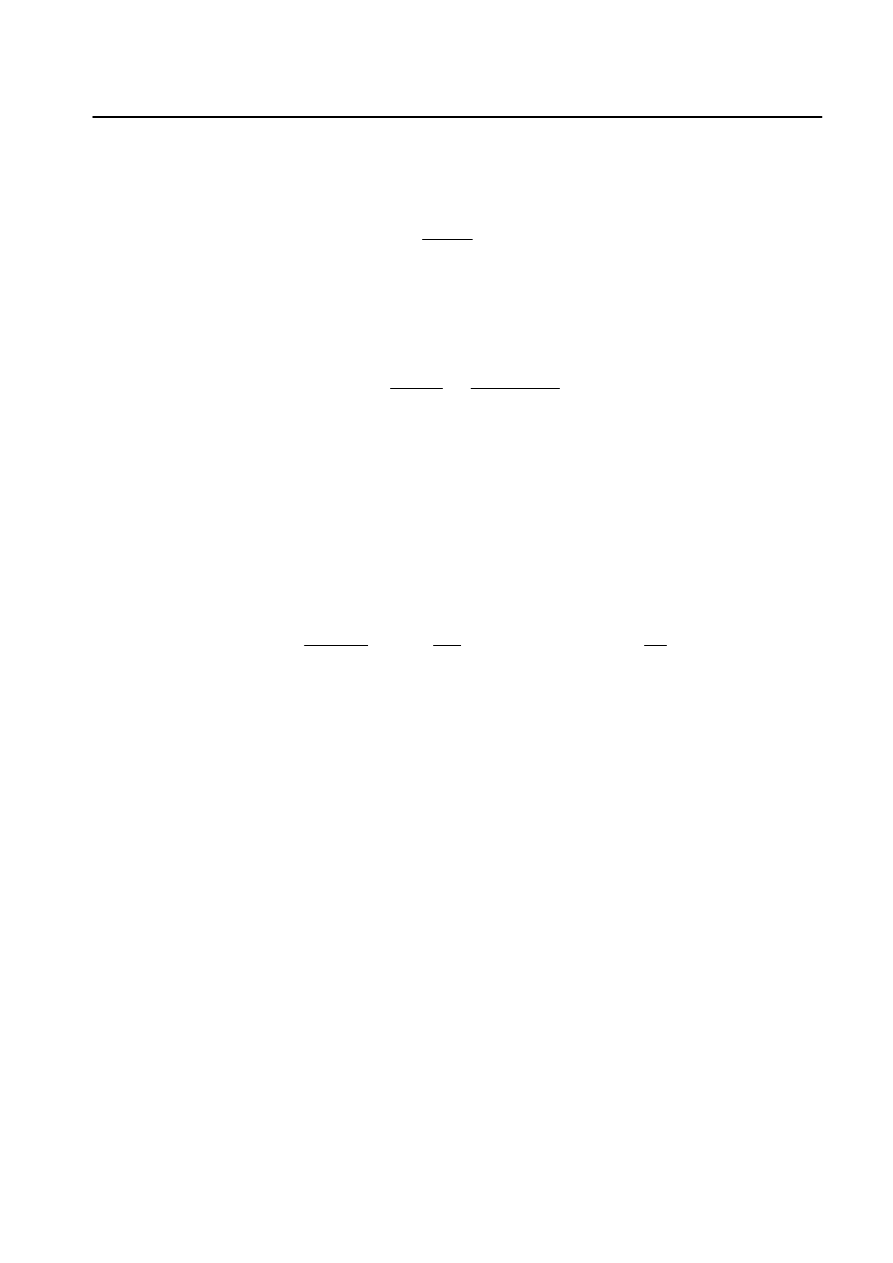
Zespół Szkół Nr 1 im. Jana Kilińskiego w Pabianicach

Przedmiot: Proces projektowania cz

ęś

ci maszyn

4

Gdy spoina pachwinowa jest obci

ąż

ona momentem zginaj

ą

cym (rys. 2c), jej wytrzymało

ść

obliczamy umownie z zale

ż

no

ś

ci

'

g

x

g

g

k

W

M

≤

=

τ

gdzie: W

x

— wska

ź

nik wytrzymało

ś

ci przekroju spoiny

6

7

,

0

6

2

2

b

h

l

a

W

x

⋅

≈

⋅

=

Odr

ę

bny przypadek stanowi

ą

poł

ą

czenia spawane, w których spoiny musz

ą

by

ć

wykonane niesymetrycznie wzgl

ę

dem linii działania siły, odpowiadaj

ą

cej linii

ś

rodków

ci

ęż

ko

ś

ci spawanej cz

ęś

ci (np. k

ą

townika). Zakłada si

ę

wówczas,

ż

e w spoinach le

żą

cych

po obu stronach linii działania siły powinny by

ć

jednakowe napr

ęż

enia. Na podstawie

warunków równowagi momentów sił działaj

ą

cych na obie spoiny (rys. 2d) mo

ż

na łatwo

ustali

ć

obci

ąż

enie poszczególnych szwów

b

e

F

b

e

b

F

F

2

1

1

⋅

=

−

=

oraz

b

e

F

F

1

2

⋅

=