PRĘTY ZAKRZYWIONE

Pręt zakrzywiony – gdy oś pręta jest krzywą (pręty zakrzywione płasko i przestrzennie).

pręty słabo zakrzywione

r/h > 5

, przyjmujemy wzory jak dla prętów prostych,

pręty silnie zakrzywione

r/h < 5.

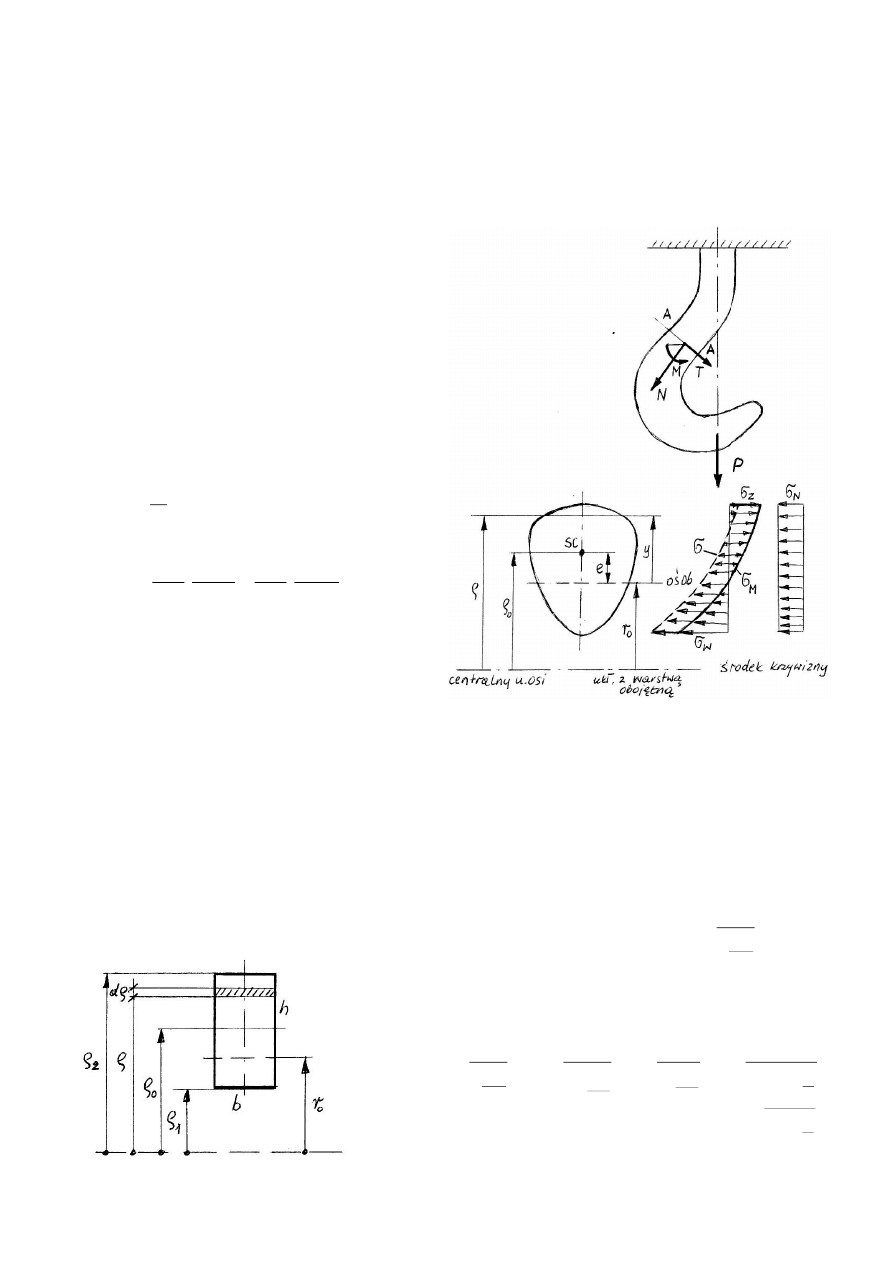
Omówimy stan naprężenia w prętach silnie zakrzywionych.
W przekroju poprzecznym wystąpią N,M i T (T- pominiemy).

Zakładamy podobnie jak dla prętów

prostych:
-

płaskie przekroje,

-

odległości w kierunku promieniowym nie

zmieniają się,
- naciski w kierunku



są pomijalne.

Rozpatrując element klinowy pręta –
warunki:
geometryczne, fizyczne i równowagi
otrzymamy wyrażenia na naprężenia.

1.

Działa tylko siła rozciągająca N:

F

N

N





-

rozkład równomierny

2. Zginanie momentem M:







0

0

r

e

F

M

y

r

y

e

F

M

M













F e

–

moment statyczny wzgl. osi oboj.

3.

Równoczesne działanie N i M:

r

M

k

N













UWAGA !

Siły z założenia są

przykładane w środku przekroju,
M

odnosimy również do środka

ciężkości przekroju.

Gdy przekrój ma dwie osie symetrii



w



>



z



WYZNACZENIE PROMIENIA WARSTWY OBOJĘTNEJ

ogólnie





F

dF

F

r



0

np. dla prostokąta

2

2

ln

ln

0

0

1

2

0

2

1

h

h

h

h

d

b

h

b

dF

F

r

F





































dF=bd



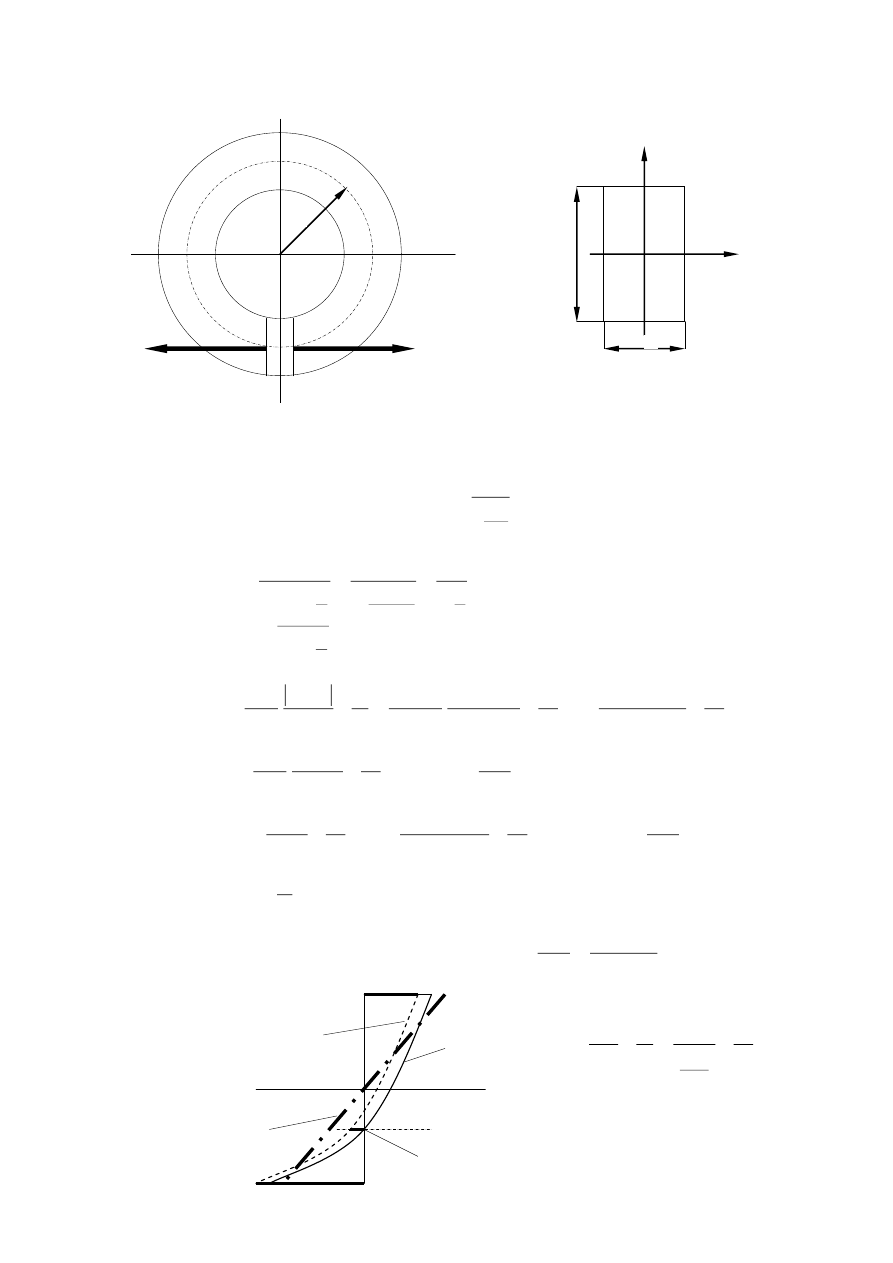
Przykład. Ustalić wartości siły dopuszczalnej P przykładanej do pręta zakrzywionego o
przekroju prostokątnym. Naprężenie dopuszczalne k=140 MPa, b=5 cm, h=8 cm,



0

=20 cm.

M

g

=P 2



0

N=P -

rozciąganie

Wyznaczamy położenie osi obojętnej:





F

dF

F

r



0

dla prostokąta

cm

h

h

h

r

o

73

,

19

3

2

ln

8

4

20

4

20

ln

8

2

2

ln

0

0





















e=



0

-r

0

=20-19,73=0,27 cm

Naprężenia

P

P

bh

P

e

h

b

P

F

N

r

e

F

M

g

888

,

0

40

1

16

27

,

0

40

73

,

3

40

16

16

73

,

19

2

0

0







































































2

1

1

0

1

888

,

0

cm

N

P

bh

P

r

e

F

M

g





















































2

2

634

,

0

40

1

24

27

,

0

40

27

,

4

40

2

cm

N

P

P

bh

P

e

F

r

P



 

P

F

P

025

,

0

0









k

P





89

,

0

1



 

N

k

P

15730

10

89

,

0

10

140

89

,

0

4

6











gdy P = P

dop

to:

licząc naprężenia jak dla pręta prostego



1

=140 MPa













bh

P

bh

P

F

N

W

M

g

6

2

2

0







2

=-99 MPa



c

=114,1 MPa



0

=3,9 MPa



r

=121,8 MPa

oś obojętna

zginanie
proste



2

=-99 MPa



N

+



g



g



0

=3,9 MPa



1

=140 MPa





P

h

b

y

z