Zadanie.

Maszynopis liczący 35 stron dano do przepisywania trzem różnym osobom a następnie sprawdzono liczbę
błędów popełnionych przez te osoby na każdej stronie maszynopisu. Wyniki przedstawia tablica:

Liczba błędów na stronie

maszynopis 1

maszynopis 2

maszynopis 3

0

3

4

1

1

4

10

3

2

6

8

4

3

9

5

5

4

6

4

8

5

4

3

10

6

3

1

4

razem stron:

35

35

35

Co można powiedzieć o pracy trzech osób przepisujących maszynopis? Która z nich najlepiej wykonała
zadanie?
Po wykonaniu niezbędnych obliczeń uzyskano następujące wielkości miar tendencji centralnej, rozrzutu i
asymetrii:

Miara

x

S

x

Me

Do

Q

1

Q

3

V

Sx

W

s

maszynopis1

3

1,67

3

3

2

4

0,558

0

maszynopis2

2,23

1,46

2

1

1

3

0,655

0,84

maszynopis3

3,77

1,59

4

5

3

5

0,422

-0,77

Interpretacja wyników:

Przeciętna liczba błędów była najmniejsza w przypadku maszynopisu 2 (średnio 2,23 błędu na stronę)

zaś największa w przypadku maszynopisu 3 (średnio 3,77 błędu na stronę).

W przypadku maszynopisu 1 na połowie stron były co najwyżej 3 błędy, na 1/4 stron – co najwyżej 2

błędy a na 3/4 stron – co najwyżej 4 błędy. W maszynopisie 2 – 50% stron zawierało nie więcej niż 2
błędy, 25% nie więcej niż 1 błąd a 75% nie więcej niż 3 błędy. W przypadku maszynopisu 3 – na połowie
stron były co najwyżej 4 błędy, na 1/4 stron – nie więcej niż 3 błędy zaś na 3/4 stron nie więcej niż 5
błędów.

W maszynopisie 1 najczęściej na stronie były 3 błędy, w maszynopisie 2 – 1 błąd zaś w maszynopisie

3 – 5 błędów.

Zróżnicowanie liczby błędów mierzone odchyleniem standardowym było najmniejsze w przypadku

maszynopisu 3 i stanowiło 42,2% średniej, zaś największe w przypadku maszynopisu 2, gdzie stanowiło
65,5% średniej arytmetycznej.

Szereg obrazujący liczbę błędów na stronach maszynopisu 1 był symetryczny czyli

x

=Me=Do.

W przypadku szeregu dla maszynopisu 2 zaobserwowano występowanie asymetrii dodatniej

(prawostronnej) o dużej sile. Oznacza to, że najczęściej spotykana liczba błędów na stronie była niższa od
przeciętnej.

Szereg nr 3 cechowała silna asymetria ujemna (lewostronna), co oznacza, że na większości stron

zaobserwowano liczbę błędów wyższą od przeciętnej.

Wniosek: najlepiej wykonała pracę osoba przepisująca maszynopis 2.

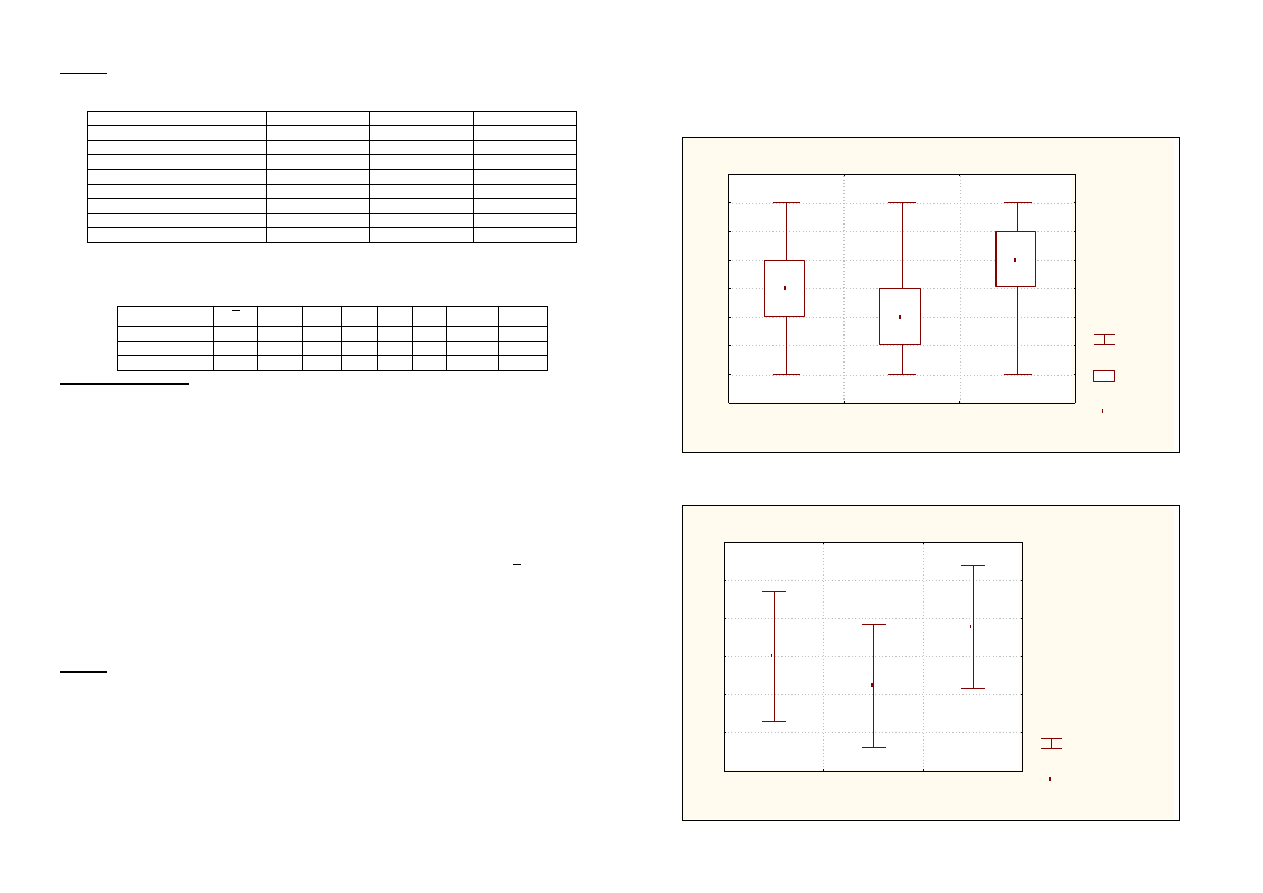
Otrzymane wyniki można zilustrować za pomocą tzw. wykresów pudełkowych (ramkowych; typu

„pudełko z wąsami” – ang. box-and-whisker), które w schematyczny sposób przedstawiają zakresy
wybranych zmiennych oraz statystyki opisowe (średnia, mediana, kwartyle, odchylenie standardowe) i
wartości nietypowe.

Wykres pudełkowy ma kształt prostokąta z dołączonymi po bokach odcinkami. Może być

umieszczony zarówno w pionie jak i w poziomie. Równolegle do boku pudełka i wąsów biegnie skala
przedstawiająca zakres wartości danej cechy.

W klasycznym wykresie pudełkowym punktem centralnym jest mediana, boki prostokąta (prostopadłe

do skali) wyznaczone są przez wartości pierwszego i trzeciego kwartyla, a końce wąsów wskazują
odpowiednio największą i najmniejszą wartość cechy. Taki wykres przedstawiony jest poniżej. Boki i

poprzeczka prostokąta dzielą całą populację na cztery części, z których każda zawiera po 25% wszystkich
elementów. Proporcje poszczególnych części pudełka i wąsów umożliwiają także przeprowadzenie
analizy dotyczącej asymetrii badanej cechy – dla maszynopisu 1 – rozkład jest symetryczny, dla
maszynopisu 2 – dłuższy prawy wąs wskazuje na asymetrię prawostronną, zaś dla maszynopisu 3 –
dłuższy lewy wąs – na asymetrię lewostronną.

M

a

k

s

M

in

7

5

%

2

5

%

M

e

d

ia

n

a

W

y

k

re

s

ra

m

k

o

w

y

M

a

s

z

y

n

o

p

is

Liczba

błędów

-1

0

1

2

3

4

5

6

7

M

1

M

2

M

3

Poniższy wykres, z kolei, przedstawia wartości średniej liczby błędów dla poszczególnych

maszynopisów oraz wielkości odchyleń standardowych. Łatwo zauważyć, że przeciętna liczba błędów jest
najmniejsza w maszynopisie 2.

Ś

re

d

n

ia

+

O

d

c

h

.s

td

Ś

re

d

n

ia

-O

d

c

h

.s

td

Ś

re

d

n

ia

W

y

k

re

s

ra

m

k

o

w

y

M

a

s

z

y

n

o

p

is

Liczba

błędów

0

1

2

3

4

5

6

M

1

M

2

M

3