BIOFIZYKA – egzamin – sesja zimowa – część 1
ZADANIA RACHUNKOWE
1. Ślimak pokonuje drogę 3cm w 3 minuty. Podaj prędkość w
s
m
.
s
m
,
s
m
,
t
s
V
s
s
t
m
,
cm
s
4
10
67
1
180
03
0
180
60
3
min
3
03
0
3
−
⋅
=
=
=
=
⋅
=
=
=
=
2. Oblicz prędkość
V
cząsteczek gazu doskonałego, mając dane: ciśnienie
hPa
p 1000
=
i gęstość
3
2
,
1
m
kg
=
ρ
.
=
=
⋅
=
⋅
=
=
⇒
=
⇒
⋅
⋅
=
=
=
=
s
m
s
m
m
kg
s
m
kg
m
kg
Pa
V
p
V
p
V
V
p
Pa
hPa
p
m
kg
2
2
3
2
3
2
2
3
250000
2
,
1
100000
3
3
3
3
:
/
3
1
100000
1000
2
,
1
ρ
ρ
ρ
ρ
ρ
3. Oblicz temperaturę T dla gazu doskonałego, mając dane:
J
E
k
21
10
657
,
1
−
⋅
=
oraz
1
23
10
022
,
6
−
⋅
⋅
=
mol
N
A
.
K
K
J
J
K
J
J
T
k
E
T
T
k
E
K
J
mol
K
mol
J
N
R
k
k
k
A
05
,
80
10
14
,
4
10
314
,
3
10
38
,
1
3
10
657
,
1
2
3
2
2
3
10
38
,
1
10
022
,
6
31
,
8
23
21
23
21
23
1
23
=
⋅
⋅
=
⋅
⋅
⋅
⋅
=
=
⇒
⋅
=
⋅
=
⋅
⋅
⋅
=
=
−
−
−
−
−
−
4. Oblicz liczbę moli gazu doskonałego w przemianie izobarycznej, mając dane:
J
U
7479
=
∆
,
C
T
°
=
∆
300
,
K
mol
J
R
⋅
=
31
,
8
.
mole
K
K
mol
J
J
T
C
U
n
K
C
T
K
mol
J
K
mol
J
R
i
C
T
C
n
U
V
V
V
2
300
465
,
12
7479
300
300
465
,
12
31
,
8
2
3
2
=
⋅
⋅
=
∆
⋅
∆
=
=
°
=
∆
⋅
=
⋅
⋅
=
⋅
=
∆
⋅
⋅
=
∆
5. Oblicz parametr kappa
χ
dla 3 moli gazu 1 atomowego.
3
5
3
2
3
2
=
+
=
+
=
i
i
χ

6. Oblicz pracę wykonaną przez 2 mole gazu dwuatomowego w przemianie izobarycznej, wiedząc, że
K
T
60
=
∆
i
hPa
p 1000
=
.
(
)
m
N
J
J
m
m
N
V
p
W
m
dm
hPa
K
K
mol
dm
hPa
mole
p
T
R
n
V
1
1
1
2
,
997
009972
,
0
100000
009972
,
0
972
,
9
1000
60
1
,
83
2
3
2
3
3
3
⋅
=
−
=
⋅
−
=
∆
⋅
−
=
=
=
⋅
⋅
⋅
⋅
=
∆
⋅
⋅
=
∆
7. Entropia układu w stanie końcowym jest 3 razy większa od entropii układu w stanie początkowym. Oblicz
prawdopodobieństwo termodynamiczne stanu końcowego, jeżeli dla stanu początkowego wynosi
200
.
8000000
8000000
ln
ln
200
ln
ln
200
ln
3
ln
:
/
200
ln
3
ln
200
ln
ln
3
3
=
=
=
⋅
=
⋅
⋅
=
⋅
⋅
=
⋅
=
=
W
W
W
W
k
k
W
k
k
S
W
k
S
S
S
p
p
p
k
8. Oblicz zmianę entalpii dla 3 moli gazu doskonałego ogrzewanego w przemianie izobarycznej od
temperatury
C
°
127
do
K
450 . Gaz ten jest gazem dwuatomowym.
J
K
K
mol
J
mole
H
H
T
R
i
n
T
C
n
Q
R
i
C
K
K
K
T
T
T
K
T
K
T
p
p
75
,
4362
50
31
,
8
2
2
5
3
2
2
2
2
50
400
450
450
400
273
127
0
1
1
0
=
⋅
⋅
⋅
+
⋅
=
∆
∆
=
∆
⋅
⋅
+
⋅
=
∆
⋅
⋅
=
∆
⋅
+
=
=
−
=
−
=
∆
=
=
+
=
9. Oblicz potencjał chemiczny składnika, jeżeli zmiana ilości moli tego składnika o
mola
25
,
0
spowodowała
zmianę jego entalpii swobodnej o
J
05
,
0
.
mol
J
mola
J
n
G
n
n
G
2
,
0
25
,
0
05
,
0
:
/
=
=
∆
∆
=
∆
∆
⋅
=
∆
µ
µ
µ
10. Oblicz zmianę entalpii swobodnej spowodowanej przeniesieniem
mola
005
,
0
jonów dwuwartościowych
w polu elektrycznym o napięciu kV
10
. Stała Faradaya wynosi
mol
C
96500
.
J
mola
mol
C
V
n
F
z
W
G
i
el
i
9650000
005
,
0
96500
2
10000
=
⋅
⋅
⋅
=
∆
⋅
⋅
⋅
=
∆
=
∆
ϕ
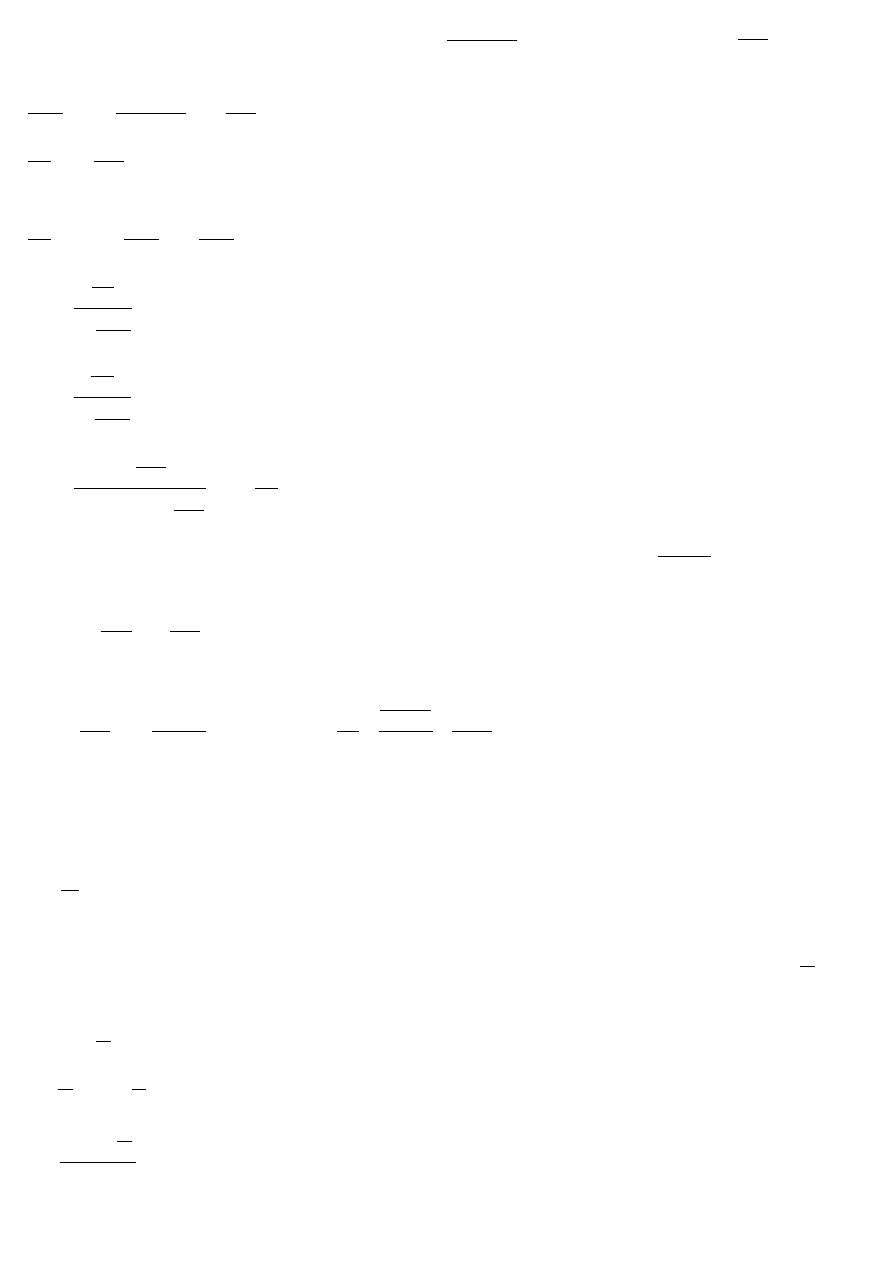
11. Oblicz stałą dyfuzji, jeżeli przy gradiencie stężeń
m
dm
mol
3
/
02
,
0
, szybkość dyfuzji wynosi
s
mol
3
,
0
.
Powierzchnia, przez którą substancja dyfunduje wynosi
2
2cm .
( )
1
/
:
/
0002
,
0
2
3
,
0
20
/
02
,
0
2
2
4
3
−
⋅
∆
∆
⋅
∆
∆
=
−
∆
∆
⋅
∆
∆
⋅
⋅
−
=
∆
∆
=
=
=
∆
∆
=
=
∆
∆
x
C
S
t
n
D
x
C
S
x
C
S
D
t
n
m
cm
S
s
mol
t
n
m
mol
m
dm
mol
x
C
m
m
m
m
s
m
m
mol
m
s
mol
D
x
C
S
t
n
D
m
2
4
2
75
20
0002
,
0
3
,
0
−
=
⋅
−
=
∆
∆
⋅
∆
∆
−
=
12. Oblicz ciśnienie osmotyczne, mając dane:
3
/
05
,
0
dm
mol
C
m
=
,
C
T
°
=
57
,
K
mol
J
R
⋅
=
31
,
8
.
=
⋅
=
⋅
=
=
⋅
⋅
⋅
=
Π
⋅
⋅
=
Π
=
=
=
+
=
Pa
s
m
kg
m
s
m
kg
m
J
K
K
mol
J
m
mol
T
R
C
m
mol
dm
mol
C
K
T
m
m
K
2
3
2
2
3
3
3
3
137115
330
31
,
8
50
50
05
,
0
330
273
57
13. Oblicz pracę W , mając dane: wartość ładunku
nC
q 30
=
oraz napięcie elektryczne
kV
U 100
=
.
J
J
C
V
W
q
U
W
q
W
U
V
kV
U
C
nC
q
3
4
9
5
5
9
10
3
10
30
10
30
10
10
100
10
30
30
−
−
−
−
⋅
=
⋅
=
⋅
⋅
=
⋅
=
⇒
=
=
=
⋅
=
=
14. Oblicz częstotliwość f fali mechanicznej, mając dane: jej długość
m
µ
λ
2
,
0
=
oraz prędkość
s
m
V 1200
=
.
(
)
1
9
6
3
6
10
6
10
2
,
0
10
2
,
1
1200
10
2
,
0
2
,
0
−
−
−
=
⋅
=
⋅
⋅
=
=
⇒
=
=
⋅
=
=
s
Hz
m
s
m
f
V
f
f
V
s
m
V
m
m
λ
λ
µ
λ
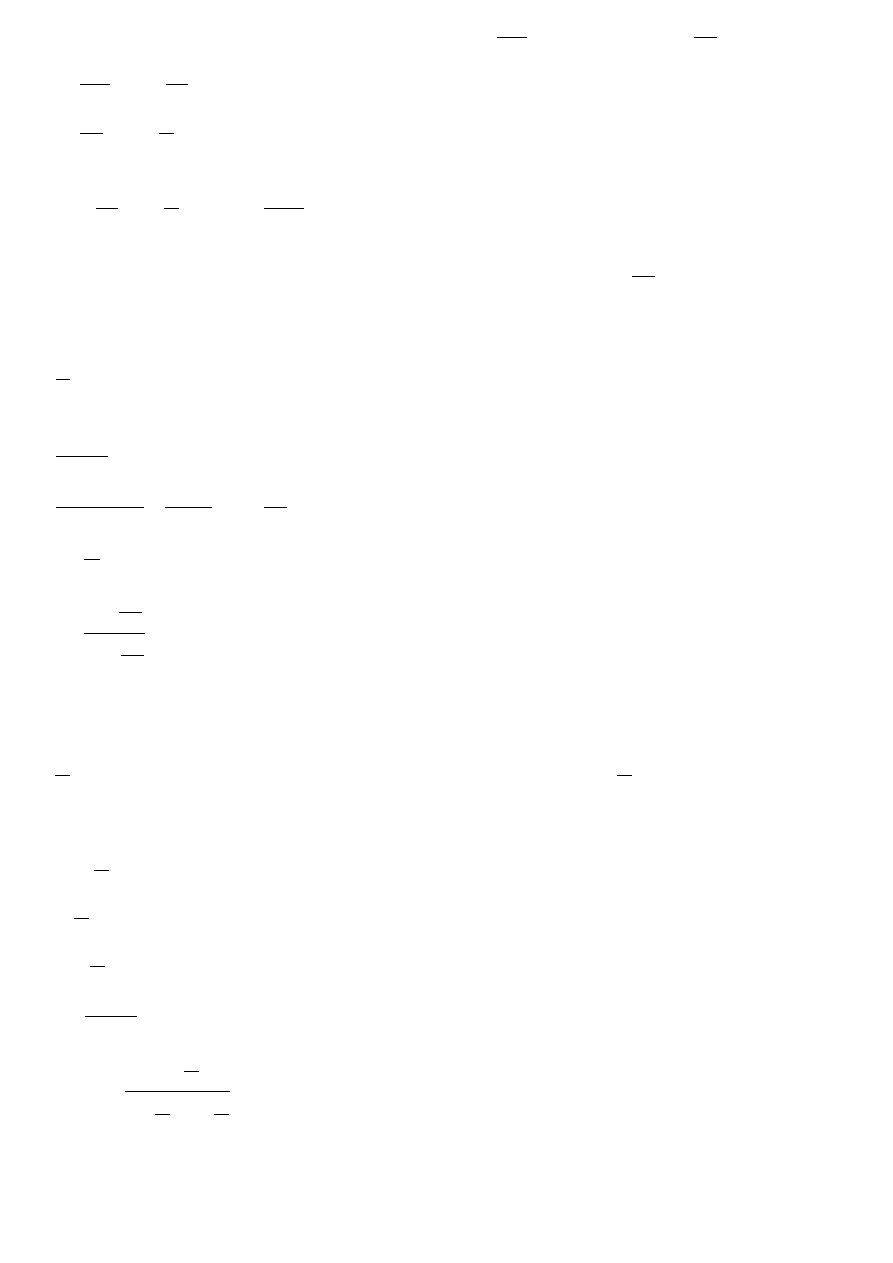
15. Oblicz opór akustyczny ośrodka, mając dane: gęstość
3
5
,
1
cm
g
=
ρ
oraz prędkość
s
km
V
5
,
1
=
.
s
m
kg
s
m
m
kg
Z
V
Z
s
m
s
km
V
m
kg
cm
g
⋅
=
⋅
=
⋅
=
=
=
=
=
2
3
3
3
2250000
1500
1500
1500
5
,
1
1500
5
,
1
ρ
ρ
16. Oblicz poziom natężenia dźwięku w odległości
m
100 od źródła dźwięku. Moc dźwięku to
mW
P
π
4
=
,
natomiast jego częstotliwość wynosi
Hz
f
100
=
. Natężenie wzorcowe to
2
12
0
10
m
W
I
−
=
.
(
)
B
L
B
L
B
m
W
m
W
L
B
I
I
L
m
W
m
W
m
W
I
R
P
I
R
S
S
P
I
m
R
W
mW
P
5
10
log
10
10
log
log
10
10
10
100
4
10
4
4
4
100
10
4
4
5
2
12
2
7
0
2
7
2
4
3
2
3
2
2
3
=
=
=
=
=
=
⋅
⋅
=
⋅
=
⋅
=
=
=
⋅
=
=
−
−
−
−
−
−
π
π
π
π
π
π
17. Fala akustyczna o częstości
Hz
1000
jest emitowana przez źródło dźwięku, które zbliża się z prędkością
s
m
144
w kierunku obserwatora. Fala rozchodzi się w powietrzu z prędkością
s
m
340
. Jaką częstotliwość
zarejestruje nieruchomy obserwator?
Hz
s
m
s
m
s
m
Hz
f
V
V
V
f
f
s
m
V
s
m
V
s
m
V
Hz
f
z
f
f
z
o
f
69
,
1734
144
340
340
1000
144
0
340
1000
0
0
=
−
⋅
=
−
⋅
=
=
=
=
=
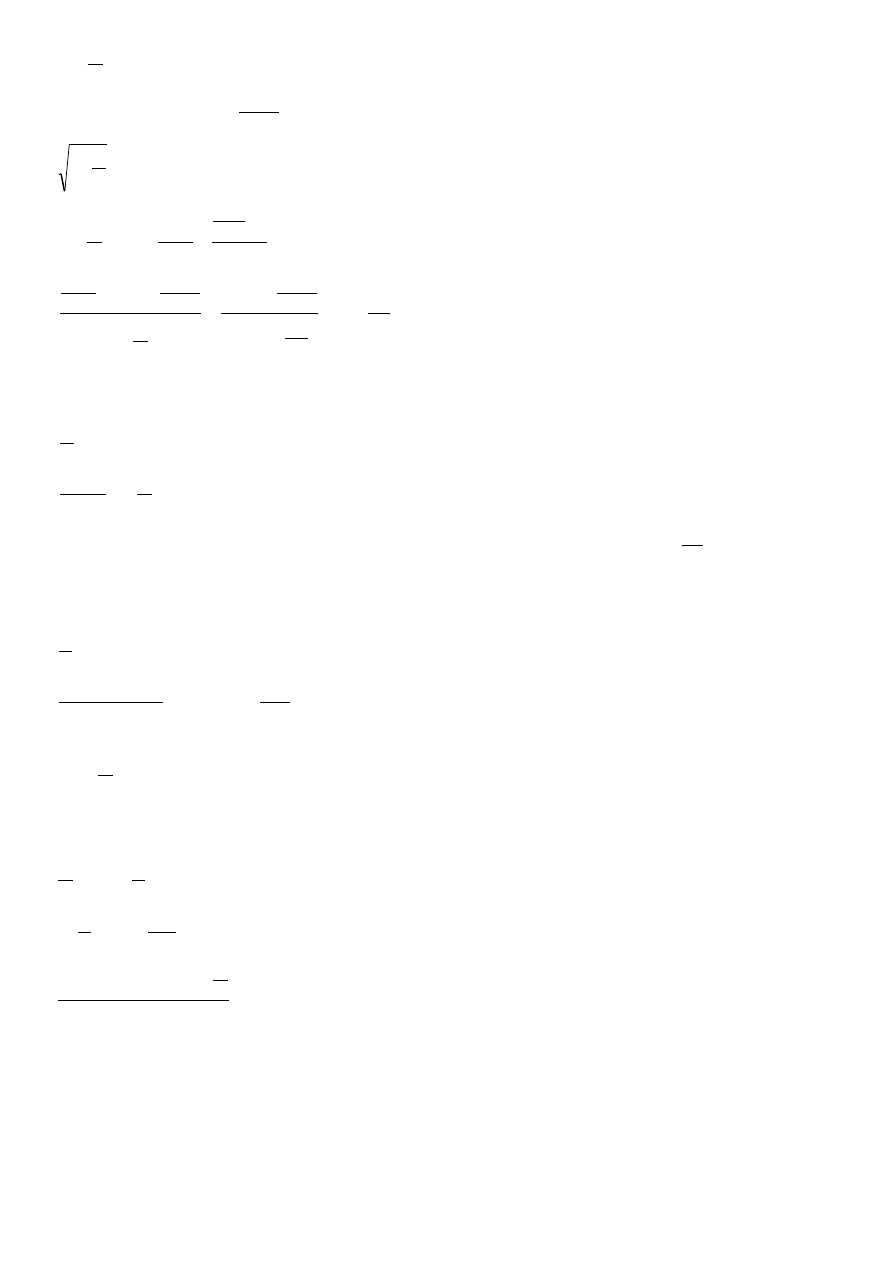
18. Jaka jest gęstość gazu dwuatomowego, w którym rozchodzi się fala akustyczna, której prędkość wynosi
s
m
V
340
=
. Ciśnienie gazu to
hPa
p 1013
=
.
2
2
2
2
2
101300
1013
V
p
i
i
V
p
p
V
p
V
s
m
kg
Pa
hPa
p
⋅
+
=
⋅
=
⇒
⋅
=
⋅
=
⋅
=
=
=
χ
ρ
ρ
χ
ρ
χ
3
2
2
2
2
2
23
,
1
115600
141820
340
101300
5
2
5
m
kg
s
m
s
m
kg
s
m
s
m
kg
=
⋅
=
⋅
⋅
+
=
ρ
19. Oblicz zdolność zbierającą soczewki o ogniskowej
cm
f
25
=
.
D
m
m
Z
f
Z
m
cm
f
4
1
4
25
,
0
1
1
25
,
0
25
=
=
=
=
=
=
Jednostką zdolności zbierającej (skupiającej) soczewki w układzie SI jest 1 dioptria
=
m
D
1
1
1
.
20. Oblicz pęd fotonu, mając podane: długość fali
m
µ
λ
3
,
0
=
oraz stałą Plancka
s
J
h
⋅
⋅
=
−
34
10
63
,
6
.
m
s
J
m
s
J
p
h
p
m
m
⋅
⋅
=
⋅
⋅
⋅
=
=
⋅
=
=
−
−
−
−
27
7
34
7
10
21
,
2
10
3
10
63
,
6
10
3
3
,
0
λ
µ
λ
21. Oblicz długość fali odpowiadającej fotonowi o energii
J
E
19
10
6575
,
1
−
⋅
=
.
m
J
s
m
s
J
E
c
h
c
h
E
c
f
f
c
f
h
E
s
J
h
s
m
c
7
19
8
34
34
8
10
12
10
6575
,
1
10
3
10
63
,
6
10
63
,
6
10
3
−
−
−
−
⋅
=
⋅
⋅
⋅
⋅
⋅
=
⋅
=
⇒
⋅
=
=
⇒
=
⋅
=
⋅
⋅
=
⋅
=
λ
λ
λ
λ
λ
22. Jądro atomowe o liczbie masowej
286
=
A
i liczbie atomowej
82
=
Z
uległo 3 razy przemianie
α
oraz 4
razy przemianie
−
β
. Ile będzie wynosić liczba masowa
( )
A oraz liczba atomowa
( )
Z po następujących
przemianach promieniotwórczych?
I przemiana
α
:
He
B
A
4
2
282
80
286
82
+
→
II przemiana
α
:
He
C
B
4
2
278
78
282
80
+
→
III przemiana
α
:
He
D
C
4
2
274
76
278
78
+
→
I przemiana
−
β
:
e
E
D
0
1
274
77
274
76
−
+
→
II przemiana
−
β
:
e
F
E
0
1
274
78
274
77
−
+
→
III przemiana
−
β
:
e
G
F
0
1
274
79
274
78
−
+
→
IV przemiana
−
β
:
e
H
G
0
1
274
80
274
79
−
+
→
Odpowiedź: Liczba masowa
274
=
A
, a liczba atomowa
80
=
Z
.
23. Oblicz stałą rozpadu, mając dane
ms
T
20
2
1
=
.
1
2
1
65
,
34
02
,
0
693
,
0
2
ln
02
,
0
20
−
=
=
=
=
s
s
T
s
ms
λ
λ
24. Jaka część z początkowej liczby jąder pozostanie po czasie
h
t 8
=
, gdy czas połowicznego rozpadu wynosi
h
T
2
2
1
=
?
0
4
0
2
1
0
16
1
2
4
2
8
2
N
N
N
h
h
T
t
n
N
N
n
⋅
=
=
=
=
=
=
Odpowiedź: Po czasie
h
t 8
=
pozostanie
16
1
początkowej liczby jąder.
25. Jak zmniejszy się natężenie promieniowania, jeżeli liniowy współczynnik osłabienia wynosi
1
25
−
=
m
µ
, a
warstwa pochłaniająca ma grubość
cm
x 20
=
?
(
)
(
)
88
,
148
12
0067166927
,
0
:
/
12
0067166927
,
0
1
:
/
12
0067166927
,
0
72
,
2
72
,
2
2
,
0
20
0
0
0
5
0
2
,
0
1
25
0
0
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
=
=
−
⋅
−
−
I
I
I
I
I
I
I
I
I
I
I
e
I
I
m
cm
x
m
m
x
µ
Odpowiedź: Natężenie promieniowania zmniejszy się 148,88 razy.
Wyszukiwarka
Podobne podstrony:
Biofizyka - egzamin - część 1, pytania rachunkowe i odpowiedzi
Biofizyka egzamin część 3 pytania rachunkowe i odpowiedzi
Biofizyka egzamin część 2 pytania rachunkowe i odpowiedzi
egzamin z chemii pytania plus odpowiedzi
Rachunkowosc egzamin - pytania bez odpowiedzi, rachunkowość
Biofizyka egzamin pytania teoretyczne
SBD pytania i same odpowiedzi, PJWSTK, 0sem, SBD, egzaminy
zadanie-z-zakresu-prawa-administracyjnego-na-egzamin-radcowski-31.08.2012-r , EGZAMIN RADCOWSKI - py
egzamin-radcowski--z-2011-r.---zadanie---prawo-karne, EGZAMIN RADCOWSKI - pytania, odpowiedzi, rozwi
Pytania egzaminacyjne Zarządzanie, Wykłady rachunkowość bankowość
www.wsb2.pl egzamin-finanse-pytania odpowiedz, Finanse przedsiębiorstwa wykłady
EGZAMIN USTNY- 3 PYTANIA, PDF i , RACHUNKOWOŚĆ I ANALIZA FINANSOWA
Biofizyka - Egzamin (Pytania), far, biofizyka, egzamin, materiały na ćwiczenia
egzamin z NOPu - pytania i odpowiedzi, EKONOMIA, Rok 2, Nauka o przedsiębiorstwie
Pytania na egzamin - biofizyka, far, biofizyka, egzamin, materiały na ćwiczenia
Materialy do egzaminu z LA, pytania i odpowiedzi stare
Przykładowe pytania egzaminacyjne Część I
więcej podobnych podstron