1

Automatyka i sterowanie

Część III

Zestaw ilustracji do wykładu „Automatyka i sterowanie”

kurs 10 godz. dla studiów magisterskich uzupełniających

opracował dr inż. Grzegorz Rogacki

2

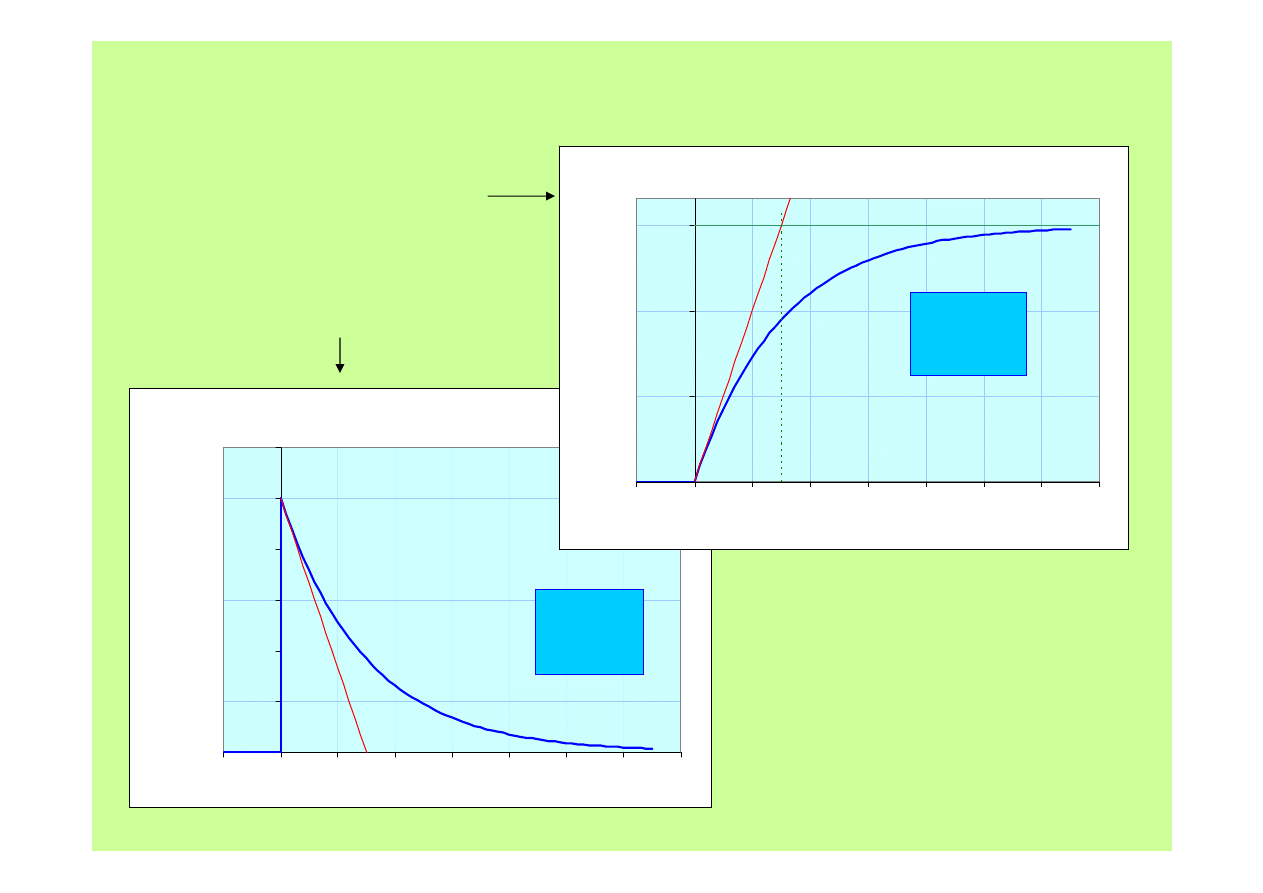
Odpowiedzi członu inercyjnego I-go rzędu

Skok 1(t)

0

0.1

0.2

0.3

0.4

0.5

0.6

-1

0

1

2

3

4

5

6

7

K = 0.75
T = 1.5

y(

t)

0

0.25

0.5

0.75

-1

0

1

2

3

4

5

6

7

K = 0.75
T = 1.5

y(

t)

Impuls Diraca

3

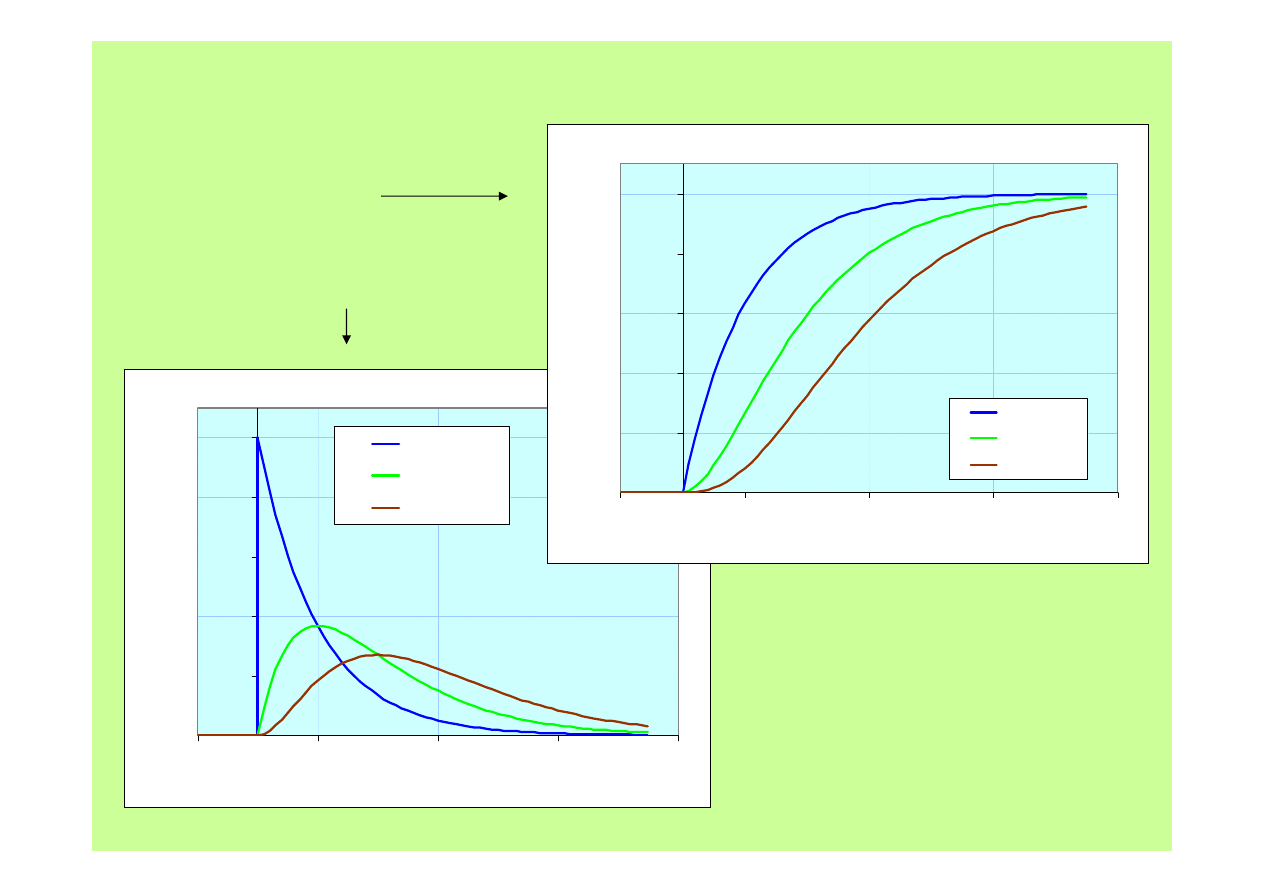
Odpowiedzi członów wyższych rzędów

0.0

0.2

0.4

0.6

0.8

1.0

-1

1

3

5

7

czas

I-szy rząd

II-gi

III-ci

0

0.2

0.4

0.6

0.8

1

-1

1

3

5

7

czas

I-szy rząd
II-gi
III-ci

Skok 1(t)

Impuls Diraca

4

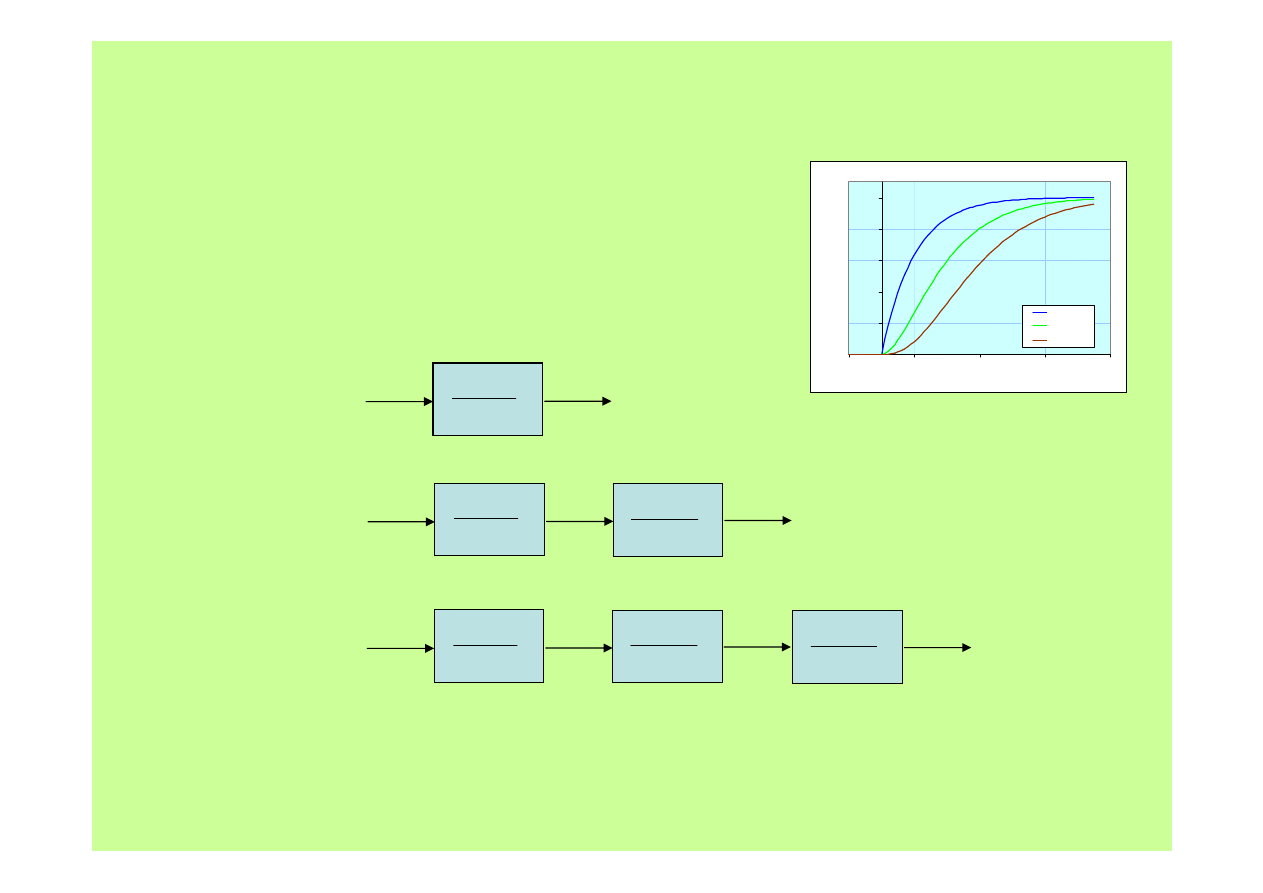
Obiekty złożone

0

0.2

0.4

0.6

0.8

1

-1

1

3

5

7

czas

I-szy rząd
II-gi
III-ci

X

Y

1

1

1

+

s

T

K

I-szy rząd

X

Y

Y

2

1

1

1

1

+

s

T

K

1

2

2

+

s

T

K

II-gi rząd

X

Y

Y

2

Y

3

1

1

1

1

+

s

T

K

1

2

2

+

s

T

K

1

3

3

+

s

T

K

III-ci rząd

5

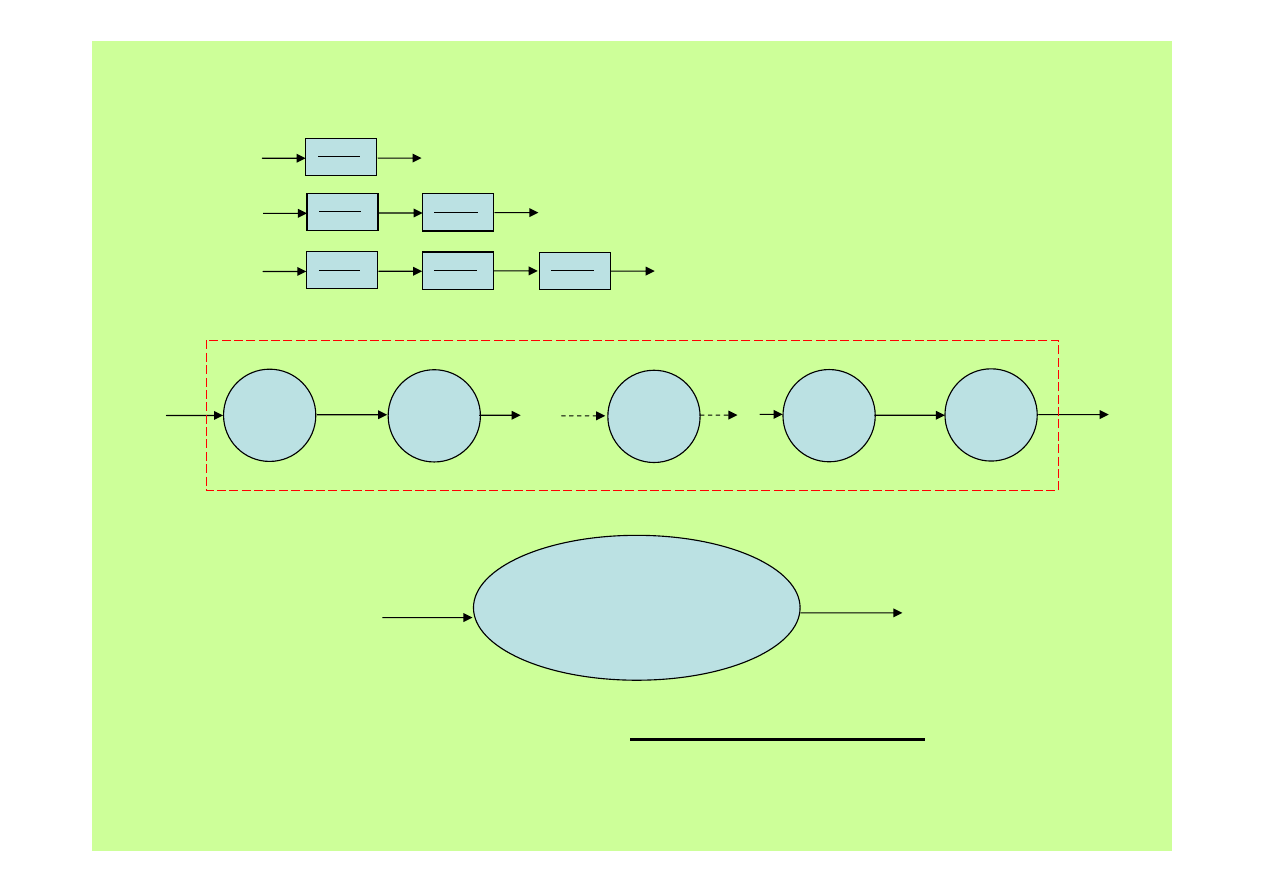
Obiekty złożone – układ szeregowy

X

Y

1

1

+

s

T

K

I-szy rząd

X

Y

1

1

1

+

s

T

K

1

2

+

s

T

K

Y

2

II-gi rząd

X

Y

1

1

1

+

s

T

K

1

2

+

s

T

K

Y

2

1

3

+

s

T

K

Y

3

III-ci rząd

G

1

G

2

G

i

G

N-1

G

N

Y

X

∏

=

N

i

i

G

1

Y

X

Transmitancja układu szeregowego bez oddziaływania wstecz jest iloczynem

transmitancji elementów tego szeregu.

6

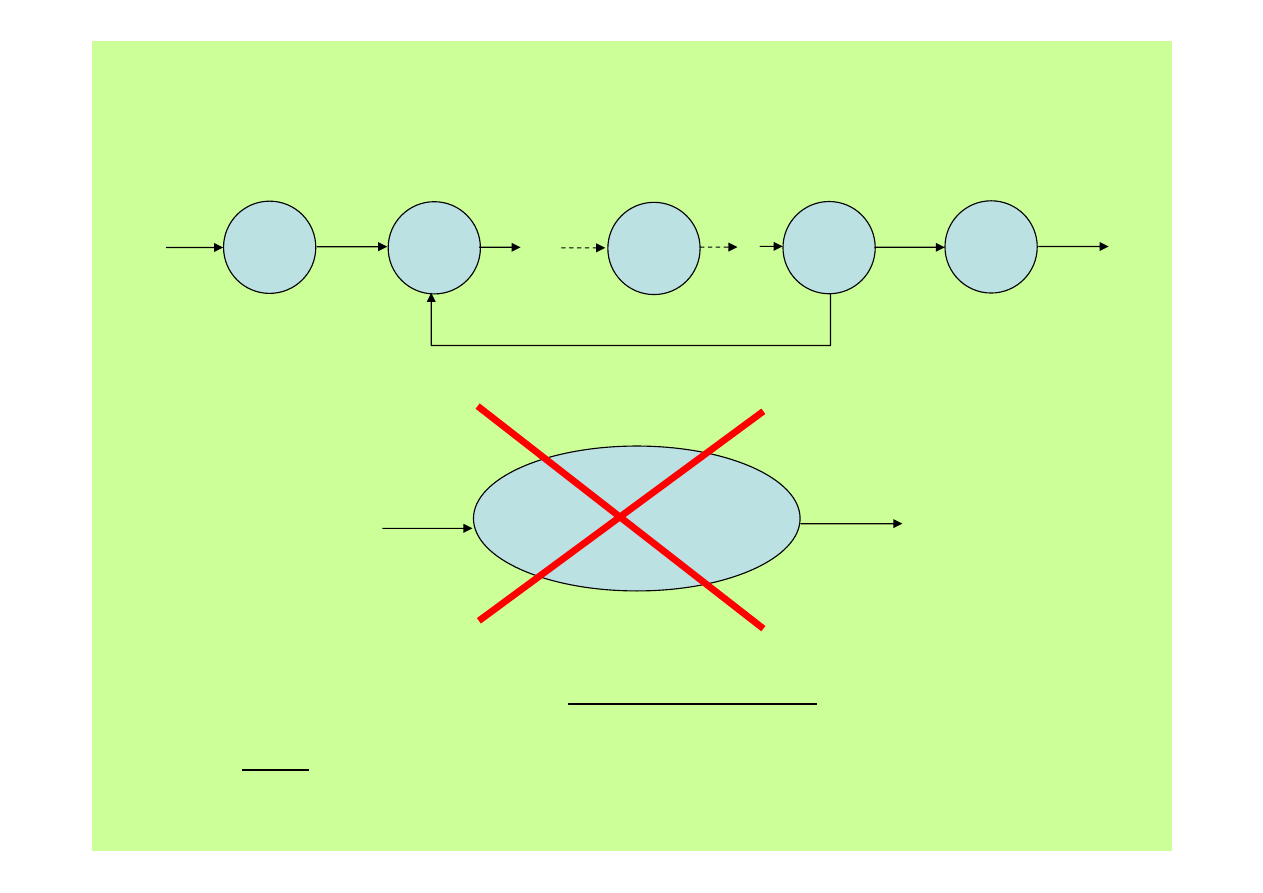
Obiekty złożone

G

1

G

2

G

i

G

N-1

G

N

Y

X

∏

=

N

i

i

G

1

Y

X

Jeśli w układzie występuje oddziaływanie wstecz to zagadnienie trzeba

analizować indywidualnie w zależności od natury tego oddziaływania i nie istnieje
żadna formuła na transmitancję.

szkoda!

7

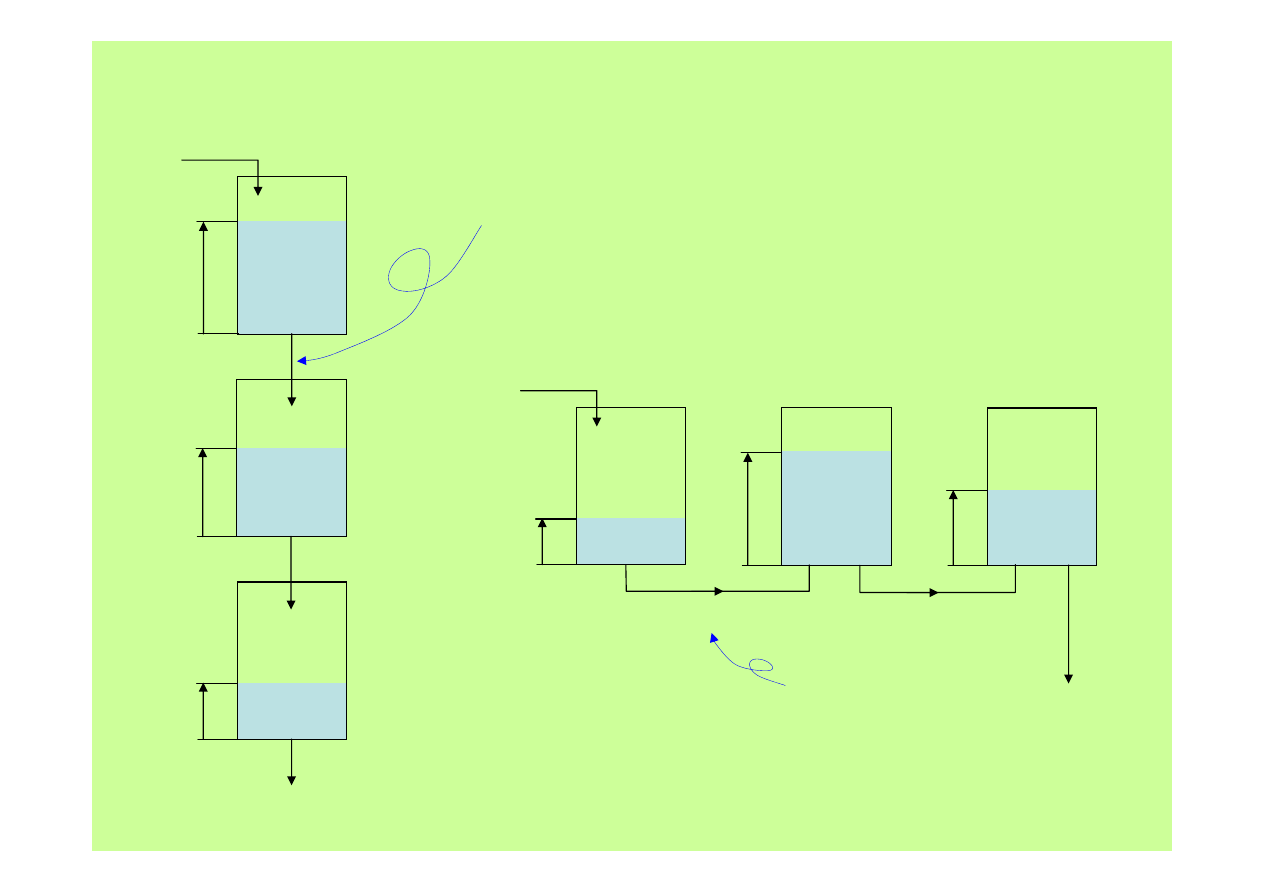
Obiekty złożone - przykład

Q

0

h

1

Q

1

Q

0

h

2

Q

2

Q

3

h

2

h

3

h

1

Q

2

Q

1

1

1

1

h

k

Q

=

(

)

2

1

12

1

h

h

k

Q

−

=

nie ma oddziaływania wst

ecz

jest oddzia

ływanie

wstecz

Q

3

h

3

8

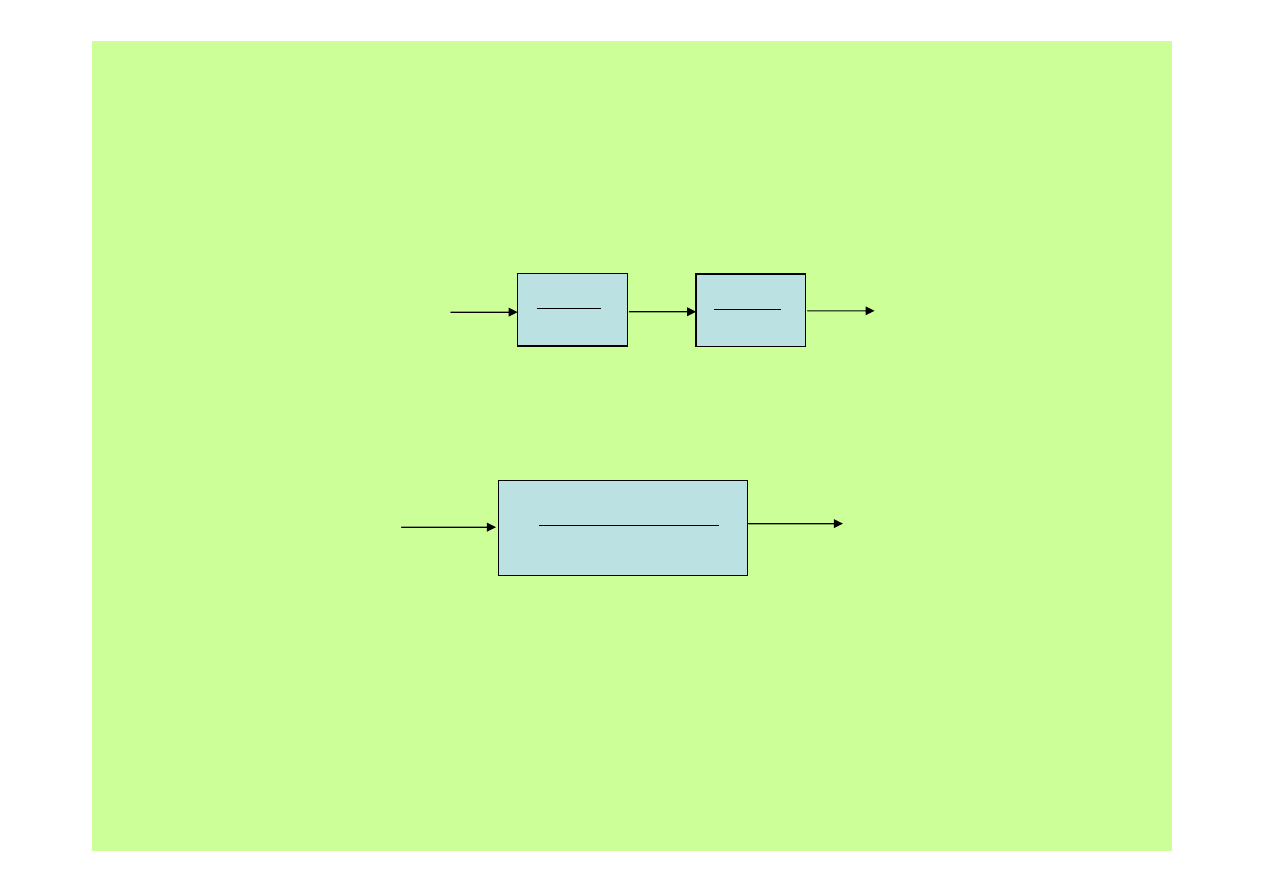
Człon inercyjny II- go rzędu

X

Y

Y

2

1

1

1

1

+

s

T

K

1

2

2

+

s

T

K

II-gi rząd

(

)(

)

1

1

2

1

+

+

s

T

s

T

K

Y

X

Człon inercyjny II-go rzędu ma dwie stałe czasowe (T

1

, T

2

)

i współczynnik wzmocnienia K.

9

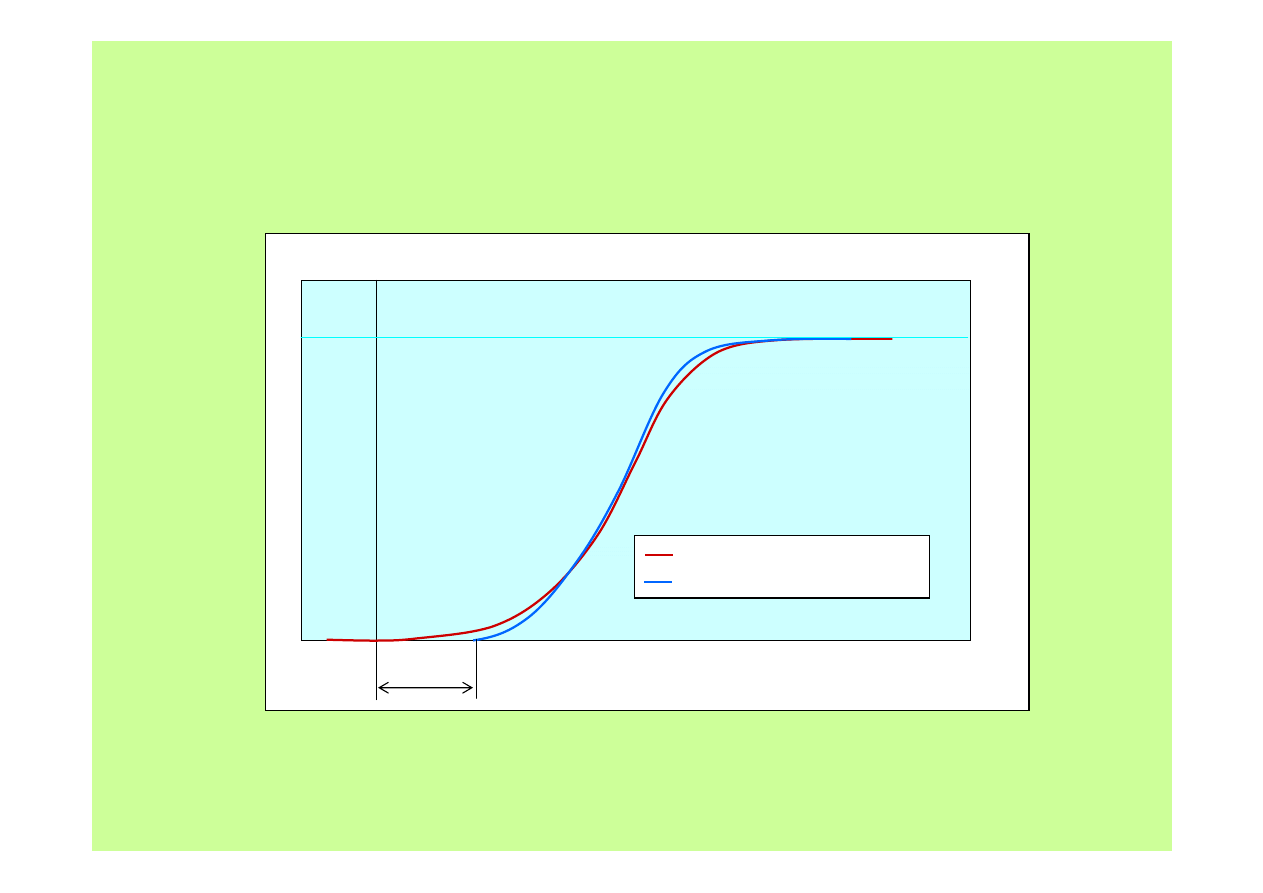
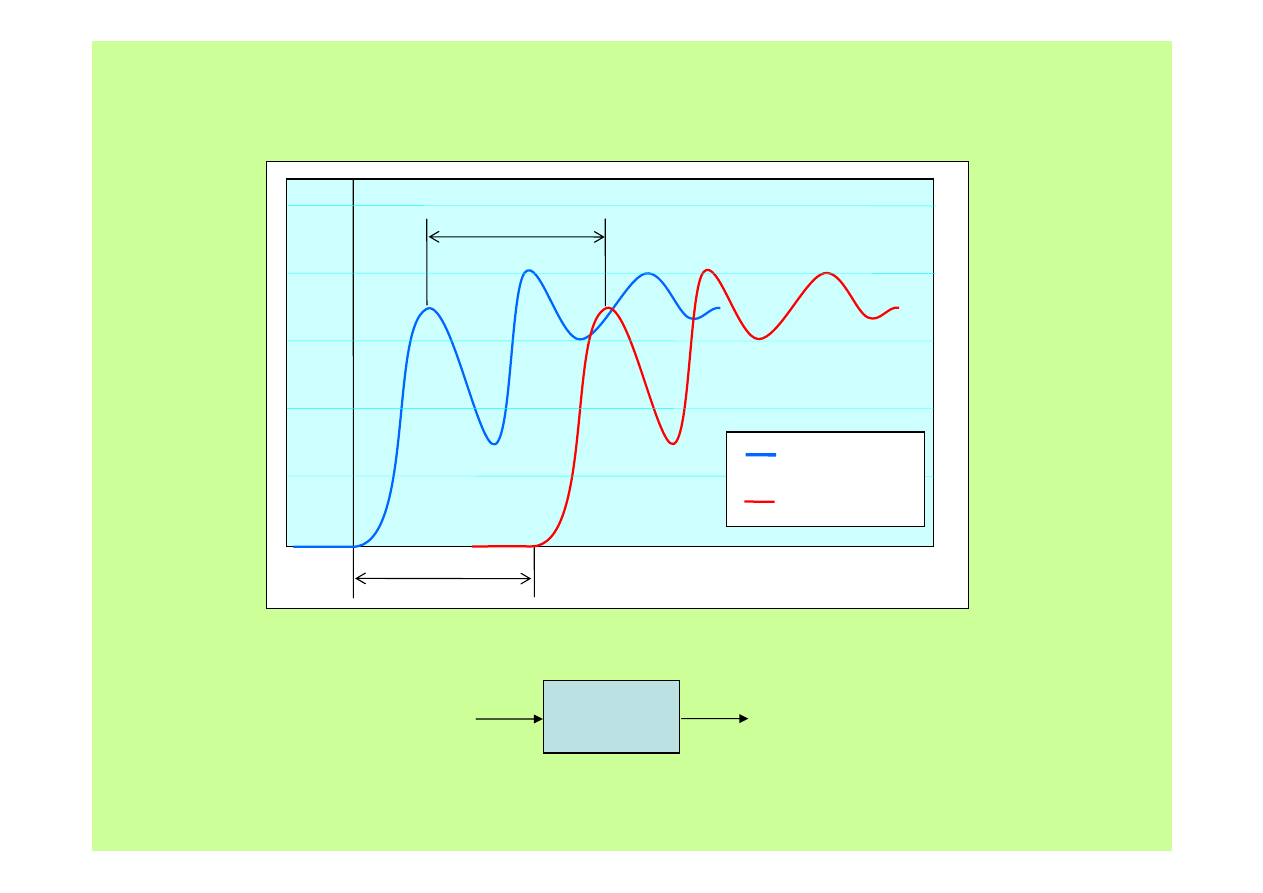
Odpowiedzi obiektów rzeczywistych

T

0

sygnał rzeczywisty
przybliżenie

czas

jak uwzględnić matematycznie opó

źnienie?

10

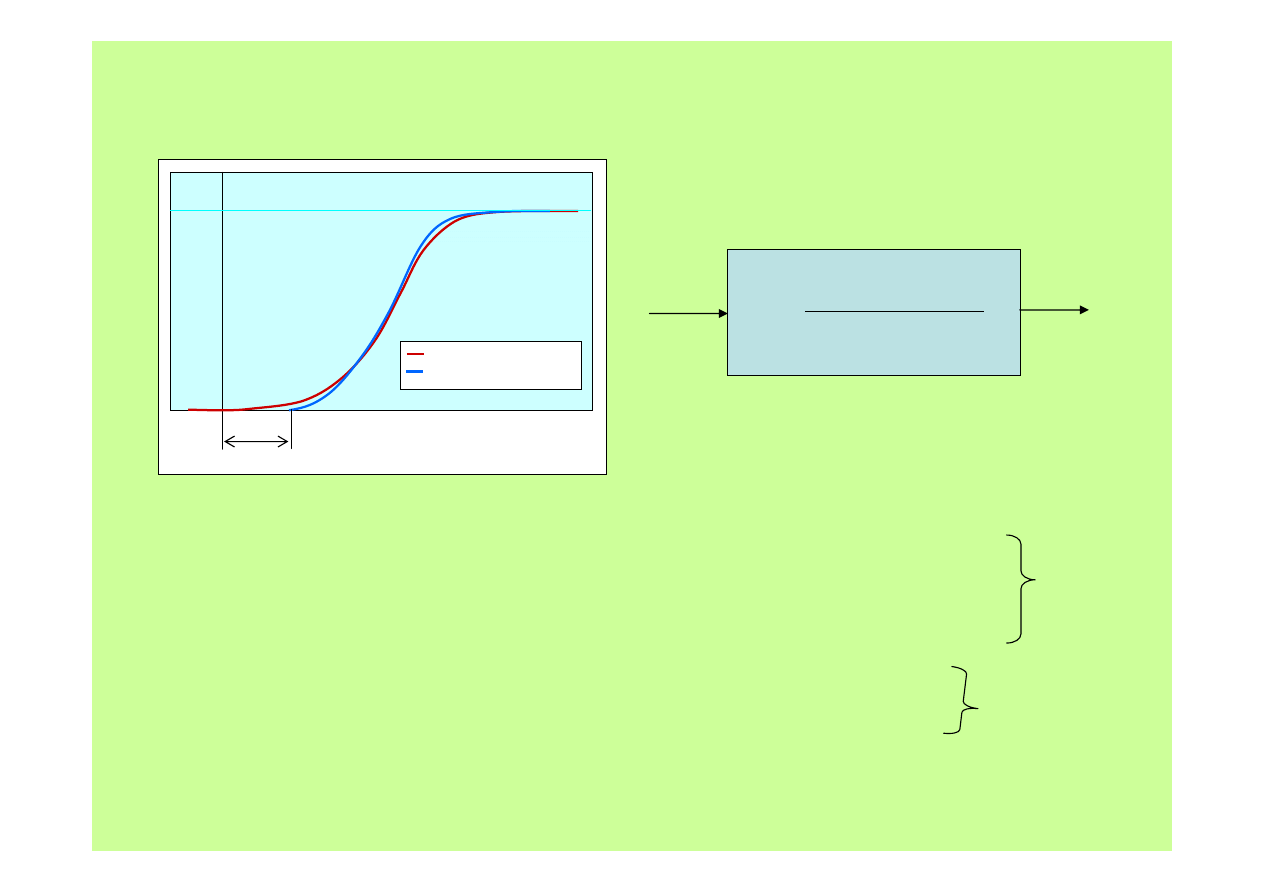
Człon opóźniający

T

0

czas

L

T

0

)

(t

f

y

=

)

(

0

T

t

f

y

−

=

X

Y

)

exp(

0

s

T

−

11

Odpowiedzi obiektów rzeczywistych

T

0

sygnał rzeczywisty
przybliżenie

czas

(

)(

)

1

1

)

exp(

2

1

0

+

+

−

s

T

s

T

s

T

K

Y

X

• W wielu przypadkach odpowiedź układu rzeczywistego daje się przybliżyć

odpowiedzią członu inercyjnego II-go rzędu z opóźnieniem.

• Do opisu dynamiki obiektu „wystarczą” wtedy trzy stałe czasowe: T

0

, T

1

, T

2

.

• Trzeba oczywiście umieć je wyznaczyć.
• Wyznaczanie stałych dla obiektów nazywamy

identyfikacją.

dob

rze

nie

dob

rze

12

Sterowanie, regulacja,

automatyka

(Process Control)

13

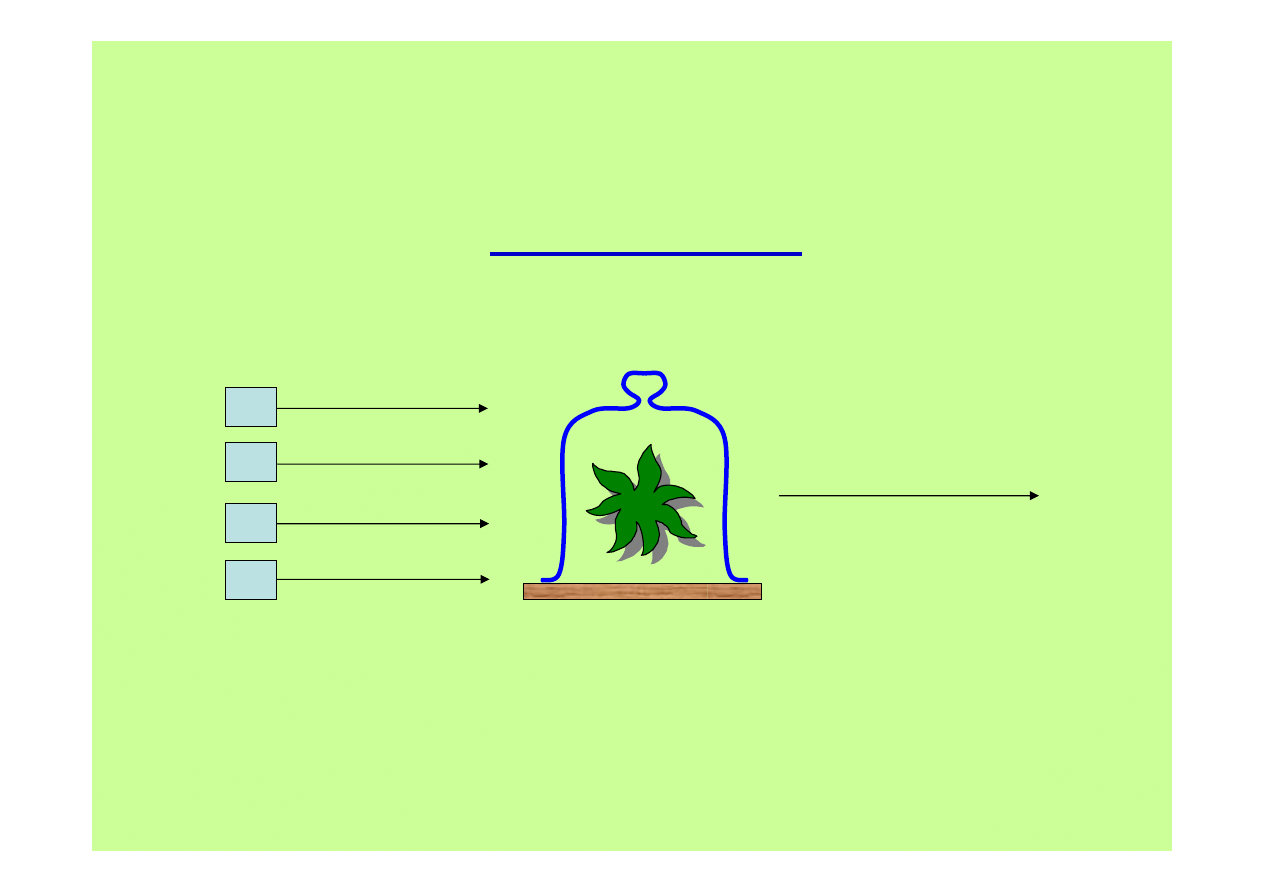
Strategie regulacji

A. Sterowanie w układzie otwartym

wilgotność

temperatura

oświetlenie

NPK

ϕ

R

C

R

°

L

R

X

R

zgodny z normą UE

14

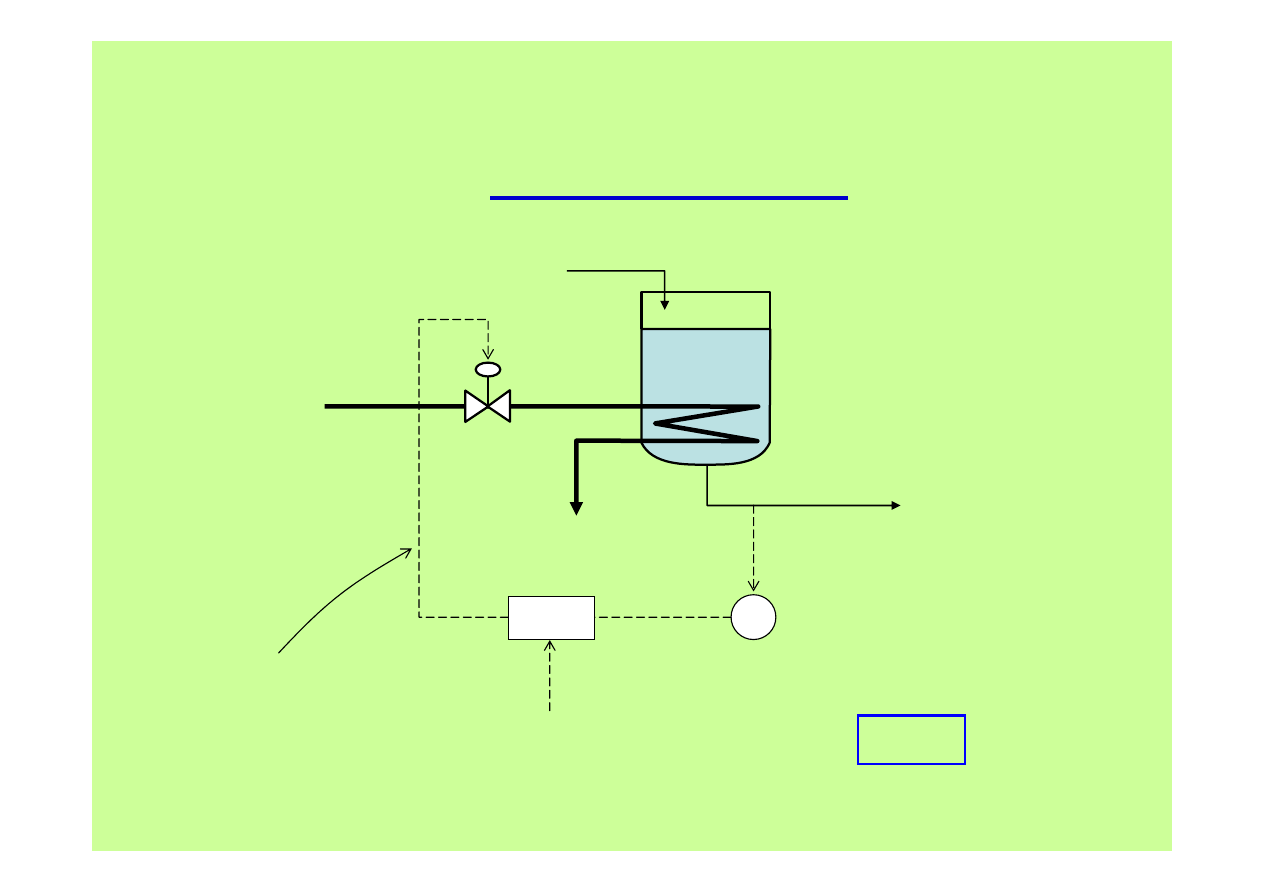
Strategie regulacji

B. Sterowanie w układzie zamkniętym

IN

Q

ϑ

,

OUT

ϑ

R

ϑ

z

ϑ

para
grzejna

z

out

ϑ

ϑ

−

to jest to

„słynne

”

sprzężen

ie zwrotn

e

Uchyb regulacji:

15

Strategie regulacji

A. Sterowanie w układzie otwartym

B. Sterowanie w układzie zamkniętym

Obie stra

tegie są

możliwe

niezależn

ie, czy re

gulacja j

est

ręczna c

zy autom

atyczna.

16

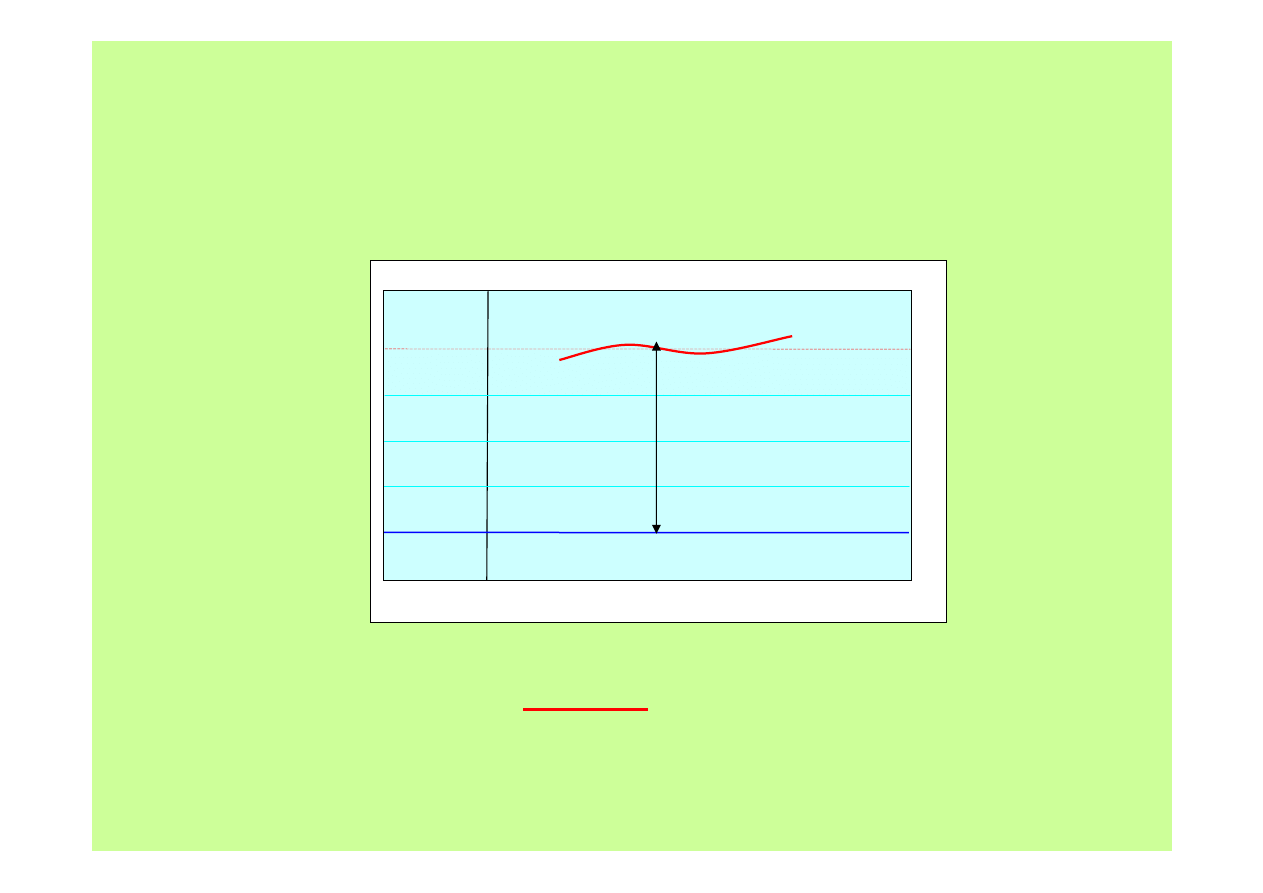
Regulacja – dobroć regulacji

Kiedy jest źle? Kiedy trzeba interweniować?

czas

36,6°C

42°

∆X

∆

X

uchyb

1. Gdy dany parametr

znacznie

odbiega od wartości zadanej.

17

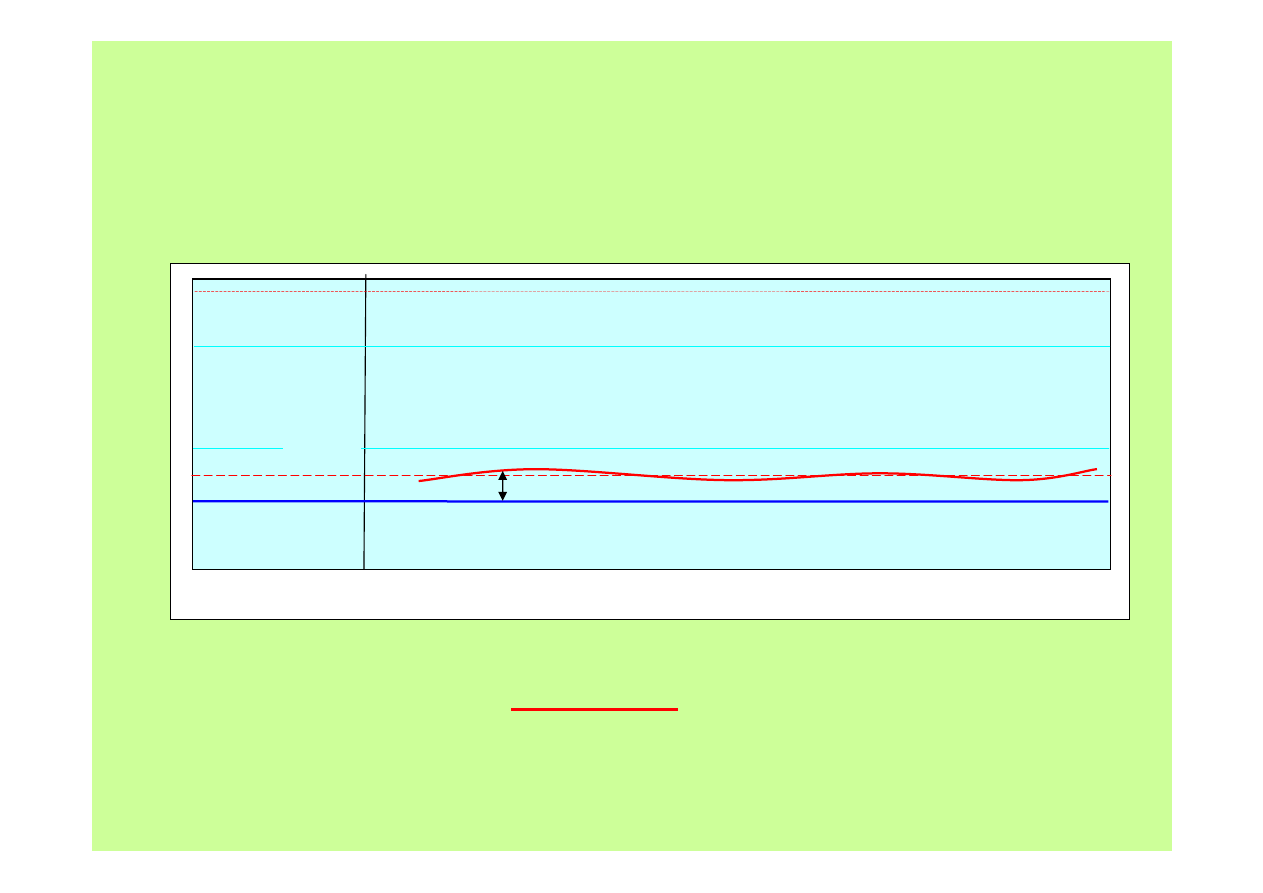
Regulacja – dobroć regulacji

Kiedy jest źle? Kiedy trzeba interweniować?

czas

36,6°C

42°

37,5°

∆X

∆

X

uchyb

2. Gdy dany parametr

chronicznie

odbiega od wartości zadanej

choć uchyb nie jest duży.

18

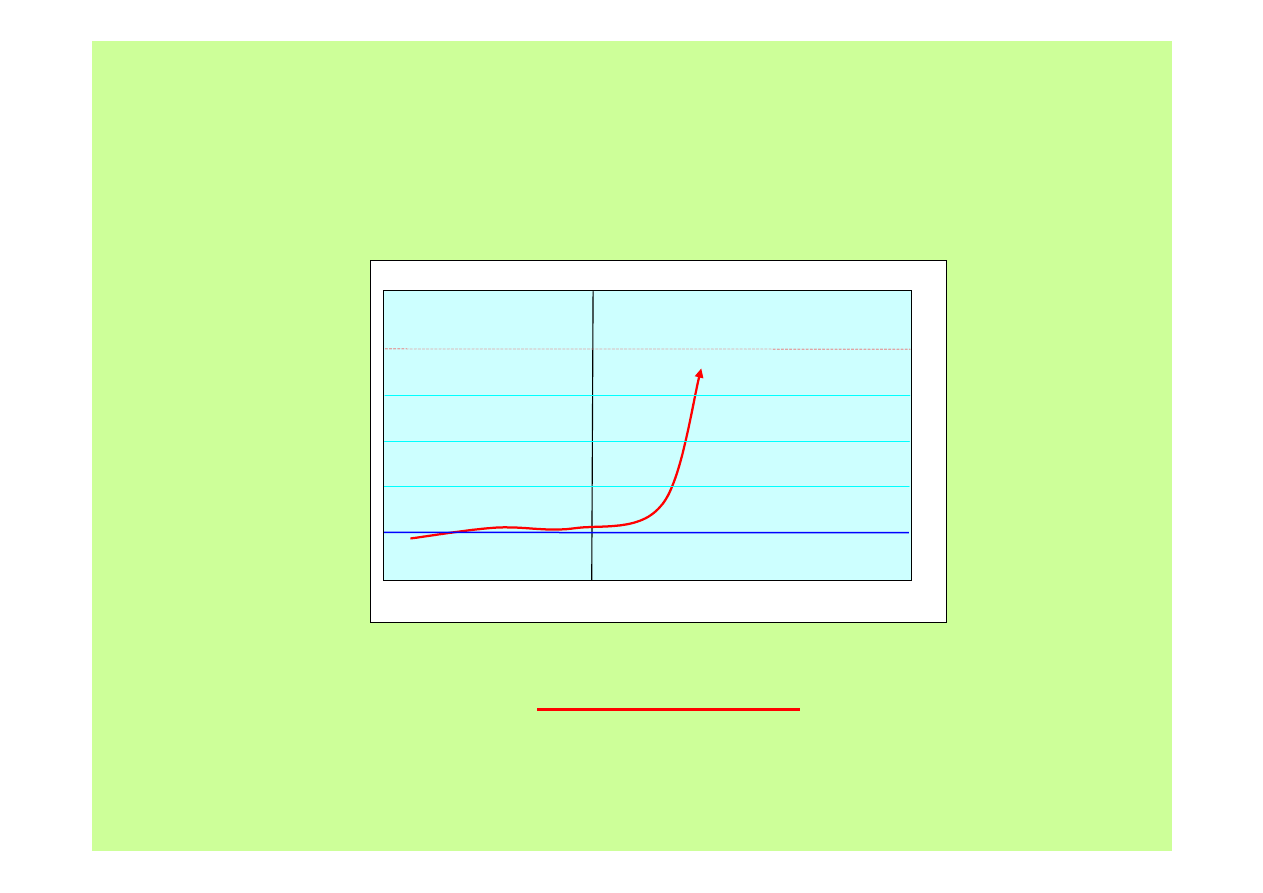
Regulacja – dobroć regulacji

Kiedy jest źle? Kiedy trzeba interweniować?

czas

36,6°C

42°

∆

X

uchyb

rośnie

3. Gdy dany parametr

gwałtownie ucieka

od wartości zadanej.

19

Metody regulacji

1. Gdy dany parametr znacznie odbiega od wartości zadanej.

2. Gdy dany parametr chronicznie odbiega od wartości zadanej.

3. Gdy dany parametr gwałtownie ucieka od wartości zadanej.

1. Współmiernie do uchybu.

2. Współmiernie do całki uchybu.

3. Współmiernie do pochodnej uchybu.

20

Metody regulacji

1. Współmiernie (proporcjonalnie) do uchybu.
2. Współmiernie do całki uchybu.
3. Współmiernie do pochodnej uchybu.

proporcja

proportio

P

całkowity

integer

I

różnica (pochodna)

differentia

D

nikt mni

e nie ucz

yl łaciny!

21

Metody regulacji

1. regulacja proporcjonalna

P

2. regulacja całkująca

I

3. regulacja różniczkująca

D

aha, r

egula

tor PI

D

mam

coś t

akieg

o

w mo

im Fe

rrari

Wszystkie

trzy metody

są ciągle m

ożliwe

niezależnie

, czy regulac

ja jest ręcz

na czy

automatyc

zna.

22

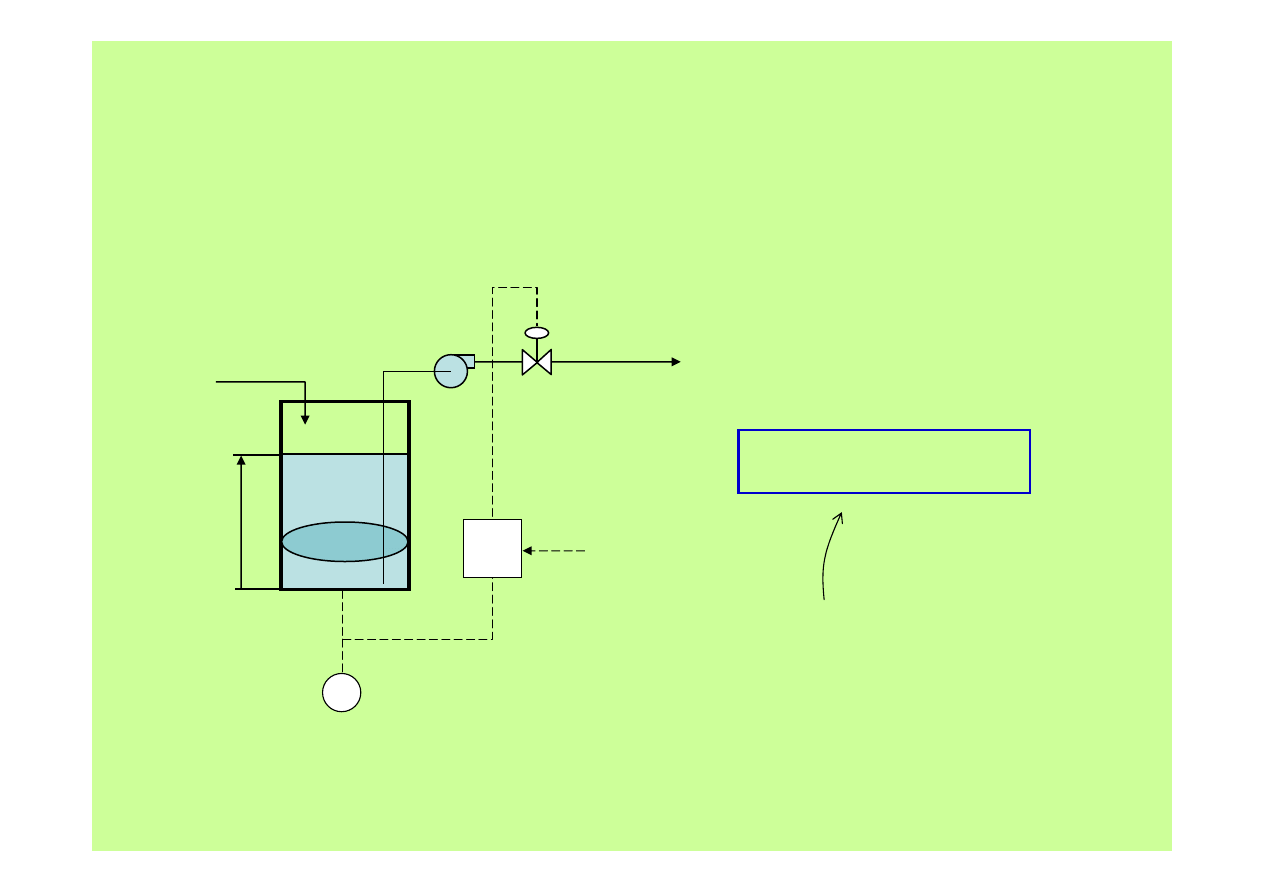
Metody regulacji

1. Regulacja proporcjonalna zbiornika magazynującego

Q

OUT

Q

IN

A

V

h

R

(

)

z

OUT

h

h

k

Q

−

⋅

=

h

h

z

matematyczny

zapis

działania regul

acji

proporcjonalnej

23

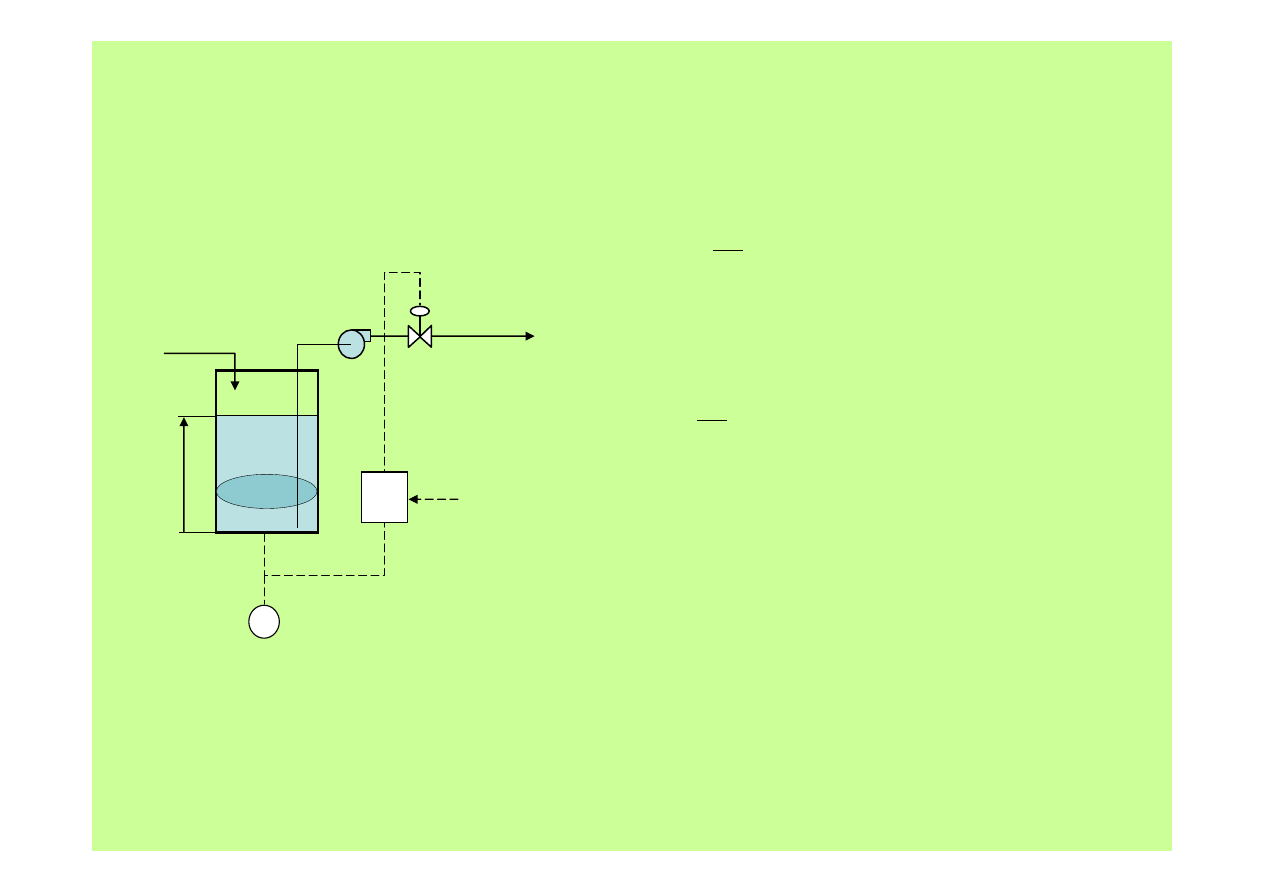
Metody regulacji

1. Regulacja proporcjonalna …

1. Bilans cieczy

OUT

IN

Q

Q

dt

dh

A

−

=

Q

OUT

Q

IN

h

A

V

h

R

2. Plus działanie regulatora

(

)

z

IN

h

h

k

Q

dt

dh

A

−

−

=

h

z

3. Definiujemy uchyb

∆

h -

uchyb

z

h

h

h

−

≡

∆

4. Zakładamy, że dla

t

= 0 układ był „w porządku” czyli

ciecz w zbiorniku była na poziomie zadanym

0

,

,

0

=

∆

=

=

h

h

h

t

z

24

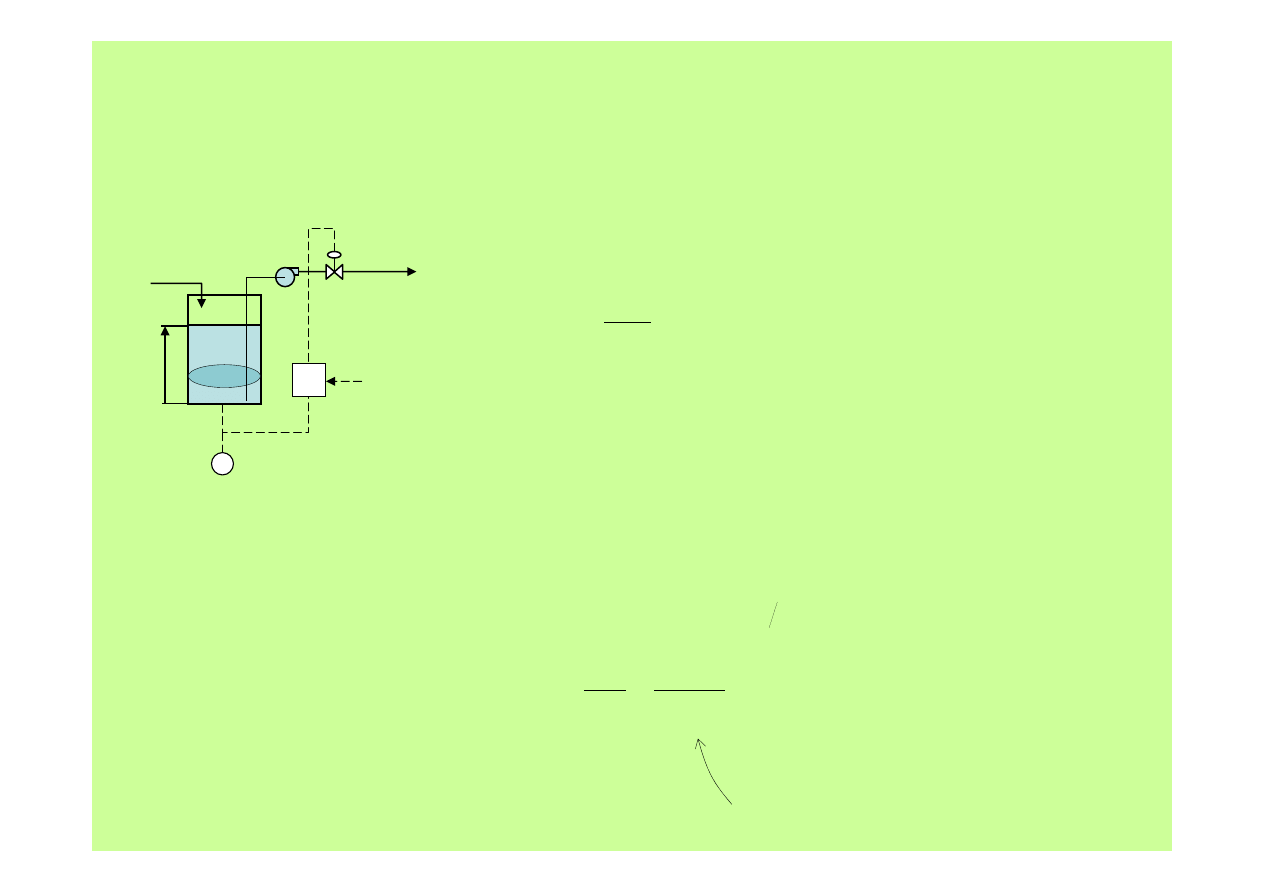
Metody regulacji

1. Regulacja proporcjonalna …

5. Wracamy do równania z punktu 2

Q

IN

A

V

Q

OUT

h

R

h

z

h

k

Q

dt

h

d

A

IN

∆

⋅

−

=

∆

0

,

0

=

∆

=

h

t

h

6. Stosujemy przekształcenia Laplace’a

h

k

Q

h

As

IN

∆

⋅

−

=

∆

7. Obliczamy stosunek

IN

Q

h

∆

k

As

Q

h

IN

+

=

∆

1

gdzieś ju

z to widz

ieliśmy

25

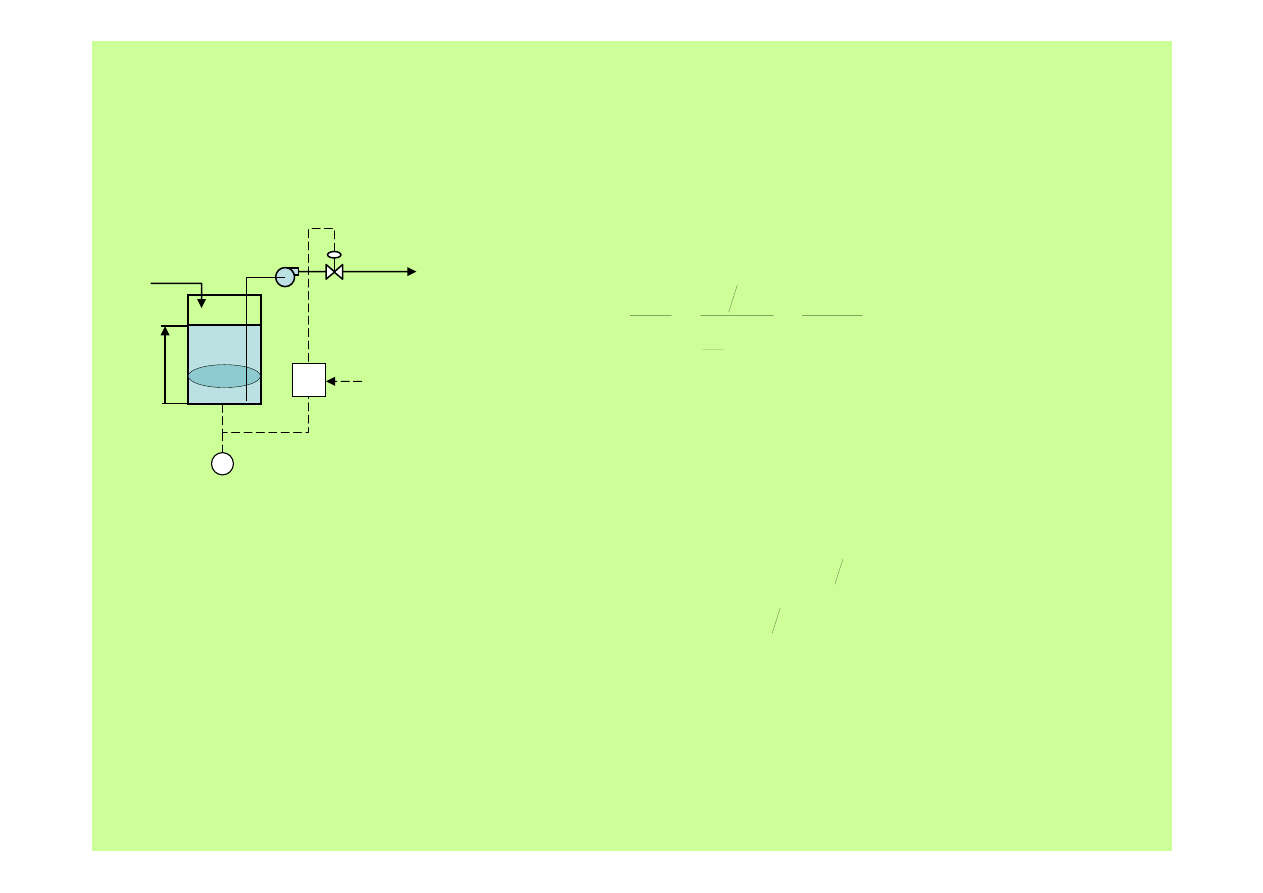
Metody regulacji

1. Regulacja proporcjonalna …

8. No pewnie!

Q

IN

A

V

Q

OUT

h

R

h

z

1

1

1

+

=

+

=

∆

Ts

K

s

k

A

k

Q

h

IN

1. Zbiornik magazynujący (całkujący) z regulacją proporcjonalną

poziomu cieczy ma dynamikę członu inercyjnego I-go rzędu.

2. Stała czasowa tego członu wynosi .

3. Wzmocnienie członu wynosi .

4.

A – przekrój zbiornika; k – wzmocnienie regulacji P.

k

A

k

1

h

26

Metody regulacji

1. Regulacja proporcjonalna …

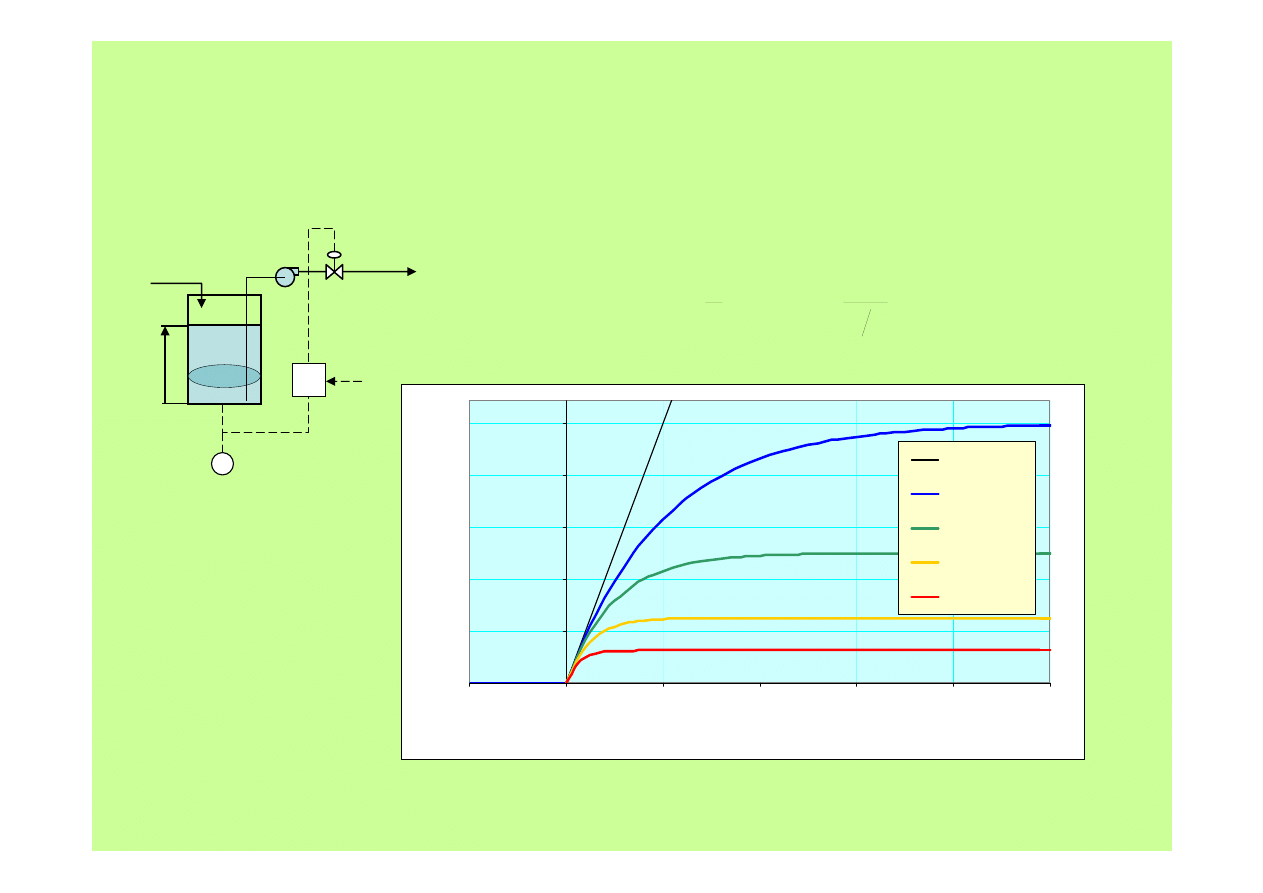
8. Odpowiedź czasowa na skok Q

IN

= 1(t)

Q

IN

A

V

Q

OUT

h

R

h

z

( )

⎥

⎥

⎦

⎤

⎢

⎢

⎣

⎡

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

−

−

⋅

=

∆

k

A

t

k

Q

t

h

IN

exp

1

1

0.0

0.2

0.4

0.6

0.8

1.0

-1

0

1

2

3

4

5

czas

uc

hy

b

bez regulacji

k = 1

k = 2

k = 4

k = 8

h

bez regul

acji – ka

tastrofa!

27

Metody regulacji

1. Regulacja proporcjonalna …

Q

IN

A

V

Q

OUT

h

R

h

z

0.0

0.2

0.4

0.6

0.8

1.0

-0.25

0

0.25

0.5

0.75

1

1.25

1.5

1.75

2

czas

uc

hy

b

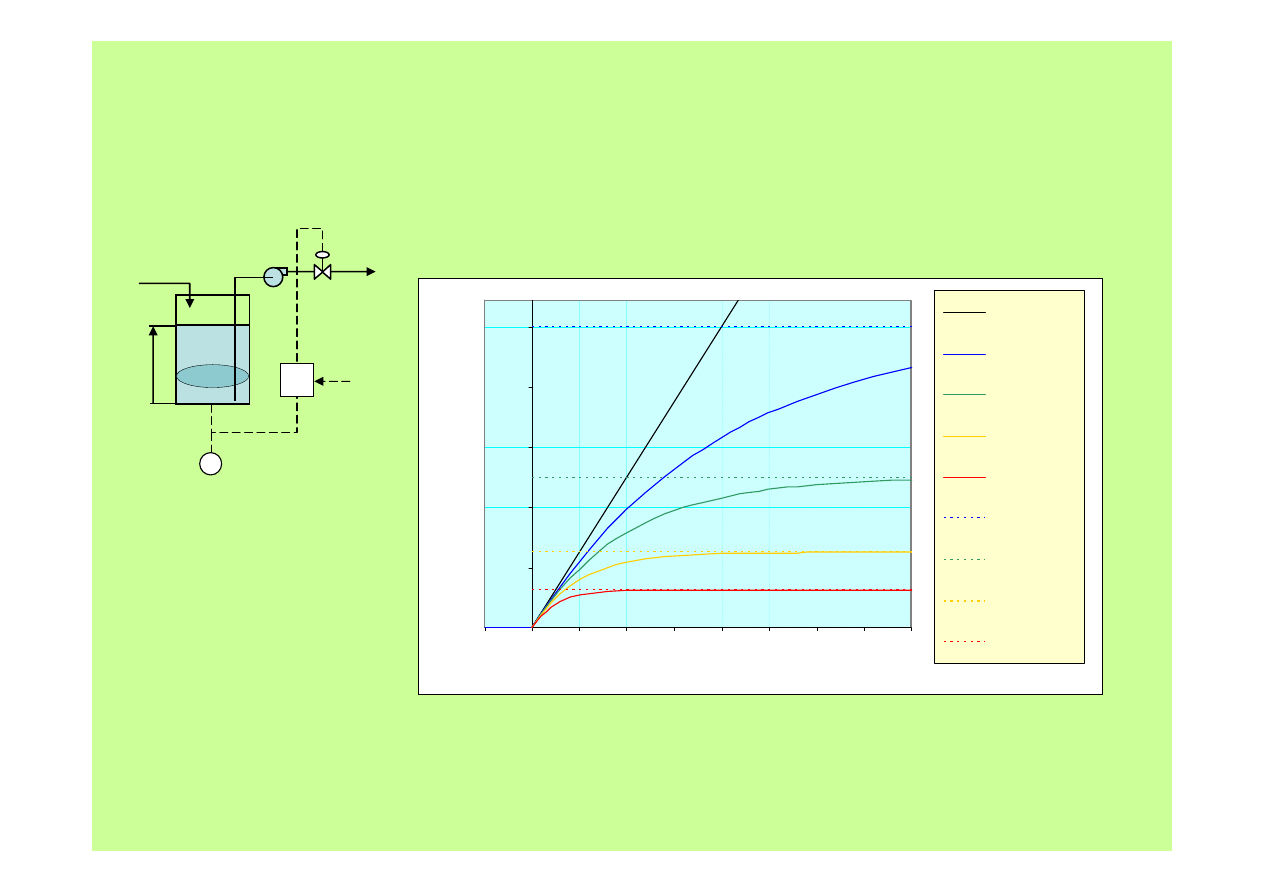
bez regulacji

k = 1

k = 2

k = 4

k = 8

uchyb k = 1

k = 2

k = 4

k = 8

h

gdy k rośnie cor

az szybciej doch

odzimy do

stanu ustaloneg

o – maleje sta

ła czasowa T

28

Metody regulacji

1. Regulacja proporcjonalna zbiornika magazynującego

Q

IN

A

V

Q

OUT

h

R

h

z

tu z

adac

k =

∞

Czy nie wystarczyłby zatem regulator
proporcjonalny z bardzo dużym
(„nieskończonym”) wzmocnieniem?

h

Nie!

Gdyż wzmocnieniu uległyby również nie uwzględnione

w teorii zakłócenie (szumy) i rzeczywisty obiekt z taką
regulacją stałby się NIESTABILNY!

29

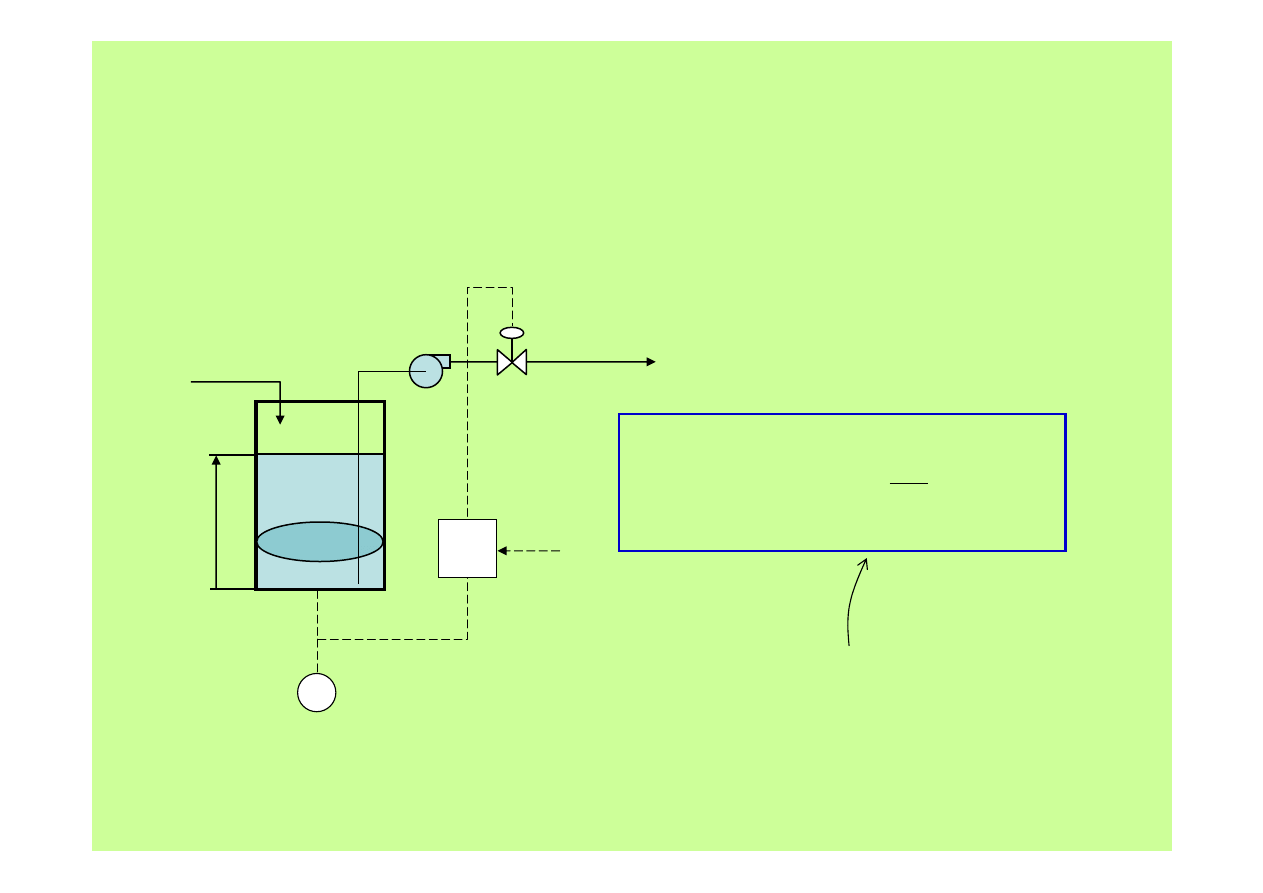
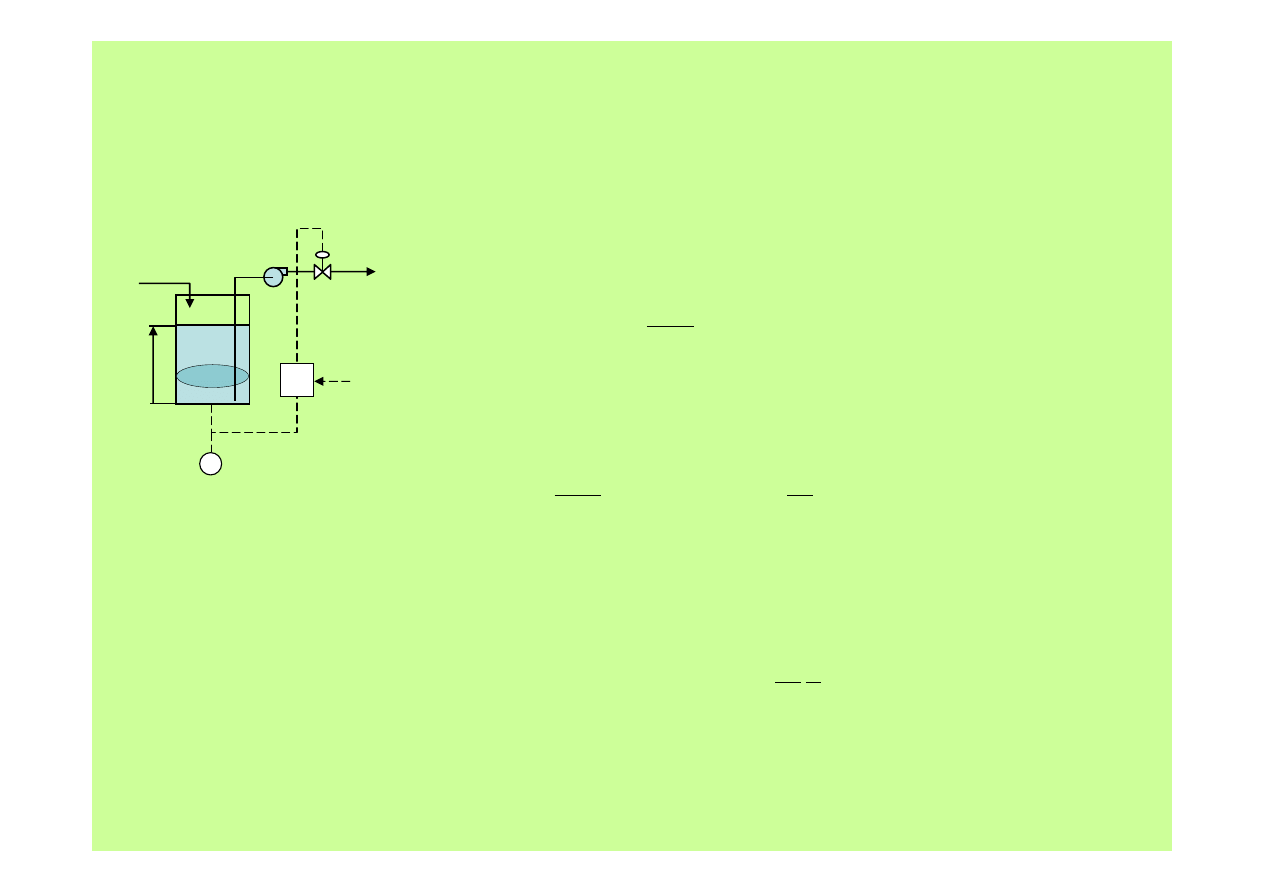
Metody regulacji

2. Regulacja

PI

zbiornika magazynującego

Q

OUT

Q

IN

A

V

h

R

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∆

+

∆

⋅

=

∫

t

I

OUT

hdt

T

h

k

Q

0

1

matematyczny

zapis

działania regul

acji PI

h

h

z

30

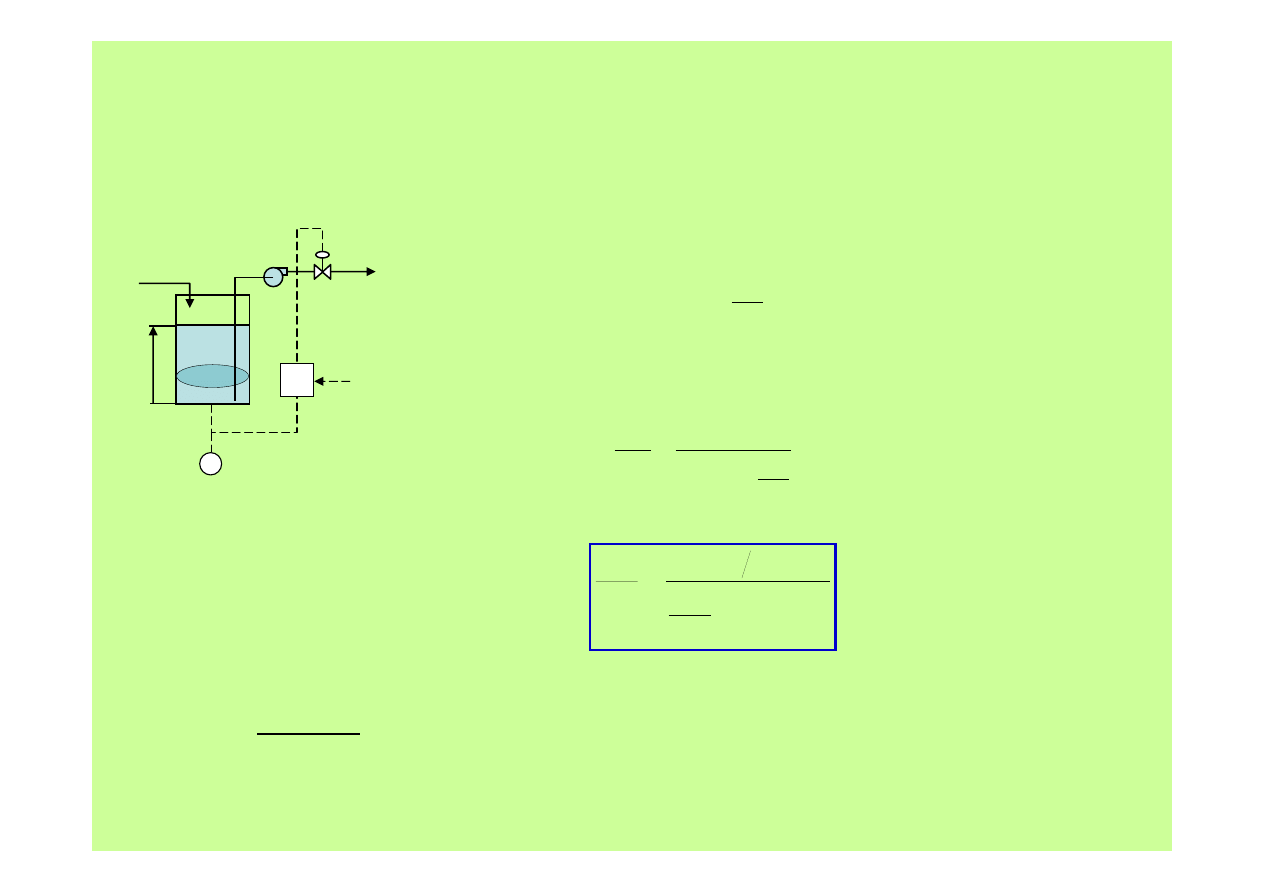
Metody regulacji

2. Regulacja PI zbiornika magazynującego

OUT

IN

Q

Q

dt

h

d

A

−

=

∆

1. Do bilansu cieczy

Q

IN

A

V

Q

OUT

h

R

h

z

h

2. Wstawiamy wzór na działanie regulatora PI

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∆

+

∆

⋅

−

=

∆

∫

t

I

IN

hdt

T

h

k

Q

dt

h

d

A

0

1

0

,

0

=

∆

=

h

t

3. Poddajemy równanie transformacji Laplace’a

h

s

T

k

h

k

Q

h

As

I

IN

∆

−

∆

⋅

−

=

∆

1

31

Metody regulacji

2. Regulacja PI zbiornika magazynującego

4. Porządkujemy

Q

IN

A

V

Q

OUT

h

R

h

z

IN

I

Q

s

T

k

k

As

h

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

∆

h

IN

Q

h /

∆

5. Wyliczamy

s

T

k

k

As

Q

h

I

IN

+

+

=

∆

1

(

)

1

2

+

+

=

∆

s

T

s

k

A

T

s

k

T

Q

h

I

I

I

IN

Otrzymany wynik oznacza, że rozpatrywany układ posiada dynamikę członu

drugiego rzędu – bez przymiotnika „inercyjny”.

O jego zachowaniu decydują wartości stojące przy s

2

i s.

32

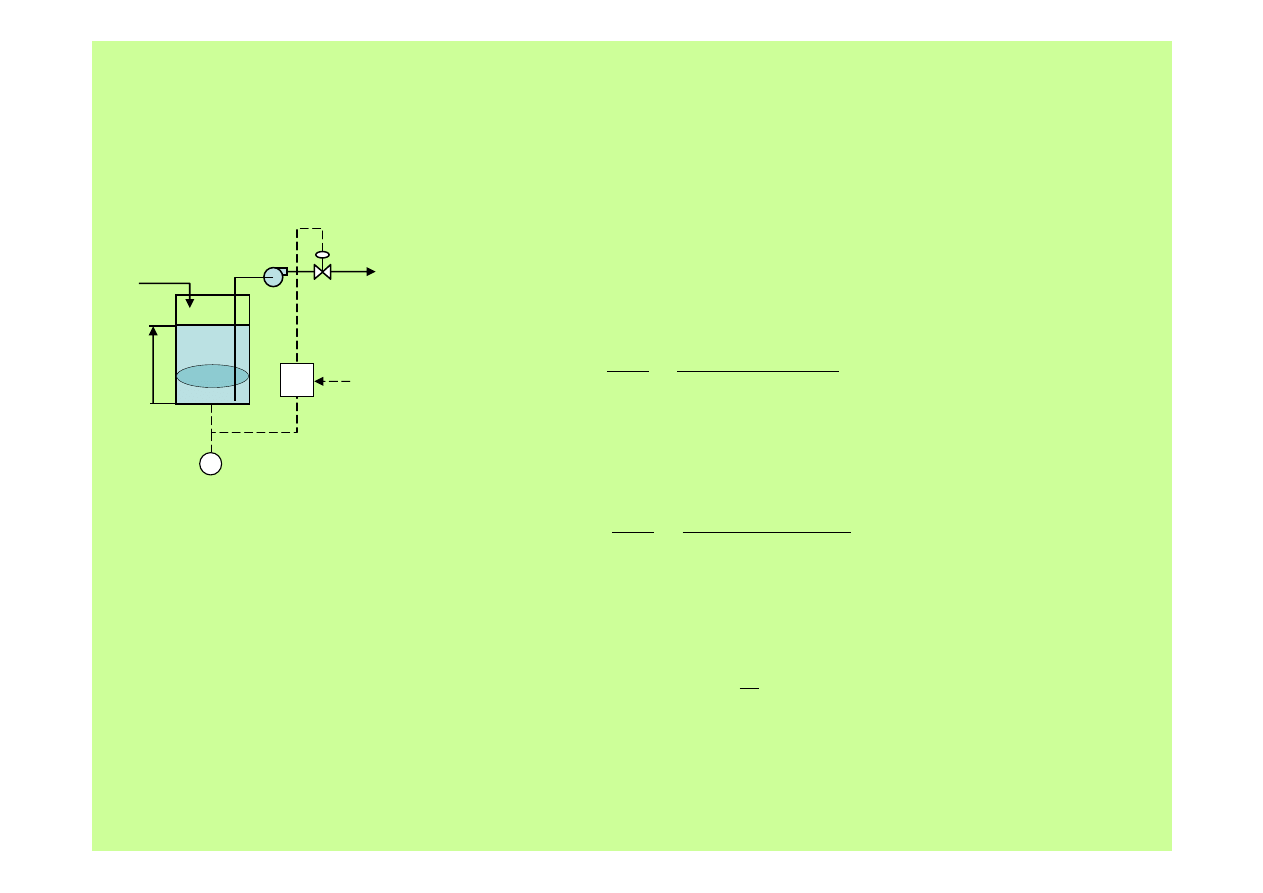
Metody regulacji

2. Regulacja PI zbiornika magazynującego

Q

IN

A

V

Q

OUT

h

R

h

z

6. Aby korzystać z tablic transformacji Laplace’a

musimy otrzymanemu wyrażeniu nadać postać:

1

2

2

2

+

+

=

∆

s

T

s

T

Ks

Q

h

IN

ξ

h

lub

2

2

2

n

n

n

IN

s

s

s

K

Q

h

ω

ξ

ω

ω

+

+

=

∆

gdzie:

T

n

1

≡

ω

33

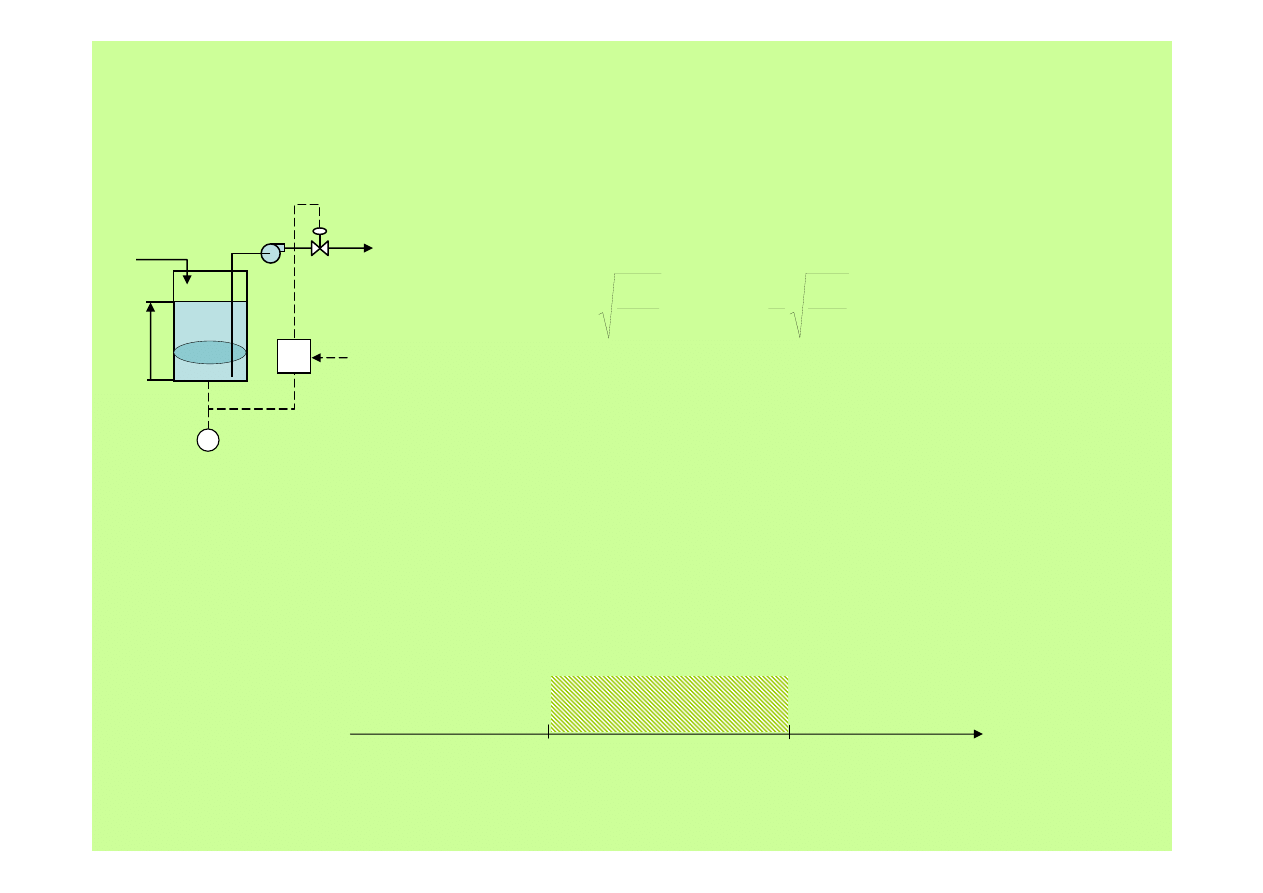
Metody regulacji

2. Regulacja PI zbiornika magazynującego

Q

IN

A

V

Q

OUT

h

R

h

z

7. W tym przypadku jest to możliwe, gdy:

A

k

T

k

A

T

T

I

I

2

1

;

=

=

ξ

h

T

-

stała czasowa

-

pulsacja własna

-

współczynnik tłumienia

n

ω

ξ

T

(zamiennie z ) decyduje o szybkości reakcji układu („żwawość”, „refleks”).

decyduje, czy w układzie wystąpią drgania czy nie.

ξ

n

ω

ξ

drgania

niestabilność

inercja

0

1

34

Metody regulacji

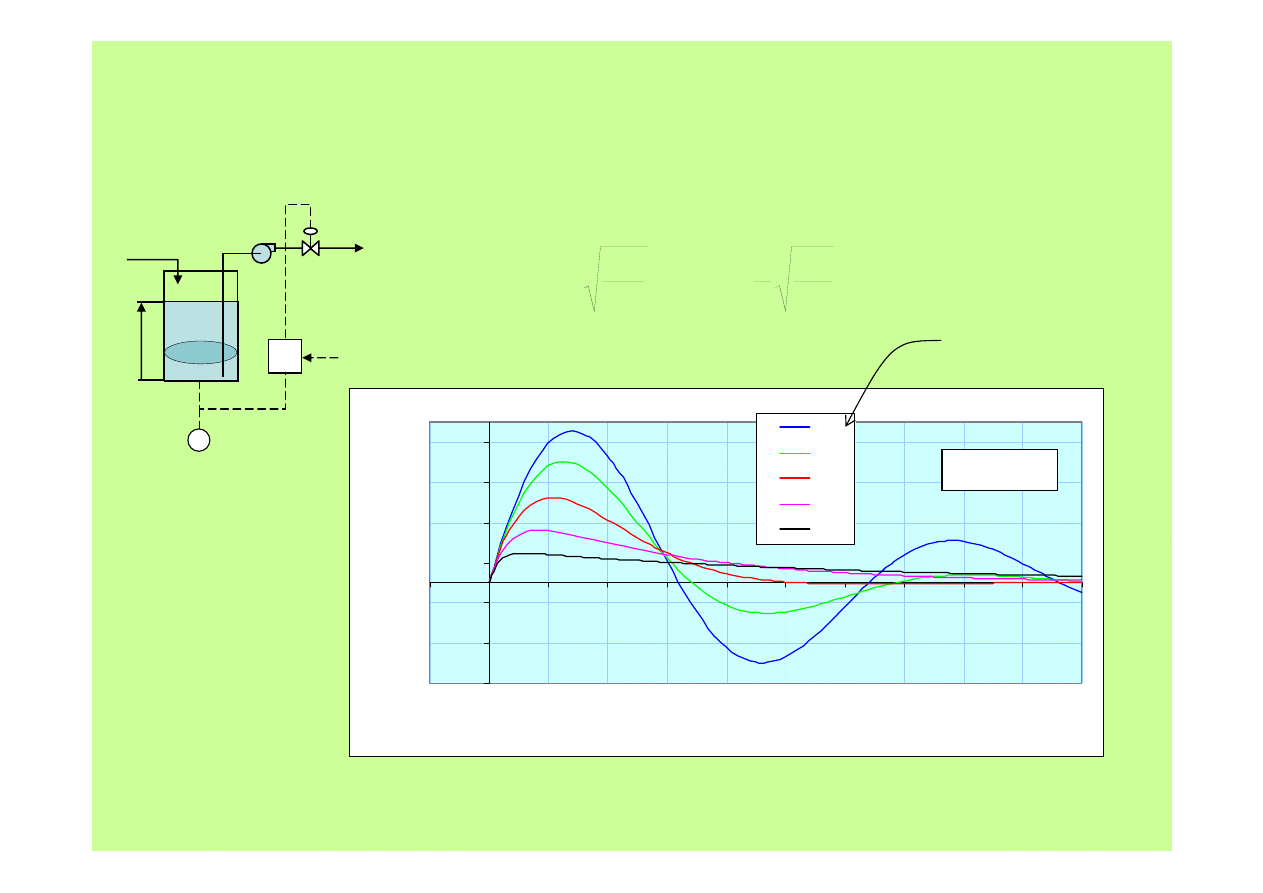
2. Regulacja PI zbiornika magazynującego – odpowiedź na skok Q

IN

= 1(t)

Q

IN

A

V

Q

OUT

h

R

h

z

A

k

T

k

A

T

T

I

I

2

1

;

=

=

ξ

-0.5

-0.3

-0.1

0.1

0.3

0.5

0.7

-1

0

1

2

3

4

5

6

7

8

9

10

czas

uc

hy

b

0.2
0.4
0.8
1.6
3.2

T = const

ξ

h

35

Metody regulacji

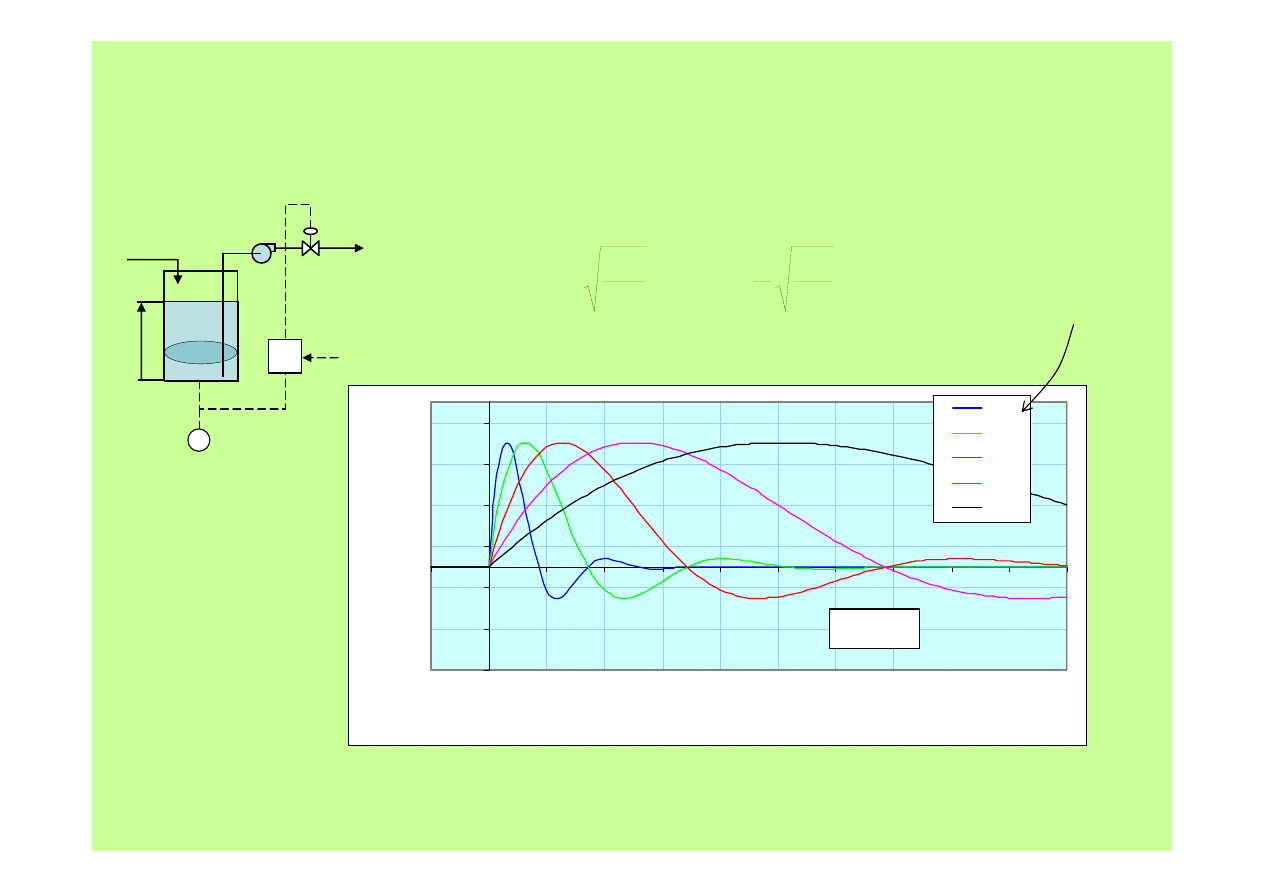
2. Regulacja PI zbiornika magazynującego – odpowiedź na skok Q

IN

= 1(t)

Q

IN

A

V

Q

OUT

h

R

h

z

A

k

T

k

A

T

T

I

I

2

1

;

=

=

ξ

-0.5

-0.3

-0.1

0.1

0.3

0.5

0.7

-1

0

1

2

3

4

5

6

7

8

9

10

czas

u

c

hy

b

0.25
0.5
1
2
4

T

4

.

0

=

ξ

h

36

Metody regulacji

2. Regulacja PI zbiornika magazynującego

Q

OUT

Q

IN

A

V

h

R

h

h

z

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∆

+

∆

⋅

=

∫

t

I

OUT

hdt

T

h

k

Q

0

1

Dobór nas

taw k i T

I

regulatora

nosi nazw

ę

strojenia

i jest w du

żej mierze

sztuką.

37

Metody regulacji

2. Regulacja

PID

zbiornika magazynującego

Q

OUT

Q

IN

A

V

h

R

h

h

z

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

∆

+

∆

+

∆

⋅

=

∫

t

D

I

OUT

dt

h

d

T

hdt

T

h

k

Q

0

1

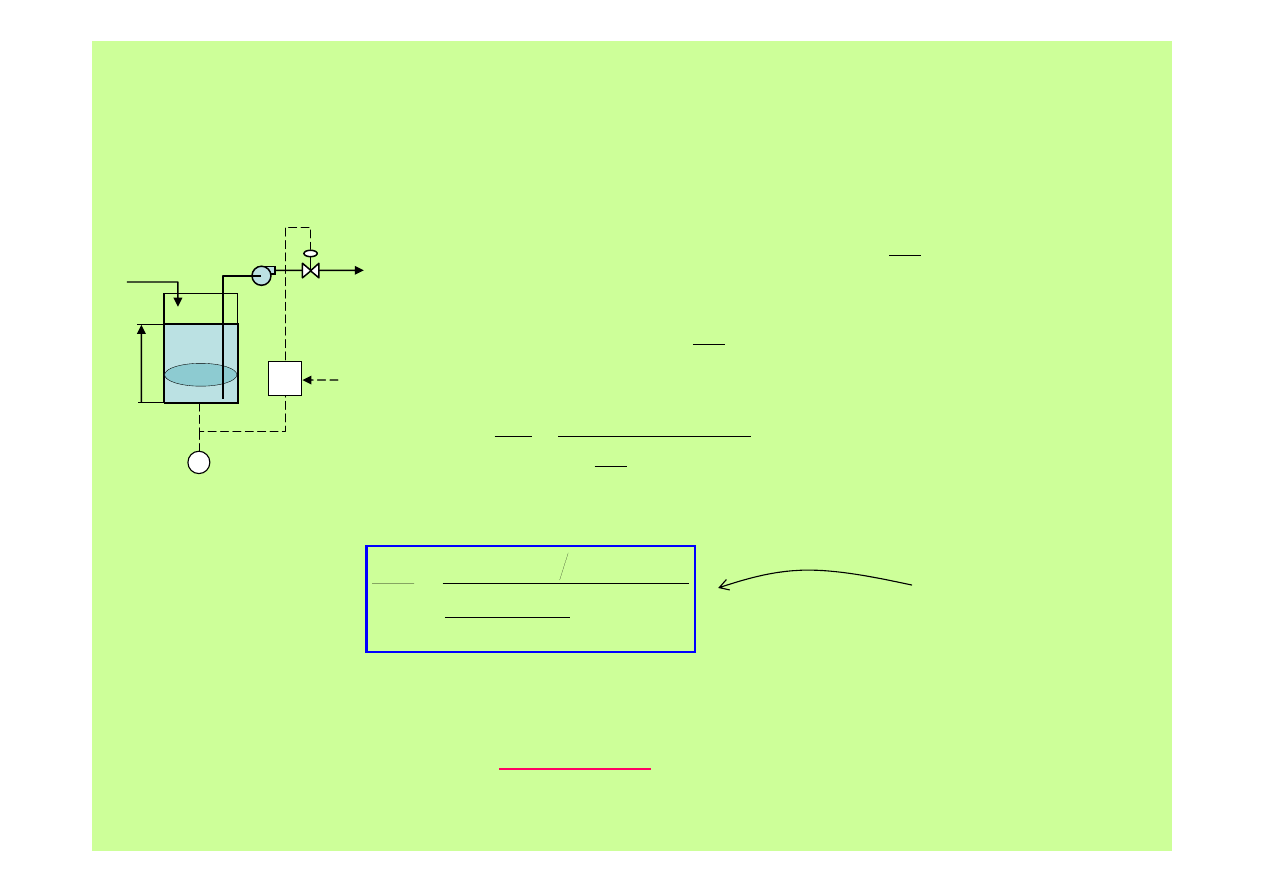
matematyczny

zapis

działania regul

acji PID

38

Metody regulacji

2. Regulacja

PID

zbiornika magazynującego

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

∆

−

=

∆

s

kT

s

T

k

k

h

Q

h

As

D

I

IN

Q

IN

A

V

Q

OUT

h

R

h

z

(

)

IN

D

I

Q

s

A

kT

s

T

k

k

h

=

⎟⎟

⎠

⎞

⎜⎜

⎝

⎛

+

+

+

∆

h

(

)

s

A

kT

s

T

k

k

Q

h

D

I

IN

+

+

+

=

∆

1

(

)

(

)

1

2

+

+

+

=

∆

s

T

s

k

A

kT

T

s

k

T

Q

h

I

D

I

I

IN

Nie warto

dalej przek

ształca

ć

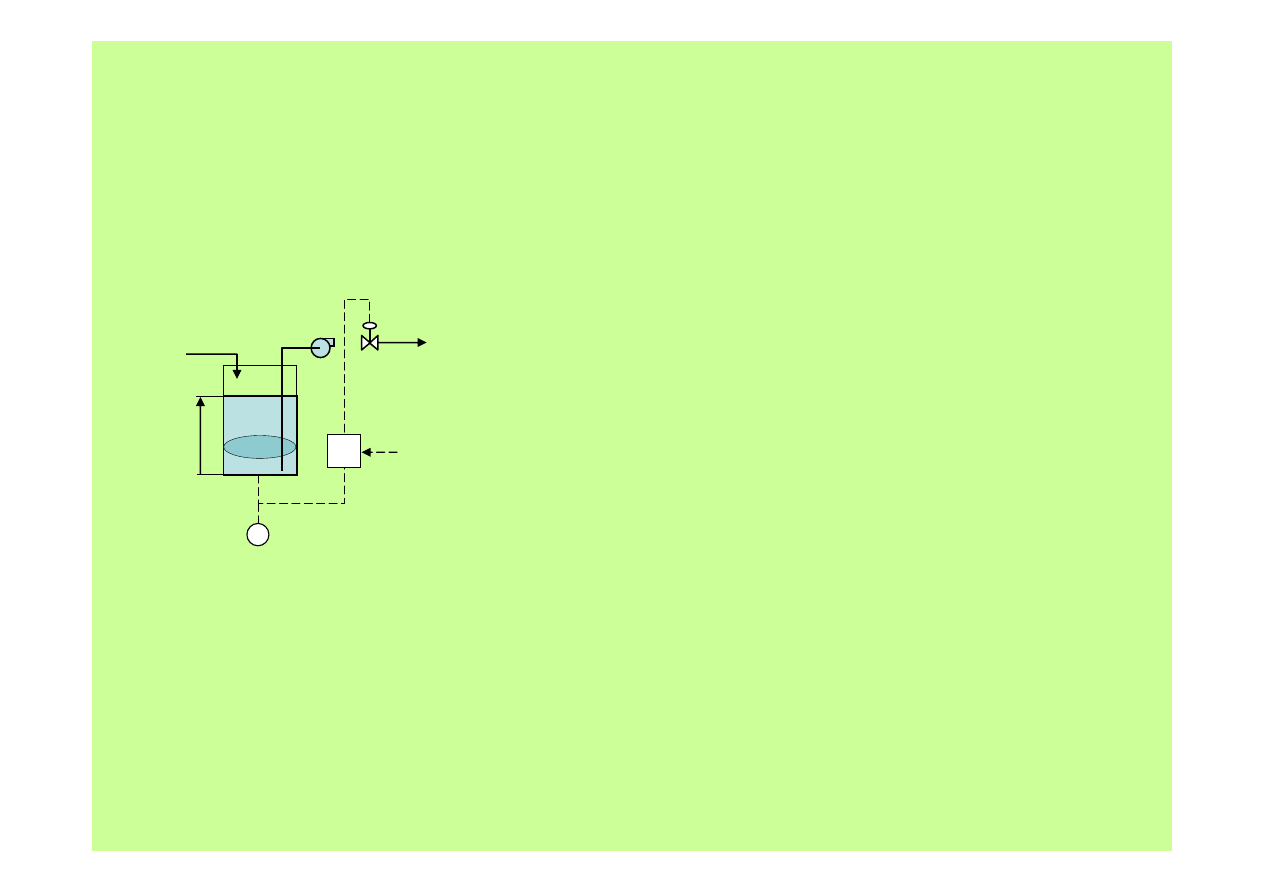
Stwierdzamy (z pewnym zdziwieniem), że wprowadzenie różniczkowania

do regulacji nie przynosi

jakościowej

zmiany – szykuje się też II-gi rząd, tylko

trochę inny!

39

Metody regulacji

2. Regulacja

PID

zbiornika magazynującego

Q

IN

A

V

Q

OUT

h

R

h

z

Rzeczyw

iście, w

wielu pr

zypadka

ch

wprowa

dzenie r

óżniczk

owania

do układ

u

regulacj

i nie pop

rawia je

j i jest b

ezcelow

e.

Ale f

ajnie

! Nie

będz

iemy

nicze

go da

lej wy

prow

adza

ć

h

40

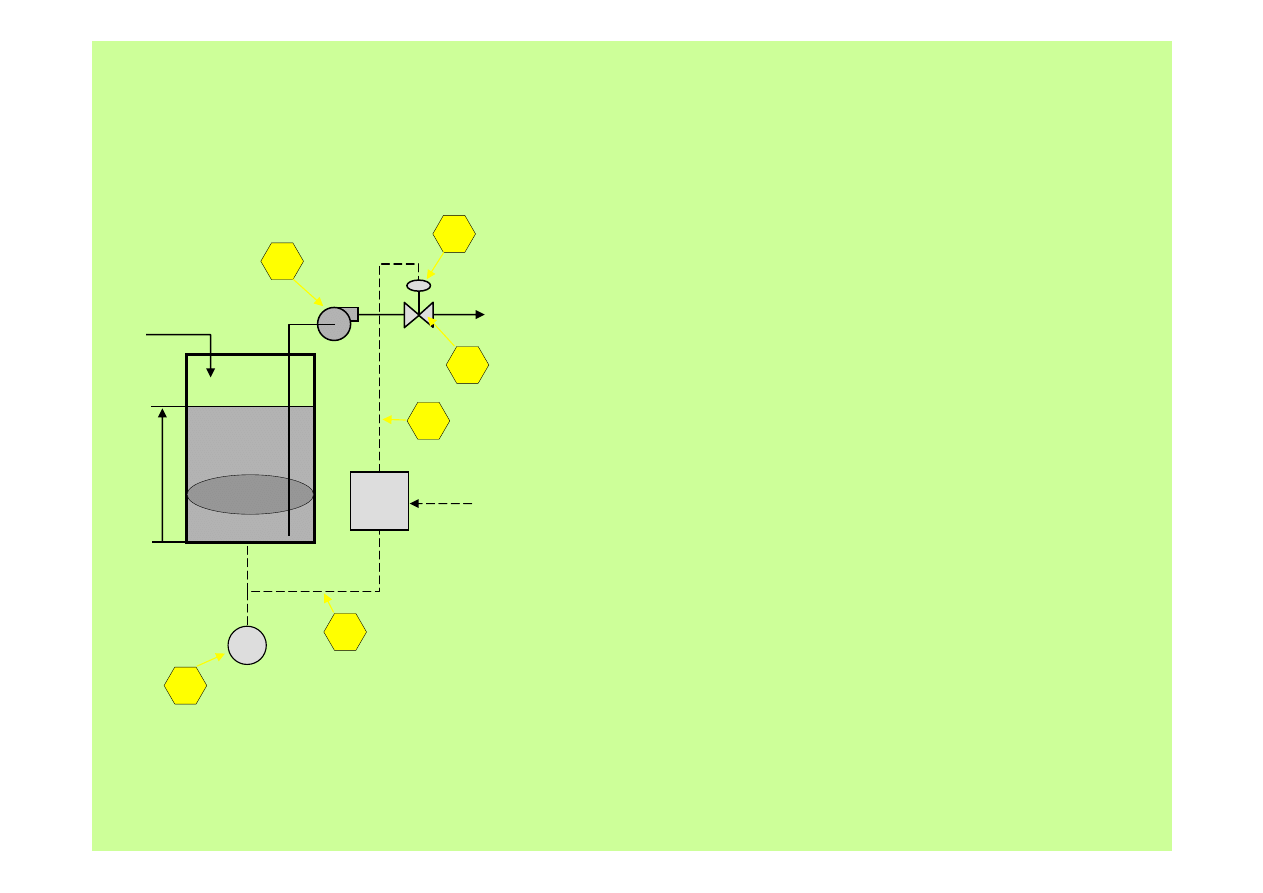
Regulacja

3. Trochę realizmu

1 – miernik poziomu cieczy, mierzy z określoną

dokładnością, ma własną dynamikę.

2 – linia przesyłowa z miernika do regulatora,

wprowadza szumy i może opóźniać.

3 – linia sygnału z regulatora do elementu

wykonawczego, to samo.

4 – element wykonawczy (siłownik), jako urządzenie

mechaniczne, ma własną dynamikę i zapewne
tzw. histerezę tzn. ruch „do góry” przebiega po
nieco innej drodze niż ruch „w dół”.

5 – zawór, nie reaguje natychmiast na ruch siłownika.
6 – pompa, nie może natychmiast dostosować się

do stanu otwarcia zaworu.

Q

IN

A

V

Q

OUT

h

R

1

2

h

h

z

3

4

5

6

Wszystko to powoduje, że

regulacja mimo

rozbudowanej teorii jest ci

ągle

sztuką

.

41

Regulacja

4. Ważna refleksja

Wszystkie pokazane tu zagadnienia obowiązują (i są tak samo

proste lub skomplikowane) niezależnie od

budowy regulatora

.

Regulator może być:

• człowiekiem

• XIX-to wiecznym mechanizmem

• XX-to wiecznym elektro-, hydro- lub pneumomechanizmem

• XXI-szo wiecznym cudem elektroniczno-cyfrowym

tzw.

awta

mat

s ma

lczik

am

Zawsze trzeba znać obiekt

poddany regulacji

oraz podjąć decyzję co do

strategii i metody

jego sterowania.

42

Podsumowanie

Dynamika i automatyka ma jeszcze wiele

nieporuszonych tu zagadnień i problemów
ale w tym kursie to już koniec.

Ufff

f…

43

Dziękuję

Do zobaczenia

na kolokwium

???!!!

…

44

Koniec cz. III ostatniej