Mariusz PYRZ

SIMR (PW), Instytut Pojazdów

Metody numeryczne w mechanice

Rozwiązywanie układów równań nieliniowych

4.

Układ równań nieliniowych

Układ n równań

z n niewiadomymi

x

1

, x

2

, ..., x

n

(funkcje f

1

, f

2

, ..., f

n

są znane).

f x x

x

f

x x

x

f

x x

x

n

n

n

n

1

1

2

2

1

2

1

2

0

0

0

( ,

,...,

)

( ,

,...,

)

( ,

,...,

)

=

=

=

⋯

2

Wprowadzamy

wektory

kolumnowe

Układ równań można wtedy zapisać jako

f(x)=0

.

f x

x

0

( )

( ,

,...,

)

( ,

,...,

)

( ,

,...,

)

=

L

N

M

M

M

M

O

Q

P

P

P

P

=

L

N

M

M

M

M

O

Q

P

P

P

P

=

L

N

M

M

M

M

O

Q

P

P

P

P

f x x

x

f

x x

x

f

x x

x

x

x

x

n

n

n

n

n

1

1

2

2

1

2

1

2

1

2

0

0

0

⋯

⋯

⋯

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

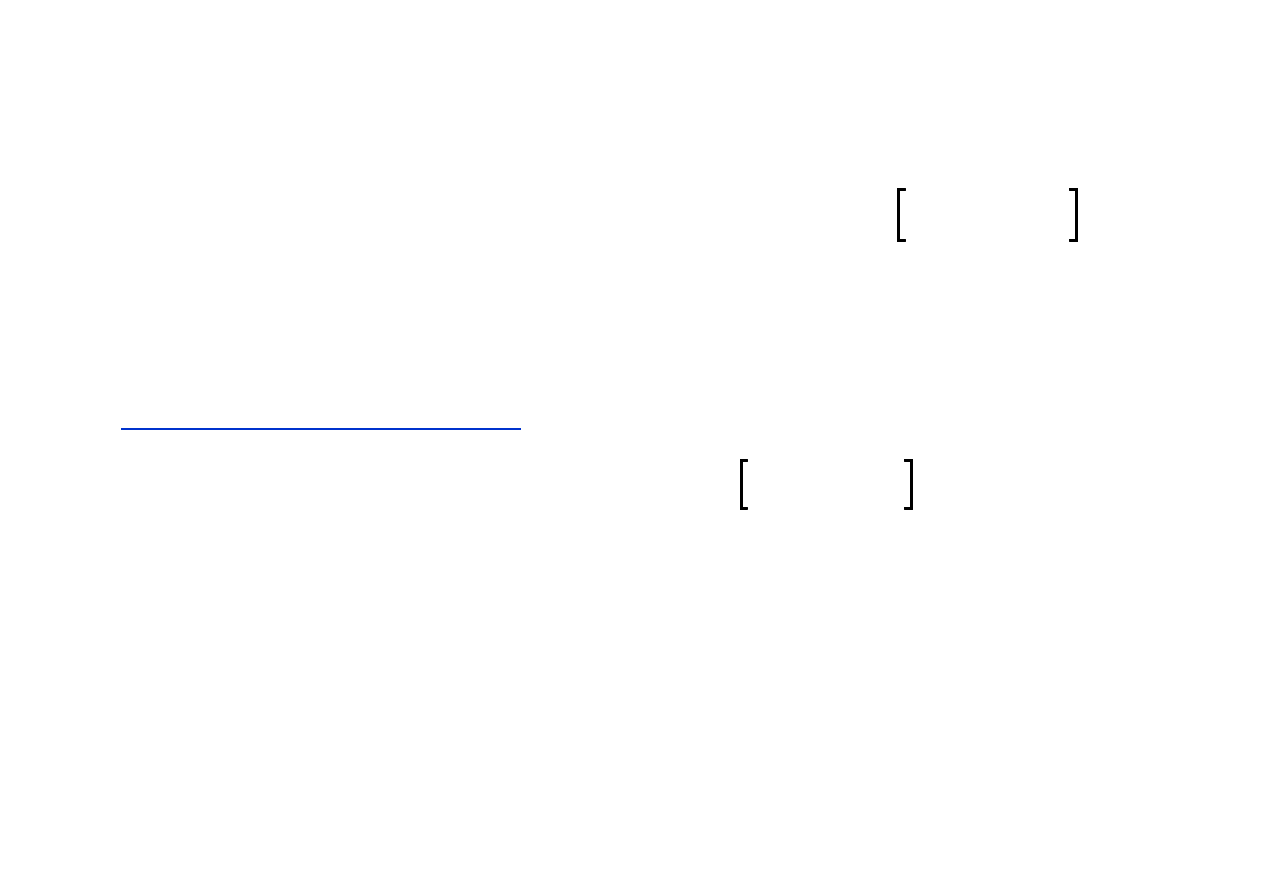
Rozwiązywanie układu równań nieliniowych

Rozwiązanie układu równań f(x)=0 oznaczmy jako

f(x*)=0

Metoda kolejnych przybliżeń

x

*

T

=

x x

x

n

1

2

*

*

*

⋯

3

Wychodząc z początkowego wektora

budujemy ciąg wektorów przybliżających rozwiązanie x

i

(i – numer iteracji).

Dla i dążącego do nieskończoności ciąg x

i

dąży do granicy x*.

x

T

0

1

0

2

0

0

=

x x

x

n

⋯

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

Przykład: metoda Newtona

Stosowana zwykle w celu zwiększenia dokładności rozwiązań wyznaczonych
innymi metodami (ponieważ napotykamy trudności w dobrym oszacowaniu
wektora początkowego x

0

).

Zbieżność ma charakter kwadratowy, macierz Jacobiego (drugich
pochodnych cząstkowych) jest przeliczana na każdym kroku iteracyjnym.

Oznaczenie: x

i

to i-ta aproksymacja wektora rozwiązań

4

Oznaczenie: x

i

to i-ta aproksymacja wektora rozwiązań

x

i+1

= x

i

- J

-1

(x

i

) f(x

i

)

x

f(x )

i

i

=

L

N

M

M

M

M

O

Q

P

P

P

P

=

L

N

M

M

M

M

O

Q

P

P

P

P

x

x

x

f x x

x

f

x x

x

f

x x

x

i

i

n

i

i

i

n

i

i

i

n

i

n

i

i

n

i

1

2

1

1

2

2

1

2

1

2

⋯

⋯

⋯

⋯

⋯

( ,

,

,

)

( ,

,

,

)

( ,

,

,

)

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

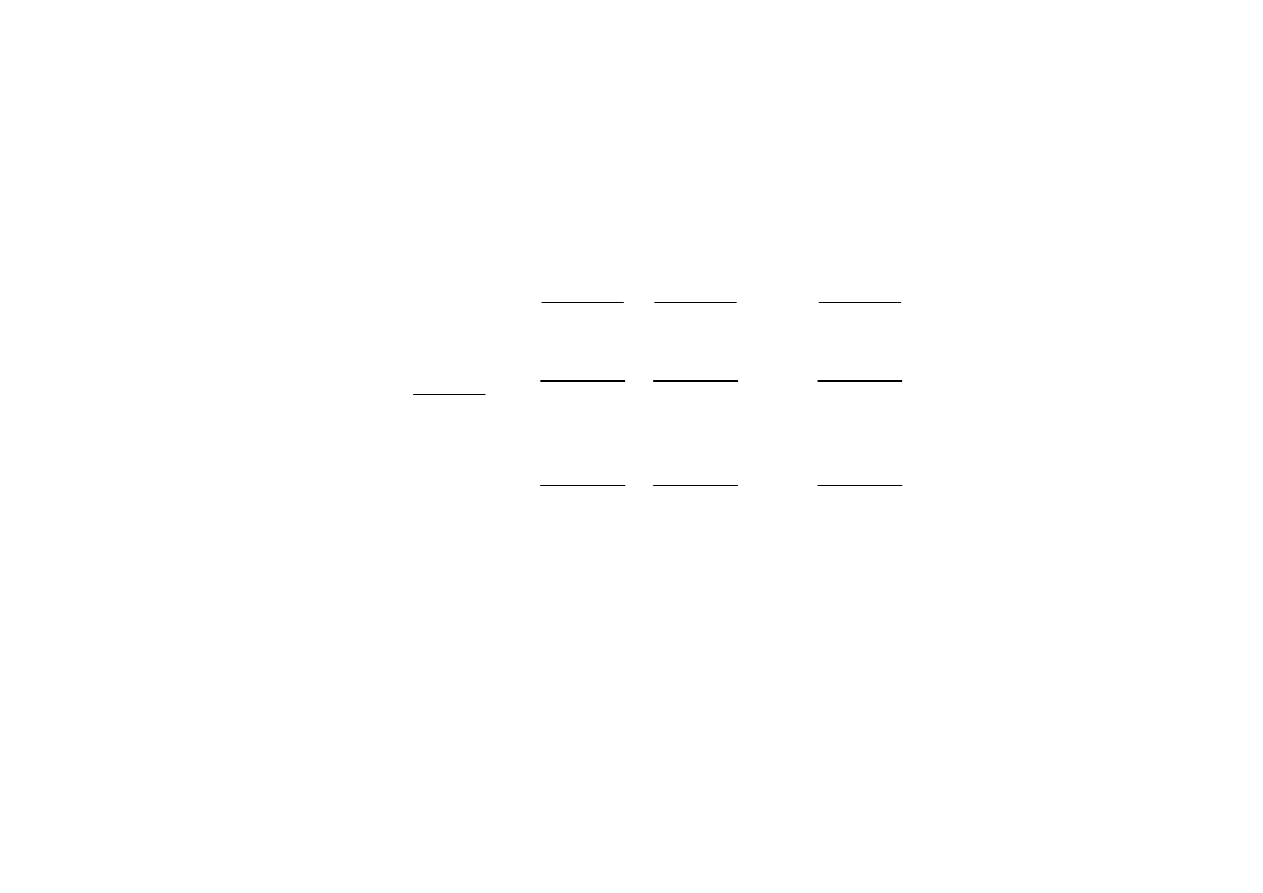
Metoda Newtona

Macierz Jacobiego układu równań nieliniowych określonego za pomocą funkcji
f

1

,f

2

, ...,f

n

J(x )

f(x )

x

x

x

x

x

x

i

i

i

i

i

i

i

i

= ∂

∂

L
N

M

M

O
Q

P

P

=

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

∂

L

M

M

M

M

M

M

M

O

P

P

P

P

P

P

P

x

f

x

f

x

f

x

f

x

f

x

f

x

j

n

n

1

1

1

2

1

2

1

2

2

2

( )

( )

( )

( )

( )

( )

⋯

⋯

⋯

⋯

⋯

⋯

5

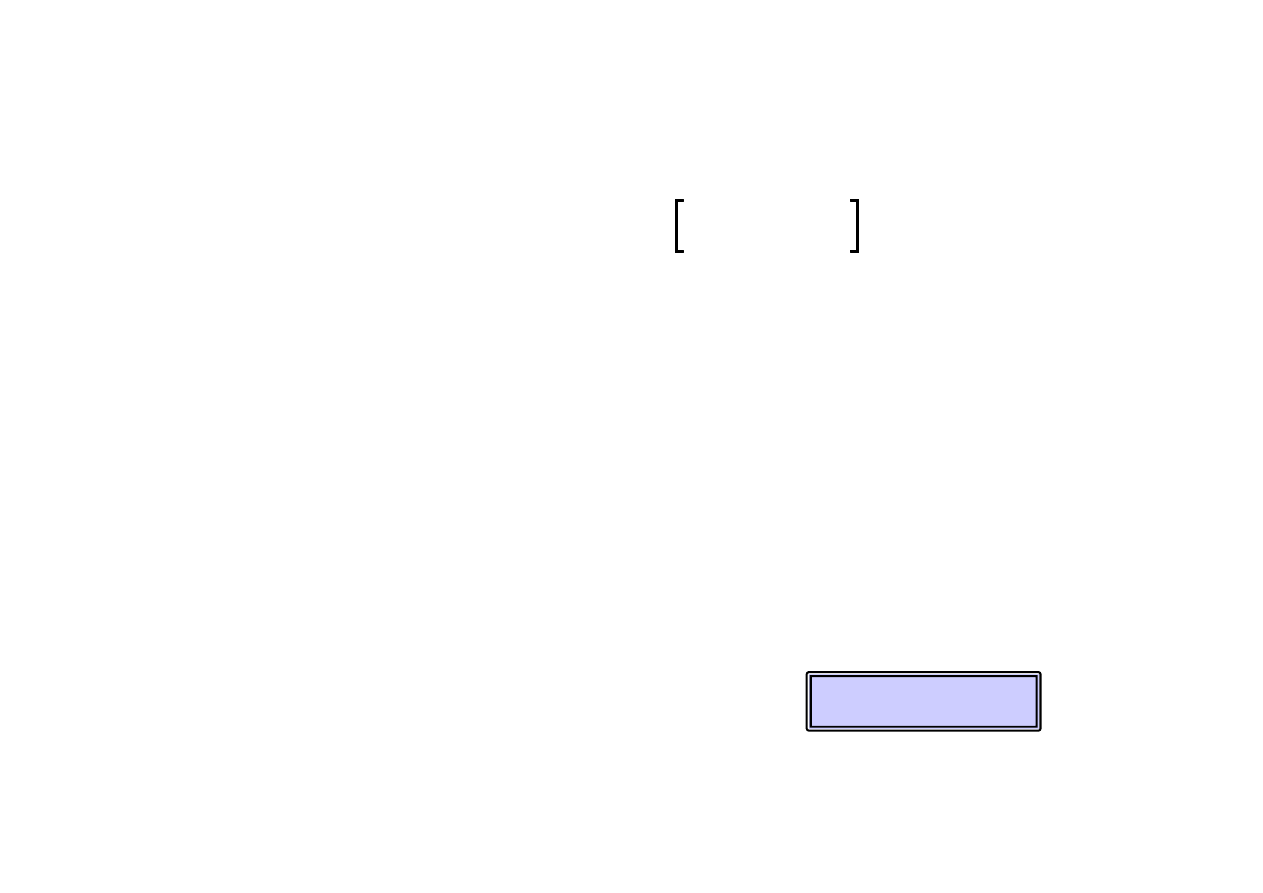
Oznaczając przez

∆

x

i

wektor « poprawiający » rozwiązania można zapisać

∆

x

i

= J

-1

(x

i

) f(x

i

).

Wektor

∆

x

i

jest obliczany w każdej iteracji rozwiązując układ równań liniowych

J(x

i

)

∆

x

i

= f(x

i

)

x

x

x

i

i

i

N

Q

∂

∂

∂

∂

∂

∂

N

M

M

M

Q

P

P

P

f

x

f

x

f

x

n

n

n

n

1

2

( )

( )

( )

⋯

⋯

⋯

⋯

⋯

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

Metoda Newtona - algorytm

Wybrać początkowe przybliżenie

Dla każdego przybliżenia x

i+1

, i=0,1,2,…

- Oblicz wartości wektora funkcji f(x

i

) w punkcie x

i

- Oblicz składowe macierzy Jacobiego J(x

i

) w punkcie x

i

- Oblicz wektor poprawek

∆

x

i

korzystając z układu równań liniowych

x

T

0

1

0

2

0

0

=

x x

x

n

⋯

6

- Oblicz wektor poprawek

∆

x

i

korzystając z układu równań liniowych

J(x

i

)

∆

x

i

= f(x

i

)

- Oblicz (i+1)–te przybliżenie rozwiązania x

i+1

= x

i

-

∆

x

i

Kryterium zatrzymania :

|| x

i+1

|| - || x

i

|| <

ε

.

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

Przykład 1

Metody rozwiązywania układów równań nieliniowych

Metody quasi-newtonowskie

Stanowią modyfikację metody Newtona.

Macierz Jacobiego jest aktualizowana co p iteracji (p jest wybierane przez
użytkownika). Prowadzi to do zmniejszenia liczby wykonywanych operacji
ale tracona jest kwadratowa zbieżność.

7

Metoda siecznych

Uogólnienie metody siecznych (patrz rozwiązywanie równania
nieliniowego) na przypadek n równań nieliniowych

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

Rysunek 1

Rozwiązywanie układów równań nieliniowych

Metody wykorzystujące techniki minimalizacji

Metody iteracyjne mogą bazować na technikach minimalizacji
« długości » wektora funkcji f

i

(x

i

) :

2

1

2

1

2

( )

( ,

,

,

)

( ,

,

,

)

min

n

n

i

n

Q

Q x x

x

f

x x

x

=

=

→

∑

x

⋯

⋯

8

Funkcja Q(x) osiąga minimum równe zero w punkcie x który jest
rozwiązaniem układu równań nieliniowych f(x)=0.

Wykorzystać można np. metody spadku, gradientów sprzężonych, …

1

2

1

2

1

n

i

n

i

=

∑

⋯

⋯

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011

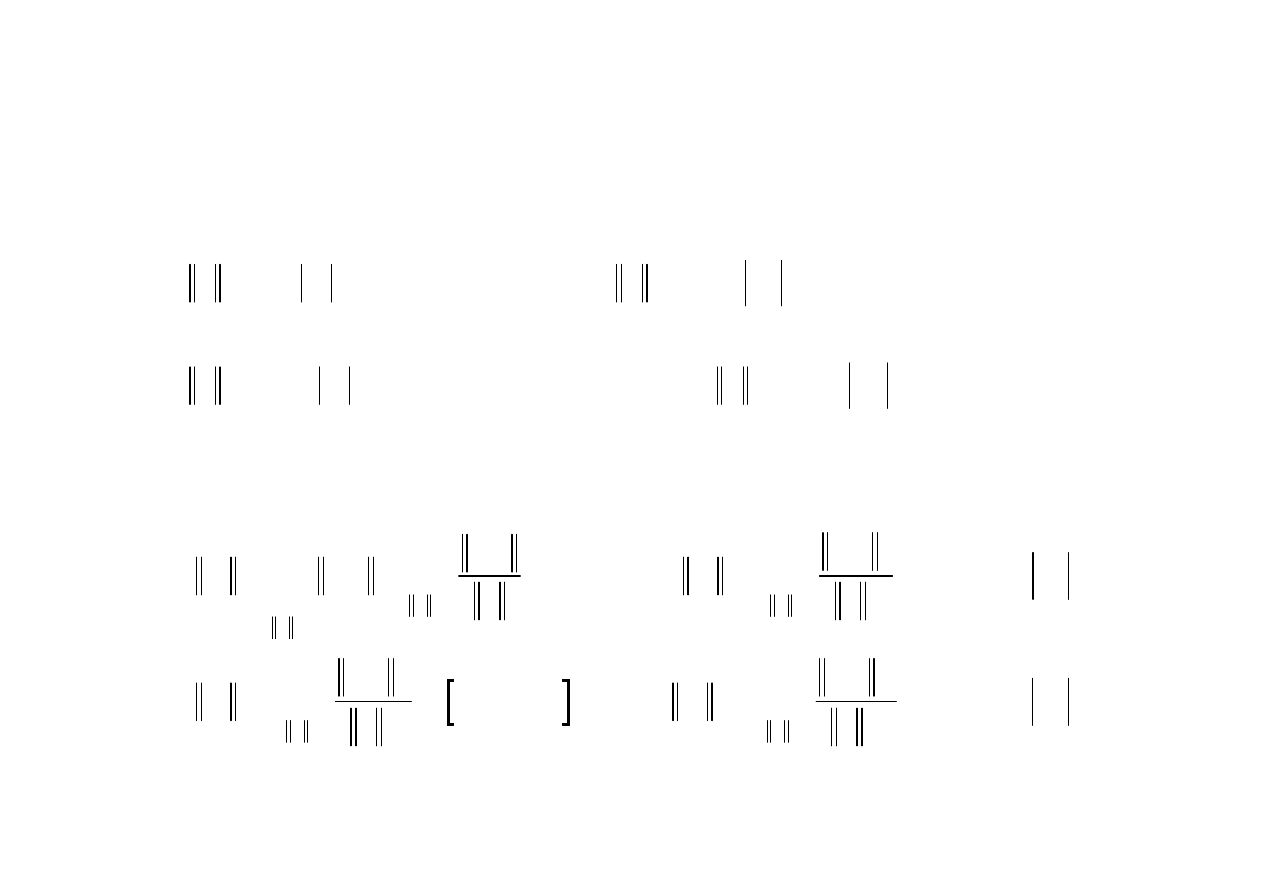
Normy wektorowe i macierzowe

normy wektorowe

1/ 2

2

1

2

1

1

1/

1

1

1

sup

n

n

i

i

i

i

p

n

p

i

i

p

i n

i

x

norma

x

norma euklidesowa

x

norma nieskonczona

x

=

=

∞

≤ ≤

=





=

=













=

=









∑

∑

∑

x

x

x

x

9

normy macierzowe (stowarzyszone z normami wektorowymi)

A

Ax

Ax

x

A

Ax

x

A

Ax

x

A A

A

Ax

x

x C

x

x

x

x

*

x

n

=

=

=

=

L

NM

O

QP

=

=

=

=

L
N

M

O
Q

P

∈

=

≠

≠

≤ ≤

=

≠

∞

≠

∞

∞

≤ ≤

=

∑

∑

sup

sup

sup

sup

sup

(

)

sup

sup

/

1

0

1

0

1

1

1

1

2

0

2

2

1 2

0

1

1

j n

ij

i

n

i n

ij

j

n

a

a

ρ

M.Pyrz Metody numeryczne w mechanice – Układy równań nieliniowych 10.2011