PODSTAWY TOPOLOGII
OBWODÓW
Topologia obwodów
– zajmuje się ustaleniem
związków dotyczących połączeń elementów
obwody
zawierające tylko elementy dwójnikowe
.
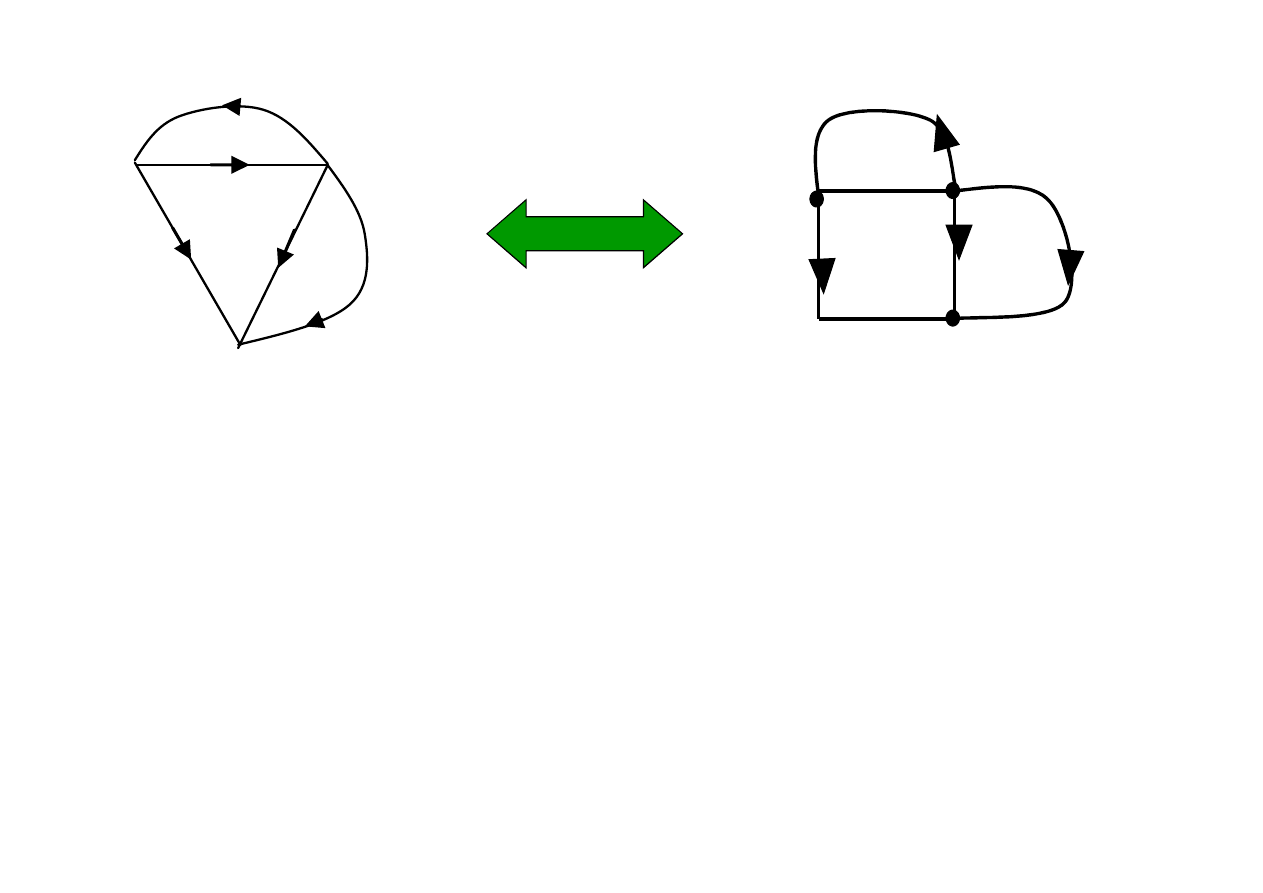
Badając strukturę geometryczną obwodu
zastępujemy elementy występujące w schemacie
gałęziami
(
reprezentowanymi przez linie
), na
końcu każdej gałęzi umieszczamy
kropkę
, zwaną
węzłem
.
Jeżeli każdej gałęzi grafu przyporządkujemy
zwrot, to otrzymamy
graf zorientowany
.
Przyjmujemy, że
orientacja gałęzi grafu jest
zgodna ze strzałką prądu
w odpowiedniej
gałęzi.
gałęzi.
UWAGA
Na grafie nie zaznaczamy strzałek napięć, których
groty są skierowane przeciwnie do grotów strzałek
prądów.
W rezultacie otrzymujemy
graf
obwodu
.
Graf
- zbiór węzłów i gałęzi, przy
Graf
- zbiór węzłów i gałęzi, przy
czym każda gałąź łączy się każdym
końcem z odpowiednim węzłem
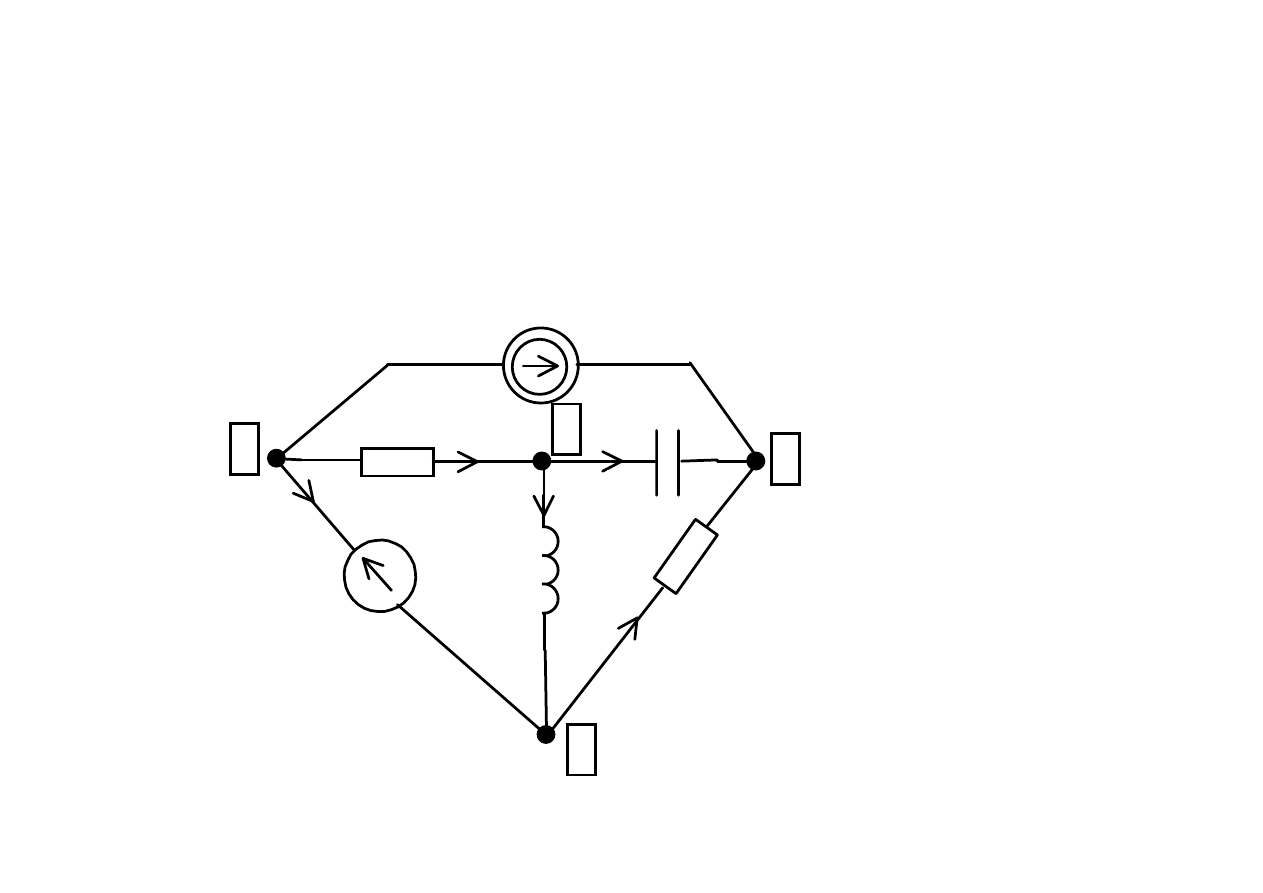
Przykład 1
Dla obwodu z rysunku narysuj graf i graf
zorientowany
1
2
3
j
1
R
2
C
3
i
2
1
2
3
4
e
6
R
5
L
4
i
3
i
4
i
5
i
6
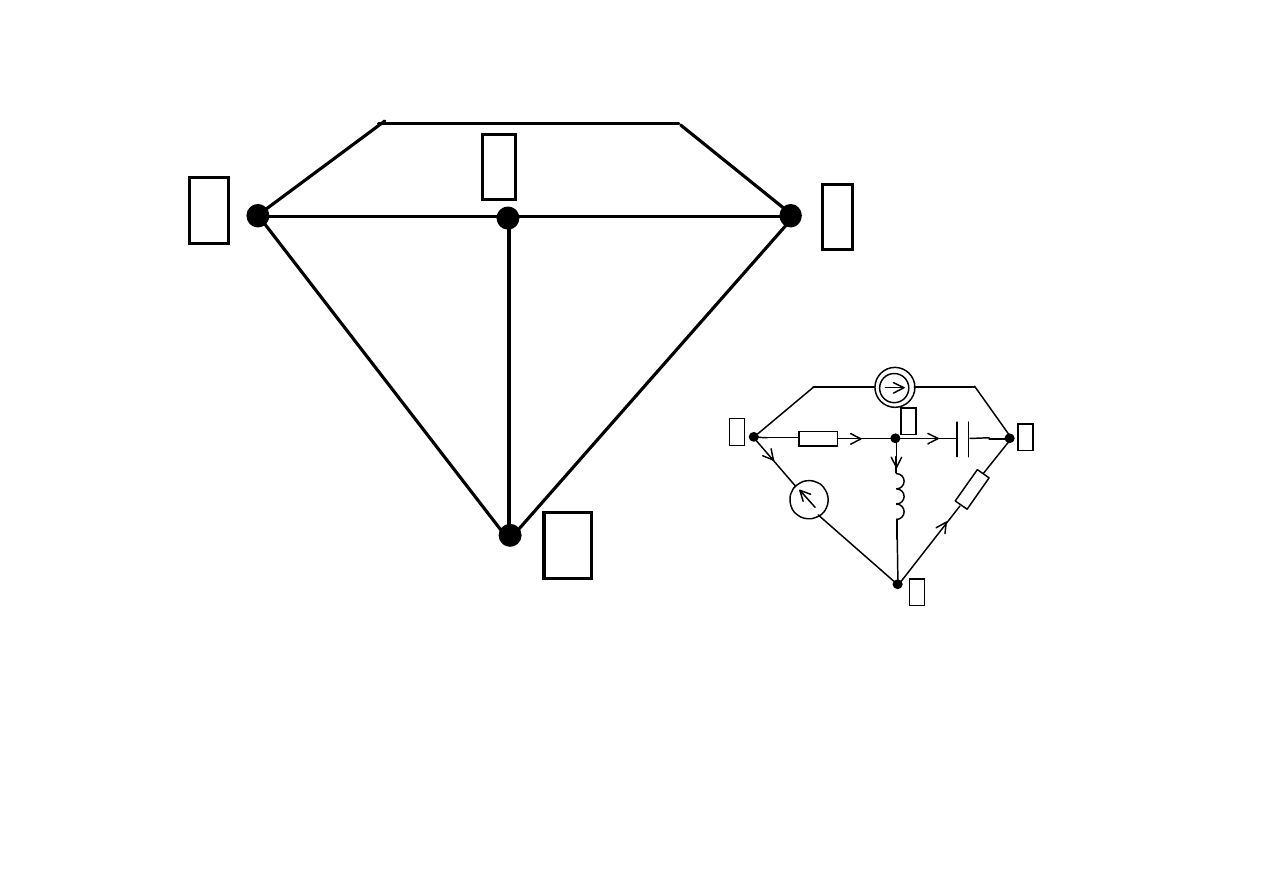
1
2
3
6
2
3
1
5
4
1
2
3
j
1
R
2
C
3
i
2
i
4
Graf
3
4
e
6
R
5
L
4
i
3
i
4
i
5
i
6
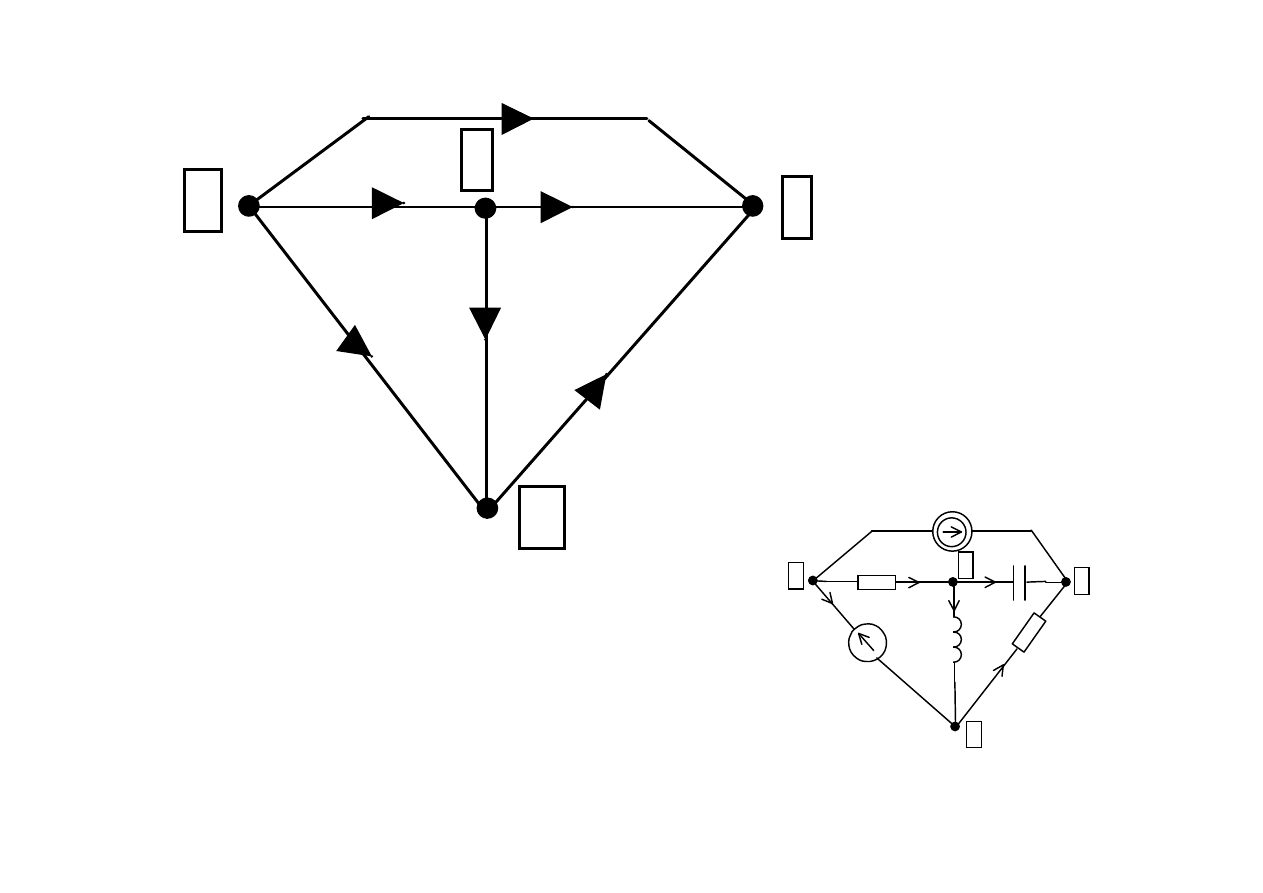
1
2
3
6
2
3
1
5
4
4
Graf zorientowany
1
2
3
4
j
1
e
6
R
2
C
3
R
5
L
4
i
2
i
3
i
4
i
5
i
6
Najważniejsze pojęcia topologiczne
Rozważamy obwód o n - węzłach i b - gałęziach
Droga
– między węzłami j oraz k
- zbiór
gałęzi grafu utworzonych w ten sposób, że
gałęzi grafu utworzonych w ten sposób, że
- kolejne gałęzie mają wspólny węzeł
- w żadnym węźle nie łączą się więcej niż dwie
gałęzie
- z węzłem j oraz k łączy się dokładnie jedna
gałąź zbioru
Przekrój grafu spójnego
– to zbiór gałęzi
spełniających następujące warunki:
---
usunięcie wszystkich gałęzi przekroju bez
węzłów końcowych powoduje podział grafu na
dwa podgrafy
dwa podgrafy
---
usunięcie wszystkich gałęzi, poza jedna
dowolnie wybraną, nie narusza spójności grafu
Graf spójny
– to graf, w którym istnieje droga
utworzona
z
gałęzi
pomiędzy
dwoma
dowolnymi węzłami grafu
Pętla
– to podgraf spełniający dwa warunki:
Pętla
– to podgraf spełniający dwa warunki:
---
podgraf jest spójny
---
w każdym węźle łączą się dwie i tylko dwie
gałęzie
Twierdzenie Tellegena
Wynika bezpośrednio z praw Kirchhoffa i topologii,
może być stosowane do dowolnego obwodu o
elementach skupionych, utworzonego z dwójników
liniowych i nieliniowych, pasywnych i aktywnych,
liniowych i nieliniowych, pasywnych i aktywnych,
stacjonarnych i niestacjonarnych.
Jeżeli prądy gałęziowe i
k
spełniają PPK w
każdym węźle grafu oraz napięcia gałęziowe uk
spełniają NPK w każdej pętli grafu, to
Twierdzenie
0
1
=
∑
=
b
k
k
k
i
u
gdzie b-liczba gałęzi grafu.
Uwaga!!!
Prądy i napięcia muszą dotyczyć tego samego
grafu, ale nie muszą odnosić się do tego samego
obwodu
Jeżeli rozpatrujemy prądy i napięcia tego samego
obwodu można podać następującą interpretację
fizyczną tw. Tellegena:
Suma mocy chwilowych wszystkich gałęzi obwodu
jest równa zeru.
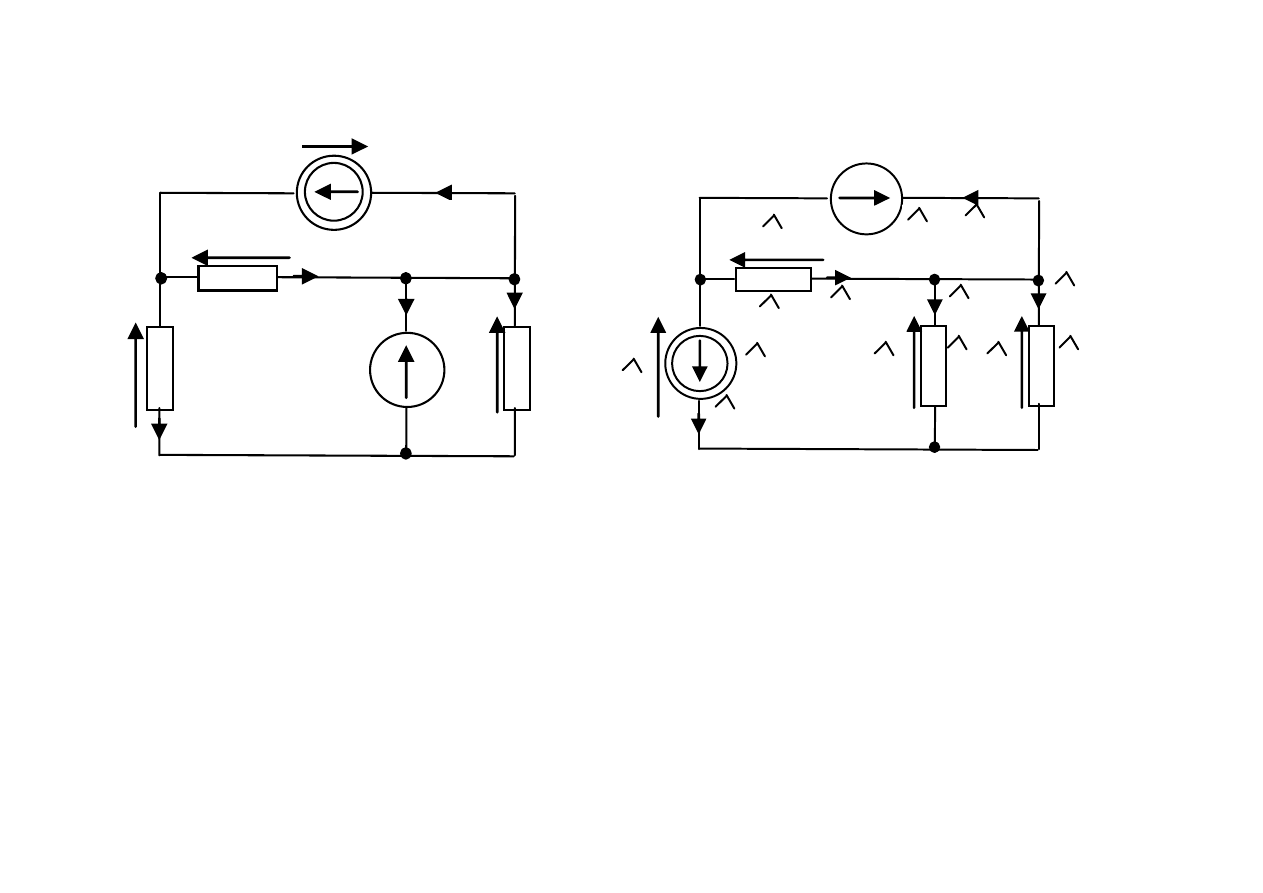
Przykład
R
1
R
2
R
3
e
4
j
5
i
5
i
4
i
3
i
2
i
1
u
1
u
2
u
5
u
3
R
2
R
3
j
1
i
5
i
4
i
3
i
2
i
1
u
1
u
2
e
5
u
3
R
4
u
4
(
)
A
j
i
R
V
e
i
2
3
,
2
,
1
1
6
5
4
=
=
Ω
=
=
(
)
A
j
i
R
V
e
i
2
ˆ
4
,
3
,
2
2
ˆ
12
ˆ
1
5
=
=
Ω
=
=
1
2
5
3
4
Po obliczeniach
ˆ
ˆ
−
=
=
=
5
1
2
4
3
równoważne
V
u
A
j
i
V
e
u
A
i
V
u
A
i
V
u
A
i
V
u
A
i
2
2
6
10
6
6
2
2
4
4
5
5
5
4
4
4
3
3
2
2
1
1
=
=
=
=
=
−
=
=
=
−
=
−
=
=
=
V
e
u
A
i
V
u
A
i
V
u
A
i
V
u
A
i
V
u
A
j
i
12
ˆ
ˆ
2
ˆ
2
ˆ
1
ˆ
2
ˆ
1
ˆ
12
ˆ
6
ˆ
14
ˆ
2
ˆ
ˆ
5
5
5
4
4
3
3
2
2
1
1
1
=
=
=
−
=
−
=
−
=
−
=
−
=
−
=
−
=
=
=
tw. Tellegena dla I obwodu
(bilans mocy)
0
4
60
36
4
16
5
5
4
4
3
3
2
2
1
1
=
+
−
+
+
=
+
+
+
+
i
u
i
u
i
u
i
u
i
u
tw. Tellegena dla II obwodu
(bilans mocy)
0
48
2
2
72
28
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
ˆ
5
5
4
4
3
3
2
2
1
1
=
−
+
+
+
−
=
+
+
+
+
i
u
i
u
i
u
i
u
i
u
tw. Tellegena
dla: prądu z I obwodu napięcia z II
0
24
20
12
24
56
ˆ
ˆ
ˆ
ˆ
ˆ
5
5
4
4
3
3
2
2
1
1
=
+
+
−
+
−
=
+
+
+
+
i
u
i
u
i
u
i
u
i
u
tw. Tellegena
dla:
napięcia z I obwodu prądy z II
0
8
6
6
12
8
ˆ
ˆ
ˆ
ˆ
ˆ
5
5
4
4
3
3
2
2
1
1
=
−
−
−
+
=
+
+
+
+
i
u
i
u
i
u
i
u
i
u
METODA POTENCJAŁÓW
WĘZŁOWYCH
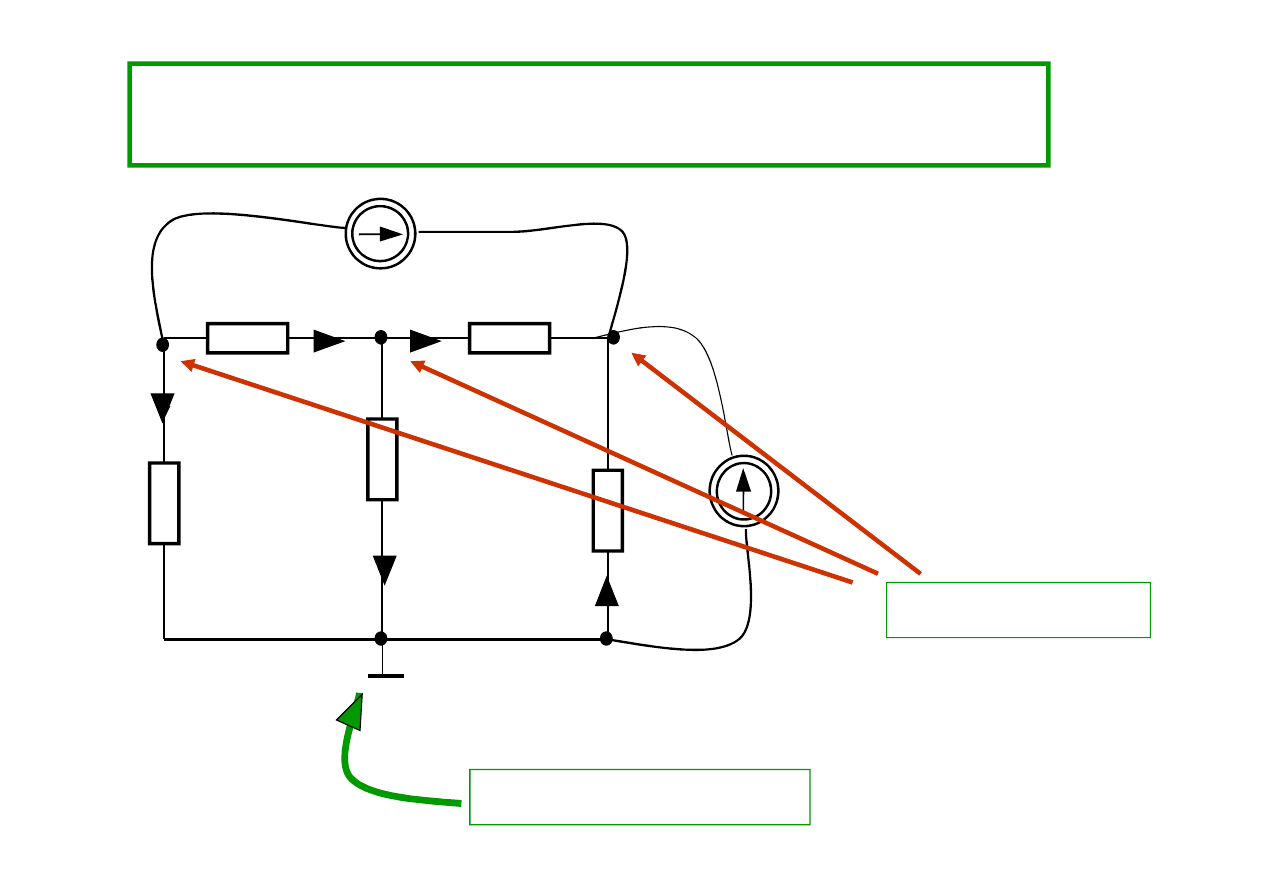
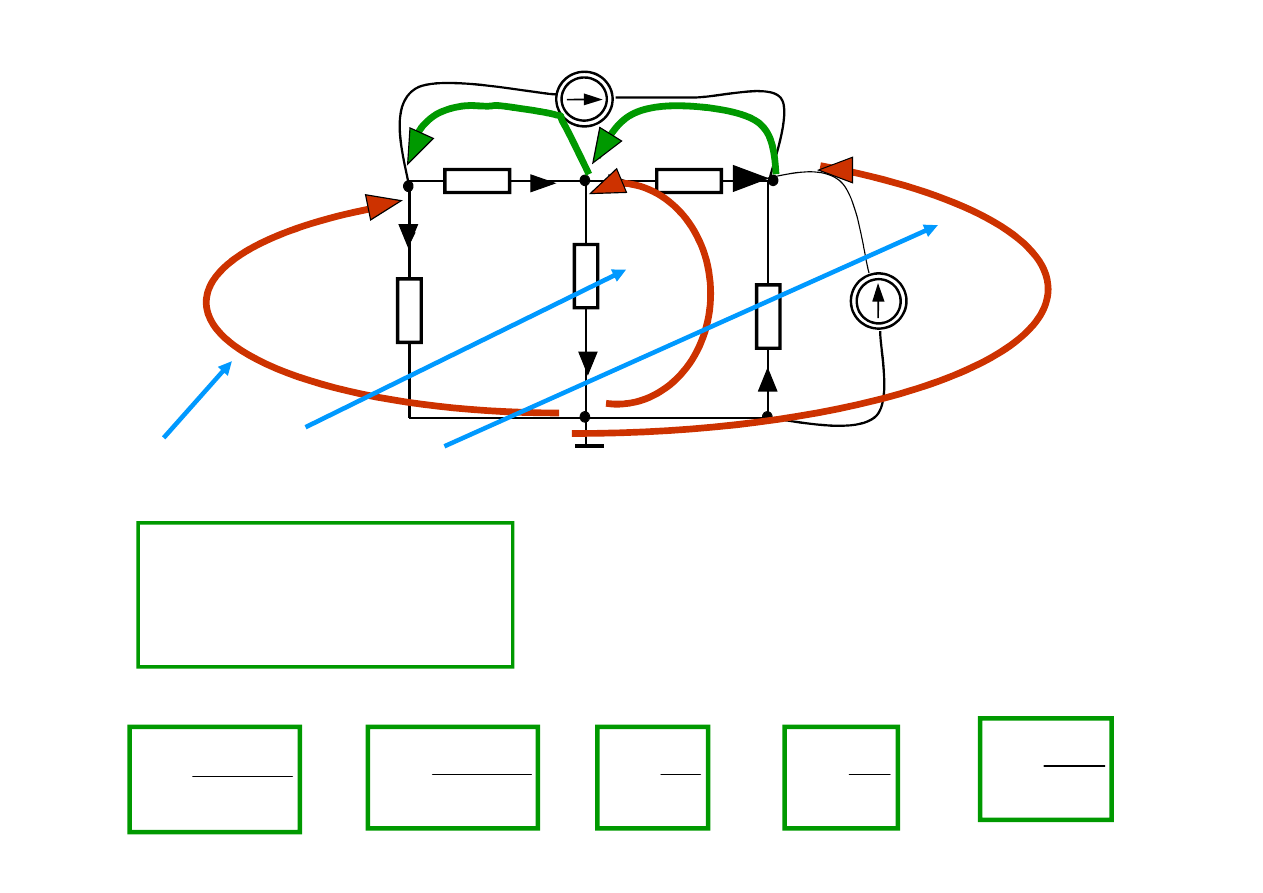
W obwodzie są 4 węzły i 7 gałęzi. Jeśli prądy źródeł są znane
– mamy 5 niewiadomych prądów.
j
6
1
2
3
R
1
R
2
j
i
4
i
1
i
2
R
4
R
5
j
7
i
3
i
5
Węzeł odniesienia
R
3
Węzły obwodu
0
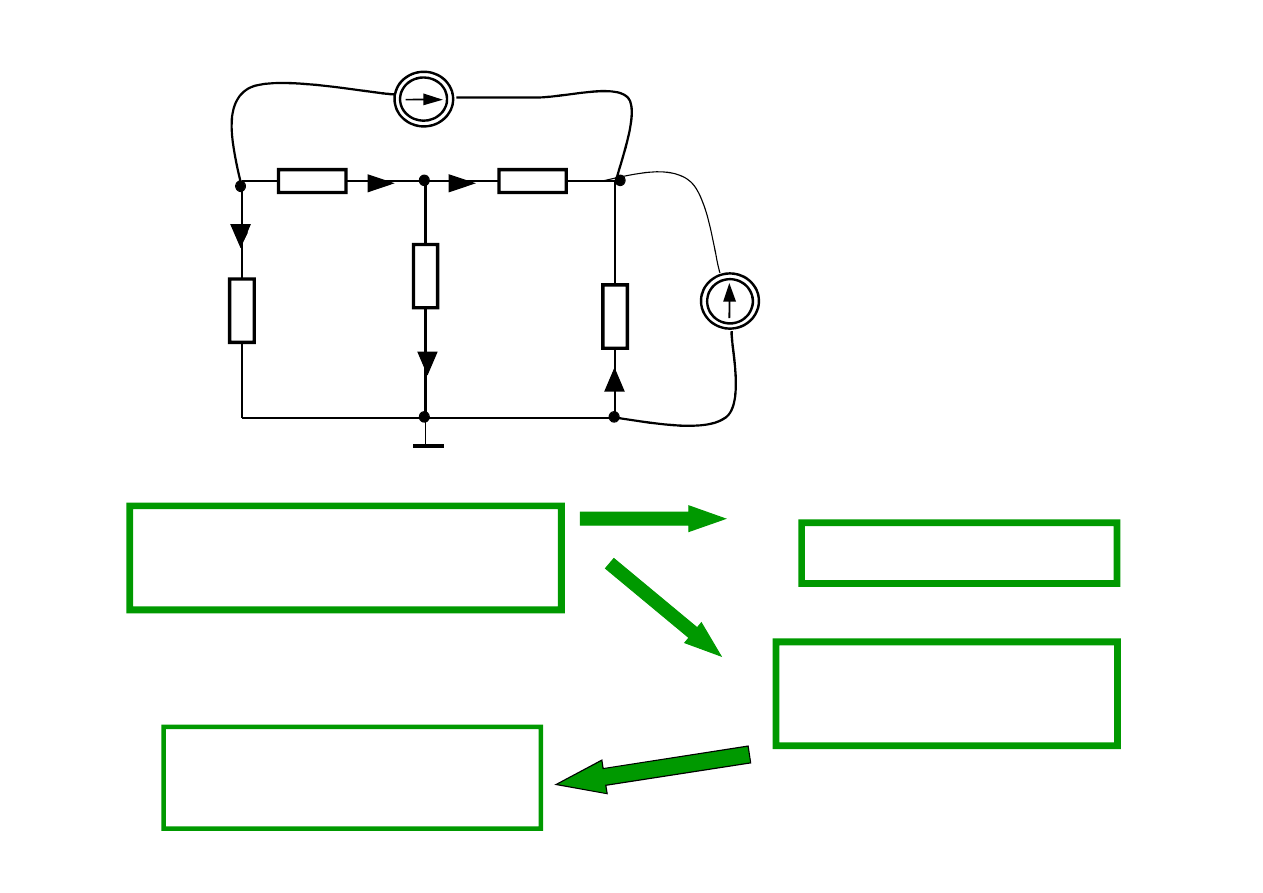
R
4
1
2
3
R
1
R
2
R
3
R
5
j
7
i
4
i
3
i
1
i
2
i
5
j
6
0
Ile można napisać równań
liniowo niezależnych?
Z PPK 3 równania
Z NPK potrzebne są
2 równania
Mamy do rozwiązania
układ 5 równań
0
1
2
3
R
1
R
2
R
3
R
5
j
7
i
4
i
1
i
5
j
6
V
1
V
2
V
3
Napięcia ( potencjały) węzłowe
i
3
i
2
0
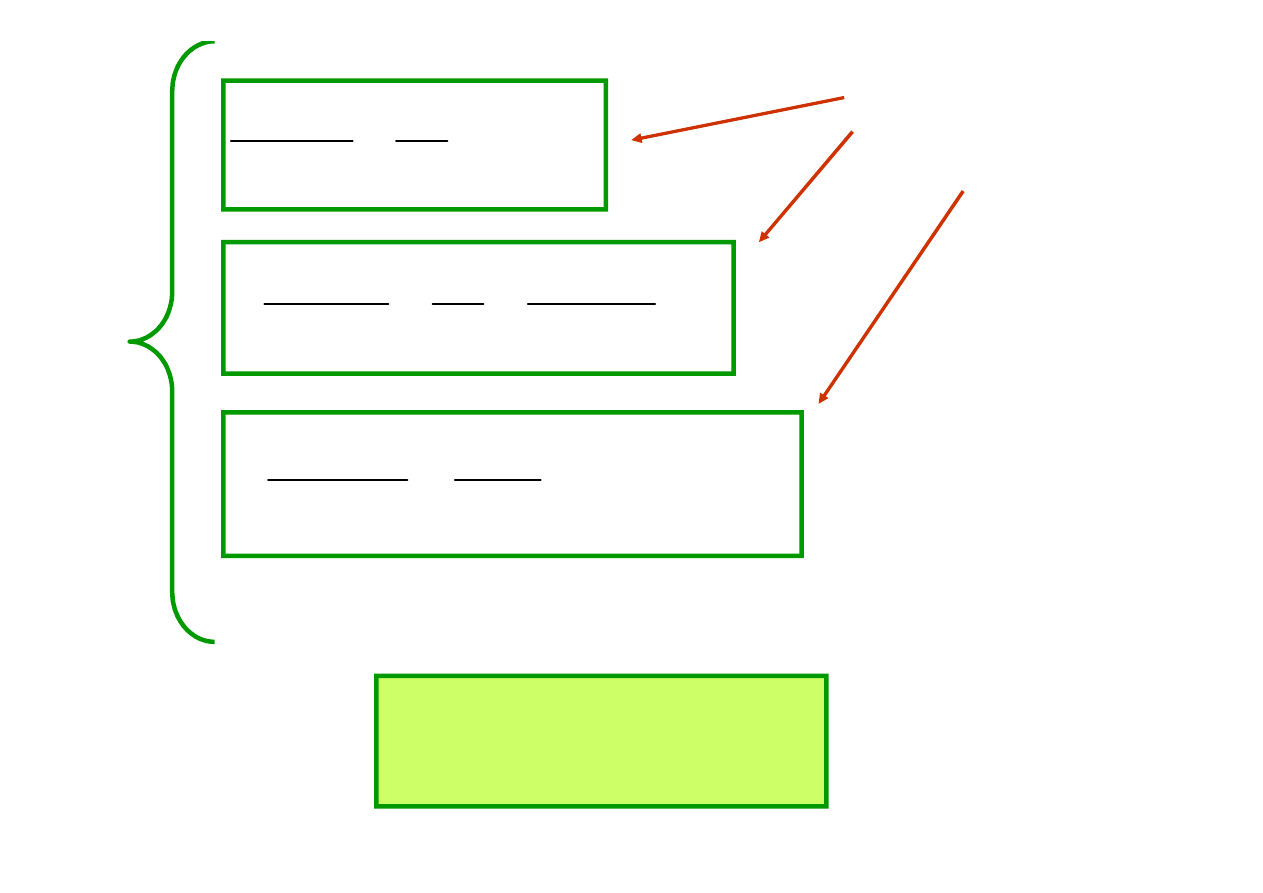
Pokażemy, że
wystarczy znajomość
trzech potencjałów węzłowych
tzn. układ trzech równań
0
.
1
6
4
1
=
+
+
j
i
i
dla
0
.
2
2
3
1
=
+
+
−
i
i
i
dla
0
.
3
7
6
5
2
=
−
−
−
−
j
j
i
i
dla
1
2
1
1
R
V
V
i
−
=
2
3
2
2
R
V
V
i
−
=
3
2
3
R
V
i =
4
1
4
R
V
i =
5
3
5
R
V
i
−
=
Napięcia ( potencjały) węzłowe
0
0
6
4
1
1
2
1
=
+
+
−
j
R
V
R
V
V
0
2
3
2
3
2
1
2
1
=
−
+
+
−
−
R
V
V
R
V
R
V
V
=
−
−
−
−
−
−
V
V
V
0
.
1
6
4
1
=
+
+
j
i
i
dla
0
.
2
2
3
1
=
+
+
−
i
i
i
dla
0
.
3
7
6
5
2
=
−
−
−
−
j
j
i
i
dla
0
7
6
5
3
2
3
2
=
−
−
−
−
−
−
j
j
R
V
R
V
V
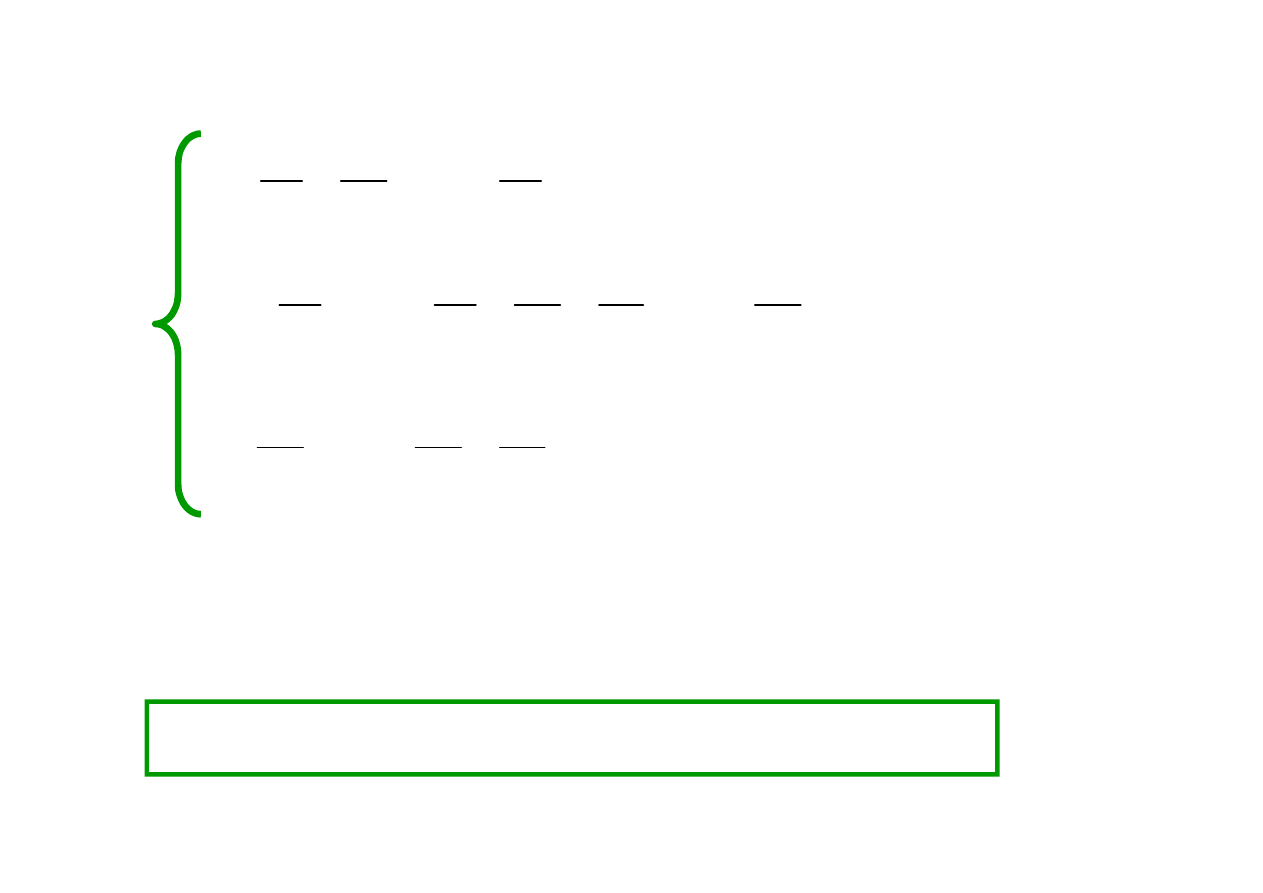
Po uporządkowaniu
otrzymamy:
6
1
2
4
1
1
1
1
1
j
R
V
R
R
V
−
=
−
+
0
1
1
1
1
1
2
3
3
2
1
2
1
1
=
−
+
+
+
−
R
V
R
R
R
V
R
V
1
1
1
j
j
V
V
+
=
+
+
−
7
6
5
2
3
2
2
j
j
R
R
V
R
V
+
=
+
+
−
a niewiadome są potencjały: V
1
, V
2
, V
3
.
Jest to opis węzłowy układu
i
G
V
G
G
V
−
=
−
+
1
2
4
1
1
)
(
0
)
(
2
3
3
2
1
2
1
1
=
−
+
+
+
−
G
V
G
G
G
V
G
V
)
(
j
j
G
G
V
G
V
+
=
+
+
−
Nasze równania możemy też zapisać następująco
7
6
5
2
3
2
2
)
(
j
j
G
G
V
G
V
+
=
+
+
−
A konduktancje G
i
użyte w opisie są równe
odwrotnością rezystancji
V
1
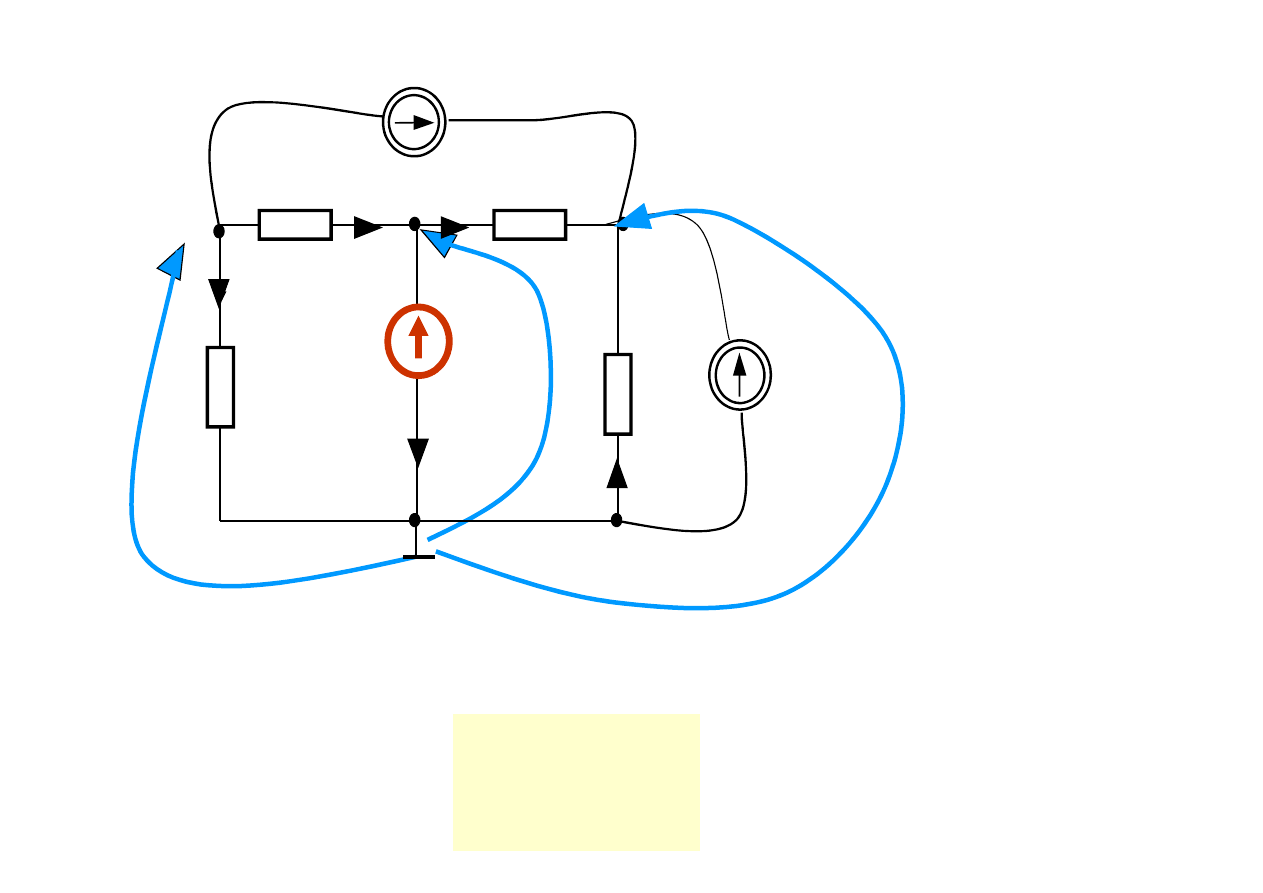
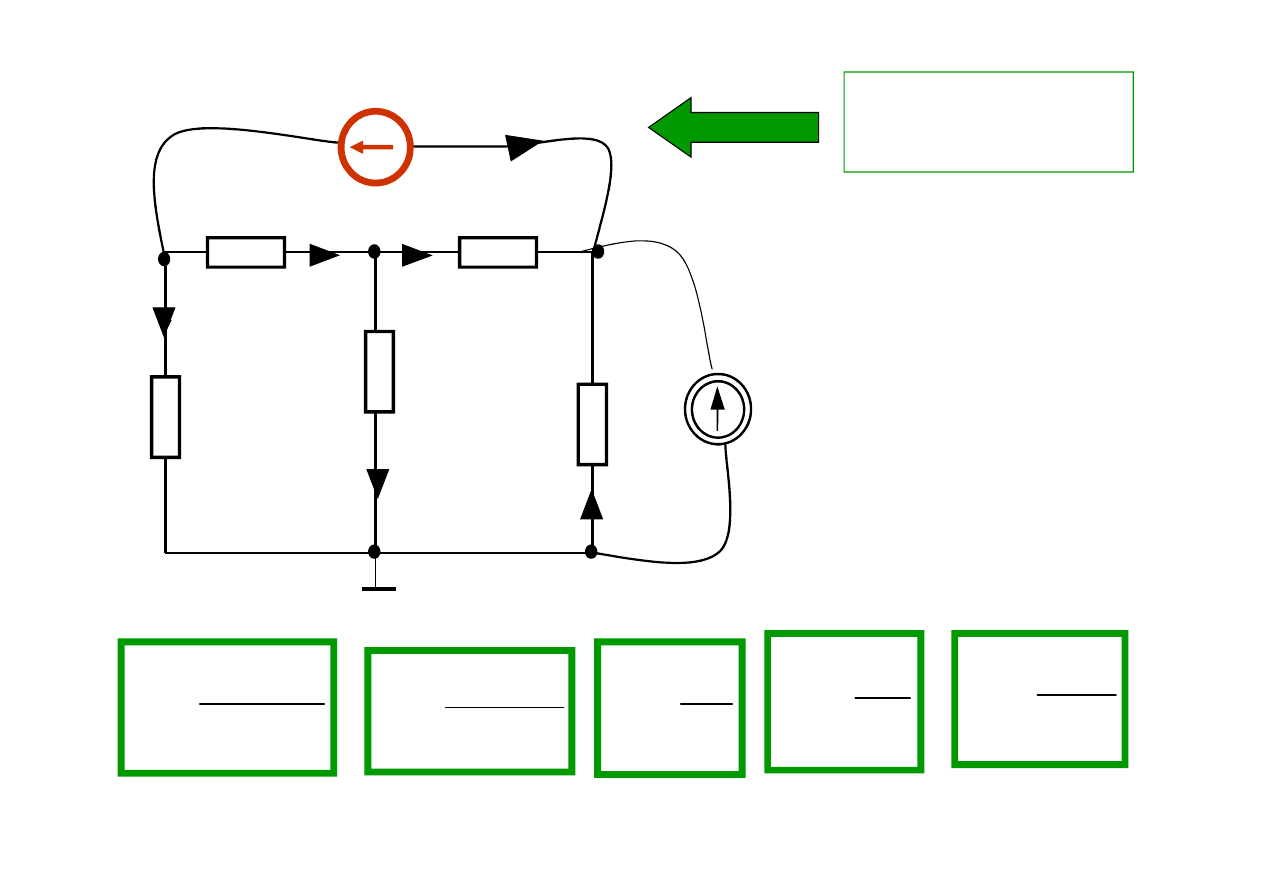
Przykład 2
V
2
j
6
1
2
3
R
1
R
2
R
5
j
7
i
4
i
i
1
i
2
e
V
3
R
4
V
1
pojawienia się idealnego źródła napięciowego dało nam
znajomość potencjału jednego węzła
e
V =
2
i
3
i
5
0
0
6
4
1
1
2
1
=
+
+
−
j
R
V
R
V
V
0
2
3
2
3
2
1
2
1
=
−
+
+
−
−
R
V
V
R
V
R
V
V
−
−
V
V
V
e
V =
2
0
7
6
5
3
2
3
2
=
−
−
−
−
−
−
j
j
R
V
R
V
V
0
6
4
1
1
2
1
=
+
+
−
j
R
V
R
V
V
0
7
6
5
3
2
3
2
=
−
−
−
−
−
−
j
j
R
V
R
V
V
3
2
e
V =
Więc układ równań ma postać
2
3
7
6
5
2
3
6
1
3
4
1
1
1
1
1
1
R
e
j
j
R
R
V
j
R
e
R
R
V
+
+
=
+
−
=
+
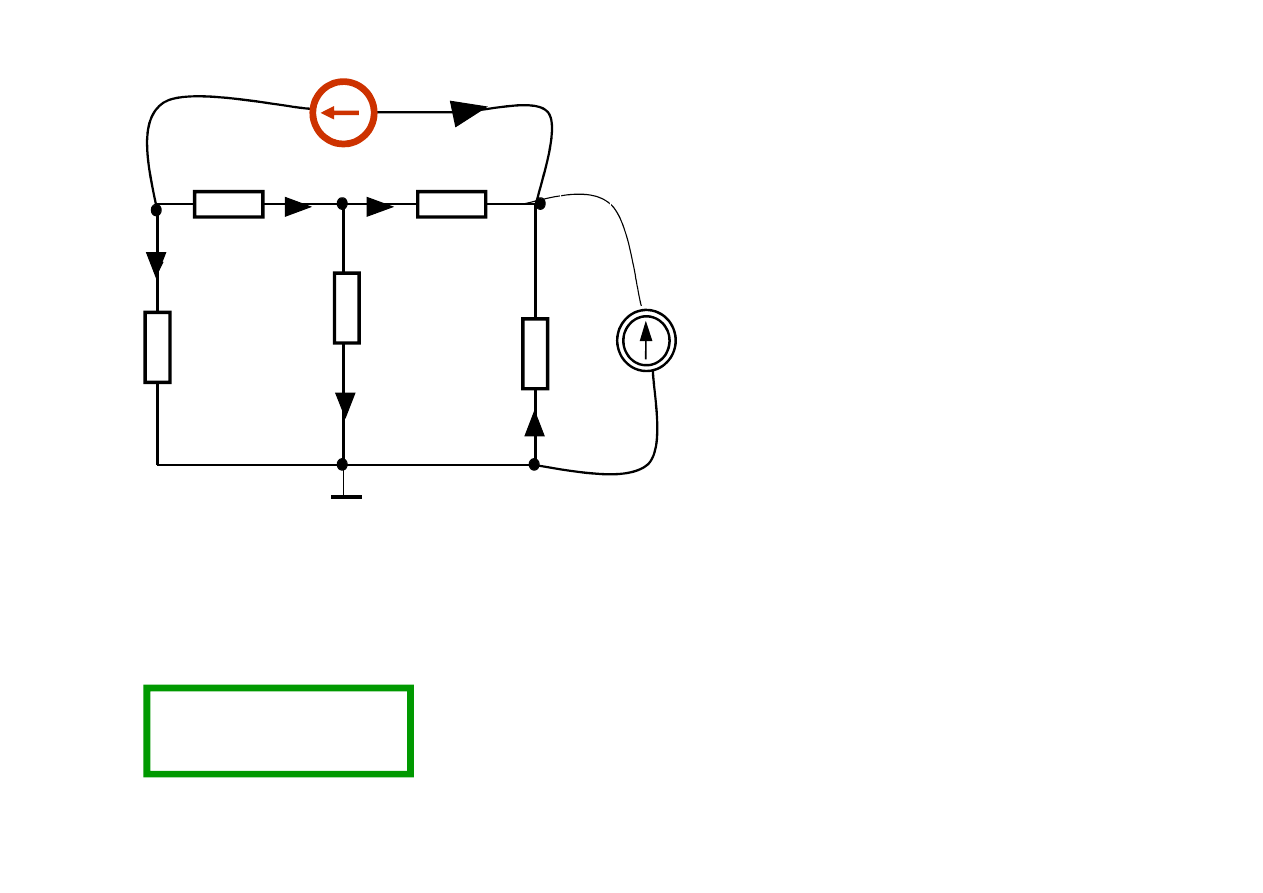
Przykład 3
e
V
V
=
−
3
1
e
j
7
1
2
3
R
1
R
2
R
5
i
4
i
1
i
2
i
R
4
1
2
1
1
R
V
V
i
−
=
2
3
2
2
R
V
V
i
−
=
3
2
3
R
V
i =
4
1
4
R
V
i =
5
3
5
R
V
i
−
=
R
5
i
3
i
5
0
e
j
7
1
2
3
R
1
R
2
R
5
i
4
i
1
i
2
i
5
i
Rozpatrzmy poprzednie
zadanie jeszcze raz
Napiszmy równania z
i
3
R
4
i
5
0
Napiszmy równania z
PPK
0
.
3
0
.
2
0
.
1
7
5
2
2
3
1
1
4
=
−
−
−
−
=
+
+
−
=
+
+
j
i
i
i
i
i
i
i
i
i
6
3
1
e
V
V
=
−
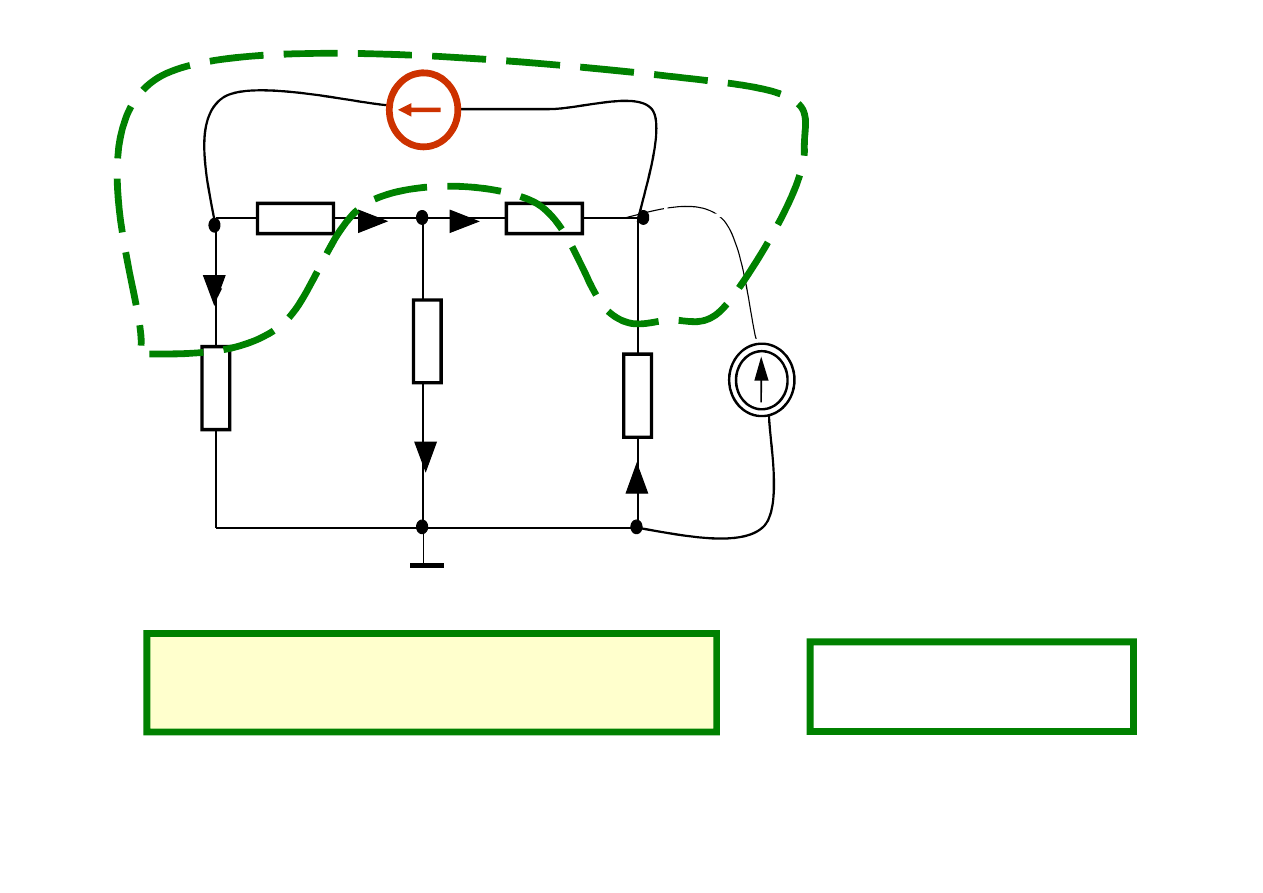
Tu w równaniach 1 i 3 mamy niewiadomy prąd
i
0
.
3
0
.
2
0
.
1
7
5
2
2
3
1
1
4
=
−
−
−
−
=
+
+
−
=
+
+
j
i
i
i
i
i
i
i
i
i
Możemy go usunąć dodając stronami oba równania
0
7
5
2
1
4
=
−
−
−
−
+
+
j
i
i
i
i
i
i
0
7
5
2
1
4
=
−
−
−
+
j
i
i
i
i
A to jest równanie dla
przekroju
4 1 2 5 7
e
j
7
1
2
3
R
1
R
2
R
5
i
4
i
i
1
i
2
R
4
i
3
i
5
0
0
7
5
2
1
4
=
−
−
−
+
j
i
i
i
i
A to jest równanie dla
przekroju 4 1 2 5 7
Procedura formułowania równań węzłowych
1. Przyjmujemy jeden węzeł za węzeł odniesienia
oraz rozpatrujemy napięcia węzłowe pozostałych węzłów
(względem odniesienia).
Napięcia węzłowe wraz z prądami źródeł napięciowych
Napięcia węzłowe wraz z prądami źródeł napięciowych
(niezależnych i sterowanych) traktujemy jako niewiadome
w budowanym układzie równań.
2. Piszemy równania, na podstawie PPK,
w poszczególnych węzłach z wykluczeniem węzła odniesienia.
3. Prądy w gałęziach z opornikiem oraz napięcia sterujące
uzależniamy od napięć węzłowych i podstawiamy do równań
wyznaczonych w p.2.
4. Napięcia niezależnych i sterowanych źródeł napięciowych
uzależniamy od napięć węzłowych, podstawiając jednocześnie
uzależniamy od napięć węzłowych, podstawiając jednocześnie
wyznaczone w p.3 zależności określające prądy i napięcia
sterujące.