1

Dynamika

Dynamika w przeciwieństwie do kinematyki zajmuje się
związkiem ruchu z jego przyczyną, tzn. z siłą.

PODSTAWOWE WIELKOŚCI

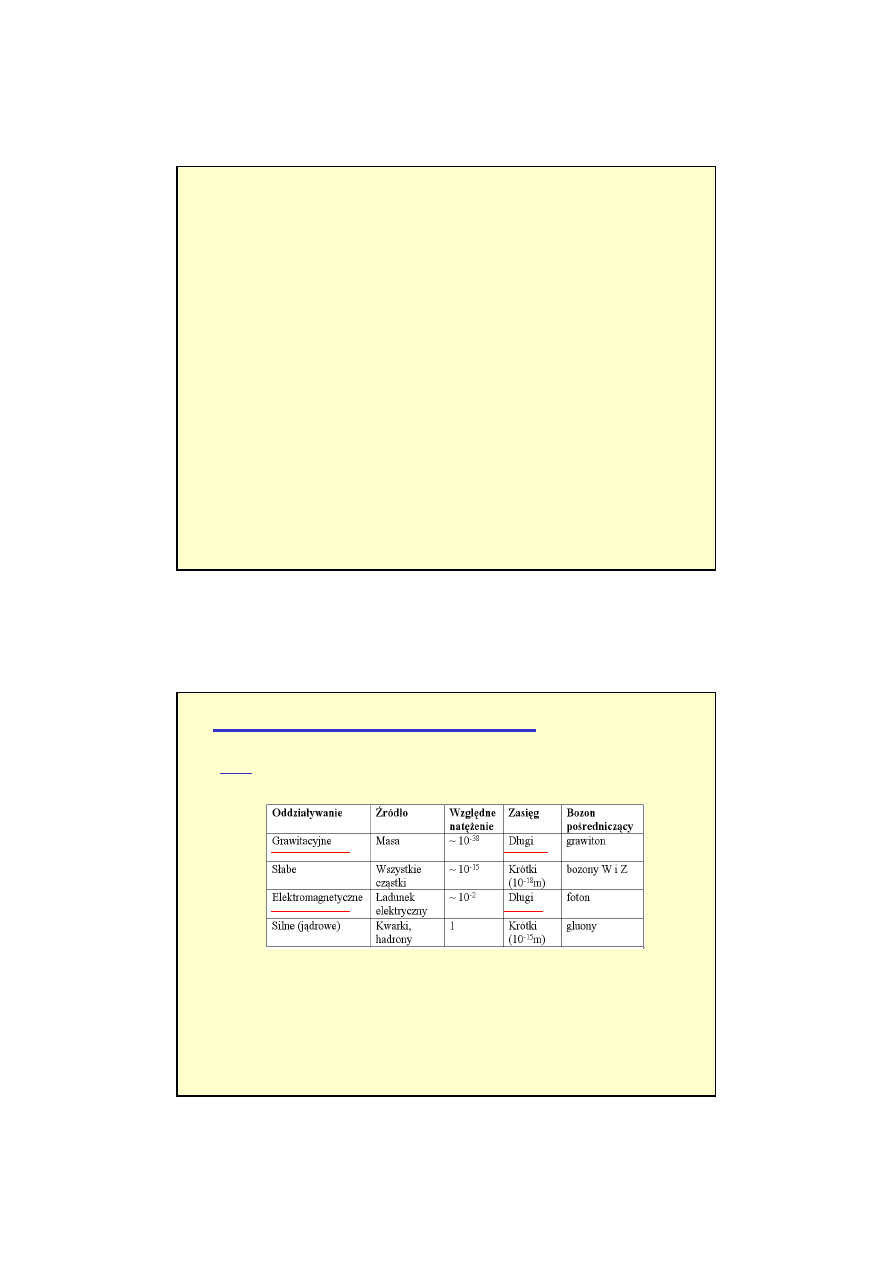
• Siła jest sposobem opisu oddziaływania ciał.

- Siła ma zdolno

ść

nadawania ciału (ciałom) przyspieszenia, czyli

rozp

ę

dzania ciała.

- Skutkiem działania siły mo

ż

e by

ć

te

ż

deformacja ciała.

- Siła jest wielko

ś

ci

ą

wektorow

ą

:

F

.

2

Masa (bezwładna) jest miar

ą

bezwładno

ś

ci ciała. Bezwładno

ść

, to

pewna cecha ciała, która objawia si

ę

podczas rozp

ę

dzania lub

zatrzymywania, czyli gdy wskutek działania siły ciało doznaje
przyspieszenia lub opó

ź

nienia.

Im wi

ę

ksza masa tym wi

ę

kszej siły (proporcjonalnie do masy)

nale

ż

y u

ż

y

ć

aby uzyska

ć

dane przyspieszenie:

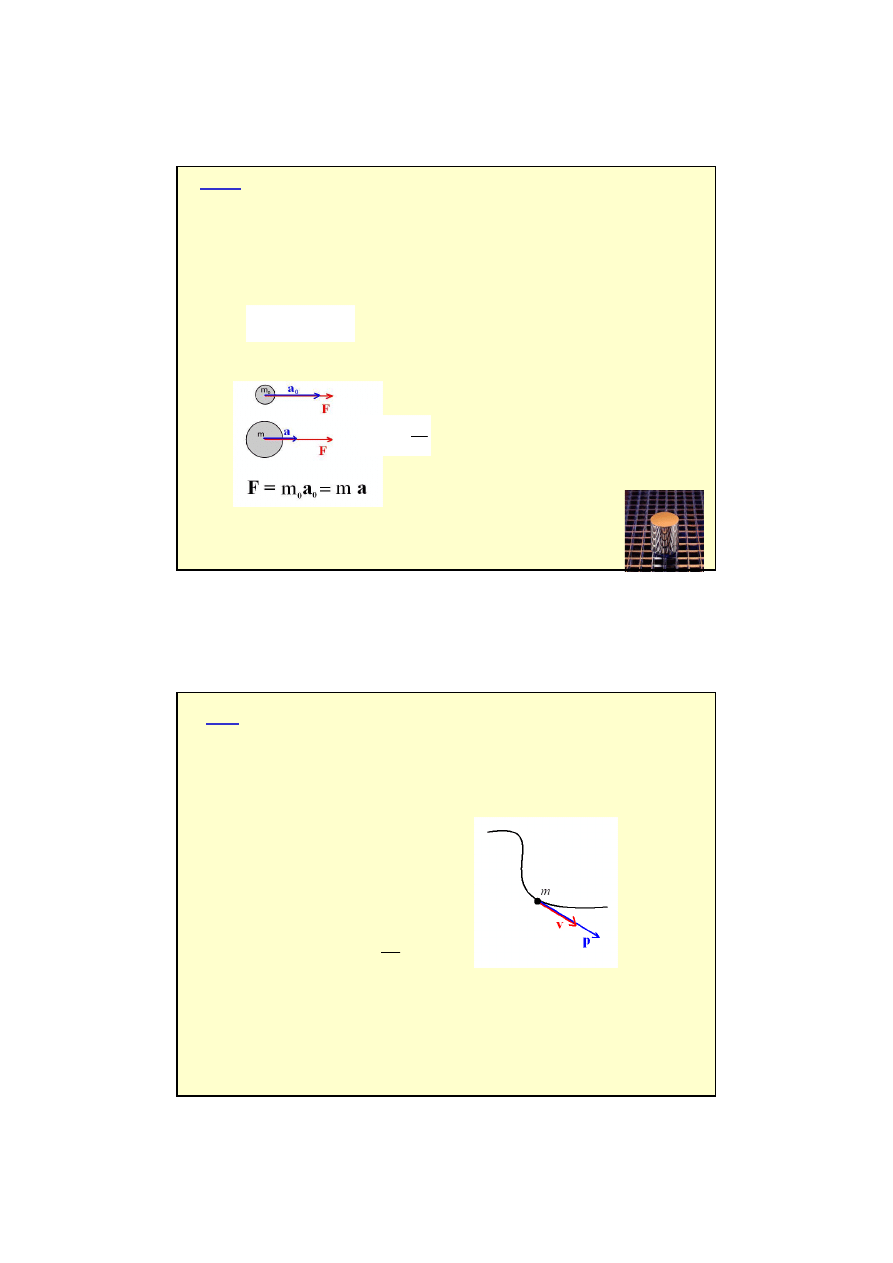
masy mo

ż

na porównywa

ć

:

a

a

m

m

0

0

=

Jednostk

ą

masy jest kilogram: 1 kg

wzorzec jest wykonany ze stopu platyny z irydem i przechowywany w
Międzynarodowym Biurze Miar w Sèvres koło Paryża.

a

F

m

=

• P

ę

d jest wielko

ś

ci

ą

stosowan

ą

do opisu ciał w ruchu.

Im wi

ę

kszy p

ę

d tym „trudniej” zatrzyma

ć

ciało (tzn. trzeba u

ż

y

ć

wi

ę

kszej siły w okre

ś

lonym czasie).

Na wielko

ść

p

ę

du wpływa masa ciała oraz pr

ę

dko

ść

z jak

ą

si

ę

ciało porusza.

Jednostk

ą

p

ę

du jest

Ś

cisła definicja p

ę

du:

v

p

m

=

s

m

kg

3

const

dt

d

wyp

=

⇒

=

=

=

=

∑

v

v

a

F

F

0

0

I.

Jeżeli na ciało (o stałej masie) nie działa żadna siła lub

wypadkowa działających sił wynosi zero to ciało porusza się
ruchem jednostajnym prostoliniowym lub pozostaje w
spoczynku.

II.

Jeśli na ciało o stałej masie m działa siła

F

to nadaje

ona ciału przyspieszenie

a

, przy czym związek między

tymi wielkościami jest następujący:

a

F

m

=

ZASADY (PRAWA) DYNAMIKI NEWTONA

1686 –Isaac Newton: „Philosophiae
Naturalis Principia Mathematica”

(Matematyczne podstawy filozofii przyrody)

III.

Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na ciało

pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na
drugie (siła akcji równa jest sile reakcji).

F

akcji

F

reakcji

a)

B

A

F

AB

F

BA

b)

BA

AB

F

F

−

=

* Definicja układu inercjalnego: jest to taki układ, w którym spełnione są
zasady dynamiki Newtona.

UWAGA:

const

m

dla

m

dt

d

m

=

=

=

a

v

F

WNIOSKI:

1)

II zas. dynamiki Newtona

.

0

0

const

dt

d

wyp

=

⇒

=

⇒

=

=

∑

p

p

F

F

2)

zasada zachowania pędu

dt

d

m

dt

m

d

dt

)

d(m

v

v

v

F

+

=

=

czyli:

Ogólniejsze prawo (analogiczne do drugiej zasady dynamiki Newtona) mówi, że tempo
zmian pędu ciała jest równe sile wypadkowej działającej na to ciało:

Punkt materialny: uogólnienie II zasady dynamiki Newtona
i zasada zachowania p

ę

du.

t

t

const

dla

t

∆

=

∆

⇒

∆

∆

=

=

=

F

p

p

F

F

p

F

.

d

d

4

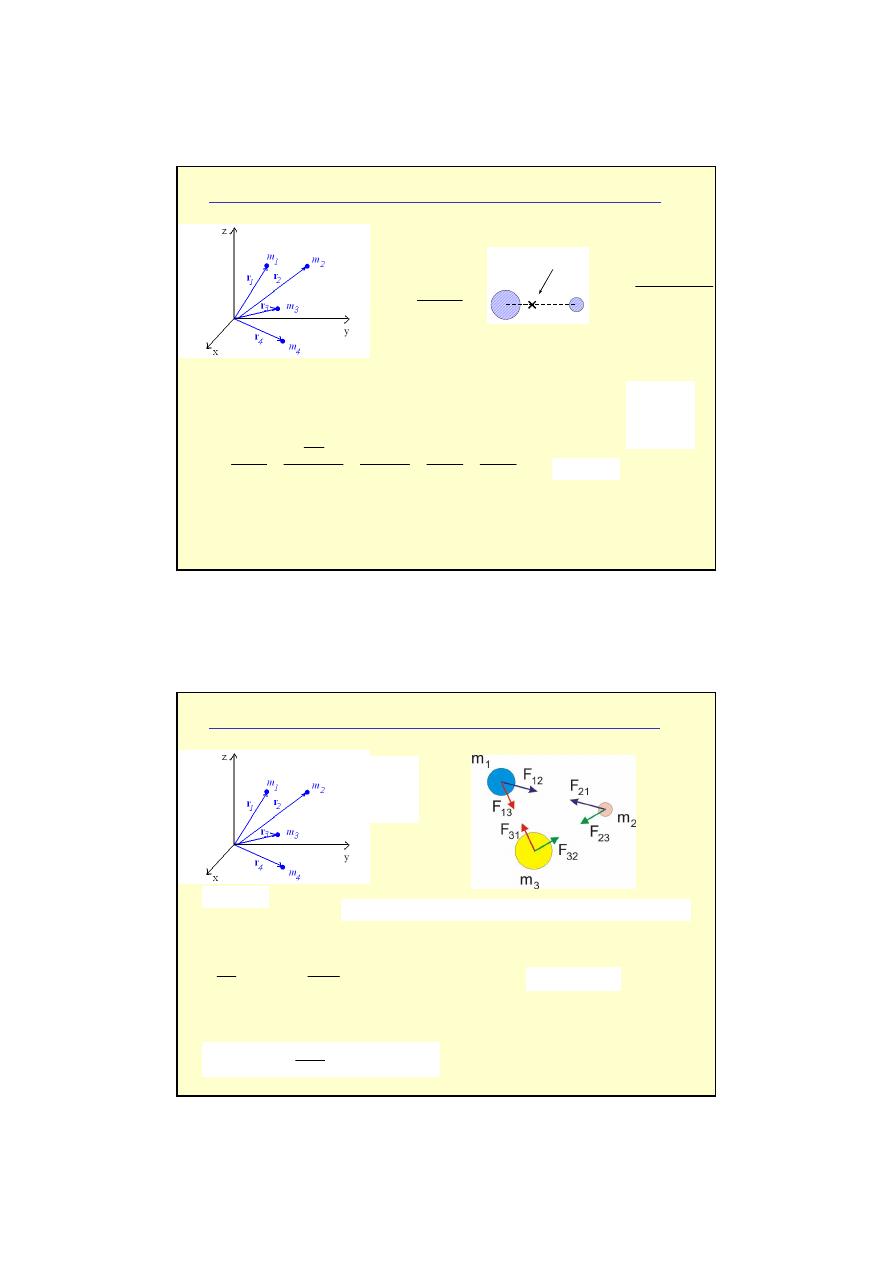
Układ ciał –

ś

rodek masy i zasady dynamiki Newtona

m

m

=

i

N

=1

i

i

N

=1

i

∑

∑

r

R

i

sm

m

+

m

m

+

m

=

2

1

2

1

r

r

R

2

1

sm

ś

rodek masy

∑

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

=

=

=

=

=

=

N

i

i

N

i

i

N

i

N

i

i

N

i

i

N

i

i

N

i

i

m

m

m

m

m

m

dt

dt

d

1

1

1

1

1

1

1

d

ca ł

i

i

i

sm

sm

p

p

v

r

R

V

⇒

∑

=

=

N

i

i

m

M

1

oznaczmy:

sm

V

P

M

=

całkowity pęd = pęd sm

cał

p

P

=

Układ ciał – zasady dynamiki Newtona i srodek masy

sm

sm

a

V

F

P

M

dt

d

M

dt

d

zew

=

=

=

⇒

sm

a

F

M

zew

=

siła zewnętrzna powoduje przyspieszenie sm

const.

t

=

⇒

=

⇒

=

∑

cał

cał

zew

p

p

F

0

d

d

0

zasada zachowania pędu dla układu ciał

0

:

32

23

31

13

21

12

=

+

+

+

+

+

F

F

F

F

F

F

ch

wewnetrzny

sił

suma

∑

=

=

N

i

i

m

M

1

cał

p

P

=

sm

V

P

M

=

5

Przykład zasady zachowania p

ę

du

-

wystrzał z armatki

prawo zachowania pędu:









+

+

=

+

=

Ziemi

Ziemi

a

py

p

a

a

px

p

M

M

m

M

m

)v

v

v

v

(

0

0













>>

≈

+

−

=

−

=

−

=

p

Ziemi

Ziemi

a

py

p

Ziemi

a

p

p

a

px

p

a

m

M

ponieważ

M

M

m

M

m

M

m

0

(

cos

)

v

v

v

v

v

α

Pomimo, że siła wypadkowa = 0 to ciało może być wprawione w ruch - obrót

ZASADY DYNAMIKI NEWTONA
DLA RUCHU OBROTOWEGO

0

=

wyp

F

0

d

d

=

t

p

0

=

a

p

r

L

×

=

⊥

=

=

p

r

p

r

L

θ

sin

Wielkościami, używaną do opisu ruchu obrotowego są:
moment pędu L (analogiczny do pędu) i moment siły M (analogiczny do siły)

F

r

M

×

=

⊥

=

=

F

r

F

r

M

θ

sin

6

t

d

dL

M

=

Zmiana pędu w czasie jest równa sile (F), a zmiana momentu pędu w czasie momentowi
siły (M). Uwaga: moment siły i moment pędu zdefiniowane są względem tego samego
punktu.

t

d

dp

F

=

II zas. dynamiki Newtona:

Druga zasada dynamiki dla ruchu obrotowego:

0

=

M

.

const

=

L

Jeśli wypadkowy moment sił działających na ciało jest równy zeru, to moment pędu
tego ciała jest zachowany (względem okreslonego punktu).

Zasada zachowania momentu pędu dla ruchu obrotowego:

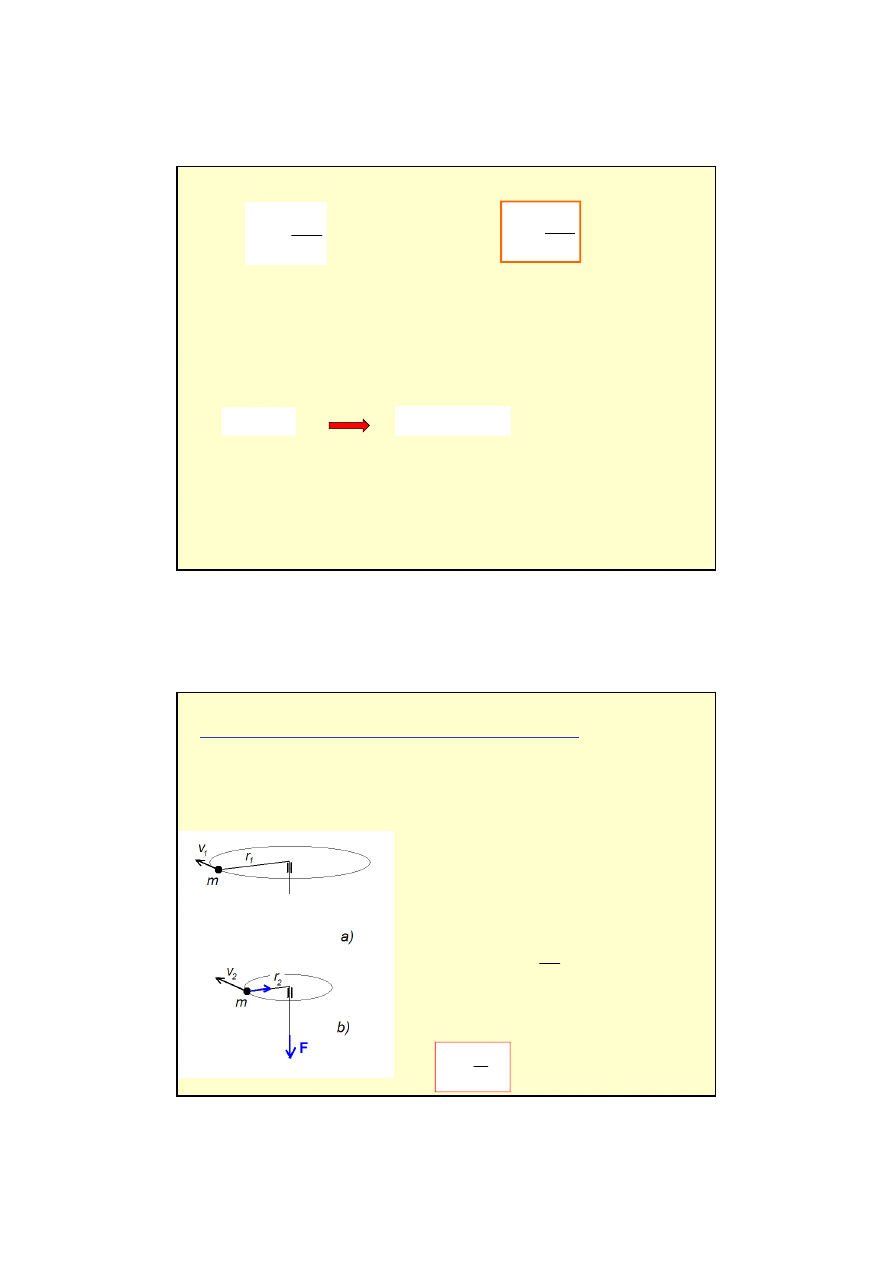
Przykład zasady zachowania momentu p

ę

du

Ciało o masie m porusza się w płaszczyźnie poziomej po okręgu o promieniu r

1

(a). Prędkość

liniowa ciała wynosi v

1

. Ile razy zmieni się prędkość liniowa ciała, jeśli pociągając za sznurek

jak na rys (b) zmniejszymy promień okręgu do długości r

2

(b) . Zakładamy, że nie działa siła

grawitacji.

a)

1

1

v

r

m

L

m

=

=

1

1

v

r

L

x

1

1

v

r

⊥

const.

0

d

d

0

=

⇒

=

⇒

=

=

L

L

F

r

M

1

t

x

b)

siła F działa wzdłuż sznurka i zawsze prostopadle

do prędkości ciała , czyli:

F

r

1

||

2

2

1

1

v

v

r

m

r

m

L

=

=

1

2

1

2

v

v

r

r

=

1

1

v

r

m

L

m

=

=

1

1

v

r

L

x

7

const.

t

wyp

=

⇒

=

⇒

=

p

p

F

0

d

d

0

Zasada zachowania pędu :

const.

t

wyp

=

⇒

=

⇒

=

L

L

M

0

d

d

0

Zasada zachowania momentu pędu :

ZASADY ZACHOWANIA:
PĘDU I MOMENTU PĘDU

Punkt materialny:

Układ punktów materialnych:

const.

t

=

⇒

=

⇒

=

∑

cał

cał

zew

p

p

F

0

d

d

0

Zasada zachowania pędu :

const.

t

=

⇒

=

⇒

=

∑

cał

cał

zew

L

L

M

0

d

d

0

Zasada zachowania momentu pędu :

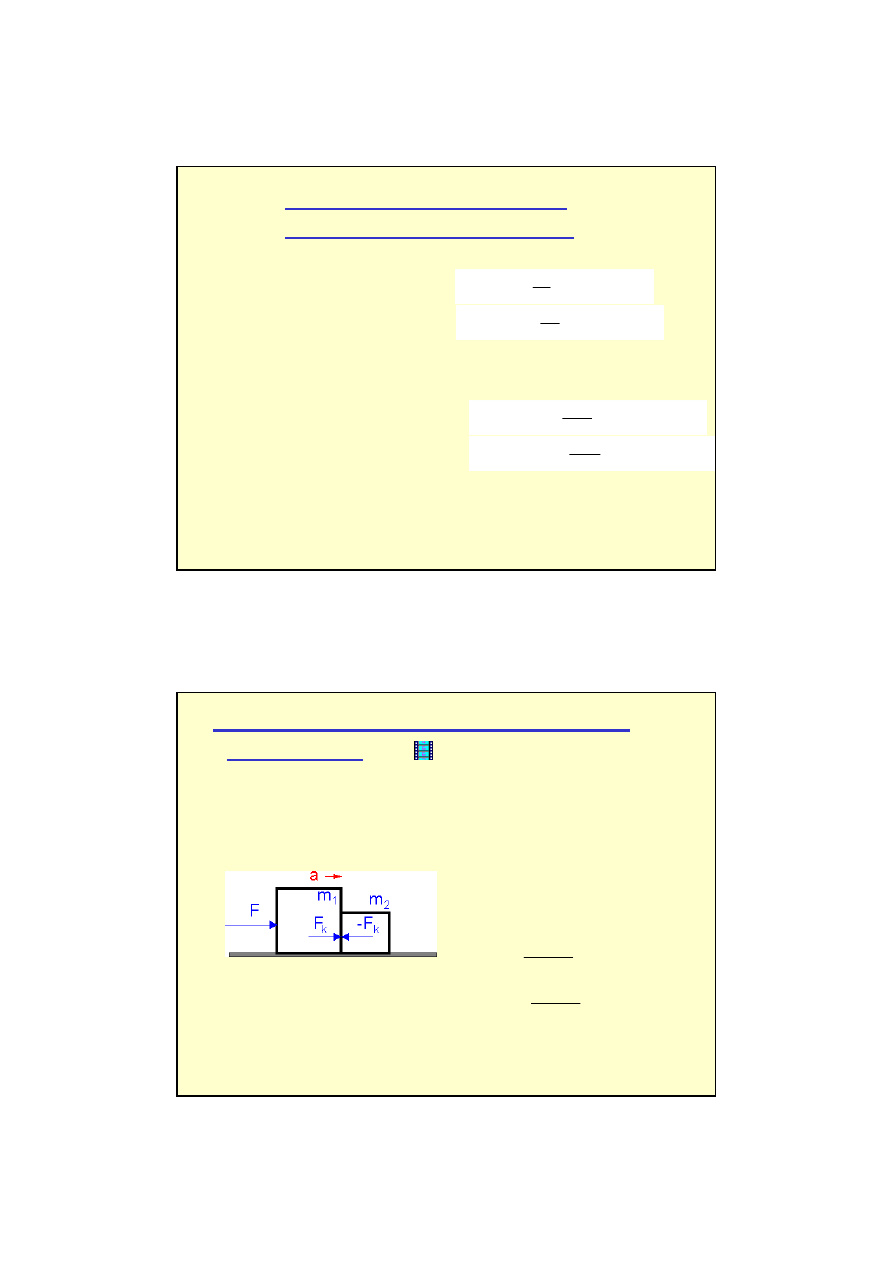
Siły kontaktowe

Gdy dwa ciała są dociskane do siebie to występują między nimi

siły kontaktowe

.

PRZYKŁADY SIŁ RZECZYWISTYCH

Źródłem tych sił jest odpychanie pomiędzy atomami, jest to siła elektromagnetyczna.

a

a

F

1

2

m

m

=

−

Siła kontaktowa

F

k

to siła z jaką klocek o masie m

1

działa na klocek o masie m

2

nadając mu przyspieszenie.







=

=

−

a

F

a

F

F

2

1

m

m

k

k













+

=

+

=

F

F

F

a

2

1

2

2

1

m

m

m

m

m

k

8

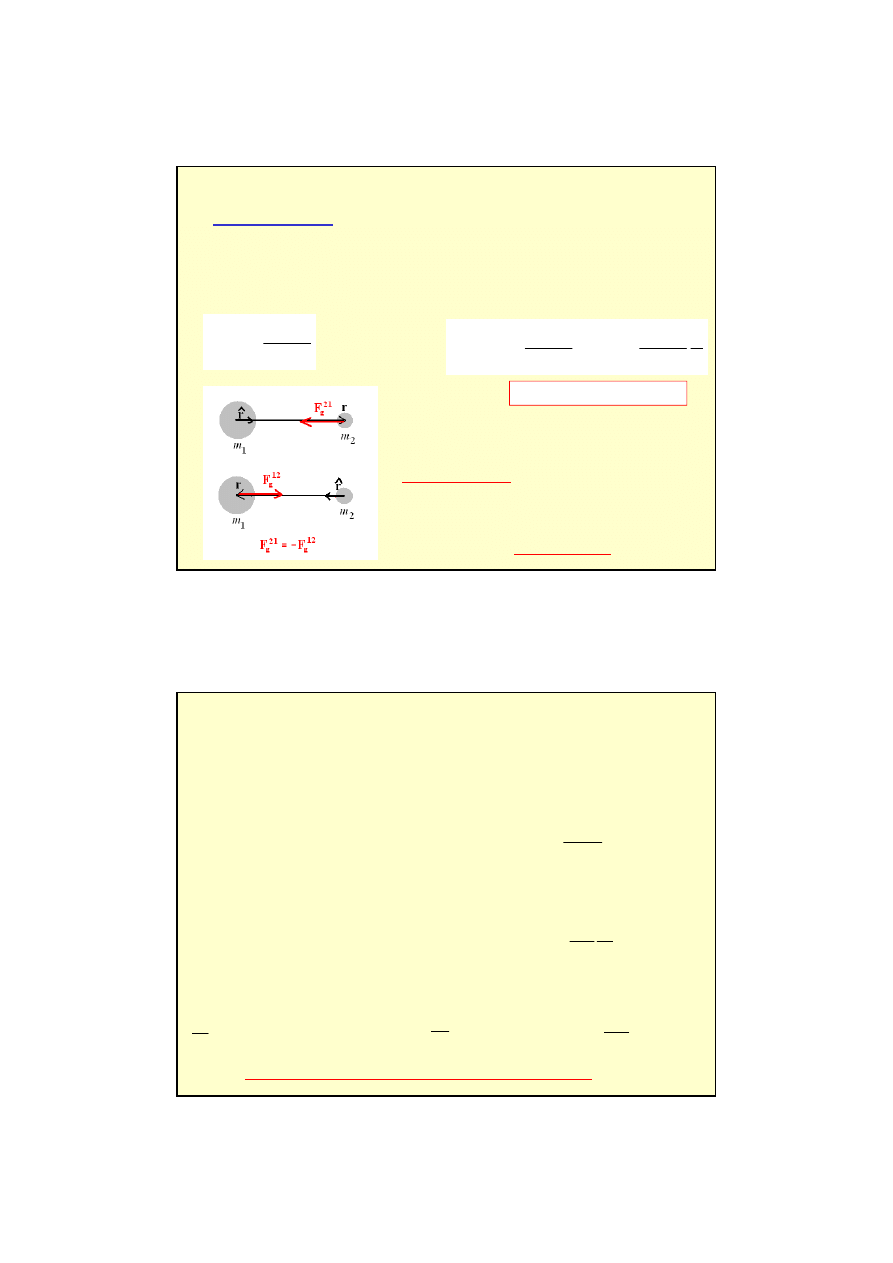
Każde dwa ciała o masach m

1

i m

2

przyciągają się wzajemnie siłą grawitacji wprost

proporcjonalną do iloczynu mas, a odwrotnie proporcjonalną do kwadratu odległości
między nimi (tj. między ich środkami mas).

2

2

1

r

m

m

G

F

=

r

r

m

m

G

r

m

m

G

g

r

r

F

2

2

1

2

2

1

ˆ

−

=

−

=

lub wektorowo

Masy m

1

i m

2

występującą we powyższym wzorze

nazywamy masami grawitacyjnymi.

Siła grawitacji

Masa występująca w II zasadzie dynamiki
Newtona ( F=ma) to masa bezwładna.

Masa grawitacyjna jest źródłem oddziaływania
grawitacyjnego.

2

2

11

kg

Nm

10

6754

.

6

G

−

−

×

=

Siła grawitacji – masa grawitacyjna i bezwładna

Czy masa bezwładna i masa grawitacyjna ciała są sobie równe ???

Obliczamy przyspieszenia jakie uzyskuje masa

m (bezwładna)

spadająca swobodnie w

pobliżu powierzchni Ziemi.

ma

Q

=

II zasada dynamiki Newtona mówi, że:

m

m

R

M

G

a

Z

Z

'

2

=

Obliczamy przyspieszenie:

Masa grawitacyjna i bezwładna są sobie równe !!!

Doświadczalnie stwierdzono, że wszystkie ciała spadają (w próżni) w pobliżu Ziemi z tym
samym przyspieszeniem a = g.

const

m

m

=

'

dobierzmy G tak aby:

1

'

=

m

m

wtedy:

2

Z

Z

R

M

G

g

=

2

'

Z

Z

R

M

m

G

Q

=

Na masę

m’ (grawitacyjną)

działa siła ciężkości:

9

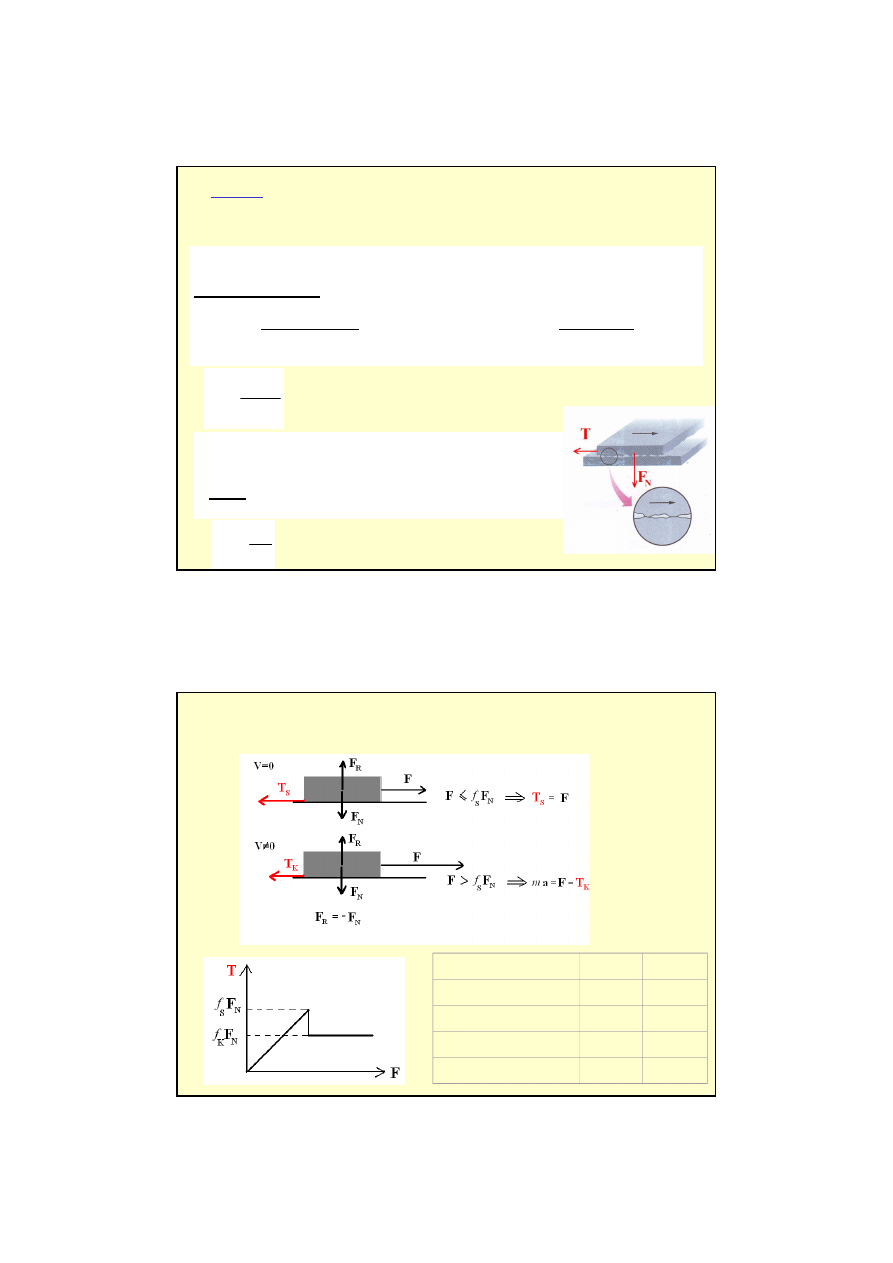
Siła tarcia to siła, która działa stycznie do powierzchni zetknięcia ciał i przeciwdziała
przesunięciu jednego ciała po drugim.

• Siłę tarcia działającą między nieruchomymi powierzchniami nazywamy

tarciem statycznym T

s

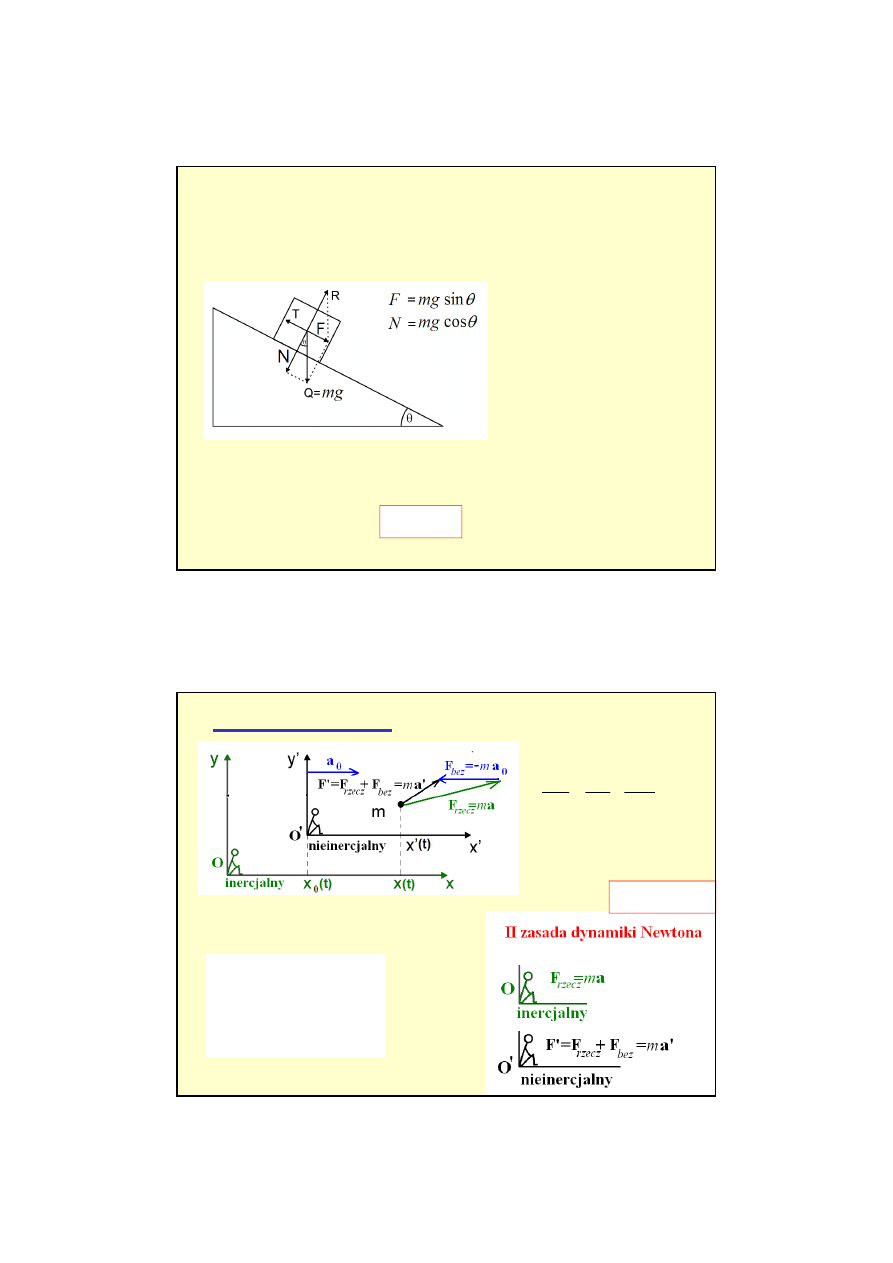
Prawa dotyczące tarcia:
- T

s (max)

(maksymale tarcie statyczne) jest w przybliżeniu niezależna od wielkości pola

powierzchni makroskopowego styku ciał (uwaga powierzchnia styku rzeczywistego może być
nawet 10000 razy mniejsza),
- T

s (max)

jest proporcjonalna do siły z jaką jedna powierzchnia naciska na drugą.

N

s

s

F

T

f

(max)

=

Stosunek maksymalnej siły T

s(max)

do siły nacisku F

N

nazywamy

współczynnikiem tarcia statycznego f

s

Tarcie

Stosunek siły T

k

do siły nacisku F

N

nazywamy

współczynnikiem tarcia kinetycznego f

k

• Gdy ciało porusza się, to mamy do czynienia z siłą

tarcia

kinetycznego T

k

Prawo:
T

k

nie zależy od prędkości względnej poruszania się powierzchni.

N

k

k

F

T

f

=

Tarcie – przykład 1

Rodzaj powierzchni

f

s

f

k

Stal po stali

0.15

0.03- 0.09

Drewno po drewnie

0.54

0.34

Drewno po kamieniu

0.7

0.3

Stal po lodzie (np. łyżwy)

0.027

0.014

10

Tarcie – przykład 2

Ciało o masie m spoczywa na równi pochyłej, której kąt nachylenia θ stopniowo zwiększamy.
Przy jakim granicznym kącie nachylenia ciało zacznie się zsuwać jeżeli współczynnik
tarcia statycznego klocka o równię wynosi f

s

?

θ

cos

max

Q

f

T

s

=







=

=

θ

θ

cos

sin

Q

N

Q

F

θ

tg

f

s

<

θ

θ

sin

cos

max

Q

Q

f

F

T

s

<

⇒

<

ciało zsuwa się

SIŁY POZORNE

0

bez

a

F

m

−

=

)

(

)

(

)

(

'

0

t

x

t

x

t

x

−

=

x

x

x

a

a

a

,

0

'

−

=

2

0

2

2

2

2

2

'

t

d

x

d

t

d

x

d

t

d

x

d

−

=

rozpatrzmy składową x:

bez

rzecz

0

0

F

F

a'

a

a

a'

a

a

a'

+

=

−

+

=

−

=

m

m

m

m

)

(

Iloczyn masy i przyspieszenia unoszenia (ze
znakiem minus) nazywamy siłą bezwładności F

bez

.

Ogólnie:

11

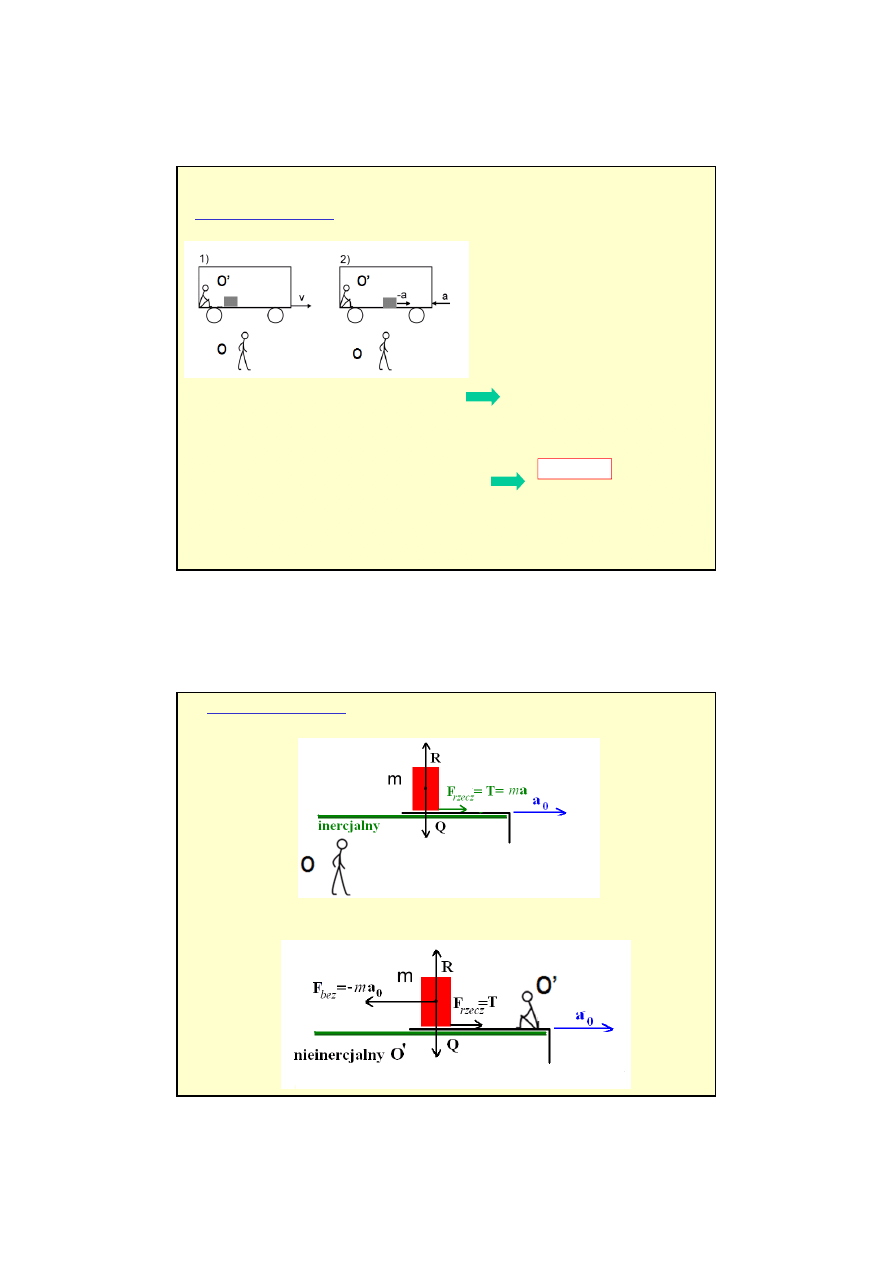
Ruch prostoliniowy

- dwaj obserwatorzy opisuj

ą

ruch klocka znajduj

ą

cego

si

ę

w samochodzie

jeden z obserwatorów stoi na Ziemi,
a drugi znajduje się w samochodzie,

samochód jedzie ze stałą prędkością (rys. 1)

v

klocka

= 0 ⇒

⇒

⇒

⇒ F = 0

(O’ )

v

klocka

= v = const. ⇒

⇒

⇒

⇒ F = 0

(O)

(obserwatorzy O i O’ znajdują się w inercjalnych układach odniesienia)

samochód hamuje ze stałym opóźnieniem a (rys. 2),

(między klockiem, a podłogą samochodu nie ma tarcia)

a

F

klocka

m

−

=

(O’)

(obserwator O’ znajduje się w układzie nieinercjalnym a obserwator O jest w układzie inercjalnym)

v

klocka

= v = const. ⇒

⇒

⇒

⇒ F = 0 (O)

Ruch prostoliniowy

- wyrywanie obrusu

mg

f

T

≤

12

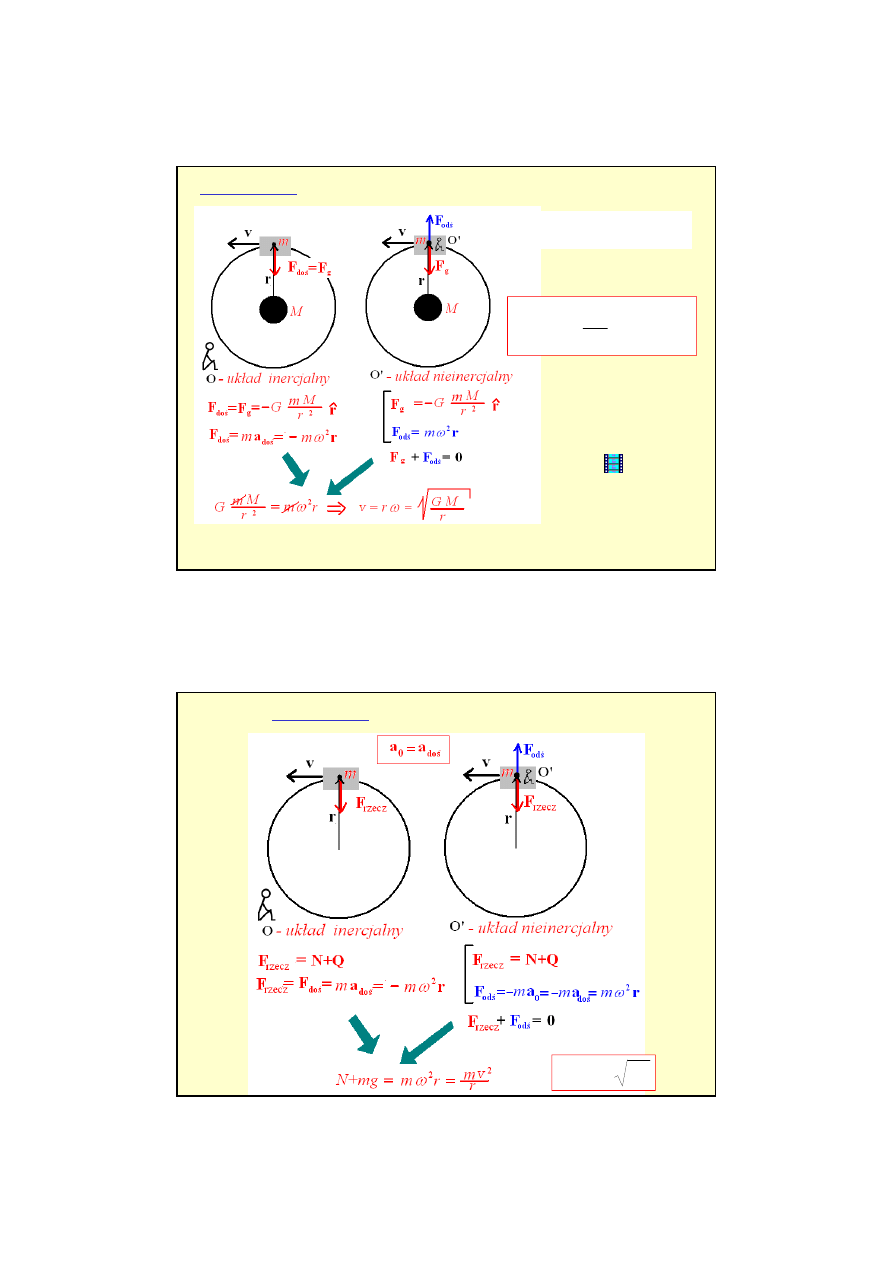
Siła odśrodkowa

– stan nieważkości

r

r

F

odś

2

2

ˆ

ω

m

r

m

=

=

v

jeden z obserwatorów (O) stoi na Ziemi,
a drugi znajduje się w sputniku (O’)

Siła odśrodkowa

- kamień na sznurku

rg

=

min

v

13

Biedronka porusza się wzdłuż
promienia tarczy ze stałą prędkością v

r

(względem tarczy !!)

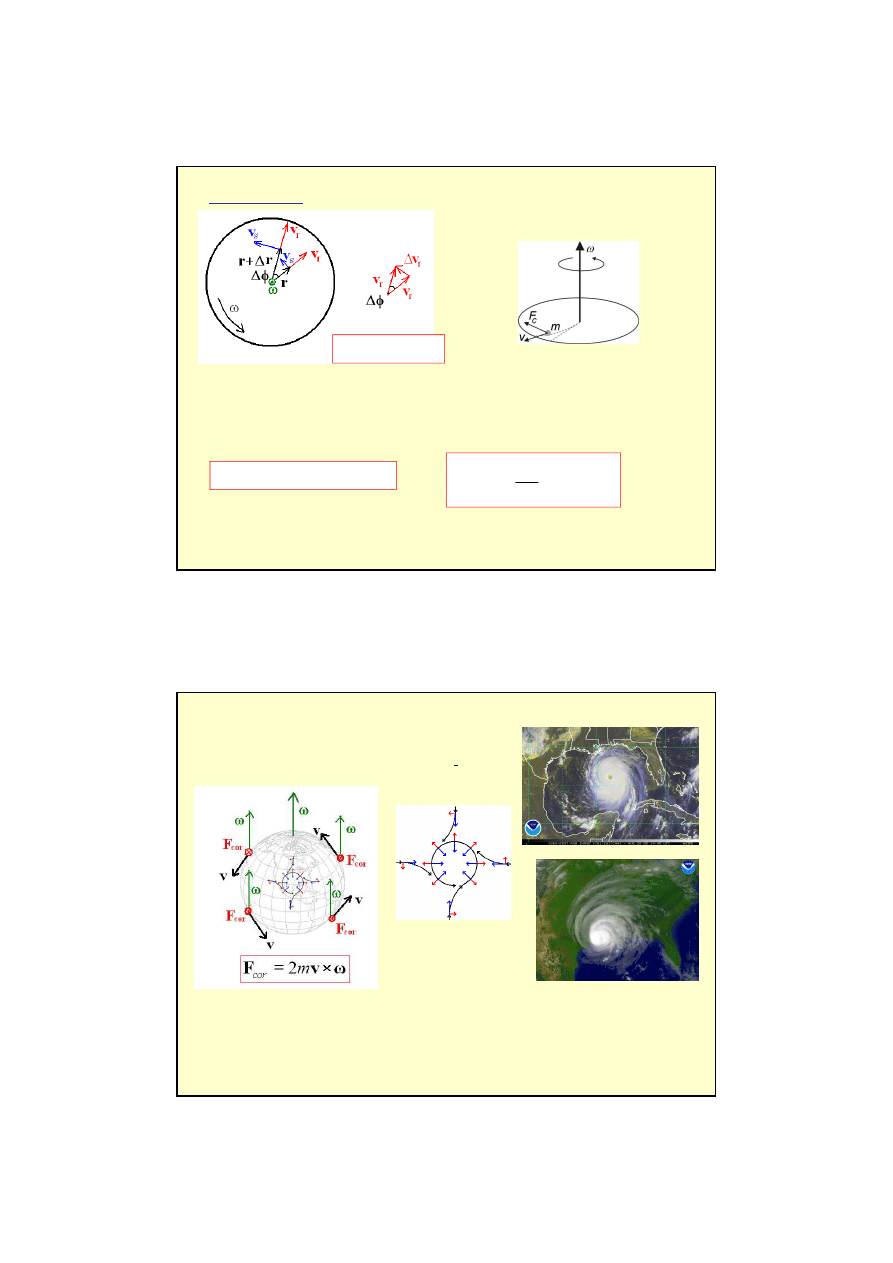
Siła Coriolisa

r

r

F

odś

2

2

ˆ

ω

m

r

m

=

=

v

ω

v

a

F

cor

cor

×

=

−

=

m

m

2

Siły bezwładno

ś

ci działaj

ą

ce w układzie obracaj

ą

cym si

ę

:

ω

v

a

cor

×

−

=

2

Mieszkamy na Ziemi – wirującej planecie

Ruch obrotowy Ziemi powoduje zmianę kierunku poruszających się po jej powierzchni ciał.
• silniejsze podmywanie prawych brzegów rzek na półkuli północnej i lewych na

półkuli południowej

• odchylenie kierunków wiatrów stałych
• układ prądów morskich
• odchylenie toru ciał spadających

RITA 2005

KATRINA 2005

Siła Coriolisa

na Ziemi

14

Siła Coriolisa

- wahadło Foucaulta

Wahadło Foucaulta w Muzeum Sztuk i Rzemiosł
w Paryżu; w miarę obrotu wahadło przewraca
ustawione wokoło klocki.

Wahadło Foucaulta - Kościół św. Piotra i Pawła w Krakowie: 46,5m , 25 kg