21

CZĘŚĆ DZIESIĄTA

OBLICZENIA STATYCZNE

KONSTRUKCJI MUROWYCH

22

Do obliczeń statycznych konstrukcji murowych wykorzystuje się polską normę
PN-B-03002 oraz euronormę - EC6 (Eurokod).

Obliczenia wg normy polskiej PN-B-03002
Norma pochodzi z lipca 2007 roku. Jest ona dostosowana do obliczeń
metodą stanów granicznych różnego rodzaju konstrukcji murowych (zarówno
murów niezbrojonych, jak i zbrojonych - poprzecznie i podłużnie). Procedury
obliczeniowe są dostosowane do murów z różnych materiałów (cegły pełnej,
gazobetonu, cegły silikatowej, cegieł pustakowych, bloczków z betonów
lekkich, kamienia naturalnego…) - kiedyś istniały odrębne normy. Norma ta
nie dotyczy obliczeń kominów fabrycznych ani murów oporowych, a poza
tym stosuje się ją do obliczeń wszystkich konstrukcji lądowych.

Przydatna literatura
1) prof. B. Lewicki - „Podstawy projektowania niezbrojonych konstrukcji

murowych”, Wydawnictwo ITB, 2001,

2) P. Matysek, T. Seruga - „Konstrukcje murowe - przykłady obliczeń”,

Wydawnictwo Politechniki Krakowskiej, 2005,

3) J. Hoła, P. Pietraszek, H. Schabowicz - „Obliczanie konstrukcji budowlanych,

wznoszonych tradycyjnie”, Dolnośląskie Wydawnictwo Edukacyjne, 2006,

4) PN-EN 1996-3:2010 - Eurokod 6 - Uproszczone metody obliczania murów

niezbrojonych,

Konstrukcje murowe są często pomijane w projektach - niektórzy projektanci
przyjmują je „na wiarę” - nie obliczają ich tak, jak np. w przypadku żelbetu.
Dzieje się tak, ponieważ w przypadku małych konstrukcji (np. domki
jednorodzinne), w porównaniu do niekiedy złożonych schematów obliczeń,
nie opłaca się obliczać (nie jest to do końca w porządku).

Materiały

(punkt 3. normy)

Z uwagi na rodzaj tworzywa rozróżnia się następujące rodzaje elementów murowych:
- ceramiczne,
- silikatowe,
- z betonu kruszywowego,
- z autoklawizowanego betonu komórkowego,
- z kamienia sztucznego i naturalnego.

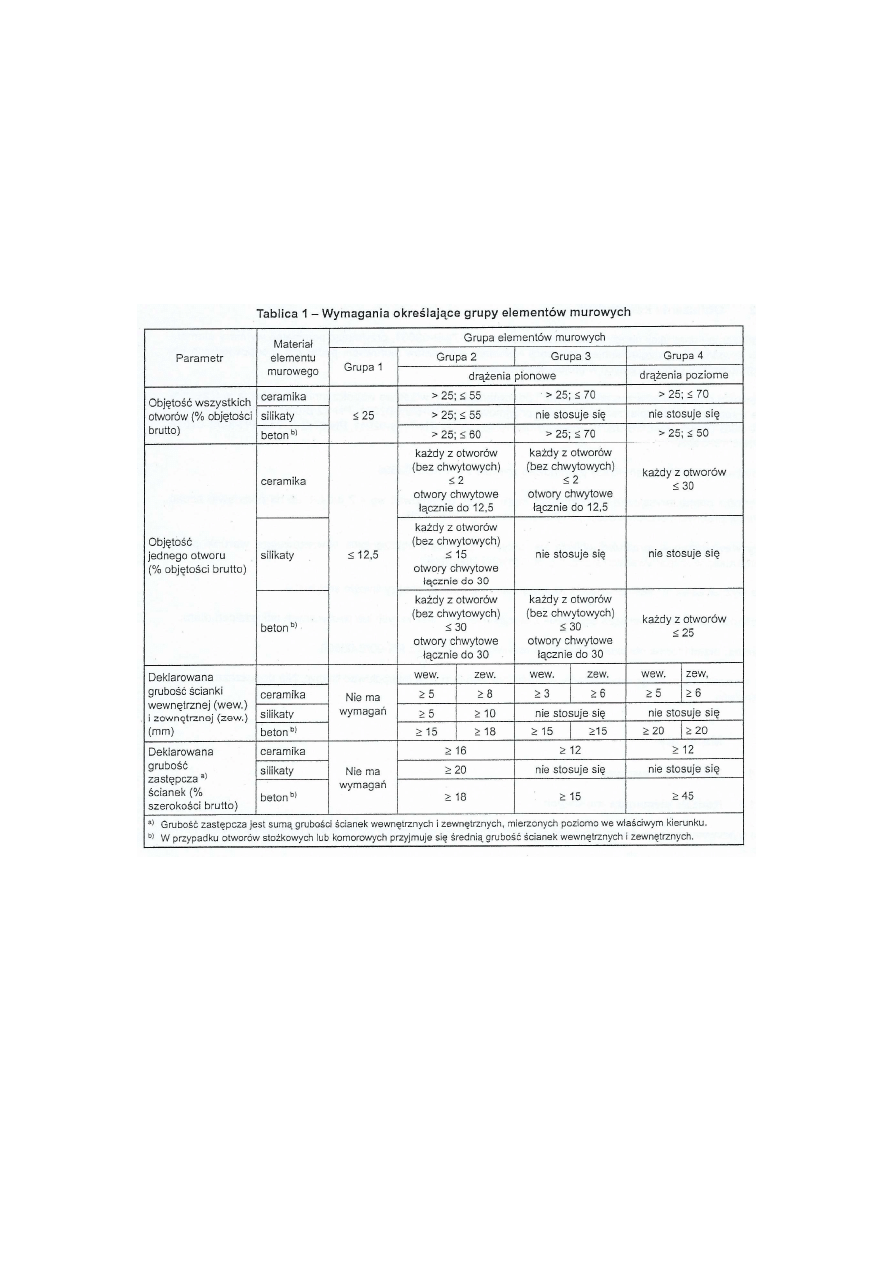
Wyróżnia się poszczególne grupy elementów murowych

(Tablica 1 - Wymagania

określające grupy elementów murowych)

. Tutaj pierwszy raz pojawiają się cztery grupy

(do tej pory wyróżniano tylko trzy). Po lewej podane są parametry
elementów, wg których określa się przynależność do odpowiedniej grupy:
objętość wszystkich otworów, objętość jednego otworu, deklarowana
grubość ścianki wewnętrznej i zewnętrznej, deklarowana grubość zastępcza
ścianek. Poza tym o grupie decyduje także to, czy otwory są pionowe czy
poziome. Tabela niestety nie ma praktycznego zastosowania, choćby ze
względu na fakt, iż bardzo trudno jest określić powierzchnię otworów w
danym elemencie (o ile ta wartość nie jest podana przez producenta, a

23

zwykle nie jest). Łatwo jest określić wyrób pełny (bo to zawsze grupa 1), ale
problem pojawia się w przypadku wyrobów pustakowych.
Warto zwrócić uwagę na czwartą grupę (wyroby o drążeniach poziomych),
ponieważ nie powinno się ich stosować w konstrukcjach murowych. Takie
elementy mogą co najwyżej stanowić wypełnienie szkieletu, ale nie powinny
stanowić muru nośnego. Otwory w pustakach przeznaczonych do konstrukcji
nośnych powinny być zawsze ułożone prostopadle do spoiny wspornej.
Np. pustaki Wienerbergera (rombowy układ drążeń) należą do grupy trzeciej,
a z kolei pustaki UNI lub MAX - grupy drugiej.

Kategorie elementów murowych

(punkt 3.1.3 normy)

W normie nie ma podanej charakteryzacji poszczególnych kategorii (I i II), ale
jest odniesienie do innej normy.

Kategoria I - wytrzymałość elementów podaje producent, mają one

określoną wytrzymałość na ściskanie, a w zakładzie prowadzona jest
kontrola jakości z prawdopodobieństwem nie odbiegania średniej
wytrzymałości od deklarowanej o więcej niż 5%. (zakład podaje
wytrzymałość na ściskanie i na bieżąco prowadzi kontrolę jakości)

Kategoria II - producent deklaruje średnią wytrzymałość, a pozostałe

wymagania, jak w kategorii I nie są spełnione. Kategoria ta dotyczy zwykle
mniejszych przedsiębiorstw, które nie mają bardzo rozwiniętego zaplecza
laboratoryjnego, wobec czego deklarowane wartości wytrzymałości
ustalane są na podstawie badań okresowych.

24

Zaprawy murarskie

(punkt 3.2 normy)

Do wykonania murów stosuje się:
- zaprawy murarskie zwykłe,

- zaprawy murarskie do cienkich spoin,
- zaprawy murarskie lekkie.

Z zapraw murarskich zwykłych najczęściej stosuje się zaprawy cementowo-
wapienne

(dawno

zaprzestano

używania

zapraw

glinianych

czy

wapiennych). Przed wojną powszechna była zaprawa wapienna (panował
pogląd, iż wapno jest zdrowsze od cementu).
Zaprawy do cienkich spoin nakłada się za pomocą wałka (nie kielni). Mają
one grubość nawet 1-2mm. Zaprawy takie są przygotowywane na bazie
polimerów. Są one jednak o wiele droższe od zaprawy cementowo-
wapiennej. Cienkie spoiny mają trzy ważne zalety względem spoin
wykonanych z zapraw zwykłych. W przypadku ich zastosowania osiadania
muru w czasie jego wznoszenia są znacznie mniejsze. Ponadto, im cieńsza
spoina, tym mniejsze osłabienie wytrzymałości muru (zaprawa ma znacznie
mniejszą wytrzymałość niż np. cegła). Co więcej, przewodność cieplna przez
spoiny jest większa niż przez elementy murowe. Dlatego czasem na tynku
odbijał się „obraz” spoin. Własność nie ma już obecnie dużego znaczenia,
ponieważ mury i tak są dodatkowo docieplane. O przewodności cieplnej
decyduje rdzeń termoizolacyjny, grubość muru ma znaczenie dla
wytrzymałości.
Zaprawy murarskie lekkie obecnie można praktycznie pominąć. Były one
kiedyś stosowane w jednorodnych murach z gazobetonu (grubości np. 37cm
lub 24cm). Zamiast piasku do zaprawy dodawano zmielony keramzyt, żużel
lub nawet granulki styropianu. Takie ściany określano jako „Murfor”. Zaprawy
lekkie były też określany jako zaprawy ciepłochronne lub ciepłe. Obecnie już
nie stosuje się takich zapraw, ale warto o nich pamiętać, ponieważ czasem
potrzebne są obliczenia sprawdzające dla murów już istniejących.

Wytrzymałość charakterystyczna muru na ściskanie

(punkt 4.3 normy)

W normie określone są wzory, które służą do obliczania wytrzymałości.
Przykładowo dla murów wykonanych na zaprawie zwykłej lub lekkiej wzór ma
postać:

30

.

0

70

.

0

m

b

k

f

f

K

f

⋅

⋅

=

k

f - wytrzymałość charakterystyczna muru na ściskanie

K - współczynnik wg odpowiedniej tablicy (z uwagi na kształt elementu)

b

f - znormalizowana wytrzymałość elementu murowego na ściskanie

m

f - wytrzymałość zaprawy murarskiej na ściskanie

W praktyce nie korzysta się ze wzorów. Bardziej praktyczny jest bowiem
załącznik C do normy. Są w nim tablicowane

(tablice C.1 - C.7)

wartości

charakterystyczne wytrzymałości na ściskanie w zależności od rodzaju
elementu murowego i zaprawy. Wadą tych tablic jest fakt, iż nie przewidują
one zaprawy M

0

. Wielkość ta była przydatna wtedy, gdy zaprawa jeszcze nie

związała (wartość tę stosowano do obliczeń wytrzymałości muru w czasie
montażu, wznoszenia). W starej normie był też tłustym drukiem wyróżniony

25

logiczny zakres stosowania elementu murowego z odpowiednią zaprawą (np.
nie ma sensu łączyć bardzo słabej cegły z silną zaprawą). W projektach
stosujemy najczęściej cegły o wytrzymałości 10-15MPa. Wyżej mielibyśmy już
cegły półklinkierowa i klinkierowe.

Wytrzymałości obliczeniowe muru

(punkt 4.8 normy)

Do obliczeń metodą stanów granicznych stosuje się wartości obliczeniowe.
Poniższy wzór nie jest umieszczony w normie, ale jest mowa o procedurze
obliczania.

A

m

k

d

f

f

η

γ

⋅

=

d

f - wytrzymałość obliczeniowa muru

k

f - wytrzymałość charakterystyczna muru

(tabele C.1 - C.7 z załącznika C do normy)

m

γ

- częściowy współczynnik bezpieczeństwa

(tablica 9)

A

η

- współczynnik uzależniony od wielkości przekroju poprzecznego

(tablica 10)

Wzór ten jest ogólny i można go stosować do wytrzymałości na ściskanie,
ścinanie i zginanie (dodaje się wówczas odpowiednie indeksy).

Częściowy współczynnik bezpieczeństwa -

m

γ

(punkt 4.7 normy)

Jego wartość zależy od kategorii elementu murowego oraz od kategorii
wykonania robót.

Rozróżnia się:
- kategorię A wykonania robót - kiedy roboty murarskie wykonuje należycie wyszkolony
zespół pod nadzorem mistrza murarskiego, stosuje się zaprawy produkowane fabrycznie,
a jeżeli zaprawy wytwarzane są na budowie, kontroluje się dozowanie składników, a
także wytrzymałość zaprawy, a jakość robót kontroluje inspektor nadzoru inwestorskiego,
- kategorię B wykonania robót - kiedy warunki określające kategorię A nie są spełnione;
w takim przypadku nadzór nad jakością robót może wykonywać osoba odpowiednio
wykwalifikowana, upoważniona przez wykonawcę.

Zaprawy produkowane fabrycznie, to specjalnie przygotowane, suche
mieszaniny piasku, wapna i cementu. Na budowie dodaje się jedynie wody i
można od razu murować. Na worku mamy informację o deklarowanej
wytrzymałości (np. 3MPa). Wtedy przyjmujemy kategorię A.
Powyższe rozwiązanie stosuje się w przypadku niedużych budów - jest ono za
drogie do masowego zastosowania. W przypadku większych przedsięwzięć
budowlanych zaprawę wykonuje się na placu budowy - miesza się składniki w
odpowiednich proporcjach (np. 1 do 2 do 5: w część cementu, dwie wapna i
5 wody). Mamy wówczas do czynienia z kategorią B.

26

Widać, że rozrzut wartości jest znaczny (1.7-2.5). Stosowanie tego
współczynnika nie jest łatwe dla projektanta, ponieważ na etapie
projektowania nie może on przewidzieć tego, kto będzie wykonywał dane
roboty. W praktyce często przyjmuje się wartość 2.2 (pozostaje się wtedy po
stronie bezpiecznej).

Współczynnik zmniejszający wytrzymałość w zależności od wielkości
przekroju poprzecznego elementu -

A

η

(punkt 4.8 normy)

Kiedy pole przekroju poprzecznego elementu konstrukcji murowej jest mniejsze niż 0.30m

2

,

wytrzymałość obliczeniową muru należy dodatkowo podzielić przez współczynnik

A

η

o

wartości podanej w tablicy 10.

Wymaga się jego zastosowania tylko dla małych przekrojów, co jest logiczne.
W przypadku dużego przekroju (np. filar 1.5 cegły na 1 metr) niedokładne
wypełnienie spoiny, czy też wyszczerbienie naroża lub krawędzi cegły nie
odgrywa znaczącej roli. Jeżeli jednak przekrój jest nieduży (np. filar cegła na
1.5 cegły), to jakiekolwiek imperfekcje wykonawcze mogą mieć ogromny
wpływ na wytrzymałość tej konstrukcji murowej.

W zasadzie należałoby mówić o przekroju pracującym, a nie poprzecznym.
Jako przykład może posłużyć obliczanie wytrzymałości ściany (grubości
25cm), na której z obu stron oparte są stropy.
Obliczenia wykonuje się w odniesieniu do
jednego metra jej długości. Przekrój pracujący
nie jest jednak przekrojem 1m x 0.25m (0.25m

2

),

ale całym przekrojem przegrody od otworu do
otworu (drzwiowego lub okiennego). Trzeba
zawsze uważać, aby odpowiednio przyjąć
wartość współczynnika

A

η

.

Cecha sprężystości muru

(punkt 4.9 normy)

Jest to bezwymiarowy współczynnik, wykorzystywany przy określaniu
odkształceń konstrukcji murowych.

Doraźny moduł sprężystości muru E (wartość średnia) zaleca się przyjmować jako:

k

c

f

E

⋅

=

α

gdzie:

c

α

- cecha sprężystości muru, której wartość można przyjąć:

- dla murów wykonanych na zaprawie

≥

m

f

5 MPa, z wyjątkiem murów z

autoklawizowanego betonu komórkowego -

=

c

α

1000,

- dla murów z autoklawizowanego betonu komórkowego, niezależnie od rodzaju

zaprawy, a także dla murów z innego rodzaju elementów murowych na zaprawie

<

m

f

5 MPa -

=

c

α

600.

27

Długotrwały moduł sprężystości muru E

∞

(wartość średnia) wyznacza się jako:

k

c

E

k

c

f

f

E

⋅

=

⋅

+

⋅

=

∞

∞

∞

,

1

α

φ

η

α

gdzie:

E

η

- współczynnik uwzględniający zmniejszenie pełzania muru na skutek redystrybucji sił

wewnętrznych w konstrukcji oraz stosunek obciążenia działającego długotrwale do
obciążenia całkowitego elementu konstrukcji murowej, którego wartość można
przyjąć

E

η

= 0.3,

∞

φ

- końcowa wartość współczynnika pełzania, którego wartość można przyjąć

∞

φ

= 1.5,

∞

∞

⋅

+

=

φ

η

α

α

E

c

c

1

,

∞

,

c

α

- cecha sprężystości muru pod obciążeniem długotrwałym, której wartość można

przyjąć:
- dla murów wykonanych na zaprawie

≥

m

f

5 MPa, z wyjątkiem murów z

autoklawizowanego betonu komórkowego -

=

∞

,

c

α

700,

- dla murów z autoklawizowanego betonu komórkowego, niezależnie od rodzaju

zaprawy, a także dla murów z innego rodzaju elementów murowych na zaprawie

<

m

f

5 MPa -

=

∞

,

c

α

400.

Wymiarowanie konstrukcji murowych w stanie granicznym nośności

(punkt 5.1

normy)

Stan graniczny nośności ścian obciążonych głównie pionowo sprawdzać należy z
warunku:

Rd

Sd

N

N

≤

w którym:

Sd

N

- siła pionowa w ścianie wywołana działaniem obciążenia obliczeniowego

Rd

N

- nośność obliczeniowa ściany z uwagi na obciążenia pionowe.

Mówiąc prościej: Nośność musi być większa od siły normalnej.

Nośność ściany należy sprawdzać w przekrojach pod i nad stropem oraz w środkowej
strefie ściany - z uwzględnieniem geometrii ścian, mimośrodowego działania obciążenia
pionowego i właściwości materiałowych muru. W ścianach z otworami sprawdzać
należy także nośność nadproży.

Najistotniejsze ze względów praktycznych są obliczenia w połowie wysokości
ściany.

Nośność obliczeniową ściany z uwagi na obciążenia pionowe wyznacza się (…) w
środkowej strefie ściany - ze wzoru:

d

m

d

mR

f

A

N

⋅

⋅

=

Φ

,

w którym:
-

m

Φ

- współczynnik redukcyjny wyrażający wpływ efektów drugiego rzędu na nośność

ściany, zależny od wielkości mimośrodu całkowitego działania wypadkowej siły pionowej
w środkowym przekroju ściany e

0

= e

m

, smukłości ściany h

eff

/t, zależności

σ

(

ε

) muru i czasu

działania obciążenia.
[- A - pole przekroju poprzecznego ściany;
- f

d

- wytrzymałość obliczeniowa muru na ściskanie.]

28

Wzór wydaje się być prosty, ale korzystanie z niego nie jest łatwe ze względu
na trudność określenia wartości współczynnika redukcyjnego nośności muru

m

Φ

. Wcześniej był on nazywany współczynnikiem wyboczeniowym. Ważne

jest, że współczynnik ten określa się z uwzględnieniem efektów drugiego
rzędu, a więc istotne są odkształcenia konstrukcji.

Zazwyczaj decydujący jest wynik obliczeń dla ściany w połowie jej
wysokości, wobec czego obliczenia pod i nad stropem pomija się ze względu
na większe przekroje pracujące w tych miejscach. Warto jednak wspomnieć,
że w ich przypadku nie ma współczynnika wyboczeniowego, ale
współczynniki wynikające z mimośrodowego obciążenia.

Możliwości w przypadku, gdy warunek nośności nie jest spełniony:
1) Można zwiększyć wartość obliczeniowej wytrzymałości muru na ściskanie

(f

d

) poprzez zwiększenie wartości charakterystycznej wytrzymałości muru. W

praktyce osiąga się to wyniku podniesienia klasy elementów, z których mur
ma być wykonany (lepsza cegła i mocniejsza zaprawa).

2) Można również zwiększyć wartość przekroju pracującego A. Wykonuje się

to poprzez pogrubienie muru (niekiedy pogrubienie wykonuje się np. w
piwnicy i na parterze, a wyżej pozostawia się mniejszą grubość).

3) Można też zwiększyć wartość f

d

poprzez zazbrojenie muru zbrojeniem

poprzecznym.

Jeżeli mur nie jest zbrojony, to w przypadku osiągnięcia siły krytycznej, na
murze powstaną pionowe pęknięcia. Przy jej przekroczeniu może wystąpić
„rozszczypanie” muru, będące wynikiem działania sił poziomych o znacznej
wartości.
Zbrojenie wykonuje się w postaci siatki z prętów, albo jako wężyki, układane
w co drugiej lub co trzeciej spoinie.
Stosowanie zbrojenia poprzecznego pozwala na zwiększenie nośności
nawet o 100%.

4) Ostatecznym rozwiązaniem jest wmurowanie wewnątrz filara ceglanego

czy gazobetonowego, filara stalowego. Tak ukształtowany słup żelbetowy
przenosi całość obciążeń.

Istnieje też bardzo trudne rozwiązanie z murem skrępowanym. Po bokach są
cienkie filary żelbetowe, które współpracują z ceramiką.

Najczęściej stosowane są rozwiązania 2) i 3).

29

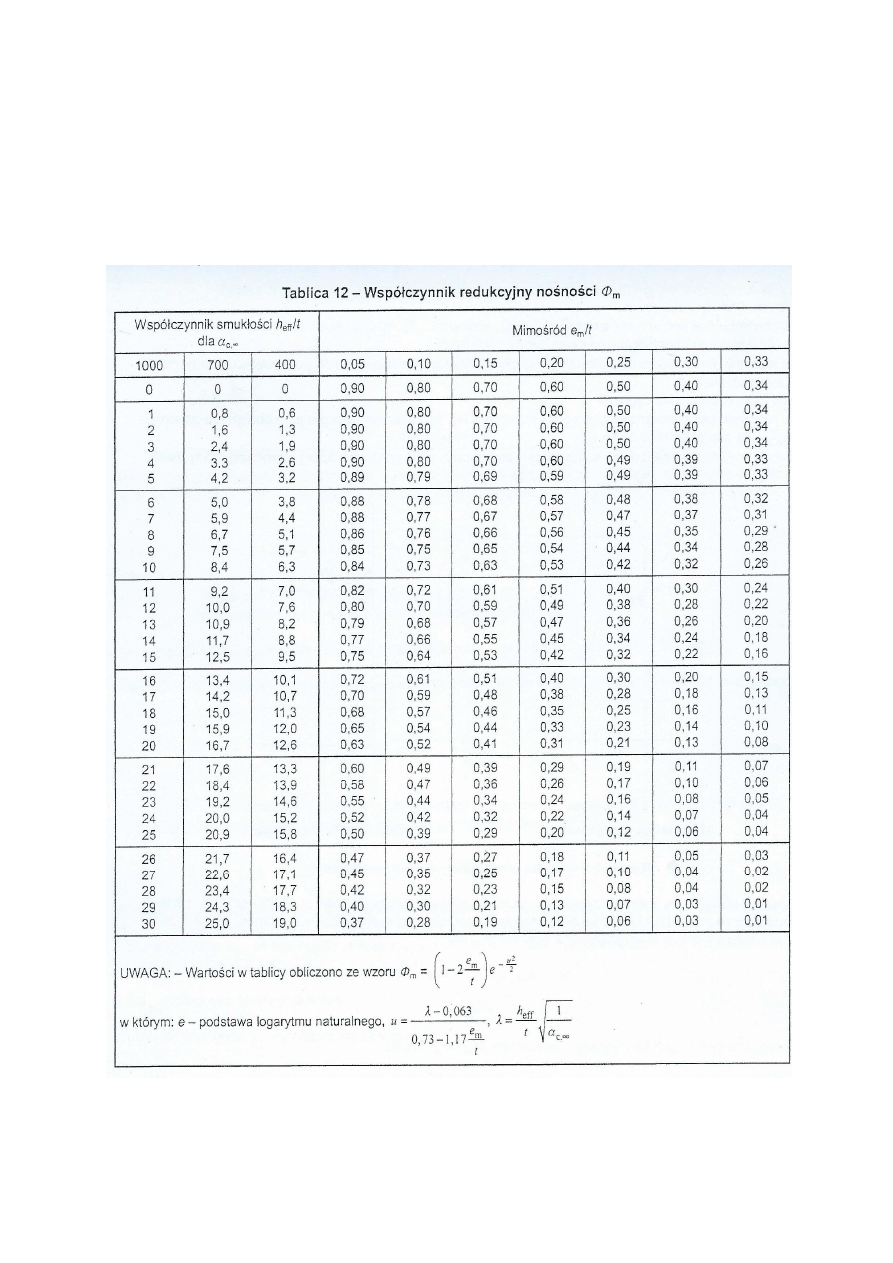
Do określania wartości współczynnika

m

Φ

stosuje się odpowiednio

przygotowaną tabelę

(tablica 12 z normy)

. Odczytana wartość jest uzależniona od

współczynnika smukłości muru dla cechy sprężystości pod obciążeniem
długotrwałym oraz stosunku mimośrodu względnego e

m

do grubości ściany t.

Smukłość muru (λ) jest stosunkiem jego wysokości obliczeniowej (efektywnej)
h

eff

do jego grubości t. Główna trudność polega jednak na wyznaczeniu

mimośrodu e

m

.

W projektach będziemy stosować wartości cechy sprężystości 400 lub 700.

30

Wysokość obliczeniowa muru

(punkt 5.1.4 normy)

Wysokość efektywną ściany oblicza się ze wzoru:

h

h

n

h

eff

⋅

⋅

=

ρ

ρ

w którym:

h

ρ

- współczynnik zależny od przestrzennego usztywnienia budynku, jak podano w

Tablicy 13;

n

ρ

- współczynnik zależny od usztywnienia ściany wzdłuż dwóch (

ρ

2

), trzech (

ρ

3

) lub

czterech (

ρ

4

) krawędzi;

h

- wysokość kondygnacji równa: przy posługiwaniu się modelem ciągłym - wysokości

kondygnacji w osiach modelu ramy (h

1

), przy posługiwaniu się modelem przegubowym -

wysokości kondygnacji w świetle.

Można zauważyć, że stropy z wieńcami żelbetowymi posiadają mniejsze
wartości współczynnika

n

ρ

- są mniej podatne na wyboczenie. Ale np. stropy

na belkach drewnianych lub stalowych (inne) mają większe wartości tego
współczynnika. Największe wartości posiadają ściany wolno stojące (mury
wspornikowe), np. niepodparty płot murowany ustawiony na parceli.

Ściany uważać można za usztywnione wzdłuż krawędzi pionowej, jeżeli:
- połączone są wiązaniem murarskim lub za pomocą zbrojenia ze ścianami
usztywniającymi usytuowanymi do nich prostopadle, wykonanymi z muru o podobnych
właściwościach odkształceniowych,
- długość ścian usztywniających jest nie mniejsza niż 0.2 wysokości ściany, a grubość nie
mniejsza niż 0.3 grubości ściany usztywnianej i nie mniejsza niż minimalna grubość ściany
określona w 7.3.1.

Modele obliczeniowe ścian
Wg normy polskiej wyróżnia się dwa modele obliczeniowe: model
przegubowy i model ciągły. W praktyce niemalże zawsze stosuje się
obliczenia wg modelu przegubowego. Niestety Eurokod przewiduje jedynie
model ciągły, zakładając, że ściana i strop tworzą razem sztywną ramę.

Model przegubowy

(punkt 5.1.3 normy)

W normie zostało uwzględnione tylko współczesne rozwiązanie (wieniec nie
posiadający ocieplenia).
W

starszych

konstrukcjach,

ściana

musiała

spełniać

wymogi

termoizolacyjności i wytrzymałości. Wobec tego potrzebne było docieplenie
wieńca. Stosowano w tym celu np. supremę, dziurawkę, styropian obłożony
siatką Rabitza. Teraz jej zadaniem jest jedynie przenoszenie obciążeń -
ochrona cieplna jest zapewniona przez rdzeń termoizolacyjny („kołderkę”) i

31

wieńców nie dociepla się. Takie rozwiązanie jest
korzystniejsze ze względu na naprężenia panujące na
połączeniu stropu i ściany - mają przebieg trójkątny.

Norma jednak powinna być uniwersalna, ponieważ obliczenia projektowe
wykonuje się nie tylko dla nowych konstrukcji, ale też dla konstrukcji
istniejących (obliczenia sprawdzające).

Przekazywanie obciążeń
Na etapie projektowania należy uwzględnić wynikające z niedokładności
wykonania imperfekcje takie, jak:
- niewielkie wychylenie ściany od pionu,
- nieznaczne przesunięcie osi ściany,
- niecałkowite wypełnienie spoin (czasem się stosuje spoinę odsuniętą od lica
o ok. 1cm np. w celu zapewnienia lepszej przyczepności tynku - tzw. puste
fugi).

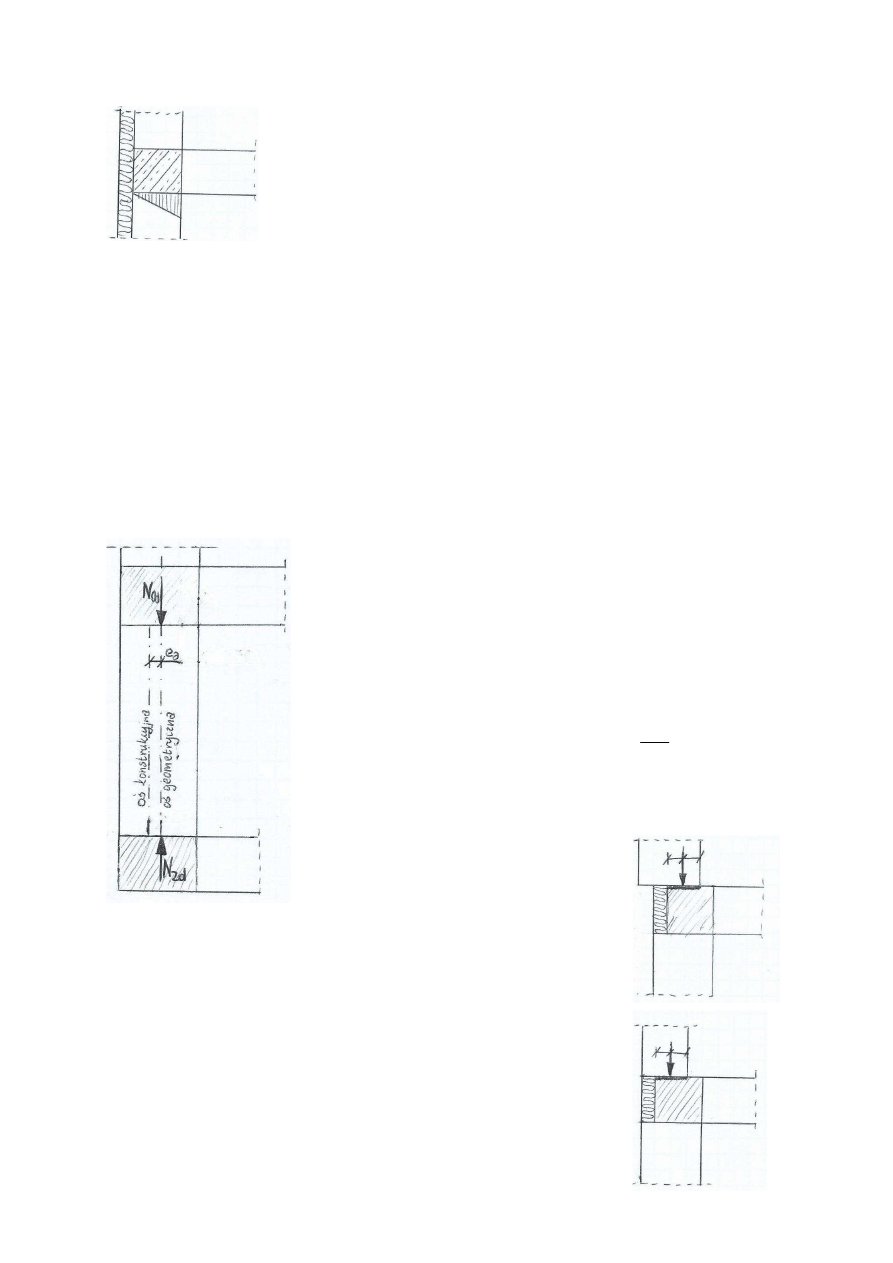
W ścianie wyróżnia się oś geometryczną, którą
umieszcza się w połowie jej grubości oraz oś
konstrukcyjną, przesuniętą względem geometrycznej o
tzw. mimośród niezamierzony (techniczny) e

a

. Jego

wielkość określają dwa warunki:

300

h

e

a

=

i

cm

e

a

1

≥

(h

jest wysokością ściany w mm).

Obciążenia z wyższej kondygnacji N

od

przekazywane są w

postaci siły skupionej umieszczonej w środku wspólnego
rzutu wyższej i niższej części kondygnacji. Wobec tego,
jeżeli ściany są tej samej grubości, a wieniec nie jest
ocieplony,

to

siła

przekazywana

jest

w

środku

geometrycznym ściany (przypadek najprostszy). Są też
trudniejsze przypadki, np. gdy mamy ściany o różnej
grubości z wieńcem ocieplonym albo gdy występuje
cokół. Ustalenie linii działania siły N

0d

względem osi

geometrycznej jest wtedy kwestią arytmetyki.

32

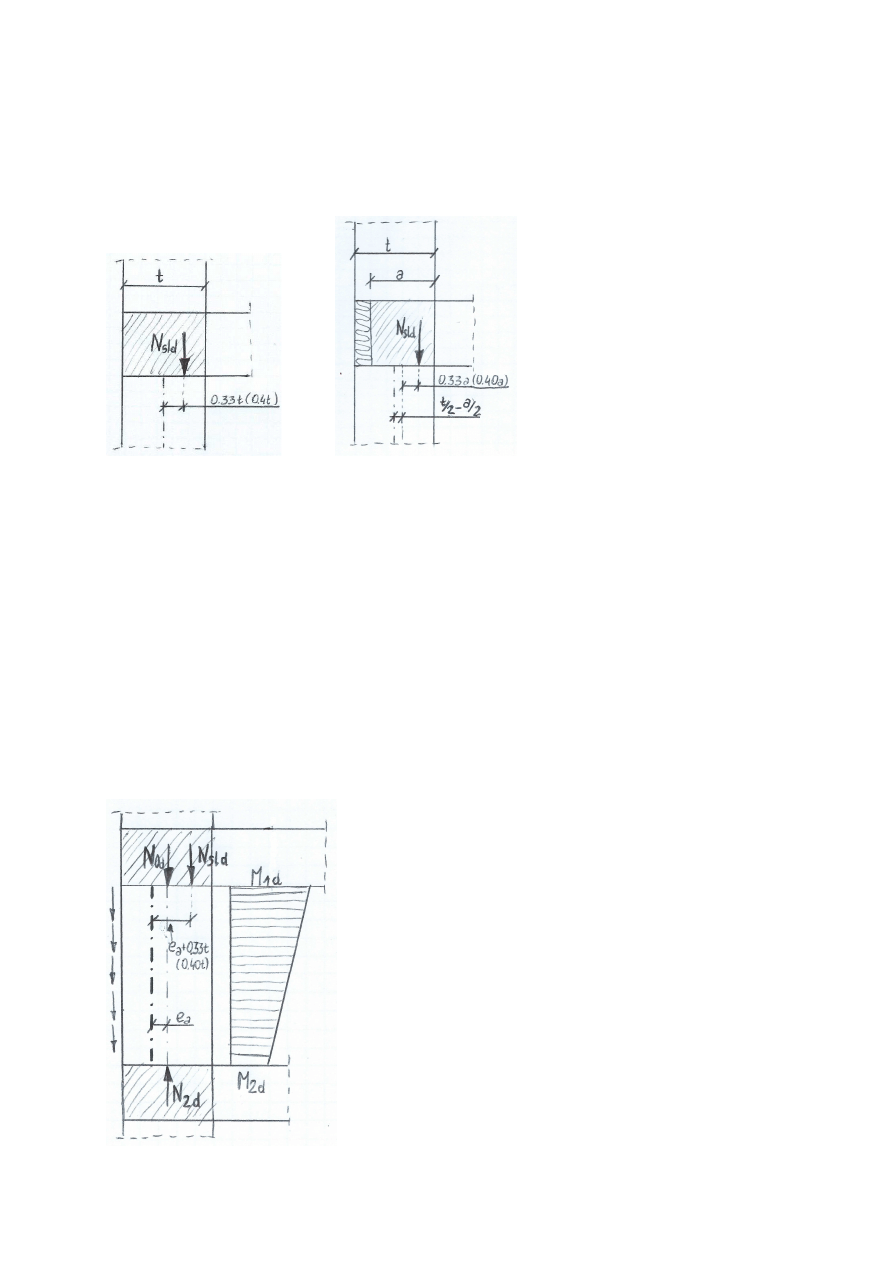
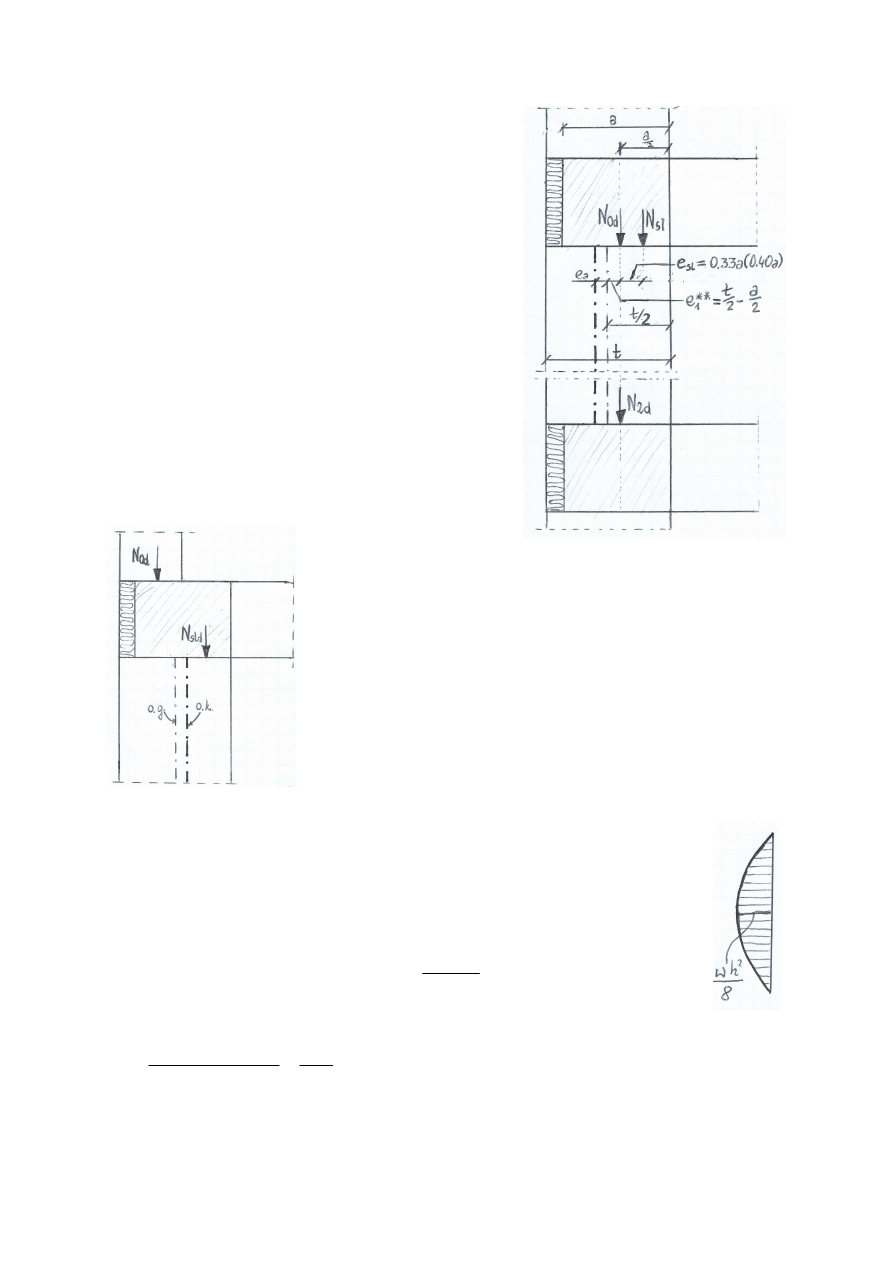
Obciążenie od stropów N

sld

przekazywane jest jako siła skupiona umieszczona

w odległości 0.33 szerokości wieńca od jego osi geometrycznej dla stropów
kondygnacji powtarzalnej, a w odległości 0.4 tejże szerokości dla
stropodachu (stropodach nie ma górnego stężenia i w związku z tym jest
bardziej podatny na odkształcenia).

Jeżeli wieniec nie jest ocieplony, to szerokość ściany jest także szerokością
wieńca. W przeciwnym wypadku wielkości te trzeba rozgraniczyć. Środek
wieńca jest przesunięty względem osi geometrycznej ściany o odległość
równą połowie różnicy szerokości ściany i wieńca.

Ważne! Odległość 0.33a (0.40a) odmierzamy względem środka wieńca a nie
ściany.

Ważne! Wszystkie momenty, zarówno pod jak i nad stropem obliczamy
względem osi konstrukcyjnej, a nie geometrycznej ściany.

Oddziaływania na dole ściany są przekazywane podobnie jak na górze -
także jako siła skupiona umieszczona w środku wspólnego rzutu. Zmienia się
jedynie oznaczenie (N

2d

). Siła ta działa w dół, na rysunkach często zamiast

niej oznacza się reakcję (w górę).

Łączny

schemat

sił

powoduje

powstanie

momentów pod stropem i nad stropem niższej
kondygnacji. Momenty te oblicza się względem
ustalonej osi konstrukcyjnej.

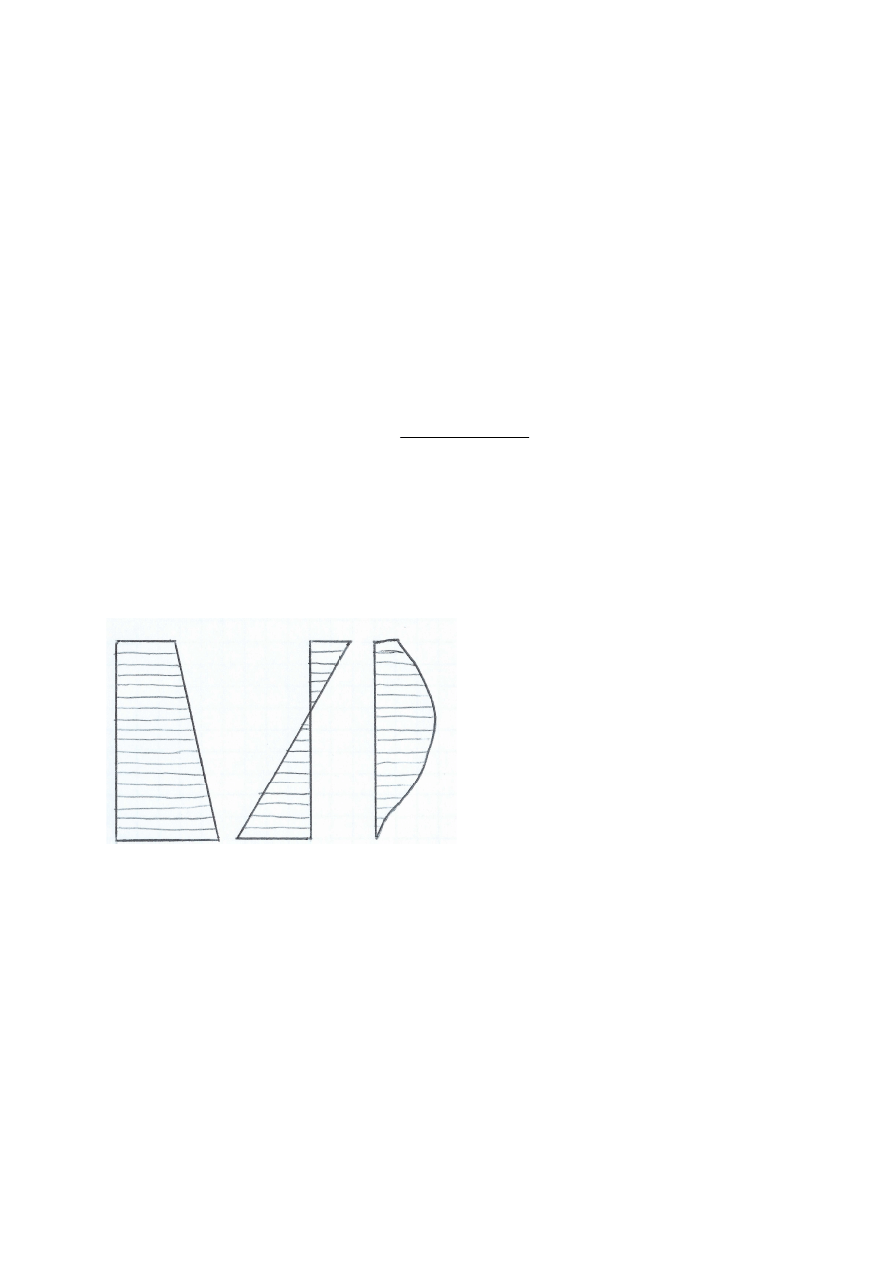
33

Siła N

2d

musi równoważyć siły N

0d

i N

sld

. Trzeba jeszcze uwzględnić narastający

ciężar własny muru. W praktyce często zbiera się wypadkową tego ciężaru
G

m

i rozkłada ją po połowie na N

2d

i N

0d

. Wobec tego:

sld

d

m

d

N

N

G

N

+

+

=

0

2

5

.

0

.

W tym wzorze N

0d

zawiera już w sobie połowę ciężaru muru.

Przy takim układzie sił, można prognozować wykres momentów jak na
rysunku. Dla stropu kondygnacji powtarzalnej mamy:

(

)

a

sld

a

d

d

e

t

N

e

N

M

+

⋅

+

⋅

=

33

.

0

0

1

a

d

d

e

N

M

⋅

=

2

2

W przypadku stropodachu zmienia się jedynie mimośród siły N

sld

(

)

a

sld

a

d

d

e

t

N

e

N

M

+

⋅

+

⋅

=

40

.

0

0

1

a

d

d

e

N

M

⋅

=

2

2

Na podstawie powyższych wielkości można wyznaczyć wartość mimośrodu
e

m

(potrzebnego do określenia wielkości współczynnika wyboczenia

m

Φ

).

Mimośród ten wyznacza się ze wzoru:

md

d

d

m

N

M

M

e

2

1

4

.

0

6

.

0

+

=

gdzie:
M

1d

i M

2d

- oznaczają momenty nad i pod stropem, przy czym co do

wartości większy jest moment M

1d,

N

md

- obliczeniowa siła pionowa w połowie wysokości ściany.

Wykresy momentów nie zawsze wyglądają tak, jak na rysunku powyżej. W
zależności od układu sił, mogą one mieć kształt np.:

Ważne! Mając powyższe wielkości możemy wrócić do tablicy 12. Jeżeli ze
stosunku otrzymamy wielkość, która znajduje się pomiędzy dwiema
określonymi

wartościami,

to

w

celu

wyznaczenia

odpowiedniego

współczynnika wyboczenia stosujemy interpolację liniową.

34

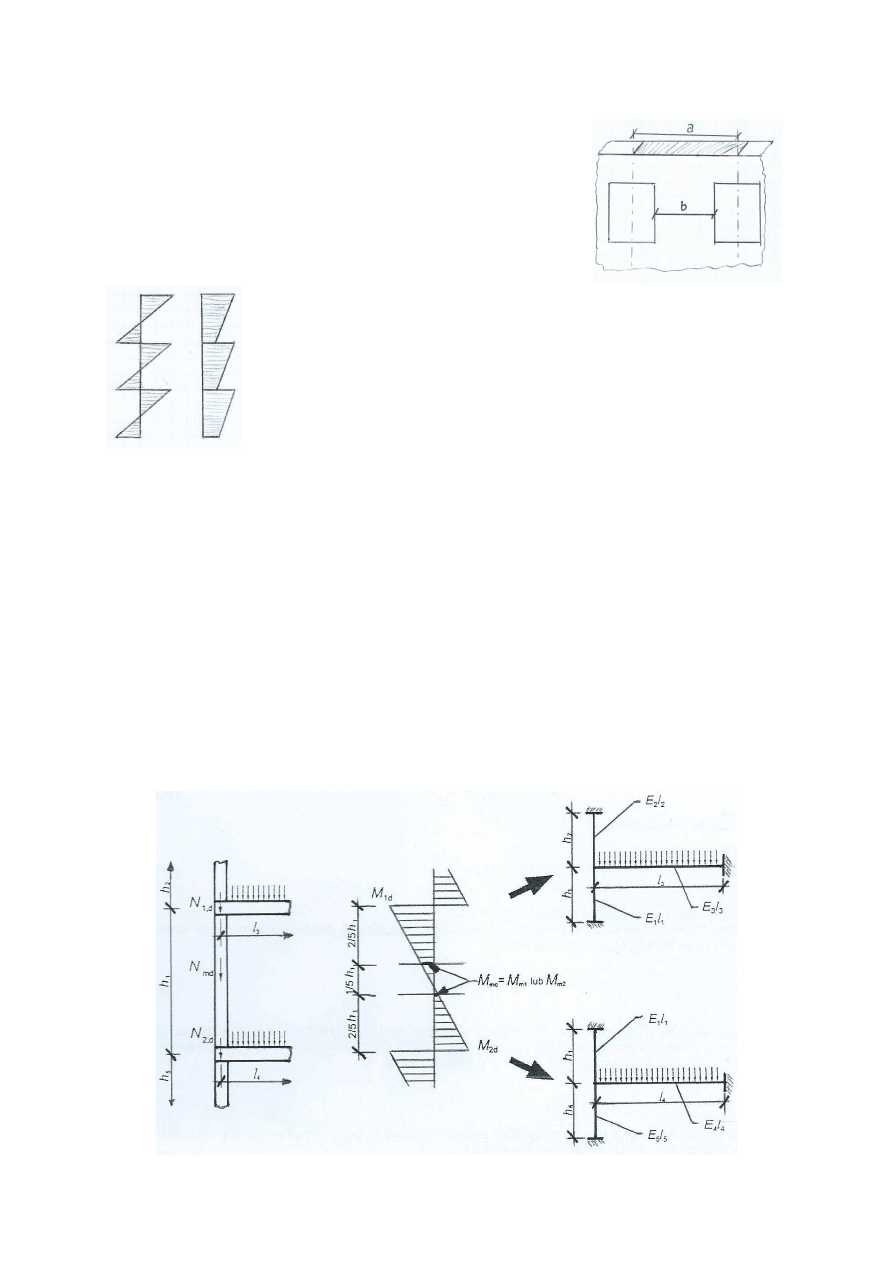
Przypadek z wieńcem ocieplonym
Mamy do czynienia z przypadkiem bardziej
ogólnym. Najistotniejsze są tutaj wielkości
mimośrodów sił, ponieważ są one niezbędne
do prawidłowego wyznaczenia momentów
pod i nad stropem. Dla siły od wyższej ściany
N

0d

mimośród wynosi: e

a

+ e

1

**

, gdzie ostatnia

wielkość

określa

odległość

pomiędzy

środkiem wieńca a osią geometryczną ściany.
Z kolei dla siły od stropu N

sl

mamy mimośród

równy: e

a

+ e

1

**

+ e

sl

, gdzie e

sl

określa się jako

0.33 szerokości wieńca dla stropu kondygnacji
powtarzalnej, 0.4 dla stropodachu

(jak

wcześniej). Natomiast dla siły N

2d

mimośród

jest taki sam jak dla siły N

0d

.

Ważne! Oś konstrukcyjna nie zawsze jest po lewej
stronie osi geometrycznej! Należy sprawdzić, jakie
przesunięcie

osi

konstrukcyjnej

względem

osi

geometrycznej (czy w prawo czy w lewo) daje mniej
korzystny przypadek ze względu na momenty
wywołane przez siły układu (ponieważ wartości
momentów zależą od przyjętej osi konstrukcyjnej).
Przyjmujemy oś tak, aby wypadkowy moment był
większy. Czasem bez dogłębnej analizy widać, która
wersja jest bardziej niekorzystna, a jeżeli nie jest to
jasne, to wykonujemy obliczenia.

Wpływ wiatru na konstrukcję
W małych budynkach (np. nasze projekty) oddziaływanie wiatru
jest pomijalnie małe. Jeżeli jednak mamy do czynienia z większymi
budynkami: kina, teatry, sale gimnastyczne, kościoły, ogromne sale
zebrań, to należy uwzględnić parcie wiatru.
Przyjmuje się moment, jak dla belki wolnopodpartej - standardowo

wartość maksymalna wynosi:

8

2

1

h

w

M

d

wd

⋅

=

Powstały moment należy uwzględnić przy określaniu wartości
mimośrodu względnego:

md

w

md

d

d

m

N

M

N

M

M

e

+

+

=

2

1

4

.

0

6

.

0

35

Model ciągły

(punkt 5.1.2 normy)

Przy modelu ciągłym zakłada się, że połączenie
pomiędzy pionowym prętem (ścianą) a poziomym
prętem (stropem) jest sztywne.
Jeżeli mamy filar międzyokienny, to do obliczeń stropu
bierze się odległość od w osiach otworów (a). Inaczej
jest

w

przypadku

wyznaczania

sztywności

-

uwzględnia się jedynie szerokość samego filara (b).

W konsekwencji, wykresy momentów (na wysokości
kondygnacji) mają w przybliżeniu postać, jak poniżej (dla
porównania z prawej mamy rozkład momentów dla modelu
przegubowego).

Rozpatrując pojedynczy element, należy myślowo wydzielić odpowiednie
pręty (ściany i stropy).

Warunkiem zastosowania modelu ciągłego jest oparcie stropu żelbetowego
na ścianie co najmniej na szerokości ściany i nie mniej jak wysokość wieńca.
Jeżeli strop nie jest żelbetowy, np. strop drewniany lub na belkach stalowych,
to w modelu przegubowym zwiększano długość wyboczeniową przez
odpowiedni współczynnik i można było dalej prowadzić obliczenia. W
modelu ciągłym w ogóle nie rozpatruje się przypadków tych stropów.
Na wykresie momentów (jak poniżej) wydziela się w środku wysokości
kondygnacji część o wysokości 1/5 tejże wysokości. Wyznaczone w ten
sposób momenty M

m1

i M

m2

porównuje się, wybiera większy i opisuje jako M

md

- wartość ta służy do obliczania mimośrodu. Jeżeli mamy tę samą rozpiętość
stropu i te same grubości ścian na kolejnych kondygnacjach, to obie
wielkości są równe, a pośrodku mamy wartość zerową.

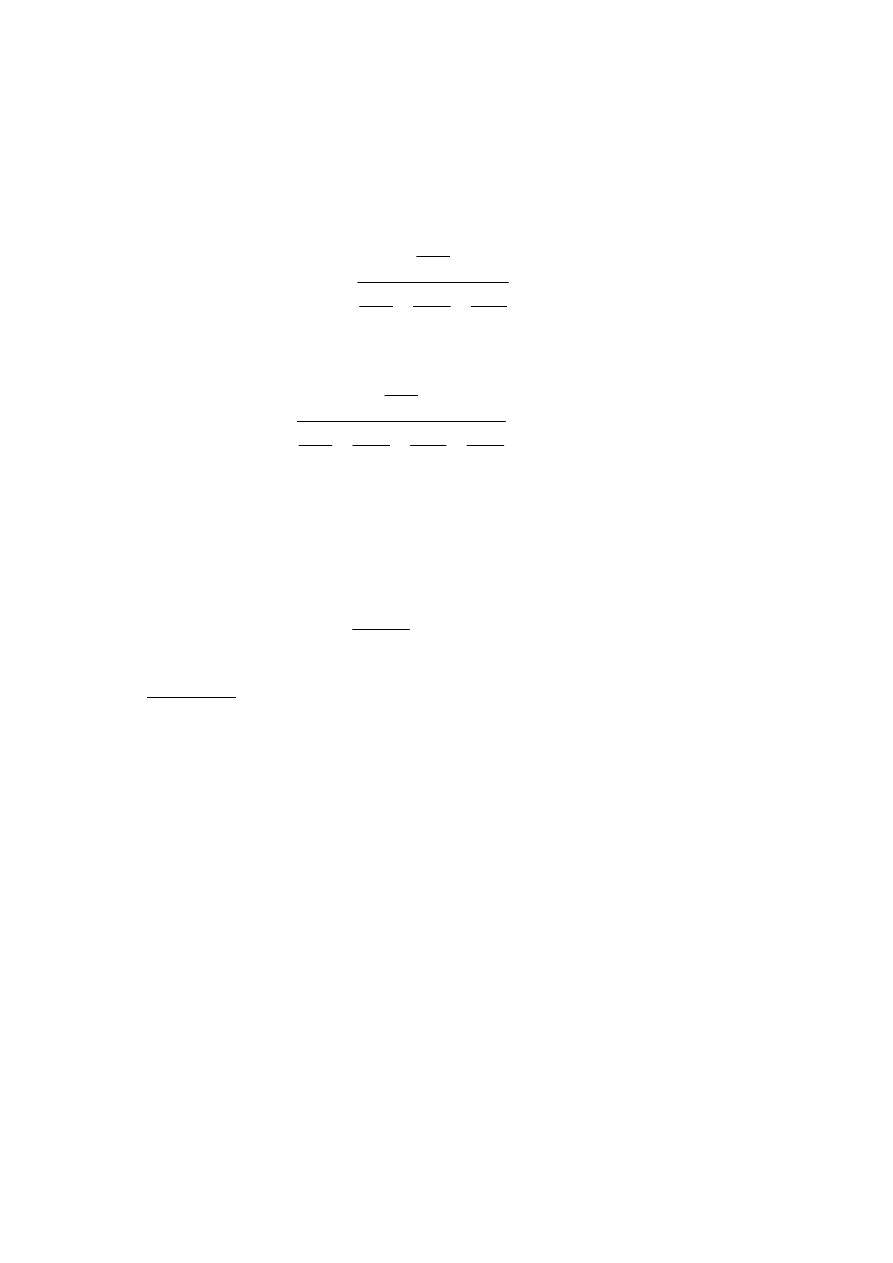
36

Obliczanie momentu pod stropem M

1d

Moment utwierdzenia stropu (w domyśle pełnego, a nie częściowego)
rozdziela się proporcjonalnie do sztywności wszystkich prętów w danym węźle.

Moment M

1d

w przekroju ściany pod stropem wyznaczać można:

- dla ściany obciążonej jednostronnie:

3

3

3

3

2

2

2

1

1

1

1

1

1

1

85

.

0

o

d

M

l

I

E

h

I

E

h

I

E

h

I

E

M

⋅

+

+

=

- dla ściany obciążonej dwustronnie:

(

)

4

3

4

4

4

3

3

3

2

2

2

1

1

1

1

1

1

1

85

.

0

o

o

d

M

M

l

I

E

l

I

E

h

I

E

h

I

E

h

I

E

M

−

⋅

+

+

+

=

W analogiczny sposób wyznacza się wartość M

2d

(różne są tylko indeksy). Dla

ściany obciążonej obustronnie musimy uwzględnić momenty węzłowe z
jednej i z drugiej strony, wobec czego pojawia się różnica. W powyższych
wzorach momenty są w sposób umowny redukowane o 15%.
Jeżeli uwzględnimy parcie wiatru na konstrukcję, to wartość momentu należy

zwiększyć o wielkość:

16

2

1

h

w

M

d

wd

⋅

=

.

Mimośród

względny

wyznacza

się

wówczas

ze

wzoru:

t

e

N

M

M

e

a

md

wd

md

m

05

.

0

≥

+

+

=

. Obliczoną wielkość odnosimy do tablicy 12 i

wyznaczamy współczynnik redukcyjny nośności muru.

W modelu ciągłym istnieje pewna niekonsekwencja. W ścianach mamy
otwory okienne i drzwiowe, w których występują nadproża. Ponieważ
moment jest przekazywany przez ścianę, to trafia on także na nadproża. W
efekcie moment zginający ścianę staje się momentem skręcającym
nadproże. Należałoby więc obliczać nadproże w odniesieniu do skręcania,
czego się nie wykonuje (bardzo trudne). Wpływa to na małą praktyczność
modelu ciągłego i dużą popularność modelu przegubowego.

Ściany obciążone siłą skupioną

(punkt 5.2 normy)

Mówimy o ścianach obciążonych głównie pionowo. Są też elementy
obciążone poziomo, np. komory ciepłownicze usytuowane pod ziemią. Jest
w nich bardzo mały ciężar własny, ale duże parcie gruntu. W projekcie ściany
są jednak obciążone głównie pionowo.

Obliczenia od siły skupionej są przydatne np. dla stropów na belkach
stalowych. Mówimy wówczas o obliczaniu docisku ściany.
Obliczenia te w starszej normie były znacznie prostsze niż obecnie.

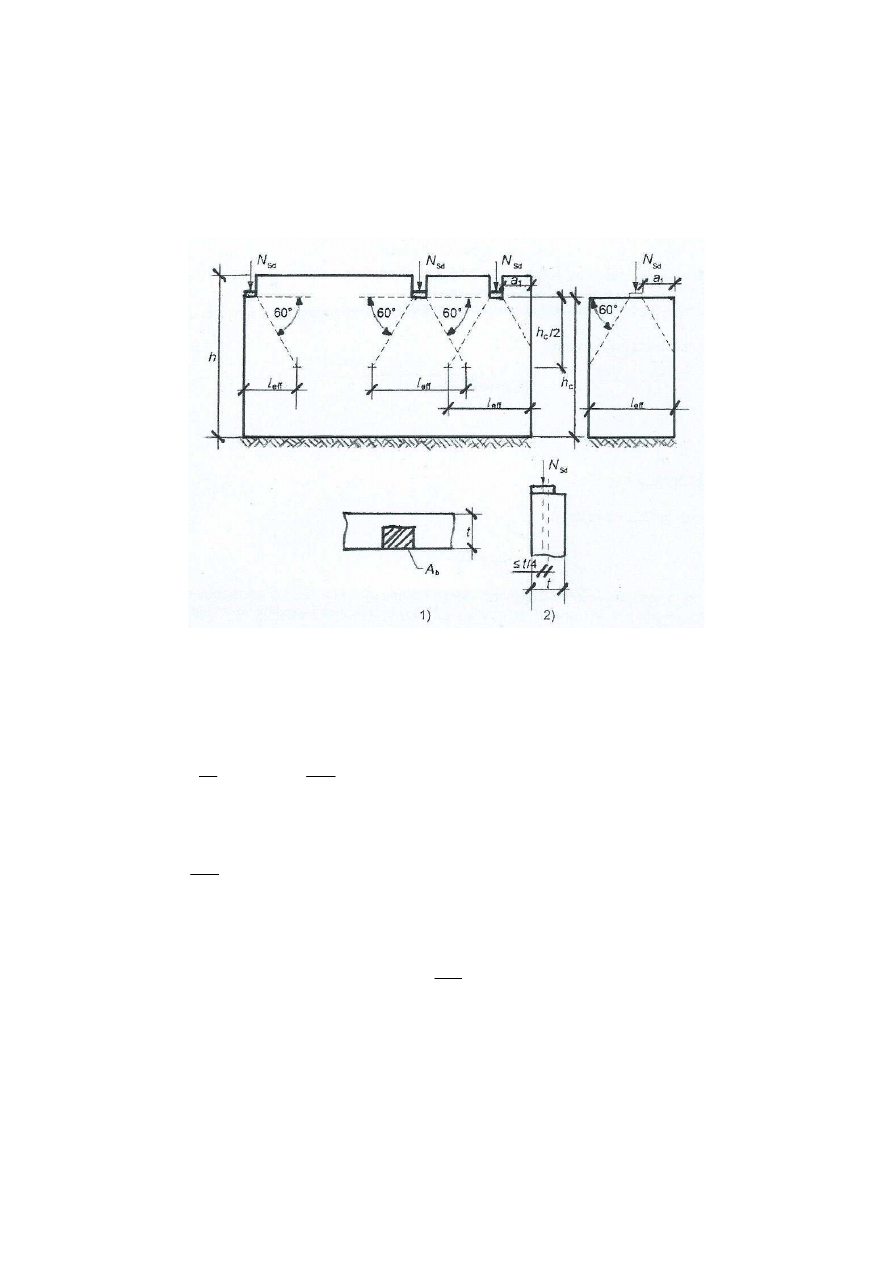
37

Mamy np. dźwigary stalowe oparte na ścianie za pomocą podkładki
żelbetowej, bloczka gazobetonu, 3 szycht cegieł (na płask) lub poduszki
betonowej. Siła przekazywana na ścianę musi zostać rozłożona na pewnej
szerokości. Rozkład następuje pod kątem 60° do poziomu do środka
wysokości ściany. W ten sposób otrzymujemy l

eff

- długość efektywną.

Uwzględnia się także odległość siły skupionej od brzegu filara.

Wytrzymałość na miejscowy docisk jest spełniona wtedy, gdy:

d

b

Rd

f

A

N

⋅

⋅

=

β

A

b

- pole oddziaływania bezpośredniego docisku, określona jako iloczyn

głębokości oparcia belki i szerokości poduszki,
f

d

- wytrzymałość na ściskanie,

β

- współczynnik wyrażający wpływ siły skupionej na nośność.















−

⋅













+

=

eff

b

c

A

A

h

a

1

.

1

5

.

1

3

.

0

1

1

β

A

eff

- efektywne pole przekroju ściany, równe iloczynowi długości efektywnej i

grubości ściany.

Stosunek

eff

b

A

A

nie może być większy niż 0.45.

Dla cegieł pustakowych (grupy 2, 3, 4) przyjmuje się, że

β

= 1.

Ponadto są pewne ograniczenia na współczynnik

β

- nie może on być

większy niż mniejsza z wartości: 1.25 +

c

h

a

2

1

lub 1.5.