E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
1
WYKŁAD 4
MODELOWANIE WYBRANYCH MECHANIZMÓW
Cz.1. MECHANIZM PODNOSZENIA
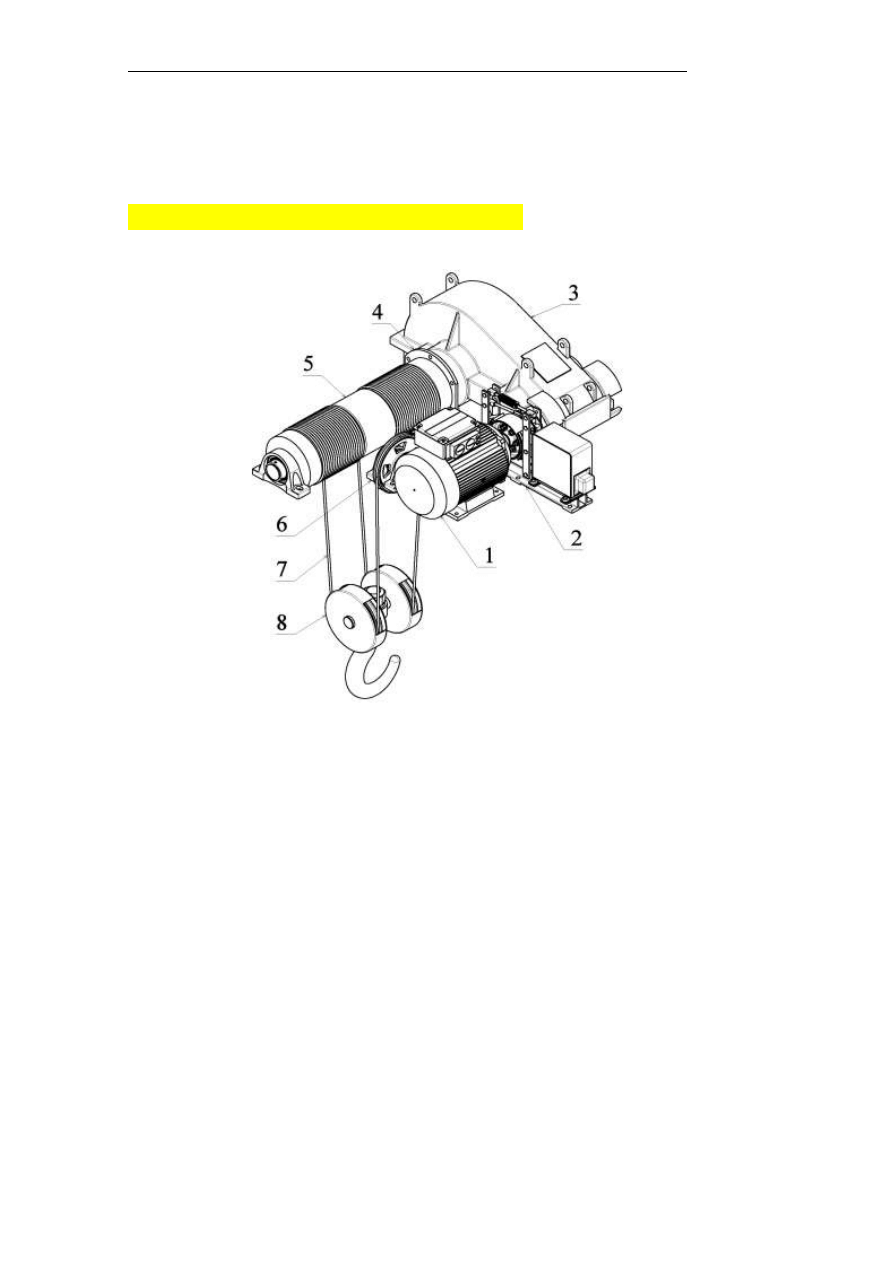
Mechanizm podnoszenia –
1 – silnik,
2 - sprzęgło hamulcowe wkładkowe wraz z hamulcem,
3 - przekładnia zębata zamknięta,
4 - sprzęgło zębate przybębnowe,
5 – bęben,
6 - krążek wyrównawczy,
7 – lina,
8 – zblocze hakowe.
1. Stany nieustalone w ruchu mechanizmu podnoszenia
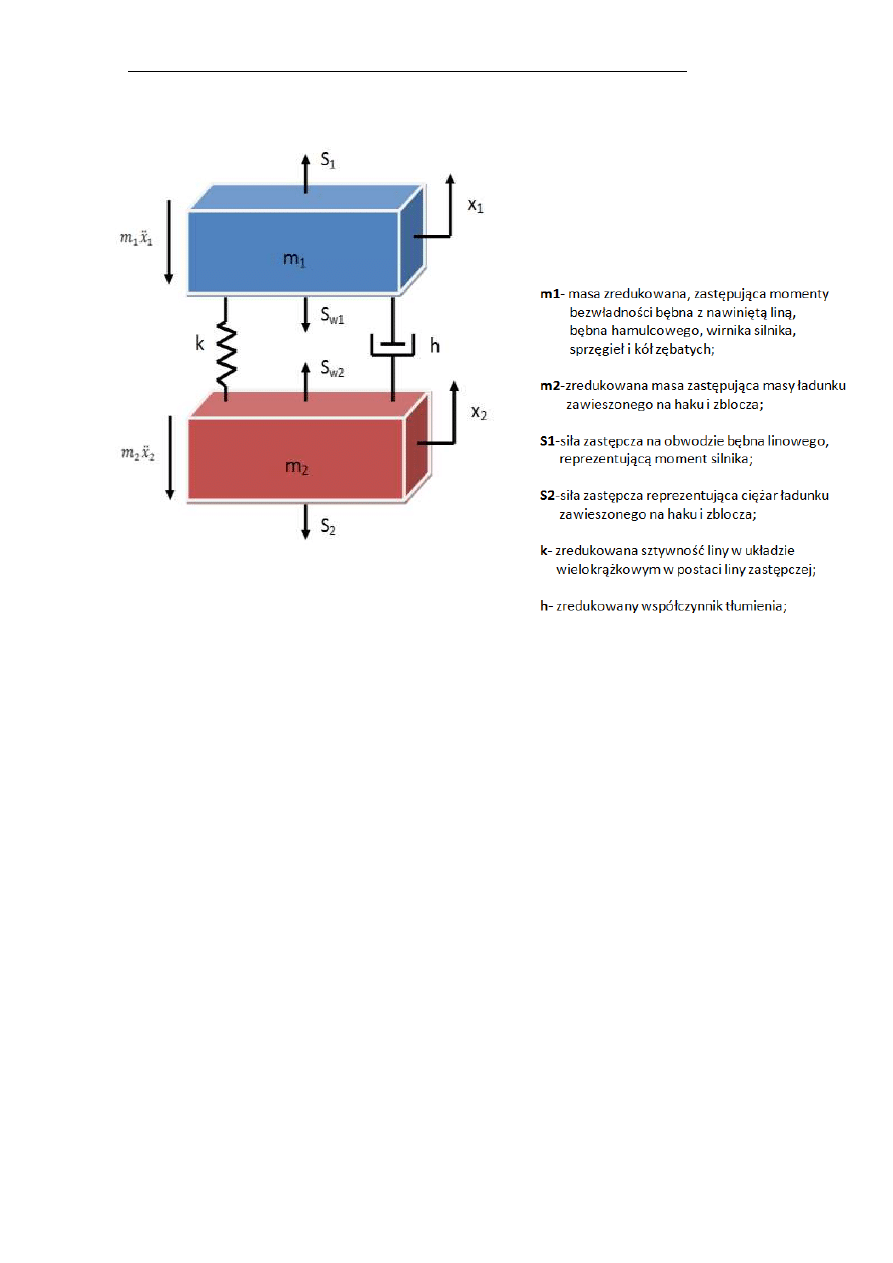
Model mechanizmu podnoszenia służący do badania ruchu to układ dwóch
mas zredukowanych, które są ze sobą połączone elementem sprężystym jak to
widać na poniższym rysunku. Masa m
1
to masa zredukowana na linę
napinającą na bęben, zastępuje ona momenty bezwładności elementów
obrotowych: bębna z nawiniętą liną, bębna hamulcowego, wirnika silnika,
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
2
sprzęgieł i kół zębatych. Masa m
2
jest natomiast masą zredukowaną,
zastępującą masę ładunku,
zawieszonego na linie oraz
masę zblocza (rys.1.).
Rys. 1. Model dwumasowy mechanizmu podnoszenia
Najogólniej można rozpatrywać kilka stanów nieustalonych mechanizmu
podnoszenia (z ciężarem lub tylko hak ze zbloczem):
1.Rozruch przy podnoszeniu,
2.Rozruch przy opuszczaniu,
3.Hamowanie przy podnoszeniu,
4.Hamowanie przy opuszczaniu.
2.
Równania ruchu
2.1.Rozruch przy podnoszeniu
Wartości początkowe mogą przyjmować różne wartości, a jest to zależne od
warunków, w jakich rozpoczyna się rozruch.
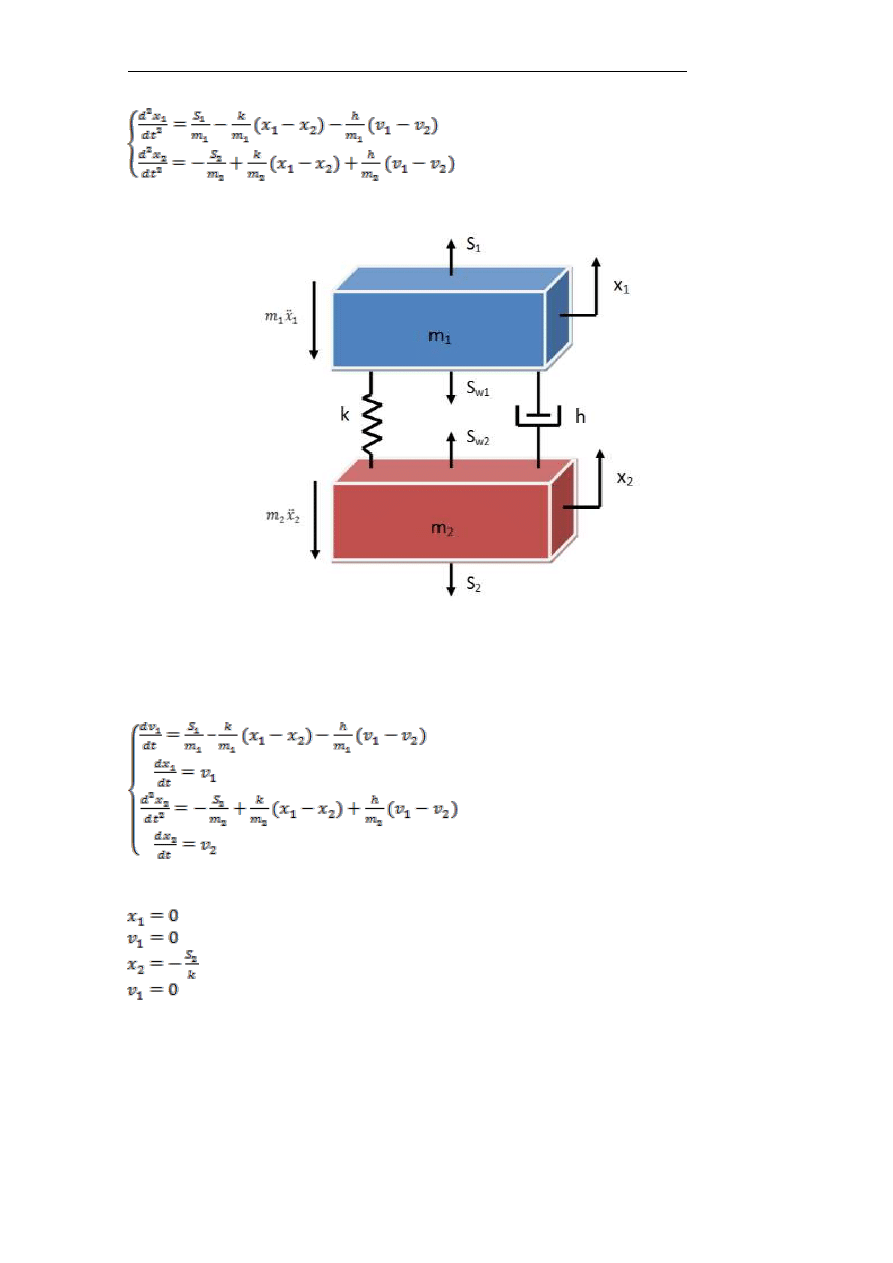
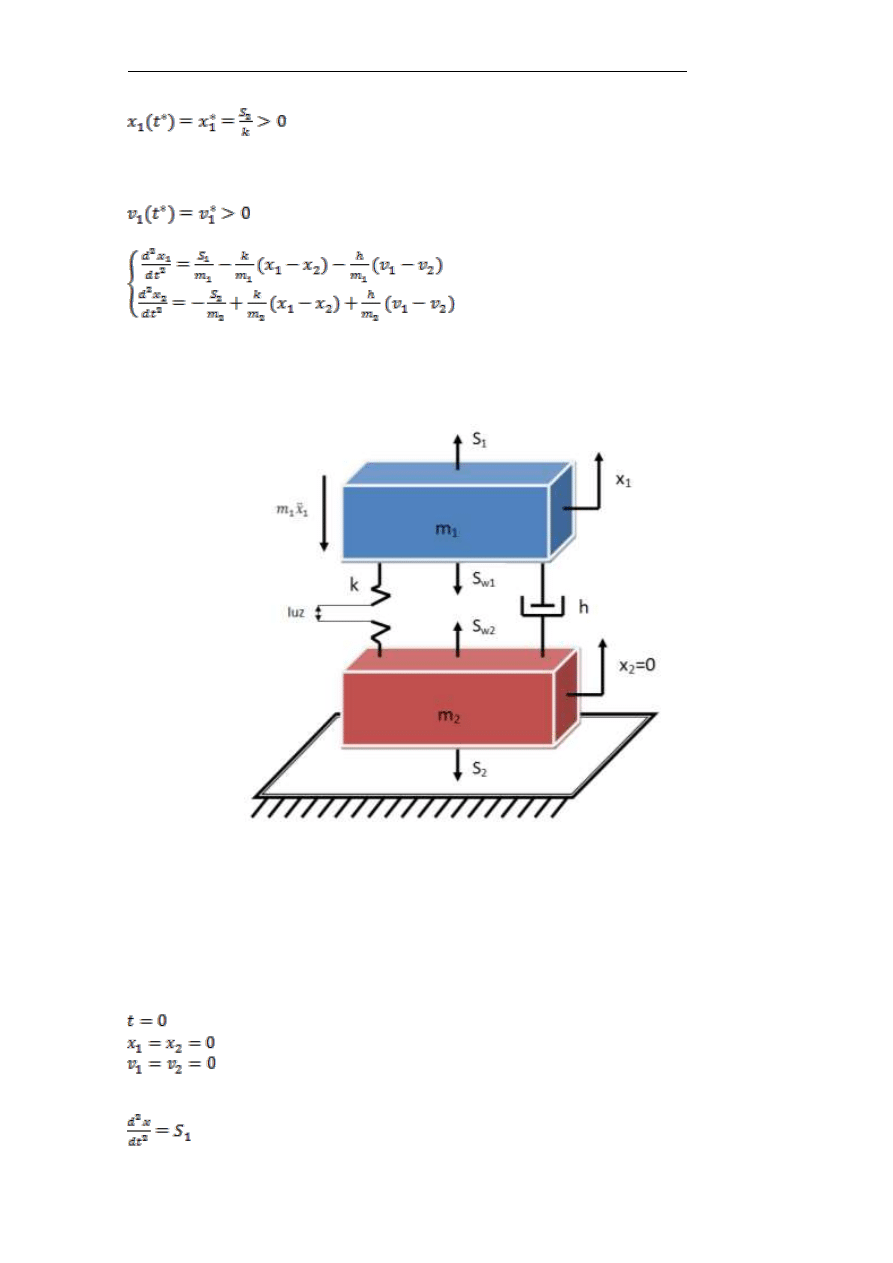
a) Przypadek z napiętymi więzami
Na rysunku 2 przedstawiono przypadek, w którym obydwie masy zaczynają
ruch jednocześnie a więzy między masami są napięte.
W tym przypadku równania ruchu mają postać:
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
3
(1.1)
Rys. 2. Model matematyczny – przypadek z napiętymi więzami
Dwa równania drugiego rzędu (1.1) można zastąpić układem czterech
równań różniczkowych pierwszego rzędu (1.2).
(1.2)
Wartości początkowe w chwili t=0 wynoszą:
(1.3)
b) Przypadek ze zluzowanymi więzami
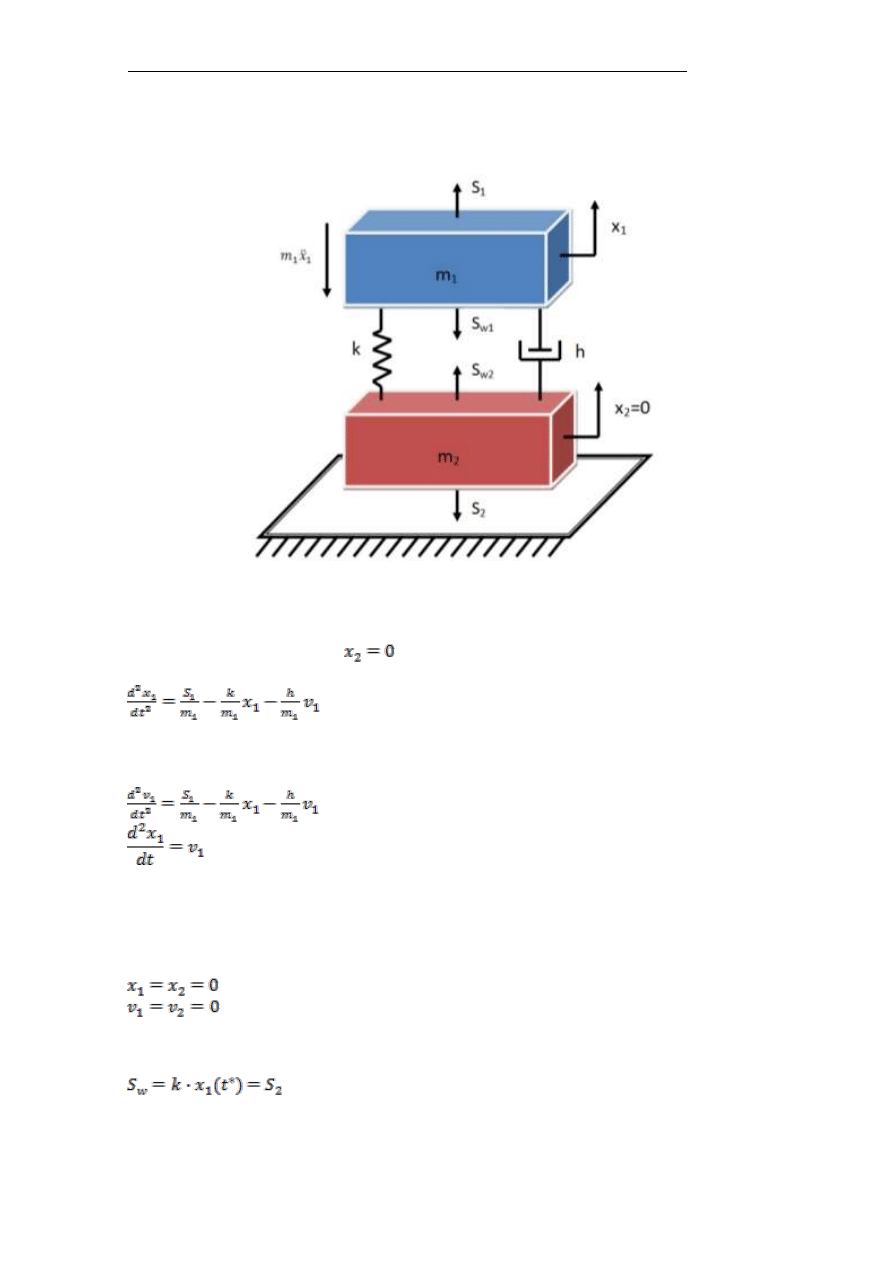
Rysunek 3 przedstawia ładunek spoczywający na podłożu, lina nie jest
napięta. Ruch takiego układu rozpoczyna się od fazy napinania więzów, tj.
początkowo porusza się tylko masa m
1
, co powoduje stopniowe rozciąganie
więzów. Faza ta trwa do chwili, w której siła odkształcająca więzy osiągnie
wartość równą sile S
2
.
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
4
Układ ma tylko jeden stopień swobody, a więc ruch układu opisuje jedno
równanie drugiego rzędu lub układ dwóch równań pierwszego rzędu.
Rys. 3. Model matematyczny – przypadek ze zluzowanymi więzami
Pierwsza faza ruchu
(1.4)
lub
(1.5)
Druga faza ruchu
Warunki początkowe dla t=0
(1.6)
t
*
- czas, po którym siła rozciąganych więzów równa się sile S
2
(1.7)
Odkształcenie, jakie osiągają więzy:
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
5
(1.8)
Wartość prędkości masy 1
(1.9)
(1.10)
c) Przypadek z nadmiernym luzem w linie
Rys. 4. Model matematyczny – przypadek z nadmiernym luzem w linie
Na rysunku 4 ładunek również jak w poprzednim przykładzie (rys. 3.)
spoczywa na podłożu, lecz tym razem liny są bardziej luźne. Ruch takiego
układu rozpoczyna się od fazy kasowania luzu w więzach – porusza się tylko
masa m
1
pociągając za sobą linę bez oporu, a masa m
2
spoczywa swobodnie
na podłożu.
Wartości początkowe są równe zero:
(1.11)
W równaniu nie występują zewnętrzne ani wewnętrzne siły oporu.
(1.12)
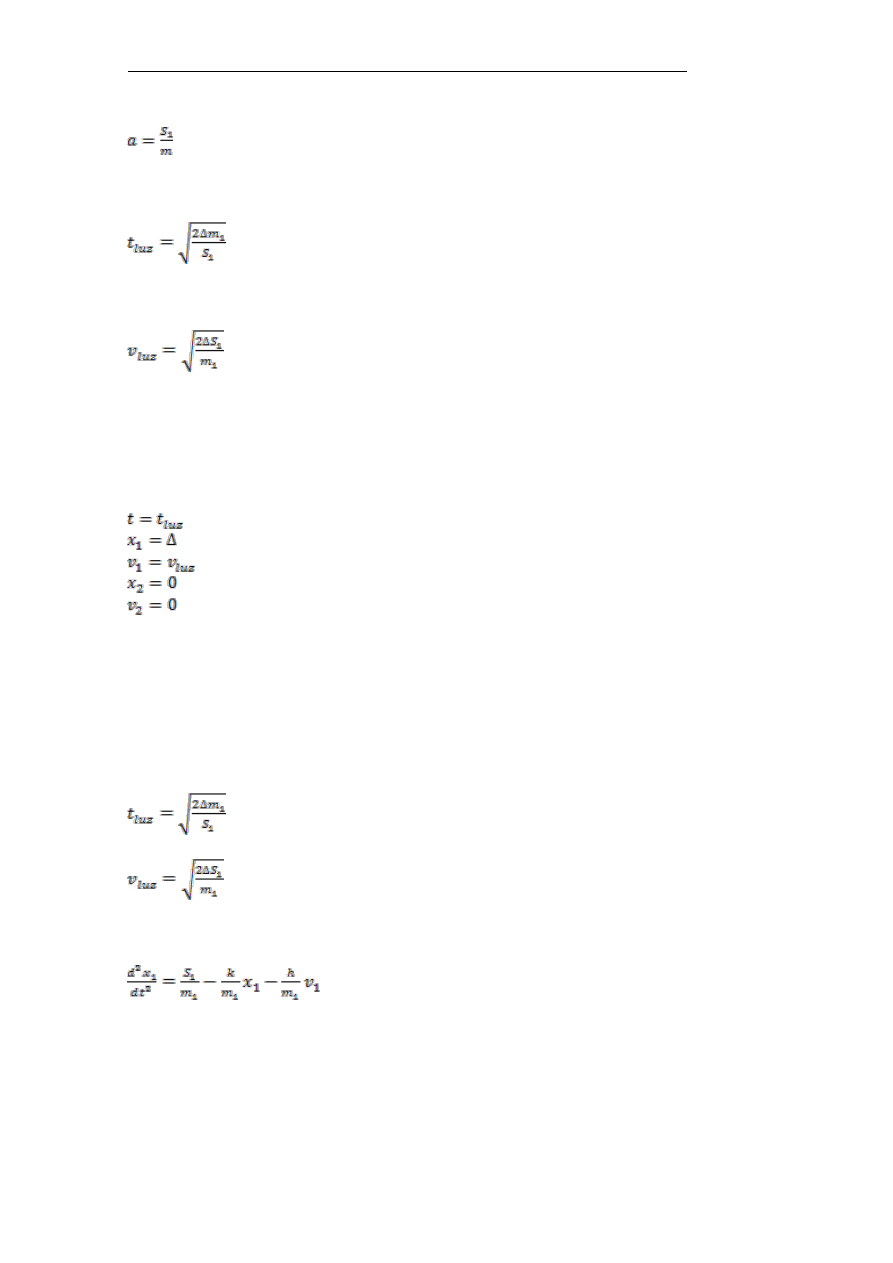
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
6
Ruch jest jednostajnie przyspieszony i trwa do chwili wyczerpania luzu:
(1.13)
Czas kasowania luzów wyraża się wzorem:
(1.14)
Prędkość masy m1 w chwili skasowania luzu jest równa:
(1.15)
Drugą fazą tego układu jest napinanie więzów, tj. początkowo porusza
się tylko masa m
1
, co powoduje stopniowe rozciąganie więzów. Faza ta trwa
do chwili, w której siła odkształcająca więzy osiągnie wartość równą sile S
2
.
Równanie ruchu nie zmienia się, natomiast występują inne warunki
początkowe:
(1.16)
Faza ta trwa aż do chwili, w której napięcie więzów zrównoważy siłę
obciążającą więź S
2
. Wartości t
*
, x
1
*
, v
1
*
na końcu drugiej fazy są odpowiednio
wartościami początkowymi trzeciej fazy ruchu obu mas. Faza ta rozpoczyna się
w chwili t > t
*
, gdy siła naciągu liny zaczyna przekraczać wartość S
2
.
Pierwsza faza kasowanie luzu
(1.17)
(1.18)
Druga faza napinanie więzów (x
1
=Δ, v
1
=v
luz
)
(1.19)
Trzecia faza ruch obu mas (x
1
=x
1
(t
*
), v
1
=v
1
(t
*
))
t
*
- czas po którym siła rozciąganych więzów równa się sile S
2
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
7
(1.20)
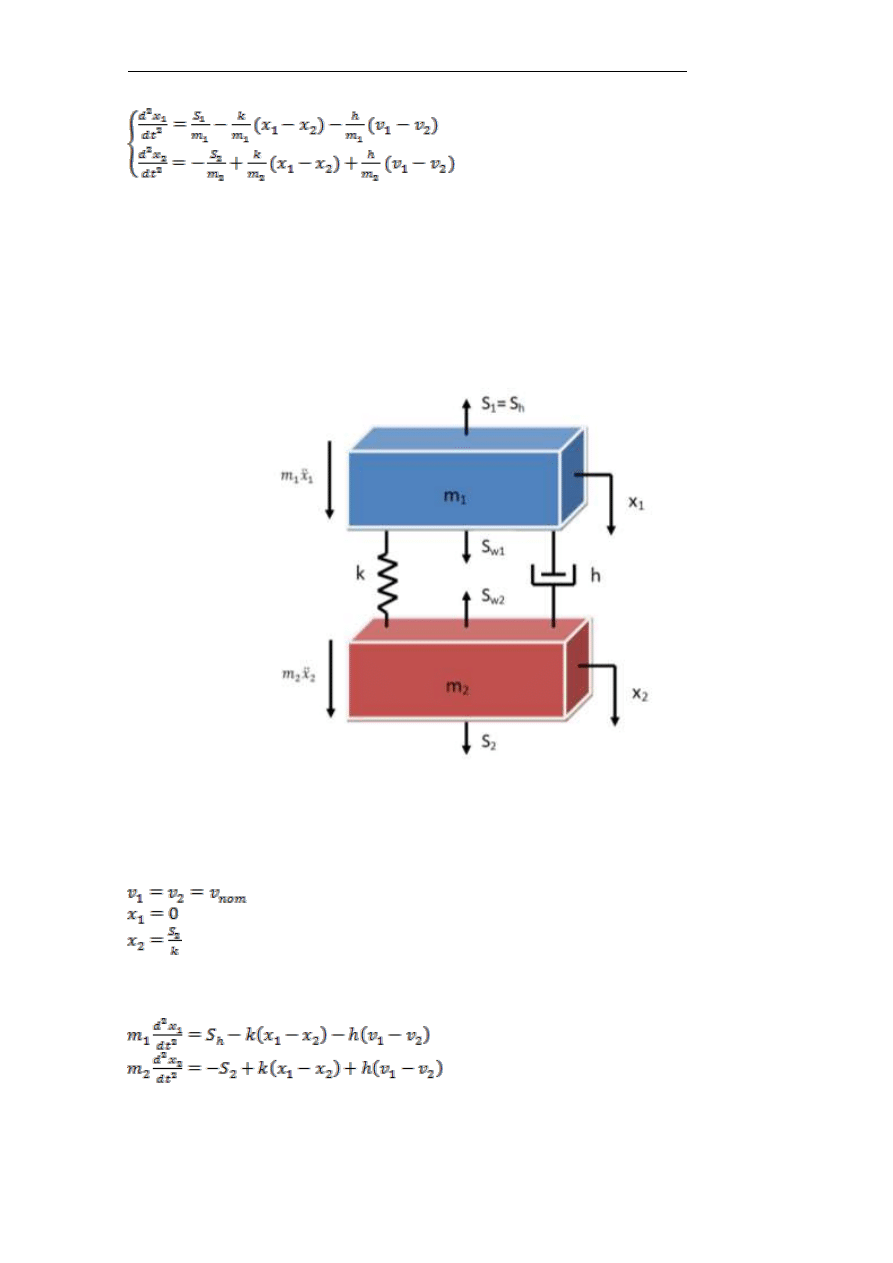
2.2. Hamowanie przy opuszczaniu
Podczas hamowania przy opuszczaniu układ sił jest bardzo podobny jak
przy rozruchu - przedstawia nam rysunek 5. Zasadnicza różnica polega na
zmianie kierunku ruchu mas oraz na tym, że siła S
1
pochodzi od hamulca
umieszczonego na wale silnika.
Rys. 5. Model matematyczny – przypadek hamowania przy opuszczaniu
Warunki początkowe określone są przez prędkość ruchu przy opuszczaniu oraz
wydłużenie układu linowego pod wpływem zawieszonego ciężaru:
(1.21)
Ruch opisują dwa równania różniczkowe:
(1.22)
Ruch tego układu składa się z dwóch faz:
- ruch obu mas trwa do zatrzymania masy m
1
siłą hamulca (t= t
*
, v
1
= 0),
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
8
- po zatrzymaniu masy m
1
(x
1
= x
1
*
= const) następuje faza, w której masa m
2
wykonuje swobodne wahania pionowe opisane równaniem:
(1.23)
Pierwsza faza obie masy w ruchu (v
1
= v
2
= v
nom
, x
1
= 0, x
2
= S
2
/k)
(1.24)
Druga faza ruch jednej masy (x
1
=x
1
*
= const, v
1
*
=0, x
2
=x
2
(t
*
), v
2
=v
2
(t
*
) )
t
*
- czas po którym zakończyła się faza pierwsza.
(1.25)
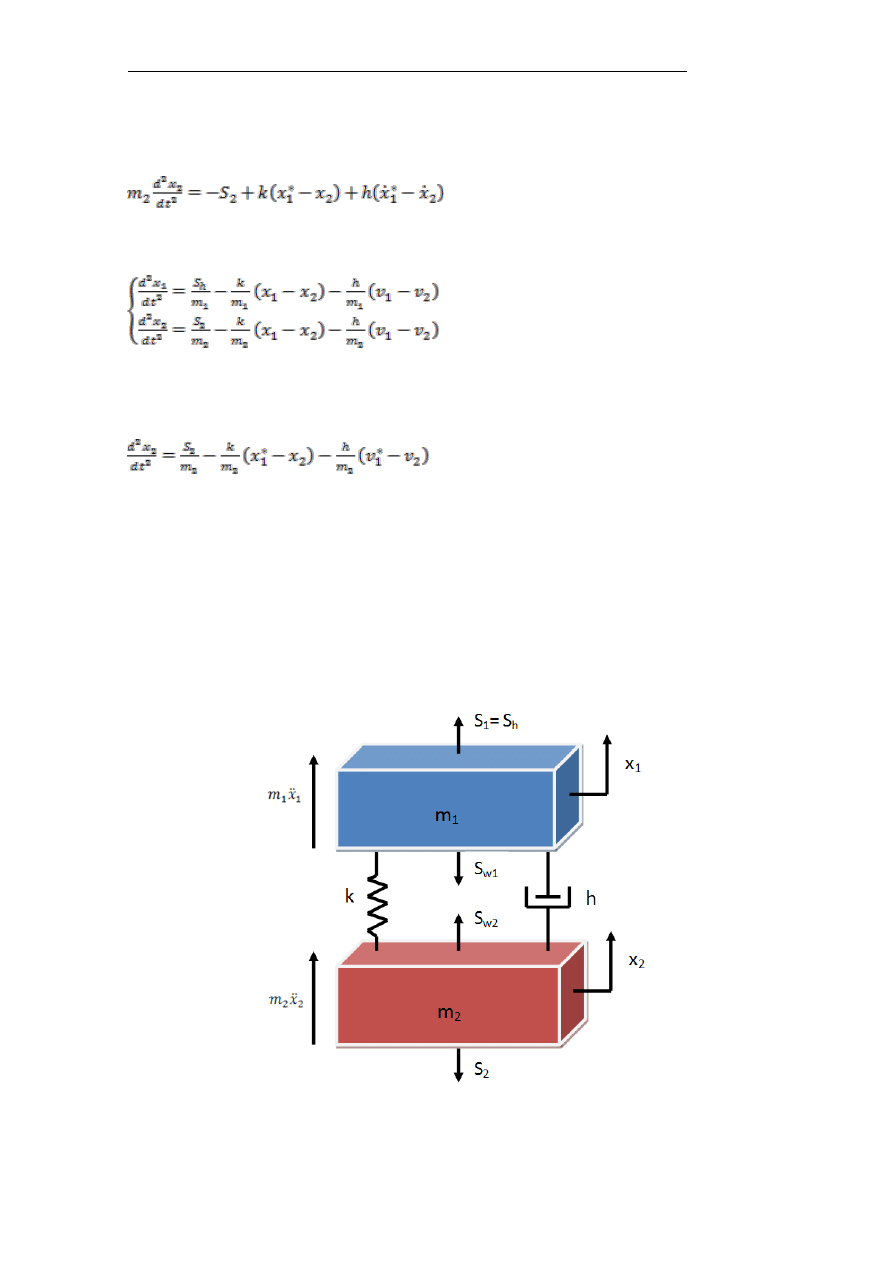
2.3. Hamowanie przy podnoszeniu
Hamowanie podczas podnoszenia można opisać podobnie jak hamowanie
podczas opuszczania – rysunek 5. Istotna różnica polega tylko na tym, że siła
S
2
pochodząca od ciężaru współdziała z hamulcem, co przyspiesza proces
hamowania (rys. 6).
Rys.6. Model matematyczny – przypadek hamowania przy podnoszenia
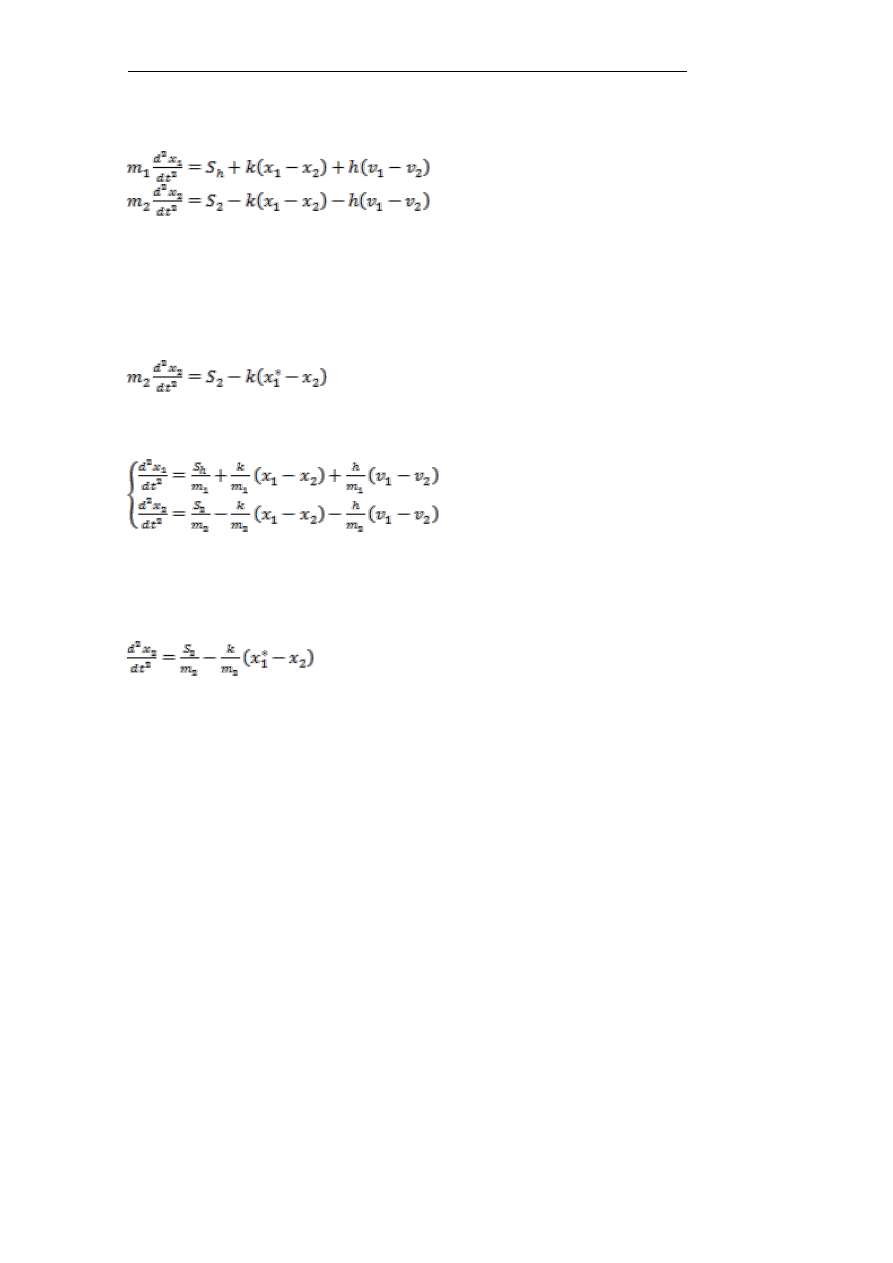
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
9
Równania ruchu w fazie pierwszej – ruch obu mas:
(1.26)
Faza ta trwa aż do chwili t= t
*
, w której nastąpi zatrzymanie pierwszej masy
m
1
, v= 0.
Druga faza po zatrzymaniu masy m
1
(x
1
= x
1
*
= const) to ruch wahadłowy
drugiej masy m
2
:
(1.27)
Pierwsza faza - obie masy w ruchu (v
1
= v
2
= v
nom
, x
1
= 0, x
2
= S
2
/k)
(1.28)
Druga faza - ruch jednej masy (x
1
= x
1
*
= const, x
2
=x
2
(t
*
))
t
*
- czas, po którym zakończyła się faza pierwsza
(1.29)
3. Parametry do identyfikacji
Z rozważań zawartych w punktach 1-2 wynika, że każdorazowo do
pełnego opisu równań ruch należy wyznaczyć sześć parametrów:
k – współczynnik sprężystości więzi (np. liny),
h – współczynnik tłumienia więzi,
m
1
– masę zredukowaną na linę nabiegającą na bęben linowy – od
strony silnika,
m
2
– masę zredukowaną na linę – od strony zblocza,
S
1
lub S
h
– obciążenie czynne – od silnika lub hamulca,
S
2
– obciążenie bierne – od podnoszonego lub opuszczanego
ciężaru.
Ważne uwagi:
- przy redukcji sił lub momentów sił korzystamy z zasady zachowania mocy
w układzie (z uwzględnieniem odpowiedniej sprawności),
- przy redukcji mas lub momentów bezwładności korzystamy z zasady
zachowania energii badanego układu.
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
10
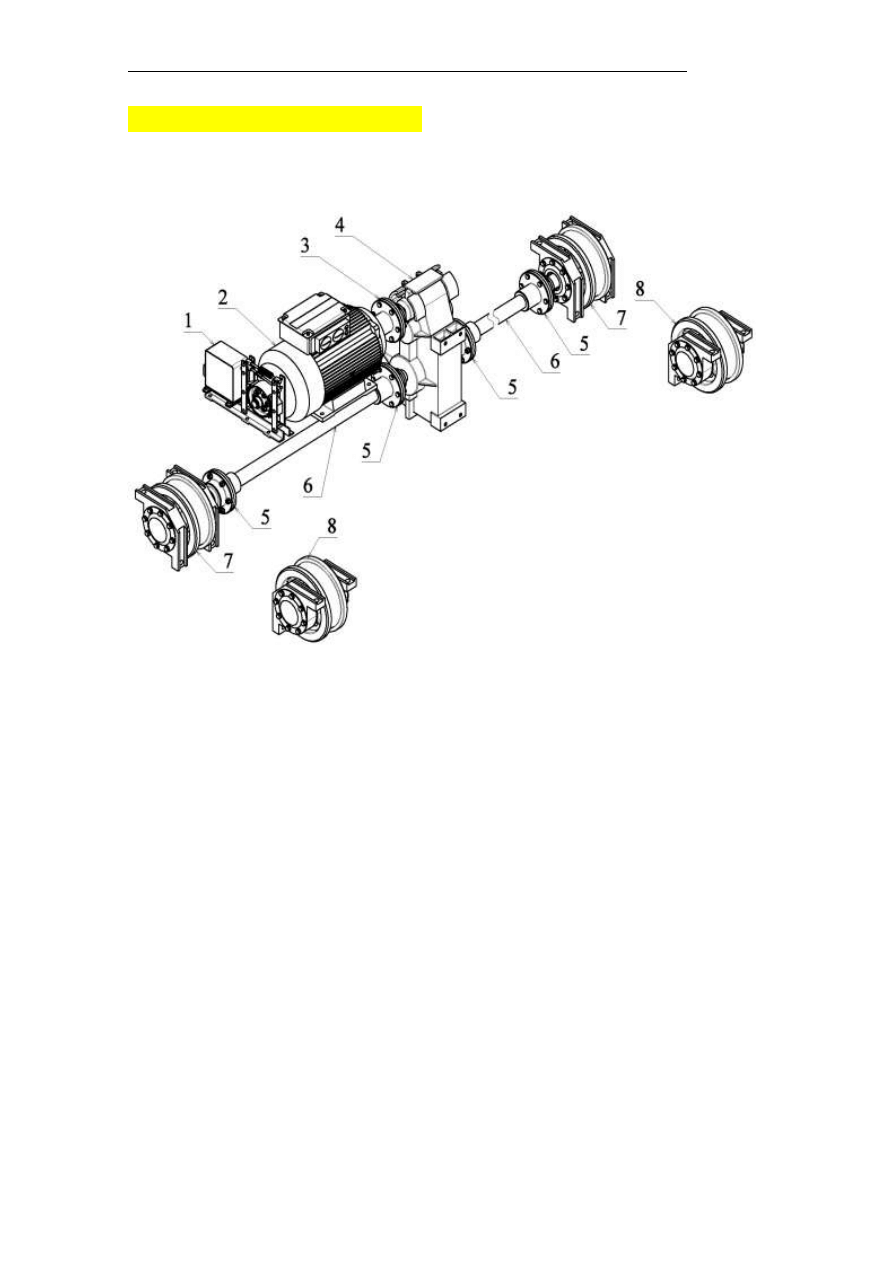
Cz.2. MECHANIZM JAZDY
Mechanizm jazdy –
1 – hamulec,
2 – silnik,
3 – sprzęgło zębate dwustronne,
4 – przekładnia zębata,
5 - sprzęgło zębate dwustronne,
6 - sprzęgło zębate jednostronne,
7 – wał wolnobieżny,
8 – zestaw kołowy napędzany,
9 – zestaw kołowy nienapędzany.
1. Stany nieustalone w ruchu mechanizmu jazdy
Model mechanizmu jazdy najlepiej sprowadzić do modelu obrotowego,
ponieważ elementy układu poruszają się ruchem obrotowym zarówno od
strony napędowej (wał silnika, sprzęgło hamulcowe, koła zębate), jak i od
strony napędzanej (sprzęgła zębate, koła jezdne). Zobrazowane jest to na
rysunku 1.
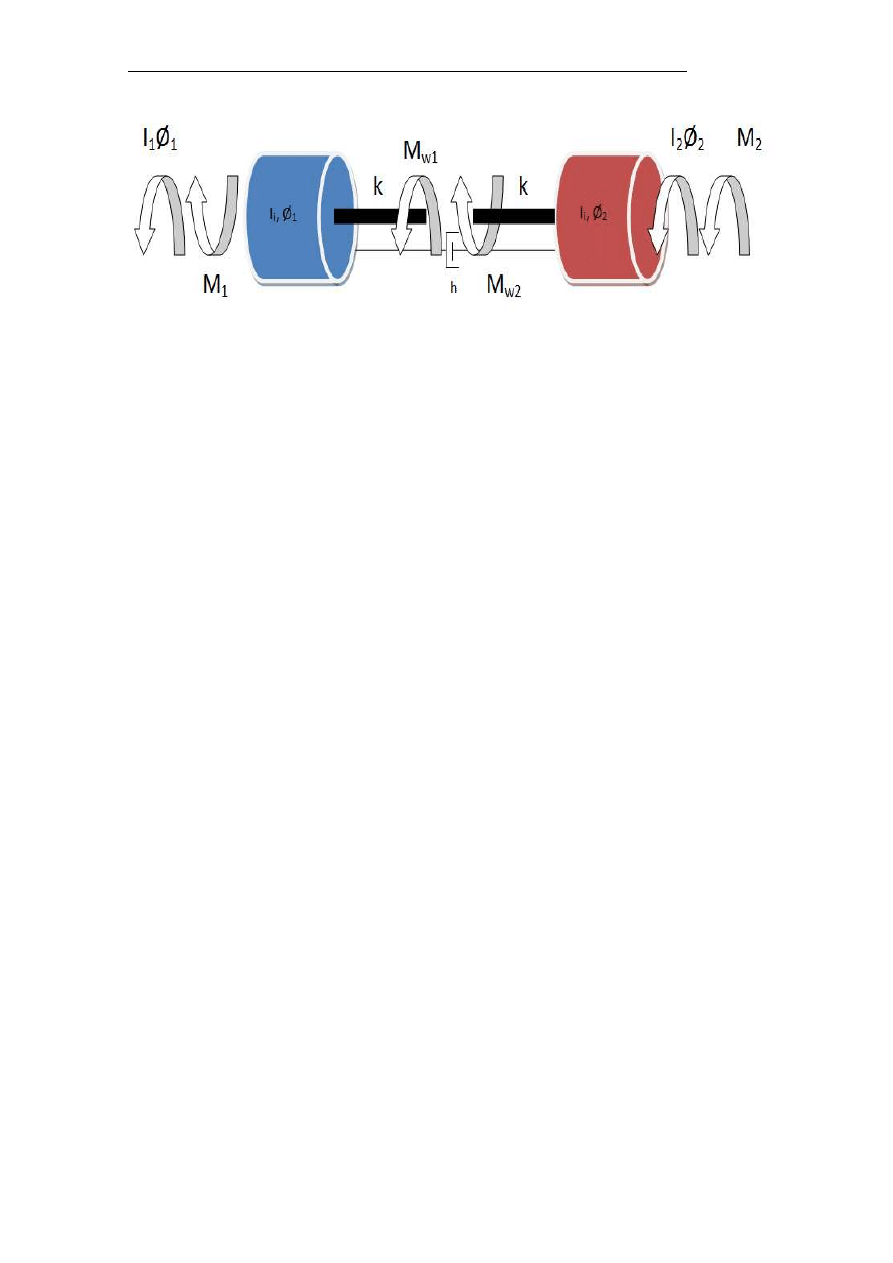
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
11
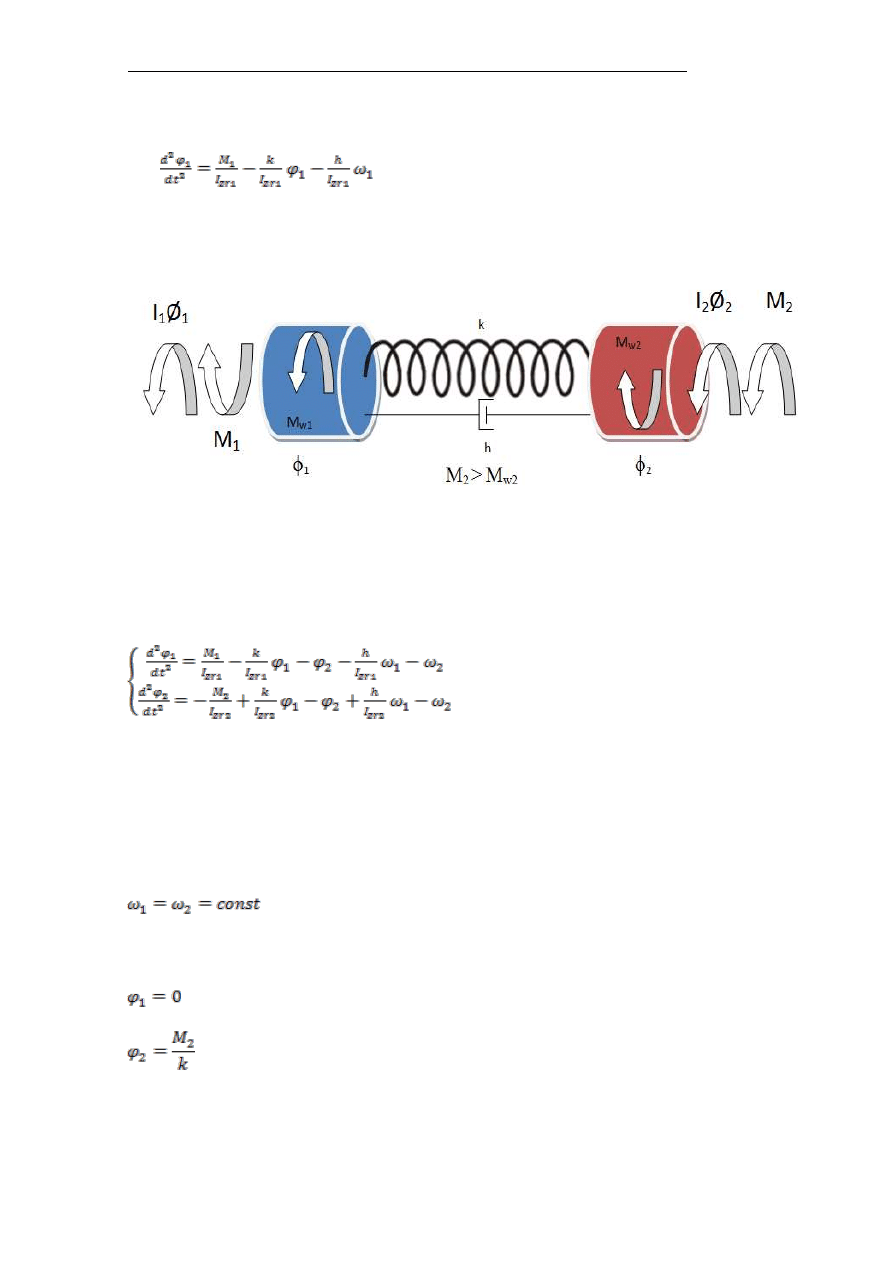
Rys. 1. Model matematyczny – mechanizmu jazdy
I
ZR1
– moment bezwładności zredukowany na wał wolnobieżny przekładni,
zastępujący moment bezwładności wirnika silnika ( I
S
), sprzęgła ( I
SP
), bębna
hamulca( I
H
), kół zębatych, sprzęgieł przy przekładni ( I
SP1
);
I
ZR2
– moment bezwładności zredukowany na wał wolnobieżny przekładni,
zastępujący moment bezwładności kół jezdnych ( I
K
), i sprzęgieł ( I
SP2
);
M
1
– moment siły na wale wolnoobrotowym przekładni, pochodzący od
momentu silnika ( M );
M
2
– moment siły na wale wolnoobrotowym przekładni, pochodzący od oporów
jazdy wózka ( W );
k – zastępczy współczynnik sztywności wolnoobrotowych wałów napędzających
koła jezdne;
h – zastępczy współczynnik tłumienia w wałach napędzających koła jezdne.
2. Równania ruchu
2.1. Rozruch
Mechanizm jazdy pokonuje siłę oporów jazdy W, która wynika z oporów
toczenia kół jezdnych wózka po szynach oraz oporów w łożyskach kół. Koła
jezdne obciążone są ciężarem masy m
2
, która obciąża mechanizm podnoszenia
oraz masy wózka m
w
. Zakładamy, że w fazie rozruchu bezwładność ładunku
zawieszonego na haku, a także jego wahania mają pomijalnie mały wpływ.
W mechanizmie jazdy podobnie jak w mechanizmie podnoszenia występują
trzy fazy ruchu. W fazie pierwszej występuje kasowanie luzów (głównie
międzyzębnych w przekładni zębatej).
W tej fazie ruchu masa m
1
obraca się bez oporu ze strony więzów.
Przebyta droga jest równa wielkości luzu w elementach więzów. Po niej
zaczyna się faza druga, którą jest napinanie więzów. Trwa ona do chwili
pokonania oporu momentu obciążenia przez moment skręcenia wału M
w
= k(φ
1
– φ
2
).
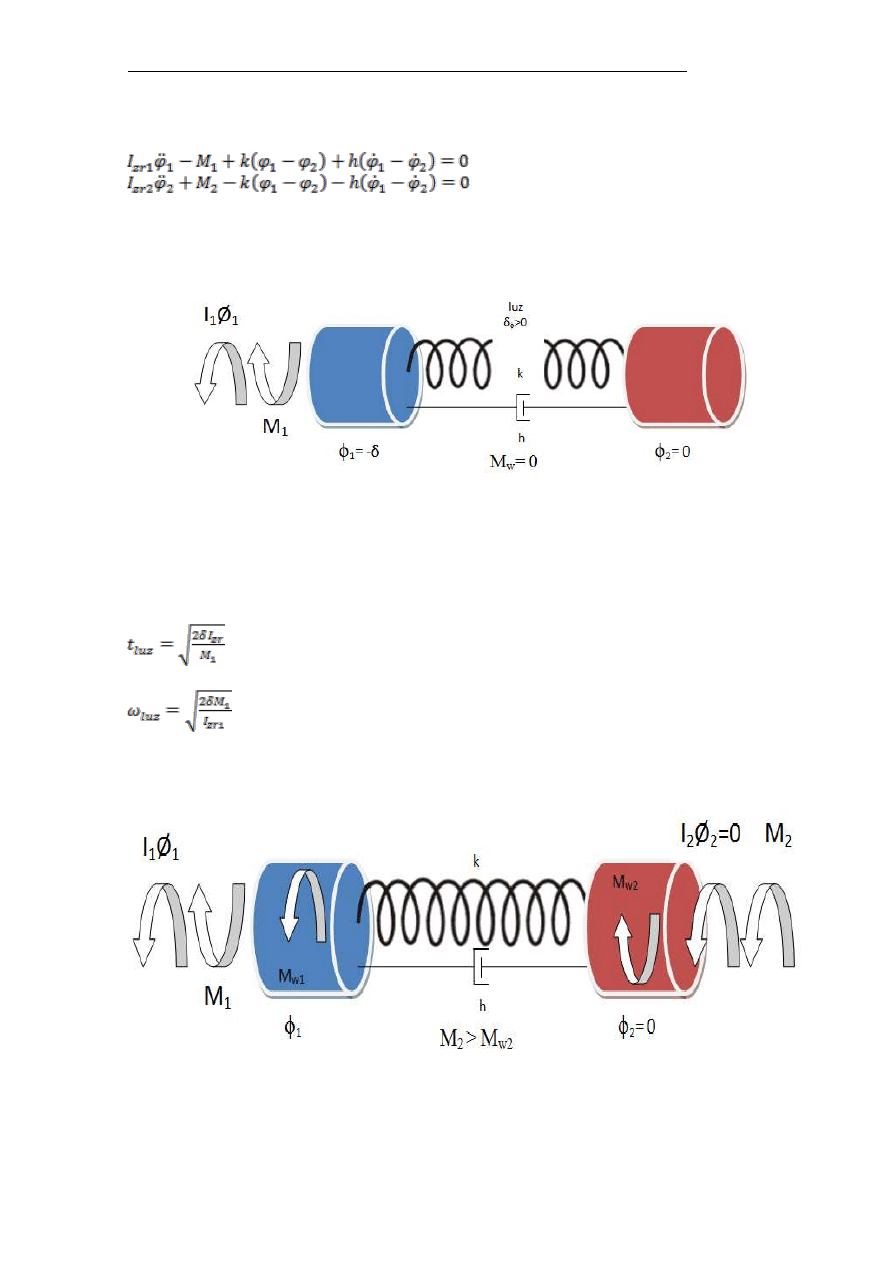
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
12
Ostatnia faza ruchu to ruch obu mas opisany układem równań:
(2.1)
a) faza pierwsza
Rys. 2. Schemat sił działających w mechanizmie jazdy podczas rozruchu –
faza pierwsza
- kasowanie luzów (ω
1
=0, φ
1
=-δ, ω
2
=0, φ
2
=0 )
(2.2)
(2.3)
b) faza druga
Rys. 3. Schemat sił działających w mechanizmie jazdy podczas rozruchu –
faza druga
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
13
- napinanie więzów (φ
1
= , ω
1
= ω
luz
)
(2.4)
c) faza trzecia
Rys.4. Schemat sił działających w mechanizmie jazdy podczas rozruchu –
faza trzecia
- faza, w której obie masy są w ruchu (φ
1
= φ
1
(t
*
), ω
1
= ω(t
*
))
t
*
- czas napinania więzów
(2.5)
2.2. Hamowanie
W chwili rozpoczęcia hamowania ruch jest ustalony tj. prędkości obrotowe
obu końców wału napędowego są stałe i jednakowe:
a więź jest napięta momentem oporu jazdy:
W pierwszej fazie hamowania następuje kasowanie luzów. Aby proces
ten był łagodniejszy pomiędzy chwilą wyłączenia silnika i włączenia hamulca
E. Michlowicz: IMiU – W04: Modelowanie mechanizmu podnoszenia
14
stosuje się krótką przerwę, aby nastąpiło zwolnienie więzów. Pozwala to
uniknąć negatywnych skutków kasowania luzów przy pełnej wartości momentu
hamowania.
Druga faza zaczyna się od skasowania luzów, a koniec następuję w
momencie zatrzymania się masy m
1
. Występuje tu ruch opóźniony obu mas,
który można opisać układem równań różniczkowych.
Po zatrzymaniu masy m
1
rozpoczyna się faza trzecia, jest nią ruch masy
m
2
(kół wózka) hamowany oporami ruchu, w trakcie tej fazy następuje
zwolnienie więzów.
Pierwsza faza obie masy w ruchu (ω
1
= ω
2
= ω
nom
= const , φ
1
= 0, φ
2
= M
2
/k)
(2.6)
Druga faza jedna masa w ruchu (φ
2
= φ
2
(t
*
), ω
2
= ω
2
(t
*
))
t
*
- czas, po którym zatrzymała się masa 1
(2.7)
3. Parametry do identyfikacji
Z rozważań zawartych w punktach 1-2 wynika, że każdorazowo do
pełnego opisu równań ruch należy wyznaczyć sześć parametrów:
k – współczynnik sprężystości więzi (np. wału wolnoobrotowego),
h – współczynnik tłumienia więzi,
I
zr1
- moment bezwładności zredukowany na wał wolnoobrotowy –
od strony silnika,
I
zr2
– moment bezwładności zredukowany na wał – od strony kół
jezdnych wraz z przemieszczaną masą (wózek i ciężar),
M
1
lub M
h
– obciążenie czynne – od silnika lub hamulca,
M
2
– obciążenie bierne – od oporów jazdy (ciężar i wózek).
Ważne uwagi:
- przy redukcji sił lub momentów sił korzystamy z zasady zachowania
mocy w układzie (z uwzględnieniem odpowiedniej sprawności),
- przy redukcji mas lub momentów bezwładności korzystamy z zasady
zachowania energii badanego układu.